चोटियों की निकटता के बारे में

“इससे पहले कि आप इसे समझें, यह एक चमत्कार जैसा लगता है। लेकिन उसके बाद कुछ खास नहीं है। ”

नहीं, पहाड़ों के बारे में नहीं, - गिनती के बारे में। गणित में, ऐसे प्रश्न होते हैं जिनका निरूपण सभी के लिए सुलभ होता है, लेकिन समाधान निर्विवाद है और विशेष तैयारी के बिना समझाना मुश्किल है। इन समस्याओं में से एक को संक्षेप में निम्नानुसार व्यक्त किया जा सकता है: निर्देशित ग्राफ़ में दूरी की सही गणना कैसे करें? यह कुछ हद तक अमूर्त समस्या को एक बहुत ही विशिष्ट प्रेरक कार्य के लिए कम किया जा सकता है। यह एक तस्वीर में फिट बैठता है:

1. समस्या का विवरण। मैं एक पर रहता हूं, लेकिन आप दूसरे पर।

एक छोटा शहर विभाजित है (उदाहरण के लिए, एक नदी के द्वारा, हालाँकि चोटियों के संदर्भ में कण्ठ अधिक उपयुक्त है) दो जिलों (भागों) में $$$ए$ और $$$ब$ । जिलों के बीच संचार एक एकल सड़क (पुल) के साथ किया जाता है, जिसमें दो लेन हैं: की तरफ $$$ए$ को $$$ब$ और इसके विपरीत। जनसंख्या वृद्धि के संबंध में, सड़क की क्षमता बढ़ाने पर सवाल उठे। हमेशा की तरह पैसा मुश्किल से पर्याप्त होता है और केवल एक दिशा में एक लेन के लिए पर्याप्त होता है। यह स्पष्ट है कि यहां तक ​​कि एक लेन क्षेत्रों को एक साथ करीब लाएगा, लेकिन सवाल यह है कि वास्तव में कितना सही है? आप एक शहरी पागल गणितज्ञ हैं, और यह आप थे जिन्हें उचित उत्तर प्राप्त करने के लिए आमंत्रित किया गया था।

यदि आप एक दिशा में एक और पट्टी बनाते हैं, तो क्षेत्र कितने करीब हैं?

उन्नत के लिए रिकॉर्डिंग

कोनिग्सबर्ग पुलों के बजाय, थोड़ा अधिक कठोर ग्राफ सिद्धांत भाषा का उपयोग किया जा सकता है। तो, दो सिरों (नोड्स) के साथ एक निर्देशित ग्राफ है $$$ए$ और $$$ब$ । आगे और रिवर्स दिशा में कनेक्शन (चालकता, बैंडविड्थ) का परिमाण शुरू में बराबर है। सवाल यह है कि यदि किसी एक दिशा में चालकता दोगुनी हो जाए तो नोड्स के बीच की दूरी कितनी बदल जाएगी?

और हाँ, यदि आप एक वास्तविक गणितज्ञ वेल्डर हैं , तो आप किसी भी प्रत्यक्ष और प्रतिक्रिया मूल्यों के लिए समाधान (और औचित्य) पेश कर सकते हैं। आदर्श रूप में, किसी भी संख्या में नोड्स और लिंक के साथ एक ग्राफ के लिए।

अंतरंगता और शराबी भटकना

यह स्पष्ट है कि क्षेत्रों के बीच सामान्य (किलोमीटर) की दूरी सड़क की उपस्थिति या अनुपस्थिति पर निर्भर नहीं करती है। इसलिए, यह यहां फिट नहीं है - हमें संचार पर भरोसा करने की आवश्यकता है। जितने अधिक जिले जुड़े हैं - वे उतने ही अधिक हैं - जितने अधिक निवासी समय के प्रति यूनिट दूसरे क्षेत्र में जा सकते हैं।

एक अप्रत्यक्ष ग्राफ के नोड्स के बीच निकटता के माप का आकलन करने के लिए, तथाकथित प्रतिरोधक दूरी का उपयोग किया जा सकता है। इससे पहले, हमने पहले से ही कई लेखों में इस दूरी के गुणों का वर्णन किया है।

प्रतिरोधक दूरी प्रभावी प्रतिरोध की अवधारणा के बराबर है, जब यह विद्युत नेटवर्क की बात आती है। इसलिए, इलेक्ट्रिक भाषा में, समस्या को निम्नानुसार तैयार किया जा सकता है। दो नोड्स के बीच, समान चालकता के दो डायोड वामावर्त जुड़े होते हैं। यदि आप एक और डायोड जोड़ते हैं तो इन बिंदुओं के बीच प्रतिरोध कैसे बदल जाएगा? (यदि इलेक्ट्रिक भाषा विफल हो गई और मैंने यहां बकवास लिखा है तो मैं माफी मांगता हूं)।

इसके अलावा, ड्रंक रैंडम वॉक की संभावनाओं के लिए मार्कोव भाषा में प्रभावी प्रतिरोध की व्याख्या की जा सकती है (इस विषय के लिए इच्छुक लोगों के लिए - Google "रैंडम वॉक और इलेक्ट्रिक नेटवर्क")।

प्रतिरोधक दूरी द्विघात है, - रैखिक दूरी के वर्ग से मेल खाती है। द्विघात दूरियों को चतुष्कोण भी कहा जाता है। लेकिन चूंकि इस समस्या में अन्य (रैखिक) दूरियों का उपयोग नहीं किया जाता है, इसलिए हमें यहाँ चतुर्भुज शब्द की आवश्यकता नहीं है। (इसके बिना भी पर्याप्त पक्षी की जीभ है)

सामान्य तौर पर, "प्रतिरोधक दूरी" शब्द भी अच्छा नहीं लगता है। उनका तात्पर्य है कि हम विज्ञान से अनजान किसी प्रकार की असामान्य दूरी के बारे में बात कर रहे हैं। वास्तव में, प्रतिरोधक दूरी सामान्य यूक्लिडियन दूरी है । लेकिन affine स्पेस में। हम इसकी इस विशेषता का आगे उपयोग करते हैं।

और क्या, वास्तव में, समस्या है?

यदि हम जानते हैं कि एक "प्रतिरोधी दूरी" क्या है, तो हम किसी दिए गए ग्राफ़ के लिए "बस इसे ले और गणना" क्यों नहीं कर सकते हैं?

हम्म। सिद्धांत रूप में, आसान। यदि हम एक अप्रत्यक्ष ग्राफ के बारे में बात कर रहे हैं। यदि शहर ने दोनों दिशाओं में स्ट्रिप्स का निर्माण किया होता, तो प्रतिरोधक दूरी बिलकुल आधी हो जाती। चूंकि प्रतिरोध चालकता के विपरीत आनुपातिक है, और चालकता (थ्रूपुट) दोगुनी हो गई है। और अगर मैंने प्रत्येक दिशा में दो बैंड जोड़े, तो दूरी 3 गुना कम हो जाएगी। यहां सब कुछ काफी तुच्छ है। (और शायद, कोई व्यक्ति पहले से ही समाधान के सामान्य रूप का अनुमान लगा सकता है। और हम आगे बढ़ते हैं)।

जब विरोधी रिश्ते समान नहीं होते हैं, तो सब कुछ जटिल हो जाता है। और काफी गंभीर रूप से।

दिशात्मक ग्राफ में चोटियों (प्रतिरोधक दूरी) की निकटता निर्धारित करने के लिए आम तौर पर स्वीकृत कोई कानूनी तरीका नहीं है।

(यह मेरी थीसिस है - शायद कोई मुझे मना सकता है)। "नहीं" - यहां इसका मतलब है कि यह पाठ्यपुस्तकों, विकी और प्रमुखों में नहीं है (अधिक सटीक रूप से - विभिन्न लेखकों से कई अलग-अलग तरीके हैं जो अलग-अलग मान्यताओं और परिभाषाओं की आवश्यकता होती है)। एक तरीका है (हालांकि इतना सरल नहीं है)। इस लेख में, हम इसका वर्णन कर रहे हैं।

निर्देशित कनेक्शन की उपस्थिति में दूरी के बहुत निर्धारण के लिए स्पष्टीकरण की आवश्यकता होती है अगर हम एक निर्देशित ग्राफ (गैर-कम्यूटेटिव मीट्रिक, मैं माफी माँगता हूं) के बारे में बात कर रहा हूं। से दूरी के बारे में बात कर सकते हैं $$$ए$ को $$$ब$ , लेकिन आप से कर सकते हैं $$$ब$ को $$$ए$ । और सबसे अधिक संभावना है कि ये दूरी हमेशा बराबर नहीं होती हैं। समस्या में हम किस तरह की दूरियों की बात कर रहे हैं?

यूक्लिडियन दूरी नियम

हम उभरेंगे और गहरी सांस लेंगे। हमने पहले ही उल्लेख किया है कि प्रतिरोधक दूरी सामान्य यूक्लिडियन है। इसका मतलब यह है कि इसकी परिभाषा को यूक्लिडियन दूरी की परिभाषा में दो तत्वों के अंतर के रूप में कम किया जा सकता है:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

यह परिभाषा तत्वों के क्रम पर निर्भर नहीं करती है - यह तत्वों की कम्यूटेटिव दूरी, निकटता (अधिक सटीक, दूरी) है। एक अभिव्यक्ति में एक बिंदु का अर्थ है एक स्केलर उत्पाद ऑपरेशन (मीट्रिक स्थान)। तदनुसार, अभिव्यक्ति (1) का खुलासा किया जा सकता है:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

यहां $$$A ^ 2 = A \ cdot A$ । $$$B ^ 2 = B \ cdot B$ - तत्वों के मानदंड। जब ग्राफ़ की बात आती है, तो तत्वों के मानदंड आमतौर पर शून्य होते हैं। मूल समस्या में मानदंडों के बारे में कुछ भी नहीं कहा गया है, इसलिए आप उन्हें शून्य होने के लिए ले जा सकते हैं (इस बारे में अधिक जानकारी होगी कि एफाइन स्पेस में तत्वों के मानदंड क्या हैं। यहां और भी अधिक विवरण, यहां )। फिर वांछित दूरी के लिए अभिव्यक्ति का रूप लेता है:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

अभिव्यक्ति (3) के अनुसार, समस्या को हल करने के लिए सभी की जरूरत है कि तत्वों (नोड्स) के स्केलर उत्पादों को एक निर्देशित ग्राफ में (यह कहना आसान है, लेकिन यह कैसे करना है?)।

रास्ते के साथ, सूत्र (3) दर्शाता है कि तत्वों के बीच निकटता के हमारे सामान्य (कम्यूटेटिव) उपाय $$$ए$ और $$$ब$ दो निर्देशित दूरी का योग है:

$$$s_ {AB} = - A \ cdot B$ - दिशात्मक दूरी $$$ए$ को $$$ब$ ।
$$$s_ {BA} = - B \ cdot A$ - दिशात्मक दूरी $$$ब$ को $$$ए$ ।

2. निर्णय। टीलों में लंबी सड़क

अफरा तफरी मच गई। मजा आ गया। फिर एक निर्देशित ग्राफ के नोड्स के बीच स्केलर उत्पाद की गणना करने के लिए विधि के सार का सुस्त विवरण दें। यह वह हिस्सा है जिसे मैं "उंगलियों पर एक सरल तरीके से" कहना नहीं जानता। लेकिन यह वह जगह है जहां लेख में सबसे महत्वपूर्ण बात है। उस पर समय बर्बाद करने लायक कुछ।

तर्क की सामान्य रेखा इस प्रकार है। हम नई अतिरिक्त धारणाओं को ध्यान से और भावनाओं के बिना सममित स्थानों के मीट्रिक के ज्ञात गुणों को असममित लोगों में स्थानांतरित करते हैं। सभी की जरूरत है कि आत्मीय स्थानों में मीट्रिक की ख़ासियत को ध्यान में रखा जाए।

कोई भी जुड़ा हुआ ग्राफ (चाहे वह निर्देशित हो या न हो) एक परिमित मीट्रिक स्थान को परिभाषित करता है। सममित (कम्यूटेटिव) निष्पादन में ऐसे रिक्त स्थान के कुछ गुण लेखों के पहले से उल्लेखित श्रृंखला में वर्णित (अधिक) थे या अधिक सटीक रूप से और विस्तार से वर्णित दीर्घवृत्त में । स्विच करने के लिए जल्दी मत करो - नीचे हम देते हैं (हालांकि, जीभ ट्विस्टर द्वारा) मुख्य निचोड़ता है।

Affric metric space (अप्रत्यक्ष ग्राफ)

क्या महत्वपूर्ण है? सर्वप्रथम सुप्रसिद्ध

1. अंतरिक्ष की आत्मीयता का मतलब है कि अंतरिक्ष में वेक्टर और तत्व की अवधारणाएं अलग-अलग हैं। वेक्टर तत्वों का अंतर है। यदि अंतरिक्ष में एक मीट्रिक को परिभाषित किया जाता है तो यह प्रतीत होता है कि महत्वहीन सुविधा महत्वपूर्ण परिणाम देती है।

2. अंतरिक्ष तत्वों से मिलकर एक आधार द्वारा परिभाषित किया गया है। ग्राफ के कोने अंतरिक्ष के आधार हैं। एक ग्राफ में संबंध इसके मीट्रिक गुणों को निर्धारित करते हैं।

3. एक ग्राफ कनेक्टिविटी विशेषता आसन्न मैट्रिक्स है । लेकिन मीट्रिक (और अन्य) गुणों के लिए, ग्राफ का किर्लिशियन (किरचॉफ मैट्रिक्स) अधिक महत्वपूर्ण है $$$एल$ ।

4. ग्राफ का लाप्लासियन लगभग एक मीट्रिक टन है। "लगभग" - यहाँ का अर्थ है कि यह अपूर्ण है। लाप्लासियन एक अध: पतन मैट्रिक्स है और इसलिए उलटा नहीं है। और मानक मीट्रिक टेंसर पूरी तरह से प्रतिवर्ती है।

अब कम जाना जाता है।

5. एक मीट्रिक चक्कर अंतरिक्ष में तत्वों और वैक्टर के बीच का अंतर इसमें एक अशक्त वेक्टर के अस्तित्व की ओर जाता है $$$\ mathbb z$ । एक कम्यूटेटिव (सममित) स्थान में नल वेक्टर के साथ तत्वों का स्केलर उत्पाद एकता के बराबर है (गैर-कम्यूटेटिव स्पेस में यह गुणन की दिशा पर निर्भर करता है)। जीरो वेक्टर के बिना ग्राफ स्पेस पूरा नहीं होता है! यह महत्वपूर्ण है।

6. शून्य वेक्टर के संबंध में आधार का ऑर्थोगोनल केंद्र दोहरी है। $$$Z$ । यह ऐसा तत्व है जो आधार के अन्य सभी तत्वों (शून्य-वेक्टर को छोड़कर) के लिए ऑर्थोगोनल है। स्मरण करो कि तत्वों की रूढ़िवादिता का अर्थ है कि उनका अदिश उत्पाद शून्य है। एक त्रिभुज का ऑर्थोसेंटर परिचालित सर्कल है । हां, एक पूर्ण चक्कर वाली जगह में एक गैर-अक्षीय मानदंड वाला एक तत्व एक बिंदु नहीं है, बल्कि एक एन-आयामी क्षेत्र है।

7. ग्राफ का लाप्लासियन, ऑर्थोगोनल सेंटर के निर्देशांक के साथ, पूर्ण (पूर्ण मीट्रिक मीट्रिक) पूर्ण हो जाता है। दूसरे शब्दों में, पूर्ण लाप्लासियन $$$एलएम$ एक साधारण गिनती लैपलीन है $$$एल$ लेकिन ऑर्थोगोनल सेंटर के बेरेंट्रिक निर्देशांक द्वारा सीमाबद्ध है।

8. पूर्ण लाप्लासियन का उलटा एक पूर्ण ग्रामियन प्राप्त करने की अनुमति देता है $$$जीएम$ - आधार के तत्वों के स्केलर उत्पादों का मैट्रिक्स (हमारे मामले में, ग्राफ के कोने)। यह ग्रामियन अंतरिक्ष का एक पूर्ण मीट्रिक मीट्रिक भी है।

9. एक पूर्ण व्याकरण का निर्धारण इकाइयों (आधार तत्वों के अदिश उत्पादों और एक शून्य-सदिश) का एक समूह है। कोने में - शून्य, यह स्वयं शून्य-वेक्टर का आदर्श है।
प्रसिद्ध केली-मेन्जर मैट्रिक्स एक लगभग नियमित ग्रामियन है।

नतीजतन, हम यह निष्कर्ष निकालते हैं कि, दावे 8 के अनुसार, स्केलर उत्पादों के निर्धारण की समस्या (और इसलिए, इसलिए, एक ग्राफ के नोड्स के बीच की दूरी) आधार के प्रारंभिक मीट्रिक टेंसर को निर्धारित करने के लिए कम कर देती है $$$जीएम$ ।

हमें पूर्ण ग्रामियन ग्राफ बनाने के लिए एक विधि की आवश्यकता है $$$जीएम$ दिए गए (अधूरे) लाप्लासियन के लिए $$$एल$ ।

सममित बांड के मामले में, लाप्लासियन (और इसके विपरीत) से एक पूर्ण ग्रामियन का निर्माण किसी विशेष कठिनाइयों का कारण नहीं बनता है। इस मामले में, आधार के तत्वों और शून्य-वेक्टर के स्केलर उत्पाद सराहनीय हैं - वे गुणा के आदेश पर निर्भर नहीं करते हैं:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

निर्देशित ग्राफ़ (गैर-कम्यूटेटिव स्पेस) के लिए समस्या जटिल है। यदि केवल इसलिए कि निर्देशित ग्राफ में संभावित कनेक्शनों की संख्या दोगुनी है।

गैर-कम्यूटेटिव एफाइन स्पेस (निर्देशित ग्राफ)

निर्देशित ग्राफ के लाप्लासियन के गुणों के बारे में, हमने पहले से ही हैबर पर भी लिखा है । उन्होंने बताया कि वस्तुओं को रैंक करने के लिए लाप्लासियन की क्षमता का उपयोग कैसे करें। ठिकानों के संदर्भ में, लाप्लासियन की क्षमता शून्य-वेक्टर (लाप्लासियन का विनाशकर्ता) के दोहरे निर्देशांक हैं।

इस लेख में, हम मीट्रिक गुणों में रुचि रखते हैं। यदि ग्राफ़ का निर्देशन किया जाता है, तो उसके कोने के बीच का स्केलर उत्पाद ऑर्डर पर निर्भर करता है:

$$$A \ cdot B \ ne B \ cdot A$

इसका मतलब है कि निर्देशित ग्राफ़ में दोहरे निर्देशांक विभाजित हैं (बाएं और दाएं)। शून्य-वेक्टर के स्केलर उत्पादों के मूल्य और आधार के तत्व (ग्रामियन की सीमा) भी कारकों के क्रम पर निर्भर करते हैं। और इसलिए, कम्यूटेटिव स्पेस के विपरीत, यहां शून्य-वेक्टर के दोहरे निर्देशांक में से एक अज्ञात है और इसे निर्धारित किया जाना चाहिए।

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

हालांकि, कई ज्ञात मात्राएं हैं।

सबसे पहले, लाप्लासियन खुद को जाना जाता है। इसके अलावा, यह ज्ञात है कि इसकी पंक्तियों का योग शून्य है (सामान्य स्थिति में, यह एक वैकल्पिक आवश्यकता है, लेकिन निर्देशित रेखांकन के लाप्लाशियनों के लिए यह आमतौर पर मामला है)। यह भी महत्वपूर्ण है कि तत्वों के बेरेंट्रिक निर्देशांक अद्वितीय हैं, क्योंकि वे अंतरिक्ष मीट्रिक से स्वतंत्र हैं। यही है, ग्राफ़ के लाप्लासियन की सीमा निर्देशित और अप्रत्यक्ष ग्राफ दोनों के लिए सममित है (मैं तुरंत इस बिंदु को नहीं पहचानता)। अंत में, हम आधार के तत्वों के मानदंडों को जानते हैं (आमतौर पर रेखांकन में वे शून्य के बराबर होते हैं)।

यह लाप्लासियन और ग्रामियन को जोड़ने वाली पहचान में सभी ज्ञात और अज्ञात को प्रतिस्थापित करने के लिए बना हुआ है:

$$$Lm \ Gm = I$

यहां $$$मैं$ एक पहचान मैट्रिक्स है। इस पहचान में, अधूरा लाप्लासियन से एक पूर्ण के लिए संक्रमण का अर्थ है।

चुप रहो और विश्वास करो

शब्दों से कर्मों की ओर बढ़ते हैं। यह वही है जो लाप्लासियन की तरह दिखता है $$$एल$ दो नोड्स के ग्राफ के लिए:

$$$L = \ start {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

सादगी के लिए, हमने संख्याओं के साथ संबंध निर्दिष्ट किए हैं: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ । यह माना जाता है कि बांड के मूल्य ज्ञात हैं - उनके माध्यम से हम अन्य सभी मात्राओं को व्यक्त करेंगे।

पूर्ण लाप्लासियन $$$एलएम$ ऑर्थोसेंटर के निर्देशांक शामिल हैं $$$[rz, az, bz]$ :

$$$Lm = \ start {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

यहां $$$rz$ - ऑर्थोसेंटर के मानदंड (सममित मामले में त्रिज्या के वर्ग के रूप में व्याख्या की गई है), $$$az$ और $$$बज़$ - आधार पर ऑर्थोसेंटर के अपघटन के गुणांक $$$ए, बी$ (barycentric वजन)।

पूर्ण चना $$$जीएम$ यह कुछ इस तरह दिखता है:

$$$Gm = \ start {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 और 0 \ end {bmatrix}$

यहाँ टुपल्स हैं $$$[za, zb]$ और $$$[1, 1]$ नल वेक्टर के दोहरे निर्देशांक को दर्शाते हैं। ये निर्देशांक लाप्लासियन के सर्वनाशक हैं (जब लाप्लासियन द्वारा गुणा किया जाता है तो वे एक शून्य वेक्टर देते हैं - शून्य वेक्टर के साथ भ्रमित नहीं होने के लिए!)।

समस्या को हल करने के लिए, हमें ग्रामियन के मूल्यों का योग खोजने की आवश्यकता है: $$$- (g_1 + g_2)$ ।

हम अज्ञात की संख्या पर विचार करते हैं: $$$rz, az, bz, za, zb, g_1, g_2$ - केवल 7 (हाँ, हाँ - एक दुर्भाग्यपूर्ण दूरी के मूल्य का पता लगाने के लिए, हमें सात और अतिरिक्त मूल्यों की गणना करने की आवश्यकता है)। प्रवेश द्वार पर दो प्रसिद्ध कनेक्शन हैं - $$$c_1$ और $$$c_2$ । पहचान $$$Lm \ Gm = I$ 9 समीकरण देंगे। कुल 7 + 2 = 9, - सब कुछ (आश्चर्यजनक रूप से) परिवर्तित होता है। यह केवल समीकरणों की प्रणाली को हल करने के लिए बनी हुई है।

दो नोड्स के ग्राफ के लिए, समाधान (सभी अज्ञात) स्पष्ट रूप में व्यक्त किए जा सकते हैं। हम ब्याज की मात्रा के लिए परिमित भाव देते हैं। हम सामान्य ज्यामितीय कनेक्टिविटी की अवधारणा को पेश करते हैं - यह ऑर्थोगोनल केंद्र के आदर्श का पारस्परिक है $$$gc = 1 / rz$ । इसका आयाम ग्राफ लिंक के आयाम के साथ मेल खाता है। दो नोड्स (और दो कनेक्शन) के ग्राफ के लिए, ज्यामितीय कनेक्शन की एक अच्छी अभिव्यक्ति है:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

इस संबंध के माध्यम से, कोई नोड के स्केलर उत्पादों को व्यक्त कर सकता है:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

आप स्केलर उत्पादों का अनुवाद कर सकते हैं $$$जी$ दिशात्मक दूरी में $$$एस$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

नोड्स के बीच वांछित कम्यूटेटिव दूरी योग द्वारा निर्धारित की जाती है:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

दादी आ गई

अंत में। अभिव्यक्ति (4) - यह वांछित सूत्र है।

दो नोड्स के ग्राफ के कोने के बीच की दूरी काउंटर-लिंक के उत्पाद के वर्गमूल के विपरीत आनुपातिक है।

आप एक और बेकार सूत्र के साथ स्कूल की पाठ्यपुस्तक को लोड कर सकते हैं।

यदि कनेक्शन बराबर हैं, तो परिणाम अप्रत्यक्ष रेखांकन में प्रतिरोधक दूरी के साथ मेल खाता है:

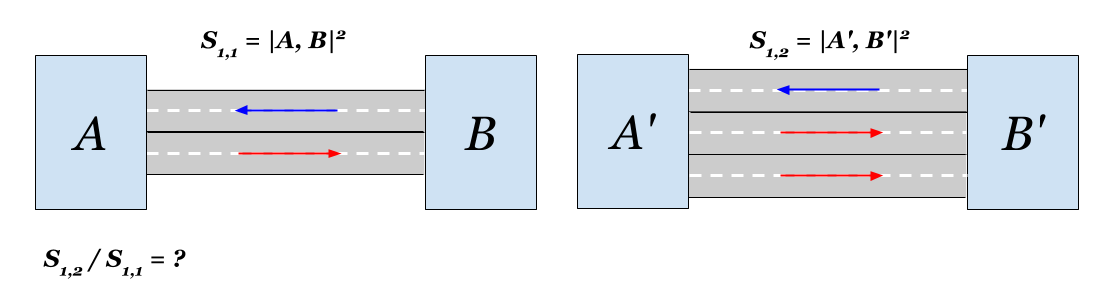
$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

हम गणना करेंगे कि हमारे शहर के साथ क्या है। यदि आप दूसरी लेन बिछाते हैं, तो एक दिशा में संचार दोगुना हो जाएगा। तदनुसार, नई दूरी $$$S_ {1, 2} (A, B)$ मूल के संदर्भ में व्यक्त किया जा सकता है:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

क्षेत्रों के बीच की दूरी में कमी होगी $$$\ sqrt {2}$ समय। यह स्पष्ट था, है ना?

यह भी पता चला है कि दूरी के संदर्भ में, प्रत्येक तरफ दो लेन वाली सड़क पर एक लेन जोड़ने से एक तरफ तीन लेन जोड़ने के बराबर है। दोनों मामलों में यूक्लिडियन निकटता दोगुनी हो जाएगी। दिलचस्प।



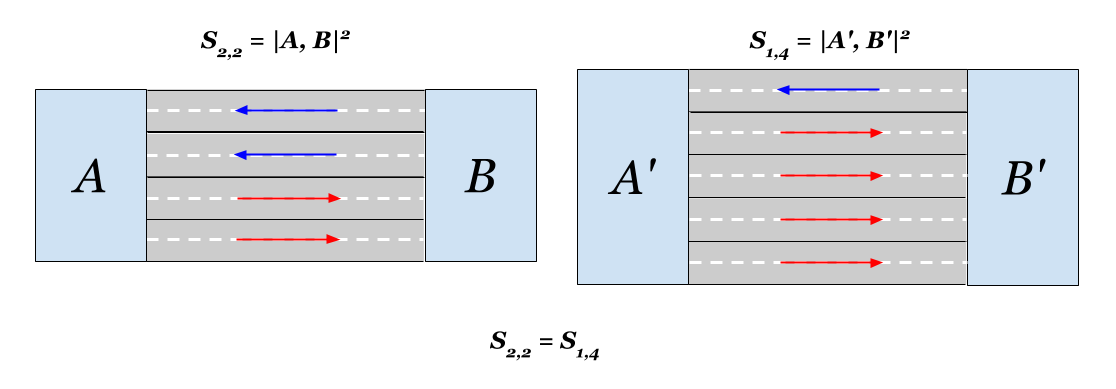
वह सब है। आपके ध्यान के लिए धन्यवाद)।