बहुमुखी और सही हैशिंग

हम सप्ताह की शुरुआत उपयोगी सामग्री "डेवलपर्स के लिए एल्गोरिदम" के लॉन्च के लिए समर्पित करते हैं। अच्छी पढाई हो।



1. अवलोकन

दिलचस्प और सूक्ष्म सिद्धांत के साथ हैशिंग एक महान व्यावहारिक उपकरण है। शब्दावली संरचना के रूप में डेटा का उपयोग करने के अलावा, हैशिंग कई अलग-अलग क्षेत्रों में भी पाया जाता है, जिसमें क्रिप्टोग्राफी और जटिलता सिद्धांत शामिल हैं। इस व्याख्यान में, हम दो महत्वपूर्ण अवधारणाओं का वर्णन करते हैं: सार्वभौमिक हैशिंग (हैश फ़ंक्शन के सार्वभौमिक परिवार के रूप में भी जाना जाता है) और आदर्श हैशिंग।

इस व्याख्यान में शामिल सामग्री में शामिल हैं:

• औपचारिक सेटिंग और हैशिंग के सामान्य विचार।
• यूनिवर्सल हैशिंग।
• बिल्कुल सही हैशिंग।

2. परिचय

हम उस शब्दकोश के साथ मुख्य समस्या पर विचार करेंगे, जिस पर हमने पहले चर्चा की थी, और दो संस्करणों पर विचार करें: स्थैतिक और गतिशील:

• स्टेटिक : बहुत सारे एस तत्वों को देखते हुए, हम इसे इस तरह से संग्रहित करना चाहते हैं कि हम जल्दी से खोज कर सकें।
• उदाहरण के लिए, एक निश्चित शब्दकोश।
• डायनामिक : यहां हमारे पास प्रविष्टि, खोज और संभवतः हटाने के लिए अनुरोधों का एक क्रम है। हम यह सब प्रभावी ढंग से करना चाहते हैं।

पहली समस्या के लिए, हम एक क्रमबद्ध सरणी और एक द्विआधारी खोज का उपयोग कर सकते हैं। दूसरे के लिए, हम एक संतुलित खोज वृक्ष का उपयोग कर सकते हैं। हालांकि, हैशिंग एक वैकल्पिक दृष्टिकोण प्रदान करता है, जो अक्सर इन समस्याओं को हल करने का सबसे तेज़ और सबसे सुविधाजनक तरीका है। उदाहरण के लिए, मान लीजिए कि आप एआई खोज के लिए एक कार्यक्रम लिख रहे हैं और उन स्थितियों को संग्रहीत करना चाहते हैं जिन्हें आपने पहले ही हल कर लिया है (बोर्ड या राज्य स्थान के तत्वों पर) ताकि जब आप उन्हें फिर से चलाएं तो समान गणनाओं को न दोहराएं। हैशिंग इस जानकारी को संग्रहीत करने का एक आसान तरीका प्रदान करता है। क्रिप्टोग्राफी, नेटवर्क, जटिलता सिद्धांत में भी कई अनुप्रयोग हैं।

3. हैश मूल बातें

हैशिंग के लिए औपचारिक सेटिंग निम्नानुसार है।

• चाबियाँ यू के कुछ बड़े सेट से संबंधित हैं (उदाहरण के लिए, कल्पना करें कि यू 80 एससीआई वर्णों की अधिकतम लंबाई के साथ सभी तारों का एक संग्रह है।)
• यू में कुछ एस कीज़ हैं जिनकी हमें वास्तव में ज़रूरत है (चाबियाँ स्थिर या गतिशील हो सकती हैं)। चलो एन = | एस | कल्पना कीजिए कि N, U के आकार से बहुत छोटा है। उदाहरण के लिए, S एक कक्षा में छात्र के नाम का सेट है, जो कि 128/80 की तुलना में बहुत छोटा है।
• हम कुछ आकार M और हैश फ़ंक्शन h: U → {0, ..., M - 1} के एक सरणी का उपयोग करके आवेषण और खोजों का प्रदर्शन करेंगे। तत्व x को देखते हुए, हैशिंग का विचार यह है कि हम इसे A [h (x)] में संग्रहीत करना चाहते हैं। ध्यान दें कि यदि U छोटा था (उदाहरण के लिए, 2-वर्ण स्ट्रिंग्स), तो आप x को A [x] में ब्लॉक छँटाई के रूप में सहेज सकते हैं। समस्या यह है कि यू बड़ा है, इसलिए हमें एक हैश फ़ंक्शन की आवश्यकता है।
• हमें टकरावों को हल करने के लिए एक विधि की आवश्यकता है। एक टकराव तब होता है जब h (x) = h (y) दो अलग-अलग कुंजियों के लिए x और y होता है। इस व्याख्यान में, हम ए के प्रत्येक तत्व को एक लिंक्ड सूची के रूप में परिभाषित करके टकराव से निपटेंगे। कई अन्य तरीके हैं, लेकिन जिन समस्याओं पर हम यहां ध्यान केंद्रित करेंगे, उनके लिए यह सबसे उपयुक्त है। इस विधि को चैनिंग विधि कहा जाता है। किसी आइटम को सम्मिलित करने के लिए, हम इसे सूची में सबसे ऊपर रखते हैं। यदि h एक अच्छा हैश फ़ंक्शन है, तो हमें उम्मीद है कि सूचियाँ छोटी होंगी।

हैशिंग के बारे में महान चीजों में से एक यह है कि सभी शब्दकोश संचालन अविश्वसनीय रूप से लागू करना आसान है। कुंजी x की खोज करने के लिए, बस इंडेक्स i = h (x) की गणना करें और तब तक ए [i] सूची में तब तक जाएं जब तक आपको यह पता न चले (या सूची से बाहर निकलें)। सम्मिलित करने के लिए, बस अपनी सूची के शीर्ष पर एक नया आइटम रखें। हटाने के लिए, आपको केवल लिंक की गई सूची में डिलीट ऑपरेशन करना होगा। अब हम इस प्रश्न की ओर मुड़ते हैं: अच्छा प्रदर्शन हासिल करने के लिए हमें क्या करने की आवश्यकता है?

वांछनीय गुण। एक अच्छी हैश योजना के लिए मुख्य वांछनीय गुण:

1. कुंजी अच्छी तरह से छितरी हुई हैं ताकि हमारे पास बहुत अधिक टक्कर न हों, क्योंकि टक्करें खोज और विलोपन के समय को प्रभावित करती हैं।
2. एम = ओ (एन): विशेष रूप से, हम चाहते हैं कि हमारे सर्किट को संपत्ति प्राप्त करने के लिए (1) टेबल एम के आकार की आवश्यकता के बिना तत्वों की संख्या से बहुत बड़ा हो।
3. फ़ंक्शन एच को जल्दी से गणना की जानी चाहिए। आज हमारे विश्लेषण में, हम h (x) की गणना करने के समय को एक स्थिरांक मानेंगे। हालांकि, यह याद रखने योग्य है कि यह बहुत जटिल नहीं होना चाहिए क्योंकि यह समग्र निष्पादन समय को प्रभावित करता है।

इसे देखते हुए, तत्व x का खोज समय O है (सूची का आकार A [h (x)]) है। हटाने के लिए भी यही सच है। सम्मिलन सूची की लंबाई की परवाह किए बिना O (1) समय लेता है। इसलिए, हम विश्लेषण करना चाहते हैं कि ये सूचियाँ कितनी बड़ी हैं।

मूल अंतर्ज्ञान: तत्वों को खूबसूरती से वितरित करने का एक तरीका उन्हें यादृच्छिक रूप से वितरित करना है। दुर्भाग्य से, हम केवल यादृच्छिक संख्या जनरेटर का उपयोग यह तय करने के लिए नहीं कर सकते हैं कि अगले तत्व को कहां निर्देशित किया जाए, क्योंकि तब हम इसे फिर से कभी नहीं पा सकते हैं। इसलिए, हम चाहते हैं कि एच कुछ औपचारिक अर्थों में "छद्म यादृच्छिक" हो।

अब हम कुछ बुरी खबरें, और फिर कुछ अच्छी खबरें पेश करेंगे।

कथन १ (बुरी खबर) किसी भी हैश फंक्शन के लिए यदि | U | − (एन )1) एम +1, एन तत्वों का एक सेट है जो सभी एक ही स्थान पर हैशेड करता है।

प्रमाण: डिरिचलेट सिद्धांत द्वारा। विशेष रूप से, काउंटरपॉइंट्स पर विचार करने के लिए, यदि प्रत्येक स्थान के पास U - 1 तत्वों से अधिक नहीं है जो कि हैश करता है, तो U का आकार M (N - 1) से अधिक नहीं हो सकता है।

यह आंशिक रूप से हैशिंग क्यों इतना रहस्यमय लगता है - यह कैसे तर्क दिया जा सकता है कि हैशिंग अच्छा है अगर किसी भी हैश फ़ंक्शन के लिए आप इसे रोकने के तरीकों के बारे में सोच सकते हैं? एक उत्तर यह है कि कई सरल हैश फ़ंक्शन हैं जो ठेठ एस सेट के लिए अभ्यास में अच्छी तरह से काम करते हैं। लेकिन क्या होगा अगर हम सबसे खराब स्थिति की अच्छी गारंटी चाहते हैं?

यहाँ मुख्य विचार है: आइए रैंडमाइज़ेशन का उपयोग रेंडमाइज़्ड क्विकॉर्ट के समान हमारे एच कंस्ट्रक्शन में करें। (कहने की जरूरत नहीं है, एच एक नियतात्मक कार्य होगा)। हम यह दिखाएंगे कि प्रविष्टि और खोज कार्यों के किसी भी अनुक्रम के लिए (हमें यह मानने की आवश्यकता नहीं है कि सम्मिलित तत्वों S का सेट यादृच्छिक है), यदि हम इस संभाव्य तरीके से h चुनते हैं, तो इस क्रम में h का प्रदर्शन प्रत्याशा में अच्छा होगा। इस प्रकार, यह रैंडमाइज्ड क्विकॉर्ट्स या ट्रैप्स के समान ही गारंटी है। विशेष रूप से, यह सार्वभौमिक हैशिंग का विचार है।

एक बार जब हम इस विचार को विकसित कर लेते हैं, तो हम इसका उपयोग "परफेक्ट हैशिंग" नामक एक विशेष रूप से आनंददायक एप्लिकेशन के लिए करेंगे।

4. यूनिवर्सल हैशिंग

परिभाषा 1. हैश फ़ंक्शंस के निर्माण के लिए एक यादृच्छिक एल्गोरिदम एच: यू → {1, ..., एम}
सार्वभौमिक अगर सभी x! = y के लिए हमारे पास है



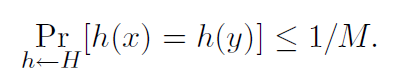
हम यह भी कह सकते हैं कि हैश फ़ंक्शंस का सेट एच, हैश फ़ंक्शंस का एक सार्वभौमिक परिवार है यदि "बेतरतीब ढंग से चयन एच universal एच" प्रक्रिया सार्वभौमिक है। (यहां हम सेट पर एक समान वितरण के साथ फ़ंक्शन के सेट की पहचान करते हैं।)

प्रमेय 2. यदि H सार्वभौमिक है, तो किसी भी सेट S ⊆ U के आकार N के लिए, किसी भी x (U (उदाहरण के लिए, जिसे हम देख सकते हैं) के लिए, यदि हम H के अनुसार अनियमित रूप से H का निर्माण करते हैं, तो x और अन्य के बीच टकराव की अपेक्षित संख्या S में तत्व N / M से अधिक नहीं हैं।

प्रमाण: प्रत्येक y (S (y! = X) में "सार्वभौमिक" की परिभाषा के अनुसार x के साथ टकराव का सबसे अधिक 1 / M मौका है। उदाहरण के लिए,

• Cxy = 1 को यदि x और y टकराते हैं, और 0 अन्यथा।
• बता दें कि Cx ने x के लिए टकराव की कुल संख्या को दर्शाया है। तो, Cx = Py∈S, y! = X Cxy।
• हम जानते हैं कि E [Cxy] = Pr (x and y collide) M. 1 / M।
• इस प्रकार, अपेक्षा की रैखिकता में, E [Cx] = Py E [Cxy] <N / M।

अब हम निम्नलिखित कोरोलरी प्राप्त करते हैं।

कोरोलरी 3. यदि H सार्वभौमिक है, तो सम्मिलन, खोज, और विलोपन संचालन L के किसी भी क्रम के लिए, जिसमें एक ही समय में सिस्टम में अधिकांश M तत्व हो सकते हैं, यादृच्छिक h is H के लिए L परिचालनों की अपेक्षित कुल लागत केवल O (L) (समय देखने) है स्थिरांक के रूप में एच की गणना करने के लिए)।

प्रमाण: अनुक्रम में किसी भी दिए गए ऑपरेशन के लिए, इसकी अपेक्षित लागत प्रमेय 2 द्वारा निरंतर है, इसलिए एल परिचालनों की अपेक्षित कुल लागत अपेक्षा की रैखिकता में O (L) है।

प्रश्न: क्या हम वास्तव में एक सार्वभौमिक एच का निर्माण कर सकते हैं? यदि नहीं, तो यह सब बहुत व्यर्थ है। सौभाग्य से, उत्तर हां है।

4.1। एक सार्वभौमिक हैश परिवार बनाना: मैट्रिक्स विधि

मान लीजिए कि चाबियाँ यू-बिट लंबी हैं। कहो, तालिका एम का आकार 2 डिग्री के बराबर है, इसलिए, एम = 2 बी के साथ सूचकांक बी-बिट लंबा है।

हम क्या करेंगे h को यादृच्छिक मैट्रिक्स 0/1 b-by-u के रूप में चुनें और h (x) = hx को परिभाषित करें, जहाँ हम mod 2 जोड़ते हैं। ये मैट्रिक्स छोटे और मोटे होते हैं। उदाहरण के लिए:



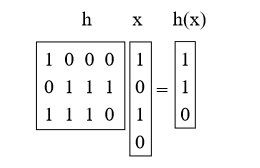
प्रस्ताव 4. x के लिए! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b।

प्रमाण: सबसे पहले, x को h से गुणा करने का क्या मतलब है? हम इसके बारे में सोच सकते हैं कि कुछ कॉलम एच (वेक्टर जोड़ मॉड 2 कर) को जोड़ रहे हैं, जहां एक्स में 1 बिट इंगित करता है कि किन लोगों को जोड़ना है। (उदाहरण के लिए, हमने ऊपर के h के पहले और तीसरे कॉलम को जोड़ा)

अब एक मनमाना कुंजी युग्म x लें, y ऐसा कि x! = Y। उन्हें कहीं अलग होना चाहिए, इसलिए, कहते हैं, वे i-वें समन्वय में भिन्न हैं, और संक्षिप्तता के लिए हम कहते हैं xi = 0 और yi = 1. कल्पना करें कि हमने पहली बार i-th कॉलम को छोड़कर सभी h को चुना था। Ith कॉलम के शेष नमूनों के लिए, h (x) तय किया गया है। हालांकि, ith कॉलम की 2b अलग-अलग सेटिंग्स प्रत्येक h (y) का एक अलग मूल्य देती हैं (विशेष रूप से, हर बार जब हम इस कॉलम में थोड़ा सा मोड़ते हैं, तो हम संबंधित बिट को h (y) में बदल देते हैं)। तो ठीक 1 / 2b मौका है कि h (x) = h (y)।

सार्वभौमिक हैश परिवारों के निर्माण के लिए अन्य विधियां हैं, जो कि अपरा के गुणन पर भी आधारित हैं (धारा 6.1 देखें)।

अगला सवाल जो हम विचार करेंगे: यदि हम सेट S को सही करते हैं, तो क्या हम एक हैश फंक्शन h पा सकते हैं, जिससे सभी खोजों में निरंतर समय होगा? इसका उत्तर हां में है, और यह सही हैशिंग के विषय की ओर जाता है।

5. परफेक्ट हैशिंग

हम कहते हैं कि एक हैश फ़ंक्शन S के लिए आदर्श है यदि सभी खोजें O (1) में होती हैं। यहां दिए गए सेट एस के लिए एकदम सही हैश फ़ंक्शन बनाने के दो तरीके हैं।

5.1 विधि 1: अंतरिक्ष O (N2) में एक समाधान

मान लें कि हम एक तालिका चाहते हैं जिसका आकार हमारे शब्दकोश एस के आकार में द्विघात है। फिर यहां आदर्श हैश फ़ंक्शन के निर्माण की एक सरल विधि है। आज्ञा देना H सार्वभौमिक और M = N2 है। तो बस एच से एक यादृच्छिक एच चुनें और इसे आज़माएं! बयान यह है कि कम से कम 50% संभावना है कि उसके पास टकराव नहीं होंगे।

प्रस्ताव 5. यदि H सार्वभौमिक है और M = N2 है, तो Prh (H (S में कोई टक्कर नहीं) is 1/2।

सबूत:

• S में कितने जोड़े (x, y) हैं? उत्तर है:
• प्रत्येक जोड़ी के लिए, उनकी टक्कर की संभावना सार्वभौमिकता की परिभाषा से M 1 / M है।
• तो पीआर (एक टक्कर है) is / एम <1/2।

यह "जन्मदिन विरोधाभास" के दूसरे पक्ष की तरह है। यदि दिनों की संख्या चुकता लोगों की संख्या की तुलना में बहुत अधिक है, तो एक उचित मौका है कि किसी भी जोड़े का एक ही जन्मदिन नहीं होगा।

तो, हम बस H से एक यादृच्छिक h उठाते हैं, और यदि कोई टक्कर होती है, तो हम बस एक नया h चुनें। औसतन, हमें केवल दो बार ऐसा करने की आवश्यकता होगी। अब, क्या होगा यदि हम केवल O (N) स्पेस का उपयोग करना चाहते हैं?

5.2 विधि 2: अंतरिक्ष ओ (एन) में एक समाधान

यह सवाल कि क्या O (N) स्पेस में परफेक्ट हैशिंग को कुछ समय के लिए खोलना संभव है: "क्या टेबल को छांटना चाहिए?" यही है, एक निश्चित सेट के लिए, आप केवल रैखिक स्थान के साथ एक निरंतर खोज समय प्राप्त कर सकते हैं? अधिक से अधिक जटिल प्रयासों की एक श्रृंखला थी, अंत में इसे दो-स्तरीय योजना में सार्वभौमिक हैश कार्यों के अच्छे विचार का उपयोग करके हल किया गया था।

विधि इस प्रकार है। सबसे पहले, हम सार्वभौमिक हैशिंग का उपयोग करते हुए आकार N की तालिका में हैश करेंगे। इससे कुछ टकराव होंगे (जब तक कि हम भाग्यशाली नहीं हैं)। हालाँकि, फिर हम प्रत्येक टोकरी को विधि 1 का उपयोग करते हुए पुनः आकार देते हैं, शून्य टक्कर प्राप्त करने के लिए टोकरी के आकार को बढ़ाते हैं। इस प्रकार, यह योजना इस तथ्य में शामिल है कि हमारे पास पहले स्तर एच का एक हैश फ़ंक्शन है और पहले स्तर का एक टेबल ए, और फिर दूसरे स्तर एच 1, ..., एचएन और एन के दूसरे स्तर ए 1 की तालिका के ए 1, ..., . ... तत्व x को खोजने के लिए, हम पहले i = h (x) की गणना करते हैं, और फिर ऐ [हाय (x)] में तत्व को खोजते हैं। (यदि आपने अभ्यास में ऐसा किया है, तो आप ध्वज को सेट कर सकते हैं ताकि आप केवल दूसरा कदम उठाएंगे यदि वास्तव में सूचकांक i के साथ संघर्ष था, अन्यथा आप केवल ए [i] में x ही डालेंगे, लेकिन चलो चलो इसके बारे में चिंता न करें।)

स्थान के आधार पर S का हैश फ़ंक्शन h हैश n तत्वों को कहें। हमने पहले ही साबित कर दिया (विधि 1 का विश्लेषण करके) कि हम h1, ..., hN पा सकते हैं, ताकि द्वितीयक तालिकाओं में प्रयुक्त कुल स्थान Pi (ni) 2 हो। यह दिखाने के लिए बना हुआ है कि हम एक प्रथम-स्तरीय फ़ंक्शन h को खोज सकते हैं, जैसे कि पि (ni) 2 = O (N)। वास्तव में, हम निम्नलिखित दिखाएंगे:

प्रमेय 6. यदि हम सार्वभौमिक सेट एच से शुरुआती बिंदु एच चुनते हैं, तो

Pr[X i (ni)2 > 4N] < 1/2. 

सबूत। आइए हम यह साबित करके दिखाते हैं कि E [Pi (ni) 2] <2N। इसका तात्पर्य है कि हम मार्कोव असमानता से क्या चाहते हैं। (यदि 1/2 की भी संभावना थी कि योग 4N से अधिक हो सकता है, तो अकेले इस तथ्य का अर्थ होगा कि उम्मीद 2N से अधिक होनी चाहिए। इस प्रकार, यदि उम्मीद 2N से कम है, तो विफलता की संभावना कम होनी चाहिए। 1/2।)

अब, मुश्किल चाल यह है कि इस राशि की गणना करने का एक तरीका उन जोड़े की संख्या की गणना करना है जिनमें टकराव होता है, अपने आप से टकराव सहित। उदाहरण के लिए, यदि टोकरी में {d, e, f} है, तो d का प्रत्येक {d, e, f} के साथ संघर्ष होगा, e का {d, e, f} के प्रत्येक के साथ संघर्ष होगा, और f के साथ संघर्ष होगा प्रत्येक {d, e, f}, इसलिए हमें 9 मिलते हैं। इसलिए, हमारे पास:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

इसलिए, हम बस H से एक यादृच्छिक h की कोशिश करते हैं, जब तक कि हम एक ऐसा नहीं ढूंढते हैं कि Pi n2 i <4N, और फिर इस फ़ंक्शन h को ठीक करते हुए, हम N माध्यमिक हैश फ़ंक्शन h1, ..., hN को विधि 1 के रूप में पाते हैं।

6. आगे की चर्चा

6.1 एक और सार्वभौमिक हैशिंग विधि

सार्वभौमिक हैश कार्यों के निर्माण के लिए यहां एक और तरीका है, जो पहले दिए गए मैट्रिक्स विधि की तुलना में थोड़ा अधिक कुशल है।

मैट्रिक्स विधि में, हमने कुंजी को बिट्स के वेक्टर के रूप में माना। इस पद्धति में, हम इसके बजाय कुंजी x को पूर्णांक [1, x2, ..., xk] के वेक्टर के रूप में विचार करेंगे, केवल इस आवश्यकता के साथ कि प्रत्येक xi सीमा {0, 1, ..., M-1} में होगी। उदाहरण के लिए, यदि हमारे पास लंबाई k का हैश है, तो xi ith वर्ण हो सकता है (यदि हमारी तालिका का आकार कम से कम 256 है) या पात्रों की ith जोड़ी (यदि हमारी तालिका का आकार कम से कम 65536 है)। इसके अलावा, हमें आवश्यकता होगी कि हमारी तालिका M का आकार एक प्रधान हो। हैश फ़ंक्शन h का चयन करने के लिए, हम k यादृच्छिक संख्या r1, r2, ..., pk से {0, 1, ..., M - 1} का चयन करते हैं और निर्धारित करते हैं:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

यह विधि सार्वभौमिक है इस प्रमाण का निर्माण मैट्रिक्स विधि के प्रमाण के समान किया गया है। आज्ञा देना x और y दो अलग-अलग कुंजी हैं। हम यह दिखाना चाहते हैं कि Prh (h (x) = h (y)) M. 1 / M. x के बाद! = Y, वहाँ कोई केस होना चाहिए जब कुछ इंडेक्स मौजूद हो जैसे कि xi! = Yi। अब कल्पना करें कि आपने सबसे पहले j के लिए सभी यादृच्छिक संख्या rj का चयन किया! = I H h (x) = Pj6 = i rjxj तो, री को चुनने पर, हमें h (x) = h x (x) + rixi मिलता है। इसका मतलब यह है कि हमारे पास x और y के बीच वास्तव में एक संघर्ष है जब

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

चूंकि M अभाज्य है, इसलिए मॉड M के नॉनज़ेरो मान से विभाजित करना मान्य है (1 से M lic1 के प्रत्येक पूर्णांक का गुणक व्युत्क्रम modulo M होता है), जिसका अर्थ है कि बिलकुल एक मान री मोडुलो M है, जिसके लिए उपरोक्त समीकरण है। सत्य, अर्थात् ri = (h ′ (y) - h x (x)) / (xi - yi) mod M. इस प्रकार, इस घटना की संभावना ठीक 1 / M है।

6.2 हैशिंग के अन्य उपयोग

मान लें कि हमारे पास तत्वों का एक लंबा अनुक्रम है, और हम यह देखना चाहते हैं कि सूची में कितने अलग-अलग तत्व हैं। क्या ऐसा करने का कोई अच्छा तरीका है?

एक तरीका हैश तालिका बनाना, और फिर प्रत्येक तत्व की खोज करके अनुक्रम से गुजरना और फिर सम्मिलित करना अगर यह तालिका में पहले से ही नहीं है। व्यक्तिगत तत्वों की संख्या आवेषण की संख्या है।

और अब, क्या होगा यदि सूची वास्तव में विशाल है और हमारे पास इसे संग्रहीत करने के लिए कोई जगह नहीं है, लेकिन एक अनुमानित उत्तर हमारे लिए उपयुक्त है। उदाहरण के लिए, कल्पना करें कि हम एक राउटर हैं और देखते हैं कि कितने पैकेट पास होते हैं, और हम (लगभग) यह देखना चाहते हैं कि कितने अलग-अलग स्रोत आईपी पते मौजूद हैं।

यहां एक अच्छा विचार है: मान लें कि हमारे पास एक हैश फ़ंक्शन एच है जो एक यादृच्छिक फ़ंक्शन की तरह व्यवहार करता है, और चलो कल्पना करते हैं कि एच (एक्स) 0 से 1 तक की वास्तविक संख्या है। एक चीज जो हम कर सकते हैं वह है न्यूनतम का ट्रैक रखना हैश मूल्य का अब तक उत्पादन किया गया है (इसलिए हमारे पास एक तालिका नहीं है)। उदाहरण के लिए, यदि कुंजियाँ 3,10,3,3,12,10,12 और h (3) = 0.4, h (10) = 0.2, h (12) = 0.7 हैं, तो हमें 0 मिलता है, 2।

तथ्य यह है कि अगर हम [0, 1] में N यादृच्छिक संख्याओं का चयन करते हैं, तो अपेक्षित न्यूनतम मूल्य 1 / (N + 1) होगा। इसके अलावा, एक अच्छा मौका है कि यह बहुत करीब है (हम कई हैश फ़ंक्शंस चलाकर और चढ़ाव के माध्य ले कर अपने अनुमान में सुधार कर सकते हैं)।

प्रश्न: हैश फ़ंक्शन का उपयोग क्यों करें, और हर बार एक यादृच्छिक संख्या न चुनें? ऐसा इसलिए है क्योंकि हम विभिन्न तत्वों की संख्या के बारे में परवाह करते हैं, और न केवल तत्वों की कुल संख्या (यह समस्या बहुत सरल है: बस एक काउंटर का उपयोग करें ...)।

दोस्तों, क्या यह लेख आपके लिए उपयोगी था? टिप्पणियों में लिखें और खुले दिन में शामिल हों, जो 25 अप्रैल को आयोजित किया जाएगा।