👩‍👦 🕺 👆🏻 लेकिन क्या हम ऑप्टिकल संचार के लिए तरंग नहीं करते हैं? लेज़र, स्पेस, क्यूबसैट 🛌🏽 🍙 👨🏿‍🤝‍👨🏻

नीचे वर्णित सामग्री एक स्थानीय पाठ्यक्रम परियोजना (उन्नत अनुसंधान परियोजना) के हिस्से के रूप में टीयू इलमेनौ के शिक्षकों के साथ संयुक्त कार्य का परिणाम है। अनुभव दिलचस्प है, लेकिन कुछ कठिनाइयों के बिना नहीं। हमने अपनी तत्कालीन दुल्हन के साथ यह प्रोजेक्ट (और एक और) किया - हाँ, और इसलिए हम एक साथ अध्ययन करने और जर्मनी में इंटर्नशिप करने के लिए भाग्यशाली थे। सच में, यह वह था जिसने इस काम को अधिक हद तक किया, लेकिन मैं इस विषय को लोकप्रिय बनाना चाहता हूं।

इसलिए, एक दिन हमने वैज्ञानिक काम के लिए एक विषय चुनने के लिए एक नियुक्ति की ...

लघु पृष्ठभूमि (चेहरों में)

जर्मन शिक्षक # 1 : ओह, मैंने सुना है कि आप घर पर क्यूबसैट उपग्रहों का अध्ययन करते हैं?

मैं और मेरी भावी पत्नी : ठीक है, आप कह सकते हैं कि ...

समझौता नंबर 1 : बढ़िया! लेकिन क्या होगा अगर आप उपग्रहों के बीच ऑप्टिकल संचार पर विचार करने की कोशिश करते हैं? मुझे पता है कि कुछ मामलों में प्रकाशिकी ऐसे छोटे उपग्रहों के लिए सबसे अच्छा ऊर्जा प्रदर्शन देता है, मुझे लगता है कि यह मुद्दा बहुत महत्वपूर्ण है। मेरा एक दोस्त है जो पेशेवर रूप से वायरलेस ऑप्टिक्स में लगा हुआ है। मुझे लगता है कि यह एक दिलचस्प परियोजना होगी!

हम : दिलचस्प लगता है!

(कुछ समय बीत जाता है)

जर्मन शिक्षक संख्या 2 के साथ बैठक।

समझौता नंबर 2 : हाँ, यह सब, ज़ाहिर है, महान है, लेकिन किस तरह के उपग्रह हैं? इतना छोटा द्रव्यमान? क्या वे संवाद भी कर सकते हैं? इसका सुझाव किसने दिया? समझ में आया ... जाहिर है, हम उसे इन बैठकों में नहीं देखेंगे। वास्तविक दुनिया के उदाहरणों के लिए खोज पर जाएं - मुझे अभी तक विश्वास नहीं है।

और हम सेट ...

और, उनकी खुशी के लिए, उन्होंने इस विषय के लिए एक संपूर्ण लेख भी पाया। एक महत्वपूर्ण अंतर यह था कि प्रकाशिकी के माध्यम से संचार पृथ्वी के साथ होना चाहिए था, न कि उपग्रहों के बीच। यह बहुत महत्वपूर्ण है क्योंकि:

सभी प्रकार के बिखरने और हस्तक्षेप, ज़ाहिर है, इस मामले में अधिक,
हालाँकि, धरती पर रिसीवर पर्याप्त रूप से सेट किया जा सकता है, और ट्रांसमीटर बहुत सटीक है। और अंतरिक्ष खंड, आप समझते हैं, चीजों को थोड़ा जटिल करता है।

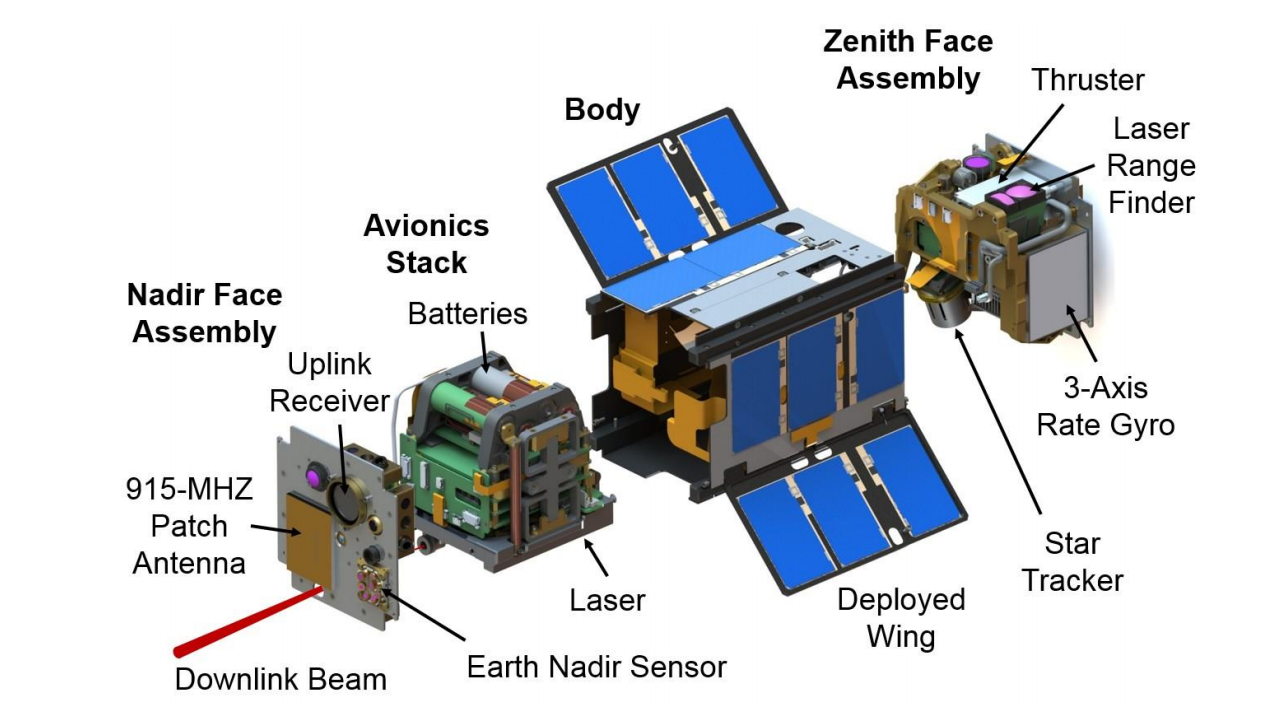
अंजीर। 1. AeroCube-OCSD नैनोसेटेलाइट [1] का योजनाबद्ध प्रतिनिधित्व।

लेकिन वह पहले से ही कुछ था, और हमने फिर से एक नियुक्ति की।

समझौता नंबर 2 : खैर, ठीक है, नासा के बाद से ... आइए ऊर्जा बजट की गणना करने की कोशिश करें और इसकी तुलना रेडियो लिंक के ऊर्जा बजट से करें। संबंधित लेख बंद करने के लिए?

और उन्होंने अपने लेख को फेंक दिया [2] (मैं आज इसे कई बार संदर्भित करूंगा) और इस मुद्दे की सामान्य समझ के लिए अन्य लेखकों द्वारा कुछ लेख।

इंटर-सैटेलाइट ऑप्टिकल लाइन के ऊर्जा बजट का क्या अर्थ है?

वायरलेस ऑप्टिकल ऊर्जा बजट

लेकिन यह अपने आप में, सामान्य रूप से, सामान्य रूप से (आवश्यक ट्रांसमीटर शक्ति, प्राप्त शक्ति, एसएनआर, आदि) के समान है - केवल शोर को रेडियो संचार के मामले की तुलना में थोड़ा अधिक दिलचस्प माना जाता है ...

चलिए मॉडलिंग शुरू करते हैं - यह थोड़ा स्पष्ट होगा:

import numpy as np from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend import matplotlib.pyplot as plt from scipy import special

मान लीजिए कि हमारे पास ऐसी प्रणाली है:

 #initial parameters for optical case R = 100*1e3 #distance between objects, eg satellites, in m (100 km) Bit_rate = 1e6 #bit rate (1 Mbps) h = 6.62607004*1e-34 # Planck constant c = 299792458 #speed of light wavelength_opt = 1550*1e-9 #optical wavelength freq_opt = c/wavelength_opt #optical frequency Ptx_opt = 1 #transmitter power in Watts Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBm

हम ऑप्टिकल रिसीवर के संभावित व्यास के एक निश्चित सेट को परिभाषित करते हैं (वास्तव में, लेंस) - हम स्वयं उपग्रहों के आकार पर प्रतिबंध को ध्यान में रखते हैं:

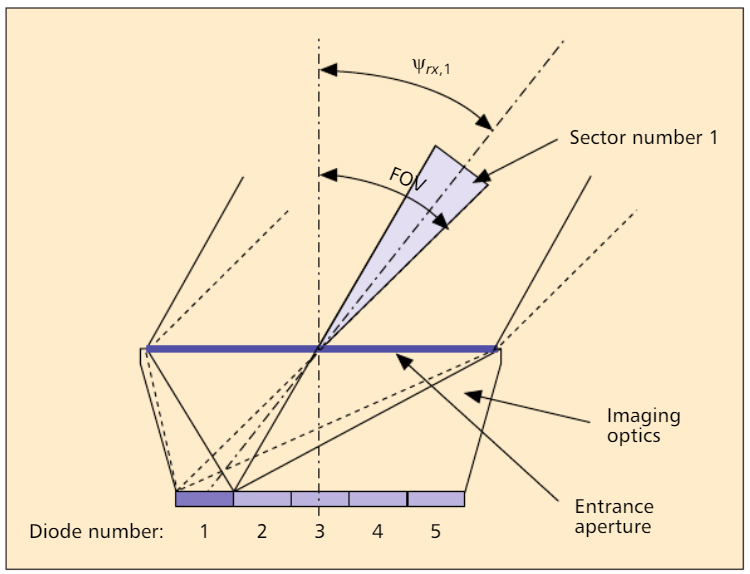
 a = [i for i in range(0,50,5)] a = np.array(a)*1e-3 #diameter of the receiver (in meters) a[0] = 1*1e-3 a_m = a*100 # for figures (in cm)

अंजीर। २। फोटोडेटेक्टर का योजनाबद्ध आरेख: सेक्टर नंबर 1 के लिए एक उदाहरण के रूप में दिखाया गया है, जिनमें से घटनाओं का कोण फोटोडायोड नंबर 1 [2] पर प्रदर्शित होता है।

और लेजर बीम (हमारे ट्रांसमीटर) के विचलन के कुछ संभावित कोण:

 div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3] div_ang = np.array(div_ang) #half of divergence angle

अंजीर। 3. लेजर बीम के विचलन के कोण का चित्रण ।

रिसीवर इनपुट पर प्राप्त शक्ति (प्राप्त शक्ति) की गणना सूत्र द्वारा की जा सकती है [2] :

$P_ {rx} = \ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ n "P_ {tx} \" क्वाड [W]$

जहाँ $A_ {rx} = \ frac {d_ {rx} ^ 2 \ pi} {4}$ स्वागत क्षेत्र है, $d_ {rx}$ - प्राप्त लेंस का व्यास, $आर$ - उपग्रहों के बीच की दूरी, $\ theta_ {div}$ आधा विचलन कोण है और $P_ {tx}$ - संचारित शक्ति।

 Prx_opt_dBm = np.zeros((len(div_ang), len(a))) Prx_opt = np.zeros((len(div_ang), len(a))) Pathloss_dBm = np.zeros((len(div_ang), len(a))) Pathloss = np.zeros((len(div_ang), len(a))) Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #received power Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3) #path loss Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)

ठीक है, कुछ पहले से ही है। लेकिन यह सब शारीरिक रूप से कितना वास्तविक है?

संवेदनशीलता की सीमाएँ

क्वांटम सीमा

फोटॉन ऊर्जा सूत्र को याद करें:

$E = hf \ quad \ left [m ^ 2 kg / s ^ 2 \ right]$

जहाँ $ज$ = 6.62607004e-34 $मी ^ 2 किलो / एस$ प्लैंक स्थिर है , और $च$ - वाहक आवृत्ति (हर्ट्ज)।

इसके बाद हमारे परामर्शों से एक छोटा सा अनुमान लगाया जाएगा। अगर किसी को सैद्धांतिक औचित्य या खंडन पता है - कृपया साझा करें!

आवश्यक ऊर्जा (कम से कम कुछ का पता लगाने के लिए रिसीवर पक्ष पर न्यूनतम जानकारी प्रति ऊर्जा):

$E_ {req, Q} = N_ {ph} hf \ quad \ left [m ^ 2 kg / s ^ 2 \ "$

जहाँ $N_ {ph}$ - 1 बिट जानकारी का पता लगाने के लिए फोटॉन की औसत संख्या।

एक ऑप्टिकल पल्स के लिए सैद्धांतिक ऊर्जा:

 E_theor = 10*h*freq_opt

ऑप्टिकल पल्स ( APD डायोड) के लिए अधिक यथार्थवादी ऊर्जा मान:

 E_real_APD = 1000*h*freq_opt

ऑप्टिकल पल्स ( पिन डायोड) के लिए अधिक यथार्थवादी ऊर्जा मूल्य:

 E_real_PIN = 10000*h*freq_opt

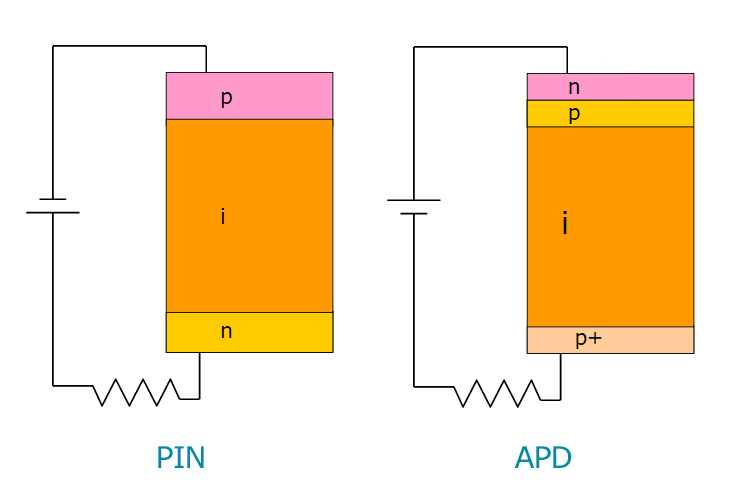
चित्र 4। विचाराधीन फोटोडायोड का सर्किट ।

आवश्यक (न्यूनतम) शक्ति प्राप्त (अधिकतम संवेदनशीलता):

$P_ {req, Q} = 10 \ log_ {10} \ left (\ frac {E_ {req, Q} B} {10 ^ {- 3}} \ right) = 10 \ log_ {10} \ left (\ _rac) {E_ {req, Q} R_b} {10 ^ {- 3}} \ right) \ quad [dBm]$

जहाँ $बी$ संचार चैनल की बैंडविड्थ है, और $R_b$ बिटरेट है।

 P_req_theor = 10*np.log10(E_theor*Bit_rate*1000) P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000) P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)

लेकिन यह सब नहीं है: मॉड्यूलेशन भी अपने सीमित योगदान देता है।

त्रुटि संभावना सीमा

एक शुरुआती बिंदु के रूप में हम मॉड्यूलेशन OOK (ऑन-ऑफ कीइंग) पर विचार करेंगे।

चित्र 5। OOK मॉडुलन के सिद्धांत का चित्रण ।

इसके लिए त्रुटियों ( BER ) की संभावना [2] होगी:

$P_b = \ frac {1} {2} ercf \ left (\ sqrt {\ frac {SNR} {2}} \ right) = \ frac {1} {2} ercf \ left (\ sqrt / \ frac {P_ {) req} ^ 2 \ gamma ^ 2} {2 \ sigma ^ 2}} \ right)$

जहाँ $SNR$ सिग्नल-टू-शोर अनुपात है, $\ सिग्मा ^ 2$ शोर विचरण (यानी शोर शक्ति), और है $\ _ गामा$ फोटोडियोड्स की संवेदनशीलता ( फोटोोडिओड रिस्पांसिबिलिटी ) है।

OOK के लिए BER (पिन डायोड):

$P_ {b, PIN} = \ frac {1} {2} ercf \ left (\ frac {\ Gamma P_ {req, PIN}} {\ sqrt {2 \ _ sigma_ {PIN} ^ 2} \ _)$

और इसलिए:

$P_ {req, PIN} = \ frac {erfcinv (2P_b) \ sqrt {2 \ _ sigma_ {PIN} ^ 2}} {\ gamma} \ quad [W]$

OOK (APD डायोड) के लिए BER:

$P_ {b, APD} = \ frac {1} {2} ercf \ left (\ frac {\ Gamma M P_ {req, APD}} {\ sqrt {2 \ _ sigma_ {APD} ^ 2}} \ right)$

और इसलिए:

$P_ {req, APD} = \ frac {erfcinv (2P_b) \ sqrt {2 \ _ sigma_ {APD} ^ 2}} {\ gamma M} \ quad [W]$

जहाँ $एम$ - यह कुछ संदर्भ लाभ है।

शोर शक्ति

जैसा कि आपने अनुमान लगाया होगा, शोर की गणना भी थोड़ा अलग तरीके से की जाएगी।

पिन डायोड के लिए शोर शक्ति

थर्मल शोर की गणना सूत्र द्वारा की जा सकती है [3, पी 11] :

$\ sigma_ {PIN} ^ 2 = \ left (\ frac {4kT} {R_f} + 2qI_ {BE} \ right) I_2R_b = N_0 + 2qI_ {BE} IRR_b \ quad [W]$

जहाँ $टी = 290 के$ । $k = 1.38064852e-23$ - बोल्ट्जमन स्थिरांक $R_f = \ frac {100} {2 \ pi C_d R_b}$ - प्रत्यक्ष प्रतिरोध $C_d$ - फोटोडायोड क्षमता, $क्ष$ एक इलेक्ट्रॉन का आवेश होता है, $I_ {BE} = \ frac {I_C} {\ beta}$ बेस-एमिटर करंट ( बेस-एमिटर या लीकेज या बायस करंट ), $I_2$ - थर्मल शोर के लिए पर्सिक इंटीग्रल का मूल्य (- मैंने हार मान ली, मुझे पर्याप्त अनुवाद नहीं मिला, कृपया बताएं) $R_b$ - बिट दर $N_0$ - शोर का वर्णक्रमीय घनत्व।

 Cd = 2*1e-12 #capacitance of the photodiode T = 290 #absolute temperature Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance k = 1.38064852*1e-23 #Bolzman constant I2 = 0.562 #depends on filter (Personick integral) for match filter q = 1.60217662*1e-19 #electron charge Ibe = (0.25*1e-3)/200 #RESULT thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate N_0 = 4*k*T/Rf #thermal noise density for PIN thermal_Noise_variance = N_0*Bit_rate*I2

APD डायोड के लिए शोर शक्ति

इस डायोड के लिए तैयार हो जाओ - कई लैटिन पत्र:

$\ sigma_ {APD} ^ 2 = \ frac {4kT} {R_f} I_2R_b + 2qI_dM_ {Si} ^ 2F_ {Si} I_2R_b = N0 + 2qI_2R_b (I_ BE) + M_ {Si} ^ 2F_ {{}} लगभग N_0 + 2qI_2I_dR_bM_ {Si} ^ 2F_ {Si} \ quadr []$

जहाँ $I_d$ - डार्क करंट (गहरा करंट), $M_ {Si}$ एक विशिष्ट लाभ (सिलिकॉन) है, $F_ {Si}$ - अतिरिक्त शोर कारक।

पैरामीटर्स निम्नलिखित से चमके हैं:

इस पत्र में, इनपुट फील्ड इफेक्ट ट्रांजिस्टर (इनपुट एफईटी शोर) और इनपुट फील्ड इफेक्ट ट्रांजिस्टर (इनपुट एफईटी लोड का शोर) के लोड के शोर को ध्यान में नहीं रखा जाता है। [3, पी 15] में इन शर्तों के बारे में और पढ़ें।

 Id = 0.05*10e-9 #dark current (500e-12) M_Si = 100 #typical gain F_Si = 7.9 #excess noise factor apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noise

मोडलिंग

शक्ति प्राप्त हुई

हम अपने सूत्रों में स्पष्ट किए गए सब कुछ को प्रतिस्थापित करते हैं:

 r = 0.53 #A/W photodiode responsivity Pb = 10e-9 #Bit error rate (BER) P_req_pin = 10*np.log10((special.erfcinv(2*Pb)* np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si) P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm fig = plt.figure(figsize=(10, 7), dpi=300) req_theor = np.ones((len(a_m),))*P_req_theor req_real_APD = np.ones((len(a_m),))*P_req_real_APD req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN PIN = np.ones((len(a_m),))*P_req_pin APD = np.ones((len(a_m),))*P_req_apd a_m = a_m.reshape((10,)) plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad') plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad') plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad') plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad') plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad') plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)') plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)') plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)') plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)') plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)') plt.gca().invert_yaxis() xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)') legend() grid() plt.show()

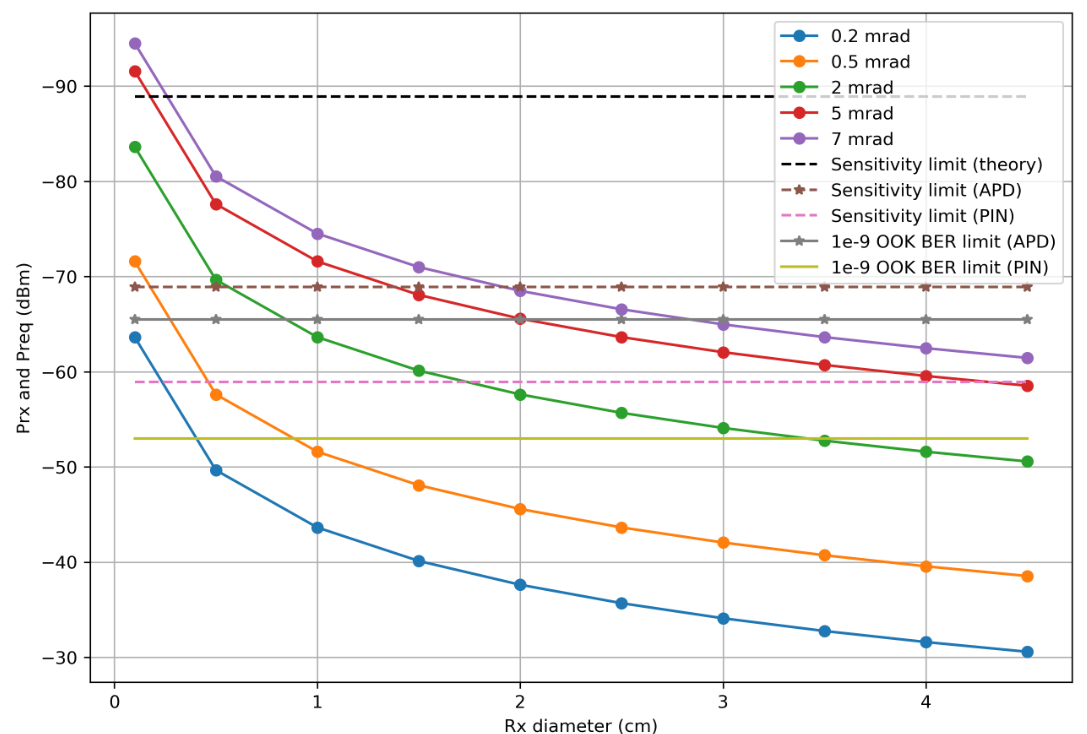
हमें समझाते हैं: आपको उन वक्रों के उन हिस्सों को देखने की जरूरत है जो संबंधित क्षैतिज रेखाओं के नीचे स्थित हैं।

संचारित शक्ति

और अब हम विपरीत समस्या को देखते हैं: हम प्राप्त पक्ष पर कुछ शक्ति को ठीक करते हैं और देखते हैं कि ट्रांसमिशन पक्ष पर किस प्रकार की शक्ति को लागू करने की आवश्यकता होगी:

$P_ {tx, dBm} = P_ {rx, dBm} + | L | + | L_ {जोड़ें} |$

जहाँ $L = 10 \ log_ {10} \ left [\ frac {A_ {rx}} {2 \ pi R ^ 2} \ left (1 - \ frac {ln2} {ln (cos \ theta_ {div)}} \ right ) सही$ पथ क्षीणन है , और $L_ {जोड़ें}$ - यह घाटे के लिए कुछ मार्जिन है।

 Prx_req_dB_APD = -65.5 Prx_req_dB_PIN = -52.9 margin = 5 Arx_m2 = np.zeros((len(a))) Ptx_variable_APD = np.zeros((len(div_ang), len(a))) Ptx_variable_PIN = np.zeros((len(div_ang), len(a))) #area rx Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #Ptx required Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin; Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin; fig = plt.figure(figsize=(10, 7), dpi=300) plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad') plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad') plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad') plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad') plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad') plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad') xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)') legend() grid() plt.show()

इलेक्ट्रोमैग्नेटिक इंटर-सैटेलाइट चैनल के मामले की तुलना हमारे पत्रिका लेख में पाई जा सकती है। यह उन कारणों का भी वर्णन करता है कि आखिरकार, हमने इस तरह के परिदृश्य से इनकार कर दिया, लेकिन मैं यहां इस बारे में अधिक कहूंगा।

नुकसान

और यहाँ हम संदर्भ पुस्तकों और गणितीय सूत्रों द्वारा पस्त हैं, लेकिन फिर भी प्राप्त परिणामों से प्रेरित हैं (हाँ क्या है - सुंदर रेखांकन के बहुत तथ्य से!), हम रक्षा से पहले एक अंतिम बैठक कर रहे हैं। और हम महत्वपूर्ण विवरणों के एक नए दौर के साथ सामना कर रहे हैं ...

समझौता नंबर 2 : ठीक है, ठीक है, यह स्पष्ट है कि जीत हैं। उन्होंने आश्वस्त किया कि पहले से ही किसी प्रकार का हार्डवेयर आधार है। लक्ष्यीकरण के बारे में क्या? आपने शायद PAT सिस्टम ( P ointing, A cquisition, and T रैकिंग) के बारे में सुना है।

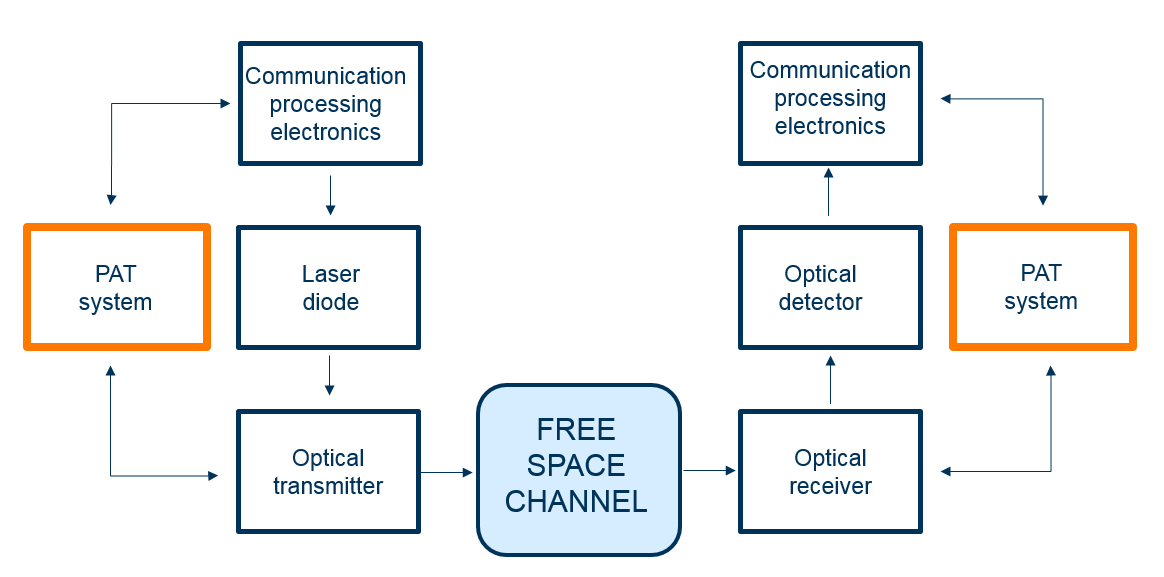
अंजीर। 6. एक वायरलेस ऑप्टिकल ट्रांसीवर सिस्टम का एक सरल आरेख।

समझौता नंबर 2 : हां, बड़े उपग्रहों [4] के लिए ऑप्टिकल चैनल के उदाहरण हैं, हालांकि, इस मामले में आप एक बड़ा रिसीवर व्यास, एक बड़ा लेजर विचलन कोण और एक उच्च संचरण शक्ति का खर्च उठा सकते हैं। इसके अलावा, क्यूबसैट, मुझे लगता है कि हिलते समय बहुत कंपन होता है । अपेक्षाकृत कम आवृत्तियों पर एक रेडियो चैनल के लिए, यह आवश्यक नहीं हो सकता है, हालांकि, प्रकाशिकी के लिए - आप स्वयं समझते हैं। क्या इस समय ऐसा सटीक स्थिरीकरण और पैट सिस्टम है?

और हम बहुत विचारशील थे ...

समझौता नंबर 2 : यही है, मेरे हिस्से के लिए, मैं आपको एक सकारात्मक मूल्यांकन देता हूं। हालाँकि, मेरी आपको सलाह: स्वर्ग से पृथ्वी पर उतरो ...

और हम थक गए, समाप्त हो गए: हमने उपग्रह प्रकाशिकी के साथ परियोजना को जारी नहीं रखने का फैसला किया। इसके अलावा, यहां तक कि हमारी लगातार बैठकों के दौरान भी हमने कुछ बर्नआउट जमा किया है ...

हालांकि, नहीं, नहीं, और यहां तक कि छात्र आशा का एक नोट भी दिल में फिसल जाएगा कि शिक्षक अपने संदेह में गलत था। नहीं, नहीं, और मैं आधुनिक तकनीक की उपलब्धियों में बहुत अवधारणा खोजना चाहता हूं। और टकटकी ऊपर की ओर उठती है ...

साहित्य

Janson SW, Welle RP नासा ऑप्टिकल संचार और सेंसर प्रदर्शन कार्यक्रम: लघु उपग्रहों पर एक अद्यतन // 28 वाँ वार्षिक AIAA / USU सम्मेलन। - 2014 ।-- एस 4-7।
भेड़िया, एम।, और क्रेओ, डी। (2003)। शॉर्ट रेंज वायरलेस इंफ्रारेड ट्रांसमिशन: आरएफ की तुलना में लिंक बोगेट । आईईईई वायरलेस संचार, 10 (2), 8-14।
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B. एट अल। 5.6 Gbps ऑप्टिकल चौराहा संचार लिंक // फ्री-स्पेस लेजर कम्युनिकेशन टेक्नोलॉजीज XXI। - इंटरनेशनल सोसायटी फॉर ऑप्टिक्स एंड फोटोनिक्स, 2009.- टी। 7199. - एस 719906।

लेकिन क्या हम ऑप्टिकल संचार के लिए तरंग नहीं करते हैं? लेज़र, स्पेस, क्यूबसैट