नमस्कार प्रिय पाठक! मैं आपके लिए क्रिस हेकर के "फिजिक्स, द नेक्स्ट फ्रंटियर" लेख के अंग्रेजी से अनुवाद प्रस्तुत करता हूं।

मैं, एक नौसिखिया जावा डेवलपर, इस तथ्य से सामना किया गया था कि भौतिक-इन-गेम इंजन बनाने की सामग्री केवल अंग्रेजी में प्रस्तुत की जाती है, इसलिए इस लेख का अनुवाद किया गया था। श्रृंखला में तीन और लेख होंगे, मैं उन्हें जल्द से जल्द पोस्ट करूंगा। अच्छा पढ़ लो!

भौतिकी में नए मोर्चे

इसमें कोई शक नहीं है कि हर साल इन-गेम ग्राफिक्स अधिक यथार्थवादी होते जा रहे हैं। पहले से ही आज, हर कोई बनावट के नक्शे के साथ (या कम से कम स्क्रीनशॉट दिखाता है) 3 डी दुनिया बनाता है, और जब पर्याप्त मेहनती लोग एक परियोजना पर काम करने के लिए एक साथ हो जाते हैं, तो प्रत्येक डेवलपर प्रति सेकंड अरबों यथार्थवादी बनावट और छाया के बहुभुज आकर्षित कर सकता है। तकनीकी शब्दों में, उच्च स्तर पर खेल बनाने के लिए क्या किया जाना चाहिए? क्या “डेव टू यूज़ 3 डी हार्डवेयर इन 21 डेज़” पुस्तक की एक प्रति के साथ हर डेवलपर वास्तव में प्रभावशाली खेल बनाने में सक्षम होगा?

बिलकुल नहीं। Upscale डेवलपर्स कई अलग-अलग तकनीकों (जैसे GUI जटिलता, कृत्रिम बुद्धिमत्ता और नेटवर्किंग) में बार बढ़ाते रहेंगे। बेशक, यह सब बहुत महत्वपूर्ण है, हम विवरणों को निर्दिष्ट किए बिना उनमें से किसी पर भी गंभीरता से चर्चा नहीं कर सकते। फिर भी, हर चीज पर एक तकनीक लागू होती है, जो मेरी राय में, निकट भविष्य में एक निर्णायक कारक बन जाएगी: भौतिकी।

निम्नलिखित उदाहरण पर विचार करें: क्या आपको ड्यूक नुकेम 3 डी के शुरुआती स्तरों में से एक में इन विशाल कताई गियर याद हैं?



चित्रा 1. खेल "ड्यूक Nukem 3 डी" से स्क्रीनशॉट

ज़रा सोचिए कि उनके घूमने का वर्णन चक्रीय एनीमेशन द्वारा नहीं, बल्कि वास्तविक भौतिक इंजन द्वारा किया जाएगा। अचानक, गियर गेम डेकोरेशन से कुछ अधिक हो जाते हैं, जैसे उनमें से एक दिए गए कोण से भटक जाता है, और इंडियाना जोन्स फिल्मों की तरह आपके पीछे गलियारे को रोल करता है। या कल्पना करें कि रॉकेट लॉन्चर से एक गियर की शूटिंग के बाद, यह गलियारे को नीचे गिरा देगा और आपके दोस्त को कुचल देगा, जिसने आपको मारने के लिए पीछे छोड़ दिया है! भौतिक इंजन ऐसी स्थितियों को वास्तविक बनाते हैं।

भौतिक अनुकरण वह है जो खेल की दुनिया को संपूर्ण बनाता है: इसके लिए धन्यवाद, "यहां" यहां स्थित है, अगर आप समझते हैं कि मेरा क्या मतलब है। दुनिया में ग्राफिक्स के किसी भी जादू खिलाड़ी को खेल प्रक्रिया में डुबकी लगाने की अनुमति नहीं देगा यदि वह किसी अन्य खिलाड़ी में, या स्तर की दीवारों में, या यदि द्रव्यमान और द्रव्यमान के क्षण को महसूस नहीं किया जाएगा। डिज्नी के एनिमेटरों ने जनता की इस भावना को पाया कि क्या अच्छा एनीमेशन खराब एनीमेशन से अलग करता है। फ्रैंक थॉमस और ओली जॉनसन के अनुसार, महाकाव्य पुस्तक डिज़नी एनिमेशन: द इल्यूज़न ऑफ़ लाइफ, डिज़नी एनिमेटर्स, यहां तक ​​कि स्टूडियो में एक पोस्टर को लटकाते हुए, हमेशा खुद से सवाल पूछना चाहिए: "क्या उनके ड्राइंग में वजन, गहराई और संतुलन है?" ? "

लेकिन आज लगभग हर खेल में एक भौतिकी इंजन है, है ना? निस्संदेह, यह वही है जो आपकी कार को खेल की दुनिया के किनारे पर गिरने से बचाता है, इसकी बदौलत आपके पात्र अंतरिक्ष में तब नहीं उड़ते हैं जब वे कूदते हैं, और यह आपकी नाव को उस तरफ फेंक देता है जब कोई रॉकेट पास में फट जाता है। हालांकि, आधुनिक खेलों में अधिकांश भौतिक इंजन बहुत कमजोर हैं। वे केवल दुनिया के किनारे पर गिरने से कार को रखने के कार्य के साथ सामना करते हैं, लेकिन उनकी क्षमताएं खेल को एक नए स्तर पर ले जाने के लिए पर्याप्त नहीं हैं - जहां एक मलबे वाली कार का मलबा ट्रैक पर सही तरीके से विस्फोट हो सकता है, जिससे दीवारों और अन्य कारों का एक रोल हो सकता है।

अन्य शारीरिक प्रभावों की जिन्हें अक्सर अनदेखा किया जाता है, उनमें शामिल हैं: एक स्पर्शरेखा हड़ताल के परिणामस्वरूप सरल मोड़ प्रभाव से, खेल में पात्रों को अपने संतुलन को बनाए रखना और सांख्यिकीय रूप से एनिमेटेड लोगों के विपरीत चलना। मेरा मानना ​​है कि कई डेवलपर्स इन संभावनाओं को अनदेखा करते हैं क्योंकि वे गणित को नहीं समझते हैं जो भौतिकी का वर्णन करते हैं, या इसे सीखने के लिए बनावट के नक्शे बनाने में बहुत व्यस्त थे। 3 डी के साथ काम करने के लिए हार्डवेयर का आक्रमण बाद की देखभाल करेगा, और मैं लेखों की एक नई श्रृंखला शुरू कर रहा हूं। पहला लेख औपचारिकताओं का ध्यान रखेगा। हमारे चक्र के अंत तक, आप स्वयं एक भौतिक इंजन बना सकते हैं, जो खिलाड़ियों को गेमप्ले में पूरी तरह से डूबने का मौका देगा, अविश्वसनीय यथार्थवाद, या एक मनोरंजक लेकिन लगातार अतियथार्थवाद के कारण।

चेतावनी! भौतिकी = गणित, एक दिलचस्प परियोजना को पूरा करने के लिए, आपको दोनों का उपयोग करना होगा। इससे पहले कि यह आपको डराए, मुझे ध्यान दें कि भौतिकी का वर्णन करने वाला गणित केवल सुरुचिपूर्ण और सुंदर नहीं है, इसमें एक लागू चरित्र भी है। यही है, यह गणित के लिए अमूर्त गणित नहीं है। हमारे द्वारा उपयोग किए जाने वाले प्रत्येक समीकरण का वास्तविक भौतिक अर्थ होता है। हम एक भौतिक मॉडल से समीकरण बनाते हैं, और बदले में समीकरण हमें बताते हैं कि मॉडल समय में कैसे व्यवहार करता है।

भव्य उद्यम

भौतिकी एक विस्तृत वैज्ञानिक क्षेत्र है। लेकिन हम वास्तव में "डायनेमिक्स", या उससे अधिक सटीक रूप से, "ठोस पदार्थों की गतिशीलता" नामक इसके छोटे खंड में रुचि रखते हैं। गतिशीलता को संबंधित खंड - कीनेमेटीक्स (समय में आंदोलन के सिद्धांत) के रूप में परिभाषित किया जा सकता है। काइनेमेटिक्स इस बात पर ध्यान केंद्रित नहीं करता है कि आंदोलन के कारण क्या हैं या शरीर कैसे समाप्त हो गए हैं, यह केवल आंदोलन का वर्णन करता है। डायनेमिक्स, इसके विपरीत, सेनाओं और जनता का वर्णन करता है जो समय के साथ बदलने के लिए किनेमैटिक्स से मूल्यों में योगदान करते हैं। यदि उड़ान का समय 10 सेकंड है और बेसबॉल की गति 50 किलोमीटर / घंटा है, और प्रक्षेपवक्र - कितनी सीधी रेखा है - एक सीधी रेखा है - तो बेसबॉल बॉल कितनी दूर तक उड़ जाएगी? बेसबॉल बॉल पृथ्वी के गुरुत्वाकर्षण क्षेत्र में कितनी दूर तक उड़ जाएगी, अगर मैं इसे बल्ले से मारता हूं - यह एक गतिशील समस्या है।

डायनामिक्स का वह भाग जो ठोस का वर्णन करता है, वह उन बाधाओं से संबंधित होता है जिन्हें हम सिम्युलेटेड ऑब्जेक्ट के लिए जोड़ते हैं। सिमुलेशन के दौरान एक ठोस शरीर का आकार नहीं बदलता है - शरीर जेली की तरह लकड़ी या धातु से अधिक संभावना है। हम एक व्यक्ति की, उदाहरण के लिए, एक ठोस शरीर से आकृति के प्रत्येक भाग का निर्माण करके और उनके बीच लिगामेंट्स बनाकर, व्यक्त किए गए आंकड़े बना सकते हैं, लेकिन हम तनाव या इसी तरह के प्रभाव के तहत झुकने वाली हड्डियों पर भरोसा नहीं करते हैं। यह हमें निकायों के दिलचस्प गतिशील व्यवहार की गुणवत्ता को खोने के बिना हमारे समीकरणों को सरल बनाने की अनुमति देगा।

भले ही हम गतिशीलता के इतने छोटे हिस्से पर विचार करेंगे, लेकिन कठोर शरीर की गतिशीलता को सार की व्याख्या करने के लिए लेखों की एक श्रृंखला की आवश्यकता होगी। हम बलों की कार्रवाई के तहत एक विमान के कठोर शरीर की गति का वर्णन करने के लिए कंप्यूटर प्रोग्रामिंग की मूल बातें का अध्ययन करके अपनी यात्रा शुरू करते हैं। मैं लगातार "कंप्यूटर प्रोग्रामिंग" दोहराता हूं, क्योंकि हम जो किनेमेटिक्स और गतिकी के लिए लिखते हैं, उसके समीकरणों के अलावा, हम फ्लोटिंग-पॉइंट गणनाओं का उपयोग करके इन समीकरणों को हल करना सीखेंगे, जो हर प्रोग्रामर के लिए जानना महत्वपूर्ण है। मैं कहता हूं कि "सपाट ठोस" क्योंकि हम केवल अगले लेख में और उससे आगे के दो आयामी दुनिया से निपटेंगे। सिद्धांत - और वास्तव में केवल समीकरणों से अधिक - को तीन-आयामी दुनिया में भी स्थानांतरित किया जा सकता है, लेकिन निश्चित रूप से दो-आयामी दुनिया में सब कुछ बहुत सरल है, इसलिए हम तब तक अध्ययन करेंगे जब तक हम तीन-आयामी अंतरिक्ष में प्रवेश करने का आत्मविश्वास महसूस नहीं करते। भविष्य के लेखों में, हम रोटेशन के प्रभाव, निकायों के संपर्कों के प्रसंस्करण, और निश्चित रूप से, यह सब तीन-आयामी दुनिया में कैसे करना है, इसका वर्णन करना सीखेंगे। खैर, पर्याप्त शब्द! चलो शुरू हो जाओ!

एक व्युत्पन्न के साथ काम करें

यह आपके लिए एक आश्चर्य के रूप में आ सकता है, लेकिन आप वास्तव में इसे धक्का देकर किसी वस्तु को नहीं हिला सकते। मुझे पता है, आपको लगता है कि इस तरह की बकवास लिखने के लिए इस पत्रिका को कूड़ेदान में फेंककर मेरे विपरीत साबित करना गलत है, लेकिन यह सच है! केवल एक पत्रिका पर दबाव डालना कभी भी अंतरिक्ष में अपनी स्थिति को प्रभावित नहीं करेगा। वास्तव में, दबाव भी इसकी गति को सीधे प्रभावित नहीं करता है। वास्तव में जो दबाव प्रभावित करता है वह पत्रिका का त्वरण है, और वास्तव में यह विज्ञान के इतिहास में सबसे महत्वपूर्ण निष्कर्षों में से एक है।

कुछ रोचक करने के लिए इस तथ्य का उपयोग करने के लिए, हमें पहले गति और त्वरण के साथ शरीर की स्थिति के संबंध के बारे में बात करनी होगी। वास्तव में, ये सभी मूल्य बहुत निकट से संबंधित हैं (जैसा कि आप शायद जानते हैं): गति समय के साथ शरीर के निर्देशांक में परिवर्तन का एक संकेतक है, और त्वरण गति में परिवर्तन का एक संकेतक है। समय के साथ इन मात्राओं में परिवर्तन का अध्ययन करने के लिए प्राथमिक उपकरण अंतर कैलकुलस है। यदि आप इसे समझते हैं, तो हम आगे बढ़ते हैं। मुझे लगता है कि आप गणित में अच्छे हैं। हम केवल साधारण स्केलर और वेक्टर गणना (डेरिवेटिव और इंटीग्रल) का उपयोग करेंगे, लेकिन अगर आप समग्र रूप से गणित से परिचित हैं तो यह अतिश्योक्तिपूर्ण नहीं होगा। संदर्भ के लिए: कंप्यूटिंग पर मेरी पसंदीदा पुस्तक थॉमस एंड फिन द्वारा एनालिटिक ज्यामिति के साथ कैलकुलस है।

समन्वय, गति और त्वरण किनेमैटिक्स हैं जिन्हें इस लेख में चर्चा की जाएगी। दो-आयामी दुनिया में एक ठोस का स्थान, स्पष्ट रूप से, निर्देशांक X और Y की एक जोड़ी है, जो शरीर के कुछ बिंदुओं के स्थान के निर्देशांक को दर्शाता है। निर्देशांक वेक्टर के लिए व्युत्पन्न वेग वेक्टर है, और यह हमें दिखाता है कि बिंदु किस दिशा में आगे बढ़ रहा है (और शरीर, अगर हम रोटेशन को अनदेखा करते हैं, जो अभी हो रहा है) और कितनी तेजी से आगे बढ़ रहा है। सदिश पथरी सदिश के प्रत्येक तत्व का मात्रक कलन है, अतः X निर्देशांक का व्युत्पन्न X के संबंध में शरीर का वेग है, और इसी तरह। हम निम्नलिखित संकेतन का परिचय देते हैं। बता दें कि शरीर का समन्वय सदिश r है, और वेग सदिश v या सदिश r एक अभाज्य है। हमें समीकरण मिलता है:

$$

$${{dx} \ over {dt}} = v = r '$$

समीकरण 1

यदि हम समय के साथ वेग वेक्टर को अलग करते हैं, तो यह दिखाएगा कि समय के साथ समन्वय वेक्टर कैसे बदलता है। त्वरण सादृश्य द्वारा निर्धारित किया जाता है। यह गति की पहली व्युत्पन्न या समन्वय वेक्टर की दूसरी व्युत्पन्न है:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '= {{dr'} \ over {dt}} = = {{DV} \ over {dt}} = v '= a$$

समीकरण २

त्वरण का अभिन्न अंग हमें गति देगा, और दो बार त्वरण को एकीकृत करने से हमें समन्वय प्राप्त होगा।

किनेमैटिक्स में इन संबंधों से पता चलता है कि हम किसी वस्तु के त्वरण को पा सकते हैं, हम गति और समन्वय प्राप्त करने के लिए इसे समय के साथ एकीकृत कर सकते हैं। जैसा कि हम बाद में देखेंगे, हम अपने सिमुलेशन कोड में कई बार एकीकरण की ओर मुड़ेंगे और प्रत्येक फ्रेम के लिए हमारे ठोस के लिए एक नई स्थिति की गणना करेंगे। हुर्रे एनीमेशन!

यहां एक आयामी दुनिया के लिए एक सरल उदाहरण है जिसे हम विश्लेषणात्मक रूप से एकीकृत कर सकते हैं। आइए सहमत हैं कि हम वर्तमान फ्रेम को खींचने के लिए अंतिम फ्रेम के अंत से वर्तमान फ्रेम के समय तक समन्वय को खोजना चाहते हैं। अगला, हम कहते हैं कि हमारे ठोस का त्वरण 5 मनमानी इकाइयों / दूसरे ^ 2 के बराबर था। हम अंतिम फ्रेम के अंत से बीते हुए समय का उपयोग एक चर टी (एकीकरण तत्व डीटी में) के रूप में करेंगे।

$$

$$v (t) = ∫adt = d5dt = 5t + C$$

समीकरण ३

उपरोक्त समीकरणों से पता चलता है कि गति अंतिम फ्रेम से गुजरे समय का एक कार्य है। हमने एकीकरण को स्थिर पाया, सी, जो एकीकरण अवधि की शुरुआत में प्रारंभिक वेग के बराबर है (टी = 0 पर)।

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

समीकरण ४

$$

$$v (t) = 5t + v_0 {}$$

अब हम समन्वय को खोजने के लिए अपने वेग समीकरण को फिर से एकीकृत करते हैं (फिर से, एकीकरण निरंतर के बारे में मत भूलना):

$$

$$r (t) = (v (t) dt = t5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

समीकरण ५

समीकरण 5 के आधार पर, हम वर्तमान स्थिति को किसी दिए गए त्वरण द्वारा ही पा सकते हैं यदि हम प्रारंभिक समन्वय और गति (जिसे हम अंतिम फ्रेम से लेंगे) और बीता हुआ समय जानते हैं। इनपुट चर समय है, और फ़ंक्शन का मान वर्तमान स्थिति है। हम अंतिम गति की गणना करने के लिए समीकरण 4 में समय का भी संकेत देंगे ताकि हम इसे अगले फ्रेम के लिए प्रारंभिक स्थिति के रूप में उपयोग कर सकें।

बल आपके साथ हो सकता है

अब हमें यह अहसास है कि एनिमेशन पाने के लिए हमें गतिज समीकरणों को एकीकृत करने के लिए त्वरण को सही ढंग से सेट करने की आवश्यकता है। मंच पर वक्ताओं का उत्पादन। याद रखें, जैसा कि मैंने कहा, किसी चीज़ पर दबाव डालने से, आप सीधे शरीर के त्वरण को प्रभावित करते हैं? खैर, "दबाव को कम करना" वाक्यांश "बल लागू करें" के लिए एक व्यंजना है - गतिशीलता में दो प्रमुख चर में से एक - और अब हम यह जानने के लिए न्यूटन की ओर मुड़ सकते हैं कि बल त्वरण को कैसे प्रभावित करते हैं। न्यूटन का दूसरा नियम F को द्रव्यमान के व्युत्पन्न के साथ जोड़ता है - गतिकी का दूसरा परिमाण - गुणा वेग। द्रव्यमान और गति के उत्पाद को "शरीर की गति" कहा जाता है, जिसे p द्वारा दर्शाया गया है:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

समीकरण ६

द्रव्यमान उस गति के लिए एक निरंतरता है जो हम अभी के साथ काम कर रहे हैं, यह समीकरण 6 में व्युत्पन्न से निम्नानुसार है, और हमें प्रसिद्ध समीकरण F = ma मिला है (हालांकि मुझे यकीन है कि न्यूटन ने शुरुआत में गति के व्युत्पन्न के माध्यम से बल निर्धारित किया था)।

यदि हम केवल भौतिक बिंदुओं के साथ काम कर रहे थे, तो समीकरण 6 की आवश्यकता है जो हमें गतिशीलता में चाहिए। किसी दिए गए भौतिक बिंदु के एक बल के लिए, बल द्वारा द्रव्यमान को विभाजित करके त्वरण पाया जाता है। यह हमें त्वरण देता है, जो ऊपर दिए गए उदाहरण से गति के समीकरण को हल करने में मदद करेगा। फिर भी, हम एक निश्चित क्षेत्र (मात्रा, जब यह तीन आयामी दुनिया की बात आती है) पर वितरित द्रव्यमान के साथ ठोस काम कर रहे हैं, इसलिए हमें अभी भी काम करने की आवश्यकता है।

सबसे पहले, ठोस को बिंदु द्रव्यमान के समूह के रूप में मानें। हम एक ठोस के लिए कुल गति, पीटी को परिभाषित करेंगे, शरीर बनाने वाले सभी बिंदुओं की गति के योग के रूप में (मैं ऊपरी अनुक्रमण का उपयोग करता हूं, क्योंकि मैं अधिक स्पष्ट रूप से दिखाना चाहता हूं कि इन बिंदुओं का क्या मात्रात्मक मूल्य है):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

समीकरण 7

हम द्रव्यमान के केंद्र (CM) की अवधारणा को पेश करके एक कठोर शरीर की गतिशीलता के विश्लेषण को सरल बना सकते हैं। द्रव्यमान के केंद्र के लिए निर्देशित एक वेक्टर वैक्टर का एक रैखिक योग है जो पूरे शरीर के द्रव्यमान द्वारा विभाजित ठोस शरीर के द्रव्यमान के सभी बिंदुओं से निर्देशित होता है:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ over {M}}$$

समीकरण 8

द्रव्यमान के केंद्र की परिभाषा का उपयोग करते हुए, हम समीकरण 7 के दोनों पक्षों को M से गुणा करके, उन्हें भिन्न करते हुए समीकरण 7 को सरल बना सकते हैं, और फिर समीकरण 7 में परिणाम को प्रतिस्थापित कर सकते हैं:

$$

$${{d (Mr ^ {CM})} \ ओवर {dt}} = {\ _ sum_ {i} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ _ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

समीकरण ९

समीकरण 9 के दाईं ओर समीकरण 7 में परिभाषित कुल गति है। अब आइए समीकरण के बाईं ओर देखें: यह पूरे शरीर के द्रव्यमान के द्रव्यमान के केंद्र में गति है। दाईं ओर बाईं ओर ले जाएं और प्राप्त करें:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

समीकरण 10

यह समीकरण 10 से इस प्रकार है कि रेखीय गति द्रव्यमान के केंद्र से निर्देशित वेग के कुल द्रव्यमान समय के बराबर होती है, इसलिए यदि हम शरीर के द्रव्यमान और द्रव्यमान के केंद्र के वेग वेक्टर की दिशा जानते हैं तो गति ज्ञात करने के लिए समीकरण 7 में योग करने की आवश्यकता नहीं है। इसके अलावा, गणना के सभी अंतिम परिणाम पूरे शरीर के लिए अभिन्न अंग हैं, लेकिन द्रव्यमान का केंद्र मौजूद है और समीकरण 10 से कुल गति के निर्धारण को बहुत सरल करता है, इसलिए हम चिंता नहीं कर सकते हैं - रैखिक गति को खोजने के लिए हम शरीर को दिए गए गति और द्रव्यमान के साथ एक भौतिक बिंदु के रूप में विचार कर सकते हैं।

सादृश्य द्वारा, कुल बल कुल गति का व्युत्पन्न है, इसलिए द्रव्यमान के केंद्र की अवधारणा का उपयोग बल के समीकरण को सरल बनाने के लिए किया जा सकता है:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

समीकरण 11

संक्षेप में, समीकरण 11 से यह निकलता है कि हम एक ठोस के साथ बातचीत करने वाली सभी ताकतों पर विचार कर सकते हैं, जैसे कि उनके योग वेक्टर का द्रव्यमान के केंद्र पर प्रभाव पड़ता है, जिसमें पूरे शरीर का द्रव्यमान होता है। हम द्रव्यमान के केंद्र के त्वरण को खोजने के लिए एम द्वारा बल (पढ़ें गुरुत्वाकर्षण) को विभाजित करते हैं, और फिर शरीर की गति और समन्वय प्राप्त करने के लिए समय में त्वरण को एकीकृत करते हैं। क्योंकि हम अगले लेख तक रोटेशन के प्रभावों की उपेक्षा करते हैं; हमारे पास पहले से ही सभी समीकरण हैं जिन्हें हमें एक कठोर शरीर की गतिशीलता का वर्णन करने की आवश्यकता है। ध्यान दें कि समीकरण 11 में इस बात की जानकारी नहीं है कि शरीर पर लागू बलों को कहाँ निर्देशित किया गया है। जब हम रैखिक गति और द्रव्यमान के केंद्र से निपटते हैं, तो यह पॉप हो जाएगा, और हम द्रव्यमान के केंद्र को त्वरण खोजने के लिए CM पर बल लगाते हैं। जब हम अगले लेख में इन ताकतों के प्रभाव में शरीर के रोटेशन की गणना करते हैं, तो हम देखेंगे कि बल के आवेदन का समन्वय कैसे किया जाता है।

ओड टू जॉय

इस स्तर पर, हम विश्लेषणात्मक एकीकरण के एक और उदाहरण पर विचार कर सकते हैं, समीकरण 11 के उपयोग से समीकरण के बजाय मनमाने ढंग से चुने गए मूल्य के केंद्र के त्वरण को खोजने के लिए = 5. फिर भी, हम एक गंभीर समस्या का सामना करते हैं, क्योंकि विश्लेषणात्मक एकीकरण में आमतौर पर एक लागू मूल्य नहीं होता है, क्योंकि यह बहुत जटिल है, इसलिए हम साधारण अंतर समीकरणों (ODE) के तथाकथित संख्यात्मक एकीकरण पर ध्यान केंद्रित करेंगे। वाह, अब यह असली गणित जैसा लगता है! एक बार जब आप इसे सीख लेते हैं, तो बार को बढ़ाने का समय होगा। सौभाग्य से, ODEs का संख्यात्मक एकीकरण उतना मुश्किल नहीं है जितना पहली नज़र में लग सकता है! इसका अर्थ समझने के लिए, हम शब्दों से कर्मों की ओर बढ़ते हैं!

तो, एक विभेदक समीकरण एक समीकरण है जिसमें फ़ंक्शन, स्वतंत्र चर और मापदंडों के अलावा निर्भर मात्रा के डेरिवेटिव होते हैं। यह क्रिया है, लेकिन यहां एक आयामी दुनिया में समय-भिन्न बल के लिए एक उदाहरण है: एफ = 2 टी, एफ एक निर्भर मात्रा है, और टी स्वतंत्र है। F का मान केवल F से निर्धारित होता है। बल का समीकरण केवल हमारे शरीर की गति पर निर्भर करता है।विमान की बढ़ती गति के साथ वायु प्रतिरोध की शक्ति बढ़ जाती है। आइए हम एक आयामी दुनिया में उदाहरण पर लौटते हैं, क्या होगा यदि F = -v का अर्थ है कि घर्षण बल गति के अनुपात में हमारे शरीर को धीमा कर देता है? हमारे पास एक समस्या है, क्योंकि हम समीकरण को निम्नानुसार हल करते हैं: F = ma = -v और, m से विभाजित करते हुए, हम प्राप्त करते हैं (याद रखें कि त्वरण गति का व्युत्पन्न है):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

समीकरण 12

इस अंतर समीकरण, (वेग समीकरण में समीकरण 12 में वेग व्युत्पन्न होता है) को सामान्य अंतर समीकरण कहा जाता है, क्योंकि इसमें केवल निर्भर मात्रा के सामान्य डेरिवेटिव होते हैं (आंशिक डेरिवेटिव के विपरीत, जो आंशिक अंतर समीकरण [पीडीएस] बनाते हैं, जिसके बारे में हम नहीं हैं) हम बात करेंगे)।

अब हमारे वाक्यांश के अगले भाग पर चलते हैं: एकीकरण। हमने इस समीकरण की स्थितियों में v को खोजने के लिए पहले DV / dt को कैसे एकीकृत किया?

यह अविश्वसनीय प्रतीत होगा, लेकिन भौतिकी में लगभग हर समीकरण का अंतर है, इसलिए ODE का अच्छी तरह से अध्ययन किया गया है। विभेदक समीकरणों को अक्सर भौतिकी में पाया जा सकता है, क्योंकि अक्सर एक मात्रात्मक मात्रा के परिवर्तन की दर स्वयं मात्रा पर निर्भर करती है। उदाहरण के लिए, हमने पहले ही नोट किया है कि ब्रेकिंग (गति में परिवर्तन की तीव्रता), वायु प्रतिरोध की गति सहित, गति पर निर्भर करता है। भौतिकी से अन्य उदाहरण: शीतलन (गर्मी के नुकसान की दर वर्तमान तापमान पर निर्भर करती है) और रेडियोधर्मी क्षय (क्षय दर इस बात पर निर्भर करती है कि रेडियोधर्मी पदार्थ कितना मौजूद है)।

हमारे वाक्यांश में अंतिम शब्द - संख्यात्मक - हमारा उद्धार है। मैं यह कहता हूं क्योंकि अंतर समीकरणों के विश्लेषणात्मक एकीकरण का सिद्धांत, यहां तक ​​कि सबसे सरल, विशाल और भ्रमित करने वाला है। हालाँकि, विडंबना यह है कि कंप्यूटर संख्यात्मक तरीकों का उपयोग करके ODEs का एकीकरण वास्तव में समझना अपेक्षाकृत आसान है। अगला, मैं यूलर विधि के आधार पर एक सरल संख्यात्मक एकीकरण का वर्णन करूंगा, और अगले लेख में इसे परिष्कृत करूंगा।

लगभग सभी संख्यात्मक इंटीग्रेटर्स, लेकिन यूलर विधि के रूप में कोई अन्य स्पष्ट नहीं है, बस झुकाव के पहले व्युत्पन्न के माध्यम से कंप्यूटिंग की पुरानी परिभाषा पर आधारित है: डाई / x x के आधार पर y की ढलान निर्धारित करता है। उदाहरण के लिए, यदि हमारे पास रैखिक समीकरण y = 5x है, तो डाई / dx = 5 का अर्थ है कि ढलान किसी भी x के लिए 5 के बराबर एक स्थिर है, और, जैसा कि आप मान सकते हैं, यह एक सीधी रेखा है। थोड़ा और अधिक कठिन उदाहरण parabola y = x2 है। इस मामले में, डाई / dx = 2x, और यह प्रत्येक x समन्वय के लिए नए तिरछा को निर्धारित करने के लिए एक फ़ंक्शन है। मैंने चित्र 2 में y = x2 को चित्रित किया: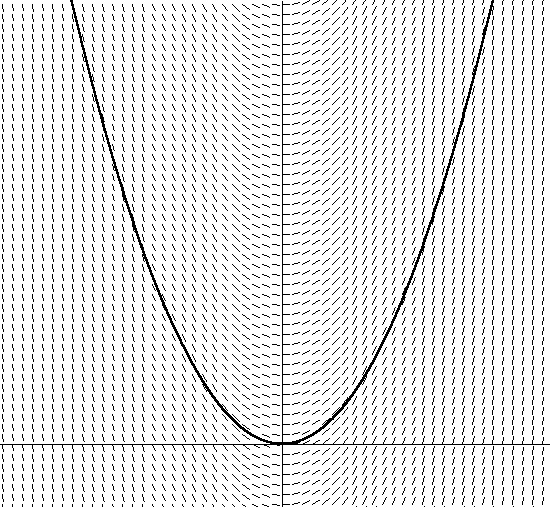



चित्र 2. y = x2

इसके अतिरिक्त, मैंने सभी x के लिए समीकरण डाई / dx = 2x + C को हल करके वेक्टर तिरछा की दिशा भी रची। इस तथ्य पर ध्यान दें कि इच्छुक वेक्टर का कोण इस बिंदु पर स्पर्शरेखा के कोण के बराबर है। ध्यान दें कि कई अलग-अलग parabolas हैं जो स्पर्शरेखा के सेट के कोण को संतुष्ट करते हैं, केवल y अक्ष के साथ एक बदलाव में भिन्न होते हैं। इनमें से प्रत्येक परवल को अलग-अलग एकीकरण स्थिरांक का उपयोग करके प्राप्त किया जाता है, जो समीकरण डाई / dx = 2x + C. में समाहित है। जिस परबोला का मैंने चित्रण किया है उसका एकीकरण निरंतर है। 0. यदि मैं एक और स्थिरांक का चयन करता हूं, उदाहरण के लिए, 1, मुझे समीकरण मिलता है y = 2x + 1. इसका अर्थ है कि y अक्ष पर 1 इकाई के बदलाव के साथ एक समान परवलय है।

अब इस तथ्य के बारे में सोचें कि यदि आप पैराबोला द्वारा परिभाषित चित्रा 2 में वैक्टर के क्षेत्र को नहीं जानते हैं, तो बस एक पोखर में बैठें। इसलिए, यदि आप स्पर्शरेखा समीकरण को हल करना चाहते हैं, तो आपको बस वेक्टर फ़ील्ड की दिशा में परिवर्तन के अनुसार दिशा बदलते हुए, प्रत्येक बिंदु पर वेक्टर की दिशा का पालन करने की आवश्यकता है। आपको आश्चर्य होगा कि कुछ समय बाद, आप देखेंगे कि आप एक परवलयिक प्रक्षेपवक्र के साथ (या परबोला के एक भाग के साथ) आगे बढ़ रहे हैं, इस पर निर्भर करता है कि आपने कहां शुरू किया था। इसे साकार करने के बिना, आपने वेक्टर फ़ील्ड के समीकरण को एकीकृत किया। आपने केवल व्युत्पन्न समीकरण (वेक्टर क्षेत्र में चलते हुए डाई / डीएक्स की गणना करते हुए) का उपयोग करते हुए एक विशिष्ट परबोला (जहां आप शुरू किया था, या प्रारंभिक स्थितियों पर निर्भर करता है) पाया।

वास्तविक अंतर समीकरण के लिए भी ऐसा करना सरल है। प्रकार डाई / dx = f (x, y) के विभेदक समीकरण के लिए, व्युत्पन्न डाई / dx को f (x, y) के रूप में स्पर्शरेखा के रूप में खोजना x, y ग्राफ पर प्रत्येक समन्वय के लिए स्पर्शरेखा के झुकाव के कोण का वर्णन करता है। यदि आप डाई / डीएक्स = एफ (एक्स, वाई) द्वारा दिए गए वेक्टर क्षेत्र की साजिश रच रहे हैं, तो आप प्रत्येक बिंदु पर व्युत्पन्न खोजने और उस दिशा में अनुसरण करके एक परवलय के साथ सादृश्य द्वारा इसका पालन कर सकते हैं। चित्रा 2 समीकरण 12 के लिए एक वेक्टर क्षेत्र दिखाता है, वायु प्रतिरोध के लिए हमारा समीकरण, ऊर्ध्वाधर अक्ष के साथ वेग और क्षैतिज के साथ समय (इस ग्राफ के लिए मैंने मनमाने ढंग से एम = 1 चुना)।



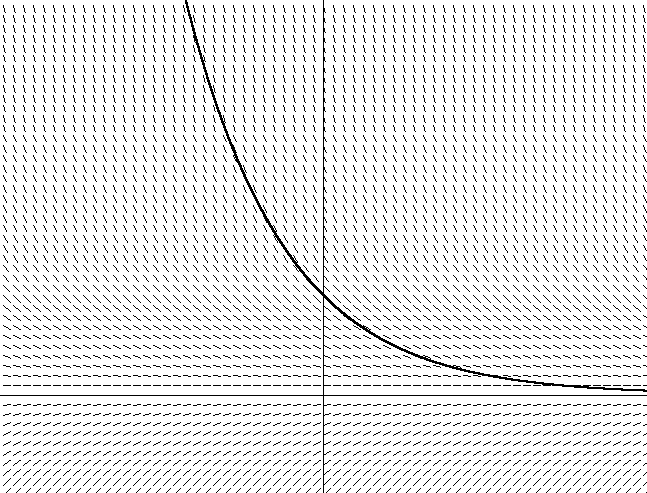चित्रा 3. DV / dt = -v / m

यह कई संभावित वक्रों में से एक को भी दर्शाता है। आप देख सकते हैं कि यदि आप ग्राफ में शुरुआती स्थिति चुनते हैं (जो समीकरण में प्रारंभिक गति पर निर्भर करता है), समय के साथ, गति शून्य हो जाएगी, क्योंकि घर्षण बल शरीर को धीमा कर देता है। आप यह भी देख सकते हैं कि गति में कमी गति के वर्तमान मूल्य पर निर्भर करती है - आप जितनी तेज़ी से आगे बढ़ते हैं, उतनी तेज़ी से घटती है। यह तब स्पष्ट हो जाता है जब समीकरण 12 से समान होता है।

न्यूमेरिकल इंटीग्रेशन भी वैसा ही है जैसा हमने चार्ट पर किया था। संख्यात्मक एकीकरण के लिए यूलर एल्गोरिथ्म बस वर्तमान बिंदु पर ढलान निर्धारित करने के लिए समीकरण (-v / m हमारे घर्षण बल के साथ उदाहरण के लिए) की व्युत्पत्ति का पता लगाकर प्रारंभिक स्थिति के अनुसार वेक्टर क्षेत्र का अनुसरण करता है, और फिर समय पर कदम से कदम पर निर्भर करता है एच के अपरिवर्तित मूल्य, ढलान के साथ। फिर एक निश्चित समय अंतराल के बाद नए ढलान को निर्धारित करने के लिए एक नई स्थिति की गणना की जाती है:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

या वायु प्रतिरोध के हमारे समीकरण के लिए अधिक सटीक:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

जाहिर है, यूलर विधि प्रत्येक समय कदम के साथ एक छोटी सी त्रुटि देती है, क्योंकि वास्तविक वेग वेक्टर (और इसलिए समाधान वक्र) प्रत्येक बिंदु पर एक विचलन के साथ झुकता है, और यूलर एल्गोरिदम झुकाव के कोण से थोड़ा विचलन करता है। लेकिन अगर समय कदम, एच बल्कि छोटी मात्रा में हैं, तो त्रुटि शून्य हो जाती है। हम भविष्य में इस पर अधिक विस्तार से चर्चा करेंगे।

यह आप सभी को Euler विधि का उपयोग करके संख्यात्मक एकीकरण के बारे में जानने की आवश्यकता है। आप पूछ सकते हैं कि हम समन्वय प्राप्त करने के लिए गति को कैसे एकीकृत करने जा रहे हैं। हम बस यू / डी = वी को एकीकृत करने के लिए फिर से यूलर विधि का उपयोग करते हैं, ठीक उसी तरह जैसे हम DV / dt = a, को सादृश्य द्वारा एकीकृत करते हैं। हमें दो जुड़े हुए अंतर समीकरण (हमारी जीत के एक और) मिलते हैं:

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

यह हमें हमारी वस्तु पर किसी भी मनमाने ढंग से लागू बल की कार्रवाई के बाद समन्वय की गणना करने के लिए एक वैकल्पिक एल्गोरिदम देता है (जो कि गति पर निर्भर हो सकता है, जैसा कि हमने देखा, या समय, या यहां तक ​​कि हमारे शरीर और अन्य निकायों की स्थिति, या एक ही बार में!)। यूलर विधि के लिए, यह कोई फर्क नहीं पड़ता कि लागू बल कैसा दिखता है, क्योंकि आप इसे किसी भी क्षण में गणना कर सकते हैं। यूलर इच्छुक बल के प्रभाव के परिमाण में रुचि रखता है, जैसा कि इच्छुक है, और यह बात है।
मैं अंतरिक्ष से बाहर भाग गया, इसलिए मेरे पास लिंक प्रदान करने का कोई तरीका नहीं है। अगली बार मैं विभिन्न अद्भुत पुस्तकों की सलाह दूंगा, और हम यह पता लगाएंगे कि ठोस पदार्थों के रोटेशन की गणना कैसे करें।

और यद्यपि उनका शरीर उतना ठोस नहीं है जितना हम चाहेंगे, क्रिस हेकर का एक गतिशील व्यक्तित्व है। यदि आप बल लागू करते हैं, तो वह ई-मेल checker@bix.com पर जवाब देगा।

अनुवादक के नोट्स: एक वाक्य यहाँ प्रस्तुत किया गया है, लेख और उसकी सामग्री के विषय को बजाया जाता है।

PS अनुवाद के लेखक ने अनुवाद के अपने संपादन के लिए berez और MarazmDed के उपयोगकर्ताओं के लिए विशेष धन्यवाद व्यक्त किया है । धन्यवाद!