परिचय
अंग्रेजी शब्द तरंगिका (फ्रांसीसी "ondelette" से) का शाब्दिक अर्थ है "लघु (छोटी) तरंग।" रूसी में विदेशी लेखों के विभिन्न अनुवादों में, शब्द भी हैं: "फट", "फंक्शन फंक्शन", "लो-वेव फंक्शन", "वेव", आदि।
तरंग विश्लेषण (वीपी) का व्यापक रूप से संकेत विश्लेषण के लिए उपयोग किया जाता है। इसके अलावा, यह डेटा कम्प्रेशन के क्षेत्र में शानदार एप्लिकेशन पाता है। एक-आयामी संकेत का वीपी एक सामान्यीकृत श्रृंखला या फूरियर के अभिन्न अंग के रूप में इसका प्रतिनिधित्व करता है जो आधार कार्यों की एक प्रणाली से अधिक है।
psiab(t)= frac1 sqrta psi left( fract−ba right) , (1)
माँ (स्रोत) तरंग से निर्मित
psi(t) टाइम शिफ्ट ऑपरेशंस (b) और टेम्पोरल स्केल चेंजेस (a) के कारण कुछ प्रॉपर्टीज रखना।
फ़ैक्टर
1/ sqrta स्केलिंग नंबर (ए) से कार्यों के मानदंड (1) की स्वतंत्रता सुनिश्चित करता है। ए और बी के मापदंडों के दिए गए मानों के लिए, फ़ंक्शन
psiab(t) और माँ तरंग द्वारा उत्पन्न एक तरंगिका है
psi(t) ।
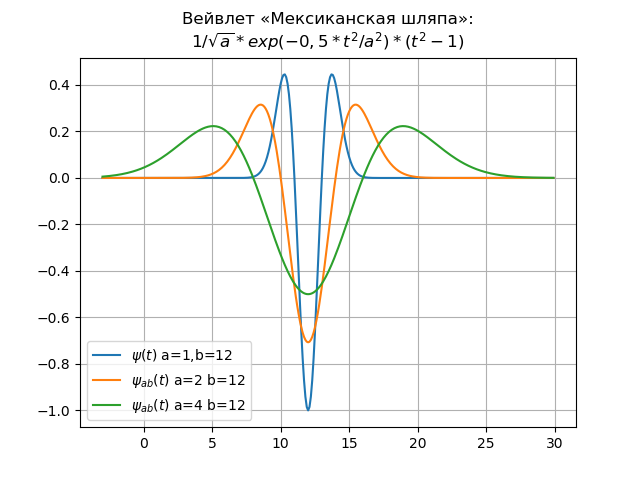
एक उदाहरण समय और आवृत्ति डोमेन में मैक्सिकन टोपी तरंग है:
समय डोमेन के लिए वेवलेट लिस्टिंगfrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
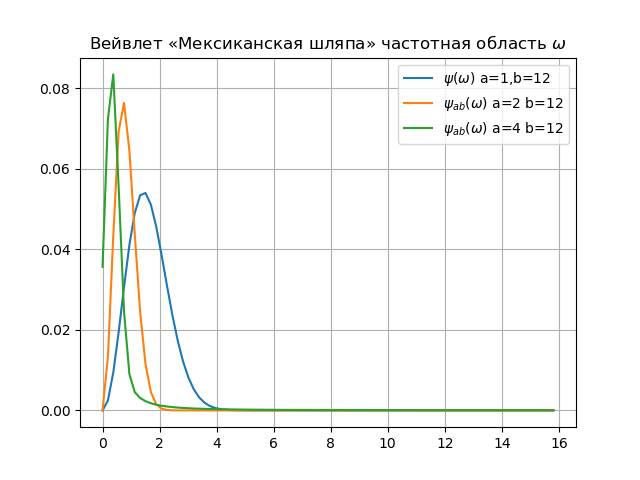
तरंगिका स्पेक्ट्रम के लिए लिस्टिंग from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 निष्कर्ष:
निष्कर्ष:1. फूरियर हार्मोनिक्स की अवधारणा और तरंगिका के पैमाने के बीच, वास्तव में एक संबंध है। इस संबंध में मुख्य बात प्राकृतिक आवृत्ति और पैमाने का व्युत्क्रम अनुपात है। इसके अलावा, पैमाने को कम करते हुए, हम तरंगिका स्पेक्ट्रम की बैंडविड्थ बढ़ाते हैं।
2. पैमाने को बदलकर (फ़ंक्शन के फूरियर स्पेक्ट्रम की संकीर्णता में वृद्धि करके)
psiab(t) ), तरंगिका अलग-अलग पैमानों (आवृत्तियों) पर विशेषताओं के अंतर का पता लगाने में सक्षम हैं, और पारी के कारण, पूरे अध्ययन किए गए अंतराल पर विभिन्न बिंदुओं पर संकेत गुणों का विश्लेषण करते हैं। इसलिए, जब गैर-स्थिर संकेतों का विश्लेषण करते हैं, तो तरंगों की स्थानीयता संपत्ति के कारण, उन्हें फूरियर ट्रांसफॉर्म पर एक महत्वपूर्ण लाभ मिलता है, जो विश्लेषण किए गए सिग्नल की आवृत्तियों (तराजू) के बारे में केवल वैश्विक जानकारी देता है, क्योंकि कार्यों की प्रणाली (जटिल घातांक या साइन और कॉज़नेस) का उपयोग किया जाता है। अनंत अंतराल।
3. स्वतंत्र रूप से वितरित उच्च-स्तरीय पायथन भाषा में लिखी गई उपरोक्त लिस्टिंग आपको निर्दिष्ट आवश्यकताओं को पूरा करने वाले तरंगों के लिए कार्यों का चयन करने की अनुमति देती है। हालांकि, तरंगिकाओं के सभी मुख्य संकेतों को ध्यान में रखना आवश्यक है।
तरंगिका के मुख्य लक्षण
सीमाओं। फ़ंक्शन के मानदंड का वर्ग परिमित होना चाहिए:
left | psi right |2= int infty− infty left| psi(t) right|2dt< infty । (2)
स्थानीयकरण। वीपी, फूरियर ट्रांसफॉर्म के विपरीत, समय और आवृत्ति दोनों में एक स्थानीयकृत प्रारंभिक फ़ंक्शन का उपयोग करता है। ऐसा करने के लिए, यह पर्याप्त है कि निम्नलिखित शर्तें पूरी हों:
बाएं| psi(t) right| leqC(1+ बाएँ|t right|)−1− varepsilon और
\ _ बाएं | S _ {\ psi} (\ omega) \ right | \ leq C (1+ \ left | \ omega \ right।) ^ ^ - 1- 1- \ varepsilon}\ _ बाएं | S _ {\ psi} (\ omega) \ right | \ leq C (1+ \ left | \ omega \ right।) ^ ^ - 1- 1- \ varepsilon} पर
varepsilon>0 , (3)
उदाहरण के लिए, एक डेल्टा फ़ंक्शन
डेल्टा(टी) और हार्मोनिक फ़ंक्शन समय और आवृत्ति डोमेन में एक साथ स्थानीयकरण के लिए आवश्यक स्थिति को संतुष्ट नहीं करते हैं।
शून्य औसत। मूल फ़ंक्शन का ग्राफ समय अक्ष पर शून्य के आसपास (बारी-बारी से) होना चाहिए और शून्य क्षेत्र होना चाहिए:
int infty− infty psi(t)dt=0 । (4)
इस स्थिति से, यह "तरंगिका" नाम की पसंद स्पष्ट हो जाती है - एक छोटी लहर।
शून्य फ़ंक्शन क्षेत्र के बराबर
psi(t) , यानी। शून्य क्षण, इस तथ्य की ओर जाता है कि फूरियर बदल जाता है
S psi( omega) यह फ़ंक्शन शून्य के बराबर है
ओमेगा=0 और एक बैंड-पास फिल्टर का रूप है। विभिन्न मूल्यों (ए) के लिए, यह बैंडपास फिल्टर का एक सेट होगा।
अक्सर अनुप्रयोगों के लिए यह आवश्यक है कि न केवल शून्य, बल्कि सभी पहले n क्षण शून्य के बराबर हों:
int infty− inftytn psi(t)dt=0 । (5)
एन-वें तरंगिकाएं सिग्नल की बारीक (उच्च-आवृत्ति) संरचना का विश्लेषण करने की अनुमति देती हैं, जिससे इसके धीरे-धीरे बदलते घटकों को दबा दिया जाता है।
स्केलिंग। वीपी की एक विशेषता इसकी आत्म-समानता है। एक विशिष्ट परिवार की सभी तरंगें
psiab(t) माता तरंगिका के समान दोलनों की संख्या है
psi(t) , क्योंकि स्केल ट्रांसफॉर्मेशन (ए) और शिफ्ट (बी) के माध्यम से इसे प्राप्त किया गया है।
निरंतर तरंगिका रूपांतरण
निरंतर (इंटीग्रल) तरंगिका परिवर्तन (एनवीपी या WT - निरंतर तरंग परिवर्तन)। हम आधार का निर्माण करते हैं
psiab(t) माँ तरंगिका के निरंतर पैमाने पर रूपांतरण (ए) और स्थानांतरण (बी) का उपयोग करना
psi(t) फार्मूला (1) में आधार पैरामीटर a और b के मनमाने मूल्यों के साथ।
फिर, परिभाषा के अनुसार, संकेत एस (टी) के प्रत्यक्ष (विश्लेषण) और रिवर्स (संश्लेषण) एनवीपी (यानी, पीएनवीपी और ओएनवीपी) निम्नानुसार हैं:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi left( fractba right)dt , (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(,,b)) psiab(t) fracपिताa2 , (7)
जहाँ
C psi गुणांक को सामान्य बनाना,
C psi= int infty− infty left| psi( omega) right|2 left| omega right|−1d omega< inftyजहां: (•, •) संबंधित कारकों का अदिश उत्पाद है,
mathbf psi( omega) - एक तरंगिका का फूरियर रूपांतरण
psi(t) । असामान्य तरंगों के लिए
C psi=1 ।
यह (6) से है कि वेवलेट स्पेक्ट्रम
Ws(बी,ए) (वेवलेट स्पेक्ट्रम, या टाइम-स्केल-स्पेक्ट्रम), फूरियर स्पेक्ट्रम (सिंगल स्पेक्ट्रम) के विपरीत, दो तर्कों का एक कार्य है: पहला तर्क ए (टाइम स्केल) दोलन अवधि के समान है, अर्थात आवृत्ति के विपरीत है, और दूसरा b –– समय अक्ष के साथ सिग्नल ऑफ़सेट के समान है।
यह ध्यान दिया जाना चाहिए कि
Ws(b,a0) समय निर्भरता (पर) की विशेषता है
a=a0) , जबकि निर्भरता
Ws(a,b0) आवृत्ति निर्भरता से मेल खाना संभव है (के लिए)
b=b0 )।
यदि अध्ययन किया गया संकेत S (t) अवधि का एक एकल नाड़ी है
tauu पड़ोस में केंद्रित है
t=t0 , तो इसके तरंगिका स्पेक्ट्रम में निर्देशांक के साथ बिंदु के आसपास के क्षेत्र में सबसे बड़ा मूल्य होगा
a= tauu,b=t0 ।
प्रस्तुति के तरीके Ws(बी,ए) अलग हो सकता है। की सीमा
Ws(बी,ए) तीन आयामी अंतरिक्ष में एक सतह है। हालांकि, अक्सर सतह की छवि के बजाय, एब विमान पर इसका प्रक्षेपण आईएसओ स्तर (या विभिन्न रंगों के आंकड़े) के साथ प्रस्तुत किया जाता है, जो विभिन्न आयामों (ए) और समय (ई) में ईपी एम्पलीट्यूड की तीव्रता में परिवर्तन का पता लगाना संभव बनाता है।
इसके अलावा, वे इन सतहों, तथाकथित कंकाल (sceleton) की स्थानीय विलुप्त होने की रेखाओं का चित्रण करते हैं, जो विश्लेषण किए गए संकेत की संरचना को प्रकट करता है।
मदर वेवलेट पर आधारित वेवलेट स्पेक्ट्रम का निर्धारण करते समय निरंतर तरंगिका परिवर्तन - "मैक्सिकन टोपी"।
NVP के लिए प्रयुक्त अन्य मातृ तरंगों का भी उपयोग किया जाता है:

सिग्नल प्रोसेसिंग में निरंतर वीपी का व्यापक रूप से उपयोग किया जाता है। विशेष रूप से, तरंग विश्लेषण (वीए) संकेतों (कार्यों) की स्थानीय और "सूक्ष्म" विशेषताओं को पहचानने के लिए अद्वितीय अवसर प्रदान करता है, जो रेडियो इंजीनियरिंग, संचार, रेडियो इलेक्ट्रॉनिक्स, भूभौतिकी और विज्ञान और प्रौद्योगिकी की अन्य शाखाओं के कई क्षेत्रों में महत्वपूर्ण है। आइए कुछ सरल उदाहरणों के साथ इस संभावना पर विचार करें।
हार्मोनिक दोलन।संकेत का रूप है:
s(t)=असिन( omegat− phi)जहां:
A=1V, omega= frac2 piT= frac2 pi50, psi=0वेवलेट बनाने का कार्य:
MHAT(t):= fracd2dt2exp(−t2/2) ।
तरंगिकाओं:
psi(a,b,t)= frac1 sqrtaMHAT left( fract−ba right) ।
वेवलेट स्पेक्ट्रम: N: = 256, a: = 1..30, b: = 0..50
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b)$ ।
कार्यक्रम सूचीकरण from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
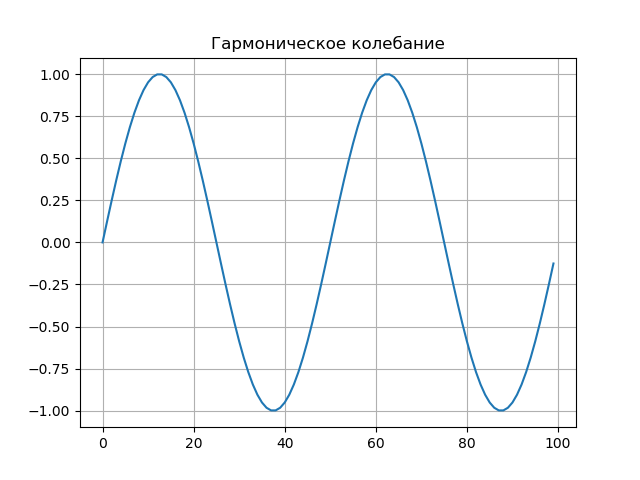
सिग्नल ग्राफ।

दो-पैरामीटर स्पेक्ट्रम का ग्राफ
Nab=W(ab) तीन-आयामी अंतरिक्ष में एक सतह के रूप में प्रदर्शित किया जाता है।

यह ध्यान दिया जाना चाहिए कि अनुभाग डब्ल्यू (ए, बी) समय के पैमाने के लिए
a=a0 प्रारंभिक दोलन एस (टी) की विशेषता है। इसके अलावा, इसका आयाम अधिकतम है
a0:1/ omega । पर निर्भर करता है
W(a0,b0) पर दोलनों के वर्तमान वर्णक्रम से मेल खा सकता है
b=b0 ।
दो हार्मोनिक दोलनों का योग।संकेत का रूप है:
s(t):=A1पाप( omega1t)+A2पाप( omega2t)जहां:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2piT2,T1=50s,T2=10s ।
MHAT(t):= fracd2dt2 left[e−t2/2 right] , एन: = 256,
psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) ।
कार्यक्रम सूचीकरण from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

सिग्नल ग्राफ।
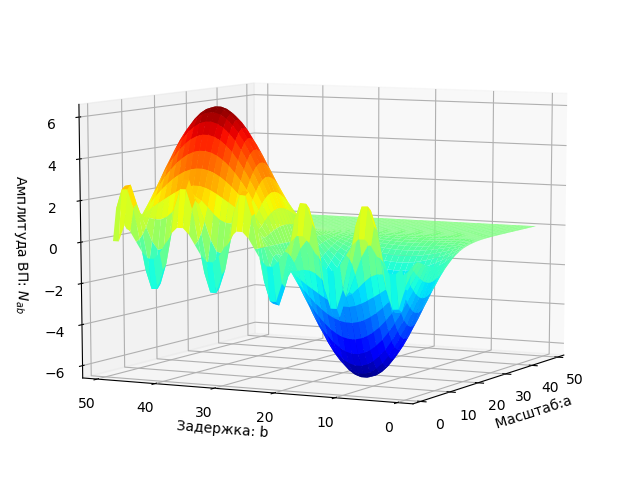
दो-पैरामीटर स्पेक्ट्रम डब्ल्यू (ए, बी) की साजिश को तीन-आयामी अंतरिक्ष में एक सतह के रूप में प्रदर्शित किया जाता है।
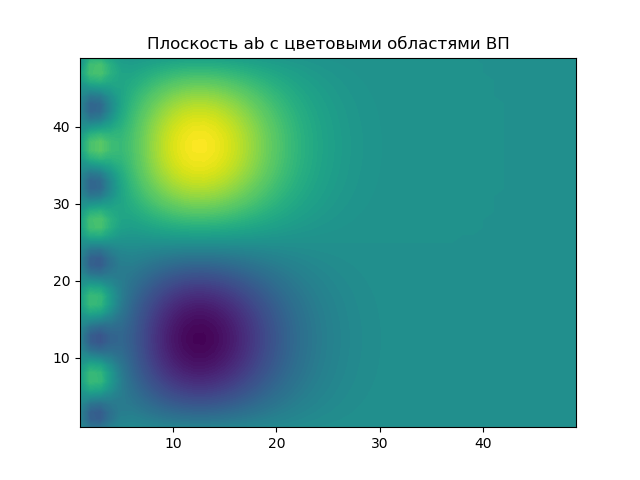
मापदंडों का विमान a, b जिस पर रंगीन क्षेत्रों में EP के परिणामों को उजागर किया गया है।

ग्राफ पैरामीटर के दो मानों के लिए तरंगिका स्पेक्ट्रम के "क्रॉस सेक्शन" को दर्शाता है। समय के पैमाने के एक अपेक्षाकृत छोटे पैरामीटर के साथ, के लिए
a1=2(a1:1/ omega2) स्पेक्ट्रम का क्रॉस सेक्शन केवल सिग्नल की उच्च-आवृत्ति घटक के बारे में जानकारी करता है, इसके कम-आवृत्ति घटक को फ़िल्टर करना (दबाना)।
एक वृद्धि के रूप में, आधार फ़ंक्शन का विस्तार
\ psi (\ frac {t-b} {{a}) , इसलिए, इसके स्पेक्ट्रम को संकीर्ण करना, और आवृत्ति "विंडो" की बैंडविड्थ को कम करना। नतीजतन, जब
a2=15(a2:1/ omega1) स्पेक्ट्रम का क्रॉस सेक्शन सिग्नल का केवल कम आवृत्ति वाला घटक है।
एक और वृद्धि के साथ, विंडो बैंड अभी भी घटता है और इस कम-आवृत्ति घटक का स्तर एक निरंतर घटक (एक> 25 के लिए) तक घट जाता है, जो विश्लेषण सिग्नल के लिए शून्य के बराबर है।

ग्राफ तरंग स्पेक्ट्रम डब्ल्यू (ए, बी) के वर्गों को दर्शाता है
पर वर्तमान संकेत स्पेक्ट्रम
b1=13 और
b2=17 । हार्मोनिक के विपरीत माना जाने वाला सिग्नल का स्पेक्ट्रम, टाइम स्केल a (a: 1..3) के छोटे मानों के क्षेत्र में उच्च आवृत्ति वाला घटक होता है, जो सिग्नल के दूसरे घटक से मेल खाता है
A2पाप( omega2t) ।
आयताकार गति।U:=5,t0:=20, tau:=60s(t):= startvmatrixU,अगरt0 leqt leqt0+ tau0,अन्यथा endvmatrixMHAT(t):= fracd2dt2exp left( frac−t22 right)N:=128, psi(a,b,t):=MHAT left( fractba right),W(a,b):= intN−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)कार्यक्रम सूचीकरण from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
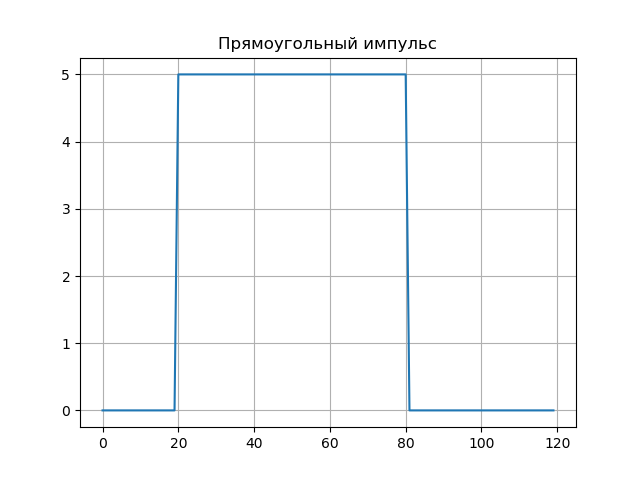


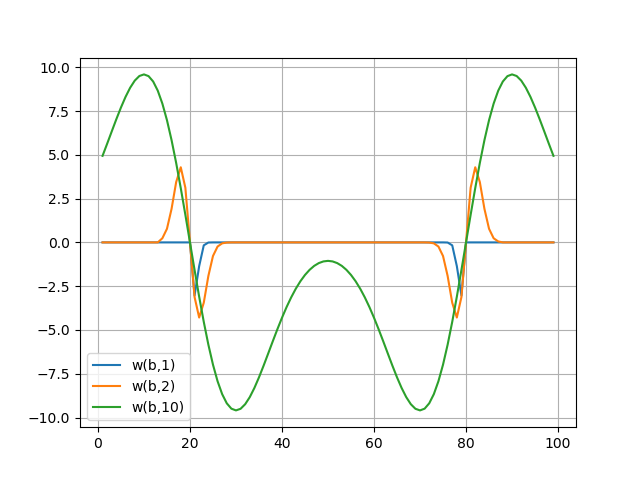
वेवलेट स्पेक्ट्रा को रेखांकन में दिखाया गया है, वेवलेट स्पेक्ट्रम अच्छी तरह से सिग्नल की सूक्ष्म विशेषताओं को बताता है - इसके नमूने नमूने पर b = 20 और b = 80 (a: 1..10 के लिए)।
निष्कर्ष
यह प्रकाशन प्रकृति में शैक्षिक है, यह सामान्य रूप से तरंगिका विश्लेषण के बारे में बुनियादी जानकारी प्रदान करता है, और स्वतंत्र रूप से वितरित उच्च स्तरीय प्रोग्रामिंग भाषा पायथन पर सरल उदाहरण व्यापक ग्राफिकल 3 डी और 2 डी विज़ुअलाइज़ेशन के साथ निरंतर तरंग विश्लेषण की विशेषताएं दिखाते हैं।
PS लेखक तरंगों की संख्या और गति दोनों के संदर्भ में मतलाब का उपयोग करके तरंगिका विश्लेषण के बिना शर्त लाभ से अलग नहीं होता है। लेकिन पायथन में अभी भी आगे के विकास के लिए जगह है: scipy.signal और PyWavelets।