अनुकूली एंटीना: यह कैसे काम करता है? (आधार)

शुभ दिन।

पिछले कुछ वर्षों में मैंने अनुकूली एंटीना सरणियों में संकेतों के स्थानिक प्रसंस्करण के लिए विभिन्न एल्गोरिदम के अनुसंधान और निर्माण के लिए समर्पित किया है, और मैं वर्तमान समय में अपने काम के हिस्से के रूप में यह करना जारी रखता हूं। यहां मैं अपने द्वारा खोजे गए ज्ञान और चिप्स को साझा करना चाहूंगा। मुझे उम्मीद है कि यह सिग्नल प्रोसेसिंग के इस क्षेत्र का अध्ययन करने वाले लोगों के लिए उपयोगी होगा या बस दिलचस्पी होगी।

एक अनुकूली एंटीना सरणी क्या है?

एक ऐन्टेना सरणी ऐन्टेना तत्वों का एक सेट है, जिसे अंतरिक्ष में किसी तरह से व्यवस्थित किया जाता है। अनुकूली ऐन्टेना सरणी की संरचना को सरल बनाने के लिए, जिस पर हम विचार करेंगे, निम्नलिखित रूप में प्रस्तुत किया जा सकता है:


अनुकूली एंटीना सरणियों को अक्सर "स्मार्ट एंटेना" ( स्मार्ट एंटेना) कहा जाता है। "स्मार्ट" एंटीना सरणी स्थानिक सिग्नल प्रोसेसिंग यूनिट और इसमें लागू किए गए एल्गोरिदम द्वारा बनाई गई है। ये एल्गोरिदम प्राप्त सिग्नल का विश्लेषण करते हैं और वजन का एक सेट बनाते हैं$$ $ इनलाइन $ w_1 ... w_N $ इनलाइन $ जो प्रत्येक तत्व के लिए संकेत के आयाम और प्रारंभिक चरण का निर्धारण करते हैं। दिए गए आयाम-चरण वितरण संपूर्ण रूप से पूरे जाली के निर्देशन पैटर्न को निर्धारित करता है । आवश्यक आकार के विकिरण पैटर्न को संश्लेषित करने और सिग्नल प्रोसेसिंग के दौरान इसे बदलने की क्षमता अनुकूली एंटीना सरणियों की मुख्य विशेषताओं में से एक है, जो समस्याओं की एक विस्तृत श्रृंखला को हल करने की अनुमति देती है । लेकिन पहले बातें पहले।

विकिरण पैटर्न कैसे बनता है?

एक विकिरण पैटर्न एक निश्चित दिशा में विकीर्ण सिग्नल की शक्ति की विशेषता है। सादगी के लिए, हम जाली तत्वों को आइसोट्रोपिक कहते हैं, अर्थात्। उनमें से प्रत्येक के लिए, उत्सर्जित संकेत की शक्ति दिशा पर निर्भर नहीं करती है। एक निश्चित दिशा में सरणी द्वारा उत्सर्जित शक्ति का प्रवर्धन या क्षीणन ऐन्टेना सरणी के विभिन्न तत्वों द्वारा उत्सर्जित विद्युत चुम्बकीय तरंगों के हस्तक्षेप के कारण प्राप्त होता है। EMW के लिए एक स्थिर हस्तक्षेप पैटर्न केवल तभी संभव है जब वे सुसंगत हों , अर्थात। संकेतों का चरण अंतर समय के साथ नहीं बदलना चाहिए। आदर्श मामले में, एंटीना सरणी के प्रत्येक तत्व को एक ही वाहक आवृत्ति पर एक हार्मोनिक सिग्नल का उत्सर्जन करना चाहिए$$ $ इनलाइन $ f_ {0} $ इनलाइन $ । हालांकि, व्यवहार में, संकीर्ण-बैंड संकेतों के साथ परिमित चौड़ाई के स्पेक्ट्रम के साथ काम करना आवश्यक है$$ $ इनलाइन $ \ Delta f << f_ {0} $ इनलाइन $ ।
सभी एआर तत्वों को जटिल आयाम के साथ एक ही संकेत देते हैं$$ $ इनलाइन $ x_n (t) = u (t) $ इनलाइन $ । फिर, दूरस्थ रिसीवर पर, nth तत्व से प्राप्त सिग्नल को विश्लेषणात्मक रूप में दर्शाया जा सकता है:

$$$ $ प्रदर्शन $ $ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $ $ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ \ tau_n $ इनलाइन $ - एंटीना तत्व से रिसेप्शन के बिंदु तक संकेत के प्रसार में देरी।
ऐसा संकेत "अर्ध-हार्मोनिक" है, और सुसंगतता की स्थिति को संतुष्ट करने के लिए, यह आवश्यक है कि किसी भी दो तत्वों के बीच विद्युत चुम्बकीय तरंगों के प्रसार में अधिकतम देरी सिग्नल लिफाफे के परिवर्तन की विशेषता समय से बहुत कम हो।$$ $ इनलाइन $ T $ इनलाइन $ , यानी।$$ $ इनलाइन $ u (t- \ tau_n) t u (t- \ tau_m) $ इनलाइन $ । इस प्रकार, एक संकरी संकेत के सुसंगतता के लिए स्थिति निम्नानुसार लिखी जा सकती है:

$$$ $ प्रदर्शन $ $ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = max (\ tau_k- \ tau_m) $ $ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ डी_ {अधिकतम} $ इनलाइन $ - एआर के तत्वों के बीच अधिकतम दूरी, और$$ $ इनलाइन $ के साथ $ इनलाइन $ प्रकाश की गति है।

संकेत प्राप्त करते समय, स्थानिक प्रसंस्करण इकाई में डिजिटल रूप से सुसंगत योग का प्रदर्शन किया जाता है। इस स्थिति में, इस ब्लॉक के आउटपुट में डिजिटल सिग्नल का जटिल मूल्य अभिव्यक्ति द्वारा निर्धारित किया जाता है:

$$$ $ प्रदर्शन $ $ y = \ sum_ {n = 1} ^ Nw_n ^ * x_n $ $ प्रदर्शन $ $

मैट्रिक्स के रूप में एन-आयामी जटिल वैक्टर के स्केलर उत्पाद के रूप में अंतिम अभिव्यक्ति पेश करना अधिक सुविधाजनक है:

$$$ $ प्रदर्शन $ $ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $ $ प्रदर्शन $ $

जहां w और x कॉलम वैक्टर हैं, और$$ $ इनलाइन $ (।) ^ एच $ इनलाइन $ - हर्मिटियन पेयरिंग का संचालन।

ऐन्टेना सरणियों के साथ काम करते समय संकेतों का वेक्टर प्रतिनिधित्व बुनियादी में से एक है, क्योंकि अक्सर बोझिल गणितीय गणनाओं से बचा जाता है। इसके अलावा, एक वेक्टर के साथ कुछ बिंदु पर प्राप्त सिग्नल की पहचान अक्सर हमें वास्तविक भौतिक प्रणाली से अमूर्त करने की अनुमति देती है और समझती है कि ज्यामिति के दृष्टिकोण से वास्तव में क्या होता है।

ऐन्टेना सरणी की प्रत्यक्षता पैटर्न की गणना करने के लिए, यह सभी संभावित दिशाओं से विमान तरंगों के एक सेट पर मानसिक और लगातार "रन" करने के लिए आवश्यक है। इस मामले में, वेक्टर x के तत्वों के मूल्यों को निम्नानुसार दर्शाया जा सकता है:

$$$ $ प्रदर्शन $ $ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $ $ प्रदर्शन $ $

जहां k वेव वेक्टर है$$ $ इनलाइन $ \ phi $ इनलाइन $ और$$ $ इनलाइन $ \ थीटा $ इनलाइन $ - अज़ीमुथल कोण और ऊँचाई का कोण , जो एक विमान तरंग के आगमन की दिशा को दर्शाता है,$$ $ इनलाइन $ \ textbf {r} _n $ इनलाइन $ - एंटीना तत्व का समन्वय,$$ $ इनलाइन $ s_n $ इनलाइन $ - वेव वेक्टर k (अंग्रेजी साहित्य में, फासिंग वेक्टर को स्टीयरेज वेक्टर कहा जाता है) के साथ एक प्लेन वेव के चरणबद्ध वेक्टर एस का एक तत्व। Y के आयाम के वर्ग की निर्भरता$$ $ इनलाइन $ \ phi $ इनलाइन $ और$$ $ इनलाइन $ \ थीटा $ इनलाइन $ वजन गुणांक w के दिए गए वेक्टर के लिए रिसेप्शन पर एंटीना सरणी की प्रत्यक्षता पैटर्न निर्धारित करता है।

एंटीना सरणी की विशेषताएं

क्षैतिज विमान में एक रैखिक समवर्ती ऐन्टेना सरणी पर एंटीना सरणी विकिरण पैटर्न के सामान्य गुणों का अध्ययन करना सुविधाजनक है (यानी, बीम पैटर्न केवल अज़ीमुथल कोण पर निर्भर करता है$$ $ इनलाइन $ \ phi $ इनलाइन $ )। यह दो दृष्टिकोणों से सुविधाजनक है: विश्लेषणात्मक गणना और दृश्य प्रस्तुति।

हम यूनिट वेट वेक्टर के लिए DN की गणना करते हैं ($$ $ इनलाइन $ w_n = 1, n = 1 ... एन $ इनलाइन $ ), ऊपर वर्णित दृष्टिकोण के बाद।


नतीजतन, हम प्राप्त करते हैं:

$$$ $ प्रदर्शन $ $ F (\ phi) = | y | ^ 2 = \ frac {\ _ पाप ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ _i) \ frac {d} {\ lambda} \ sin \ phi)} $ $ प्रदर्शन $ $

विकिरण पैटर्न आवृत्ति

एंटीना सरणी का परिणामी विकिरण पैटर्न कोण के साइन का आवधिक कार्य है। इसका मतलब यह है कि डी / λ अनुपात के कुछ मूल्यों के लिए, इसमें विवर्तन (अतिरिक्त) मैक्सिमा है।
N = 5 के लिए असामान्य ऐन्टेना पैटर्न
ध्रुवीय समन्वय प्रणाली में एन = 5 के लिए एंटीना सरणी का सामान्यीकृत विकिरण पैटर्न

"विवर्तनवादियों" की स्थिति को सीधे NAM के सूत्र से देखा जा सकता है। हालांकि, हम यह समझने की कोशिश करेंगे कि वे शारीरिक और ज्यामितीय रूप से (एन-आयामी अंतरिक्ष में) कहाँ से आते हैं।

चरणबद्ध वेक्टर के तत्व जटिल घातांक हैं$$ $ इनलाइन $ e ^ {i \ Psi n} $ इनलाइन $ जिनका मान सामान्यीकृत कोण के मान से निर्धारित होता है$$ $ इनलाइन $ \ psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi इनलाइन $ । यदि एक विमान तरंग के आगमन की विभिन्न दिशाओं के अनुरूप दो सामान्यीकृत कोण हैं, जिसके लिए$$ $ इनलाइन $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ इनलाइन $ , तो इसका मतलब दो चीजें हैं:

• शारीरिक रूप से: इन दिशाओं से आने वाले प्लेन वेव मोहरे एंटीना सरणी के तत्वों पर विद्युतचुंबकीय तरंगों के समान आयाम-चरण वितरण को प्रेरित करते हैं।
• ज्यामितीय रूप से: इन दो दिशाओं के लिए चरणबद्ध वैक्टर संयोग करते हैं।

एक समान तरीके से जुड़े तरंग आगमन की दिशाएं एंटीना सरणी के दृष्टिकोण से बराबर होती हैं और एक दूसरे से अलग नहीं होती हैं।

कोणों के क्षेत्र का निर्धारण कैसे करें जिसमें एमडी का केवल एक मुख्य अधिकतम हमेशा झूठ होता है? हम निम्नलिखित कारणों से शून्य azimuth के आसपास के क्षेत्र में यह करेंगे: दो आसन्न तत्वों के बीच चरण बदलाव अंतराल से झूठ होना चाहिए$$ $ इनलाइन $ - \ pi $ इनलाइन $ को$$ $ इनलाइन $ \ pi $ इनलाइन $ ।

$$$ $ प्रदर्शन $ $ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $ $ प्रदर्शन $ $

इस असमानता को हल करते हुए, हम शून्य के पड़ोस में विशिष्टता के क्षेत्र पर स्थिति प्राप्त करते हैं:

$$$ $ प्रदर्शन $ $ | \ sin \ phi | <\ frac {\ lambda} {2d} $ $ प्रदर्शन $ $

यह देखा जा सकता है कि कोण में विशिष्टता के क्षेत्र का आकार अनुपात d / λ पर निर्भर करता है। यदि d = 0.5 λ है , तो संकेत के आगमन की प्रत्येक दिशा "व्यक्तिगत" है, और विशिष्टता का क्षेत्र कोणों की पूरी श्रृंखला को कवर करता है। यदि d = 2.0 λ , तो दिशाएं 0, ± 30, equivalent 90 समतुल्य हैं। विवर्तन लोब विकिरण के पैटर्न पर दिखाई देते हैं।

आमतौर पर, विवर्तन लोब दिशात्मक एंटीना तत्वों का उपयोग करते हुए दब जाते हैं। इस मामले में, एंटीना सरणी का पूर्ण विकिरण पैटर्न एक तत्व के पैटर्न और आइसोट्रोपिक तत्वों के सरणी का उत्पाद है। एक तत्व के डीएन पैरामीटर आमतौर पर ऐन्टेना सरणी की विशिष्टता क्षेत्र पर स्थिति के आधार पर चुने जाते हैं।

मुख्य पालि की चौड़ाई

ऐन्टेना प्रणाली के मुख्य पालि की चौड़ाई का आकलन करने के लिए इंजीनियरिंग सूत्र व्यापक रूप से जाना जाता है :$$ $ इनलाइन $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ इनलाइन $ जहां D एंटीना का चारित्रिक आकार है। सूत्र का उपयोग विभिन्न प्रकार के एंटेना के लिए किया जाता है, जिसमें एसएलआर वाले भी शामिल हैं। हम बताते हैं कि यह ऐन्टेना सरणियों के लिए भी मान्य है।

हम मुख्य अधिकतम के आसपास के क्षेत्र में एमडी के पहले शून्य द्वारा मुख्य लोब की चौड़ाई निर्धारित करते हैं। के लिए अभिव्यक्ति का संचालक$$ $ इनलाइन $ F (\ phi) $ इनलाइन $ पर गायब हो जाता है$$ $ इनलाइन $ \ sin \ phi = m \ frac {\ lambda} {dN} $ इनलाइन $ । पहला शून्य m = correspond 1 के अनुरूप है। विश्वास$$ $ इनलाइन $ \ frac {\ lambda} {dN} << 1 $ इनलाइन $ हमें मिलता है$$ $ इनलाइन $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ इनलाइन $ ।

आमतौर पर, दिशा बीम की चौड़ाई एआर आधा शक्ति स्तर (-3 डीबी) द्वारा निर्धारित की जाती है। इस स्थिति में, अभिव्यक्ति का उपयोग करें:

$$$ $ प्रदर्शन $ $ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $ $ प्रदर्शन $ $

एंटीना सरणी के वजन गुणांक के लिए आयाम के विभिन्न मूल्यों को सेट करके मुख्य लोब की चौड़ाई को नियंत्रित किया जा सकता है। तीन वितरणों पर विचार करें:

• वर्दी आयाम वितरण (वजन 1):$$ $ इनलाइन $ w_n = 1 $ इनलाइन $ ।
• जाली के किनारों पर पड़ने वाले आयाम मान (भार 2):$$ $ इनलाइन $ w_n = 0.5 + 0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ इनलाइन $
• झंझरी के किनारों पर बढ़ते आयाम मान (वजन 3):$$ $ इनलाइन $ w_n = 0.5-0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ इनलाइन $

आकृति एक लघुगणकीय पैमाने पर परिणामस्वरूप सामान्यीकृत विकिरण पैटर्न दिखाती है:
निम्नलिखित प्रवृत्तियों को आंकड़े से देखा जा सकता है: जाली के किनारों की ओर घटने वाले वजन गुणांक के आयाम के वितरण से एमडी के मुख्य लोब का चौड़ीकरण होता है, लेकिन साइड लॉब्स के स्तर में कमी। ऐन्टेना सरणी के किनारों की ओर बढ़ते हुए आयाम, इसके विपरीत, मुख्य लोब की एक संकीर्णता और पक्षों के स्तर में वृद्धि होती है। यहां मामलों को सीमित करना सुविधाजनक है:

1. चरम को छोड़कर सभी तत्वों के भारांक गुणांक के आयाम शून्य के बराबर हैं। चरम तत्वों के लिए वजन एकता के बराबर हैं। इस मामले में, डी = (एन -1) डी की अवधि के साथ जाली दो-तत्व एआर के बराबर हो जाती है। उपरोक्त सूत्र के अनुसार मुख्य पंखुड़ी की चौड़ाई का अनुमान लगाना मुश्किल नहीं है। इस मामले में, पार्श्व विवर्तन मैक्सिमा में बदल जाएगा और मुख्य अधिकतम के साथ संरेखित होगा।
2. केंद्रीय तत्व का वजन एक के बराबर है, और शेष सभी शून्य के बराबर है। इस मामले में, हमें अनिवार्य रूप से एक आइसोट्रोपिक विकिरण पैटर्न के साथ एक एंटीना मिला।

मुख्य अधिकतम की दिशा

इसलिए, हमने देखा कि आप एपी एआर के मुख्य लोब की चौड़ाई को कैसे समायोजित कर सकते हैं। अब देखते हैं कि दिशा को कैसे आगे बढ़ाया जाए। प्राप्त संकेत के लिए वेक्टर अभिव्यक्ति को याद करें। मान लें कि हम एक निश्चित दिशा में अधिकतम विकिरण पैटर्न देखना चाहते हैं$$ $ इनलाइन $ \ phi_0 $ इनलाइन $ । इसका मतलब है कि इस दिशा से अधिकतम शक्ति ली जानी चाहिए। चरणबद्ध वेक्टर इस दिशा से मेल खाती है$$ $ इनलाइन $ \ textbf {s} (\ phi_0) $ इनलाइन $ एन -डायमेंशनल वेक्टर स्पेस में, और प्राप्त शक्ति को वज़न गुणांक w के वेक्टर द्वारा इस चरणबद्ध वेक्टर के स्केलर उत्पाद के वर्ग के रूप में परिभाषित किया गया है। दो वैक्टर के स्केलर उत्पाद अधिकतम होते हैं जब वे कोलीनियर होते हैं , अर्थात।$$ $ इनलाइन $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ इनलाइन $ , जहां β कुछ सामान्यीकरण कारक है। इस प्रकार, यदि हम वांछित दिशा के लिए चरणबद्ध वेक्टर के बराबर एक वजन वेक्टर चुनते हैं, तो हम अधिकतम विकिरण पैटर्न को घुमाएंगे।

एक उदाहरण के रूप में निम्नलिखित भार पर विचार करें:$$ $ इनलाइन $ \ textbf {w} = \ textbf {s} (10 °) $ इनलाइन $

$$$ $ प्रदर्शन $ $ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $ $ प्रदर्शन $ $

नतीजतन, हम 10 ° की दिशा में मुख्य अधिकतम के साथ एक विकिरण पैटर्न प्राप्त करते हैं।

अब हम समान भार लागू करते हैं, लेकिन सिग्नल रिसेप्शन के लिए नहीं, बल्कि ट्रांसमिशन के लिए। यहां यह विचार करने योग्य है कि सिग्नल ट्रांसमिट करते समय, वेव वेक्टर की दिशा उलट जाती है। इसका मतलब यह है कि रिसेप्शन और ट्रांसमिशन के लिए चरणबद्ध वेक्टर के तत्व घातांक में साइन में भिन्न होते हैं, अर्थात। जटिल संयुग्मन द्वारा परस्पर जुड़ा हुआ। नतीजतन, हम -10 ° की दिशा में अधिकतम विकिरण पैटर्न प्राप्त करते हैं, जो एक ही वजन गुणांक पर प्राप्त संकेत के अधिकतम के साथ मेल नहीं खाता है। स्थिति को सही करने के लिए, जटिल संयुग्मन को भी वजन गुणांक पर लागू करना आवश्यक है।

ऐन्टेना सरणियों के साथ काम करते समय रिसेप्शन और ट्रांसमिशन के लिए बीम के गठन की वर्णित विशेषता को हमेशा ध्यान में रखा जाना चाहिए।

चलो विकिरण पैटर्न के साथ खेलते हैं

कुछ ऊँचा

हम समस्या को दिशा में विकिरण पैटर्न के दो मुख्य अधिकतम बनाने के लिए कहते हैं: -5 ° और 10 °। ऐसा करने के लिए, हम वेट वेक्टर के रूप में संबंधित दिशाओं के लिए चरणबद्ध वैक्टर का भारित योग चुनते हैं।

$$$ $ प्रदर्शन $ $ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ बीटा) \ textbf {s} (- 5 °) $ $ प्रदर्शन $ $

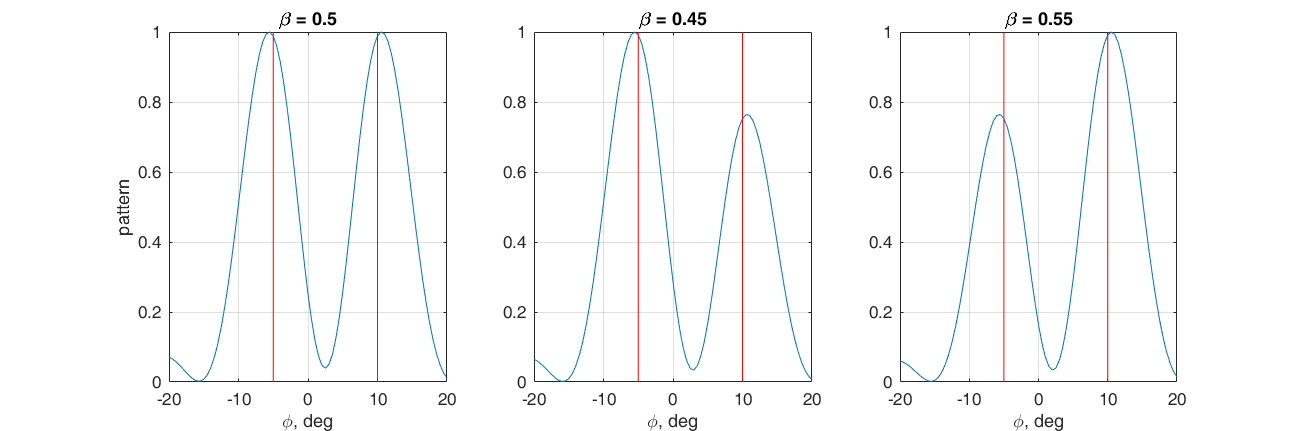
गुणांक e को समायोजित करके, मुख्य लोब के बीच का अनुपात समायोजित किया जा सकता है। यहाँ फिर से, यह देखना सुविधाजनक है कि वेक्टर अंतरिक्ष में क्या हो रहा है। यदि, 0.5 से अधिक है, तो वजन का सदिश s (10 °) के करीब होता है, अन्यथा s (-5 °) तक। किसी एक चरण के लिए वजन वेक्टर के करीब, अधिक से अधिक स्केलर उत्पाद, और इसलिए एनडी की इसी अधिकतम की परिमाण।

हालांकि, यह विचार करने योग्य है कि दोनों मुख्य पंखुड़ियों की परिमित चौड़ाई है, और अगर हम दो करीबी दिशाओं में ट्यून करना चाहते हैं, तो ये पंखुड़ियों को एक में विलय कर देंगे, कुछ मध्य दिशा में उन्मुख होंगे।

एक अधिकतम और शून्य

अब आइए दिशा में अधिकतम विकिरण पैटर्न को समायोजित करने का प्रयास करें$$ $ इनलाइन $ \ phi_1 = 10 ° $ इनलाइन $ और साथ ही दिशा से आने वाले सिग्नल को दबा देते हैं$$ $ इनलाइन $ \ phi_2 = -5 ° $ इनलाइन $ । इसके लिए, संबंधित कोण के लिए शून्य सेट करना आवश्यक है। आप इस प्रकार कर सकते हैं:

$$$ $ प्रदर्शन $ $ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf / s} _2 $ $ प्रदर्शन $ $

जहाँ$$ $ इनलाइन $ \ textbf {s} _1 = \ textbf {s} (10 °) $ इनलाइन $ , और$$ $ इनलाइन $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ इनलाइन $ ।

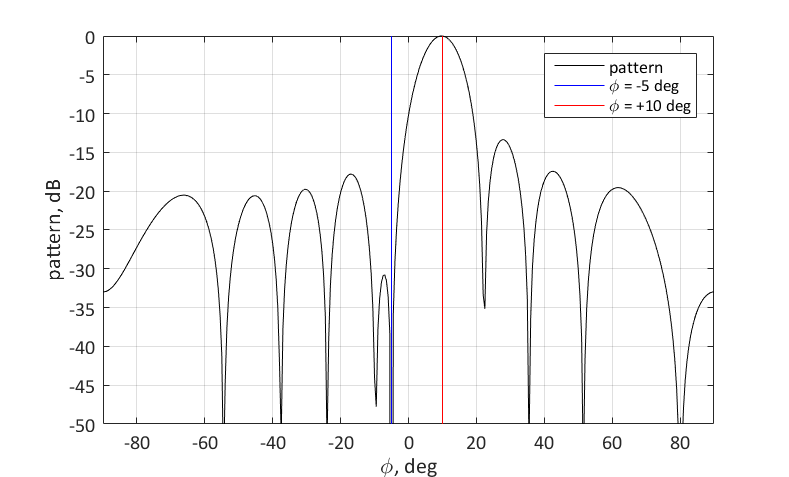
वेट वेक्टर की पसंद का ज्यामितीय अर्थ इस प्रकार है। हम चाहते हैं कि यह वेक्टर w पर अधिकतम प्रक्षेपण हो$$ $ इनलाइन $ \ textbf {s} _1 $ इनलाइन $ और वेक्टर के लिए रूढ़िवादी था$$ $ इनलाइन $ \ textbf {s} _2 $ इनलाइन $ । वेक्टर$$ $ इनलाइन $ \ textbf {s} _1 $ इनलाइन $ दो शब्दों के रूप में प्रतिनिधित्व किया जा सकता है: कोलियर वेक्टर$$ $ इनलाइन $ \ textbf {s} _2 $ इनलाइन $ और ओर्थोगोनल वेक्टर$$ $ इनलाइन $ \ textbf {s} _2 $ इनलाइन $ । समस्या कथन को संतुष्ट करने के लिए, वजन गुणांक w के वेक्टर के रूप में दूसरा घटक चुनना आवश्यक है। कोलिनियर घटक की गणना एक वेक्टर डिजाइन करके की जा सकती है$$ $ इनलाइन $ \ textbf {s} _1 $ इनलाइन $ सामान्यीकृत वेक्टर के लिए$$ $ इनलाइन $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ इनलाइन $ अदिश उत्पाद का उपयोग करना।

$$$$ $ $ $ \ textbf {s} _ {1}} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H's textbf {s} _1} {\ sqrt {N}} $ $ प्रदर्शन $ $

तदनुसार, प्रारंभिक चरणबद्ध वेक्टर से घटाना$$ $ इनलाइन $ \ textbf {s} _1 $ इनलाइन $ इसका कोलिनियर घटक, हम वांछित वजन वेक्टर प्राप्त करते हैं।

कुछ अतिरिक्त नोट

1. हर जगह, मैंने वजन वेक्टर को सामान्य करने के सवाल को छोड़ दिया, अर्थात। इसकी लंबाई। तो, वेट वेक्टर का सामान्यीकरण एंटीना सरणी विकिरण पैटर्न की विशेषताओं को प्रभावित नहीं करता है: मुख्य अधिकतम की दिशा, मुख्य लोब की चौड़ाई, आदि। यह भी दिखाया जा सकता है कि यह सामान्यीकरण स्थानिक प्रसंस्करण ब्लॉक के आउटपुट पर एसएनआर को प्रभावित नहीं करता है। इस संबंध में, जब स्थानिक संकेत प्रसंस्करण एल्गोरिदम पर विचार करते हैं, तो मैं आमतौर पर वेट वेक्टर के एक इकाई सामान्यीकरण को स्वीकार करता हूं, अर्थात।$$ $ इनलाइन $ \ textbf {w} ^ H \ textbf {w} = 1 $ इनलाइन $
2. एंटीना सरणी तल के गठन की संभावनाएं तत्वों एन की संख्या से निर्धारित होती हैं। अधिक तत्व, व्यापक संभावनाएं। स्थानिक भार प्रसंस्करण के कार्यान्वयन में स्वतंत्रता की अधिक डिग्री, एन-आयामी अंतरिक्ष में वजन वेक्टर को "मोड़" करने के लिए और अधिक विकल्प।
3. ऐन्टेना बीम पैटर्न प्राप्त करते समय , एंटीना सरणी भौतिक रूप से मौजूद नहीं है, और यह सब केवल उस कंप्यूटिंग इकाई की "कल्पना" में मौजूद है जो सिग्नल को संसाधित करता है। इसका मतलब यह है कि एक ही समय में, कई दिशाओं से आने वाले कई एमडी और स्वतंत्र रूप से सिग्नल सिग्नल को संश्लेषित करना संभव है। ट्रांसमिशन के मामले में, सब कुछ कुछ अधिक जटिल है, लेकिन विभिन्न डेटा धाराओं को प्रसारित करने के लिए कई एमडी को संश्लेषित करना भी संभव है। संचार प्रणालियों में इस तकनीक को MIMO कहा जाता है।
4. प्रदान किए गए matlab कोड का उपयोग करके, आप स्वयं NAM के साथ खेल सकते हैं
   
   कोड

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

अनुकूली एंटीना सरणी की मदद से कौन से कार्य हल किए जा सकते हैं?

आपका ध्यान के लिए धन्यवाद