एफएफटी एल्गोरिदम को समझना

नमस्कार दोस्तों। डेवलपर्स कोर्स के लिए एल्गोरिदम कल शुरू होता है, और हमारे पास अभी भी एक अप्रकाशित अनुवाद है। वास्तव में हम आपके साथ सामग्री को सही और साझा करते हैं। चलो चलते हैं।

फास्ट फूरियर ट्रांसफॉर्म (एफएफटी) सबसे महत्वपूर्ण सिग्नल प्रोसेसिंग और डेटा विश्लेषण एल्गोरिदम में से एक है। मैंने कंप्यूटर विज्ञान में बिना औपचारिक ज्ञान के वर्षों तक इसका उपयोग किया। लेकिन इस हफ्ते मेरे साथ ऐसा हुआ कि मैंने कभी नहीं सोचा कि एफएफटी इतनी जल्दी फूरियर ट्रांसफॉर्म की गणना कैसे करता है। मैंने एल्गोरिदम पर एक पुरानी किताब से धूल को हटा दिया, इसे खोल दिया, और भ्रामक सरल कम्प्यूटेशनल चाल के बारे में खुशी के साथ पढ़ा कि जेवी कोइले और जॉन टके ने इस विषय पर अपने क्लासिक 1965 के काम में वर्णित किया।



इस पोस्ट का लक्ष्य Cooley-Tukey FFT एल्गोरिथ्म में डुबकी लगाना है, जो इसे ले जाने वाले समरूपता को समझाता है, और कुछ सरल पायथन कार्यान्वयन दिखाता है जो अभ्यास में सिद्धांत को लागू करते हैं। मुझे उम्मीद है कि इस अध्ययन से डेटा विश्लेषण विशेषज्ञ, जैसे कि खुद को, हमारे द्वारा उपयोग किए जाने वाले एल्गोरिदम के तहत क्या हो रहा है, की एक और पूरी तस्वीर मिल जाएगी।

असतत फूरियर रूपांतरण

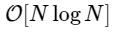
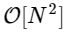
एफएफटी तेज है असतत फूरियर ट्रांसफॉर्म (डीएफटी) की गणना के लिए एक एल्गोरिथ्म, जिसकी सीधे गणना की जाती है । डीएफटी, फूरियर ट्रांसफॉर्म के अधिक परिचित निरंतर संस्करण की तरह, एक प्रत्यक्ष और उलटा रूप है, जिसे निम्नानुसार परिभाषित किया गया है:

प्रत्यक्ष असतत फूरियर ट्रांसफॉर्म (DFT):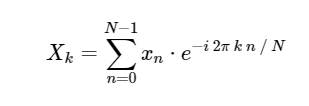



उलटा असतत फूरियर रूपांतरण (ODPF):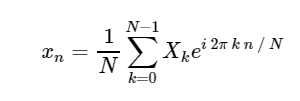



xn → Xk से रूपांतरण कॉन्फ़िगरेशन स्थान से आवृत्ति स्थान पर एक अनुवाद है और सिग्नल पावर स्पेक्ट्रम का अध्ययन करने और अधिक कुशल गणना के लिए कुछ कार्यों को परिवर्तित करने के लिए दोनों के लिए बहुत उपयोगी हो सकता है। आप खगोल विज्ञान और सांख्यिकी पर हमारी भविष्य की पुस्तक के अध्याय 10 में कार्रवाई में इसके कुछ उदाहरण पा सकते हैं, जहां आप चित्र और पायथन स्रोत कोड भी पा सकते हैं। अन्यथा जटिल अंतर समीकरणों के एकीकरण को आसान बनाने के लिए एफएफटी का उपयोग करने के एक उदाहरण के लिए, मेरी पोस्ट "पायथन में श्रोडिंगर समीकरण को हल करना" देखें ।

एफएफटी के महत्व के कारण (बाद में, पायथन के कई क्षेत्रों में समकक्ष एफएफटी - फास्ट फूरियर ट्रांसफॉर्म का उपयोग किया जा सकता है) इसमें गणना के लिए कई मानक उपकरण और गोले शामिल हैं। NumPy और SciPy दोनों के पास बहुत अच्छी तरह से परीक्षण किए गए FFTPACK लाइब्रेरी के गोले हैं, जो क्रमशः numpy.fft और scipy.fftpack numpy.fft में स्थित हैं। सबसे तेज़ FFT जो मुझे पता है कि FFTW पैकेज में है, जो PyFFTW पैकेज के माध्यम से Python में भी उपलब्ध है।

फिलहाल, आइए इन कार्यान्वयनों को एक तरफ छोड़ दें और आश्चर्य करें कि हम स्क्रैच से पायथन में एफएफटी की गणना कैसे कर सकते हैं।

असतत फूरियर रूपांतरण गणना

सरलता के लिए, हम केवल सीधे रूपांतरण से निपटेंगे, क्योंकि व्युत्क्रम परिवर्तन को बहुत ही समान तरीके से लागू किया जा सकता है। डीएफटी के उपरोक्त अभिव्यक्ति को देखते हुए, हम देखते हैं कि यह एक सीधा रैखिक ऑपरेशन से अधिक कुछ नहीं है: एक वेक्टर द्वारा मैट्रिक्स को गुणा करना





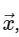
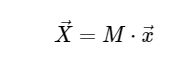
मैट्रिक्स एम के साथ दिया



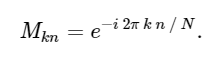
इसे ध्यान में रखते हुए, हम एक सरल मैट्रिक्स गुणा का उपयोग करके डीएफटी की गणना कर सकते हैं:

[1] में:

 import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x) 

हम परिणाम की जांच एफपीटी फंक्शन के साथ तुलना करके इसे दोहरा सकते हैं:

[2] में:

 x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x)) 

0ut [2]:

True

बस हमारे एल्गोरिथ्म की सुस्ती की पुष्टि करने के लिए, हम इन दो तरीकों के निष्पादन समय की तुलना कर सकते हैं:

[3] में:

 %timeit DFT_slow(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop 

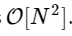
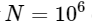
हम 1000 से अधिक बार धीमे हैं, जो कि इस तरह के सरलीकृत कार्यान्वयन के लिए अपेक्षित है। लेकिन यह सबसे बुरा नहीं है। लंबाई एन के इनपुट वेक्टर के लिए, एफएफटी एल्गोरिथ्म के रूप में जबकि हमारे धीमी एल्गोरिथ्म तराजू की तरह । इसका मतलब है कि के लिए तत्वों, हम FFT को लगभग 50 एमएस में पूरा करने की उम्मीद करते हैं, जबकि हमारे धीमी एल्गोरिथ्म में लगभग 20 घंटे लगेंगे!

तो एफएफटी इस तरह के त्वरण को कैसे प्राप्त करता है? इसका उत्तर समरूपता का उपयोग करना है।

असतत फूरियर रूपांतरण में समरूपता

एल्गोरिदम के निर्माण में सबसे महत्वपूर्ण उपकरणों में से एक कार्य समरूपता का उपयोग है। यदि आप विश्लेषणात्मक रूप से दिखा सकते हैं कि समस्या का एक हिस्सा बस दूसरे से संबंधित है, तो आप केवल एक बार उप-परिणाम की गणना कर सकते हैं और इस कम्प्यूटेशनल लागत को बचा सकते हैं। Cooley और Tukey ने एफएफटी प्राप्त करने के लिए इस दृष्टिकोण का बिल्कुल उपयोग किया।
हम अर्थ के प्रश्न से शुरू करते हैं । ऊपर हमारी अभिव्यक्ति से:



जहाँ हमने पहचान ऍक्स्प का उपयोग किया [2π] in = 1, जो किसी भी पूर्णांक n के लिए है।

अंतिम पंक्ति DFT की समरूपता संपत्ति को अच्छी तरह से दिखाती है:



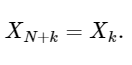
एक साधारण विस्तार



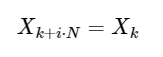
किसी भी पूर्णांक के लिए मैं। जैसा कि हम नीचे देखेंगे, इस समरूपता का उपयोग डीएफटी की गणना करने के लिए बहुत तेजी से किया जा सकता है।

FFT में DFT: समरूपता का उपयोग करना

Cooley और Tukey ने दिखाया कि FFT गणना को दो छोटे भागों में विभाजित किया जा सकता है। हमारे पास डीएफटी की परिभाषा से:



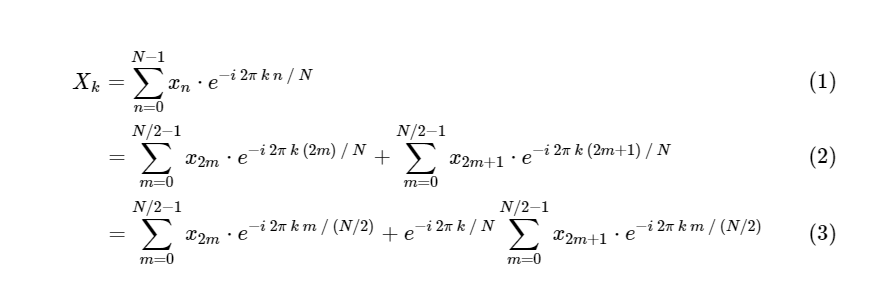
हमने एक असतत फूरियर ट्रांसफॉर्म को दो शब्दों में विभाजित किया है, जो अपने आप में छोटे असतत फूरियर ट्रांसफॉर्म के समान है, एक विषम संख्या वाले मान और एक सम संख्या वाले मान। हालाँकि, अभी तक हमने कोई संगणक चक्र नहीं बचाया है। प्रत्येक पद में (N / 2) consists N गणनाएँ होती हैं ।

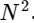
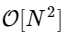
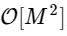
चाल इन स्थितियों में से प्रत्येक में समरूपता का उपयोग करना है। चूँकि k की श्रेणी 0≤k <N है, और n की सीमा 0 <n <M≡N / 2 है, हम ऊपर के समरूप गुणों से देखते हैं कि हमें प्रत्येक उपमा के लिए केवल आधी गणना करने की आवश्यकता है। हमारी गणना बन गया है जहाँ M, N से दो गुना कम है।

लेकिन इस पर ध्यान केंद्रित करने का कोई कारण नहीं है: जब तक हमारे छोटे फूरियर रूपांतरणों में एक भी एम है, हम इस विभाजन को फिर से लागू कर सकते हैं और दृष्टिकोण को जीत सकते हैं, हर बार कम्प्यूटेशनल लागत को आधा कर सकते हैं, जब तक कि हमारे सरणियां पर्याप्त रूप से छोटी न हों, ताकि रणनीति को अब लाभ न हो। स्पर्शोन्मुख सीमा में, यह पुनरावर्ती दृष्टिकोण O [NlogN] के रूप में होता है।

पायथन में इस पुनरावर्ती एल्गोरिदम को बहुत तेज़ी से लागू किया जा सकता है, हमारे धीमे डीएफटी कोड से शुरू होता है, जब उपमा का आकार बहुत छोटा हो जाता है:

[४] में:

 def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32: # this cutoff should be optimized return DFT_slow(x) else: X_even = FFT(x[::2]) X_odd = FFT(x[1::2]) factor = np.exp(-2j * np.pi * np.arange(N) / N) return np.concatenate([X_even + factor[:N / 2] * X_odd, X_even + factor[N / 2:] * X_odd]) 

यहाँ हम एक त्वरित जाँच करेंगे कि हमारा एल्गोरिथ्म सही परिणाम देता है:
[५] में:

 x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x)) 

बाहर [5]:
True

हमारे धीमे संस्करण के साथ इस एल्गोरिथ्म की तुलना करें:
-इन [6] में:

 %timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop 

हमारी गणना प्रत्यक्ष संस्करण की तुलना में तेज़ है! इसके अलावा, हमारे पुनरावर्ती एल्गोरिथ्म asymptotically है : हमने तेजी से फूरियर ट्रांसफॉर्म लागू किया।

ध्यान दें कि हम अभी भी सुदूर निर्मित एफएफटी एल्गोरिथ्म की गति के करीब नहीं हैं, और यह उम्मीद की जानी चाहिए। Fft सुपी के पीछे FFTPACK एल्गोरिथ्म एक फोरट्रान कार्यान्वयन है जिसे शोधन और अनुकूलन के वर्ष प्राप्त हुए हैं। इसके अलावा, हमारे NumPy समाधान में पायथन स्टैक की पुनरावृत्ति और कई अस्थायी सरणियों का आवंटन शामिल है, जो कम्प्यूटेशनल समय को बढ़ाता है।

पायथन / न्यूमपी के साथ काम करते समय कोड को गति देने के लिए एक अच्छी रणनीति जब भी संभव हो गणना दोहराएगी। हम ऐसा कर सकते हैं - इस प्रक्रिया में, हमारे पुनरावर्ती फ़ंक्शन कॉल को हटा दें, जो हमारे पायथन एफएफटी को और भी अधिक कुशल बना देगा।

सदिश Numpy संस्करण

कृपया ध्यान दें कि FFT के उपरोक्त पुनरावर्ती कार्यान्वयन में, पुनरावृत्ति के निम्नतम स्तर पर, हम N / 32 समान मैट्रिक्स-वेक्टर उत्पादों का प्रदर्शन करते हैं। यदि हम एक साथ एक मैट्रिक्स मैट्रिक्स उत्पाद के रूप में इन मैट्रिक्स-वेक्टर उत्पादों की गणना करते हैं, तो हमारे एल्गोरिथ्म की प्रभावशीलता जीत जाएगी। प्रत्येक बाद की पुनरावृत्ति के स्तर पर, हम दोहराए जाने वाले ऑपरेशन भी करते हैं जिसे वेक्टर किया जा सकता है। NumPy इस तरह के ऑपरेशन का एक उत्कृष्ट काम करता है, और हम इस तथ्य का उपयोग तेजी से फूरियर के इस वेक्टरकृत संस्करण को बनाने के लिए कर सकते हैं:

[7] में:

 def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0]) / X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel() 

यद्यपि एल्गोरिथ्म थोड़ा अधिक अपारदर्शी है, यह केवल एक अपवाद के साथ पुनरावर्ती संस्करण में उपयोग किए जाने वाले संचालन का पुनर्व्यवस्था है: हम गुणांक की गणना में समरूपता का उपयोग करते हैं और केवल आधा सरणी का निर्माण करते हैं। फिर, हम पुष्टि करते हैं कि हमारा कार्य सही परिणाम देता है:

[8] में:

 x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x)) 

बाहर [8]:
True

जैसे-जैसे हमारे एल्गोरिदम अधिक कुशल होते जाते हैं, हम समय की तुलना करने के लिए एक बड़े सरणी का उपयोग कर सकते हैं, DFT_slow छोड़कर:
[९] में:

 x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x) 

 10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop 

हमने परिमाण के एक क्रम से हमारे कार्यान्वयन में सुधार किया है! अब हम FFTPACK बेंचमार्क से लगभग 10 गुना दूर हैं, शुद्ध पायथन + न्यूपी की सिर्फ एक-दो दर्जन पंक्तियों का उपयोग कर रहे हैं। यद्यपि यह अभी भी कम्प्यूटेशनल रूप से सुसंगत नहीं है, पठनीयता के संदर्भ में, पायथन संस्करण FFTPACK स्रोत कोड से बहुत बेहतर है, जिसे आप यहां देख सकते हैं ।

तो FFTPACK इस अंतिम त्वरण को कैसे प्राप्त करता है? खैर, मूल रूप से, यह केवल विस्तृत बहीखाता की बात है। FFTPACK किसी भी मध्यवर्ती गणना का पुन: उपयोग करने में बहुत समय व्यतीत करता है जिसे पुन: उपयोग किया जा सकता है। हमारे रैग्ड संस्करण में अभी भी अतिरिक्त मेमोरी आवंटन और कॉपी करना शामिल है; एक निम्न-स्तरीय भाषा जैसे कि फोरट्रान में, स्मृति उपयोग को नियंत्रित करना और कम करना आसान है। इसके अलावा, Cooley-Tukey एल्गोरिथ्म को 2 के अलावा किसी अन्य आकार के विभाजनों का उपयोग करने के लिए बढ़ाया जा सकता है (जो हमने यहां लागू किया है उसे 2 के आधार पर Cooley-Tukey Radix FFT के रूप में जाना जाता है)। अन्य अधिक जटिल एफएफटी एल्गोरिदम का भी उपयोग किया जा सकता है, जिसमें कन्वेंशन डेटा के आधार पर मौलिक रूप से अलग-अलग दृष्टिकोण शामिल हैं (उदाहरण के लिए, ब्लूशेटिन एल्गोरिथ्म और रेडर एल्गोरिदम)। उपरोक्त एक्सटेंशन और विधियों के संयोजन से उन एफआर पर भी बहुत तेजी से एफएफटी हो सकते हैं, जिनका आकार दो की शक्ति नहीं है।

यद्यपि शुद्ध पायथन में कार्य संभवतः अभ्यास में बेकार हैं, मुझे आशा है कि वे एफएफटी पर आधारित डेटा विश्लेषण की पृष्ठभूमि में क्या हो रहा है, इसके बारे में कुछ जानकारी प्रदान करते हैं। डेटा विशेषज्ञों के रूप में, हम अपने अधिक एल्गोरिथम-दिमाग वाले सहयोगियों द्वारा बनाए गए मूलभूत साधनों के "ब्लैक बॉक्स" के कार्यान्वयन का सामना कर सकते हैं, लेकिन मेरा दृढ़ता से मानना ​​है कि हम अपने डेटा पर लागू होने वाले निम्न-स्तरीय एल्गोरिदम के बारे में अधिक समझ रखते हैं, बेहतर अभ्यास। हम करेंगे।

यह पोस्ट पूरी तरह से IPython Notepad में लिखी गई थी। पूर्ण नोटबुक को यहां डाउनलोड किया जा सकता है या स्टेटिक रूप से यहां देखा जा सकता है ।

कई लोग यह देख सकते हैं कि सामग्री नए से बहुत दूर है, लेकिन जैसा कि हमें लगता है, काफी प्रासंगिक है। सामान्य तौर पर, यह लिखें कि क्या लेख उपयोगी था। आपकी टिप्पणियों की प्रतीक्षा है।