प्रस्तावना

अपने हालिया लेख के अलावा , मैं MU ( M ulti U ser) MIMO के विषय पर भी बात करना चाहूंगा। मैंने पहले ही प्रोफेसर हार्ड्ट के एक बहुत प्रसिद्ध लेख का उल्लेख किया है, जहां वह अपने सहयोगियों के साथ मिलकर, उपयोगकर्ताओं को एक चैनल के ब्लॉक डायगनैलाइज़ेशन, जैसे रैखिक तरीकों पर आधारित डाउन लिंक में उपयोगकर्ताओं को अलग करने के लिए एक एल्गोरिथ्म का प्रस्ताव देता है। लेख में उद्धरणों की एक प्रभावशाली संख्या है , और परीक्षा असाइनमेंट में से एक के लिए आधारशिला प्रकाशन भी है। इसलिए, प्रस्तावित एल्गोरिथ्म की मूल बातें क्यों नहीं बनाई गई हैं?

समस्या का बयान

सबसे पहले, तय करते हैं कि अब हम किस क्षेत्र में MIMO थीम पर काम करेंगे।
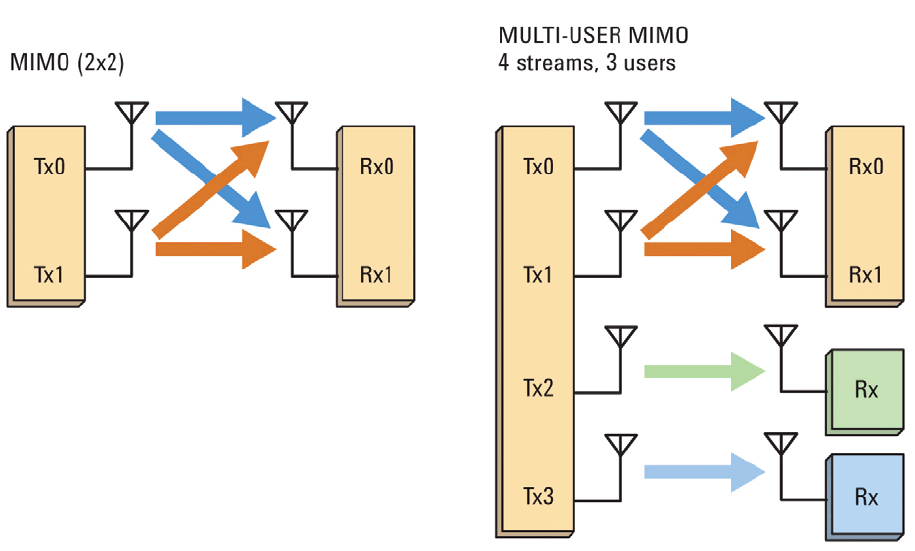
परंपरागत रूप से, MIMO प्रौद्योगिकी के ढांचे के भीतर सभी हस्तांतरण विधियों को दो मुख्य समूहों में विभाजित किया जा सकता है:

• स्थानिक विविधता

ट्रांसमिशन का शोर प्रतिरक्षा बढ़ाने के लिए मुख्य लक्ष्य है। स्थानिक चैनल, यदि सरलीकृत किया जाता है, तो एक-दूसरे की नकल करते हैं, जिसके कारण हमें सर्वोत्तम संचरण गुणवत्ता मिलती है।

उदाहरण:
- ब्लॉक कोड (उदाहरण के लिए, अलमुती योजना );
- विटर्बी एल्गोरिथ्म पर आधारित कोड।

• स्थानिक बहुसंकेतन

ट्रांसमिशन स्पीड को बढ़ाना मुख्य लक्ष्य है। हमने पहले ही एक पिछले लेख में चर्चा की थी कि कुछ शर्तों के तहत MIMO चैनल को समानांतर SISO चैनलों की एक श्रृंखला के रूप में माना जा सकता है। दरअसल, यह स्थानिक बहुसंकेतन का केंद्रीय विचार है: अधिकतम संख्या में स्वतंत्र सूचना प्रवाह प्राप्त करना। इस मामले में मुख्य समस्या अंतर-चैनल हस्तक्षेप (इंटर-चैनल हस्तक्षेप) का दमन है, जिसके लिए कई वर्ग हैं:

- क्षैतिज चैनल जुदाई;
- ऊर्ध्वाधर (उदाहरण के लिए, वी-ब्लास्ट एल्गोरिथ्म);
- विकर्ण (उदाहरण के लिए, डी-ब्लास्ट एल्गोरिथ्म)।

लेकिन यह, बिल्कुल नहीं है।

स्थानिक बहुसंकेतन के विचार का विस्तार किया जा सकता है: न केवल चैनलों को विभाजित करने के लिए, बल्कि उपयोगकर्ताओं (एसडीएमए - स्पेस डिवीजन मल्टीपल एक्सेस) के लिए भी।

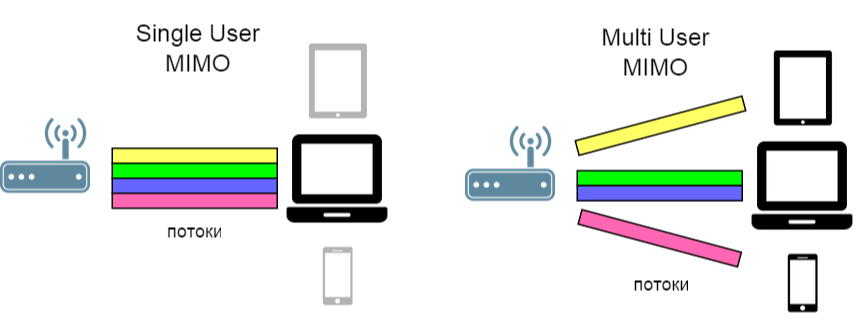
( चित्रण के स्रोत से लिंक )

नतीजतन, इस मामले में, अंतर-उपयोगकर्ता हस्तक्षेप के खिलाफ लड़ने के लिए पहले से ही आवश्यक है। इसके लिए, ब्लॉक डायगोलाइज़ेशन जीरो-फोर्सिंग नामक एक एल्गोरिथ्म प्रस्तावित किया गया था , जिसे हम आज विचार कर रहे हैं।

गणितीय विवरण

चलो, पहले से प्राप्त सिग्नल मॉडल के साथ शुरू करते हैं। अधिक सटीक रूप से, हम आरेख पर दिखाते हैं कि क्या और कहाँ से आता है:

इस मामले में चैनल मैट्रिक्स का रूप है:

संचारण एंटेना की कुल संख्या के साथ , और एंटेना प्राप्त करने की कुल संख्या ।

महत्वपूर्ण :
इस एल्गोरिथम को केवल तभी लागू किया जा सकता है जब एंटेना प्राप्त करने की कुल संख्या एंटेना प्राप्त करने की कुल संख्या से अधिक या बराबर हो:

यह स्थिति विकर्णीकरण के गुणों को सीधे प्रभावित करती है।

तो, प्राप्त प्रतीकों (संकेतों) के मॉडल को वेक्टर रूप में लिखा जा सकता है:

हालाँकि, किसी विशिष्ट उपयोगकर्ता के लिए सूत्र देखना अधिक दिलचस्प है:

वास्तव में:

• K- वें उपयोगकर्ता के लिए एक उपयोगी संकेत है,

  
  

• - यह अन्य उपयोगकर्ताओं से हस्तक्षेप है,

  
  

• - योजक शोर।

तो हम मुख्य कार्य के सूत्रीकरण पर आते हैं:

आप ऐसे मेट्रिसेस पा सकते हैं ताकि हस्तक्षेप का हिस्सा शून्य हो जाए!

यही हम करेंगे।

एल्गोरिथम विवरण

हम एक उदाहरण के साथ विवरण को आगे बढ़ाएंगे, और एक दृष्टांत के रूप में मैं पहले हाथ के स्क्रीनशॉट दूंगा , उन पर थोड़ी टिप्पणी करूंगा।

पहले उपयोगकर्ता पर विचार करें:

चलिए मुख्य चरणों के बारे में बात करते हैं:

• हम कुछ मैट्रिक्स बनाते हैं अन्य सभी उपयोगकर्ताओं के चैनल मैट्रिसेस से।

• हम एसवीडी विधि का उपयोग करके इसे विघटित करते हैं।

  
  

• मैट्रिक्स में हम शोर उप-स्थान (नल-उप-स्थान) - मैट्रिक्स को ढूंढते हैं (यानी, वह सब कुछ जो मैट्रिक्स की रैंक से आगे जाता है - इसे निरूपित करें )।

  
  

• हम इस शोर मैट्रिक्स और इसके हर्मिटियन संयुग्मन से कुछ प्रक्षेपण मैट्रिक्स की रचना करते हैं ।

  
  

आगे बढ़ो:

• अब चैनल मैट्रिक्स का मूल भाग परिणामी प्रक्षेपण मैट्रिक्स के साथ गुणा करें ।

  
  

• हम एसवीडी के माध्यम से परिणाम को विघटित करते हैं।

  
  

• मैट्रिक्स में चुनना लाइनें जहां - रैंक ।

  
  

• उन्हें स्थानांतरित करें और मैट्रिक्स प्राप्त करें (या - जहां जैसा संकेत दिया गया है)।

  
  

और इसलिए यह प्रक्रिया प्रत्येक उपयोगकर्ता के लिए दोहराई जाएगी। क्या यह गणित का जादू नहीं है: रैखिक बीजगणित की विधियों का उपयोग करके, हम पूरी तरह से तकनीकी समस्याओं को हल करते हैं!

ध्यान दें कि व्यवहार में न केवल प्राप्त पूर्व-कोडिंग मैट्रिस का उपयोग किया जाता है, बल्कि पोस्ट-प्रोसेसिंग मैट्रिसेस और मैट्रिक्स मूल्यों के मैट्रिक्स ( स्लाइड देखें) भी। उत्तरार्द्ध, उदाहरण के लिए, पहले से ही ज्ञात पानी डालने वाले एल्गोरिदम के अनुसार शक्ति को संतुलित करने के लिए।

हम एल्गोरिथ्म मॉडल

मुझे लगता है कि परिणाम को मजबूत करने के लिए एक छोटे से सिमुलेशन का संचालन करना बेहतर नहीं होगा। ऐसा करने के लिए, हम पायथन 3 का उपयोग करेंगे, अर्थात्:

import numpy as np 

बुनियादी गणना के लिए, और:

 import pandas as pd 

परिणाम प्रदर्शित करने के लिए।

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

मान लें कि हमारे पास 8 संचारण वाले एंटेना और 3 उपयोगकर्ता हैं, जिनके पास क्रमशः 3, 2 और 3 प्राप्त करने वाले एंटेना हैं:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

हम अपनी कक्षा को इनिशियलाइज़ करते हैं और उपयुक्त तरीके अपनाते हैं:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

हम एक पठनीय रूप में लाते हैं:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

और स्पष्टता के लिए थोड़ा लिफ्ट करें (हालांकि आप इसके बिना कर सकते हैं):

 print(pd.DataFrame(np.round(np.real(df),100))) 

आपको कुछ इस तरह से मिलना चाहिए:

दरअसल, यहां वे ब्लॉक हैं, यहां यह है और विकर्ण है। और हस्तक्षेप को कम करना।

ऐसी बातें।

साहित्य

1. स्पेंसर, क्वेंटिन एच।, ए ली स्विंडलहर्स्ट, और मार्टिन हैर्ड। "बहु-स्तरीय MIMO चैनलों में डाउनलिंक स्थानिक बहुसंकेतन के लिए शून्य-मजबूर करने के तरीके।" सिग्नल प्रोसेसिंग पर आईईईई लेनदेन 52.2 (2004): 461-471।
2. मार्टिन Haard " मल्टी-उपयोगकर्ता MIMO सिस्टम के लिए रोबोट ट्रांसमिशन प्रक्रिया "

पुनश्च

शिक्षण स्टाफ और मेरे मूल पेशे के छात्र बिरादरी को मैं नमस्ते कहता हूं!