यादृच्छिक क्रमपरिवर्तन और यादृच्छिक विभाजन

कई वर्षों से मैं गणित और कंप्यूटर वैज्ञानिकों (यह रूसी, कंप्यूटर वैज्ञानिकों में कैसे है?) के छात्रों के लिए कॉम्बिनेटरिक्स और ग्राफ़ में पाठ्यक्रम दे रहा है, पहले अकादमिक विश्वविद्यालय में और अब सेंट पीटर्सबर्ग स्टेट यूनिवर्सिटी में । हमारे कार्यक्रम को इस तरह से डिज़ाइन किया गया है कि इन विषयों को "सैद्धांतिक कंप्यूटर विज्ञान" के हिस्से के रूप में रखा गया है (इसमें अन्य विषय एल्गोरिदम, जटिलता, भाषा और व्याकरण हैं)। मैं यह नहीं कह सकता कि कैसे आध्यात्मिक या ऐतिहासिक रूप से उचित है: फिर भी, कंप्यूटर के आगमन से बहुत पहले, दहनशील वस्तुएं (रेखांकन, सेट सिस्टम, क्रमपरिवर्तन, चेक किए गए आंकड़े, आदि) का अध्ययन किया जाना शुरू हुआ, और अब यह महत्वपूर्ण है, हालांकि यह महत्वपूर्ण है, यह दिलचस्पी के एकमात्र कारण से बहुत दूर है। उन्हें। लेकिन कॉम्बिनेटरिक्स और सैद्धांतिक कंप्यूटर विज्ञान में बहुत विशेषज्ञों को देखकर आश्चर्यजनक रूप से अक्सर एक ही लोग हैं: लोवास, अलोन, सेमेरी, रज़ोरोव और उससे आगे। शायद इसके कारण हैं। मेरे पाठों में, ओलम्पिक प्रोग्रामिंग चैंपियन अक्सर जटिल समस्याओं के लिए बहुत ही गैर-तुच्छ समाधान पेश करते हैं (मैं उन्हें सूचीबद्ध नहीं करूंगा, किसी को भी शीर्ष कोडफोर्स देखने के लिए उत्सुक हूं।) सामान्य तौर पर, मुझे लगता है कि कॉम्बिनेटरिक्स की कुछ चीजें समुदाय के लिए रुचि हो सकती हैं। बोले कि कुछ है या नहीं।

आपको 1 से संख्याओं का एक यादृच्छिक क्रमांकन बनाने की आवश्यकता है$$ $ इनलाइन $ n $ इनलाइन $ ताकि सभी क्रमपरिवर्तन समान रूप से संभावित हों। यह कई तरीकों से किया जा सकता है: उदाहरण के लिए, पहले बेतरतीब ढंग से पहले तत्व का चयन करें, फिर शेष दूसरे से और इसी तरह। या आप अन्यथा कर सकते हैं: बेतरतीब ढंग से अंक का चयन करें$$ $ इनलाइन $ t_1, t_2, \ ldots, t_n $ इनलाइन $ खंड में$$ $ इनलाइन $ [0,1] $ इनलाइन $ , और देखें कि उन्हें कैसे आदेश दिया जाता है। 1 के साथ सबसे छोटी संख्याओं को बदलना, 2 के साथ दूसरा, और इसी तरह, हमें एक यादृच्छिक क्रमपरिवर्तन मिलता है। यह सब कुछ देखना आसान है$$ $ इनलाइन $ n! $ इनलाइन $ क्रमपरिवर्तन समान रूप से संभावित हैं। यह संभव है और सेगमेंट में नहीं$$ $ इनलाइन $ 0.1 $ इनलाइन $ अंक चुनें, और, उदाहरण के लिए, 1 से संख्याओं के बीच$$ $ इनलाइन $ n $ इनलाइन $ । संयोग यहां संभव हैं (एक खंड के लिए, वे भी संभव हैं, लेकिन शून्य संभावना के साथ, इसलिए वे हमें परेशान नहीं करते हैं) - आप उनके साथ विभिन्न तरीकों से निपट सकते हैं, उदाहरण के लिए, इसके अलावा संयोग संख्याओं को फिर से व्यवस्थित करना। या एन को बड़ा लें ताकि संयोग की संभावना छोटी हो (जब मामला हो$$ $ इनलाइन $ N = 365 $ इनलाइन $ , और$$ $ इनलाइन $ n $ इनलाइन $ आपकी कक्षा में छात्रों की संख्या है, और हम दो जन्मदिनों के संयोग के बारे में बात कर रहे हैं।) इस पद्धति पर एक विविधता यादृच्छिक रूप से ध्यान दें।$$ $ इनलाइन $ n $ इनलाइन $ एक इकाई वर्ग में इंगित करता है और देखता है कि उनके निर्देशांक कैसे एब्सिस के सापेक्ष दिए जाते हैं। एक और भिन्नता: खंड में निशान$$ $ इनलाइन $ n-1 $ इनलाइन $ इंगित करें और देखें कि यह किस खंड में विभाजित है, इसकी लंबाई कितनी है। इन दृष्टिकोणों में मुख्य बिंदु परीक्षणों की स्वतंत्रता है, जिसके परिणामों के अनुसार एक यादृच्छिक पुनर्व्यवस्था का निर्माण किया जाता है। आंद्रेई निकोलायेविच कोलमोगोरोव ने कहा कि संभाव्यता सिद्धांत उपाय प्लस स्वतंत्रता का एक सिद्धांत है - और इसकी पुष्टि किसी भी व्यक्ति द्वारा की जाएगी, जिसने संभावना से निपटा है।

मैं दिखाऊंगा कि यह कैसे मदद करता है, पेड़ों के लिए हुक फार्मूले के उदाहरण का उपयोग करते हुए:



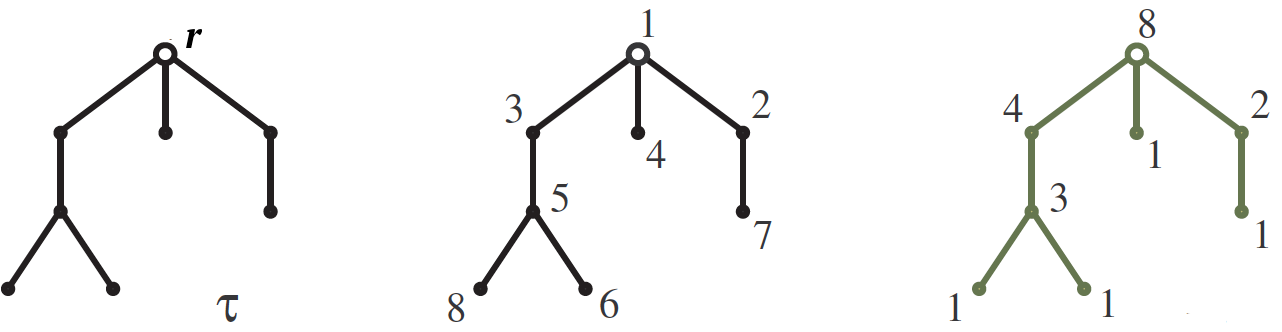
चलो$$ $ इनलाइन $ \ tau $ इनलाइन $ - रूट द्वारा निलंबित$$ $ इनलाइन $ आर $ इनलाइन $ के साथ पेड़$$ $ इनलाइन $ n $ इनलाइन $ चित्र की तरह नीचे बढ़ती चोटियाँ। हमारा लक्ष्य संख्या की गणना करना है$$ $ इनलाइन $ S (\ tau) $ इनलाइन $ नंबरिंग ट्री टॉप$$ $ इनलाइन $ \ tau $ इनलाइन $ संख्या 1 से$$ $ इनलाइन $ n $ इनलाइन $ ऐसा है कि प्रत्येक किनारे के लिए इसके शीर्ष पर संख्या नीचे की तुलना में अधिक है। इनमें से एक नंबर को मध्य चित्र में दिखाया गया है। हुक आकार का उपयोग करके उत्तर तैयार किया जाता है। अंकुड़ा$$ $ इनलाइन $ H (v) $ इनलाइन $ कोने$$ $ इनलाइन $ v $ इनलाइन $ आइए इस शीर्ष से बढ़ते हुए एक सबट्री को कॉल करें, और इसका आकार बस इसमें लंब की संख्या है। हुक की लंबाई सही चित्र में इसी कोने के बगल में लिखी जाती है। तो, संख्या की संख्या है$$ $ इनलाइन $ n! $ इनलाइन $ हुक आकार के उत्पाद से विभाजित, इसलिए हमारे उदाहरण के लिए

$$$ $ प्रदर्शन $ $ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $ $ प्रदर्शन $ $

हम उस सूत्र को विभिन्न तरीकों से साबित कर सकते हैं, उदाहरण के लिए कोने की संख्या पर प्रेरण द्वारा, लेकिन यादृच्छिक क्रमपरिवर्तन के बारे में हमारा दृष्टिकोण हमें बिना किसी गणना के प्रमाण को पूरा करने की अनुमति देता है। यह न केवल लालित्य से बेहतर है, बल्कि इसलिए भी है क्योंकि यह निर्धारित असमानताओं के साथ अंकन के बारे में अधिक सूक्ष्म सवालों को अच्छी तरह से सामान्य करता है, लेकिन अब इसके बारे में नहीं। तो, n अलग-अलग वास्तविक संख्याएं लें और उन्हें पेड़ के शीर्ष पर रखें, प्रत्येक में एक संख्या, सभी के साथ$$ $ इनलाइन $ n! $ इनलाइन $ क्रमपरिवर्तन समान रूप से संभावित हैं। क्या संभावना है कि प्रत्येक किनारे के लिए, किनारे के शीर्ष शीर्ष पर संख्या अपने निचले शीर्ष पर संख्या से अधिक है? उत्तर है:$$ $ इनलाइन $ S (\ tau) / n! $ इनलाइन $ , और यह संख्याओं के एक सेट पर निर्भर नहीं करता है। और अगर यह निर्भर नहीं करता है, तो चलो संख्याओं को यादृच्छिक रूप से चयनित - निश्चितता के लिए, अंतराल में विचार करें$$ $ इनलाइन $ [0,1] $ इनलाइन $ । पहले नंबर पर यादृच्छिक रूप से चयन करने के बजाय, और फिर उन्हें पेड़ के शीर्ष पर बेतरतीब ढंग से व्यवस्थित करने के बजाय, हम बस बेतरतीब ढंग से और स्वतंत्र रूप से प्रत्येक शीर्ष पर एक संख्या का चयन कर सकते हैं: उनकी पुनर्व्यवस्था स्वचालित रूप से यादृच्छिक होगी। इस तरह से$$ $ इनलाइन $ S (\ tau) / n! $ इनलाइन $ यह संभावना है कि यादृच्छिक स्वतंत्र संख्याओं के लिए$$ $ इनलाइन $ \ xi (v) $ इनलाइन $ प्रत्येक शीर्ष के लिए एक का चयन किया$$ $ इनलाइन $ v $ इनलाइन $ लकड़ी$$ $ इनलाइन $ \ tau $ इनलाइन $ , फार्म की सभी असमानताएं$$ $ इनलाइन $ \ xi (v)> \ xi (u) $ इनलाइन $ सभी किनारों के लिए$$ $ इनलाइन $ v \ u से u $ इनलाइन $ ।$$ $ इनलाइन $ v $ इनलाइन $ रिब के शीर्ष शीर्ष है, और$$ $ इनलाइन $ यू $ इनलाइन $ - नीचे। हम इन स्थितियों को एक समान रूप में तैयार करते हैं, लेकिन कुछ अलग तरीके से: प्रत्येक शीर्ष के लिए$$ $ इनलाइन $ v $ इनलाइन $ इस तरह की घटना होनी चाहिए - मैं इसे निर्दिष्ट करूंगा

$$$ इनलाइन $ Q (v) $ इनलाइन $ : संख्या$$ $ इनलाइन $ \ xi (v) $ इनलाइन $ - हुक सबट्री के कोने पर सभी नंबरों के बीच अधिकतम$$ $ इनलाइन $ H (v) $ इनलाइन $ ।

ध्यान दें$$ $ इनलाइन $ \ frac {1} {| H (v) |} $ इनलाइन $ यह एक घटना की संभावना है$$ $ इनलाइन $ Q (v) $ इनलाइन $ । वास्तव में, हुक में$$ $ इनलाइन $ H (v) $ इनलाइन $ उपलब्ध है$$ $ इनलाइन $ | H (v) | $ इनलाइन $ कोने और अधिकतम हुक संख्या उनमें से प्रत्येक के लिए समान संभावना के साथ मैप की जाती है$$ $ इनलाइन $ \ frac {1} {| H (v) |} $ इनलाइन $ । तो हुक सूत्र$$ $ इनलाइन $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ इनलाइन $ निम्नानुसार तैयार किया जा सकता है: संभावना है कि सभी घटनाएं एक ही बार में होती हैं$$ $ इनलाइन $ Q (v) $ इनलाइन $ इन घटनाओं की संभावनाओं के उत्पाद के बराबर है। इसके कारण कई अलग-अलग हो सकते हैं, लेकिन सबसे पहले जो दिमाग में आता है वह यहां काम करता है: ये घटनाएँ स्वतंत्र हैं। इसे समझने के लिए, आइए देखें, उदाहरण के लिए, किसी घटना पर$$ $ इनलाइन $ Q (r) $ इनलाइन $ (जड़ के अनुरूप)। यह इस तथ्य में सम्‍मिलित है कि जड़ में संख्‍या सभी संख्‍याओं की अन्‍य संख्‍याओं से अधिक होती है, और अन्‍य घटनाएँ जड़ में न लिखे गए आपस में तुलना से संबंधित होती हैं। वह है$$ $ इनलाइन $ Q (r) $ इनलाइन $ संख्या के बारे में$$ $ इनलाइन $ \ xi (r) $ इनलाइन $ और अन्य कोने पर संख्याओं के सेट , और अन्य सभी घटनाएं रूट के अलावा अन्य संख्याओं के क्रम की हैं । जैसा कि हमने पहले ही चर्चा की है, "आदेश" और "भीड़" स्वतंत्र हैं, इसलिए घटना$$ $ इनलाइन $ Q (r) $ इनलाइन $ दूसरों से स्वतंत्र। पेड़ के नीचे जाने पर, हमें पता चलता है कि ये सभी घटनाएँ स्वतंत्र हैं, जहाँ से आवश्यक है।

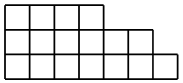
आमतौर पर, हुक के लिए फार्मूला पेड़ में कोने नहीं बल्कि यंग आरेख में कोशिकाओं की संख्या के लिए सूत्र है समन्वय अक्षों की दिशा में बढ़ते हुए, और हुक पेड़ों की तुलना में अधिक हुक जैसे होते हैं। लेकिन यह सूत्र अधिक जटिल साबित होता है और एक अलग पद का हकदार होता है।

चूंकि मेरे पास रास्ते थे, मैं मदद नहीं कर सकता लेकिन एक यादृच्छिक युवा आरेख के मॉडल के बारे में बात कर सकता हूं। यंग डायग्राम एक ऐसा फिगर है$$ $ इनलाइन $ n $ इनलाइन $ इकाई वर्ग, इसकी पंक्तियों की लंबाई नीचे से ऊपर तक और स्तंभों की लंबाई बाईं से दाईं ओर बढ़ती है। यंग के एरिया चार्ट की संख्या$$ $ इनलाइन $ n $ इनलाइन $ इंगित किया गया है$$ $ इनलाइन $ p (n) $ इनलाइन $ , यह महत्वपूर्ण कार्य एक दिलचस्प और असामान्य तरीके से व्यवहार करता है: उदाहरण के लिए, यह किसी भी बहुपद की तुलना में तेजी से बढ़ता है, लेकिन इसके घातांक की तुलना में धीमा है। इसलिए, विशेष रूप से, एक यादृच्छिक युवा आरेख उत्पन्न करें (यदि हम सभी क्षेत्र आरेख चाहते हैं$$ $ इनलाइन $ n $ इनलाइन $ समान रूप से संभावना थी$$ $ इनलाइन $ 1 / p (n) $ इनलाइन $ ) कोई मामूली बात नहीं है। उदाहरण के लिए, यदि आप एक समय में एक को जोड़ते हैं, तो बेतरतीब ढंग से जोड़ने के लिए जगह का चयन करते हुए, विभिन्न चार्ट में अलग-अलग संभावनाएं होंगी (इसलिए, एकल-लाइन चार्ट की संभावना बराबर हो जाती है$$ $ इनलाइन $ 1/2 ^ {n-1} $ इनलाइन $ ।) यह आरेख पर एक मनोरंजक उपाय निकला, लेकिन एक समान नहीं है। निम्नानुसार वर्दी प्राप्त की जा सकती है। नंबर लो$$ $ इनलाइन $ t \ in (0,1) $ इनलाइन $ , हमारे उद्देश्यों के लिए, क्षेत्र में संख्या सबसे उपयुक्त हैं$$ $ इनलाइन $ 1- \ mathrm {const} / \ sqrt {n} $ इनलाइन $ । प्रत्येक के लिए$$ $ इनलाइन $ k = 1,2, \ ldots $ इनलाइन $
गैर-नकारात्मक पूर्णांक पर ज्यामितीय वितरण पर विचार करें$$ $ इनलाइन $ t ^ k $ इनलाइन $ (यानी संख्या की संभावना$$ $ इनलाइन $ m = 0,1, \ ldots $ इनलाइन $ के बराबर है$$ $ इनलाइन $ t ^ {किमी} (1-t ^ k) $ इनलाइन $ )। हम इसके अनुसार एक यादृच्छिक चर चुनते हैं$$ $ इनलाइन $ m_k $ इनलाइन $ (इसे व्यवस्थित करने के कई तरीके हैं)। बड़े पैमाने पर$$ $ इनलाइन $ k $ इनलाइन $ सबसे अधिक संभावना है। चलो यंग आरेख को देखें$$ $ इनलाइन $ m_k $ इनलाइन $ पंक्तियाँ लंबाई हैं$$ $ इनलाइन $ k $ इनलाइन $ हर पर$$ $ इनलाइन $ k = 1,2, \ ldots $ इनलाइन $ । मैं इसे जहाज विधि कहता हूं क्योंकि कुल क्षेत्र कभी-कभी बराबर होता है$$ $ इनलाइन $ n $ इनलाइन $ । यदि बराबर नहीं है, तो प्रयोग को दोहराएं। वास्तव में बराबर$$ $ इनलाइन $ n $ इनलाइन $ अगर वह चालाकी से चुने तो वह अक्सर पर्याप्त है$$ $ इनलाइन $ t \ in (0,1) $ इनलाइन $ । मैं पाठक को स्वतंत्र रूप से यह साबित करने के लिए आमंत्रित करता हूं कि किसी दिए गए क्षेत्र के सभी आरेख समान रूप से संभावित हैं और चरणों की संख्या का अनुमान लगाते हैं।