परिचय
जब PyWavelets पुस्तकालय (एमआईटी लाइसेंस के तहत जारी एक मुफ्त खुला स्रोत सॉफ्टवेयर) का उपयोग करके सीडब्ल्यूटी विश्लेषण का आयोजन किया जाता है, तो परिणाम की कल्पना करने में समस्याएं होती हैं। डेवलपर्स द्वारा प्रस्तावित विज़ुअलाइज़ेशन परीक्षण
कार्यक्रम निम्नलिखित सूची में दिखाया गया है:
लिस्टिंगimport pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max())
जब जटिल तरंगों के साथ काम करते हैं, उदाहरण के लिए 'cmor1-1.5' के साथ, कार्यक्रम एक त्रुटि पैदा करता है:
File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float
यह त्रुटि, साथ ही आवश्यक समय रिज़ॉल्यूशन प्रदान करने के लिए स्केल (चौड़ाई) चुनने के साथ कठिनाइयाँ, विशेष रूप से नौसिखिए उपयोगकर्ताओं के लिए, सीडब्ल्यूटी विश्लेषण का अध्ययन करना मुश्किल बना देती है, जिसने मुझे एक शैक्षिक प्रकृति के इस लेख को लिखने के लिए प्रेरित किया।
इस प्रकाशन का उद्देश्य सरल और विशेष संकेतों के विश्लेषण के लिए नए
स्केलोग्राम विज़ुअलाइज़ेशन
मॉड्यूल के उपयोग पर विचार करना है, साथ ही साथ सामान्यीकरण विधियों, लॉगरिदमिक स्केलिंग और संश्लेषण का उपयोग करना है, जो समय श्रृंखला के विश्लेषण में अतिरिक्त जानकारी प्रदान करते हैं।
लेख ने प्रकाशन से जानकारी का उपयोग किया
"डेटा विश्लेषण के लिए तरंगिका के लिए एक सौम्य परिचय" । प्रकाशन में दिए गए उदाहरणों की सूचियों में, त्रुटियों को ठीक किया जाता है, और उदाहरण की प्रत्येक सूची को उसके समाप्त रूप में लाया जाता है, जो इसे पिछले वाले के साथ परिचित होने के बिना उपयोग करने की अनुमति देता है। विशेष संकेतों के तरंग विश्लेषण के लिए, PyWavelets
नमूना डेटाबेस के डेटा का उपयोग किया गया था।
एक तरंगिका स्केलोग्राम एक आयामी डेटा का दो-आयामी प्रतिनिधित्व है। समय एक्स अक्ष पर प्लॉट किया जाता है, और वाई अक्ष पर एक स्केल दिखाया जाता है - समय पर सिग्नल आयाम के अनुरूप सिग्नल के तरंगिका परिवर्तन का परिणाम एक्स। सिग्नल के ऐसे ग्राफिक डिस्प्ले का विश्लेषणात्मक मूल्य यह है कि वाई अक्ष पर समय रिज़ॉल्यूशन प्रदर्शित होता है, जो अतिरिक्त जानकारी देता है। संकेत के गतिशील गुणों के बारे में।
वेवलेट - सिंपल सिग्नल स्कैग्लोग्राम्स
1. गॉसियन लिफाफे के साथ कोसाइन तरंग (रिप्लेसमेंट वेवलेट्स। आप पैमाने पर समय संकल्प की निर्भरता का अध्ययन कर सकते हैं):
लिस्टिंग from numpy import* from pylab import* import scaleogram as scg import pywt
सिग्नल रूपांतरण के लिए वेवलेट फ़ंक्शन: cmor1-1.5 (कॉम्प्लेक्स मोरलेट वेवलेट्स)


आवधिक संकेत अब बिंदु Y = p1 पर एक क्षैतिज निरंतर पट्टी के रूप में प्रकट होता है, जिसकी तीव्रता आवधिक संकेत के आयाम के आधार पर भिन्न होती है।
पता लगाने में कुछ फ़िज़नेस है, चूंकि बैंडविड्थ शून्य के बराबर नहीं है, यह इस तथ्य के कारण है कि तरंगिका एक आवृत्ति का पता नहीं लगाती है, बल्कि एक बैंड है। यह प्रभाव तरंगिका बैंडविड्थ के साथ जुड़ा हुआ है।
2. तीन दालों को एक बढ़ती हुई अवधि के साथ क्रमिक रूप से जोड़ा जाता है (विभिन्न पैमानों पर समय-समय पर बदलाव पर विचार करने के लिए: बहु-रिज़ॉल्यूशन विश्लेषण)
लिस्टिंग from numpy import* import pandas as pd from pylab import* import scaleogram as scg

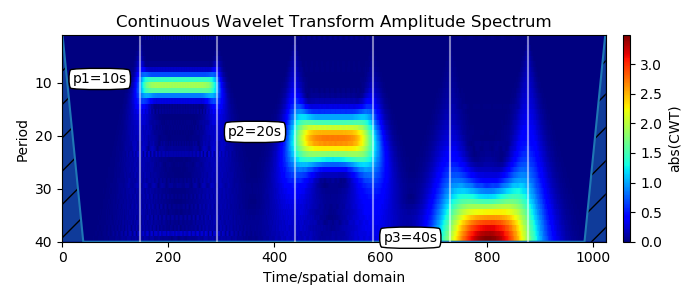
आवेग उनकी आवधिकता के अनुरूप अपेक्षित स्थान Y में दिखाई देते हैं, वे आवृत्ति और समय में स्थानीय होते हैं। पट्टी की शुरुआत और अंत गति के अनुरूप हैं।
अवधि की लंबाई के साथ बैंडविड्थ तराजू। यह तरंगिका परिवर्तन की एक प्रसिद्ध संपत्ति है: जब पैमाने बढ़ता है, तो समय संकल्प कम हो जाता है। यह समय और आवृत्ति के बीच व्यापार बंद के रूप में भी जाना जाता है। जब आप इस प्रकार के स्पेक्ट्रोग्राम को देखते हैं, तो आप बहुत अधिक रिज़ॉल्यूशन विश्लेषण करते हैं।
3. एक ही समय में विभिन्न आवृत्तियों के तीन आवधिक दोलन (वेवलेट - विश्लेषण आवृत्ति के संकेत के घटकों को अलग करने में सक्षम है, यदि उनके अंतर महत्वपूर्ण हैं):
लिस्टिंग from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5')


4. एक गैर-साइनसॉइडल आवधिक संकेत (पहले से माना जाता है कि 30 सेकंड की अवधि के साथ एक त्रिकोणीय लहर संकेत के तरंग परिवर्तनों में अंतर):
लिस्टिंग from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5')

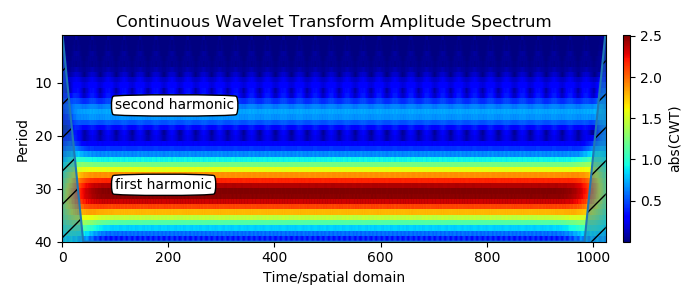
एक बड़ा बैंड पहला हार्मोनिक है। दूसरा हार्मोनिक पहले हार्मोनिक की अवधि के आधे मूल्य पर बिल्कुल दिखाई देता है। यह आवधिक गैर-साइनसॉइडल संकेतों के लिए अपेक्षित परिणाम है। फजी ऊर्ध्वाधर तत्व दूसरे हार्मोनिक के आसपास दिखाई देते हैं, जो कमजोर है और त्रिकोणीय तरंग के लिए पहले का 1/4 आयाम है।
5. चिकनी आवेग (गाऊसी) वास्तविक डेटा संरचनाओं के समान हैं। (यह उदाहरण दिखाता है कि समय के साथ स्थानीयकृत सिग्नल परिवर्तनों का पता लगाने के लिए तरंग विश्लेषण का उपयोग कैसे किया जाता है):
विभिन्न सिग्मा मूल्यों के साथ चिकनी दालों की एक श्रृंखला:
पल्स चौड़ाई:
लिस्टिंग from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5')

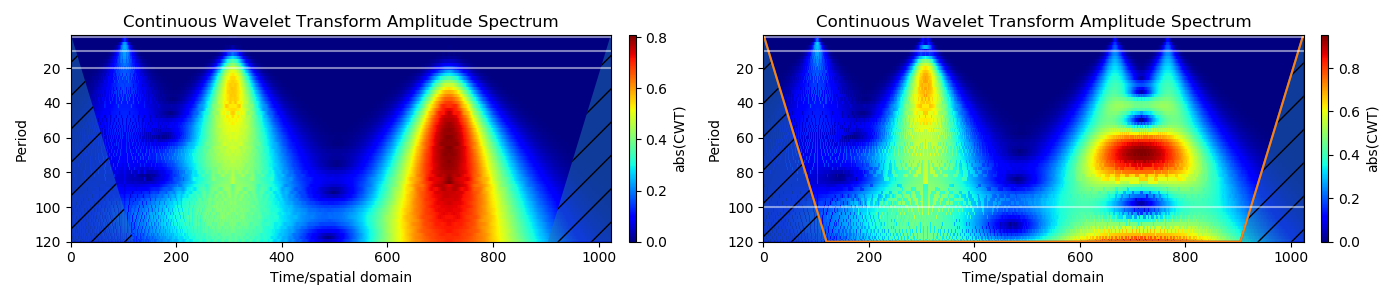
असतत दालें सियालोग्राम पर शंक्वाकार संरचनाएं बनाती हैं, जिन्हें प्रभाव शंकु के रूप में भी जाना जाता है। चिकनी आवेग (गाऊसी) वास्तविक डेटा संरचनाओं के समान हैं और बड़े पैमाने पर शंकु का विस्तार करते हैं। क्षैतिज गाइड लाइनें लगभग समय अवधि (2 एस, 10 एस, 20 एस) के अनुरूप हैं। इसलिए, पल्स एक अवधि के साथ आवधिक संकेत के समान है।
6. शोर (सियालोग्राम पर प्रदर्शन शोर):
लिस्टिंग from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5')


शोर को आमतौर पर तत्वों के एक सेट के रूप में प्रदर्शित किया जाता है, और कुछ अनियमितताएं वास्तविक डेटा की वस्तुओं की तरह दिख सकती हैं, इसलिए वास्तविक डेटा का उपयोग करते समय, आपको सावधान रहना चाहिए और यदि आवश्यक हो, तो शोर के स्तर की जांच करें। कार्यक्रम शुरू होने पर हर बार ऊपरी शेड्यूल अलग होगा।
विशेष सिग्नल के वेवलेट स्केग्लोग्राम्स
PyWavelets डेटाबेस में बीस विशेष तरंगिका परिवर्तन संकेत शामिल हैं जो अध्ययन और विकास दोनों के लिए उपयोगी होंगे। इसलिए, मैं एक सूची दूंगा जो आपको सभी बीस संकेतों का तरंगिका विश्लेषण करने की अनुमति देता है:
मैं डॉपलर सिग्नल के तरंगिका परिवर्तन का केवल एक परिणाम दूंगा:
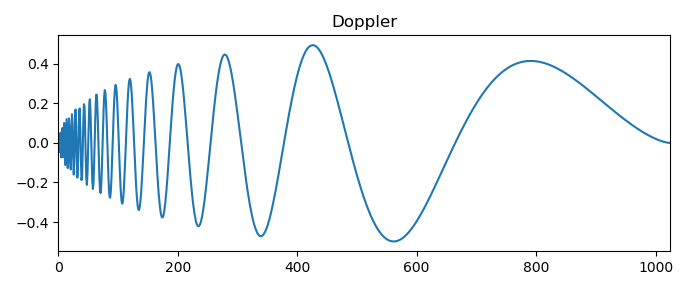

सरल और विशेष संकेतों की सबसे आम किस्मों पर विचार किया जाता है, जो हमें समय श्रृंखला विश्लेषण की कुछ समस्याओं को हल करने के लिए स्केलोग्राम का उपयोग करने के लिए स्विच करने की अनुमति देता है।
वेवलेट टाइमलाइन स्केलोग्राम
1. यूएसए 1969-2008 में सीडीसी प्रजनन डेटा (प्रजनन डेटा में आवधिक विशेषताएं शामिल हैं, दोनों वार्षिक पैमाने पर और एक छोटे स्तर पर):
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()


एक क्षैतिज रेखा लगभग 7 दिनों की आवृत्ति के साथ दिखाई देती है। उच्च मान पैमाने की सीमाओं के पास दिखाई देते हैं, जो तरंग प्रसंस्करण का सामान्य व्यवहार है। इन प्रभावों को अच्छी तरह से प्रभाव के शंकु के रूप में जाना जाता है, यही वजह है कि एक (वैकल्पिक) मुखौटा इस क्षेत्र को ओवरले करता है।
2. सामान्यीकरण (औसत मान को
हटाते हुए -
जन्मों_नमूर्त = जन्मों-जन्मों का) () अनिवार्य है, अन्यथा डेटा सीमाओं को चरणों के रूप में माना जाता है जो बहुत सारे झूठे शंकु के आकार के
निरोध बनाते हैं):
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
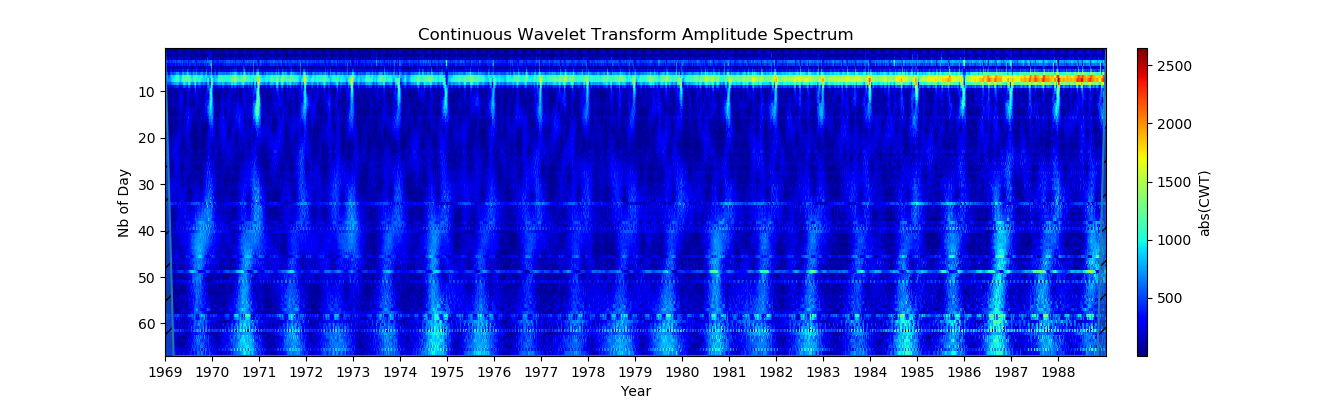
3. आयाम में पैमाने में परिवर्तन (वार्षिक वस्तुओं को देखने के लिए,
पी 2 अक्ष का उपयोग करके
) ( Y अक्ष निर्दिष्ट किया गया है)।
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
रंग मानचित्र (Y अक्ष) की आयाम सीमा अब चढ़ाई = (0.2500) से निर्धारित होती है। दोलनों के आयाम के लिए सटीक मान तरंग पर निर्भर करता है, लेकिन वास्तविक मूल्य के क्रम के करीब रहेगा। यह बहुत बेहतर है, अब हम बहुत अच्छी तरह से वार्षिक भिन्नता, साथ ही लगभग 6 महीने देखते हैं!
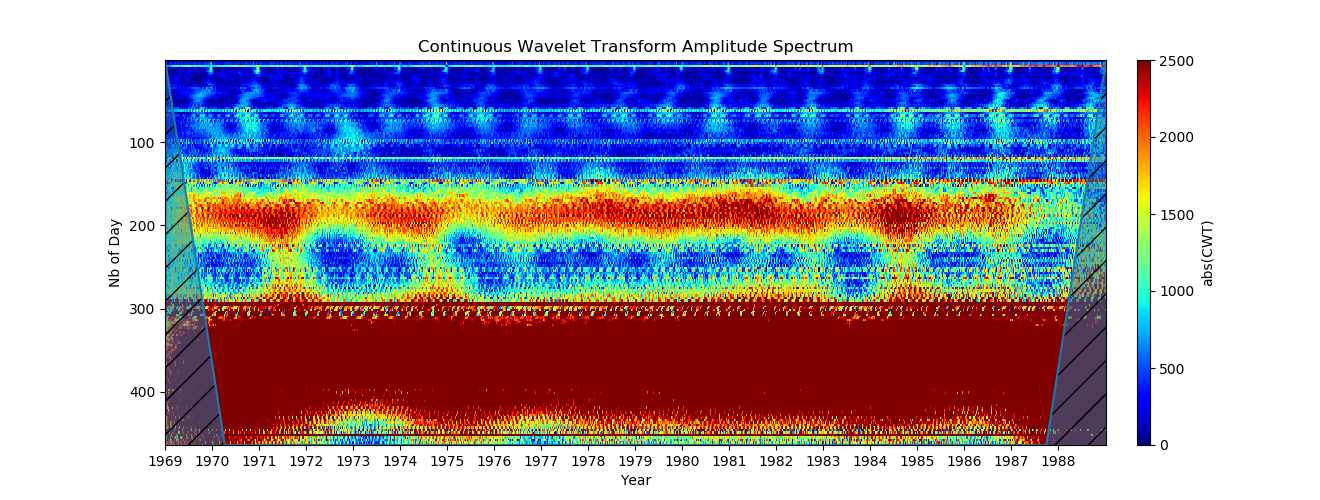
4. लघुगणक पैमाने का उपयोग करना (एक ही समय में छोटे और बड़े समय को देखने में सक्षम होने के लिए, वाई अक्ष पर लघुगणकीय पैमाने का उपयोग करना बेहतर होता है। यह xscale = log विकल्प का उपयोग करके प्राप्त किया जाता है।)
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

परिणाम बहुत बेहतर है, लेकिन अब पीरियड्स के कम मूल्यों पर पिक्सल वाई अक्ष के साथ बढ़े हुए हैं।
5. एक लघुगणकीय पैमाने पर एक समान वितरण (एक पैमाने पर एक समान वितरण प्राप्त करने के लिए, अवधि मान समान रूप से वितरित किए जाने चाहिए और फिर पैमाने मानों में परिवर्तित किए जाते हैं, जैसा कि नीचे दिखाया गया है :):
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
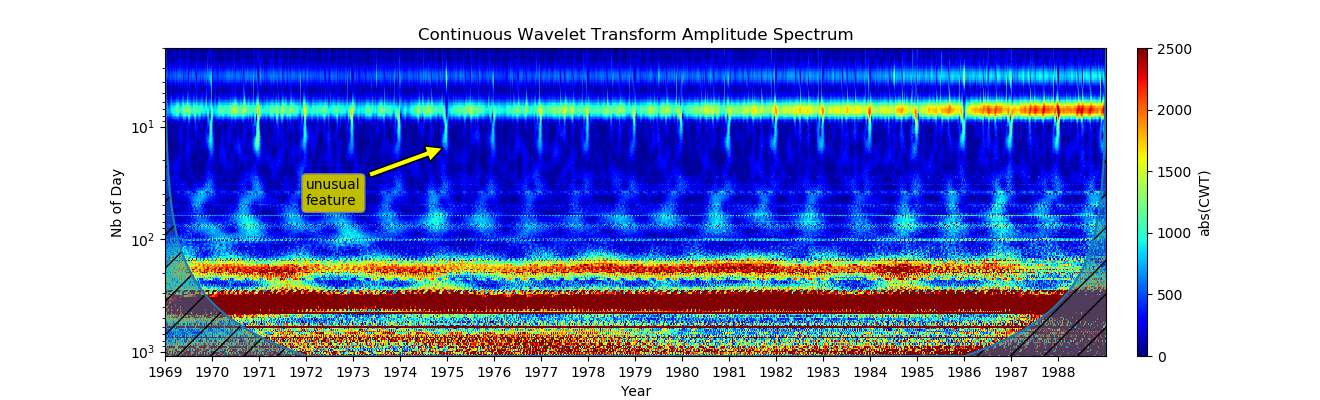
हम सभी पैमानों पर संकेत परिवर्तन देख सकते हैं। सियालोग्राम प्रत्येक वर्ष समान अवधि में दिखाई देता है।
6. समयरेखा का हाइलाइटिंग हिस्सा (कलाकृतियों या लापता डेटा की खोज में टाइमलाइन के निशान के बीच मध्यवर्ती डेटा की जाँच करना।):
लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
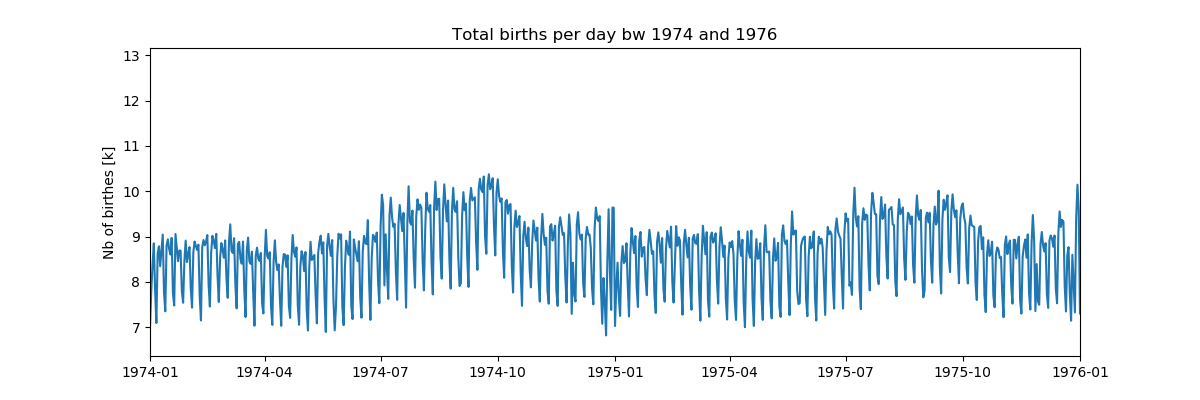
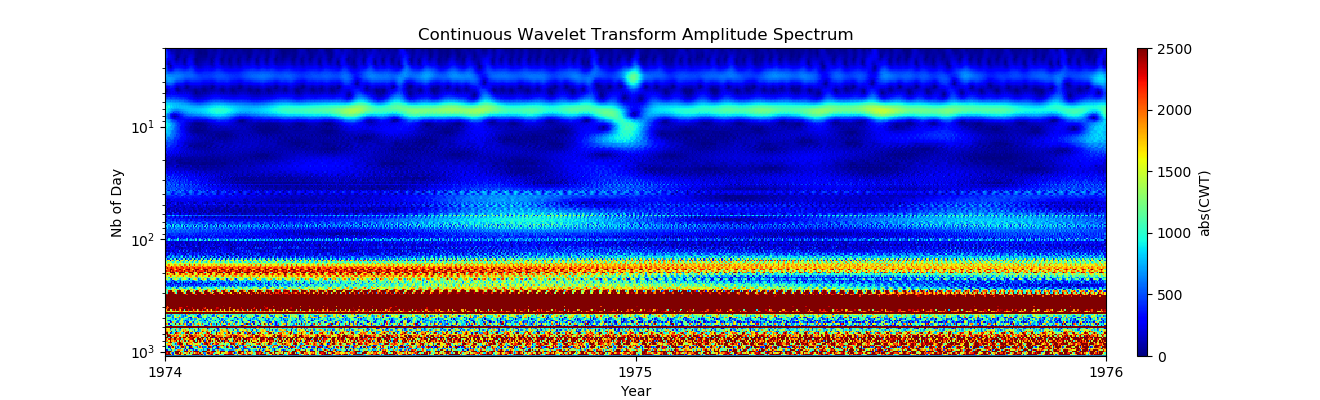 पहली नज़र में, साप्ताहिक पैटर्न बहुत अच्छे लगते हैं, लेकिन क्रिसमस के दिन कुछ होता है, आइए इस अवधि को फिर से देखें:
पहली नज़र में, साप्ताहिक पैटर्न बहुत अच्छे लगते हैं, लेकिन क्रिसमस के दिन कुछ होता है, आइए इस अवधि को फिर से देखें:लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

 अब यह स्पष्ट है कि यह वर्ष के अंत का प्रभाव है:
अब यह स्पष्ट है कि यह वर्ष के अंत का प्रभाव है:- क्रिसमस: दिसंबर 23/24/25 जन्मों की असामान्य रूप से कम संख्या दर्शाता है, और इन दिनों साप्ताहिक कार्यक्रम से विचलन होता है;
- दिसंबर के लिए डेटा है, जो 1 और 2 जनवरी को प्रभावित तारीखों के लिए कुछ मूल्य की उपस्थिति के साथ संगत है, ये तिथियां आमतौर पर कई अन्य घटनाओं की तुलना में कम हैं
7. संश्लेषण (सभी आकार के लिए बेहतर पठनीयता के साथ सामान्य डेटा से एक सियालोग्राम बनाया गया है):लिस्टिंग import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
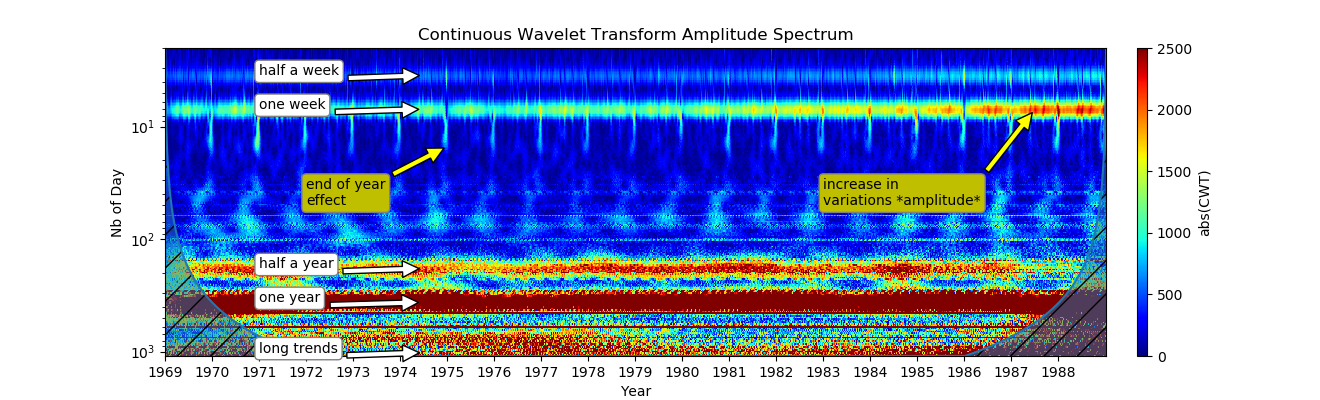 सीडब्ल्यूटी ने बहुत कम समय में बहुत सी जानकारी का खुलासा किया है:अस्पताल की आदतों को दिखाने वाला एक साप्ताहिक रूपांतर कई दशकों से मौजूद है;80 के दशक में साप्ताहिक संकेतक में वृद्धि हुई थी, जो अस्पतालों की कामकाजी आदतों में बदलाव, प्रजनन क्षमता में बदलाव या जनसंख्या में साधारण बदलाव के कारण हो सकती है;दूसरा छमाही वर्ष स्पष्ट रूप से दूसरा हार्मोनिक है। ज़ोन में फ़ज़ी पैटर्न 3 से 1 महीने तक दिखाई देते हैं, जो तीसरे हार्मोनिक के कारण हो सकता है, क्योंकि वार्षिक उतार-चढ़ाव बहुत मजबूत है। यह प्रजनन क्षमता पर छुट्टियों के प्रभाव के कारण भी हो सकता है और आगे के अध्ययन की आवश्यकता हो सकती है;साल के अंत का प्रभाव क्रिसमस और 1 जनवरी को नोट किया गया था। यह एक और आवृत्ति विधि के साथ अदृश्य रह सकता है।
सीडब्ल्यूटी ने बहुत कम समय में बहुत सी जानकारी का खुलासा किया है:अस्पताल की आदतों को दिखाने वाला एक साप्ताहिक रूपांतर कई दशकों से मौजूद है;80 के दशक में साप्ताहिक संकेतक में वृद्धि हुई थी, जो अस्पतालों की कामकाजी आदतों में बदलाव, प्रजनन क्षमता में बदलाव या जनसंख्या में साधारण बदलाव के कारण हो सकती है;दूसरा छमाही वर्ष स्पष्ट रूप से दूसरा हार्मोनिक है। ज़ोन में फ़ज़ी पैटर्न 3 से 1 महीने तक दिखाई देते हैं, जो तीसरे हार्मोनिक के कारण हो सकता है, क्योंकि वार्षिक उतार-चढ़ाव बहुत मजबूत है। यह प्रजनन क्षमता पर छुट्टियों के प्रभाव के कारण भी हो सकता है और आगे के अध्ययन की आवश्यकता हो सकती है;साल के अंत का प्रभाव क्रिसमस और 1 जनवरी को नोट किया गया था। यह एक और आवृत्ति विधि के साथ अदृश्य रह सकता है।निष्कर्ष:
इस प्रकाशन में, हमने देखा कि कैसे संकेत रूपांतरों का मूल रूप स्केलोग्राम में बदल जाता है। एक समय-क्रमित डेटासेट का एक उदाहरण तब चरणबद्ध तरीके से प्रदर्शित करने के लिए उपयोग किया गया था कि मानक डेटा पर CWT कैसे लागू किया जाता है।नेटवर्क तकनीक का विश्लेषण करने और वस्तुओं के असामान्य व्यवहार का पता लगाने के लिए उपरोक्त तकनीक का विस्तार किया जा सकता है। CWT एक शक्तिशाली उपकरण है जो तेजी से तंत्रिका नेटवर्क के इनपुट के रूप में उपयोग किया जा रहा है और इसका उपयोग विसंगतियों को वर्गीकृत या पता लगाने के लिए नए कार्यों को बनाने के लिए किया जा सकता है।प्रत्येक उदाहरण को एक स्वतंत्र कार्यक्रम के रूप में लागू किया जाता है, जो आपको अपने कार्य के लिए एक उदाहरण चुनने की अनुमति देता है, बिना पिछले और बाद के उदाहरणों में। उपयोगकर्ता किसी भी वेवलेट की कोशिश कर सकता है - प्रत्येक कार्यक्रम की शुरुआत में दी गई सूची से कार्य करता है, उदाहरण के लिए, जैसे कि मेक्सिको या गौस 5। उदाहरण के लिए 1, क्रमशः:
 पीएस लिस्टिंग के व्यावहारिक उपयोग के लिए, मैं उनमें इस्तेमाल किए गए मॉड्यूल के संस्करणों को दूंगा:
पीएस लिस्टिंग के व्यावहारिक उपयोग के लिए, मैं उनमें इस्तेमाल किए गए मॉड्यूल के संस्करणों को दूंगा: >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2
* .Csv फ़ाइल में डेटा के एक स्वतंत्र सेट के लिए, मैं डेटा संरचना (एक कॉलम में) लाता हूं:वर्ष, महीना, दिन, लिंग, जन्म1969,1,1, F, 40461969,1,1, M,449 1969,1,2 , एफ, 44541969.1.2, एम, 4548...
संस्करण 0.24.1 पांडा के लिए, आपको स्पष्ट रूप से matplotlib कन्वर्टर्स को पंजीकृत करने की आवश्यकता होगी।कन्वर्टर्स रजिस्टर करने के लिए: from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()