प्रतिभा बनाम किस्मत: सफलता और असफलता में संभावना की भूमिका

हाल ही में, मुझे इतालवी वैज्ञानिकों द्वारा हमारे जीवन में भाग्य और मौका की बहुत कम आंका जाने वाली भूमिका के बारे में एक दिलचस्प काम मिला। दुर्भाग्य से, मुझे रूसी में पूर्ण संस्करण नहीं मिला (शायद मैं बुरी तरह से देख रहा था?), लेकिन मैं वास्तव में अपने गैर-धाराप्रवाह अंग्रेजी साथियों के साथ जो भी पढ़ा था उसे साझा करना चाहता था। इसलिए, अपनी आस्तीन को रोल करते हुए, उन्होंने अपने कारीगर अनुवाद के बारे में निर्धारित किया। लेखकों, एलेसेंड्रो, एलेसियो और एंड्रिया ने कृपया इसे सार्वजनिक डोमेन में प्रकाशित करने की अनुमति दी है, इसलिए यदि आप रुचि रखते हैं, तो बिल्ली का स्वागत करें।

लेखक

• ए। प्लूचिनो - भौतिकी और खगोल विज्ञान विभाग, कैटेनिया विश्वविद्यालय और राष्ट्रीय भौतिकी संस्थान, इटली के कैटेनिया शाखा; alessandro.pluchino@ct.infn.it
• ए। ई। बियोनडो - अर्थशास्त्र और व्यवसाय विभाग, कैटेनिया विश्वविद्यालय, इटली; ae.biondo@unict.it
• ए। रैपिसर्ड - भौतिकी और खगोल विज्ञान विभाग, कैटेनिया विश्वविद्यालय और राष्ट्रीय भौतिकी संस्थान, इटली के कैटेनिया शाखा; जटिल प्रणालियों के अध्ययन के लिए केंद्र, वियना; andrea.rapisarda@ct.infn.it

अमूर्त

काफी हद तक, प्रमुख गुणात्मक ( मेरिटोक्रेसी मैनेजमेंट सिद्धांत है, जिसके अनुसार सबसे सक्षम लोग, चाहे उनकी सामाजिक उत्पत्ति और वित्तीय धन ) नेतृत्व के पदों पर हों, उच्च प्रतिस्पर्धी पश्चिमी संस्कृतियों का मॉडल इस विश्वास से उत्पन्न होता है कि सफलता मुख्य रूप से है, यदि पूरी तरह से नहीं, तो प्रतिभा, बुद्धिमत्ता, कौशल, संसाधनशीलता, कड़ी मेहनत, दृढ़ता, कड़ी मेहनत या जोखिम लेने जैसे व्यक्तिगत गुणों पर निर्भर करता है। कभी-कभी हम यह स्वीकार करने के लिए तैयार होते हैं कि भाग्य का एक निश्चित हिस्सा भी महत्वपूर्ण भौतिक सफलता प्राप्त करने में भूमिका निभा सकता है। लेकिन, वास्तव में, व्यक्तिगत सफलता की कहानियों में बाहरी ताकतों के महत्व को अक्सर कम करके आंका जाता है। यह सर्वविदित है कि एक जनसंख्या में खुफिया (या, आमतौर पर, प्रतिभा और व्यक्तिगत गुणों) का गौसियन वितरण होता है, जबकि मूल्यों का वितरण - अक्सर सफलता के माप के रूप में देखा जाता है - आमतौर पर एक शक्ति कानून (पारेतो कानून) का पालन करता है जब बहुमत खराब होता है अरबपतियों की एक नगण्य संख्या है। सामान्य रूप से वितरित आदानों के बीच यह विसंगति जो एक सामान्य स्तर (औसत प्रतिभा या बुद्धिमत्ता) है और आउटपुट पर एक निरंतर वितरण बताता है कि कहीं न कहीं पर्दे के पीछे एक अदृश्य घटक है। इस पत्र में, एक अत्यंत सरल और खिलौना एजेंट-आधारित सिमुलेशन के आधार पर, हम यह धारणा बनाते हैं कि इस तरह का एक घटक एक साधारण दुर्घटना है। विशेष रूप से, हम बताते हैं कि, जबकि जीवन की सफलता के लिए वास्तव में एक निश्चित मात्रा में प्रतिभा की आवश्यकता होती है, सबसे अधिक प्रतिभाशाली लोग लगभग कभी भी धन की उच्चतम चोटियों तक नहीं पहुंचते हैं, औसत दर्जे से आगे निकल जाते हैं, लेकिन बहुत अधिक सफल व्यक्तित्व। जहां तक ​​हम जानते हैं, यह सामान्य ज्ञान परिणाम का विरोधाभासी है - हालांकि स्पष्ट रूप से लाइनों के बीच माना जाता है कि किस तरह के साहित्य में बहुत कुछ है - यह यहां था कि पहली बार एक मात्रात्मक मूल्यांकन दिया गया था। यह आपको पहले से हासिल की गई सफलता के स्तर के आधार पर गुणों के मूल्यांकन की प्रभावशीलता पर एक नए सिरे से विचार करने की अनुमति देता है और उन लोगों को अत्यधिक सम्मान या संसाधन फैलाने के जोखिमों पर जोर देता है जो लंबे समय में दूसरों की तुलना में अधिक सफल हो सकते हैं। इस मॉडल का उपयोग करते हुए, हम योग्यता, विविधता और नवाचार में सुधार के लक्ष्य के साथ सार्वजनिक अनुसंधान के वित्तपोषण के लिए सबसे प्रभावी रणनीति दिखाने के लिए कई व्यवहार संबंधी परिकल्पनाओं की तुलना और तुलना करते हैं।

1. परिचय

कई भौतिक, जैविक, या सामाजिक-आर्थिक जटिल प्रणालियों में शक्ति निर्भरता की सर्वव्यापकता को एक पैमाने पर अपरिवर्तित सामयिक संरचना [1, 2, 3, 4] के साथ उनके गतिशील विशेषताओं के घनिष्ठ संबंध की विशिष्ट गणितीय विशेषता की तरह कुछ माना जा सकता है। पारेतो [५, ६, io, io, ९, ९] के काम के अनुसार सामाजिक-आर्थिक संदर्भ में, यह सर्वविदित है कि धन के वितरण में एक शक्ति निर्भरता का चरित्र होता है, जिसकी विशेषता दृढ़ता से लम्बी आकृति हमारे समाज के अमीर और गरीब के बीच मौजूदा रसातल की गहराई को दर्शाती है।

एक हालिया रिपोर्ट [10] से पता चलता है कि आज यह अंतर जितना हमें डर था उससे कहीं अधिक बड़ा है: आठ लोग 3.6 बिलियन लोगों के समान धन रखते हैं, जो मानवता का सबसे गरीब हिस्सा हैं। पिछले 20 वर्षों में, कई सैद्धांतिक मॉडल विकसित किए गए हैं जो प्रायिकता सिद्धांत और भौतिक आंकड़ों के संदर्भ में मूल्यों के वितरण की गणना करते हैं, अक्सर सरल आंतरिक गतिशीलता के साथ मल्टी-एजेंट मॉडलिंग का रूप लेते हैं [11, 12, 13, 14, 15, 16, 17]।

इस दिशा में आगे बढ़ते हुए, अगर हम व्यक्तिगत धन को सफलता का पैमाना मानते हैं, तो यह तर्क दिया जा सकता है कि लोगों के बीच इसका गहरा असममित और असमान वितरण प्रतिभा, कौशल, क्षमता, बुद्धिमत्ता, क्षमताओं या उनकी दृढ़ता, परिश्रम या उनकी माप के प्राकृतिक अंतर का परिणाम है। निरुउद्देश्यता। इस तरह की धारणा, एक निहित रूप में, तथाकथित गुणात्मक प्रतिमान का आधार है: यह न केवल हमारे समाज को रोजगार के अवसर, सम्मान और प्रसिद्धि प्रदान करता है बल्कि सरकारों द्वारा संसाधनों और वित्त को आवंटित करने के लिए अपनाई जाने वाली रणनीतियों को भी प्रभावित करता है जिन्हें सबसे अधिक माना जाता है। सम्मानित व्यक्तित्व।

हालाँकि, पिछला निष्कर्ष इस पुष्ट किए गए डेटा से बहुत भिन्न प्रतीत होता है कि लोगों के उपर्युक्त गुण और गुण सामान्य रूप से पूरी आबादी में वितरित किए जाते हैं, अर्थात्, इस औसत के सापेक्ष एक सममित गौसियन वितरण के अनुरूप है। उदाहरण के लिए, बुद्धि, जैसा कि IQ परीक्षणों द्वारा मापा गया है, निम्न पैटर्न से मेल खाती है: औसत IQ 100 है, लेकिन किसी के पास 1000 या 10000 का IQ नहीं है। काम के घंटों में गिने जाने वाले काम पर भी यही लागू होता है: कोई व्यक्ति औसत से अधिक काम करता है, कोई दूसरा कम है, लेकिन कोई भी ऐसा नहीं है जो बाकी की तुलना में एक अरब गुना अधिक घंटे काम करता है।

लेकिन हमारे समय में हमारे व्यक्तिगत और व्यावसायिक मामलों में सफलता या असफलता का निर्धारण करने में, सामान्य रूप से, यादृच्छिक कारकों में, मौका, भाग्य, या, की मूलभूत भूमिका के बारे में अधिक से अधिक सबूत हैं। विशेष रूप से, यह दिखाया गया कि सभी वैज्ञानिकों के पास अपने करियर के दौरान सफलता के काम को प्रकाशित करने का समान मौका है [18]; वर्णमाला की शुरुआत के करीब परिवार के नाम के पहले अक्षर वाले लोग विभाग के प्रमुख का पद प्राप्त करने की अधिक संभावना रखते हैं [19]; वैज्ञानिकों द्वारा एकत्र किए गए बिब्लीमेट्रिक संकेतकों का वितरण मुद्रास्फीति "प्रकाशन या मरना" तंत्र से जुड़ी बढ़ती घटनाओं के कारण यादृच्छिक और अर्थहीन हो सकता है [20]; किसी वर्णानुक्रम में सॉर्ट की गई सूची में किसी की स्थिति सार्वजनिक सेवाओं तक पहुँच निर्धारित करने में महत्वपूर्ण हो सकती है जो स्थानों की संख्या तक सीमित है [२१]; मध्य नाम का प्रारंभिक अक्षर बौद्धिक क्षमताओं का मूल्यांकन करता है [22]; जिन लोगों के नाम आसानी से उच्चारित होते हैं, उन्हें उन लोगों की तुलना में अधिक सकारात्मक दर्जा दिया जाता है जिनके नाम जटिल हैं [23]; वे जिनके नाम दूसरों की तुलना में अधिक अभिजात वर्गीय हैं, वे नेताओं के रूप में काम करते हैं और अधीनस्थों के नहीं [24]; पुरुष उपनाम वाली महिलाएं कानूनी पेशे में अधिक सफल होती हैं [25]; दुनिया भर के लोगों के बीच आय का लगभग आधा अंतर केवल उनके निवास स्थान और संबंधित देश के भीतर वेतन के वितरण द्वारा समझाया गया है [26]; निर्देशक बनने की संभावना आपके नाम और जन्म के महीने [27, 28, 29] से बहुत प्रभावित होती है; यह नवीन विचार हमारे मस्तिष्क की कोशिकाओं में यादृच्छिक प्रतिक्रियाओं का परिणाम हैं [30]; और यहां तक ​​कि कैंसर के विकास की संभावना, संभवतः एक उत्कृष्ट कैरियर को नष्ट करना, अधिकांश भाग के लिए विफलता [31, 32] पर निर्भर करती है। जीवन भर प्रजनन सफलता के विषय पर हालिया काम ऐसे बयानों की पुष्टि में योगदान करते हैं, जो दिखाते हैं कि यदि लक्षण के विचलन पूरे के रूप में आबादी के भाग्य को प्रभावित कर सकते हैं, तो विशिष्ट व्यक्तियों का जीवन अक्सर भाग्य द्वारा निर्धारित होता है।

हाल के वर्षों में, सांख्यिकीविद् और जोखिम विश्लेषक नासिम तालेब [35, 36], निवेश रणनीतिकार माइकल मोबूसिन [37] और अर्थशास्त्री रॉबर्ट फ्रैंक [38] सहित कई लेखकों ने कई वित्तीय पुस्तकों में जांच की है कि वित्तीय लेनदेन में भाग्य और कौशल के बीच संबंध हैं। व्यापार, खेल, कला, संगीत, साहित्य, विज्ञान और कई अन्य क्षेत्र। उन्होंने निष्कर्ष निकाला कि यादृच्छिक घटनाएं जीवन में बहुत बड़ी भूमिका निभाती हैं, जिसकी कल्पना कई लोगों ने की होगी। वास्तव में, वे यह नहीं मानते हैं कि सफलता प्रतिभा और प्रयासों पर निर्भर नहीं करती है, क्योंकि बेहद प्रतिस्पर्धी क्षेत्रों या बाजारों में जैसे "विजेता सब कुछ लेता है", जहां हम इस समय रहते हैं और काम करते हैं, सबसे उत्पादक लोग लगभग हमेशा असाधारण होते हैं प्रतिभाशाली और मेहनती। उन्होंने केवल यह निष्कर्ष निकाला कि प्रतिभा और प्रयास पर्याप्त नहीं हैं: आपको सही समय पर सही जगह पर रहने की आवश्यकता है। संक्षेप में, भाग्य भी प्रभावित करता है, हालांकि इसकी भूमिका लगभग हमेशा सफल लोगों द्वारा कम करके आंका जाता है। यह इस तथ्य के कारण है कि यादृच्छिकता अक्सर एक स्पष्ट तरीके से काम करती है, इसलिए उन घटनाओं की तुलना करना आसान है जो सफलता को कुछ ऐसा दिखाते हैं जो अपरिहार्य था। तालेब इस तरह के झुकाव को "एक शानदार गिरावट" [36] कहते हैं, और समाजशास्त्री पॉल लेज़र्सफेल्ड ने "पक्षपाती पूर्वव्यापी" शब्द का प्रस्ताव किया है। अपनी अंतिम पुस्तक में, "एवरीथिंग इज़ एब्रीड: व्हेन यू नो द आंसर" [39], समाजशास्त्री और नेटवर्क साइंस के प्रणेता डंकन वाट्स का सुझाव है कि दोनों शानदार भ्रम और पक्षपाती पूर्वव्यापी अपील एक विशेष घटना के लिए करते हैं जिसमें लोग असामान्य रूप से सफल परिणाम प्राप्त करते हैं, उन्हें कड़ी मेहनत और प्रतिभा का एक निस्संदेह उत्पाद मानते हैं। हालांकि, सफलता मुख्य रूप से जटिल और intertwined चरणों के माध्यम से उत्पन्न होती है, जिनमें से प्रत्येक पिछले लोगों पर निर्भर करता है: यदि उनमें से कोई भी अलग था, तो पूरा कैरियर या जीवन पथ लगभग निश्चित रूप से अलग भी होगा। यह तर्क कई वर्षों पहले खुद को अन्य लेखकों [40] के सहयोग से वाट्स द्वारा किए गए एक अभिनव प्रयोगात्मक अध्ययन के परिणामों पर भी आधारित है, जिसमें कृत्रिम संगीत बाजार पर पहले के अज्ञात गीतों की सफलता को स्वयं कार्य की गुणवत्ता के साथ सहसंबंधित नहीं दिखाया गया था। और यह, ज़ाहिर है, किसी भी भविष्यवाणियों को बहुत जटिल करता है, जैसा कि दूसरे में दिखाया गया है, हाल ही के अध्ययन [41]।

इस पत्र में, एजेंट-आधारित सांख्यिकीय दृष्टिकोण का उपयोग करते हुए, हम सफल करियर में भाग्य और प्रतिभा की भूमिका को व्यावहारिक रूप से निर्धारित करने का प्रयास करेंगे। धारा 2 में, मान्यताओं की न्यूनतम संख्या के आधार पर, अर्थात् प्रतिभा के वितरण की गॉसियन प्रकृति [42] और सफलताओं और विफलताओं [43] की गुणात्मक गतिशीलता, हम एक सरल मॉडल प्रस्तुत करते हैं, जिसे "टैलेंट बनाम लक" मॉडल (टीपीयू) कहा जाता है, जो अपने काम के 40 साल की अवधि में लोगों के समूह के पेशेवर करियर के विकास की नकल करता है। मॉडल से पता चलता है कि वास्तव में, यादृच्छिकता सबसे सफल व्यक्तियों को निर्धारित करने में एक मौलिक भूमिका निभाती है। सच्ची बात यह है कि जैसा कि कोई उम्मीद कर सकता है, कम तैयार लोगों के संबंध में प्रतिभाशाली लोग अपने स्वयं के जीवन में अमीर, प्रसिद्ध या महत्वपूर्ण बनने की संभावना रखते हैं। लेकिन, और यह कम सहज व्याख्या, प्रतिभा के एक सामान्य स्तर वाले सामान्य लोग सांख्यिकीय रूप से सफल होने के लिए किस्मत में हैं (यानी, सफलता के कुछ बिजली वितरण के अंत में स्थित होना) सबसे अधिक प्रतिभाशाली लोगों की तुलना में अधिक बार, बशर्ते कि वे भाग्य के लिए पसंदीदा हों अपने जीवन के इस तथ्य का अक्सर सामना किया जाता है, जैसा कि संदर्भों में इंगित किया गया है [35, 36, 38], लेकिन, जहां तक ​​हम जानते हैं, यह पहली बार इस काम में मॉडलिंग और मापा गया था।

साधारण प्रतिभा वाले लोगों की सफलता "योग्यता" प्रतिमान और उन सभी रणनीतियों और तंत्रों पर सवाल उठाती है, जिन्होंने अपने क्षेत्र में सबसे अच्छा माना जाने वाले लोगों को अधिक पुरस्कार, अवसर, सम्मान, प्रसिद्धि और संसाधन दिए। [४४, ४५]। तथ्य यह है कि, अधिकांश मामलों में, किसी की प्रतिभा के सभी आकलन इस तथ्य के बाद दिए गए थे, पूरी तरह से उसकी गतिविधि को देखते हुए, या प्राप्त किए गए परिणाम, हमारे समाज के एक विशिष्ट क्षेत्र में, जैसे कि खेल, व्यवसाय, वित्त, कला , विज्ञान, आदि। इस प्रकार के भ्रामक मूल्यांकन के कारण और प्रभाव का प्रतिस्थापन होता है, जो सबसे प्रतिभाशाली लोगों के रूप में मूल्यांकन करते हैं, बस, सबसे सफल [46, 47] हैं। इस दृष्टिकोण के अनुसार, पिछले कार्यों ने "योग्यता के निकट" के समान प्रकारों की चेतावनी दी और कई अलग-अलग वातावरणों में यादृच्छिक नमूनों के आधार पर अन्य रणनीतियों की प्रभावशीलता को दिखाया, जैसे कि प्रबंधन, राजनीति और वित्त [48, 49, 50, 51, 52, आदि। 53, 54, 55]। धारा 3 में, हम अपने दृष्टिकोण को लागू करते हैं और वैज्ञानिक अनुसंधान के संदर्भ में सार्वजनिक धन का वितरण कैसे संभव है, इसकी रूपरेखा तैयार करते हैं। हम विभिन्न वितरण रणनीतियों के परिणामों का अध्ययन करते हैं, जिनके बीच एक "पास" योग्यता है, जिसमें वृद्धि करने के नए तरीके तलाशने के उद्देश्य से, एक ही समय में, समाज में सबसे प्रतिभाशाली लोगों की सफलता का न्यूनतम स्तर और सरकारी खर्च की कुल प्रभावशीलता। हम सामान्य रूप से यह भी परखते हैं कि शिक्षा और आय के स्तर (यानी, देश और सामाजिक स्तर पर लोगों के आधार पर बाहरी कारक, जहां से लोग आते हैं) के रूप में प्रस्तुत किए गए वातावरण, पर्यावरण द्वारा पेश किए गए अवसरों, सफलता की संभावना बढ़ाने में महत्वपूर्ण हैं। अंतिम टिप्पणी काम पूरा करती है।

2. मॉडल

इसके अलावा, हम एक एजेंट मॉडल का प्रस्ताव करते हैं जिसे "टैलेंट बनाम गुड लक" (टीपीयू) कहा जाता है, जो कि बहुत सी मान्यताओं पर आधारित है, और इसका उद्देश्य यादृच्छिक रूप से सफल और असफल घटनाओं के प्रभाव में लोगों के एक समूह के करियर के विकास का वर्णन करना है।


चित्र 1: हमारे सिमुलेशन के लिए प्रारंभिक मापदंडों का एक उदाहरण। इस पत्र में प्रस्तुत सभी सिमुलेशन नेटलोगो एजेंट सिमुलेशन वातावरण [56] में किए गए थे। N = 1000 लोग (एजेंट) अलग-अलग डिग्री के साथ प्रतिभा (बुद्धि, कौशल, आदि) चक्रीय सीमा स्थितियों के साथ 201 × 201 वर्गों के एक वर्ग की दुनिया के भीतर तय पदों पर बेतरतीब ढंग से वितरित किए जाते हैं। प्रत्येक सिमुलेशन के दौरान, जो कई दशकों तक फैलता है, वे एक निश्चित संख्या में एन _ई सफल (हरे रंग की मंडलियों) और असफल (लाल हलकों) घटनाओं के संपर्क में आते हैं जो दुनिया भर में यादृच्छिक प्रक्षेपवक्र (यादृच्छिक चलना) के साथ चलते हैं। इस उदाहरण में, N _E = 500।

हम T _i प्रतिभा (बुद्धि, कौशल, योग्यता, आदि) के साथ एन व्यक्तियों को अंतराल में एक सामान्य वितरण मानते हैं [0; 1] मानक विचलन के साथ किसी दिए गए औसत m _{T के} चारों ओर ly _T चक्रीय सीमा के भीतर निश्चित रूप से निर्धारित स्थानों पर रखा गया है (चित्र 1 देखें) चक्रीय सीमा स्थितियों (जो कि एक टॉरॉयडल टोपोलॉजी के साथ है) और एक निश्चित संख्या " _E " से घिरा हुआ है घटनाओं (डॉट्स के साथ चिह्नित), जिनमें से कुछ सफल हैं, कोई अन्य (इस मॉडल में तटस्थ घटनाओं को ध्यान में नहीं रखा गया है, क्योंकि उनके व्यक्ति के जीवन पर कोई महत्वपूर्ण परिणाम नहीं हैं)। चित्रा 1 में, हमने इन घटनाओं को रंगीन डॉट्स के रूप में दिखाया: हरे रंग में सफल और एक सापेक्ष प्रतिशत पी _{एल के साथ} , और लाल रंग में असफल और एक प्रतिशत ( 100 - पी _एल ) के साथ। _ई अंक _ई की कुल संख्या समान रूप से वितरित की जाती है, लेकिन निश्चित रूप से, ऐसा वितरण केवल एन _ई → N के लिए आदर्श रूप से समान होगा। हमारे सिमुलेशन में, आमतौर पर एन _ई / एन / 2 होगा , इसलिए, प्रत्येक सिमुलेशन की शुरुआत में, दुनिया के विभिन्न क्षेत्रों में सफल या असफल घटना बिंदुओं का एक यादृच्छिक महत्वपूर्ण एकाग्रता है, जबकि अन्य क्षेत्र अधिक तटस्थ होंगे। एक वर्ग मैट्रिक्स के अंदर बिंदुओं के यादृच्छिक यादृच्छिक आंदोलन, अर्थात्, दुनिया, मॉडल की इस मौलिक विशेषता को नहीं बदलती है, जो कि उनके व्यक्तिगत प्रतिभा की परवाह किए बिना, उनके जीवन भर के विभिन्न लोगों के लिए सफलता या विफलता की विभिन्न घटनाओं का संकेत देती है।


चित्र 2: आबादी के बीच प्रतिभा का सामान्य वितरण (ध्येय m _t = 0.6 के साथ धराशायी ऊर्ध्वाधर रेखा और मानक विचलन dev _T = 0.1 - मान m _T σ _{are T} को दो बिंदु ऊर्ध्वाधर रेखाओं के रूप _में प्रदर्शित किया जाता है)। यह वितरण अंतराल में आवंटित किया गया है [0; 1] और सिमुलेशन के दौरान नहीं बदलता है।

एक सिमुलेशन रन 40 वर्षों की कामकाजी जीवन अवधि पी (बीस से साठ साल की आयु) की जांच करता है, जिसमें छह महीने का समय कदम होता है। अनुकार की शुरुआत में, सभी एजेंटों को एक ही पूंजी C _i = C (0) = _i = 1, ..., N दी गई , जो उनकी सफलता के शुरुआती स्तर / भलाई का प्रतिनिधित्व करते हैं। इस विकल्प का स्पष्ट लक्ष्य है कि किसी को भी प्रारंभिक लाभ न दिया जाए। जबकि एजेंटों की प्रतिभा समय-निर्भर नहीं है, उनकी पूंजी बदल रही है। इस मॉडल के विकास के दौरान, यानी, एजेंटों के जीवन की अपेक्षित अवधि के दौरान, सभी घटना बिंदु दुनिया भर में बेतरतीब ढंग से चलते हैं और एक ही समय में, कुछ एजेंटों के स्थान के साथ अंतर हो सकता है। यदि आप विवरण में जाते हैं, तो हर बार प्रत्येक घटना बिंदु, एक यादृच्छिक दिशा में, 2 खंडों की दूरी तय करती है। हम मानते हैं कि अगर किसी एक खंड के त्रिज्या के साथ सर्कल के अंदर प्रतिनिधित्व किया जाने वाला घटना बिंदु एजेंट पर केंद्रित है (घटना बिंदु चौराहे के बाद गायब नहीं होते हैं) तो व्यक्ति के साथ एक चौराहा होता है।इस तरह की घटना के आधार पर, इस समय कदम टी (यानी, हर छह महीने में), एक निश्चित एजेंट ए _{के के साथ} , निम्नलिखित तीन संभावित विकल्प संभव हैं:

1. कोई घटना बिंदु एजेंट A _k की स्थिति को पार नहीं करता है - इसका मतलब है कि पिछले छह महीनों के दौरान ऐसी कोई घटना नहीं हुई है, एजेंट A _k कोई कार्रवाई नहीं करता है।
2. A _k – , ( , [30], , ); , A _k / , T _k . C _k (t) = 2C _k (t − 1) , rand[0; 1] < T _k , .., , .
3. A _k – , ; , A _k / , .. C _k (t) = C _k (t − 1) / 2 .

( , ), , , , . , , , ( , ). , , , , . , «», « , ». , «» , , , , , , , , . , , .

2.1।

. , , , , , .

N = 1000 C (0) = 10 ( ) T _i ϵ [0; 1], m _T = 0,6 σ _T = 0,1 (. 2). , P = 40 , , , I = 80 . N _E = 500 , p _L = 50%.

, () 3, , / , () (). , (b) , y© ≈ C ^−1,27 .

, , , , , : . , 4 500 , 20 44% , 10 . , «80/20», 80% 20% , 20% 80% . , , , , , / , . ?


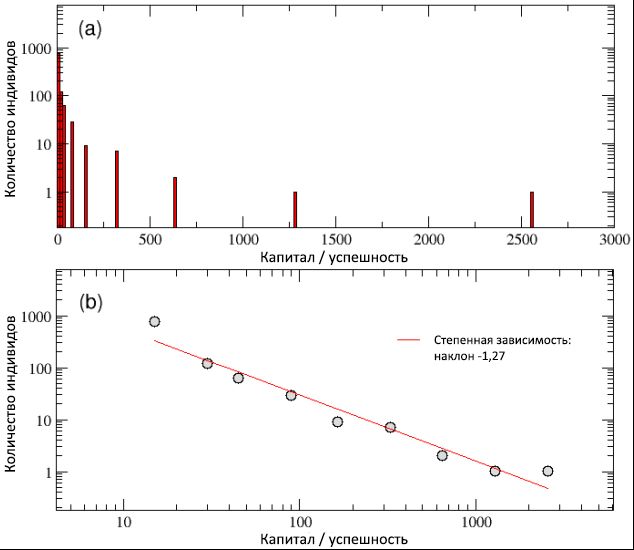चित्र 3: आबादी के बीच धन / सफलता का अंतिम वितरण, एक लघुगणकीय रैखिक (ए) और बिलोगैरिथमिक (बी) पैमाने पर। सामान्य प्रतिभा वितरण के बावजूद, सफलता वितरण की पूंछ, जैसा कि योजना (बी) से देखा जा सकता है, को ope1.27 की ढलान के साथ पावर वक्र के रूप में वर्णित किया जा सकता है। हमने यह भी पुष्टि की है कि पूंजी / सफलता का वितरण पारेतो "80/20" कानून का पालन करता है, क्योंकि 20% आबादी 80% मूल्यों का मालिक है और इसके विपरीत।

4, (a) (b), , / , ( , (a) / – ). , , , , , . , , C _max = 2560, T* = 0,61, m _T = 0,6, ( T _max = 0,89) / , 1 ( C = 0,625).

, , , , : , . , . , T > T* C ≈ 20; , / 128 , / , , . , , , , . , .


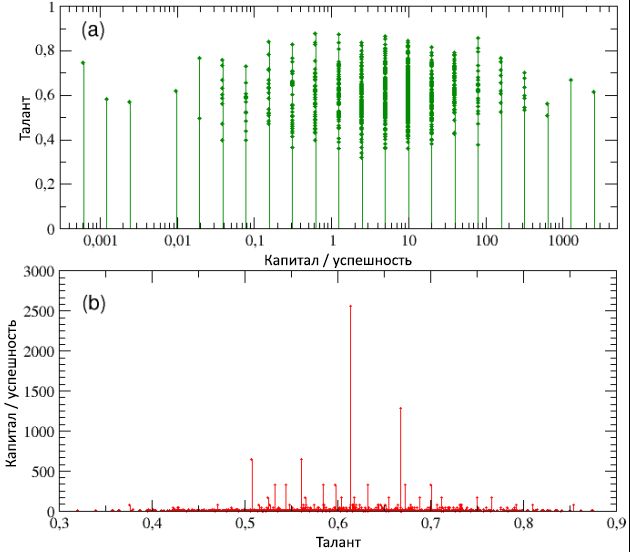
4: () / ( , ) – , , , . (b), , / – , , C _max = 2560, , m _T = 0,6, / , C = 1 , C (0). .

5 , , / . (a) , ( , , , , , ). , (b), , . , , , , . , , © (d), , 0,64 0,48, 1,35 1,66, , , , 10 15. , 16% «» , , 40% - ( ).

/ , , , 40 (80 , 6 ) . , , 6. (a) 5, , , , .


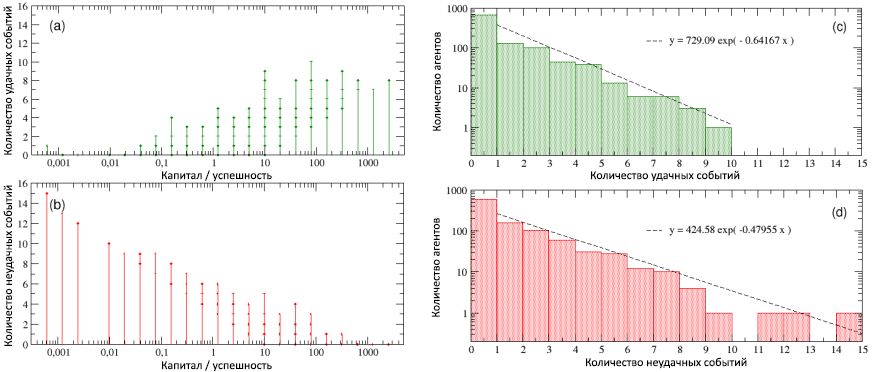
5: (a) (b) , / . : , . , - , , / . © (d) , , . , ).

( ) (a) 6, , , , , ( ), ( ), , 30 40 (.. 40- ) , 10 (.., 5 ) , C = 320 C _max = 2560.

, ( ) (b) , , , , , / , C = 0,00061. , T = 0,74, , . , . , , ( ), , , , .


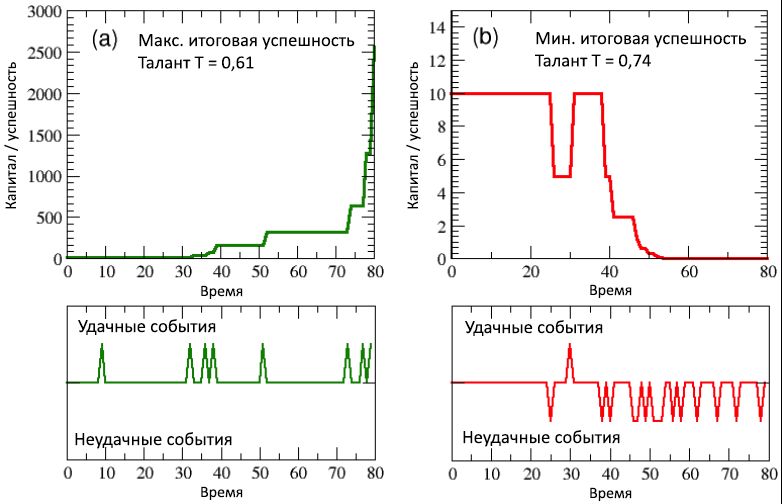
6: (a) / (b) , , ( 80 , .., 40 ). , .

(- NetLogo , , Open ABM), , , , , , , , .

2.2।

इस उपधारा में, हमने सामान्य सिमुलेशन परिणाम औसतन, 100 से अधिक रन प्रस्तुत किए, प्रत्येक ने अलग-अलग, यादृच्छिक रूप से चयनित, प्रारंभिक स्थितियों के साथ शुरू किया। नियंत्रण मापदंडों के मूल्य पिछले उपधारा में समान थे: प्रतिभा के सामान्य वितरण के लिए एन = 1000 व्यक्तियों, एम _टी = 0.6 और the _टी = 0.1, मैं = 80 पुनरावृत्तियों (प्रत्येक का प्रतिनिधित्व करता है δ _टी = 6 महीने के कामकाजी जीवन ), C (0) = प्रारंभिक पूंजी की 10 इकाइयाँ, N _E = 500 घटना बिंदु और सफल घटनाओं का प्रतिशत p _L = 50%।

चित्र 7 के आरेख (ए) में, 100 रन के परिणामस्वरूप एकत्र किए गए सभी एजेंटों के बीच कुल पूंजी / सफलता का कुल वितरण एक लघुगणकीय पैमाने पर दिखाया गया है और एक कोणीय गुणांक −1.33 के साथ एक शक्ति-कानून वक्र द्वारा अच्छी तरह से वर्णित है। पैमाने और भले ही व्यक्तियों के बीच उच्च असमानता, और साथ ही परेतो नियम "80/20" के बावजूद एक ही रन में देखी गई पूंजीगत संपत्ति की संपत्ति, इस प्रकार कई रन के मामले में संरक्षित हैं। वास्तव में, अमीर (सफल) और गरीब (असफल) एजेंटों के बीच की खाई और भी चौड़ी हो गई है, क्योंकि सबसे अमीर लोगों की पूंजी अब 40,000 इकाइयों से अधिक हो गई है।

यह परिणाम चित्र 7 की योजना (बी) को देखकर सबसे अच्छा अनुमान लगाया जा सकता है, जहां कुल पूंजी सी _{अधिकतम} केवल सबसे सफल व्यक्तियों को प्रतिभा के एक समारोह के रूप में दिखाया गया है 100 रनों में से प्रत्येक में सबसे अच्छा परिणाम दिखा। प्रतिभा के साथ एजेंट टी _{बेस्ट} = 0.6048, लगभग प्रतिभा के वितरण के माध्यिका के साथ मेल खाता है ( एम _टी = 0.6), जो चरम राजधानी सी _{बेस्ट} = 40960 पर पहुंच गया, उसे सबसे अधिक अंक प्राप्त हुए। दूसरी ओर, सबसे सफल व्यक्तियों के सबसे उपहार के साथ। प्रतिभा T _{अधिकतम} = 0.91, पूंजी C _{अधिकतम} = 2560 प्राप्त की, जो C _{सर्वश्रेष्ठ} का केवल 6% है ।


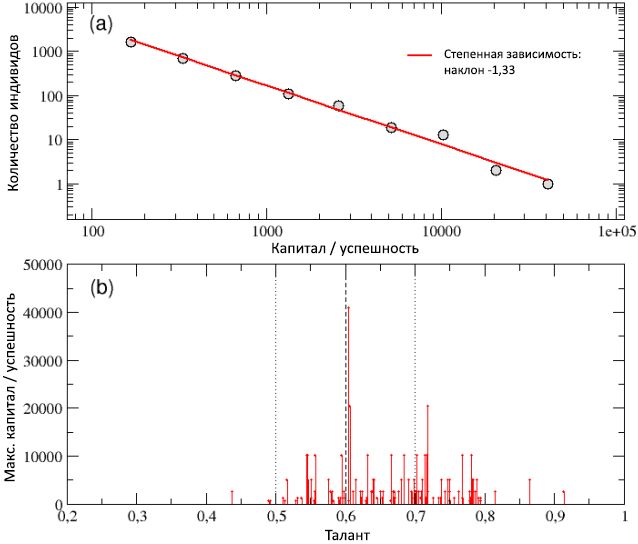
चित्र 7: योजना (ए) - विभिन्न बेतरतीब ढंग से निर्धारित प्रारंभिक स्थितियों के साथ आबादी के लिए 100 से अधिक रन की गणना की गई कुल पूंजी / सफलता का वितरण। वितरण का वर्णन पावर वक्र द्वारा −1.33 की ढलान के साथ किया जा सकता है। स्कीम (बी) - 100 रनों में से प्रत्येक में सबसे सफल व्यक्तियों की कुल पूंजी सी _{अधिकतम} , उनकी प्रतिभा के एक समारोह के रूप में दिखाया गया है। मध्यम उच्च प्रतिभा वाले लोग, औसतन, उन लोगों की तुलना में अधिक सफल होते हैं जिनके पास कम या मध्यम कम प्रतिभा होती है, और सबसे अधिक बार सबसे सफल व्यक्ति एक मामूली प्रतिभाशाली एजेंट होता है, और केवल कभी-कभी सबसे प्रतिभाशाली व्यक्ति होता है। एम _टी का मान, साथ ही साथ एम _टी σ are _टी के मूल्यों को क्रमशः ऊर्ध्वाधर धराशायी और बिंदीदार रेखाओं के रूप में दिखाया गया है।

इस बिंदु पर अधिक विस्तार से विचार करने के लिए, चित्र 8 (ए) में हमने सर्वश्रेष्ठ प्रदर्शन करने वालों की प्रतिभा के वितरण की साजिश रची, जिसकी गणना 100 रन के लिए की गई। वितरण, स्पष्ट रूप से, प्रतिभा के अक्ष के साथ दाईं ओर स्थानांतरित कर दिया जाता है, टी औसत = 0.66> मी _{टी के} औसत मूल्य के साथ - यह पुष्टि करता है, एक तरफ, कि महत्वपूर्ण सफलता प्राप्त करने के लिए, एक मामूली उच्च प्रतिभा अक्सर आवश्यक होती है; हालाँकि, दूसरी ओर, यह भी दर्शाता है कि यह स्थिति लगभग पर्याप्त नहीं है, क्योंकि उच्चतम प्रतिभा वाले एजेंट (जैसे, T > m _T = 2σ _T , या T > 0.8) केवल सर्वश्रेष्ठ प्रदर्शन करने वालों में से हैं 3% मामलों में, और उनकी पूंजी / सफलता कभी भी _{सर्वश्रेष्ठ के} 13% से अधिक नहीं होती है ।


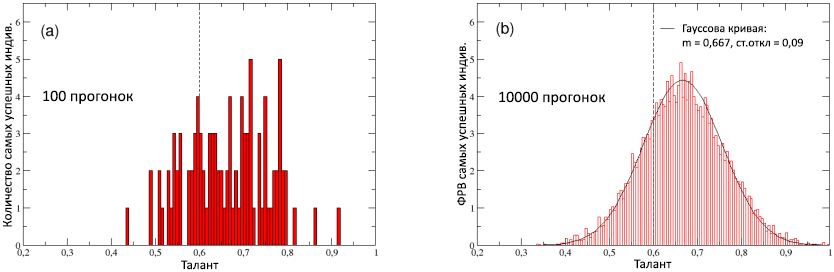
चित्र 8: (ए) 100 रनों में से प्रत्येक में सबसे सफल व्यक्तित्व (सर्वश्रेष्ठ कलाकार) का प्रतिभाशाली वितरण। (बी) 10,000 रनों में गणना की गई सबसे सफल व्यक्तियों की प्रतिभा की संभाव्यता वितरण समारोह (आरएफएफ): 0.667 के मध्य के सामान्य वितरण और 0.09 (ठोस वक्र) के मानक विचलन द्वारा अच्छी तरह से वर्णित है। तुलना के लिए, जनसंख्या में प्रतिभा के प्रारंभिक सामान्य वितरण का माध्य एम _टी = 0.6 दिखाया गया है, दोनों योजनाओं में एक घने ऊर्ध्वाधर रेखा द्वारा दिखाया गया है।

चित्र 8 के आरेख (बी) में, समान वितरण (एफआरएफ प्राप्त करने के लिए कुल क्षेत्र में कमी) की गणना 10,000 रन के लिए की जाती है, इसके वास्तविक आकार को समझने के लिए: ऐसा लगता है कि यह एक औसत टी _एवी = 0.667 के साथ गॉसियन वक्र जी (टी) में फिट बैठता है और 0.09 (ठोस लाइन) का एक मानक विचलन। यह, निश्चित रूप से, पुष्टि करता है कि सबसे अच्छे कलाकारों की प्रतिभा का वितरण प्रारंभिक वितरण की तुलना में, प्रतिभा की धुरी के सापेक्ष सही स्थानांतरित किया गया है। अधिक सटीक होने के लिए, इसका मतलब है कि सशर्त प्रायिकता P ( C _{अधिकतम} | T ) = G (T) dT को अंतराल में प्रतिभा के साथ एक व्यक्तित्व के साथ सर्वश्रेष्ठ प्रदर्शन करने वालों के बीच खोजने के लिए [ T ; टी + डीटी ] प्रतिभा टी के साथ बढ़ता है, लगभग मध्यम-मध्यम प्रतिभा टी _एवी = 0.66 के पास चोटियों, और फिर तेज प्रतिभा मूल्यों के साथ तेजी से गिरता है। दूसरे शब्दों में, सफलता के शीर्ष पर एक मामूली प्रतिभाशाली व्यक्ति को खोजने की संभावना वहाँ एक अत्यधिक प्रतिभाशाली व्यक्ति को खोजने की तुलना में अधिक है। ध्यान दें कि एक आदर्श दुनिया जिसमें प्रतिभा सफलता का मुख्य कारण था, यह उम्मीद की जाती है कि पी ( सी _{अधिकतम} | टी ) टी का एक बढ़ता हुआ कार्य होगा । इस प्रकार, हम यह निष्कर्ष निकाल सकते हैं कि मनाया गया गौसियन रूप P ( C _{अधिकतम} | T ) सफलता के उच्च स्तर को प्राप्त करने में प्रतिभा की तुलना में भाग्य का अधिक महत्व है।


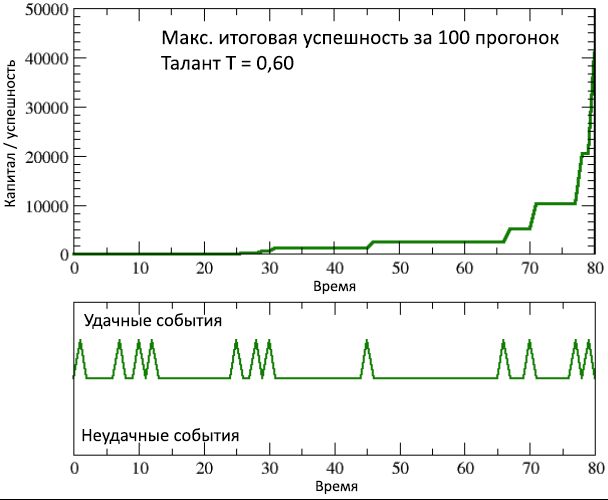
चित्र 9: सबसे सफल व्यक्ति की सफलता / पूंजी के समय में परिवर्तन (लेकिन एक ही समय में, मामूली रूप से उपहार में), 100 सिमुलेशन रन में से, उसके जीवन में होने वाली सफल घटनाओं के संबंधित असामान्य क्रम की तुलना में।

तुलनात्मक रूप से यह भी दिलचस्प है, 100 रनों से, औसत पूंजी / सफलता दर C _mt interesting 63 सबसे प्रतिभावान लोगों की औसत C के साथ of 33 है जिनकी प्रतिभा मंझला m _{T के} करीब है _। दोनों मामलों में, हमने कम संकेतक पाए (भले ही प्रारंभिक पूंजी C (0) = 10 से अधिक), लेकिन तथ्य यह है कि C _mt > C _पर संकेत मिलता है कि यद्यपि सफलता के शीर्ष पर एक मामूली प्रतिभाशाली व्यक्ति को खोजने की संभावना अधिक है। अत्यधिक उपहार वाले व्यक्ति की तुलना में, प्रत्येक रन के सबसे प्रतिभाशाली व्यक्ति औसतन, गिफ्ट किए गए लोगों की तुलना में अधिक सफल होते हैं। दूसरी ओर, 100 से अधिक रनों के औसत को देखते हुए, प्रतिभा T > 0.7 (यानी, माध्यिका से एक मानक विचलन के साथ उच्चतर) और अंतिम सफलता / पूंजी C _अंत > 10 के साथ व्यक्तियों की हिस्सेदारी, खाते की सभी विशेषताओं को ध्यान में रखते हुए प्रतिभा T > 0.7 (जिनमें से प्रत्येक रन के लिए औसतन,, 160), हमने पाया कि यह हिस्सा 32% है - इसका मतलब है कि हमारी आबादी में सबसे प्रतिभाशाली लोगों का संयुक्त प्रदर्शन, औसतन, अपेक्षाकृत छोटा है, केवल तब से उनमें से एक तिहाई मूल से अधिक की कुल पूंजी तक पहुंचते हैं।

किसी भी मामले में, यह तथ्य कि 100 सिमुलेशन रन के बीच सबसे अच्छा प्रदर्शन करने वाला व्यक्ति टी _{बेस्ट} = 0.6 के साथ एक एजेंट है, जो पूरी तरह से माध्यिका से मेल खाता है, और अंतिम सफलता के साथ सी _{बेस्ट} = 40960, जो सी _एमटी से 650 गुना अधिक है, _{अकाट्य है} । और सबसे प्रतिभाशाली लोगों के 2/3 में सी _एंड <10 की सफलता की तुलना में 4,000 गुना अधिक है। यह हुआ, अंत में, क्योंकि वह बाकी की तुलना में भाग्यशाली था। बिना शर्त भाग्यशाली, जैसा कि चित्र 9 से देखा जा सकता है, जो कि उनकी कामकाजी जीवन में उनकी पूंजी / सफलता की वृद्धि को दर्शाता है, साथ ही सफल (और केवल सफल) घटनाओं की एक प्रभावशाली श्रृंखला है, जिनमें से, असाधारण प्रतिभा की कमी के बावजूद, वह अपने लाभ में सक्षम था कैरियर।

इस बिंदु पर संक्षेप में, यह पाया गया कि अपनी सादगी के बावजूद, टीपीयू मॉडल कई विशेषताओं को ध्यान में रखने में सक्षम है जो कि विशेषता है, जैसा कि परिचय में बताया गया है, हमारे समाज में धन और सफलता के वितरण में उच्च असमानता, जो स्पष्ट रूप से प्रतिभाओं के बीच गौसियन वितरण के साथ विपरीत है। लोग। इसके अलावा, मात्रात्मक रूप में मॉडल से पता चलता है कि महान प्रतिभा एक गारंटीकृत सफल कैरियर के लिए पर्याप्त नहीं है और इसके विपरीत, कम प्रतिभाशाली लोग अक्सर सफलता के शिखर पर पहुंच जाते हैं - यह एक और "सशर्त तथ्य" है जो अक्सर वास्तविक जीवन में मनाया जाता है [35, 36, 38]।

एक प्रमुख पहलू जो सहजता से बताता है कि यह कैसे हो सकता है कि मामूली प्रतिभाशाली व्यक्ति अधिक प्रतिभाशाली लोगों के साथ तुलना में (अधिक बार) बहुत अधिक सम्मान और सफलता प्राप्त करते हैं, यह है कि भाग्य की एक छिपी हुई और अक्सर कम की भूमिका होती है, जैसा कि स्पष्ट रूप से है। हमारे सिमुलेशन से देखा। लेकिन हमारे शोध के परिणामों के सही अर्थ को समझने के लिए, स्थूल और सूक्ष्म दृष्टिकोण के बीच अंतर करना महत्वपूर्ण है।

वास्तव में, सूक्ष्म स्तर पर, टीपीयू मॉडल के गतिशील नियमों का पालन करते हुए, एक प्रतिभाशाली व्यक्ति एक मध्यम स्तर के प्रतिभाशाली व्यक्ति की तुलना में उच्च स्तर की सफलता प्राप्त करने की अधिक संभावना रखता है, क्योंकि उसके पास अवसर को जब्त करने की उच्च क्षमता है। इस प्रकार, किसी व्यक्ति के दृष्टिकोण से, हमें निष्कर्ष निकालना चाहिए कि सफल घटनाओं की उपस्थिति को प्रभावित करने में सक्षम (परिभाषा के अनुसार), सफलता की संभावना को बढ़ाने के लिए सबसे अच्छी रणनीति (किसी भी स्तर पर प्रतिभा) व्यक्तिगत गतिविधि का विस्तार करना, विचारों को उत्पन्न करना, संवाद करना अन्य लोगों के साथ, विविधता और आपसी संवर्धन की खोज। दूसरे शब्दों में, एक व्यापक दिमाग वाला व्यक्ति, जो दूसरों से संपर्क करने के लिए तैयार है, एक सफल घटना की उच्चतम संभावना देता है (जिसे व्यक्ति की प्रतिभा की सीमा तक महसूस किया जाएगा)।

दूसरी ओर, वृहद स्तर पर, पूरे समाज के दृष्टिकोण से, सफलता के शीर्ष पर मामूली रूप से प्रतिभाशाली व्यक्तियों से मिलने की संभावना वहाँ के अत्यंत प्रतिभाशाली लोगों को खोजने की तुलना में बहुत अधिक है, क्योंकि पूर्व बहुत बड़े हैं और भाग्य के लिए धन्यवाद, वे सामान्य रूप से, सांख्यिकीय हैं अपनी प्राथमिकताओं में कम व्यक्तिगत संभावना के बावजूद जबरदस्त सफलता प्राप्त करने का लाभ।

अगले भाग में, हम इस मैक्रो-लेवल के दृष्टिकोण पर विचार करेंगे, हमारे मॉडल द्वारा पेश किए गए अवसरों का पता लगाने के लिए और अधिक प्रभावी रणनीतियों और नीतियों का अध्ययन करने के लिए, आबादी में सबसे प्रतिभाशाली लोगों के प्रदर्शन के औसत स्तर को सुधारने के लिए, पुरस्कार और संसाधनों को वितरित करने के अधिक उत्पादक तरीकों को लागू करना। वास्तव में, हम अपेक्षा करते हैं कि कोई भी नीति जो सबसे प्रतिभाशाली व्यक्तियों के स्तर को बढ़ा सकती है जो हमारे समाज में प्रगति और नवाचार का इंजन हैं, उन पर संचयी लाभकारी प्रभाव पड़ेगा।

3. प्रभावी भाग्य संतुलन रणनीतियों

पिछले खंड में प्रस्तुत किए गए परिणाम स्पष्ट रूप से परिचय में प्रलेखित अनुभवजन्य साक्ष्य के साथ सुसंगत हैं, जो गुणात्मक धारणा पर सवाल उठाता है कि प्रतिभा, कौशल, योग्यता, बुद्धिमत्ता, कड़ी मेहनत या दृढ़ता में प्राकृतिक अंतर ही सफलता का एकमात्र कारण हैं। जैसा कि हमने दिखाया है, भाग्य पर भी प्रभाव पड़ता है और एक महत्वपूर्ण भूमिका निभा सकता है। चर्चा का सार यह है कि, व्यक्तिगत गुणों के कठिन औसत दर्जे (कई मामलों में, सटीक शब्दों में निर्धारित करना मुश्किल है) के कारण, योग्यता संबंधी रणनीतियों का इस्तेमाल अक्सर निजी धन या सफलता के संदर्भ में मापा जाता है, प्रायः निजी परिणामों के आधार पर किया जाता है। नतीजतन, इस तरह की रणनीतियां सकारात्मक प्रतिक्रिया तंत्र के कारण सबसे सफल व्यक्तियों के धन / सफलता को मजबूत करने और पंप करने के लिए आगे की कार्रवाई को प्रभावित करती हैं, जो कि "अमीर हो अमीर" प्रक्रिया के समान है (जिसे "मैथ्यू प्रभाव" [57, 58, 59: 59) कहा जाता है। , एक अनुचित परिणाम के साथ।

उदाहरण के लिए, इसके निपटान में एक निश्चित राशि के साथ एक सरकार द्वारा वित्त पोषित अनुसंधान और विकास परिषद की कल्पना करें। औसत शोध प्रभावशीलता बढ़ाने के लिए और अधिक प्रभावी क्या होगा: केवल कुछ निस्संदेह उत्कृष्ट वैज्ञानिकों या छोटे अनुदानों को बड़े पैमाने पर अनुदान देने के लिए स्पष्ट रूप से अधिक सामान्य वैज्ञानिकों को? हाल के एक अध्ययन [44], संबंधित प्रकाशनों के वैज्ञानिक महत्व के चार सूचकांकों के विश्लेषण के आधार पर, पाया गया कि महत्व का केवल धन के साथ कमजोर सकारात्मक संबंध है। विशेष रूप से, बड़े अनुदान धारकों के लिए डॉलर का महत्व कम था, और वैज्ञानिकों को फंडिंग में वृद्धि प्राप्त करने का महत्व उचित डिग्री तक नहीं बढ़ा। अध्ययन के लेखकों ने निष्कर्ष निकाला कि वैज्ञानिक महत्व (प्रकाशन में परिलक्षित होता है) केवल वित्त पोषण की सीमाओं को कमजोर करता है, और सुझाव दिया कि "उत्कृष्टता" के बजाय विचारों में विविधता लाने के उद्देश्य से वित्तपोषण की रणनीति अधिक उत्पादक होने की संभावना है। एक बाद के योगदान [60] ने दिखाया कि, उत्पादित और उनके वैज्ञानिक महत्व में दोनों की संख्या, केंद्रित अनुसंधान धन आम तौर पर सीमांत रिटर्न में कमी की ओर जाता है, और यह भी कि सबसे अधिक वित्त पोषित शोधकर्ता प्रदर्शन और वैज्ञानिक महत्व के मामले में बाहर खड़े नहीं होते हैं। सामान्य तौर पर, ऐसे निष्कर्षों को एक और हालिया खोज [18] के प्रकाश में आश्चर्यजनक नहीं होना चाहिए, जो बताता है कि महत्व, जैसा कि प्रभावशाली प्रकाशनों द्वारा मापा जाता है, वैज्ञानिक के कई प्रकाशनों में यादृच्छिक रूप से वितरित किया जाता है। दूसरे शब्दों में, भाग्य मायने रखता है, और अगर हम इसे स्वीकार करना चाहते हैं तो इससे अधिक प्रभावित होता है, यह आश्चर्य की बात नहीं है कि योग्यता संबंधी रणनीतियां अपेक्षा से कम प्रभावी हैं, खासकर अगर हम किसी पोस्टीरियर की योग्यता की सराहना करने की कोशिश कर रहे हैं। पिछले अध्ययनों में [४,, ४ ९, ५०, ५१, ५२, ५३, ५४, ५५] प्रबंधन, राजनीति और वित्त के क्षेत्रों में यादृच्छिक चुनावों के आधार पर वैकल्पिक रणनीतियों की प्रभावशीलता दिखाते हुए, इस तरह के "योग्यता के निकट" के खिलाफ पहले से ही चेतावनी थी। इस दृष्टिकोण के अनुसार, टीपीयू मॉडल दिखाता है कि दुनिया के अधिकांश प्रतिभाशाली लोगों के लिए सफलता का न्यूनतम स्तर कैसे बढ़ाया जा सकता है जहां भाग्य मायने रखता है, और आकस्मिक खोज अक्सर महत्वपूर्ण उपलब्धियों की ओर ले जाती है।

3.1। आकस्मिक खोज, नवाचार और प्रभावी वित्तपोषण रणनीतियों

शब्द "आकस्मिक खोज" का व्यापक रूप से ऐतिहासिक तथ्यों के साहित्यिक संदर्भों में उपयोग किया जाता है, यह दर्शाता है कि शोधकर्ता अक्सर शुद्ध मौका द्वारा अप्रत्याशित और उपयोगी खोजों को बनाते हैं, जब वे कुछ और खोज रहे होते हैं [61, 62]। संयोगों द्वारा विशेष रूप से की गई खोजों की कहानियों की एक लंबी सूची है: अलेक्जेंडर फ्लेमिंग द्वारा पेनिसिलिन से लेकर मैरी क्यूरी द्वारा रेडियोधर्मिता तक, ब्रह्मांडीय माइक्रोवेव पृष्ठभूमि विकिरण से रेडियो खगोलविदों अर्नो पेनज़ियास और रॉबर्ट वुडरोसन न्यूटन से ग्राफीन आंद्रेई जिम और कोंस्टेंटिन नोवोसियोलोव। यहाँ एक और हालिया उदाहरण है: मानव शरीर में तरल से भरे चैनलों का एक नेटवर्क, एक पूर्व अज्ञात अंग जो स्पष्ट रूप से कैंसर कोशिकाओं के प्रसार को बढ़ावा देता है, मौका द्वारा खोजा गया था, सरल एंडोस्कोपी [63] के दौरान। इसलिए, बहुत से लोग सोचते हैं कि जिज्ञासा से प्रेरित शोध को हमेशा वित्त पोषित किया जाना चाहिए, क्योंकि कोई भी वास्तव में अग्रिम रूप से नहीं जान सकता है या भविष्यवाणी कर सकता है कि वे क्या करते हैं [64]।

क्या यादृच्छिक खोज के महत्व को निर्धारित करना संभव है? यादृच्छिक खोज को अनुकरण करने के सबसे प्रभावी तरीके क्या हैं? यह कई अलग-अलग रूप ले सकता है, और इसे सीमित और मात्रा देना मुश्किल है। इसीलिए, अब तक, अकादमिक अध्ययनों ने दार्शनिक अवधारणा के रूप में, अधिकांश भाग के लिए एक आकस्मिक वैज्ञानिक खोज पर विचार किया है। लेकिन समय बदल रहा है। यूरोपीय रिसर्च काउंसिल ने हाल ही में बायोकैमिस्ट ओहिद याकूबू को विज्ञान में एक आकस्मिक खोज के महत्व की गणना करने के लिए $ 1.7 मिलियन का अनुदान दिया। [६५] याकूब ने पाया कि यादृच्छिक खोज को चार बुनियादी प्रकारों [66] में वर्गीकृत किया जा सकता है और इसके महत्वपूर्ण कारक हो सकते हैं जो इसकी उपस्थिति को प्रभावित करते हैं। उनके निष्कर्ष पहले के शोध [67, 68, 69, 70, 71, 72] के विचारों से मेल खाते हैं, जो तर्क देते हैं कि आमतौर पर स्वीकार किए जाते हैं, स्पष्ट रूप से योग्यता, श्रेष्ठता और शालीनता का पीछा करने वाली रणनीतियों को खोने के लिए किस्मत में लगता है। और अप्रभावी। कारण यह है कि वे एक प्राथमिकताओं को खारिज करते हैं, जो शुरू में कम आशाजनक दिखती थीं, लेकिन जो, विशेष रूप से, यादृच्छिक खोज के लिए, एक पोस्टवर्दी अविश्वसनीय रूप से अभिनव हो सकती है।

इस दृष्टिकोण से, हम TPU मॉडल को लागू करना चाहते हैं, जो स्वाभाविक रूप से इस उपधारा में विभिन्न वित्तपोषण परिदृश्यों की प्रभावशीलता का अध्ययन करने के लिए, रणनीति के एक मात्रात्मक पैरामीटर के रूप में भाग्य (और, परिणामस्वरूप, यादृच्छिक खोज) को व्यक्त करता है। विशेष रूप से, स्थितियों में, जैसा कि ऊपर उल्लेख किया गया है, एक मामूली प्रतिभाशाली-लेकिन-भाग्यशाली व्यक्ति अक्सर अधिक प्रतिभाशाली-लेकिन-अनलकी व्यक्तियों की तुलना में अधिक सफल होता है, सफलता के न्यूनतम स्तर को बनाए रखने की क्षमता के लिए वित्तपोषण रणनीतियों की प्रभावशीलता का मूल्यांकन करना महत्वपूर्ण है, जिसमें शामिल हैं सबसे प्रतिभाशाली लोग जो सबसे नवीन और प्रगतिशील विचारों को लाने की उम्मीद करते हैं।

उन्हीं आरंभिक मापदंडों से शुरू होता है जिनका उपयोग 2.2 में किया गया था, अर्थात्। एन = 1000, एम _टी = 0.6, 1000 _टी = 0.1, आई = 80, 6 _टी = 6, सी (0) = 10, एनई = 500, पी _एल = 50% और 100 सिमुलेशन रन, आइए कल्पना करें उपलब्ध कुल धन पूंजी एफ _टी समय-समय पर विभिन्न मानदंडों के अनुसार व्यक्ति के बीच वितरित की जाती है। उदाहरण के लिए, वित्त जारी किया जा सकता है:

1. अनुसंधान विविधता को प्रोत्साहित करने के लिए समान रूप से साझा (समतावादी मानदंड);
2. सबसे सफल ("सर्वश्रेष्ठ") व्यक्तियों (अभिजात्य कसौटी) का केवल एक निश्चित प्रतिशत, जिसे पहले पिछले प्रदर्शन के आधार पर लोगों के बीच वित्त के वितरण के लिए "निकट" योग्यता कहा जाता था।
3. सबसे सफल व्यक्तियों के एक निश्चित अनुपात के बीच "प्रीमियम" वितरण, और शेष, छोटे बराबर भागों में, बाकी (मिश्रित मानदंड) पर;
4. , ( ).

, F _T 5 , 40- , F _T = 8 . . , P _T , 100 , T > m _T + σ _T , / , .., C _end > C (0).

, 2.2. , , , / . , P _T0 ≈ 32% T > 0,7 , , / , . , , P _T P _T0 , . P ^* _T = P _T − P _T0 . : 100 , P ^* _T 2%. , P ^* _T , 40 , E , , E = P ^* _T / F _T .


10: . (1 ), E _norm (2 ), . , , , P _T P ^* _T , « », 100 . , F _T , .

, 10, (2- ), , (1 ), P _T (3- ) P ^* _T (4- ). , , F _T . E E _max , () E _norm = E / E _max . , , E _norm = 0. E _norm 11. P _T , 2%, E _norm .

11, , ( ), ( ) , , , .


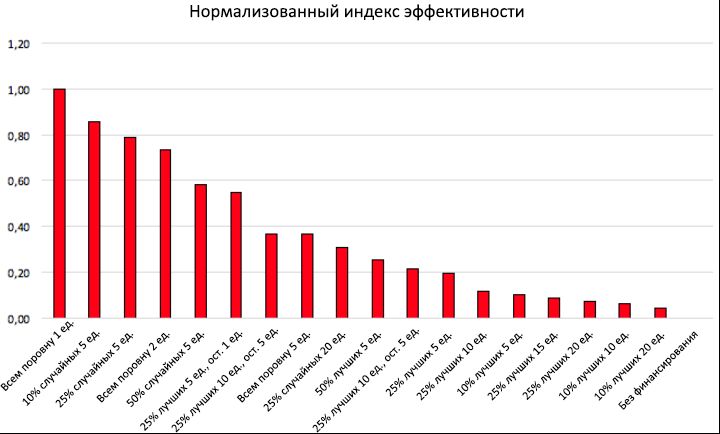
11: . E _norm . , , C _end > C (0), , , .

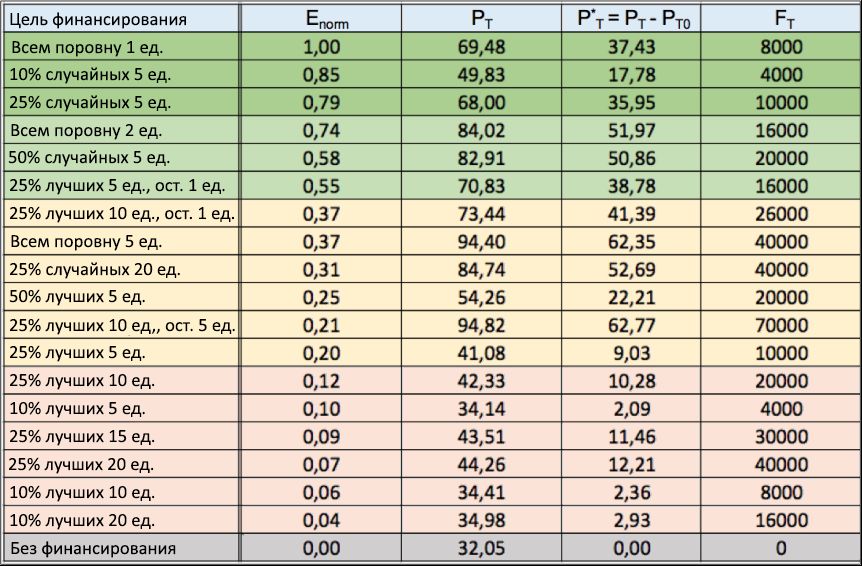
, , «» , 1 5 , , E _norm = 1 (.., E = E _max ): F _T 8000 , , « », P _T0 = 32,05% P _T = 69,48%, P ^* _T = 37,43. (, 2 5 ), ( 69,48% 94,40%), , E _norm = 1 E _norm = 0,74, E _norm = 0,37, .

, «» , 5 (5, 10, 15 20 ) 50%, 25% 10% , , E _norm < 0,25 , P ^* _T , « », ( 20%), , . , , , .

, «» , .. «» , , 25%, , , « » , . , «» . , , : 16000 , P _T , , , (70,83% 84,02%), E _norm (0,55 0,74).

( ), . , , , , : , , .

, , . , , , 5 10% , 4000 , P ^* _T = 17,78%, . , 25% ( 10000 ) P ^* _T= 35.95, जो कि सबसे अच्छी बराबरी की रणनीति द्वारा प्राप्त की गई तुलना में, जिसने समग्र स्टैंडिंग में पहला स्थान हासिल किया। यह हड़ताली है कि यह अंतिम पी ^* _टी परिणाम मूल्य ( पी ^* _{टी) के} लगभग चार गुना है = 9,03%), (. 12 ), (10000 ) (25% ). , , , , , , « » , . , , , , [48, 49, 50, 51, 52, 53, 54, 55], , , .

, 12 . , 100 F _T = 80000, 5 F _T /8 = 10000 , , , . , , , P _T 100%. ( 50% ), , 25% , , , . , , « » .


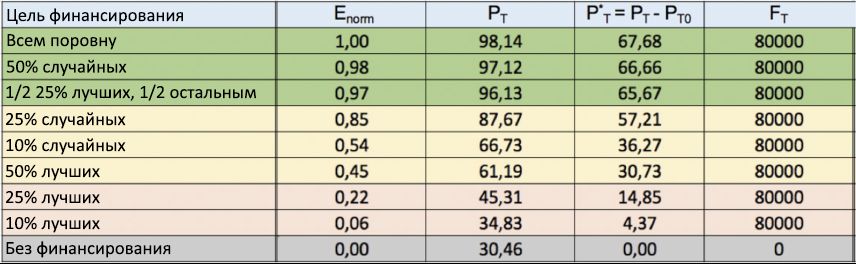
12: . E _norm (1- ) , . 10, F _T = 80000. .

, , (, , ) , . , , , , .

3.2।

, . . , , , , , m _T , σ _T , , , , .

13 / , 100 , . , 2.2 ( N = 1000, I = 80, δ _t = 6, C (0) = 10, N _E = 500 p _L = 50%), . , (a) m _T = 0,6, σ _T = 0,2, (b) , σ _T = 0,1 m _T = 0,7. , .


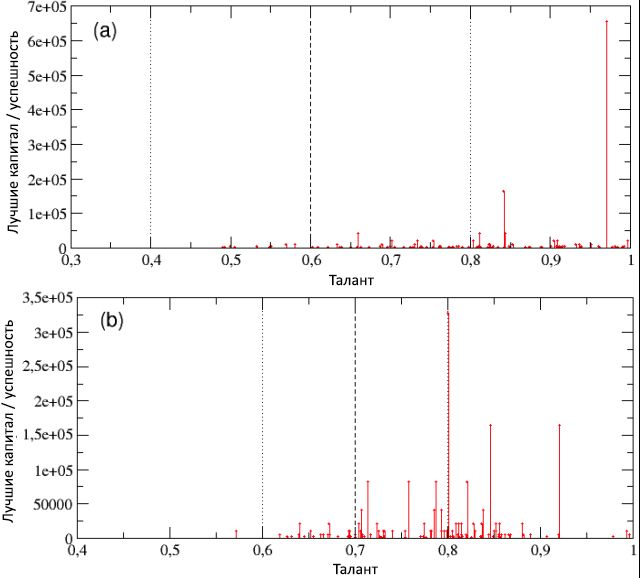
13: 100 , : (a) m _T = 0,6 σ _T = 0,2 ( ); (b) m _T = 0,7 σ _T = 0,1 ( ). m _T m _T ± σ _T , , .

, , σ _T , m _T , (a), – , T = 0,97, / C _best = 655360. , , , , , , , . (b) , m _T σ _T C _best = 327680 T = 0,8, , C = 163840 , , T = 0,85 T = 0,92. , , .

, / 100 C _mt ≈ 63, 2.2. , C _mt ≈ 319 (a) C _mt ≈ 122 (b), . , – P _T , , .. T > m _T + σ _T / C _end > 10, T > m _T + σ _T ( , , , m _T + σ _T = 0,8). , P _T = 38% (a) P _T = 37,5% (b), P _T0 = 32% ( m _T = 0,6 σ _T = 0,1).

, , , , , , . , , , , . , , , .

, , , , , .. , - , , .

14 , , , , 100 , , 2.2 ( N = 1000, m _T = 0,6, σ _T = 0,1, I = 80, C (0) = 10, N _E = 500) p _L (, 2.2 p _L = 50%). (a) p _L = 80%, , , [26]. , (b) p _L = 20% , , , , « ».


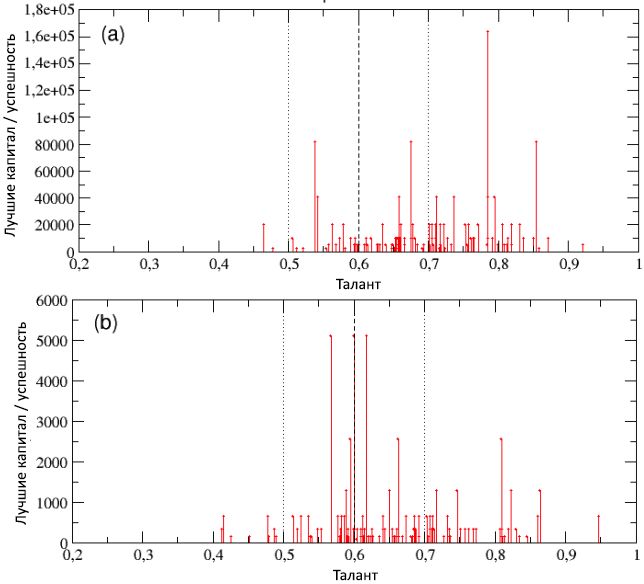
14: 100 , p _L : (a) p _L = 80%; (b) p _L = 20%. , , m _T = 0,6 m _T ± σ _T , σ _T = 0,1.

, / , , p _L .

p _L = 80%, (a), - , p _L = 50%, , C _best = 163840. , / , C _mt ≈ 149, , , P _T = 62,18% ( P _T0 = 32%), , , , .

p _L = 20%. , (b), , , 2.2, C _best 5120 – , . , P _T , , , 8.75%.

, , , , , , . , , , .

4.

, , , . , , , / , 40 , «80/20», , . , , , – , . . , , / , , . , « », , . , – , . , , , .

, .

1. Bak, P., Tang, C. and Wiesenfeld, K., Self-organized criticality. Phys. Rev. A , 38:364{374 (1988).
2. Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Science , Vol. 286, Issue 5439, pp. 509{512 (1999).
3. Newman, MEJ, Power laws, Pareto distributions and Zipf's law, Contemporary Physics , 46 (5): 323{351 (2005).
4. Tsallis, C., Introduction to Nonextensive Statistical Mechanics. Approaching a Complex World , Springer (2009).
5. Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
6. Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
7. Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
8. Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
9. Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
10. Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
11. Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
12. Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
13. Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
14. Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
15. Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
16. During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
17. During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
18. Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
19. Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
20. Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
21. Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
22. Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
23. Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
24. Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
25. Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
26. Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
27. Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
28. Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
29. Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
30. Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
31. Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
32. Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
33. Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
34. Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
35. .., . , , (2018).
36. .., . , (2018).
37. Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
38. .., . , (2019).
39. Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
40. Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
41. Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
42. Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
43. Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
44. Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
45. Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
46. O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
47. Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
48. Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
49. Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
50. Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
51. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
52. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
53. Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
54. Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
55. Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
56. Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
57. Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
58. . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
59. Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
60. Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
61. Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
62. Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
63. Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
64. Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
65. Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
66. Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
67. Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
68. Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
69. Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
70. Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
71. Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
72. Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).

: Talent vs Luck: the role of randomness in success and failure