संतुलित द्विआधारी खोज पेड़: जूलिया पर कार्यान्वयन

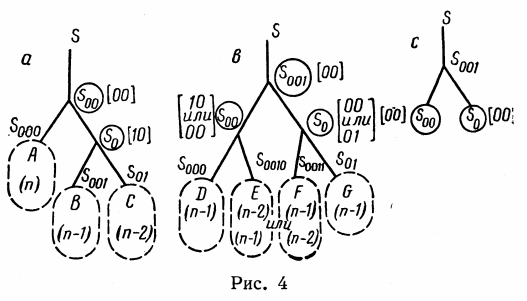
जी। एम। के काम से चित्रण। एडल्सन-वाल्स्की और ई.एम. लैंडिस 1962

खोज ट्री व्यवस्थित भंडारण और वस्तुओं की सरल खोज के लिए डेटा संरचनाएं हैं। बाइनरी सर्च ट्री व्यापक रूप से उपयोग किए जाते हैं, जिसमें प्रत्येक नोड में केवल दो बच्चे होते हैं। इस लेख में, हम द्विआधारी खोज पेड़ों को व्यवस्थित करने के लिए दो तरीकों पर विचार करते हैं: एडेल्सन-वेल्स्की और लैंडिस एल्गोरिदम (एवीएल पेड़) और कमजोर पड़े एवीएल पेड़ (डब्ल्यूएवीएल पेड़)।

चलो परिभाषाओं के साथ शुरू करते हैं। बाइनरी ट्री में नोड्स होते हैं , प्रत्येक नोड कुंजी-मूल्य जोड़े (या, सरल मामले में, केवल मूल्यों) के रूप में एक रिकॉर्ड संग्रहीत करता है और दो से अधिक बच्चे नहीं हैं । वंशज नोड्स को दाएं और बाएं से अलग किया जाता है, और चाबियों के क्रम के लिए शर्त संतुष्ट होती है: बाएं वंश की कुंजी अब और नहीं है, और दायां पैरेंट नोड की कुंजी से कम नहीं है। इसके अतिरिक्त, सेवा की जानकारी नोड्स में संग्रहीत (और आमतौर पर संग्रहीत) की जा सकती है - उदाहरण के लिए, मूल नोड या अन्य डेटा के लिए एक लिंक। विशेष मामले रूट नोड हैं जिसमें से पेड़ प्रवेश करता है, और एक खाली नोड जो किसी भी जानकारी को संग्रहीत नहीं करता है। नोड्स जिसमें दोनों वंश खाली हैं उन्हें पेड़ के पत्ते कहा जाता है। सभी वंशों के साथ एक नोड एक उपप्रकार बनाता है। इस प्रकार, प्रत्येक नोड या तो सबट्री या लीफ की जड़ है।

यह परिभाषा आपको नोड्स और पेड़ के भंडारण के लिए एक सरल संरचना बनाने की अनुमति देती है। हम मानते हैं कि एक खाली नोड में nothing प्रकार nothing विशेष मूल्य है। फिर नोड में यह दाईं और बाईं संतानों और माता-पिता के संदर्भों को संग्रहीत करने के लिए पर्याप्त है। पेड़ के भंडारण के लिए संरचना में केवल रूट नोड का लिंक होता है।

 # K -   # V -    mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end 

इस मामले में, सवाल उठता है कि एक खाली पेड़ का प्रतिनिधित्व कैसे करें। ऐसा करने के लिए, हम पुस्तक "एल्गोरिदम: निर्माण और विश्लेषण" से दृष्टिकोण का उपयोग करते हैं और पेड़ में प्रवेश के एक बिंदु के रूप में एक जड़ नहीं, बल्कि एक डमी नोड है, जो अपने स्वयं के माता-पिता होंगे। ऐसा नोड बनाने के लिए, BSTNode संरचना विवरण में कंस्ट्रक्टर जोड़ें:

 mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} #   function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end #    - function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() #     ! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing 

इस मामले में, BST संरचना को अपरिवर्तित किया जा सकता है, क्योंकि प्रवेश बिंदु के लिंक को अब बदलने की आवश्यकता नहीं होगी। इसके अलावा, हम मानते हैं कि पेड़ का रूट नोड इनपुट नोड के दाएं और बाएं वंशज है।

मुख्य ऑपरेशन जिसके लिए खोज पेड़ों की आवश्यकता होती है, स्वाभाविक रूप से, तत्वों की खोज है। चूंकि बाएं बच्चे की कुंजी अधिक नहीं है, और दायां पैरेंट कुंजी से कम नहीं है, इसलिए तत्व खोज प्रक्रिया बहुत सरल रूप से लिखी गई है: पेड़ की जड़ से शुरू होकर, वर्तमान नोड की कुंजी के साथ इनपुट कुंजी की तुलना करें; यदि कुंजियाँ मेल खाती हैं, तो हम मान लौटाते हैं, अन्यथा, कुंजियों के क्रम के आधार पर, बाईं या दाईं उप-सीमा पर जाएँ। यदि एक ही समय में वे एक खाली नोड तक पहुंच गए - पेड़ में कोई कुंजी नहीं है, तो एक अपवाद फेंक दें।

 #   Base.getindex()    #      tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

कुंजी द्वारा एक तत्व की खोज, जाहिर है, ओ ( एच ) समय लेता है, जहां एच पेड़ की ऊंचाई है, अर्थात्। जड़ से पत्ती तक अधिकतम दूरी। यह गणना करना आसान है कि ऊंचाई एच के एक द्विआधारी पेड़ में अधिकतम 2 ^{एच + 1} -1 नोड्स हो सकते हैं यदि यह घनी आबादी वाला है , अर्थात। सभी नोड्स, को छोड़कर, शायद, बहुत चरम परत, दोनों के वंशज हैं। इसके अलावा, यह स्पष्ट है कि अग्रिम में किसी भी दिए गए अनुक्रम में इस तरह के घने पेड़ हो सकते हैं। यह समय ओ (लॉग ₂ एन ) में अपने इष्टतम निर्माण के साथ एक पेड़ में एक तत्व के लिए खोज का एक बहुत ही आशावादी विषमतापूर्ण व्यवहार देता है, जहां एन तत्वों की संख्या है।

स्वाभाविक रूप से, खोज पेड़ में एक तत्व जोड़ने के लिए एल्गोरिथ्म का निर्माण इस तरह से किया जाना चाहिए कि कुंजियों के क्रम पर स्थिति संतुष्ट हो। आइए कुंजी द्वारा एक तत्व डालने का एक भोली कार्यान्वयन लिखें:

 #   Base.setindex!()    #       tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left #   -     if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end 

दुर्भाग्य से, पेड़ का भोली निर्माण यादृच्छिक इनपुट डेटा पर केवल वांछित संरचना देगा, लेकिन वास्तव में वे अक्सर काफी संरचित होते हैं। सबसे खराब स्थिति में, यदि आने वाली चाबियों का कड़ाई से आदेश दिया जाता है (कम से कम आरोही में, कम से कम अवरोही क्रम में), तो भोले वृक्ष का निर्माण हर समय नए तत्वों को एक दिशा में, एकत्रित करना, वास्तव में, एक रैखिक सूची भेजेगा। यह अनुमान लगाना आसान है कि तत्वों का सम्मिलन, यह खोज ओ ( एन ) के दौरान ऐसी संरचना के साथ होगी, जो एक जटिल डेटा संरचना के निर्माण के सभी प्रयासों को नकारती है।

निष्कर्ष: निर्माण के दौरान खोज पेड़ को संतुलित होना चाहिए, अर्थात प्रत्येक नोड पर दाएं और बाएं सबट्री की ऊंचाई को संरेखित करें। संतुलन के लिए कई दृष्टिकोण हैं। सरलतम एक निश्चित संख्या में सम्मिलित या हटाए गए संचालन को निर्दिष्ट करना है, जिसके बाद पेड़ को पुन: असंतुलित किया जाएगा। इस स्थिति में, पेड़ संतुलन बनाने से पहले "चल" स्थिति में होगा, जिसके कारण संतुलन सबसे खराब स्थिति में O ( N ) समय के बारे में होगा, लेकिन बाद में एक निश्चित सम्मिलन / विलोपन सीमा तक संचालन लॉजिस्टिक समय में किया जाएगा। एक और विकल्प तुरंत सम्मिलन और विलोपन एल्गोरिदम का निर्माण करना है ताकि पेड़ हमेशा संतुलित रहे, जो किसी भी ऑपरेशन के लिए गारंटीकृत संचालन समय ओ (लॉग ₂ एन ) देता है।

इस तथ्य के कारण कि ऐसे एल्गोरिदम हैं जिनमें पेड़ को "जंगली" जाने की अनुमति है, लेकिन उसके बाद, एक लघुगणक समय में ऑपरेशन लंबे समय तक किया जा सकता है, इससे पहले कि पेड़ को लंबे समय तक संतुलित अवस्था में लाया जाए, एक तत्व के सम्मिलन / विलोपन की गारंटी और परिशोधन समय को अलग किया जाता है। द्विआधारी खोज पेड़ों के साथ संचालन के कुछ कार्यान्वयन के लिए, हे ( एन ₂ ) को खराब करने के साथ, ओ (लॉग ₂ एन ) डालने और हटाने की जटिलता की गारंटी है।

एडल्सन-वाल्स्की और लैंडिस एल्गोरिथम (AVL)

एडलसन-वाल्स्की और लैंडिस द्वारा 1962 में एक स्व-संतुलन बाइनरी सर्च ट्री का पहला कार्यान्वयन प्रस्तावित किया गया था। उपनामों के प्रारंभिक अक्षरों पर आधुनिक साहित्य में इस संरचना को एवीएल-ट्रीज़ कहा जाता है। संरचना निम्नलिखित गुणों द्वारा वर्णित है:

1. आदेश देना: किसी भी नोड के लिए, बाएं सबट्री के शीर्ष पर स्थित कुंजी सही सबट्री के शीर्ष पर कुंजी से कम है (यदि वंशज खाली नोड नहीं हैं)।
2. ऊँचाई वृद्धि: मूल नोड की ऊँचाई उसके वंशजों की अधिकतम ऊँचाई से एक अधिक है। खाली नोड्स की ऊंचाई शून्य के बराबर मानी जा सकती है।
3. एवीएल संतुलन: किसी भी नोड के लिए, दाएं और बाएं सबटाइम्स की ऊंचाइयां 1 से अधिक नहीं होती हैं।

इन गुणों से यह निम्नानुसार है कि पूरे पेड़ की ऊँचाई हे (लॉग ₂ एन ), जहां एन पेड़ में संग्रहीत रिकॉर्ड की संख्या है, जिसका अर्थ है कि रिकॉर्ड लॉगरिदमिक समय के लिए खोजा गया है। प्रत्येक प्रविष्टि के बाद रहने के लिए एबीएल-संतुलन की स्थिति के लिए, प्रत्येक सम्मिलन एक संतुलन संचालन के साथ है। इस ऑपरेशन के प्रभावी कार्यान्वयन के लिए, प्रत्येक नोड को सेवा की जानकारी संग्रहीत करने की आवश्यकता होती है। सादगी के लिए, बस वहाँ नोड की ऊंचाई रखें।

 mutable struct AVLNode{K,V} # ,       255 # (  10^38 ) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} #   function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end #    - function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height) 

रिकॉर्ड डालें

मूल सम्मिलन मानक एल्गोरिथ्म के अनुसार किया जाता है - नीचे पेड़ को नीचे जाएं, देखें कि आप एक नया नोड कहां डाल सकते हैं और डालें। हम बाएं और दाएं के बजाय अनुक्रमित -1 और 1 का उपयोग करके बच्चे के नोड्स की जगह पाने के लिए रैपर लिखेंगे:

 function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end 

अगला, हम पेड़ के ऊपर जाते हैं और शर्तों 2 और 3 के उल्लंघन की तलाश करते हैं। अगला, हम उन विकल्पों पर विचार करते हैं जो दिखाई दे सकते हैं (आंकड़ों में, हरा उस नोड को इंगित करता है जिसने ऊंचाई को बदल दिया है, संसाधित होने वाला नोड इसका मूल है)।

केस 0
सम्मिलन के बाद, नोड की ऊंचाई बहन के समान होती है, और मूल नोड की (पुरानी) ऊंचाई से 1 कम।

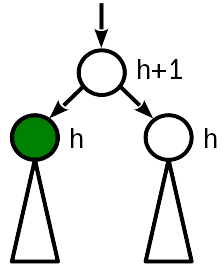
सबसे अच्छा मामला है, आगे कुछ भी छूने की जरूरत नहीं है। ऊपर, भी, आप देख नहीं सकते, क्योंकि वहां कुछ नहीं बदलेगा।

केस 1
सम्मिलन से पहले, गाँठ की ऊंचाई बहन की गाँठ की ऊंचाई के बराबर थी। डालने से सबट्री की जड़ बढ़ जाती है, और नोड की ऊंचाई की तुलना माता-पिता की ऊंचाई के साथ की जाती है।

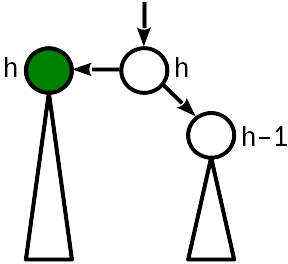
इस मामले में, यह माता-पिता नोड को "बढ़ाने" के लिए पर्याप्त है, इसकी ऊँचाई 1. से बढ़ रही है। इसी समय, आपको पेड़ की जड़ तक बढ़ना जारी रखना होगा, क्योंकि मूल नोड की ऊंचाई बदलने से स्थिति 2 के स्तर का उल्लंघन हो सकता है।

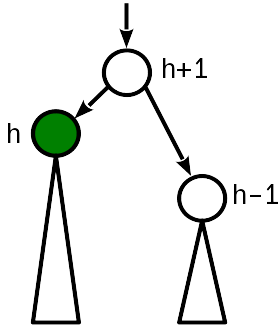
 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end 

केस 2

सम्मिलन के बाद, बहन सबट्री के साथ ऊंचाई का अंतर 2 हो गया, और बायाँ उपरी भाग ऊपर की ओर "धकेल" दिया गया:

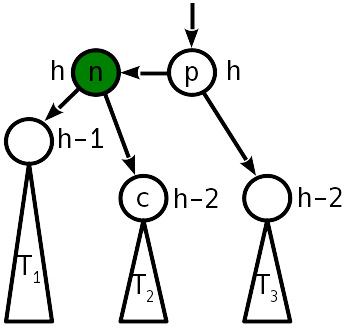
समस्या को एक "सरल रोटेशन" नामक एक ऑपरेशन के साथ इलाज किया जाता है जो पेड़ को निम्नानुसार बदल देता है:

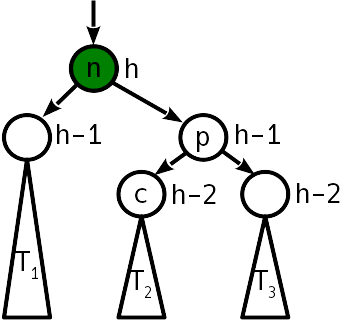
एक साधारण मोड़ के लिए 6 सूचक परिवर्तनों की आवश्यकता होती है।

ध्यान दें कि क्षैतिज अक्ष पर प्रक्षेपण में, चक्कर n , p और पेड़ों का क्रम T ₁ - T ₃ रोटेशन के पहले और बाद में समान रहता है। यह आदेश देने की स्थिति की पूर्ति है। जैसा कि आप देख सकते हैं, पेड़ को मोड़ने के बाद, संतुलन की आवश्यकता नहीं है।

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end 

केस 3
सम्मिलन के बाद, बहन सबट्री के साथ ऊंचाई का अंतर 2 हो गया, और सही सबट्री "पुश" हो गया:

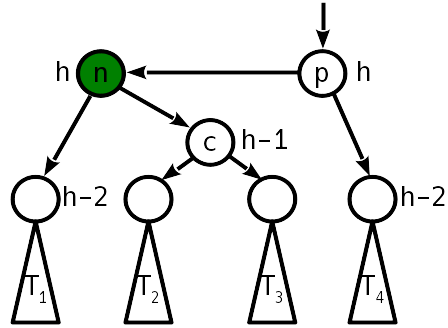
इस मामले में, एक एकल सरल मोड़ अब मदद नहीं करेगा, लेकिन आप दाएं वंश के चारों ओर एक सरल बाएं मोड़ बना सकते हैं, जिससे केस 2 को जन्म दिया जाएगा, जिसे पहले से ही एक साधारण दाहिने मोड़ के साथ इलाज किया जा रहा है।

नोड्स के "आउटवेग" की संख्या को कम करने के लिए, दो घुमावों को एक ऑपरेशन में जोड़ा जा सकता है, जिसे एक बड़ा या दोहरा मोड़ कहा जाता है। फिर, पॉइंटर्स के 12 बदलावों के बजाय, केवल 10 की आवश्यकता होगी। दोहरे घुमाव के परिणामस्वरूप, पेड़ निम्नलिखित रूप लेता है:

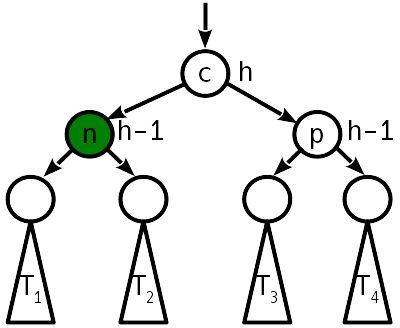
जैसा कि आप देख सकते हैं, एक डबल मोड़ के बाद, पेड़ को और संतुलित करना भी आवश्यक नहीं है।

 # pivot       funtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end 

इसलिए, जब आप एवीएल पेड़ में रिकॉर्ड डालते हैं, तो आपको नोड्स की ऊंचाई के बारे में जानकारी में ओ (लॉग ₂ एन ) की आवश्यकता होती है और दो से अधिक रोटेशन संचालन नहीं होते हैं। एक सम्मिलित फ़ंक्शन में सब कुछ मिलाएं। यह केवल मूल सम्मिलन से अलग होगा, एक नए नोड के सम्मिलन के बाद, fix_insertion!() फ़ंक्शन को fix_insertion!() , जो नए सम्मिलित नोड से रूट पर जाता है, चेक करता है और यदि आवश्यक हो, तो संतुलन को ठीक करता है।

 function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

fix_insertion!() फ़ंक्शन दो चाइल्ड नोड्स के बीच की ऊँचाई के अंतर की जाँच करता है, जो कि सम्मिलित किए गए पैरेंट नोड से शुरू होता है। यदि यह 1 के बराबर है - हम मामले 1 में हैं, तो आपको नोड की ऊंचाई बढ़ाने और अधिक जाने की आवश्यकता है। यदि यह शून्य है, तो पेड़ संतुलित है। यदि यह 2 के बराबर है - यह मामला 2 या 3 है, तो आपको उपयुक्त घुमाव लागू करने की आवश्यकता है, और पेड़ एक संतुलित स्थिति में आता है।

 #     -  , #   -  imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) #      0 - ..        while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 #       , # ..   dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end 

रिकॉर्ड हटाएं

निकालना डालने से थोड़ा अधिक कठिन है।

शुरू करने के लिए, एक द्विआधारी खोज पेड़ से एक प्रविष्टि के सामान्य विलोपन पर विचार करें।

1. यदि हटाए गए रिकॉर्ड शीट में है, तो रिकॉर्ड को बस हटा दिया जाता है, यहां सब कुछ सरल है।
2. यदि हटाए गए रिकॉर्ड एक नोड में है जिसमें केवल एक वंशज है, तो यह वंशज अपने सभी उपप्रकार के साथ रिमोट नोड के स्थान पर डाल दिया जाता है।
3. यदि दो वंशज हैं, तो या तो अधिकतम तत्व को बाएं सबट्री में खोजा जाता है, या न्यूनतम एक में सही, पेड़ से निकाला जाता है (खोज ट्री की संपत्ति के द्वारा, अधिकतम तत्व वाले नोड को सही वंश नहीं होने की गारंटी है, और एक न्यूनतम तत्व के साथ बाईं ओर है, इसलिए यह विलोपन आसान है और) हटाए गए रिकॉर्ड के स्थान पर रखें।

लेकिन उसके बाद, पेड़ का संतुलन गड़बड़ा सकता है, इसलिए आपको इसे पुनर्स्थापित करते हुए दूरस्थ नोड के माता-पिता से ऊपर जाने की आवश्यकता है। ध्यान दें कि बहुत शुरुआत में यह गारंटी दी जाती है कि प्रश्न में माता-पिता के वंशजों में से एक ने ऊंचाई कम कर दी है। 1 इसे ध्यान में रखते हुए, आपको उन विकल्पों पर विचार करने की आवश्यकता है (जो नोड्स ऊँचाई को लाल रंग में दिखाए गए हैं, संसाधित नोड लाल रंग से माता-पिता हैं):

केस 1
शून्य असंतुलन। इसलिए, हटाने से पहले, यह 1 मॉडुलो था, और अब बच्चे के नोड्स माता-पिता की तुलना में 2 कम हैं।

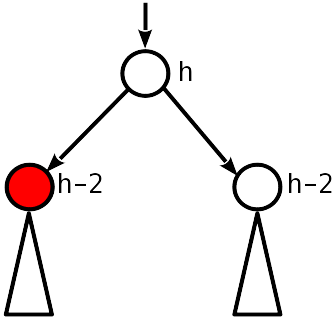
आपको मूल नोड को 1 से कम करने और आगे बढ़ने की आवश्यकता है।

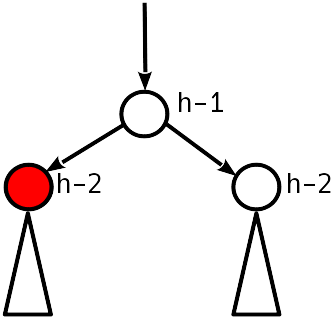
केस 2
असंतुलन 1 मोदुलो।

AVL की स्थिति संतुष्ट है, आप रोक सकते हैं।

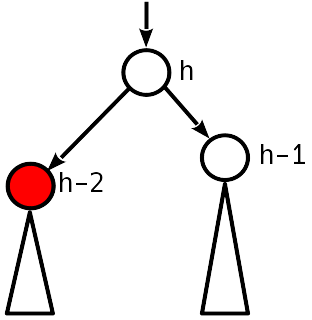
केस 3
असंतुलन 2 मोडुलो है, अवरोही के लिए बहन नोड में एक गैर-शून्य असंतुलन है।

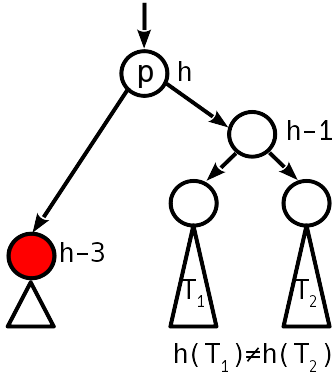
हम सरल (यदि टी ₁ टी ₂ से कम है) या डबल (अन्यथा) रोटेशन के द्वारा संतुलन बहाल करते हैं, जैसा कि सम्मिलन के दौरान किया गया था। सबट्री की ऊंचाई कम हो जाती है, अर्थात पेड़ के ऊपर उल्लंघन हो सकता है।

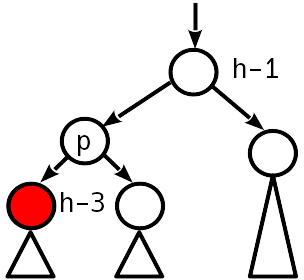
केस 4
असंतुलन 2 मोडुलो, बहन नोड में शून्य असंतुलन है।

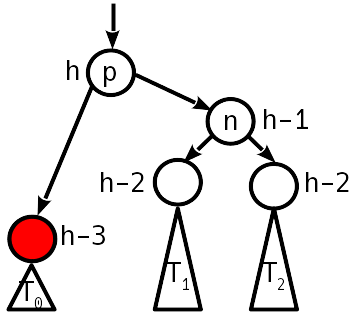
एक साधारण रोटेशन संतुलन की स्थिति को बहाल करता है, जबकि उपरी की ऊंचाई नहीं बदलती है - हम ऊपर जाना बंद कर देते हैं।

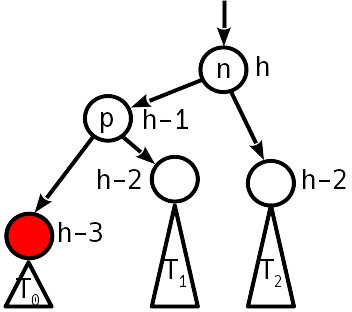
 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end 

एवीएल पेड़ों का उदय और पतन

क्लासिक एवीएल पेड़ों की एक बहुत अच्छी विशेषता एक रिकॉर्ड को हटाने की कठिनाई नहीं है: एक रोटेशन पूरे सबट्री एक स्तर को नीचे "रीसेट" कर सकता है, फिर सबसे खराब स्थिति में, हटाने के लिए ओ (लॉग ₂ एन ) ट्री रोटेशन की आवश्यकता होती है - हर बार जब आप fix_deletion!() में एक स्तर ऊपर जाते हैं।

इस अशुभ विषम व्यवहार के कारण, एवीएल पेड़ों ने लाल-काले पेड़ों को रास्ता दिया जो 1970 के दशक में दिखाई देते थे और कमजोर संतुलन की स्थिति थी - जड़ से सबसे दूर के पत्तों तक का रास्ता रूट से निकटतम पत्ती से दोगुना से अधिक नहीं है। इस वजह से, एवीएल पेड़ों के लिए लाल-काले पेड़ों की ऊंचाई सबसे खराब स्थिति में 2log ₂ N बनाम 1.44log ₂ N है , लेकिन एक रिकॉर्ड को हटाने के लिए तीन से अधिक सरल घुमाव की आवश्यकता नहीं है। इस प्रकार, पेड़ की ऊँचाई के कारण खोज और सम्मिलन संभावित रूप से प्रदर्शन में खो देते हैं, लेकिन एक संभावित लाभ होता है यदि सम्मिलन को अक्सर विलोपन के साथ जोड़ दिया जाता है।

एवीएल स्ट्राइक बैक

यह पता चलता है कि द्विआधारी खोज पेड़ों के निर्माण के लिए "आदर्श" एल्गोरिथ्म एक छोटी ऊंचाई (क्लासिक एवीएल पेड़ के स्तर पर) की गारंटी देता है और रिकॉर्ड जोड़ने या हटाने पर दोनों की एक निरंतर संख्या होती है। यह अभी तक आविष्कार नहीं किया गया है, लेकिन 2015 में एक काम प्रकाशित हुआ था, जिसने एक संरचना का प्रस्ताव किया था जो एवीएल और लाल-काले पेड़ों दोनों के गुणों में सुधार करता है। यह विचार एवीएल पेड़ों के करीब है, लेकिन रिकॉर्ड की अधिक कुशल विलोपन की अनुमति देने के लिए शेष स्थिति को शिथिल किया गया है। "कमजोर AVL पेड़" (W (eak) AVL पेड़) नामक संरचना के गुणों को निम्नानुसार तैयार किया गया है:

1. आदेश देना: किसी भी नोड के लिए, बाएं सबट्री के शीर्ष पर स्थित कुंजी सही सबट्री के शीर्ष पर कुंजी से कम है (यदि वंशज खाली नोड नहीं हैं)।
2. आरोही रैंक। प्रत्येक नोड को एक रैंक सौंपा गया है। सभी खाली नोड्स की रैंक शून्य है, चादरों की रैंक 1 है। माता-पिता नोड की रैंक बच्चे की रैंक से कड़ाई से अधिक है।
3. कमजोर ABL-balance: एक नोड की रैंक बाल नोड्स के रैंक से 2 से अधिक नहीं है।

यह पता चला है कि इस तरह की संरचना में क्लासिक एवीएल पेड़ों और लाल-काले पेड़ों दोनों के गुण शामिल हैं। विशेष रूप से, यदि हम इस शर्त का परिचय देते हैं कि दोनों बाल नोड्स माता-पिता से रैंक 2 में भिन्न नहीं हो सकते हैं, तो हमें एक नियमित एवीएल पेड़ मिलता है, और रैंक बिल्कुल उपशीर्षक की ऊंचाई से मेल खाएगा।

SAVL के पेड़ों की सुंदरता यह है कि AVL की स्थिति के थोड़ा कमजोर पड़ने से पेड़ को संतुलित किया जा सकता है, जब रिकॉर्ड को दो से अधिक नहीं हटाया जाता है! पेड़ की ऊंचाई का अनुमान h <min (1.44log ₂ M , 2log ₂ N ) है, जहां N पेड़ में प्रविष्टियों की संख्या है, M आवेषण की संख्या है, लाल-काले पेड़ों के लिए h <2log ₂ N की तुलना में। , - , , .

- , . - .

.

-, "" "". , :

 mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} #   function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end #    - function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .

 wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end 

, . , , , , -, - .

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end # pivot       function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

, — -. .

0
, ..:

1. 1, 1
2. 0, 2 , .
   .

1
2 ( 0, 2 ).
1 .

2
1, 2.

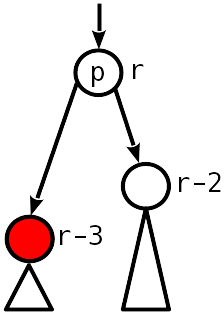
1, .

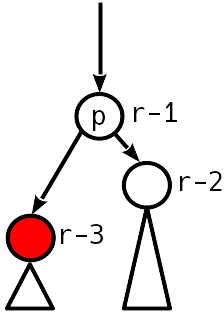
3
2 ( 1, .. ), 2 .

, . .

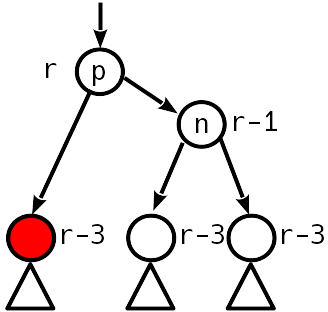
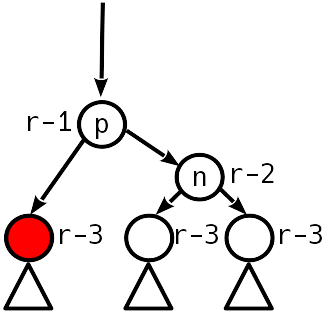
4

.

, , , .. .

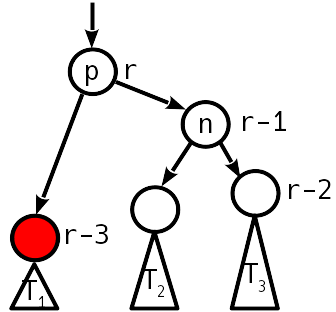
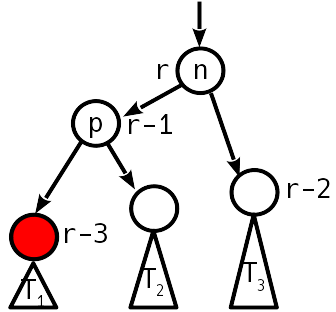
— T ₁ T ₂ , p 2, p 1.

5

.

, , .

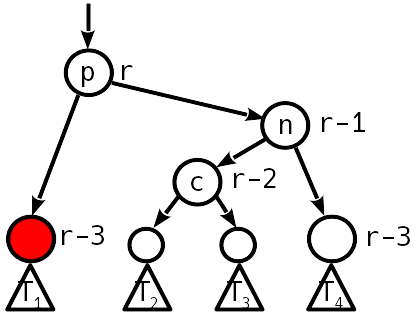
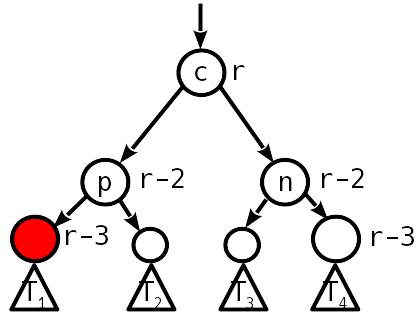
 function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end 

-.

 julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) #       ~  julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # ,     julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17 

, , . , , - , -, .

— ?
— , . , , .

.

— , . n - . , , .. , .

*

— , " ", " ", " -", " ". , , -. . , .

*
** O (1), ...

, " — ". , . — ( ) , , , . .

*
** ,

निष्कर्ष

() — , , , , , . — , .. , , .

संदर्भ

1. "-" nickme
2. Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
3. Goodrich MT, Tamassia R. Algorithm Design and Applications