🧑 🤝 👨🏿‍🤝‍👨🏼 इष्टतम रैखिक फ़िल्टरिंग: ढाल मूल से अनुकूली फिल्टर तक 👩‍⚕️ 🧚 🏦

मास्टर की विशेषता "कम्युनिकेशन एंड सिग्नल प्रोसेसिंग" (टीयू इलमेनौ) पर सार के विषय को विकसित करते हुए, मैं "एडेप्टिव एंड एरे सिग्नल प्रोसेसिंग" पाठ्यक्रम के मुख्य विषयों में से एक को जारी रखना चाहूंगा। अर्थात्, अनुकूली छानने की मूल बातें।

जिनके लिए यह लेख पहली बार लिखा गया था:

1) एक देशी विशेषता के एक छात्र भाईचारे के लिए;
2) उन शिक्षकों के लिए जो व्यावहारिक सेमिनार तैयार करते हैं, लेकिन उन्होंने अभी तक उपकरणों पर निर्णय नहीं लिया है - नीचे अजगर और मतलाब / ऑक्टेव में उदाहरण हैं;
3) छानने के विषय में रुचि रखने वाले किसी के लिए भी।

कट के तहत क्या मिल सकता है:

1) सिद्धांत से जानकारी, जिसे मैंने यथासंभव यथासंभव व्यवस्थित करने की कोशिश की, लेकिन, यह मेरे लिए, जानकारीपूर्ण रूप से लगता है;
2) फिल्टर के उपयोग के उदाहरण: विशेष रूप से, एंटीना सरणी के लिए तुल्यकारक के हिस्से के रूप में;
3) बुनियादी साहित्य और ओपन लाइब्रेरी (अजगर में) के लिए लिंक, जो अनुसंधान के लिए उपयोगी हो सकते हैं।

सामान्य तौर पर, स्वागत है और चलो सब कुछ अंक के आधार पर हल करते हैं।

तस्वीर में रहने वाला व्यक्ति कई लोगों से परिचित है, मुझे लगता है, नॉर्बर्ट वीनर। अधिकांश भाग के लिए, हम उसके नाम के फिल्टर का अध्ययन करेंगे। हालांकि, कोई भी हमारे हमवतन - आंद्रेई निकोलेविच कोलमोगोरोव का उल्लेख करने में विफल नहीं हो सकता है, जिसका 1941 का लेख भी इष्टतम फ़िल्टरिंग सिद्धांत के विकास में महत्वपूर्ण योगदान देता है, जिसे अंग्रेजी स्रोतों में भी कोलमोगोरोव-वीनर फ़िल्टरिंग सिद्धांत कहा जाता है ।

हम क्या विचार कर रहे हैं?

आज हम एक उत्कृष्ट आवेग प्रतिक्रिया (एफआईआर, परिमित आवेग प्रतिक्रिया) के साथ एक क्लासिक फिल्टर पर विचार कर रहे हैं, जिसे निम्नलिखित सरल योजना (छवि 1) द्वारा वर्णित किया जा सकता है।

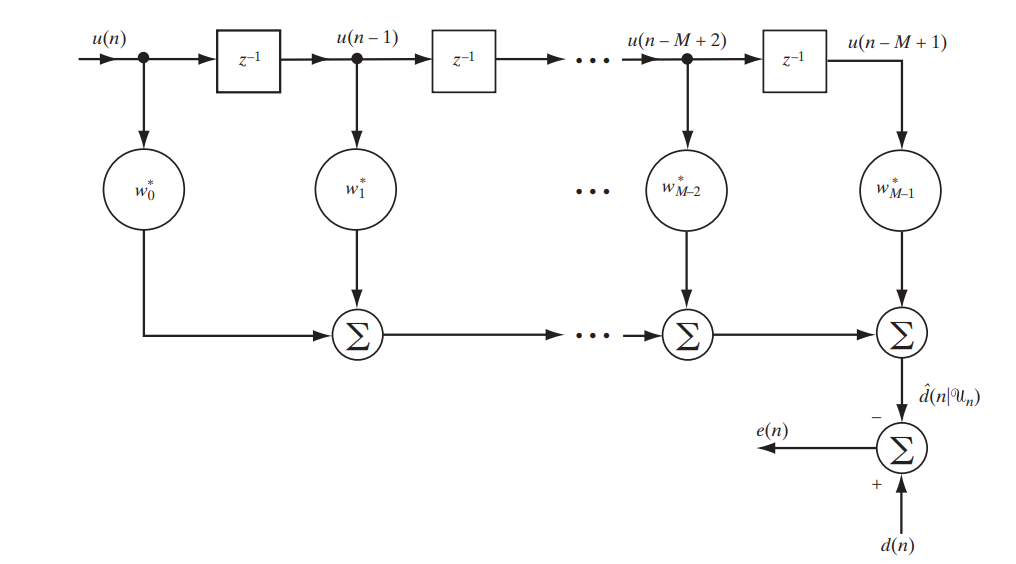
चित्र 1। वीनर फिल्टर के अध्ययन के लिए एफआईआर फ़िल्टर योजना। [१। c.117]

हम मैट्रिक्स के रूप में लिखेंगे कि इस स्टैंड के आउटपुट पर क्या होगा:

$e (n) = d (n) - \ hat {d} (n। \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

संकेतन की व्याख्या करें:

दिए गए और प्राप्त संकेतों के बीच अंतर (त्रुटि) है
कुछ पूर्वनिर्धारित संकेत है
$\ mathbf {u}$ नमूनों का वेक्टर है या, दूसरे शब्दों में, फिल्टर के इनपुट पर एक संकेत
$\ hat {d} (n | \ mathcal {U} _n)$ फिल्टर आउटपुट पर सिग्नल है
$\ mathbf {w} ^ एच$ - यह फिल्टर गुणांक वेक्टर का एक हर्मिटियन संयुग्मन है - यह उनके इष्टतम चयन में है कि फ़िल्टर की अनुकूलनशीलता झूठ

आपने शायद पहले ही अनुमान लगा लिया था कि हम दिए गए और फ़िल्टर किए गए सिग्नल के बीच सबसे छोटे अंतर के लिए प्रयास करेंगे, यानी सबसे छोटी त्रुटि। इसका मतलब है कि हम एक अनुकूलन कार्य का सामना कर रहे हैं।

हम क्या अनुकूलन करेंगे?

अनुकूलन, या कम से कम करने के लिए, हम केवल त्रुटि का मतलब नहीं करेंगे, मतलब वर्ग त्रुटि ( MSE - मीन सिकरेड एरर ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

जहाँ $J (\ mathbf {w})$ फिल्टर गुणांक के वेक्टर की लागत फ़ंक्शन को दर्शाता है, और $E \ {* \}$ निंदा करता है। उम्मीद।

इस मामले में वर्ग बहुत ही सुखद है, क्योंकि इसका मतलब है कि हमें उत्तल प्रोग्रामिंग की समस्या का सामना करना पड़ रहा है (मैंने केवल अंग्रेजी उत्तल अनुकूलन के ऐसे एनालॉग को देखा), जो बदले में, एक एकल चरम (हमारे मामले में, एक न्यूनतम) का तात्पर्य करता है।

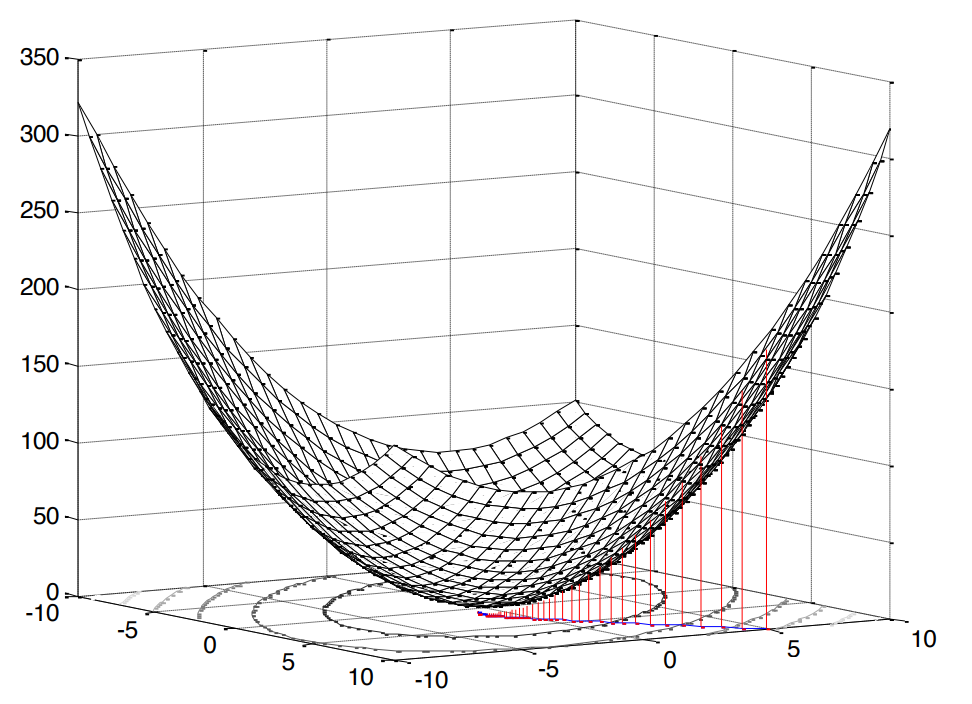
अंजीर। २। औसत वर्ग त्रुटि की सतह ।

हमारे त्रुटि समारोह में एक विहित रूप होता है [1, पी। 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

जहाँ $\ _ सिग्मा ^ 2_ डी$ अपेक्षित संकेत का विचरण है, $\ mathbf {p} = E \ {mathbf {u} (n) d ^ * * (n) \}$ इनपुट वेक्टर और अपेक्षित सिग्नल के बीच क्रॉस-सहसंबंध वेक्टर है, और $\ mathbf {R} = E \ {mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ इनपुट सिग्नल का ऑटोक्रॉलेशन मैट्रिक्स है।

इस सूत्र का निष्कर्ष यहां है (मैंने इसे और अधिक स्पष्ट रूप से आज़माया)।

जैसा कि हमने ऊपर उल्लेख किया है, अगर हम उत्तल प्रोग्रामिंग के बारे में बात कर रहे हैं, तो हमारे पास एक चरम (न्यूनतम) होगा। इसलिए, लागत फ़ंक्शन का न्यूनतम मान (न्यूनतम रूट स्क्वायर त्रुटि) खोजने के लिए, यह स्पर्शरेखा के ढलान के स्पर्श को खोजने के लिए पर्याप्त है या, दूसरे शब्दों में, हमारे अध्ययन किए गए चर के संबंध में आंशिक व्युत्पन्न :

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

सबसे अच्छे मामले में ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ), त्रुटि, निश्चित रूप से, न्यूनतम होनी चाहिए, जिसका अर्थ है कि हम व्युत्पन्न को शून्य के बराबर करते हैं:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquer (5)$

दरअसल, यहां यह हमारे स्टोव है, जिसमें से हम आगे नृत्य करेंगे: इससे पहले कि हम रैखिक समीकरणों की एक प्रणाली है ।

हम कैसे तय करेंगे?

यह तुरंत ध्यान दिया जाना चाहिए कि दोनों समाधान, जिन्हें हम नीचे विचार करेंगे, इस मामले में सैद्धांतिक और शैक्षिक हैं $\ mathbf {R}$ और $\ mathbf {p}$ पहले से ज्ञात (अर्थात, हमारे पास इनकी गणना करने के लिए पर्याप्त आँकड़े एकत्र करने की कथित क्षमता थी)। हालांकि, यहां ऐसे सरलीकृत उदाहरणों का विश्लेषण सबसे अच्छा है जिसे आप बुनियादी दृष्टिकोणों को समझने के लिए सोच सकते हैं।

विश्लेषणात्मक समाधान

इस समस्या को हल किया जा सकता है, इसलिए बोलने के लिए, माथे में - उलटा मैट्रिस का उपयोग करना:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

इस तरह की अभिव्यक्ति को वीनर - हॉपफ समीकरण कहा जाता है - यह अभी भी एक संदर्भ के रूप में हमारे लिए उपयोगी है।

बेशक, पूरी तरह से सावधानीपूर्वक होने के लिए, इस मामले को सामान्य तरीके से लिखने के लिए संभवतः अधिक सही होगा, अर्थात। साथ नहीं $^ {-}$ और के साथ ( छद्म उल्टा ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

हालाँकि, स्वतःभरण मैट्रिक्स गैर-वर्ग या एकवचन नहीं हो सकता है, इसलिए, बिल्कुल सही, हम मानते हैं कि कोई विरोधाभास नहीं है।

इस समीकरण से यह निकालना संभव है कि लागत फ़ंक्शन के न्यूनतम मूल्य के बराबर क्या होगा (यानी, हमारे मामले में MMSE - न्यूनतम औसत वर्ग त्रुटि):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {{}} \ qquad (7)$

सूत्र की व्युत्पत्ति यहाँ है (मैंने इसे और अधिक रंगीन बनाने की कोशिश की)।

खैर, एक उपाय है।

Iterative समाधान

हालांकि, हां, ऑटोकरेलेशन मैट्रिक्स - इनरेटिवली ( कम्प्यूटेशंस को बचाने के लिए ) को इनवर्ट किए बिना रैखिक समीकरणों की एक प्रणाली को हल करना संभव है। इस उद्देश्य के लिए, ग्रेडिएंट डिसेंट की मूल और समझने योग्य विधि ( स्टीपेस्ट / ग्रेडिएंट डीसेंट की विधि ) पर विचार करें।

एल्गोरिथ्म का सार निम्नलिखित को कम किया जा सकता है:

हम वांछित चर को कुछ डिफ़ॉल्ट मान पर सेट करते हैं (उदाहरण के लिए, $\ mathbf {w} (0) = \ mathbf {0}$ )
कुछ कदम चुनें $\ _ मु$ (हम वास्तव में कैसे चुनते हैं, हम नीचे बात करेंगे)।
और फिर, जैसा कि यह था, हम अपनी मूल सतह के साथ नीचे जाते हैं (हमारे मामले में, यह MSE सतह है) एक दिए गए कदम के साथ $\ _ मु$ और ढाल की भयावहता द्वारा निर्धारित एक निश्चित गति।

इसलिए नाम: ग्रेडिएंट - ग्रेडिएंट या स्टीपेस्ट - चरण-दर-चरण वंश - वंश।

हमारे मामले में ढाल पहले से ही ज्ञात है: वास्तव में, हमने इसे तब पाया जब हमने लागत फ़ंक्शन (सतह अवतल है, [1, पी। 220]) के साथ तुलना की। हम लिखते हैं कि वांछित चर (फ़िल्टर गुणांक) के पुनरावृत्ति अद्यतन के लिए सूत्र कैसा दिखेगा [1, p]। 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] / qquad (8)$

जहाँ पुनरावृति संख्या है।

अब एक चरण आकार चुनने के बारे में बात करते हैं।

हम स्पष्ट परिसर को सूचीबद्ध करते हैं:

कदम नकारात्मक या शून्य नहीं हो सकता
चरण बहुत बड़ा नहीं होना चाहिए, अन्यथा एल्गोरिथ्म अभिसरण नहीं करेगा (यह होगा, जैसा कि यह था, किनारे से किनारे तक छोड़ दें, चरम में गिरने के बिना)
कदम, ज़ाहिर है, बहुत छोटा हो सकता है, लेकिन यह भी पूरी तरह से वांछनीय नहीं है - एल्गोरिथ्म अधिक समय बिताएगा

वीनर फिल्टर के संबंध में, प्रतिबंध, निश्चित रूप से, बहुत पहले ही पाया गया है [1, पी। 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

जहाँ $\ lambda_ {अधिकतम}$ आटोक्लेररेशन मैट्रिक्स का सबसे बड़ा आइजनवेल्यू है $\ mathbf {R}$ ।

वैसे, रैखिक फ़िल्टरिंग के संदर्भ में आइजनवेल्स और वैक्टर एक अलग दिलचस्प विषय हैं। इस मामले के लिए एक पूरा Eigen फ़िल्टर भी है (देखें परिशिष्ट 1)।

लेकिन यह, सौभाग्य से, सभी नहीं है। एक इष्टतम, अनुकूली समाधान भी है:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ Gamma} (n)} \ qquad (10)$

जहाँ $\ mathbf {\ gamma} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ एक नकारात्मक ढाल है। जैसा कि सूत्र से देखा जा सकता है, चरण को प्रत्येक पुनरावृत्ति में पुनर्गणना किया जाता है, अर्थात यह adapts है।

सूत्र का निष्कर्ष यहाँ है (गणित का एक बहुत - मेरे जैसे कुख्यात नर्ड्स को ही देखें)।

ठीक है, दूसरे निर्णय के लिए, हमने भी चरण निर्धारित किया।

लेकिन क्या यह उदाहरणों से संभव है?

स्पष्टता के लिए, हम एक छोटा सिमुलेशन करेंगे। हम पायथन 3.6.4 का उपयोग करेंगे।

मैं तुरंत कहूंगा कि ये उदाहरण होमवर्क असाइनमेंट में से एक का हिस्सा हैं, जिनमें से प्रत्येक दो सप्ताह के भीतर छात्रों को समाधान के लिए पेश किया जाता है। मैं अजगर (रेडियो इंजीनियरों के बीच भाषा को लोकप्रिय बनाने के लिए) के तहत भाग को फिर से लिखता हूं। शायद आप अन्य पूर्व छात्रों से वेब पर कुछ अन्य विकल्पों में आएंगे।

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

हम चैनल समकारी समस्या के लिए अपने रैखिक फ़िल्टर का उपयोग करेंगे, जिसका मुख्य उद्देश्य इस चैनल के विभिन्न प्रभावों को उपयोगी सिग्नल पर समतल करना है।

स्रोत कोड को यहां या यहां एक फ़ाइल में डाउनलोड किया जा सकता है (हां, मुझे ऐसा शौक था - विकिपीडिया को संपादित करें)।

सिस्टम मॉडल

मान लीजिए कि एक एंटीना सरणी है (हमने पहले ही इसे संगीत के बारे में एक लेख में जांच लिया है)।

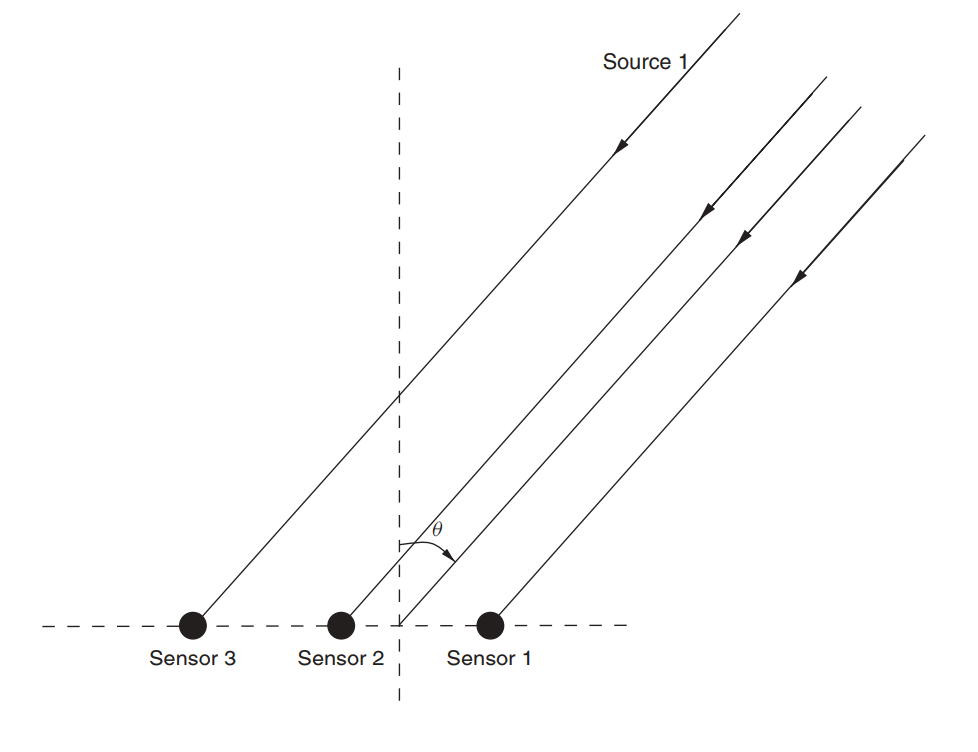
अंजीर। 3. गैर-दिशात्मक रैखिक एंटीना सरणी (ULAA - वर्दी रैखिक एंटीना सरणी) [2, पी। 32]।

प्रारंभिक जाली मापदंडों को परिभाषित करें:

 M = 5 #    (number of sensors)

इस पत्र में, हम लुप्त होती के साथ एक ब्रॉडबैंड चैनल की तरह कुछ पर विचार करेंगे, जिसकी एक विशेषता विशेषता बहु प्रचार है । ऐसे मामलों के लिए, एक दृष्टिकोण आमतौर पर लागू किया जाता है जिसमें प्रत्येक बीम को एक निश्चित परिमाण (छवि 4) की देरी का उपयोग करके तैयार किया जाता है।

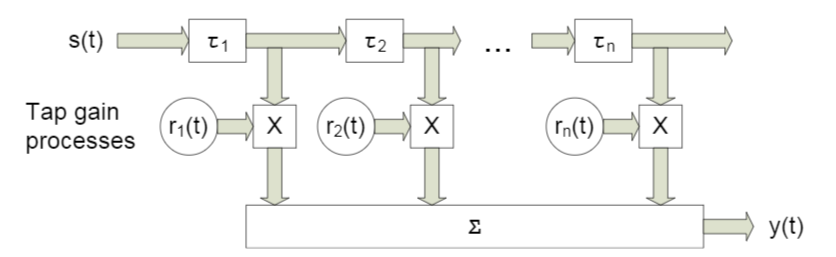
अंजीर। 4. n तय देरी के साथ ब्रॉडबैंड चैनल का मॉडल। [3, पी। 29]। जैसा कि आप समझते हैं, विशिष्ट पदनाम एक भूमिका नहीं निभाते हैं - आगे हम थोड़ा अलग का उपयोग करेंगे।

एक सेंसर के लिए प्राप्त संकेत का मॉडल निम्नानुसार व्यक्त किया गया है:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

इस मामले में संदर्भ संख्या इंगित करता है, एच (एल) क्या चैनल की प्रतिक्रिया l- th किरण के साथ है, L विलंब रजिस्टरों की संख्या है, s संचारित (उपयोगी) संकेत है, $\ n (n)$ - योजक शोर।

कई सेंसर के लिए, सूत्र फॉर्म लेगा:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

जहाँ $\ mathbf {x} (n)$ और $\ mathbf {\ nu} (n)$ - आयाम है $एम \ _ 1 बार$ आयाम $\ mathbf {H}$ के बराबर है $M \ गुना (M-L)$ , और आयाम $\ mathbf {s} (n)$ बराबरी $(एम-एल) \ _ 1 बार$ ।

मान लीजिए कि प्रत्येक सेंसर को एक निश्चित देरी के साथ एक कोण पर लहर की घटना के कारण एक संकेत भी प्राप्त होता है। मैट्रिक्स $\ mathbf {H}$ हमारे मामले में, यह प्रत्येक किरण के लिए प्रतिक्रिया सदिश के लिए एक दृढ़ मैट्रिक्स होगा। मुझे लगता है कि कोड अधिक स्पष्ट होगा:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

निष्कर्ष यह होगा:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

अगला, हम उपयोगी सिग्नल और शोर के लिए प्रारंभिक डेटा सेट करते हैं:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

अब हम सहसंबंधों से गुजरते हैं।

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

यहाँ सूत्र की व्युत्पत्ति (सबसे अधिक हताश के लिए एक पत्रक भी)।

हम वीनर के लिए एक समाधान पाते हैं:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

अब चलो ढाल मूल विधि पर चलते हैं।

सबसे बड़ा स्वदेशी खोजें ताकि चरण की ऊपरी सीमा इससे निकाली जा सके (देखें सूत्र (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

आइए अब कुछ चरणों को सेट करते हैं जो अधिकतम का एक निश्चित अंश बनाएंगे:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

पुनरावृत्तियों की अधिकतम संख्या निर्धारित करें:

 N_steps = 100

एल्गोरिथ्म चलाएँ:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

अब हम ऐसा ही करेंगे, लेकिन अनुकूली कदम (सूत्र (10)) के लिए:

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

आपको कुछ इस तरह से मिलना चाहिए:

ड्राइंग

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

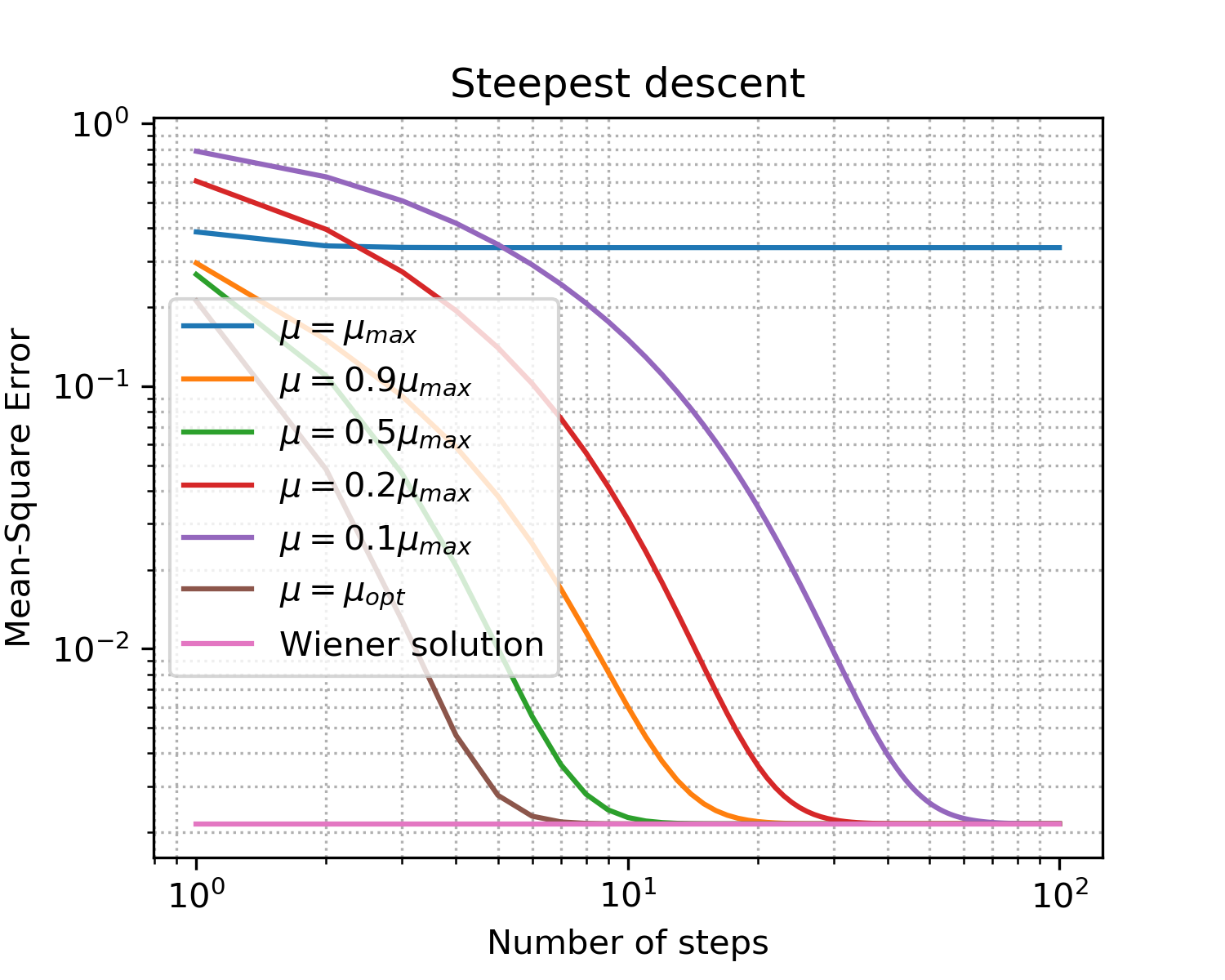
अंजीर। 5. विभिन्न आकारों के चरणों के लिए सीखना घटता है।

क्रमिक वंश पर मुख्य बिंदुओं को बोलने के लिए उपवास:

जैसा कि अपेक्षित था, इष्टतम कदम सबसे तेज़ अभिसरण देता है;
अब इसका बेहतर अर्थ नहीं है: ऊपरी सीमा से अधिक होने के कारण, हम अभिसरण तक नहीं पहुँच पाए हैं।

इसलिए हमने फिल्टर गुणांक के इष्टतम वेक्टर पाया जो चैनल के प्रभावों को सबसे अच्छा स्तर देगा - हमने तुल्यकारक को प्रशिक्षित किया ।

क्या वास्तविकता के करीब कुछ है?

बेशक! हम पहले ही कई बार कह चुके हैं कि वास्तविक समय के सिस्टम में आंकड़े एकत्र करना (यानी सहसंबंध मैट्रिक्स और वैक्टर की गणना करना) हमेशा सस्ती लक्जरी से दूर है। हालांकि, मानवता ने इन कठिनाइयों को अनुकूलित किया है: व्यवहार में एक नियतकालिक दृष्टिकोण के बजाय, अनुकूली दृष्टिकोण का उपयोग किया जाता है। उन्हें दो बड़े समूहों में विभाजित किया जा सकता है [1, पी। 246]:

संभाव्य (स्टोचस्टिक) (उदा। एसजी - स्टोचस्टिक ग्रैडिएंट)
और कम से कम वर्गों की विधि के आधार पर (उदाहरण के लिए, LMS - कम से कम वर्ग या RLS - पुनरावर्ती कमानी वर्ग)

अनुकूली फिल्टर का विषय खुले स्रोत समुदाय (अजगर के लिए उदाहरण) के भीतर अच्छी तरह से दर्शाया गया है:

दूसरे उदाहरण में, मैं विशेष रूप से प्रलेखन पसंद करता हूं। हालाँकि, सावधान रहें! जब मैंने पैडासिप पैकेज का परीक्षण किया, तो मैं जटिल संख्या को संभालने में कठिनाइयों में भाग गया (डिफ़ॉल्ट रूप से, फ्लोट64 को वहां निहित है)। कुछ अन्य कार्यान्वयनों के साथ काम करते समय शायद वही समस्याएं उत्पन्न हो सकती हैं।

बेशक, एल्गोरिदम के अपने फायदे और नुकसान हैं, जिनमें से योग एल्गोरिथम का दायरा निर्धारित करता है।

आइए उदाहरणों पर एक नज़र डालते हैं: हम तीन एल्गोरिदम एसजी , एलएमएस और आरएलएस पर विचार करेंगे, जिनका हमने पहले ही उल्लेख किया है (हम MATLAB भाषा में मॉडल करेंगे - मेरा मानना है कि पहले से ही रिक्त थे, और सब कुछ एकरूपता के लिए एकरूपता अजगर के लिए फिर से लिखना ... अच्छी तरह से ...)।

एलएमएस और आरएलएस एल्गोरिदम का विवरण पाया जा सकता है, उदाहरण के लिए, पैडासिप डॉक में।

एसजी का विवरण यहां पाया जा सकता है।

ढाल मूल से मुख्य अंतर एक चर ढाल है:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ _ mu \ left (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} {xx } [n] \ mathbf {w} [n-1] \ right)$

पर

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ right)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ एन] डी [एन] ^ * \ सही)$

1) जैसा ऊपर माना गया वैसा ही एक मामला।

स्रोत (मैटलैब / ऑक्टेव)।

सूत्रों को यहां डाउनलोड किया जा सकता है ।

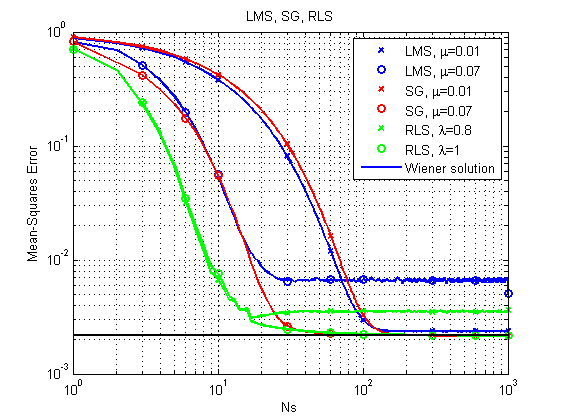
अंजीर। 6. एलएमएस, आरएलएस और एसजी के लिए सीखना घटता।

यह तुरंत नोट किया जा सकता है कि इसकी सापेक्ष सादगी के साथ, एलएमएस एल्गोरिथ्म सिद्धांत रूप में, अपेक्षाकृत बड़े कदम के साथ इष्टतम समाधान में नहीं आ सकता है। आरएलएस सबसे तेज़ परिणाम देता है, लेकिन यह अपेक्षाकृत छोटे भूलने के कारक के साथ भी विफल हो सकता है । अब तक, एसजी अच्छा कर रहा है, लेकिन आइए एक और उदाहरण देखें।

2) जब चैनल समय में बदलता है।

स्रोत (मैटलैब / ऑक्टेव)।

सूत्रों को यहां डाउनलोड किया जा सकता है ।

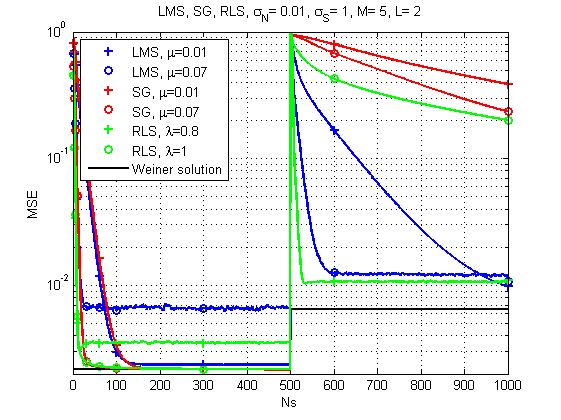
अंजीर। 7. एलएमएस, आरएलएस, और एसजी के लिए सीखना घटता (समय के साथ चैनल बदलता है)।

और यहां तस्वीर पहले से ही बहुत अधिक दिलचस्प है: चैनल की प्रतिक्रिया में तेज बदलाव के साथ, एलएमएस पहले से ही सबसे विश्वसनीय समाधान लगता है। किसने सोचा होगा। यद्यपि सही भूलने के कारक के साथ आरएलएस भी एक स्वीकार्य परिणाम प्रदान करता है।

प्रदर्शन के बारे में कुछ शब्द।

हां, निश्चित रूप से, प्रत्येक एल्गोरिथ्म की अपनी विशिष्ट कम्प्यूटेशनल जटिलता है, लेकिन मेरे माप के अनुसार, मेरी पुरानी मशीन एलएमएस और एसजी के मामले में प्रति पुनरावृत्ति लगभग 120 μs और आरएलएस के मामले में लगभग 250 μs प्रति पुनरावृत्ति का सामना कर सकती है। यही है, अंतर, सामान्य रूप से, तुलनीय है।

और वह सब आज के लिए है। सभी को धन्यवाद जो देखा!

साहित्य

हेकिन एसएस एडाप्टिव फिल्टर सिद्धांत। - पियर्सन एजुकेशन इंडिया, 2005।
हेकिन, साइमन और केजे रे लियू। सरणी प्रसंस्करण और सेंसर नेटवर्क पर हैंडबुक। वॉल्यूम। 63. जॉन विले एंड संस, 2010. पीपी। 102-107
अरंड्ट, डी। (2015)। लैंड मोबाइल सैटेलाइट रिसेप्शन के लिए चैनल मॉडलिंग (डॉक्टोरल शोध प्रबंध)।

परिशिष्ट १

आइजन फिल्टर

इस तरह के फिल्टर का मुख्य लक्ष्य सिग्नल-टू-शोर अनुपात (एसएनआर) को अधिकतम करना है।

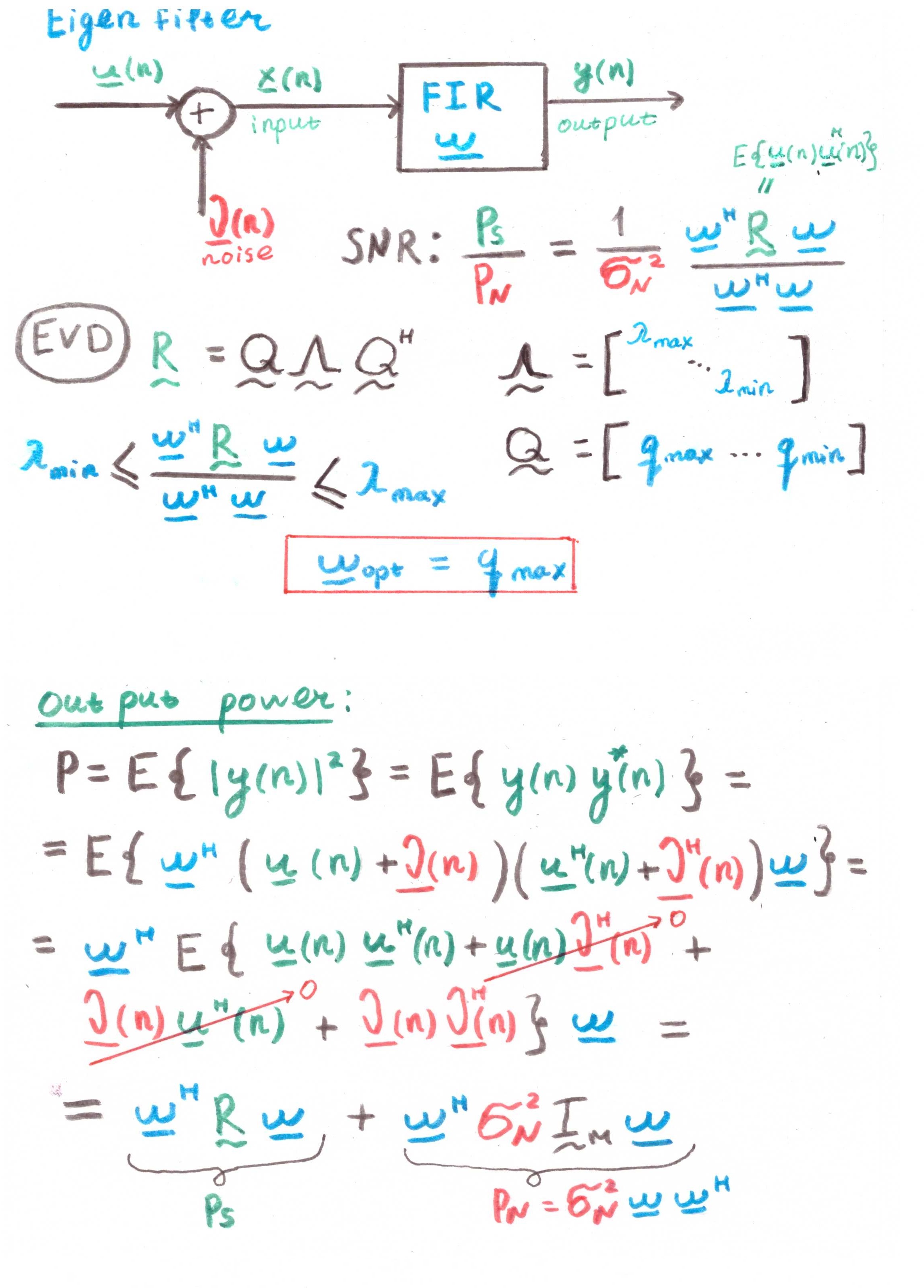
लेकिन गणना में सहसंबंधों की उपस्थिति को देखते हुए, यह एक व्यावहारिक समाधान की तुलना में सैद्धांतिक निर्माण का भी अधिक है।

इष्टतम रैखिक फ़िल्टरिंग: ढाल मूल से अनुकूली फिल्टर तक