CS231n में एक व्याख्यान में आपका स्वागत है : दृश्य मान्यता के लिए संवादात्मक तंत्रिका नेटवर्क ।

सामग्री

• वास्तुकला अवलोकन
• एक दृढ़ तंत्रिका नेटवर्क में परतें
  - दृढ़ परत
  - परत उपसमुच्चय
  - सामान्यीकरण परत
  - पूरी तरह से जुड़ी हुई परत
  - पूरी तरह से जुड़ी हुई परतों को कंफर्टेबल लेयर्स में कन्वर्ट करें
• संवादी तंत्रिका नेटवर्क वास्तुकला
  - परत टेम्पलेट्स
  - परत आकार पैटर्न
  - केस स्टडी (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
  - कम्प्यूटेशनल पहलुओं
• आगे पढ़ रहे हैं

संवैधानिक तंत्रिका नेटवर्क (CNN / ConvNets)

संवेदी तंत्रिका नेटवर्क सामान्य तंत्रिका नेटवर्क के समान हैं जो हमने पिछले अध्याय (CS231n पाठ्यक्रम के अंतिम अध्याय का उल्लेख करते हुए) में अध्ययन किया था: वे न्यूरॉन्स से मिलकर होते हैं, जो बदले में, चर भार और विस्थापन होते हैं। प्रत्येक न्यूरॉन कुछ इनपुट डेटा प्राप्त करता है, स्केलर उत्पाद की गणना करता है और, वैकल्पिक रूप से, एक nonlinear सक्रियण फ़ंक्शन का उपयोग करता है। संपूर्ण नेटवर्क, पहले की तरह, केवल अलग-अलग मूल्यांकन फ़ंक्शन है: एक छोर पर पिक्सेल के प्रारंभिक सेट (छवि) से दूसरे छोर पर एक विशेष वर्ग से संबंधित संभावना वितरण के लिए। इन नेटवर्कों में अभी भी अंतिम (पूरी तरह से जुड़ा हुआ) लेयर पर (उदाहरण के लिए, SVM / सॉफ्टमैक्स) एक लॉस फंक्शन है, और साधारण न्यूरल नेटवर्क के बारे में पिछले चैप्टर में दिए गए सभी टिप्स और सिफारिशें भी कंफर्टेबल न्यूरल नेटवर्क के लिए प्रासंगिक हैं।

तो क्या बदल गया है? दृढ़ तंत्रिका नेटवर्क की वास्तुकला में स्पष्ट रूप से इनपुट पर चित्र प्राप्त करना शामिल है, जो हमें नेटवर्क वास्तुकला में इनपुट डेटा के कुछ गुणों को ध्यान में रखने की अनुमति देता है। ये गुण आपको सीधे वितरण फ़ंक्शन को अधिक कुशलता से लागू करने और नेटवर्क में मापदंडों की कुल संख्या को कम करने की अनुमति देते हैं।

वास्तुकला अवलोकन

हम सामान्य तंत्रिका नेटवर्क को याद करते हैं। जैसा कि हमने पिछले अध्याय में देखा था, तंत्रिका नेटवर्क इनपुट डेटा (एक एकल वेक्टर) प्राप्त करते हैं और इसे छिपी हुई परतों की एक श्रृंखला के माध्यम से "पुश" करके परिवर्तित करते हैं । प्रत्येक छिपी हुई परत में एक निश्चित संख्या में न्यूरॉन्स होते हैं, जिनमें से प्रत्येक पिछली परत के सभी न्यूरॉन्स से जुड़ा होता है और जहां प्रत्येक परत पर न्यूरॉन्स एक ही स्तर पर अन्य न्यूरॉन्स से पूरी तरह से स्वतंत्र होते हैं। पिछली पूरी तरह से जुड़ी हुई परत को "आउटपुट लेयर" कहा जाता है और वर्गीकरण समस्याओं में कक्षा द्वारा ग्रेड का वितरण है।

पारंपरिक तंत्रिका नेटवर्क बड़ी छवियों के लिए अच्छी तरह से पैमाने पर नहीं है । CIFAR-10 डेटा सेट में, चित्र 32x32x3 आकार में (32 पिक्सेल ऊंचे, 32 पिक्सेल चौड़े, 3 रंग चैनल) हैं। ऐसी छवि को संसाधित करने के लिए, सामान्य तंत्रिका नेटवर्क की पहली छिपी हुई परत में एक पूरी तरह से जुड़ा हुआ न्यूरॉन 32x32x3 = 3072 वजन होगा। यह राशि अभी भी स्वीकार्य है, लेकिन यह स्पष्ट हो जाता है कि ऐसी संरचना बड़ी छवियों के साथ काम नहीं करेगी। उदाहरण के लिए, एक बड़ी छवि - 200x200x3, वजन की संख्या 200x200x3 = 120,000 हो जाएगी। इसके अलावा, हमें ऐसे एक से अधिक न्यूरॉन की आवश्यकता होगी, इसलिए कुल वजन की संख्या जल्दी से बढ़ने लगेगी। यह स्पष्ट हो जाता है कि कनेक्टिविटी अत्यधिक है और बड़ी संख्या में पैरामीटर जल्दी से नेटवर्क को फिर से चलाने के लिए नेतृत्व करेंगे।

न्यूरॉन्स के 3 डी अभ्यावेदन । संवादात्मक तंत्रिका नेटवर्क इस तथ्य का उपयोग करते हैं कि इनपुट डेटा छवियां हैं, इसलिए वे इस प्रकार के डेटा के लिए अधिक संवेदनशील वास्तुकला बनाते हैं। विशेष रूप से, पारंपरिक तंत्रिका नेटवर्क के विपरीत, दृढ़ तंत्रिका नेटवर्क में परतें 3 आयामों में न्यूरॉन्स की व्यवस्था करती हैं - चौड़ाई, ऊंचाई, गहराई ( नोट : शब्द "गहराई" सक्रियण न्यूरॉन्स के 3 आयाम को संदर्भित करता है, न कि तंत्रिका तंत्रिका की गहराई को स्वयं में मापा जाता है। परतों की संख्या)। उदाहरण के लिए, CIFAR-10 डेटासेट से इनपुट छवियां एक 3D प्रतिनिधित्व में इनपुट डेटा हैं, जिसका आयाम 32x32x3 (चौड़ाई, ऊंचाई, गहराई) है। जैसा कि हम बाद में देखेंगे, एक परत में न्यूरॉन्स परत में सभी पिछले न्यूरॉन्स से जुड़े होने के बजाय पिछली परत में कम संख्या में न्यूरॉन्स से जुड़े होंगे। इसके अलावा, CIFAR-10 डेटा सेट से छवि के लिए आउटपुट परत में 1 × 1 × 10 का आयाम होगा, क्योंकि तंत्रिका नेटवर्क के अंत में पहुंचने पर हम छवि के आकार को गहराई (3 डी आयाम) के साथ स्थित वर्ग अनुमानों के वेक्टर में कम कर देंगे।

दृश्य:

मानक तंत्रिका नेटवर्क	संवादी तंत्रिका नेटवर्क

बाईं ओर: मानक 3-परत तंत्रिका नेटवर्क।
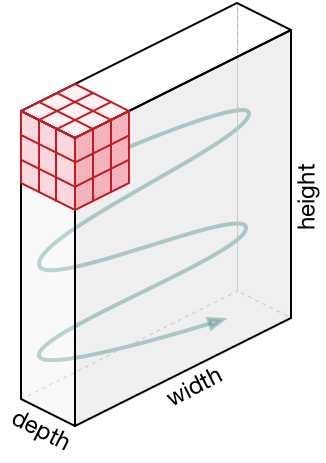
दाईं ओर: दृढ़ तंत्रिका नेटवर्क में 3 आयाम (चौड़ाई, ऊंचाई, गहराई) में न्यूरॉन्स होते हैं, जैसा कि एक परत पर दिखाया गया है। प्रत्येक दृढ़ तंत्रिका नेटवर्क परत इनपुट के 3 डी प्रतिनिधित्व को सक्रियण न्यूरॉन्स के रूप में आउटपुट के 3 डी प्रतिनिधित्व में परिवर्तित करता है। इस उदाहरण में, लाल इनपुट परत में छवि शामिल है, इसलिए इसका आकार छवि के आकार के बराबर होगा, और गहराई 3 होगी (तीन चैनल - लाल, हरा, नीला)।

दृढ़ तंत्रिका नेटवर्क में परतें होती हैं। प्रत्येक परत एक साधारण एपीआई है: इनपुट 3 डी प्रतिनिधित्व को आउटपुट में 3 डी प्रतिनिधित्व में परिवर्तित करता है, जो एक भिन्न फ़ंक्शन का प्रतिनिधित्व करता है, जिसमें पैरामीटर शामिल नहीं हो सकते हैं या हो सकते हैं।

लेयर्स कंफ्यूजनल न्यूरल नेटवर्क का निर्माण करते थे

जैसा कि हमने पहले ही ऊपर वर्णित किया है, एक सरल दृढ़ तंत्रिका नेटवर्क परतों का एक सेट है, जहां प्रत्येक परत एक प्रतिनिधित्व को दूसरे में एक परिवर्तनीय फ़ंक्शन का उपयोग करके परिवर्तित करती है। हम तीन मुख्य प्रकार के लेयर्स का उपयोग कंफ्यूज़नल न्यूरल नेटवर्क बनाने के लिए करते हैं: एक कॉनवेल्यूशनल लेयर , एक सबमाम्लिंग लेयर , और एक पूरी तरह से कनेक्टेड लेयर (जैसा कि हम एक नॉर्मल न्यूरल नेटवर्क में उपयोग करते हैं)। हम इन परतों को क्रमिक रूप से एसएनए आर्किटेक्चर प्राप्त करने के लिए व्यवस्थित करते हैं।

वास्तुकला उदाहरण: अवलोकन। नीचे, हम विवरण में डुबकी लगाएंगे, लेकिन अभी के लिए, CIFAR-10 डेटासेट के लिए, हमारे दृढ़ तंत्रिका नेटवर्क की वास्तुकला [INPUT -> CONV -> RELU -> POOL -> FC] । अब और अधिक विस्तार में:

• INPUT [32x32x3] में छवि पिक्सेल के मूल मूल्य शामिल होंगे, हमारे मामले में छवि 32px चौड़ी, 32px ऊँची और 3 रंग चैनलों R, G, B की है।
• CONV परत आउटपुट न्यूरॉन्स का एक सेट का उत्पादन करेगी जो इनपुट स्रोत छवि के स्थानीय क्षेत्र से जुड़ी होगी; प्रत्येक ऐसा न्यूरॉन अपने वजन और मूल छवि के छोटे हिस्से के बीच स्केलर उत्पाद की गणना करेगा, जिसके साथ वह जुड़ा हुआ है। आउटपुट मान 323212 का 3 डी प्रतिनिधित्व हो सकता है, यदि, उदाहरण के लिए, हम 12 फिल्टर का उपयोग करने का निर्णय लेते हैं।
• RELU परत तत्व सक्रियण फ़ंक्शन max(0, x) को लागू करेगी। यह रूपांतरण डेटा आयाम को नहीं बदलेगा - [32x32x12] ।
• POOL परत छवि को दो आयामों - ऊँचाई और चौड़ाई में नमूने के संचालन का कार्य करेगा, जिसके परिणामस्वरूप हमें एक नया 3 डी प्रतिनिधित्व [161612] ।
• FC परत (पूरी तरह से जुड़ा हुआ परत) कक्षाओं द्वारा ग्रेड की गणना करेगा, जिसके परिणामस्वरूप आयाम [1x1x10] , जहां प्रत्येक 10 मान CIFAR-10 से छवियों की 10 श्रेणियों के बीच एक विशेष वर्ग के ग्रेड के अनुरूप होंगे। पारंपरिक तंत्रिका नेटवर्क की तरह, इस परत के प्रत्येक न्यूरॉन को पिछली परत (3 डी प्रतिनिधित्व) के सभी न्यूरॉन्स के साथ जोड़ा जाएगा।

यह इस तरह से है कि कन्वेन्शियल न्यूरल नेटवर्क, प्रारंभिक पिक्सेल मान से अंतिम वर्ग के अनुमान तक, मूल छवि को परत दर परत रूपांतरित करता है। ध्यान दें कि कुछ परतों में विकल्प होते हैं, और कुछ नहीं होते हैं। विशेष रूप से, CONV/FC परतें एक परिवर्तन करती हैं, जो न केवल एक फ़ंक्शन है जो इनपुट डेटा पर निर्भर करता है, बल्कि स्वयं न्यूरॉन्स में वज़न और विस्थापन के आंतरिक मूल्यों पर भी निर्भर करता है। दूसरी ओर RELU/POOL परतें, गैर- RELU/POOL कार्यों का उपयोग करती हैं। CONV/FC परतों में पैरामीटर को ढाल वंश द्वारा प्रशिक्षित किया जाएगा ताकि इनपुट को संबंधित सही आउटपुट लेबल प्राप्त हो।

संक्षेप में:

• दृढ़ सरल तंत्रिका नेटवर्क की वास्तुकला, इसके सरलतम प्रतिनिधित्व में, परतों का एक क्रमबद्ध सेट है जो एक छवि के प्रतिनिधित्व को दूसरे प्रतिनिधित्व में बदल देता है, उदाहरण के लिए, वर्ग सदस्यता अनुमान।
• कई अलग-अलग प्रकार की परतें हैं (CONV - दृढ़ परत, FC - पूरी तरह से जुड़ा हुआ, RELU - सक्रियण फ़ंक्शन, POOL - सबमिशन लेयर - सबसे लोकप्रिय)।
• प्रत्येक इनपुट परत एक 3 डी प्रतिनिधित्व प्राप्त करता है, इसे एक भिन्न फ़ंक्शन का उपयोग करके आउटपुट 3 डी प्रतिनिधित्व में परिवर्तित करता है।
• प्रत्येक परत में पैरामीटर (CONV / FC - पैरामीटर हो सकता है, RELU / POOL - नहीं) हो सकता है।
• प्रत्येक परत में हाइपर पैरामीटर नहीं हो सकते हैं (CONV / FC / POOL - है, RELU - नहीं)

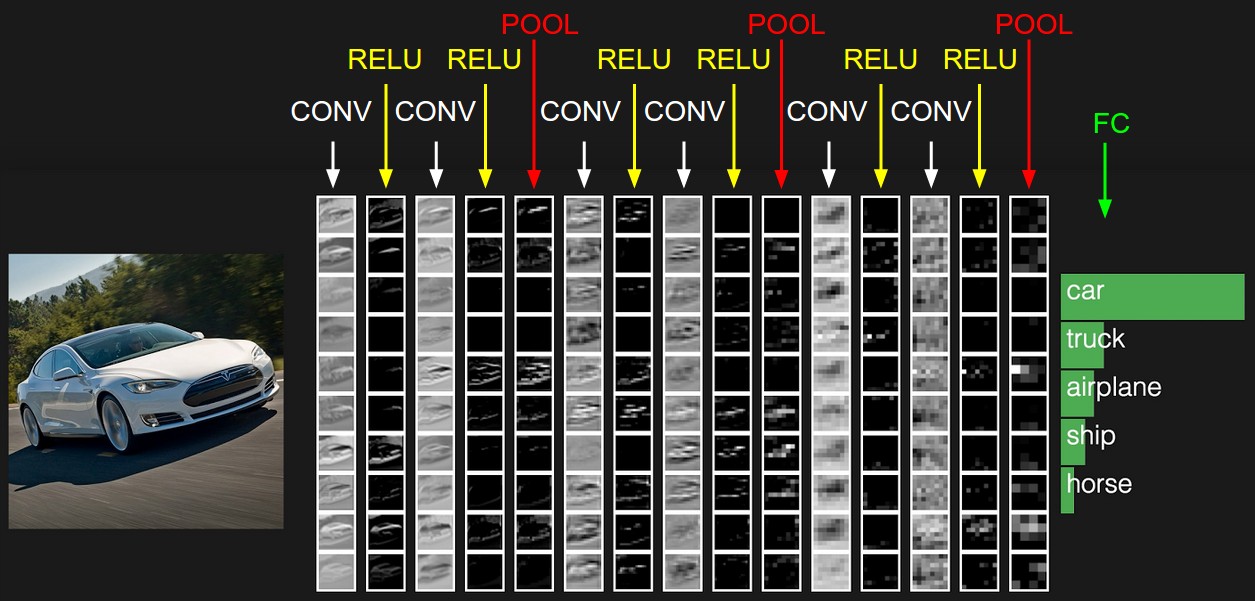
प्रारंभिक प्रतिनिधित्व में छवि के पिक्सेल मान शामिल होते हैं (बाईं ओर) और उन वर्गों के लिए अनुमान लगाते हैं, जिनके लिए छवि में ऑब्जेक्ट दाईं ओर स्थित है। प्रत्येक दृश्य परिवर्तन को एक स्तंभ के रूप में चिह्नित किया जाता है।

संवादी परत

सजा हुआ परत नेटवर्क के निर्माण में मुख्य परत है।

मस्तिष्क की विशेषताओं में गोता लगाने के बिना अवलोकन। आइए पहले यह पता लगाने की कोशिश करें कि मस्तिष्क और न्यूरॉन्स के विषय पर CONV परत अभी भी बिना डूबे और स्पर्श किए क्या गणना कर रही है। दृढ़ परत मापदंडों में प्रशिक्षित फिल्टर का एक सेट होता है। प्रत्येक फ़िल्टर चौड़ाई और ऊंचाई के साथ एक छोटा ग्रिड है, लेकिन इनपुट प्रतिनिधित्व की पूरी गहराई तक फैली हुई है।

उदाहरण के लिए, एक सजातीय तंत्रिका नेटवर्क की पहली परत पर एक मानक फ़िल्टर में 5x5x3 (5px - चौड़ाई और ऊंचाई, 3 - रंग चैनलों की संख्या) आयाम हो सकते हैं। एक प्रत्यक्ष पास के दौरान, हम इनपुट निरूपण की चौड़ाई और ऊंचाई के साथ फिल्टर को हटाते हैं (सटीक - हम ढह जाते हैं) और किसी भी बिंदु पर इनपुट मान के संगत मानों के बीच स्केलर उत्पाद की गणना करते हैं। इनपुट प्रतिनिधित्व की चौड़ाई और ऊंचाई के साथ फिल्टर को स्थानांतरित करने की प्रक्रिया में, हम एक 2-आयामी सक्रियण मानचित्र बनाते हैं जिसमें इनपुट प्रतिनिधित्व के प्रत्येक क्षेत्र में इस फ़िल्टर को लागू करने के मूल्य शामिल हैं। सहज रूप से, यह स्पष्ट हो जाता है कि नेटवर्क फ़िल्टर को सक्रिय करने के लिए सिखाएगा जब वे एक निश्चित दृश्य संकेत देखते हैं, उदाहरण के लिए, एक निश्चित कोण पर एक सीधी रेखा या उच्च स्तर पर पहिया के आकार का प्रतिनिधित्व। अब जब हमने अपने सभी फ़िल्टर मूल छवि पर लागू कर दिए हैं, उदाहरण के लिए, 12 थे। 12 फ़िल्टर लागू करने के परिणामस्वरूप, हमें आयाम के 12 सक्रियण कार्ड प्राप्त हुए। आउटपुट आउटपुट का उत्पादन करने के लिए, हम इन कार्डों (क्रमिक रूप से तृतीय आयाम में) को संयोजित करते हैं और एक प्रतिनिधित्व प्राप्त करते हैं आयाम [WxHx12]।

एक अवलोकन जिसे हम मस्तिष्क और न्यूरॉन्स से जोड़ते हैं। यदि आप मस्तिष्क और न्यूरॉन्स के प्रशंसक हैं, तो आप कल्पना कर सकते हैं कि प्रत्येक न्यूरॉन इनपुट प्रतिनिधित्व के एक बड़े हिस्से पर "दिखता है" और पड़ोसी न्यूरॉन्स को इस अनुभाग के बारे में जानकारी स्थानांतरित करता है। नीचे हम न्यूरॉन कनेक्टिविटी के विवरण, अंतरिक्ष में उनके स्थान और साझाकरण मापदंडों के लिए तंत्र पर चर्चा करेंगे।

स्थानीय संपर्क। जब हम बड़ी संख्या में आयामों के साथ इनपुट डेटा के साथ काम कर रहे हैं, उदाहरण के लिए, जैसा कि छवियों के मामले में, तब, जैसा कि हम पहले ही देख चुके हैं, पिछली परत पर सभी न्यूरॉन्स के साथ न्यूरॉन्स को जोड़ने की बिल्कुल आवश्यकता नहीं है। इसके बजाय, हम केवल इनपुट प्रतिनिधित्व के स्थानीय क्षेत्रों से न्यूरॉन्स को जोड़ेंगे। कनेक्टिविटी की स्थानिक डिग्री हाइपर-मापदंडों में से एक है और इसे रिसेप्टिव फ़ील्ड कहा जाता है (एक न्यूरॉन का ग्रहणशील क्षेत्र एक ही फिल्टर / कनवल्शन कोर का आकार है)। 3 डी आयाम (गहराई) के साथ कनेक्टिविटी की डिग्री हमेशा मूल प्रतिनिधित्व की गहराई के बराबर होती है। इस पर फिर से ध्यान देना बहुत महत्वपूर्ण है, ध्यान दें कि हम स्थानिक आयाम (चौड़ाई और ऊंचाई) और गहराई को कैसे परिभाषित करते हैं: न्यूरॉन कनेक्शन चौड़ाई और ऊंचाई में स्थानीय हैं, लेकिन हमेशा इनपुट प्रतिनिधित्व की पूरी गहराई में विस्तार करते हैं।

उदाहरण 1. कल्पना कीजिए कि इनपुट प्रतिनिधित्व का आकार 32x32x3 (RGB, CIFAR-10) है। यदि फिल्टर का आकार (न्यूरॉन का ग्रहणशील क्षेत्र) 5 × 5 है, तो कन्वेन्शियल लेयर के प्रत्येक न्यूरॉन में मूल प्रतिनिधित्व के 5 × 5 × 3 क्षेत्र में वज़न होगा, जो अंततः 5 × × × 3 = 75 बॉन्ड (वज़न) + 1 ऑफ़सेट पैरामीटर की स्थापना को बढ़ावा देगा। कृपया ध्यान दें कि गहराई में जुड़ाव की डिग्री 3 के बराबर होनी चाहिए, क्योंकि यह मूल प्रतिनिधित्व का आयाम है।

उदाहरण 2. कल्पना कीजिए कि इनपुट प्रतिनिधित्व का आकार 16x16x20 है। एक उदाहरण के रूप में 3x3 आकार के न्यूरॉन के ग्रहणशील क्षेत्र का उपयोग करते हुए, प्रत्येक दृढ़ परत न्यूरॉन में 3x3x320 = 180 कनेक्शन (भार) + 1 विस्थापन पैरामीटर होगा। ध्यान दें कि कनेक्टिविटी चौड़ाई और ऊंचाई में स्थानीय है, लेकिन गहराई (20) में पूर्ण है।

# 1	# २

बाईं ओर से: इनपुट प्रतिनिधित्व लाल रंग में प्रदर्शित होता है (उदाहरण के लिए, 32x332 CIFAR-10 आकार की एक छवि) और पहली दृढ़ परत में न्यूरॉन्स के प्रतिनिधित्व का एक उदाहरण। कन्वेन्शियल लेयर में प्रत्येक न्यूरॉन केवल इनपुट प्रतिनिधित्व के स्थानीय क्षेत्र से जुड़ा होता है, लेकिन पूरी तरह से गहराई में (उदाहरण में, सभी रंग चैनलों के साथ)। कृपया ध्यान दें कि छवि में बहुत सारे न्यूरॉन्स हैं (उदाहरण में - 5) और वे तीसरे आयाम (गहराई) के साथ स्थित हैं - इस व्यवस्था के बारे में स्पष्टीकरण नीचे दिया जाएगा।
दाईं ओर: तंत्रिका नेटवर्क से न्यूरॉन्स अभी भी अपरिवर्तित रहते हैं: वे अभी भी अपने वजन और इनपुट डेटा के बीच स्केलर उत्पाद की गणना करते हैं, सक्रियण फ़ंक्शन को लागू करते हैं, लेकिन उनकी कनेक्टिविटी अब स्थानिक स्थानीय क्षेत्र द्वारा सीमित है।

स्थानिक स्थान। हमने इनपुट प्रतिनिधित्व के साथ पहले से ही प्रत्येक न्यूरॉन की संयोजकता परत में संयोजकता का पता लगाया है, लेकिन अभी तक चर्चा नहीं की है कि इनमें से कितने न्यूरॉन हैं या वे कैसे स्थित हैं। तीन हाइपर पैरामीटर आउटपुट दृश्य के आकार को प्रभावित करते हैं: गहराई , कदम और संरेखण ।

1. आउटपुट प्रतिनिधित्व की गहराई एक हाइपर पैरामीटर है: यह उन फ़िल्टर की संख्या से मेल खाती है जिन्हें हम लागू करना चाहते हैं, जिनमें से प्रत्येक मूल प्रतिनिधित्व में कुछ और सीखता है। उदाहरण के लिए, यदि पहली दृढ़ परत एक छवि को इनपुट के रूप में प्राप्त करती है, तो 3 डी आयाम (गहराई) के साथ अलग-अलग न्यूरॉन्स को एक निश्चित क्षेत्र या एक निश्चित रंग के समूहों में लाइनों के विभिन्न झुकावों की उपस्थिति में सक्रिय किया जा सकता है। न्यूरॉन्स का सेट जो इनपुट प्रतिनिधित्व के एक ही क्षेत्र में "दिखता है", हम गहरे कॉलम (या "फाइबर" - फाइबर) को कहेंगे।
2. हमें चरण (पिक्सेल में ऑफसेट आकार) निर्धारित करने की आवश्यकता है जिसके साथ फ़िल्टर स्थानांतरित हो जाएगा। यदि चरण 1 है, तो हम एक पुनरावृत्ति में फ़िल्टर को 1 पिक्सेल से स्थानांतरित करते हैं। यदि चरण 2 (या, जो कि आमतौर पर 3 या उससे अधिक का उपयोग किया जाता है) भी कम है, तो ऑफसेट एक पुनरावृत्ति में प्रत्येक दो पिक्सेल के लिए होता है। एक छोटे आउटपुट में एक बड़ा कदम परिणाम का प्रतिनिधित्व करता है।
3. जैसा कि हम जल्द ही देखेंगे, कभी-कभी यह शून्य के साथ किनारों के साथ इनपुट प्रतिनिधित्व को पूरक करने के लिए आवश्यक होगा। संरेखण आकार (शून्य गद्देदार स्तंभों / पंक्तियों की संख्या) भी एक हाइपर पैरामीटर है। संरेखण का उपयोग करने की एक अच्छी विशेषता यह तथ्य है कि संरेखण हमें आउटपुट प्रतिनिधित्व के आयाम को नियंत्रित करने की अनुमति देगा (अक्सर हम दृश्य के मूल आयामों को रखेंगे - आउटपुट प्रतिनिधित्व की चौड़ाई और ऊंचाई के साथ इनपुट प्रतिनिधित्व की चौड़ाई और ऊंचाई को संरक्षित करना)।

हम आउटपुट प्रतिनिधित्व के अंतिम आयाम की गणना इनपुट प्रतिनिधित्व ( डब्लू ) के आकार के एक फ़ंक्शन के रूप में प्रस्तुत कर सकते हैं, जो कि दिमागी परत के न्यूरॉन्स के ग्रहणशील क्षेत्र के आकार ( एफ ), चरण ( एस ), और सीमाओं पर संरेखण ( पी ) के आकार का है। आप अपने लिए देख सकते हैं कि आउटपुट प्रतिनिधित्व में न्यूरॉन्स की संख्या की गणना करने का सही सूत्र निम्न है (डब्ल्यू - एफ + 2 पी) / एस + 1 । उदाहरण के लिए, आकार 7x7 के इनपुट प्रतिनिधित्व और 3x3 के फिल्टर आकार, चरण 1 और संरेखण 0 के लिए, हमें आकार 5x5 का आउटपुट प्रतिनिधित्व मिलता है। चरण 2 में, हमें 3x3 का आउटपुट प्रतिनिधित्व मिलेगा। आइए एक और उदाहरण देखें, इस बार रेखांकन:

एक स्थानिक व्यवस्था का चित्रण। इस उदाहरण में, केवल एक स्थानिक आयाम (एक्स-अक्ष), रिसेप्टिव फ़ील्ड F = 3 के साथ एक न्यूरॉन, इनपुट प्रतिनिधित्व आकार W = 5 और संरेखण P = 1 । बाईं ओर : न्यूरॉन का ग्रहणशील क्षेत्र एक कदम S = 1 के साथ चलता है, जिसके परिणामस्वरूप आउटपुट प्रतिनिधित्व का आकार देता है (5 - 3 + 2) / 1 + 1 = 5. दाईं ओर : न्यूरॉन आकार S = 2 के ग्रहणशील क्षेत्र का उपयोग करता है, जो परिणाम आउटपुट प्रतिनिधित्व का आकार (5 - 3 + 2) / 2 + 1 = 3. है। ध्यान दें कि चरण आकार S = 3 का उपयोग नहीं किया जा सकता है, क्योंकि इस चरण के आकार के साथ ग्रहणशील क्षेत्र छवि के भाग को कैप्चर नहीं करेगा। यदि हम अपने सूत्र का उपयोग करते हैं, तो (5 - 3 + 2) = 4 का गुणांक 3 नहीं है। इस उदाहरण में न्यूरॉन्स का वजन [1, 0, -1] (जैसा कि सबसे दाहिने चित्र में दिखाया गया है) हैं, और ऑफसेट शून्य है। ये वजन सभी पीले न्यूरॉन्स द्वारा साझा किए जाते हैं।

संरेखण का उपयोग करना । बाईं ओर के उदाहरण पर ध्यान दें, जिसमें आउटपुट में 5 तत्व और आउटपुट में 5 तत्व शामिल हैं। यह काम किया क्योंकि ग्रहणशील क्षेत्र (फिल्टर) का आकार 3 था और हमने संरेखण P = 1 का उपयोग किया। यदि कोई संरेखण नहीं था, तो आउटपुट प्रतिनिधित्व का आकार 3 के बराबर होगा, क्योंकि यह वास्तव में इतने सारे न्यूरॉन्स थे जो वहां फिट होंगे। सामान्य तौर पर, संरेखण आकार P = (F - 1) / 2 को S = 1 के बराबर चरण के साथ सेट करने से आप इनपुट प्रतिनिधित्व के समान आउटपुट प्रतिनिधित्व का आकार प्राप्त कर सकते हैं। संरेखण का उपयोग करने वाला एक समान दृष्टिकोण अक्सर व्यवहार में लागू होता है, और हम नीचे दिए गए कारणों पर चर्चा करेंगे जब हम दृढ़ तंत्रिका नेटवर्क की वास्तुकला के बारे में बात करेंगे।

चरण आकार सीमा । कृपया ध्यान दें कि स्थानिक व्यवस्था के लिए जिम्मेदार हाइपर-पैरामीटर भी सीमाओं से संबंधित हैं। उदाहरण के लिए, यदि इनपुट प्रतिनिधित्व में W = 10 , P = 0 और रिसेप्टिव फ़ील्ड F = 3 का आकार है, तो S = 2 के बराबर एक चरण आकार का उपयोग करना असंभव हो जाता है, क्योंकि (W - F + 2P) / S + 1 = (10 - 10) 3 + 0) / 2 + 1 = 4.5 , जो न्यूरॉन्स की संख्या का पूर्णांक मान देता है। इस प्रकार, हाइपर मापदंडों के इस तरह के विन्यास को अमान्य माना जाता है और सजातीय तंत्रिका नेटवर्क के साथ काम करने के लिए पुस्तकालय अपवाद, बल संरेखण, या यहां तक ​​कि इनपुट प्रतिनिधित्व को काट देंगे। जैसा कि हम इस अध्याय के अगले खंडों में देखेंगे, कंफ्यूजनल लेयर के हाइपर-मापदंडों की परिभाषा अभी भी एक सिरदर्द है जिसे कुछ सिफारिशों और "अच्छे टोन नियमों" का उपयोग करके कम किया जा सकता है, जो कंसिस्टेंट न्यूरल नेटवर्क्स की वास्तुकला को डिजाइन करते हैं।

वास्तविक जीवन उदाहरण । संवादात्मक तंत्रिका नेटवर्क वास्तुकला Krizhevsky एट अल। , जिसने 2012 में इमेजनेट प्रतियोगिता जीती, उसे 227x227x3 चित्र मिले। पहली दृढ़ परत पर, उसने F = 11 , चरण S = 4, और संरेखण आकार = 0 0 का एक ग्रहणशील क्षेत्र का उपयोग किया। चूँकि (227 - 11) / 4 + 1 = 55, और दृढ़ परत K = 96 गहरी थी, प्रस्तुति का उत्पादन आयाम 55x55x96 था। इस प्रतिनिधित्व में 55x55x96 न्यूरॉन्स में से प्रत्येक इनपुट प्रतिनिधित्व में 11x11x3 आकार के एक क्षेत्र से जुड़ा था। इसके अलावा, गहरे स्तंभ में सभी 96 न्यूरॉन्स समान 11x11x3 क्षेत्र के साथ जुड़े हैं, लेकिन अलग-अलग वजन के साथ। और अब थोड़ा हास्य - यदि आप मूल दस्तावेज (अध्ययन) से परिचित होने का निर्णय लेते हैं, तो ध्यान दें कि दस्तावेज़ का दावा है कि इनपुट 224x224 छवियां प्राप्त करता है, जो सच नहीं हो सकता, क्योंकि (224 - 11) / 4 + 1 किसी भी तरह से पूर्णांक मूल्य नहीं दें। इस तरह की स्थिति अक्सर लोगों में दृढ़ तंत्रिका नेटवर्क वाली कहानियों के लिए भ्रमित होती है। मेरा अनुमान है कि एलेक्स ने संरेखण आकार P = 3 का उपयोग किया था, लेकिन दस्तावेज़ में यह उल्लेख करना भूल गया।

विकल्प साझा करना। मापदंडों की संख्या को नियंत्रित करने के लिए, संकेंद्रित परतों में मापदंडों को साझा करने के तंत्र का उपयोग किया जाता है। ऊपर दिए गए उदाहरण पर ध्यान दें, जैसा कि आप देख सकते हैं कि पहली कनक्लूशनल लेयर पर 55x55x96 = 290,400 न्यूरॉन्स हैं और प्रत्येक न्यूरॉन्स में 11x11x3 = 363 वज़न + 1 ऑफसेट मूल्य है। कुल मिलाकर, अगर हम इन दो मूल्यों को गुणा करते हैं, तो हमें 290400x364 = 105 705 600 पैरामीटर्स केवल तंत्रिका संबंधी नेटवर्क की पहली परत पर मिलते हैं। जाहिर है, यह बहुत महत्व का है!

यह पता चला है कि एक धारणा बनाकर मापदंडों की संख्या को काफी कम करना संभव है: यदि स्थिति (x, y) में गणना की गई कुछ संपत्ति हमारे लिए मायने रखती है, तो यह स्थिति (x2, y2) में गणना की गई संपत्ति भी हमारे लिए मायने रखती है। दूसरे शब्दों में, "गहरी परत" के रूप में गहराई में एक दो-आयामी "परत" को दर्शाते हुए (उदाहरण के लिए, [55x55x96] दृश्य में 96 गहरी परतें हैं, प्रत्येक 55x55 आकार में), हम एक ही वजन और विस्थापन के साथ गहराई में न्यूरॉन्स का निर्माण करेंगे। मापदंडों को साझा करने की इस योजना के साथ, हमारे उदाहरण में पहली दोषपूर्ण परत में अब वजन के 96 अद्वितीय सेट (प्रत्येक गहराई परत के लिए प्रत्येक सेट) होंगे, कुल मिलाकर 96x11x11x3 = 34,848 अद्वितीय वजन या 34,948 पैरामीटर (+96 ऑफसेट) होंगे। इसके अलावा, प्रत्येक गहरी परत में सभी 55x55 न्यूरॉन्स अब एक ही पैरामीटर का उपयोग करेंगे। व्यवहार में, पीठ के प्रसार के दौरान, इस प्रतिनिधित्व में प्रत्येक न्यूरॉन अपने स्वयं के वजन के लिए ढाल की गणना करेगा, लेकिन इन ग्रेडिएंट को प्रत्येक गहराई परत पर अभिव्यक्त किया जाएगा और प्रत्येक स्तर पर वजन का केवल एक सेट अपडेट करेगा।

ध्यान दें कि यदि एक ही गहरी परत में सभी न्यूरॉन्स एक ही भार का उपयोग करते हैं, तो सीधे परत के माध्यम से प्रसार के लिए, न्यूरॉन वज़न और इनपुट डेटा के मूल्यों के बीच की गणना की गणना की जाएगी। यही कारण है कि वजन के एक सेट को कॉल करने के लिए प्रथागत है - एक फिल्टर (कोर) ।

फिल्टर के उदाहरण जो Krizhevsky et al। मॉडल को प्रशिक्षित करके प्राप्त किए गए थे। यहां दिखाए गए 96 फिल्टर में से प्रत्येक का आकार 11x11x3 है और उनमें से प्रत्येक को एक गहरी परत के सभी 55x55 न्यूरॉन्स द्वारा साझा किया गया है। कृपया ध्यान दें कि समान भार साझा करने की धारणा से समझ में आता है: यदि छवि के एक हिस्से में क्षैतिज रेखा का पता लगाना महत्वपूर्ण है, तो यह सहज रूप से स्पष्ट है कि इस छवि के दूसरे भाग में ऐसी पहचान महत्वपूर्ण है। इसलिए, यह कोई भी मतलब नहीं है कि प्रत्येक परत में 55x55 में से प्रत्येक में क्षैतिज रेखाओं को खोजने के लिए प्रतिक्षेपणीय परत में क्षैतिज रेखाओं का पता लगाएं।

यह ध्यान में रखा जाना चाहिए कि शेयरिंग मापदंडों की धारणा हमेशा समझ में नहीं आती है। उदाहरण के लिए, यदि कुछ केन्द्रित संरचना वाली एक छवि को एक अवक्षेपणीय तंत्रिका नेटवर्क के इनपुट को खिलाया जाता है, जहाँ हम छवि के एक भाग में एक गुण और छवि के दूसरे भाग में एक अन्य गुण को जानने में सक्षम होना चाहेंगे। एक व्यावहारिक उदाहरण केंद्रित छवि है। यह माना जा सकता है कि छवि के विभिन्न क्षेत्रों में विभिन्न आंखों या बालों के संकेतों की पहचान की जा सकती है, इसलिए, इस मामले में, वजन में छूट का उपयोग किया जाता है और परत को स्थानीय रूप से जुड़ा हुआ कहा जाता है ।

उदासीन उदाहरण । पिछली चर्चाओं को बारीकियों के विमान और कोड के साथ उदाहरणों पर स्थानांतरित किया जाना चाहिए। कल्पना कीजिए कि इनपुट प्रतिनिधित्व X का एक numpy सरणी है। तब:

• स्थिति (x,y) ) पर गहरे कॉलम ( थ्रेड ) को X[x,y,:] रूप में दर्शाया जाएगा।
• गहरी परत , या जैसा कि हमने पहले इस तरह की परत को बुलाया था - गहराई d पर सक्रियण मानचित्र को निम्नानुसार दर्शाया जाएगा X[:,:,d] ।

एक दृढ़ परत का एक उदाहरण । , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

#1	#2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
यूट्यूब
तार
VKontakte