रीसायकल के अलग संग्रह के लिए कार्रवाई का रसद

ज्वाइन करने के बजाय

जब रूस में अपशिष्ट संग्रह और प्रसंस्करण की प्रक्रियाएं पूरी तरह से समायोजित होती हैं, तो यह कहना आसान नहीं है, लेकिन मैं अब लैंडफिल्स की पुनःपूर्ति में भाग नहीं लेना चाहता हूं। इसलिए, कई बड़े शहरों में, एक तरह से या किसी अन्य, विशेष रूप से अलग संग्रह में स्वयंसेवक आंदोलन लगे हुए हैं।

नोवोसिबिर्स्क में, ग्रीन स्क्विरेल अभियान के आसपास इस तरह की गतिविधि का गठन किया जाता है, जिसके ढांचे में महीने में एक बार, पर्यावरण से संबंधित शहरी निवासी एक निश्चित समय पर पूर्वनिर्धारित स्थानों पर संचित घरेलू कचरे को जमा करते हैं। उसी समय तक, एक किराए पर ट्रक वहाँ आता है, जो एकत्रित और छंटाई योग्य रिसाइकल सामग्रियों को साइट पर ले जाता है, जहाँ से इसे विभिन्न प्रसंस्करण उद्यमों के बीच पुनर्वितरित किया जाता है। कार्रवाई 2014 से अस्तित्व में है, और तब से रिसाइकिल के लिए संग्रह बिंदुओं की संख्या, साथ ही साथ इसके संस्करणों में काफी वृद्धि हुई है। ट्रक रूटिंग के लिए, बस एक टकटकी पर्याप्त नहीं थी, और हमने परिवहन लागत को कम करने के लिए अनुकूलन मॉडल विकसित करना शुरू कर दिया। इन मॉडलों में से पहला इस लेख का विषय है।

खंड 1 में, मैं विस्तार से वर्णन करूंगा और चित्र के साथ कार्रवाई के आयोजन की योजना बनाऊंगा। इसके अलावा, धारा 2 में, परिवहन लागत को कम करने के कार्य को औपचारिक रूप दिया जाएगा क्योंकि समय के साथ विषम वाहनों के बेड़े के वाहन रूटिंग समस्या को पार करने का कार्य। धारा 3 मिश्रित पूर्णांक रैखिक गणितीय प्रोग्रामिंग समस्याओं को हल करने के लिए स्वतंत्र रूप से वितरित पैकेज का उपयोग करके इस समस्या को हल करने के लिए समर्पित है।

1. कार्रवाई "ग्रीन गिलहरी"

2014 से, लिविंग अर्थ पहल समूह नोवोसिबिर्स्क में पुनर्नवीनीकरण ग्रीन गिलहरी के संग्रह को अलग करने के लिए एक मासिक अभियान चला रहा है। लेखन के समय, कई आरक्षणों के साथ रीसाइक्लिंग पीईटी, पीई, पीपी, पीएस, ग्लास, एल्यूमीनियम, लोहा, घरेलू उपकरणों, बेकार कागज और अधिक लेबल वाले प्लास्टिक कचरे को स्वीकार किया जाता है। कार्रवाई की तैयारी और संचालन में 50 से अधिक स्वयंसेवक भाग लेते हैं। कार्रवाई वाणिज्यिक नहीं है, इसमें भागीदारी नि: शुल्क है और मौद्रिक इनाम का मतलब नहीं है।

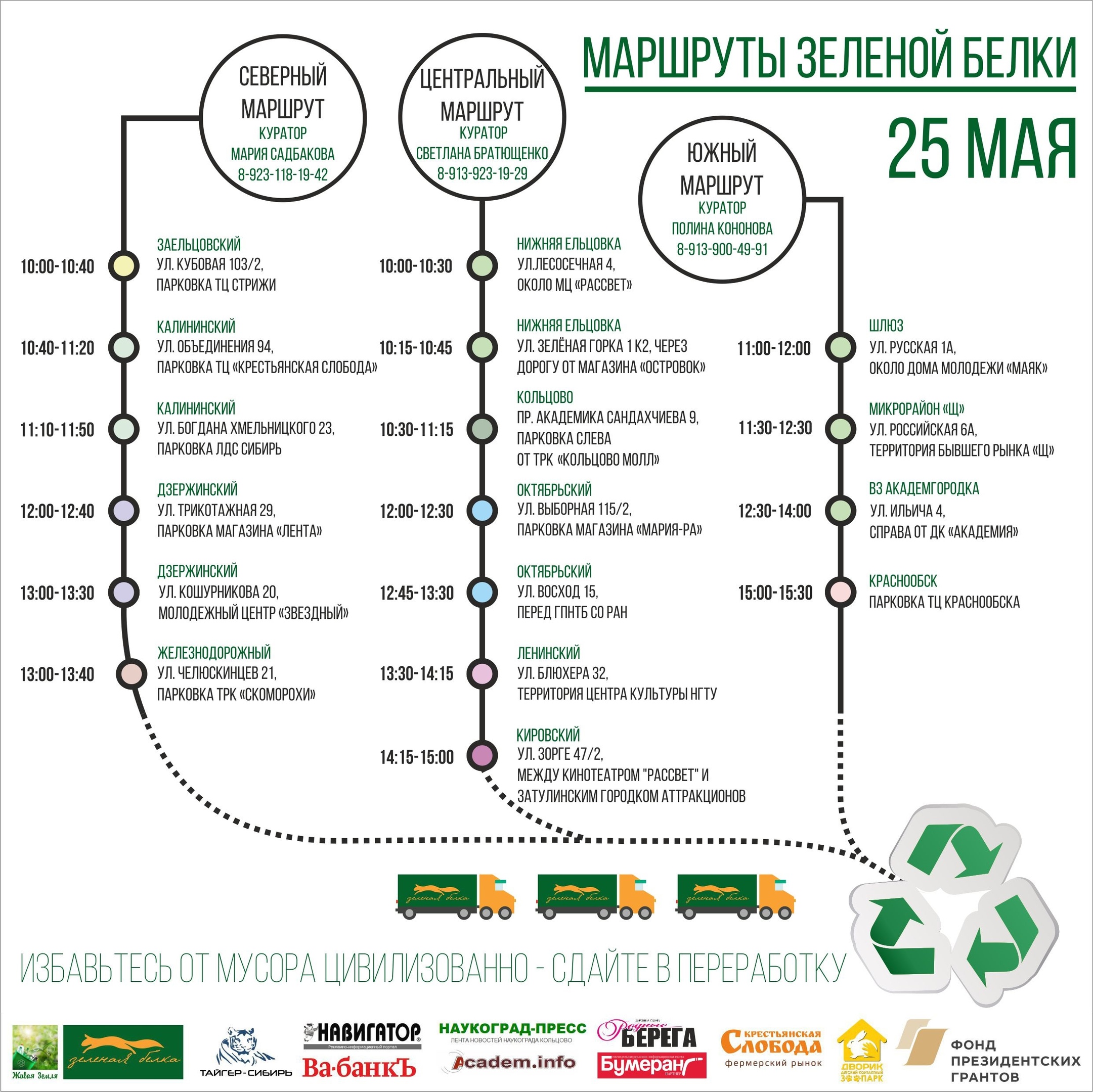
अंक

15 से 90 मिनट की अवधि में कार द्वारा कवर दूरी पर एक दूसरे से स्थित शहर के 17 बिंदुओं पर कार्रवाई की जाती है। फोटो में इन बिंदुओं में से एक: प्लास्टिक के विभिन्न अंशों को इकट्ठा करने के लिए दीवार के साथ बाईं ओर बैग, दाईं ओर - एक ट्रक, जिसमें भविष्य में सब कुछ लोड किया गया है, और केंद्र में - कानों के साथ एक स्वयंसेवक।



बिंदु पर सभी गतिविधि क्यूरेटर द्वारा आयोजित की जाती हैं जिनके पास उस समय प्रतिबंध हैं, जो वे अपने कर्तव्यों को पूरा करने के लिए तैयार हैं। कार्रवाई की योजना बनाते समय, क्यूरेटर उस समय अंतराल की रिपोर्ट करते हैं जिसके भीतर कार्रवाई को अपने बिंदु पर पारित करना होगा।

प्रत्येक बिंदु पर एकत्र किए गए रिसाइकिल के औसत वॉल्यूम पर भी डेटा है।

मार्गों

अंक उन मार्गों में व्यवस्थित होते हैं जो एक ट्रक द्वारा क्रमिक रूप से संचालित होते हैं। ट्रक आंदोलनों की निगरानी मार्ग पर्यवेक्षकों द्वारा की जाती है जो परिचालन पर्यावरण की निगरानी करते हैं और विशेष घटनाओं से निपटने पर निर्णय लेते हैं।



ट्रक

मालवाहक वाहनों के प्रति घंटे किराये के प्रस्तावों के ढांचे के भीतर एक सामान्य आधार पर किराए पर लिया जाता है। जगह में प्लास्टिक को कॉम्पैक्ट करना संभव नहीं है, इसलिए ट्रक को चिह्नित करने वाला मुख्य पैरामीटर शरीर का आयतन है। हमारे मामले में क्षमता वहन करना एक सीमित कारक नहीं है।

कार्रवाई का मुख्य खर्च ट्रक किराये के भुगतान के साथ जुड़ा हुआ है, इसलिए, हमारे हिस्से के अस्तित्व और विकास के लिए इसकी कमी महत्वपूर्ण है, जो जिम्मेदार खपत के बारे में विचार बनाने के अर्थ में संस्थागत महत्व प्राप्त करता है। अगला, इस मुद्दे को हल करने के लिए एक दृष्टिकोण का वर्णन किया जाएगा, असतत अनुकूलन विधियों के आवेदन के आधार पर, गणितीय प्रोग्रामिंग।

2. औपचारिककरण

गणितीय मॉडल के निर्माण में, हम रैखिक मिश्रित-पूर्णांक कार्यक्रमों के ढांचे के भीतर बने रहेंगे, जिसके लिए कक्षा 7 बीजगणित का ज्ञान पर्याप्त है।

एकमात्र कठिनाई सूत्रों में अमूर्त अंकन और योग संकेतों के उपयोग से जुड़ी हो सकती है। मुझे आशा है कि यह उन पाठकों को नहीं डराएगा जिनके पास गणितीय ग्रंथों के साथ असीम मुठभेड़ है।

अनुकूलन मॉडल में, चार घटकों को प्रतिष्ठित किया जा सकता है:

• एक अलग मार्ग बनाने वाले बिंदुओं के समूहों का गठन;
• प्रत्येक समूह के लिए एक सर्किट की परिभाषा;
• प्रत्येक बिंदु पर ट्रक के आगमन के समय की आवश्यकताओं को पूरा करना;
• मार्गों में से प्रत्येक की सेवा के लिए आवश्यक ट्रक के प्रकार का निर्धारण।

हम प्रत्येक भाग पर विचार करते हैं, आवश्यक संकेतन को आवश्यक रूप से पेश करते हैं।

बिंदु समूहन

चलो $$$V = \ {1, \ dots, n \}$ पुनरावर्तनीय सामग्रियों के लिए संग्रह बिंदुओं के कई सूचकांक हैं, और साइट जहां एकत्र किए गए रिसाइकिल को फिर से ले जाया जाता है - हम इसे डिपो कहेंगे - में 0. पुट का सूचकांक है। $$$\ bar {V} = V \ cup \ {0 \}$

अंकों का प्रत्येक समूह एक अलग मार्ग बनाता है। के माध्यम से $$$आर$ मार्ग संख्याओं के सेट को निरूपित करें।

मात्रा दें $$$z_ {ir}, i \ _ in, r $ R $ मे$ एक बराबर है अगर बिंदु $$$मैं$ संख्या के साथ मार्ग में शामिल $$$आर$ , और शून्य अन्यथा। फिर आवश्यकता है कि बिंदु की $$ मार्गों में से एक दर्ज करना चाहिए जैसा लिखा जा सकता है

$$

$$\ sum_ {r \ _ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$$

सभी मार्गों में डिपो दर्ज करना होगा: $$$z_ {0r} = 1, R $ R मे$


एक चक्कर की परिभाषा

रूट उनके बीच बिंदुओं और क्रॉसिंग का एक वैकल्पिक क्रम है। औपचारिक रूप से, वे सभी सेट के एक बिंदु पर शुरू करते हैं $$$V$ और डिपो में समाप्त होता है, हालांकि, यह मान लेना आसान होगा कि सभी मार्ग चक्रीय हैं। यह धारणा सार को परिवर्तित नहीं करती है, लेकिन सभी लंबों को एक समान बनाती है: इस मामले में कोई अंतिम छोर नहीं हैं, वे सभी पारगमन हैं।

अंक के लिए $$$i, j \ in \ bar {V}$ और मार्ग $$ एक चर सेट करें $$$x_ {ijr}$ संख्या के साथ मार्ग में एक के बराबर है $$$आर$ ट्रक बिंदु से आगे बढ़ रहा है $$$मैं$ इस बिंदु पर $$$ज$ , और शून्य अन्यथा।

फिर हमें आवश्यकता है, सबसे पहले, कि मार्ग के साथ आगे बढ़ने वाला ट्रक $$ इस बिंदु पर गए $$ यदि वह, समूहों में विभाजित होने के बाद, संख्या के साथ समूह में गिर गई $$$आर$ :

$$

$$\ sum_ {j \ _ in \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, R_ में R $$$

दूसरे, बिंदु पर पहुंचने के बाद ट्रक $$$i \ in \ बार {V}$ उसे छोड़ देना चाहिए।

$$

$$\ sum_ {j \ _ in \ bar {V}} x_ {jir} = \ sum_ {j \ _ in \ bar {V}} x_ {ijr}, \ quad i \ in \ bar {V}, r \ _ in R ।$$

आप देख सकते हैं कि ये प्रतिबंध मात्राओं की अनुमति देते हैं $$$x_ {ijr}$ रूटों को परिभाषित करें जो असंतुष्ट छोरों का एक समूह हैं। इस तरह के मार्ग, निश्चित रूप से, समझ में नहीं आते हैं, और इससे बचने के लिए कई प्रतिबंधों की आवश्यकता होती है।


प्रत्येक बिंदु पर ट्रक के आगमन के समय आवश्यकताओं को पूरा करना

दूसरे शब्दों में, आपको क्यूरेटरों द्वारा बताए गए समय खिड़कियों के अंदर ही बिंदुओं पर जाने की आवश्यकता है। के माध्यम से $$$B_i$ और $$$ई_आई$ क्रमशः, समय अंतराल की शुरुआत और अंत जिसमें बिंदु के क्यूरेटर $$$मैं$ इसमें शामिल हो सकते हैं।

इन प्रतिबंधों के कार्यान्वयन को ट्रैक करने के लिए, हमें मार्ग पर स्टॉप और क्रॉसिंग के दौरान ट्रक द्वारा खर्च किए गए समय के बारे में जानकारी चाहिए। के माध्यम से $$$L_i, i $ V मे$ बिंदु पर लोड करने की अवधि को निरूपित करें $$$मैं$ और के माध्यम से $$$D_ {ij}, i, j \ in \ bar {V}$ - एक बिंदु से आगे बढ़ने का समय $$$मैं$ इस बिंदु पर $$$ज$ हम एक आरक्षण बनाते हैं $$$D_ {0i} = 0$ सभी के लिए $$$i \ in \ बार {V}$ , और आम तौर पर प्रदर्शन किया जा सकता है $$$D_ {ij} \ neq D_ {ji}$ किसी के लिए $$$i \ neq j$

हम गैर-नकारात्मक चर पेश करते हैं $$$a_i, i \ in \ bar {V}$ और $$$w_ {ir}, i \ in \ bar {V}, r $ in R$ बिंदु पर आगमन के समय और प्रतीक्षा समय के बराबर $$$मैं$ जब एक मार्ग के साथ ड्राइविंग $$$आर$ , क्रमशः। प्रवेश किए गए मूल्यों के लिए, निम्नलिखित संबंधों को संतुष्ट किया जाना चाहिए।

प्रतीक्षा समय लोड करने के लिए आवश्यक समय से कम नहीं हो सकता है

$$

$$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ _ in R,$$

और यदि बिंदु मार्ग से संबंधित नहीं है तो शून्य के बराबर है $$$आर$

$$

$$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ _ in R,$$

बिंदु पर आगमन का समय $$$ज$ पिछले बिंदु के लिए उपयुक्त समय पर गणना की गई $$$मैं$ यहाँ एक बहुत बड़ा स्थिरांक है $$$एम$ के बीच चलते समय अनावश्यक निर्भरता को समाप्त करने के लिए उपयोग किया जाता है $$$मैं$ और $$$ज$ नहीं किया।

$$

$$a_i + \ sum_ {r \ _ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ _ in R} x_ {ijr}), \ quad_ \ _ in, j \ V में,$$

ट्रक का आगमन और प्रस्थान क्यूरेटर द्वारा इंगित अंतराल के भीतर होना चाहिए।

$$

$$a_i \ geq B_i, \ quad i \ _ in V,$$

$$

$$a_i + \ sum_ {r \ _ in R} w_ {ir} \ leq E_i, \ quad i \ _ V $ मे$$

प्रत्येक मार्ग की सेवा के लिए आवश्यक ट्रक के प्रकार का निर्धारण
द्वारा किराए के लिए उपलब्ध कई प्रकार के ट्रकों को अस्वीकार करें $$$T$ ट्रक का प्रकार $$$T $ T में$ शरीर की मात्रा की विशेषता $$$C_t$ और प्रति घंटे के किराए की लागत $$$P_t$ न्यूनतम ट्रक किराये का समय $$$टी$ द्वारा निरूपित करें $$$U_t ^ 0$ बिंदु पर एकत्र किए गए रिसाइकिल की मात्रा $$ द्वारा निरूपित करें $$$G_i$

हम चर का परिचय देते हैं $$$y_ {tr}, T \ T में, R $ R में$ यदि ट्रक प्रकार एक के बराबर है $$$टी$ संख्या के साथ सेवा मार्ग को सौंपा $$$आर$ , और शून्य अन्यथा।

पूर्णांक चर $$$u_ {tr}, T \ T में, r $ R $ मे$ ट्रक प्रकार को किराए पर देने का समय निर्धारित करें $$$टी$ संख्या के साथ मार्ग की सेवा $$$आर$
प्रत्येक मार्ग के लिए, $$ , आपको ट्रक का प्रकार निर्दिष्ट करना चाहिए:

$$

$$\ ___ टी में T} y_ {tr} = 1, R $ में \ quad r$$

मार्गों के बीच के बिंदुओं के टूटने के अनुसार, कुछ मार्ग तुच्छ हो सकते हैं, यानी केवल डिपो होते हैं। अगर मार्ग $$$आर$ गैर-तुच्छ, फिर उसे सौंपे गए ट्रक को कम से कम किराए पर दिया जाता है $$$U_t ^ 0$ घंटे।

$$

$$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ _ V} z_ {ir}), T में \ quad t \, R \ _ में$$

इसी समय, पट्टे की अवधि पार्किंग की कुल अवधि और मार्ग के साथ बढ़ने से भी अधिक होनी चाहिए।

$$

$$u_ {tr} \ geq \ sum_ {i_ in V} \ sum_ {j \ _ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ _ in \ bar {V}} w_ { ir} -M (1-y_ {tr}), R में \ quad r \, t $ t में$$

संपत्ति प्रदान करने वाले प्रतिबंध जोड़ें: यदि ट्रक प्रकार का है $$$टी$ एक मार्ग को नहीं सौंपा $$$आर$ , इसका किराया समय शून्य है।

$$

$$u_ {tr} \ leq My_ {tr}।$$

मार्ग बिंदुओं पर एकत्रित सभी पुनर्चक्रण ट्रक के पीछे फिट होने चाहिए।

$$

$$\ sum_ {i_ in V} G_iz_ {ir} \ leq \ sum_ {t \ _ in T} C_ty_ {tr}, R. $ में \ quad r \ _$$

अंत में, हमारा लक्ष्य ट्रकों को किराए पर देने की लागत को कम करना है, जो कि प्रस्तुत किए गए पदनामों का उपयोग करते हुए लिखा जाता है $$$\ ___ T \ _ में T} \ sum_ {r \ _ R} P_tu_ {tr} $ मे$

समाधान के लिए खोजें

यह सत्यापित करना आसान है कि अनुकूलन मॉडल में शामिल सभी अभिव्यक्तियाँ चर के रैखिक कार्य हैं, इसलिए, सटीक और अनुमानित समाधान खोजने के लिए, आप मिश्रित पूर्णांक प्रोग्रामिंग समस्याओं जैसे कि गुरोबी , CPLEX , Xpress , ORtools , को हल करने के लिए मानक पैकेज का उपयोग कर सकते हैं। SCIP , BLIS इत्यादि।
हम GMPL भाषा में परिवहन लागत को कम करने के लिए एक मॉडल लिखते हैं। यह हमें हमारे उद्देश्यों के लिए मुफ्त GLPK पैकेज का उपयोग करने की अनुमति देगा। कोड लिखने और मॉडल को डीबग करने के लिए, GUSEK विकास वातावरण डाउनलोड करना सुविधाजनक होगा, जिसमें पहले से ही इसकी संरचना में GLPK शामिल है।

GUSEK इस तरह दिखता है:



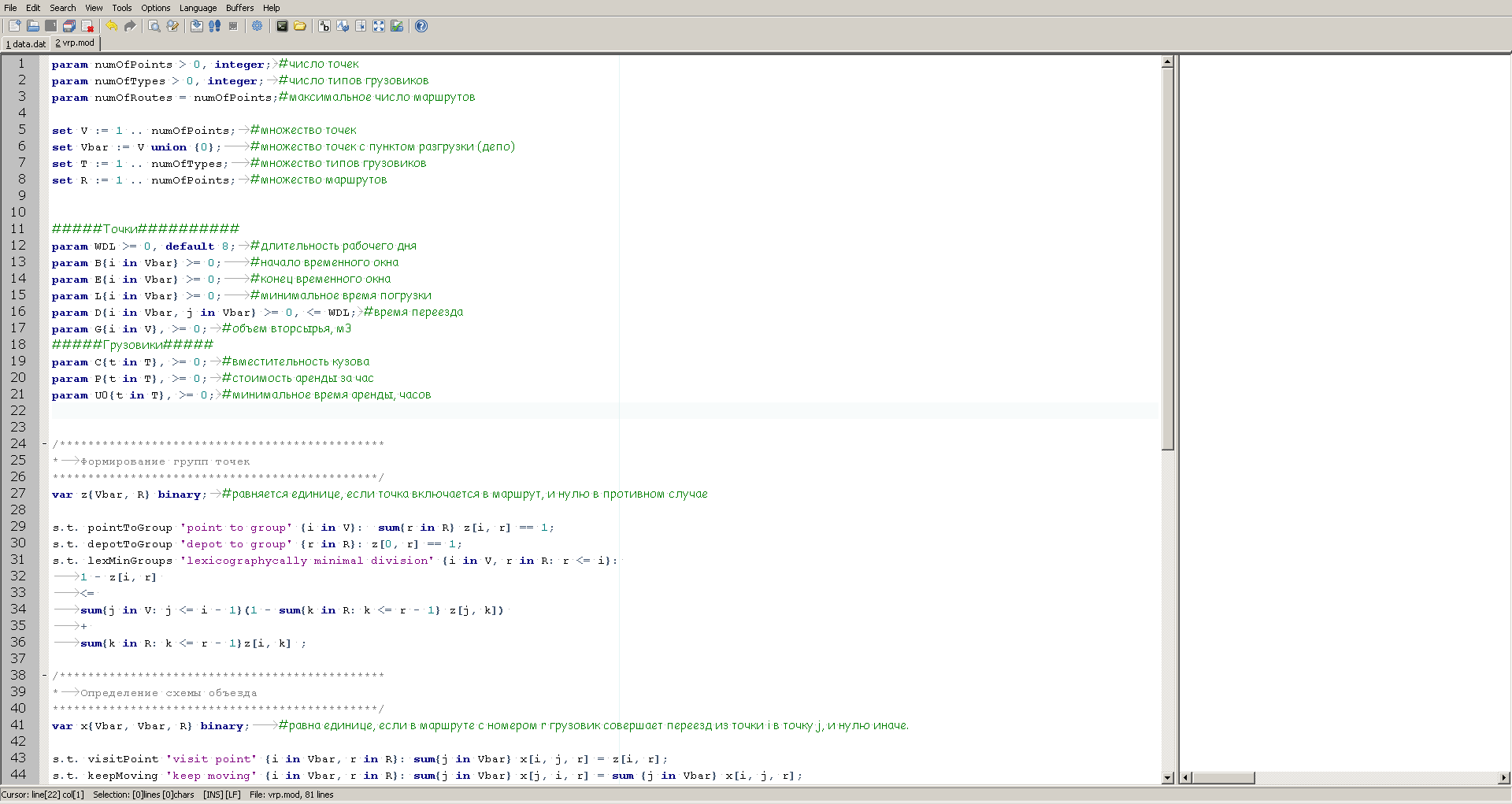
बाईं ओर हम मॉडल का विवरण देखते हैं, और दाईं ओर गणना प्रगति पर जानकारी प्रदर्शित करने के लिए एक खिड़की है, जिसे लॉन्च के बाद सॉल्वर आपूर्ति करेगा।


एक त्वरित शुरुआत के लिए, मैं मॉडल में उपयोग के लिए तैयार किए गए मेरे सिर से लिया गया डेटा भी जोड़ूंगा:


नाम के साथ फ़ाइल में मॉडल कोड कॉपी करने के बाद, उदाहरण के लिए, model.mod, और data.dat फ़ाइल में इनपुट डेटा, सब कुछ चलाने के लिए तैयार है। हमने 100 सेकंड की गणना समय पर एक सीमा निर्धारित की है (यह कुंजी --tmlim [सेकंड में समय] का उपयोग करके किया जाता है), इनपुट डेटा के साथ फ़ाइल में पथ को स्थानांतरित करना (की -d [फ़ाइल पथ] का उपयोग करके),



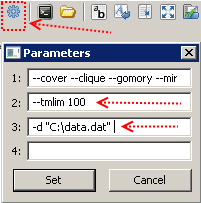
और F5 दबाएं। सफल होने पर, संदेश दाईं ओर विंडो में दिखाई देंगे, और सौ सेकंड के बाद हमारे पास सबसे अच्छा समाधान होगा जिसे GLPK आवंटित समय में खोजने में कामयाब रहे।



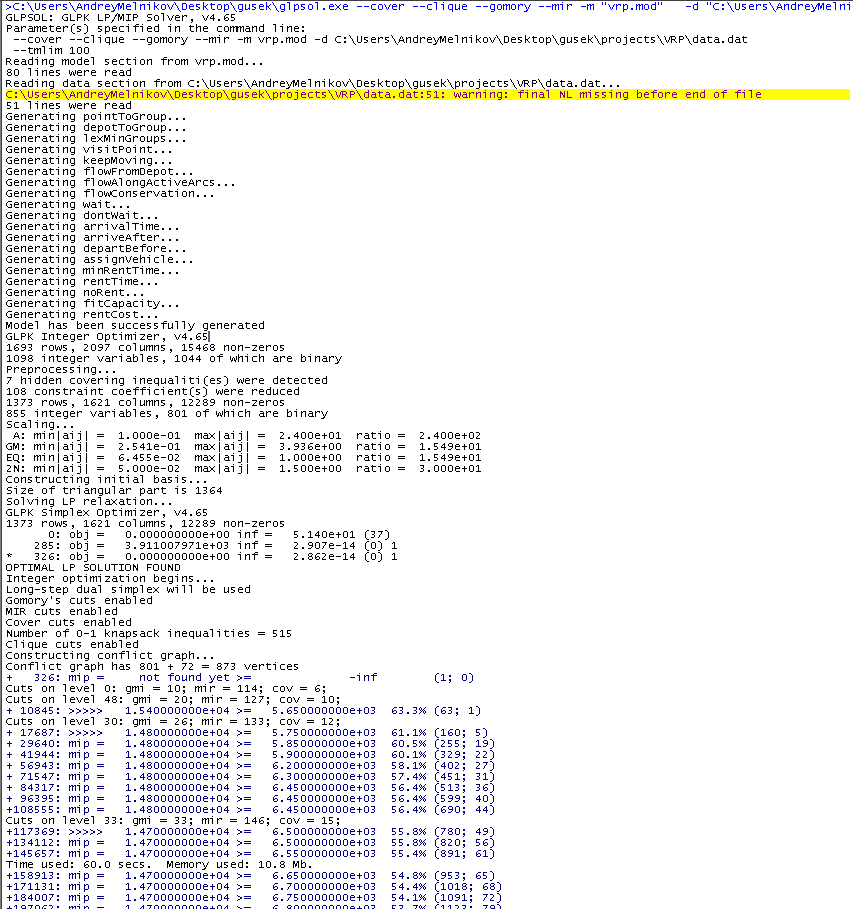
नीले पाठ में, हम शिलालेख "एमआईपी =" के बाद अर्थ में रुचि रखते हैं। जैसा कि आप देख सकते हैं, यह समय-समय पर घटता है। सभी नए समाधान काम की प्रक्रिया में हैं, सबसे अच्छे में परिवहन लागत का मूल्य इस कॉलम में प्रदर्शित किया गया है (अब तक 14700 हैं)। अगली संख्या सबसे अच्छा मौजूदा, यानी इष्टतम समाधान के लिए निचली सीमा है। प्रारंभ में, अनुमान को काफी कम आंका गया है, लेकिन समय के साथ परिष्कृत किया जाता है, अर्थात बढ़ता है। बाईं ओर और दाईं ओर स्थित मान परिवर्तित हो रहे हैं, और स्क्रीनशॉट के समय उनके बीच का सापेक्ष अंतर 54.1% है। जैसे ही यह संख्या शून्य हो जाएगी, एल्गोरिथ्म साबित करेगा कि सबसे अच्छा समाधान सबसे अच्छा संभव है। व्यवहार में इस घटना के लिए इंतजार करना हमेशा उचित नहीं है, और न केवल इसलिए कि यह एक लंबा समय है, लेकिन आरक्षण करना महत्वपूर्ण है कि, एक नियम के रूप में, एक अच्छा समाधान अपेक्षाकृत जल्दी है, और मुख्य समय लागत अनुमान के शोधन के साथ जुड़ा हुआ है जो सबसे अच्छा संभव साबित करने के लिए आवश्यक है।

एक निष्कर्ष के बजाय

रूटिंग समस्याएँ अत्यंत कम्प्यूटेशनल रूप से जटिल होती हैं, और जिन बिंदुओं पर जाने की आवश्यकता होती है, उनकी संख्या में वृद्धि के साथ, समाधान खोजने के लिए और इसकी इष्टतमता को साबित करने के लिए समय लगता है। हालांकि, काफी छोटे उदाहरणों के लिए, समय की उचित मात्रा में, सॉल्वर मार्गों का एक सफल सेट बनाने में सक्षम है और निर्णय लेने का समर्थन करने के लिए इस्तेमाल किया जा सकता है। मॉडल द्वारा प्रस्तावित रूटिंग विकल्पों के विश्लेषण से हमें लागत में कमी के महत्वपूर्ण अवसरों की खोज करने में मदद मिली, और यह स्टॉक के अस्तित्व और विकास के लिए महत्वपूर्ण है।

हमारे आगे के प्रयास अंकों में एकत्रित रिसाइकिल की मात्रा में अनिश्चितता के साथ काम की ओर बढ़ गए। हम ट्रक रूटिंग में रणनीतिक और परिचालन निर्णय लेने के लिए कई स्टोकेस्टिक प्रोग्रामिंग मॉडल विकसित कर रहे हैं। यदि विषय प्रासंगिक हो जाता है और रुचि पैदा होती है, तो मैं इस बारे में भी लिखूंगा, क्योंकि जल्द ही हम सभी को पर्यावरण के मुद्दों पर अधिक गहन रूप से गोता लगाना होगा, जो कि हम में सफलता की कामना करते हैं।