संयोग संबंध की समरूपता गुण

इस लेख का उद्देश्य समय श्रृंखला के सह-एकीकरण के अध्ययन में विरोधाभासी परिणामों को साझा करना है: यदि समय श्रृंखला $$$ए$ पास से सह-एकीकृत $$$ब$ , एक नंबर $$$ब$ हमेशा एक नंबर के साथ सह-एकीकृत नहीं $$$ए$ ।

यदि हम विशुद्ध रूप से सैद्धांतिक रूप से संयोग का अध्ययन करते हैं, तो यह साबित करना आसान है कि यदि श्रृंखला $$$ए$ के साथ सह-एकीकृत $$$ब$ फिर पंक्ति $$$ब$ के साथ सह-एकीकृत $$$ए$ । हालांकि, अगर हम संयोग से अध्ययन करना शुरू करते हैं, तो यह पता चलता है कि सैद्धांतिक गणना हमेशा पुष्टि नहीं होती है। ऐसा क्यों हो रहा है?

समरूपता

रवैया $$$ए$ अगर सममित कहा जाता है $$$A \ subseteq A ^ {- 1}$ जहाँ $$$A ^ {- 1}$ - स्थिति द्वारा उलटा अनुपात: $$$x A ^ {- 1} y$ करने के लिए tantamount $$$yAx$ । दूसरे शब्दों में, यदि संबंध $$$xAy$ फिर रिश्ता $$$yAx$ ।

दो पर विचार करें $$$I (1)$ की एक संख्या $$$x_t$ और $$$y_t$ । $$$t = 0, \ dots, T$ । संयोग अगर सममित है $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ को आकर्षित करती है $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ यदि प्रत्यक्ष प्रतिगमन की उपस्थिति व्युत्क्रम की उपस्थिति की ओर ले जाती है।

समीकरण पर विचार करें $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ । $$$\ Beta_1 \ neq 0$ । बाईं और दाईं ओर स्वैप करें और घटाएं $$$\ varepsilon_ {1t}$ दोनों भागों से: $$$\ Beta_1 x_t = y_t - \ varepsilon_ {1t}$ । क्योंकि $$$\ Beta_1 \ neq 0$ परिभाषा के अनुसार, दोनों भागों को विभाजित करें $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1} $$$

की जगह $$$1 / \ beta_1$ पर $$$\ beta_2$ , और $$$- \ varepsilon_ {1t} / \ beta_1$ पर $$$\ varepsilon_ {2t}$ हमें मिलता है $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ । इसलिए, संयोग संबंध सममित है।

यह इस प्रकार है कि अगर चर $$$X$ चर के साथ मेल खाता है $$$य$ फिर चर $$$य$ चर के साथ सह-एकीकृत होना चाहिए $$$X$ । हालांकि, एंगल-ग्रेंजर संयोग परीक्षण हमेशा इस समरूपता संपत्ति की पुष्टि नहीं करता है, क्योंकि कभी-कभी एक चर $$$य$ चर के साथ सह-एकीकृत नहीं $$$X$ इस परीक्षण के अनुसार।

मैंने एंगल-ग्रेंजर टेस्ट का उपयोग करके मॉस्को और न्यूयॉर्क एक्सचेंजों के 2017 के आंकड़ों पर समरूपता संपत्ति का परीक्षण किया। मास्को एक्सचेंज पर शेयरों के 7,975 सह-एकीकृत जोड़े थे। 7731 (97%) संयोगित जोड़े के लिए, समरूपता संपत्ति की पुष्टि की गई थी, 244 (3%) के लिए जोड़ी गई समरूपता संपत्तियों की पुष्टि नहीं की गई थी।

न्यूयॉर्क स्टॉक एक्सचेंज में 140,903 सह-एकीकृत जोड़े थे। १३६५ pairs६ (९ te%) संयोगित जोड़े के लिए, समरूपता संपत्ति की पुष्टि की गई, ४३१ ((३%) के लिए जोड़ी गई समरूपता संपत्तियों की पुष्टि नहीं हुई।

व्याख्या

इस परिणाम की व्याख्या दूसरे प्रकार के डिकी-फुलर परीक्षण की कम शक्ति और उच्च संभावना से की जा सकती है, जिस पर एंगल-ग्रेंजर परीक्षण आधारित है। दूसरी तरह की त्रुटि की संभावना को निरूपित किया जा सकता है $$$\ बीटा = पी (H_0 | H_1)$ फिर मूल्य $$$1 - \ बीटा$ परीक्षण की शक्ति कहा जाता है। दुर्भाग्य से, डिक्की-फुलर परीक्षण गैर-स्थिर और निकट-गैर-स्थिर समय श्रृंखला के बीच अंतर करने में सक्षम नहीं है।

निकट-अस्थिर समय श्रृंखला क्या है? समय श्रृंखला पर विचार करें $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ । एक स्थिर समय श्रृंखला एक श्रृंखला है जिसमें $$$0 <\ phi <1$ । एक गैर-स्थिर समय श्रृंखला एक श्रृंखला है जिसमें $$$\ phi = 1$ । निकट-अस्थिर समय श्रृंखला एक ऐसी श्रृंखला है जिसमें मान होता है $$$\ phi$ एक के करीब।

निकट-गैर-स्थिर समय श्रृंखला के मामले में, हम अक्सर गैर-स्थिर की शून्य परिकल्पना को अस्वीकार करने में सक्षम नहीं होते हैं। इसका अर्थ है कि डिकी-फुलर परीक्षण में दूसरी तरह की त्रुटि का एक उच्च जोखिम है, अर्थात, झूठे अशक्त परिकल्पना को अस्वीकार नहीं करने की संभावना।

केपीएसएस टेस्ट

डिकी-फुलर परीक्षण की कमजोरी के लिए एक संभावित प्रतिक्रिया केपीएसएस परीक्षण है, जो कि केवेटकोव्स्की, फिलिप्स, श्मिट और शीन के वैज्ञानिकों के शुरुआती नाम के कारण है। यद्यपि इस परीक्षण का पद्धतिगत दृष्टिकोण डिक्की-फुलर दृष्टिकोण से पूरी तरह से अलग है, मुख्य अंतर को अशक्त और वैकल्पिक परिकल्पना के क्रमांकन में समझा जाना चाहिए।

केपीएसएस परीक्षण में, शून्य परिकल्पना में कहा गया है कि समय श्रृंखला स्थिर है, बनाम गैर-स्थिरता की उपस्थिति के बारे में विकल्प। निकट-गैर-स्थिर समय श्रृंखला, जिन्हें अक्सर डिक्की-फुलर परीक्षण का उपयोग करके गैर-स्थिर के रूप में पहचाना जाता था, KPSS परीक्षण का उपयोग करके स्टेशनरी के रूप में सही ढंग से पहचाना जा सकता है।

हालाँकि, हमें इस बात की जानकारी होनी चाहिए कि सांख्यिकीय परीक्षण का कोई भी परिणाम केवल संभाव्य है और एक निश्चित सच्चे निर्णय के साथ भ्रमित नहीं होना चाहिए। हमेशा एक गैर-शून्य संभावना है कि हम गलत हैं। इस कारण से, डिक्सी-फुलर और केपीएसएस परीक्षणों के परिणामों को गैर-स्थिरता के लिए एक आदर्श परीक्षण के रूप में संयोजित करने का प्रस्ताव है।



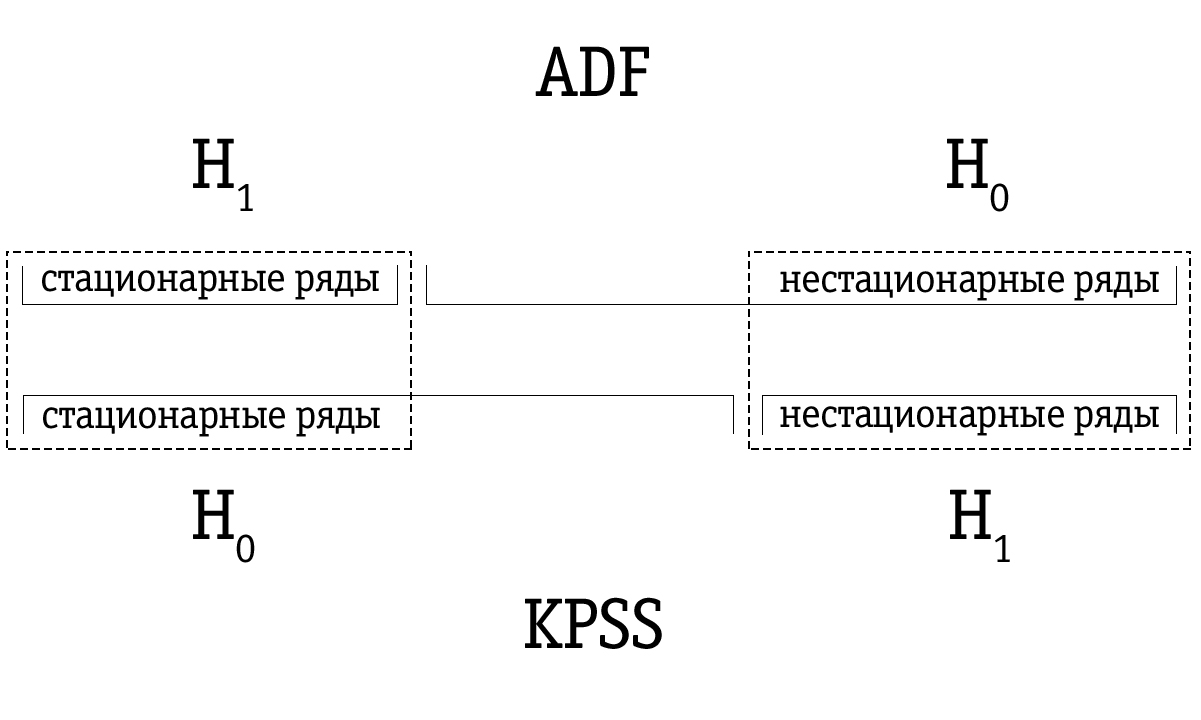
कम शक्ति के कारण, डिक्की-फुलर परीक्षण अक्सर ग़लती से एक श्रृंखला को गैर-स्थिर के रूप में पहचानता है, इसलिए परिणामी श्रृंखला को डिके-फुलर परीक्षण द्वारा पहचाना जाता है क्योंकि अस्थिरता KPSS परीक्षण का उपयोग करते हुए गैर-स्थिर की पहचान की गई कई समय श्रृंखला की तुलना में बड़ी है। इसलिए, परीक्षण का आदेश महत्वपूर्ण है।

यदि समय श्रृंखला को डिक्की-फुलर परीक्षण का उपयोग करके स्थिर के रूप में पहचाना जाता है, तो यह सबसे अधिक संभावना केपीएसएस परीक्षण का उपयोग करके स्थिर के रूप में पहचाना जाएगा; इस मामले में, हम मान सकते हैं कि श्रृंखला वास्तव में स्थिर है।

यदि समय श्रृंखला को KPSS परीक्षण का उपयोग करके अस्थिर के रूप में पहचाना गया था, तो यह सबसे अधिक संभावना है कि डिक्की-फुलर परीक्षण का उपयोग करके अस्थिर के रूप में पहचाना जाएगा; इस मामले में, हम मान सकते हैं कि श्रृंखला वास्तव में अस्थिर है।

हालांकि, अक्सर ऐसा होता है कि एक समय श्रृंखला जिसे डिकी-फुलर परीक्षण का उपयोग करके गैर-स्थिर के रूप में पहचाना गया है, केपीएसएस परीक्षण का उपयोग करके स्थिर के रूप में चिह्नित किया जाएगा। इस मामले में, हमें अपने अंतिम निष्कर्ष के साथ बहुत सावधान रहना चाहिए। हम जांच कर सकते हैं कि KPSS परीक्षण के मामले में स्थिरता के लिए आधार कितना मजबूत है और डिकी-फुलर परीक्षण के मामले में अस्थिरता के लिए और एक उचित निर्णय लेते हैं। बेशक, हम इस तरह की टाइम सीरीज़ की स्टेशनियरिटी के सवाल को भी अनसुलझा छोड़ सकते हैं।

KPSS परीक्षण दृष्टिकोण समय श्रृंखला को मानता है $$$y_t$ एक प्रवृत्ति के सापेक्ष स्थिरता के लिए परीक्षण एक निर्धारक प्रवृत्ति के योग में विघटित हो सकता है $$$\ बीटा टी$ यादृच्छिक चलना $$$r_t$ और स्थिर त्रुटि $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

जहाँ $$$u_t$ - शून्य मीन और विचरण के साथ सामान्य आईआईडी प्रक्रिया $$$\ _ सिग्मा ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ )। प्रारंभिक मूल्य $$$r_0$ तय माना जाता है और एक स्वतंत्र सदस्य की भूमिका निभाता है। स्थिर त्रुटि $$$\ varepsilon_t$ किसी भी सामान्य एआरएमए प्रक्रिया द्वारा उत्पन्न किया जा सकता है, अर्थात, इसके पास मजबूत ऑटोक्रेलेशन हो सकता है।

डिकी-फुलर परीक्षण के समान, ऑटोक्रेलेशन की एक मनमाना संरचना को ध्यान में रखने की क्षमता $$$\ varepsilon_t$ बहुत महत्वपूर्ण है क्योंकि अधिकांश आर्थिक समय श्रृंखला अत्यधिक समय पर निर्भर है और इसलिए एक मजबूत स्वायत्तता है। यदि हम क्षैतिज अक्ष के संबंध में स्थिरता की जांच करना चाहते हैं, तो शब्द $$$\ बीटा टी$ बस ऊपर दिए गए समीकरण से बाहर रखा गया है।

इसके ऊपर के समीकरण से यह माना जाता है कि अशक्त परिकल्पना $$$H_0$ स्टेशनरिटी के बारे में $$$y_t$ परिकल्पना के बराबर $$$\ _ सिग्मा ^ 2 = 0$ जिससे यह इस प्रकार है $$$r_t = r_0$ सभी के लिए $$$टी$ ( $$$r_0$ एक स्थिर है)। इसी तरह, एक वैकल्पिक परिकल्पना $$$H_1$ गैर-स्थैतिकता परिकल्पना के बराबर है $$$\ सिग्मा ^ 2 \ neq 0$ ।

परिकल्पना का परीक्षण करने के लिए $$$H_0$ : $$$\ _ सिग्मा ^ 2 = 0$ (स्थिर समय श्रृंखला) बनाम वैकल्पिक $$$H_1$ : $$$\ सिग्मा ^ 2 \ neq 0$ (गैर-स्थिर समय श्रृंखला) KPSS परीक्षण के लेखक, लैग्रेग मल्टीप्लायर टेस्ट के एक तरफ़ा आँकड़े प्राप्त करते हैं। वे इसके स्पर्शोन्मुख वितरण की गणना करते हैं और असममित महत्वपूर्ण मानों का मॉडल बनाते हैं। हम यहां सैद्धांतिक विवरणों पर विचार नहीं करते हैं, लेकिन केवल परीक्षण निष्पादन एल्गोरिथ्म को संक्षेप में रेखांकित करते हैं।

जब एक समय श्रृंखला के लिए KPSS परीक्षण करते हैं $$$y_t$ । $$$t = 1, \ dots, T$ निम्नलिखित समीकरणों में से एक का अनुमान लगाने के लिए सबसे कम वर्ग विधि (सबसे कम वर्ग) का उपयोग किया जाता है:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ Beta t + \ varepsilon_t। $$$

यदि हम क्षैतिज अक्ष के संबंध में स्थिरता की जांच करना चाहते हैं, तो हम पहले समीकरण का मूल्यांकन करते हैं। यदि हम प्रवृत्ति के संबंध में स्टेशनरी की जांच करने की योजना बनाते हैं, तो हम दूसरा समीकरण चुनते हैं।

शेष राशि $$$e_t$ अनुमानित समीकरण से Lagrange गुणक के परीक्षण के आंकड़ों की गणना करने के लिए उपयोग किया जाता है। लैग्रेंज गुणक परीक्षण इस विचार पर आधारित है कि जब शून्य परिकल्पना पूरी हो जाती है, तो सभी लाग्रेंज गुणक शून्य के बराबर होने चाहिए।

लग्र गुणक परीक्षण

Lagrange गुणक परीक्षण अधिकतम संभावना विधि (एमएल) का उपयोग करके पैरामीटर अनुमान के लिए एक अधिक सामान्य दृष्टिकोण से जुड़ा हुआ है। इस दृष्टिकोण के अनुसार, डेटा को वितरण मापदंडों से संबंधित सबूत माना जाता है। सबूत को अज्ञात मापदंडों के एक समारोह के रूप में व्यक्त किया जाता है - एक संभावना समारोह:

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k),$$

जहाँ $$$X_i$ देखे गए मूल्य हैं, और $$$\ Phi_i$ - जिन मापदंडों का हम मूल्यांकन करना चाहते हैं।

अधिकतम संभावना समारोह नमूना टिप्पणियों का संयुक्त संभावना है।

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k) = P (X_1 \ land X_2 \ land X_3 \ Nots X_n) $$$

अधिकतम संभावना विधि का लक्ष्य संभावना फ़ंक्शन को अधिकतम करना है। यह अनुमानित मापदंडों में से प्रत्येक के लिए अधिकतम संभाव्यता फ़ंक्शन को विभेदित करके और आंशिक डेरिवेटिव को शून्य के बराबर करने के द्वारा प्राप्त किया जाता है। पैरामीटर का मान जिस पर फ़ंक्शन का मान अधिकतम है, वांछित अनुमान है।

आमतौर पर, बाद के काम को आसान बनाने के लिए, सबसे पहले संभावना फ़ंक्शन का लघुगणक लिया जाता है।

एक सामान्यीकृत रैखिक मॉडल पर विचार करें $$$Y = \ beta X + \ varepsilon$ जहां यह माना जाता है कि $$$\ _ varepsilon$ सामान्य रूप से वितरित $$$N (0, \ sigma ^ 2)$ वह है $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ ।

हम इस प्रणाली की परिकल्पना का परीक्षण करना चाहते हैं $$$q$ ( $$$q <k$ ) स्वतंत्र रैखिक बाधाओं $$$आर \ बीटा = आर$ । यहां $$$आर$ - प्रसिद्ध $$$q \ गुना k$ रैंक मैट्रिक्स $$$q$ , और $$$आर$ - प्रसिद्ध $$$q \ गुना 1$ वेक्टर।

प्रेक्षित मूल्यों की प्रत्येक जोड़ी के लिए $$$X$ और $$$य$ सामान्य परिस्थितियों में, निम्नलिखित फ़ॉर्म की संभाव्यता घनत्व फ़ंक्शन मौजूद होगी:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ _ \ _ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Yi - \ beta X_i) {[सिग्मा} \ सही) ^ 2}$$

के अधीन है $$$एन$ संयुक्त अवलोकन $$$X$ और $$$य$ नमूने में सभी मूल्यों को देखने की कुल संभावना संभावना घनत्व फ़ंक्शन के व्यक्तिगत मूल्यों के उत्पाद के बराबर है। इस प्रकार, संभावना फ़ंक्शन को निम्नानुसार परिभाषित किया गया है:

$$

$$L (\ बीटा) = \ prod \ limit_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} / बाईं ({फ़्रेक {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2$$

चूंकि उत्पाद की तुलना में योग को अलग करना आसान है, इसलिए संभावना समारोह का लघुगणक आमतौर पर लिया जाता है, इस प्रकार:

$$

$$\ ln L (\ Beta) = \ sum \ limit_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {{}} 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ right)$$

यह उपयोगी रूपांतरण अंतिम परिणाम को प्रभावित नहीं करता है, क्योंकि $$$\ ln L$ एक बढ़ती हुई क्रिया है $$$एल$ । तो फिर मूल्य $$$\ बीटा$ जो अधिकतम हो $$$\ ln L$ भी अधिकतम होगा $$$एल$ ।

के लिए एमएल स्कोर $$$\ बीटा$ प्रतिबंध के साथ प्रतिगमन में () $$$आर \ बीटा = आर$ ) फ़ंक्शन को अधिकतम करके प्राप्त किया जाता है $$$\ ln L (\ beta)$ के अधीन है $$$आर \ बीटा = आर$ । इस अनुमान को खोजने के लिए, हम Lagrange फंक्शन लिखते हैं:

$$

$$\ psi (\ Beta) = \ ln L (\ Beta) - g '(R \ beta - r),$$

के माध्यम से $$$g = \ left (g_1, \ dots, g_q \ right) '$ चिह्नित वेक्टर $$$q$ लग्रि गुणक।

Lagrange गुणक परीक्षण के आँकड़े द्वारा चिह्नित $$$\ eta_ \ m $$ क्षैतिज अक्ष के संबंध में और के माध्यम से स्थिरता के मामले में $$$\ eta_ \ tau$ प्रवृत्ति के सापेक्ष स्थिरता के मामले में, यह अभिव्यक्ति द्वारा निर्धारित किया जाता है

$$

$$\ eta _ {\ _ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limit_ {t = 1} ^ T S_t ^ 2,$$

जहाँ

$$

$$S_t = \ sum \ limit_ {i = 1} ^ t e_i$$

और

$$

$$s ^ 2 (l) = T ^ {- 1} \ sum \ limit_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ sum \ limit_ {1} ^ lw (s, l) \ sum \ limit_ {t = s + 1} ^ T e_t e_ {ts},$$

जहाँ

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}$$

उपरोक्त समीकरणों में $$$S_t$ - आंशिक संतुलन की प्रक्रिया $$$e_t$ अनुमानित समीकरण से; $$$s ^ 2 (l)$ - अवशेषों के दीर्घकालिक फैलाव का आकलन $$$e_t$ ; और $$$w (s, l)$ - तथाकथित बार्टलेट स्पेक्ट्रल विंडो, जहां $$$ल$ - अंतराल ट्रंकेशन पैरामीटर।

इस एप्लिकेशन में, वर्णक्रमीय विंडो का उपयोग एक निश्चित अंतराल (खिड़की) के लिए त्रुटियों की वर्णक्रमीय घनत्व का अनुमान लगाने के लिए किया जाता है, जो श्रृंखला की पूरी श्रृंखला के साथ चलती है। अंतराल के बाहर डेटा को अनदेखा किया जाता है, क्योंकि विंडो फ़ंक्शन कुछ चयनित अंतराल (विंडो) के बाहर शून्य के बराबर एक फ़ंक्शन है।

भिन्नता का अनुमान $$$s ^ 2 (l)$ पैरामीटर पर निर्भर करता है $$$ल$ और कब से $$$ल$ बढ़ जाती है और 0 से अधिक, स्कोर $$$s ^ 2 (l)$ अवशिष्टों में संभव स्वत :संबंध को ध्यान में रखना शुरू करता है $$$e_t$ ।

अंत में, लग्र गुणक परीक्षण के आँकड़े $$$\ eta_ \ m $$ या $$$\ eta_ \ tau$ महत्वपूर्ण मूल्यों के साथ तुलना करता है। यदि लैगरेंज गुणक परीक्षण के आंकड़े संबंधित महत्वपूर्ण मूल्य से अधिक है, तो अशक्त परिकल्पना $$$H_0$ (स्थिर समय श्रृंखला) एक वैकल्पिक परिकल्पना के पक्ष में भटकती है $$$H_1$ (गैर-स्थिर समय श्रृंखला)। अन्यथा, हम अशक्त परिकल्पना को अस्वीकार नहीं कर सकते $$$H_0$ एक समय श्रृंखला की स्टेशनरी के बारे में।

महत्वपूर्ण मूल्य स्पर्शोन्मुख हैं और इसलिए, बड़े नमूना आकारों के लिए सबसे उपयुक्त हैं। हालांकि, व्यवहार में वे एक छोटे नमूने के लिए भी उपयोग किए जाते हैं। इसके अलावा, महत्वपूर्ण मान पैरामीटर से स्वतंत्र हैं $$$ल$ । हालांकि, लैग्रेग मल्टीप्लायर टेस्ट के आंकड़े पैरामीटर पर निर्भर करेंगे $$$ल$ । KPSS परीक्षण के लेखक उपयुक्त पैरामीटर चुनने के लिए कोई सामान्य एल्गोरिथ्म प्रदान नहीं करते हैं। $$$ल$ । परीक्षण आमतौर पर के लिए किया जाता है $$$ल$ 0 से 8 की सीमा में।

वृद्धि के साथ $$$ल$ हम अशक्त परिकल्पना को अस्वीकार करने की संभावना कम है $$$H_0$ स्थिरता के बारे में, जो आंशिक रूप से परीक्षण की शक्ति में कमी की ओर जाता है और मिश्रित परिणाम दे सकता है। हालांकि, सामान्य तौर पर, हम यह कह सकते हैं कि यदि अशक्त परिकल्पना $$$H_0$ छोटे मूल्यों पर भी समय श्रृंखला की स्थिरता को अस्वीकार नहीं किया जाता है $$$ल$ (0, 1 या 2), हम यह निष्कर्ष निकालते हैं कि सत्यापित समय श्रृंखला स्थिर है।

परीक्षा परिणाम तुलना

समरूपता की संभावना का आकलन करने के लिए निम्नलिखित पद्धति विकसित की गई थी।

1. सभी समय श्रृंखला 0.05 के महत्व स्तर पर डिकी-फुलर परीक्षण का उपयोग करके 1 आदेश पूर्णता के लिए जाँच की जाती है। केवल पहले क्रम के पूर्णांक श्रृंखला को नीचे माना जाता है।
2. प्रथम क्रम के पूर्णांक श्रृंखला में प्राप्त धारा 1 में पुनरावृत्ति के बिना संयोजन के जोड़े शामिल हैं।
3. क्लॉज 2 में जोड़े गए शेयरों के जोड़े को एंगल-ग्रेंजर टेस्ट का उपयोग करके संयोग के लिए परीक्षण किया जाता है। नतीजतन, संयोग से जोड़े की पहचान की जाती है।
4. पैराग्राफ 3 में परीक्षण के परिणामस्वरूप प्राप्त प्रतिगमन अवशेषों को KPSS परीक्षण का उपयोग करके स्थिरता के लिए परीक्षण किया जाता है। इस प्रकार, दो परीक्षणों के परिणाम संयुक्त हैं।
5. आइटम 2 से सह-एकीकृत जोड़े में समय श्रृंखला को एंग्ल-ग्रेंजर परीक्षण का उपयोग करके सह-एकीकरण के लिए फिर से बदल दिया गया है और जांच की गई है, अर्थात हम यह जांचते हैं कि क्या समय श्रृंखला के बीच संबंध सममित है।
6. आइटम 4 से सह-एकीकृत जोड़े में समय श्रृंखला परस्पर जुड़ी हुई है और प्रतिगमन से अवशिष्टों को KPSS परीक्षण का उपयोग करते हुए फिर से स्थिरता के लिए जाँच की जाती है, अर्थात हम यह जाँच करेंगे कि क्या समय श्रृंखला के बीच संबंध सममित है।

सभी गणना MATLAB पैकेज का उपयोग करके की जाती हैं। परिणाम नीचे दी गई तालिका में प्रस्तुत किए गए हैं। प्रत्येक परीक्षण के लिए, हमारे पास कई संबंध हैं जो परीक्षण परिणामों के अनुसार सममित हैं (चिह्नित हैं $$$एस$ ); हमारे पास कई रिश्ते हैं जो परीक्षण परिणामों के अनुसार सममित नहीं हैं $$$$S$ ); और हमारे पास एक अनुभवजन्य संभावना है कि परीक्षण परिणामों के अनुसार अनुपात सममित है ( $$$P (S) = \ frac {S} {S + }S}$ )।

मॉस्को एक्सचेंज पर:


न्यूयॉर्क स्टॉक एक्सचेंज में:

बैकस्टेस्ट परिणाम तुलना

आइए एंगल-ग्रेंजर टेस्ट का उपयोग करके चयनित सह-एकीकृत जोड़े और केपीएसएस टेस्ट का उपयोग करके चयनित सह-एकीकृत जोड़े के लिए ऐतिहासिक डेटा पर ट्रेडिंग रणनीति के परिणामों की तुलना करें।

जैसा कि तालिका से देखा जा सकता है, शेयरों की सह-एकीकृत जोड़े की अधिक सटीक पहचान के कारण 9.21% द्वारा एक अलग सह-एकीकृत जोड़ी का व्यापार करते समय औसत वार्षिक उपज में वृद्धि करना संभव था। इस प्रकार, प्रस्तावित पद्धति बाजार-तटस्थ रणनीतियों का उपयोग करके एल्गोरिथम ट्रेडिंग की लाभप्रदता बढ़ा सकती है।

वैकल्पिक व्याख्या

जैसा कि हमने ऊपर देखा, एंगल-ग्रेंजर टेस्ट के परिणाम एक लॉटरी हैं। कुछ के लिए, मेरे विचार अत्यधिक स्पष्ट प्रतीत होंगे, लेकिन मुझे लगता है कि यह विश्वास पर सांख्यिकीय विश्लेषण द्वारा पुष्टि की गई शून्य परिकल्पना को नहीं लेने के लिए बहुत अच्छा अर्थ है।

परिकल्पनाओं के परीक्षण के लिए वैज्ञानिक पद्धति की रूढ़िवादिता यह है कि जब डेटा का विश्लेषण करते हैं तो हम केवल एक वैध निष्कर्ष निकाल सकते हैं: शून्य परिकल्पना को महत्व के चुने हुए स्तर पर खारिज कर दिया जाता है। इसका मतलब यह नहीं है कि विकल्प सही है। $$$H_1$ - हमें बस एक विशिष्ट "इसके विपरीत से साक्ष्य के आधार पर इसकी विश्वसनीयता का अप्रत्यक्ष प्रमाण मिला है।" मामले में जब यह सच है $$$H_0$ शोधकर्ता को एक सतर्क निष्कर्ष निकालने के लिए भी निर्देश दिया जाता है: प्रयोगात्मक परिस्थितियों में प्राप्त आंकड़ों के आधार पर, अशक्त परिकल्पना को अस्वीकार करने के लिए पर्याप्त सबूत मिलना संभव नहीं था।

सितंबर 2018 में मेरे विचारों के साथ, एक लेख में प्रभावशाली लोगों द्वारा "सांख्यिकीय महत्व" की अवधारणा को छोड़ने और अशक्त परिकल्पना के परीक्षण के प्रतिमान को छोड़ने के लिए लिखा गया था।

सबसे महत्वपूर्ण: “सुझाव जैसे कि सीमा स्तर को बदलना $$$पी$ - डिफ़ॉल्ट मान, इस बात पर जोर देने के साथ कि वे शून्य हैं या नहीं, या एक समान या समान समस्याओं से आने वाले साक्ष्य की ताकत का आकलन करने के लिए सार्वभौमिक रूप से स्वीकृत वर्गीकरणों के साथ बाय्स गुणांक के उपयोग पर जोर के साथ अंतराल का उपयोग करें। $$$पी$ 0.05 के स्तर के साथ संकेत ... सांख्यिकीय कीमिया का एक रूप है जो विश्वसनीयता में यादृच्छिकता को बदलने का एक झूठा वादा करता है, तथाकथित "अनिश्चितता का धुलाई" (गेलमैन, 2016), जो डेटा से शुरू होता है और सच्चाई या मिथ्या के बारे में विचित्र निष्कर्ष के साथ समाप्त होता है - द्विआधारी कथन कि "कोई प्रभाव है" या "कोई प्रभाव नहीं" - कुछ हासिल करने के आधार पर $$$पी$ - .

(Carlin, 2016; Gelman, 2016), , ( ) , , .»

निष्कर्ष

हमने देखा कि हालांकि संयोग संबंध की समरूपता संपत्ति सैद्धांतिक रूप से संतुष्ट होनी चाहिए, सैद्धांतिक गणना से प्रयोगात्मक डेटा विचलन। इस विरोधाभास की व्याख्या में से एक डिकी-फुलर परीक्षण की कम शक्ति है।

सह-एकीकृत परिसंपत्ति जोड़े की पहचान करने के लिए एक नई पद्धति के रूप में, केपीएसएस परीक्षण का उपयोग करते हुए स्थिरता के लिए कोण-ग्रेंजर परीक्षण का उपयोग करके प्राप्त प्रतिगमन अवशेषों का परीक्षण करने और इन परीक्षणों के परिणामों को संयोजित करने का प्रस्ताव किया गया था; और एंगल-ग्रेंजर टेस्ट और केपीएसएस टेस्ट के परिणामों को प्रत्यक्ष और रिवर्स रिग्रेशन दोनों के लिए संयोजित करें।

2017 के लिए मॉस्को एक्सचेंज के डेटा पर बैकस्टेस आयोजित किए गए थे। बैकस्टेस्ट के परिणामों के अनुसार, ऊपर प्रस्तावित शेयरों के संयोगित जोड़े की पहचान के लिए कार्यप्रणाली का उपयोग करते समय औसत वार्षिक उपज 22.72% थी। इस प्रकार, एंगल-ग्रेंजर परीक्षण का उपयोग करके सह-एकीकृत स्टॉक जोड़े की पहचान के साथ तुलना में, औसत वार्षिक उपज 9.21% बढ़ाना संभव था।

विरोधाभास की एक वैकल्पिक व्याख्या, विश्वास पर, सांख्यिकीय विश्लेषण द्वारा पुष्टि की गई शून्य परिकल्पना को नहीं लेना है। इस तरह के एक प्रतिमान द्वारा प्रस्तुत अशक्त परिकल्पना परीक्षण प्रतिमान और द्विभाजन हमें बाजार के ज्ञान का एक गलत अर्थ देते हैं।

जब मैंने अभी अपना शोध शुरू किया, तो मुझे ऐसा लगा कि आप बाज़ार ले जा सकते हैं, इसे सांख्यिकीय परीक्षणों के "मांस की चक्की" में डाल सकते हैं और बाहर निकलने पर स्वादिष्ट पंक्तियों को फ़िल्टर कर सकते हैं। दुर्भाग्य से, अब मैं देखता हूं कि सांख्यिकीय बल बल की यह अवधारणा काम नहीं करेगी।

बाजार पर संयोग है या नहीं - मेरे लिए यह सवाल खुला है। इस सिद्धांत के संस्थापकों के लिए मेरे पास अभी भी बड़े प्रश्न हैं। मुझे पश्चिम में कुछ ख़बरें आती थीं और उन वैज्ञानिकों ने एक समय में वित्तीय गणित विकसित किया था जब सोवियत संघ में अर्थमिति को एक भ्रष्ट पूंजीपति माना जाता था। ऐसा लग रहा था कि हम बहुत पीछे हैं, और यूरोप और अमेरिका में कहीं वित्त के देवता बैठे हैं, जो सत्य की पवित्र कब्र को जानते थे।

अब मैं समझता हूं कि यूरोपीय और अमेरिकी वैज्ञानिक हमारे बीच से बहुत अलग नहीं हैं, केवल अंतर खदान के पैमाने में है। हमारे वैज्ञानिक हाथी दांत के महल में बैठे हैं, वे कुछ बकवास लिखते हैं और 500 हजार रूबल की राशि में अनुदान प्राप्त करते हैं। पश्चिम में, लगभग एक ही हाथी दांत के बारे में एक ही वैज्ञानिक बैठे हैं, वे एक ही बकवास के बारे में लिखते हैं और इसके लिए "नॉबेल" और 500 हजार डॉलर की राशि में अनुदान प्राप्त करते हैं। वह सारा अंतर है।

फिलहाल, मेरे शोध के विषय के बारे में मेरा स्पष्ट दृष्टिकोण नहीं है। यह कहना गलत है कि "सभी हेज फंड जोड़ी ट्रेडिंग का उपयोग करते हैं" क्योंकि ज्यादातर हेज फंड दिवालिया हो जाते हैं।

दुर्भाग्य से, आपको हमेशा अपने स्वयं के सिर के साथ सोचना और निर्णय लेना होगा, खासकर जब हम पैसे का जोखिम उठाते हैं।