कोड लिखे बिना विचारों, वास्तुकला और एल्गोरिदम का परीक्षण कैसे करें? उनकी संपत्तियों को कैसे तैयार और सत्यापित किया जाए? मॉडल-चेकर और मॉडल-खोजक क्या हैं? आवश्यकताओं और विनिर्देशों - अतीत का एक अवशेष?
नमस्कार। मेरा नाम वासिल डियाडोव है, अब मैं यांडेक्स में एक प्रोग्रामर के रूप में काम करता हूं, इससे पहले मैंने इंटेल में काम किया था, मैं एएसआईसी / एफपीजीए के लिए वेरिलोग / वीएचडीएल पर आरटीएल कोड (रजिस्टर ट्रांसफर लेवल) विकसित करता था। मैं लंबे समय से सॉफ्टवेयर और हार्डवेयर की विश्वसनीयता, गणित, उपकरण और गारंटीकृत, पूर्वनिर्धारित गुणों के साथ सॉफ्टवेयर और तर्क विकसित करने के तरीकों के विषय का शौकीन रहा हूं।
सॉफ्टवेयर विकास के लिए इंजीनियरिंग दृष्टिकोण के लिए डेवलपर्स और प्रबंधकों का ध्यान आकर्षित करने के लिए डिज़ाइन की गई श्रृंखला में यह मेरा पहला लेख है। हाल ही में, उनके दृष्टिकोण और समर्थन साधनों में क्रांतिकारी बदलाव के बावजूद, उन्हें अवांछनीय रूप से अनदेखा किया गया है।
मैं भंग नहीं करूंगा: लेख का मुख्य कार्य रुचि जगाना है। तो कम से कम लम्बे तर्क और अधिकतम विशिष्टता होगी।

लेख के दो भाग हैं। पहले में मैं वर्णन करूंगा कि इंजीनियरिंग दृष्टिकोण से मेरा क्या अभिप्राय है, दूसरे में मैं एक सरल कार्य के ढांचे में दृष्टिकोण का उपयोग करने का एक उदाहरण दिखाऊंगा (माइक्रोसेस्क आर्किटेक्चर के क्षेत्र के करीब)।
मैं सॉफ्टवेयर विकास से संबंधित मुद्दों पर चर्चा करने के लिए हमेशा खुला हूं, और मुझे पाठकों के साथ बातचीत करने में खुशी होगी (संचार के लिए निर्देशांक मेरी प्रोफाइल में हैं)।
भाग 1. विकास के लिए इंजीनियरिंग दृष्टिकोण
यह क्या है मैं आपको एक पुल बनाने का उदाहरण दिखाऊंगा:
- स्टेज 1 पुल के लिए आवश्यकताओं का संग्रह है: पुल का प्रकार, भार क्षमता, आदि।
- स्टेज 2 - संरचनाओं की आवश्यकताओं और गणना का विनिर्देश (विनिर्देश)।
- स्टेज 3 - इंजीनियरिंग गणना (विनिर्देशों) के आधार पर वास्तविक निर्माण।
बेशक, यह एक सरलीकृत सादृश्य है। आवश्यकताओं और चश्मे को स्पष्ट करने के लिए कोई भी प्रोटोटाइप पुल नहीं बनाता है। पैरामीटर को पुल में नहीं जोड़ा जा सकता है ताकि यह या तो धनुषाकार हो जाए या निलंबित हो जाए। लेकिन कुल मिलाकर, मुझे लगता है कि सादृश्य स्पष्ट है।
सॉफ्टवेयर विकास में, चरण 1 और 2 अक्सर अनुपस्थित या बहुत कमजोर रूप से व्यक्त किए जाते हैं। यदि आवश्यकताओं को तय किया जाता है, तो यह अस्पष्ट, अपूर्ण और अनौपचारिक है। केवल कुछ विस्तार की आवश्यकताएं और स्पष्ट विनिर्देश विकसित करना।
बहुत से लोग सोचते हैं कि यह समय की बर्बादी है, अतीत का एक अवशेष, खासकर अगर विकास के लिए चुस्त दृष्टिकोण चुना जाता है (विशेषकर कम पुनरावृत्तियों के साथ)। और यह एक बड़ी गलती है।
क्यों?
शुरू करने के लिए, हम यह समझेंगे कि ऐसी आवश्यकता और विनिर्देश क्या हैं और उनका महत्वपूर्ण अंतर क्या है, जो कई पेशेवरों के लिए हमेशा स्पष्ट नहीं होता है।
आवश्यकताएं क्या हैं?
संक्षेप में, विषय क्षेत्र के संदर्भ में आवश्यकताएँ उत्पाद गुणों का निर्माण हैं। उदाहरण के लिए, इस तरह: "कार्यक्रम के सभी उदाहरणों को समान रूप से इनपुट अनुरोधों को संसाधित करना चाहिए।"
आवश्यकताएँ कार्यान्वयन के दायरे की शर्तों का उपयोग नहीं करती हैं। जैसे ही शब्द "राज्य सिंक्रनाइज़ेशन", रफ़, पैक्सोस, "लॉगरिदमिक जटिलता समय में" आवश्यकताओं में लीक हो जाते हैं, फिर आवश्यकताएं और विनिर्देश मिश्रण करने लगते हैं।
यह समझना महत्वपूर्ण है और स्पष्ट रूप से एक को दूसरे से अलग करना है।
क्यों?
सॉफ़्टवेयर के उपभोक्ताओं के लिए आवश्यकताएँ स्पष्ट होनी चाहिए, इसलिए, उन्हें उस विषय क्षेत्र से होना चाहिए, जिसके लिए सॉफ़्टवेयर विकसित किया जा रहा है (अक्सर, जो विशेषज्ञ विकास से बहुत दूर हैं, उन्हें आवश्यकताओं को तैयार करने और सॉफ़्टवेयर विकास के लिए कार्य सेट करने में शामिल होना होगा)।
सॉफ्टवेयर गुण जो एक उपभोक्ता देखता है का मूल्यांकन विषय क्षेत्र मैट्रिक्स द्वारा किया जाता है। 1 में सक्षम होने के लिए आवश्यकताओं और विनिर्देशों को अलग करना आवश्यक है) मुख्य उत्पाद मीट्रिक की पहचान करें जिसके द्वारा उपभोक्ता हमारे सॉफ़्टवेयर का मूल्यांकन करेगा, और 2) स्पष्ट रूप से समझें कि उपयोगकर्ता के लिए कौन से उत्पाद गुण महत्वपूर्ण हैं और जो नहीं हैं।
अन्यथा, यह इस तरह से बदल सकता है: डेवलपर्स, समय सीमा को पूरा नहीं करते हुए, महत्वपूर्ण गुणों का त्याग करेंगे और महत्वहीन लोगों के लिए बहुत समय और ध्यान समर्पित करेंगे। इसके अलावा, सॉफ्टवेयर विकास के दृष्टिकोण से जो महत्वपूर्ण लगता है वह उपयोगकर्ता के दृष्टिकोण से महत्वपूर्ण नहीं हो सकता है।
इस तरह की विसंगति का एक क्लासिक उदाहरण उपयोगकर्ता इंटरफ़ेस विकास और लेखों में विभिन्न प्रकार के साहित्य में दिया गया है (उदाहरण के लिए: सिस्टम प्रतिक्रिया समय और उपयोगकर्ता संतुष्टि: ब्राउज़र-आधारित अनुप्रयोगों का एक प्रायोगिक अध्ययन , कंप्यूटर विलंबता: 1977–2017 )। डेवलपर्स आमतौर पर किसी ऑपरेशन के निष्पादन समय को अनुकूलित करने का प्रयास करते हैं, उदाहरण के लिए, डेटाबेस में जानकारी खोजना और उपयोगकर्ता की प्रतिक्रिया समय महत्वपूर्ण है। और यदि खोज धीमी है, लेकिन उपयोगकर्ता लौटाए गए परिणामों को जितनी जल्दी हो सके देखना शुरू कर देता है, तो उसे ऐसा लगता है कि ऐसा सॉफ़्टवेयर उस खोज से बेहतर काम करता है जो जल्दी खोजता है, लेकिन पहले परिणामों को जमा करता है और अंत में उन सभी को प्रदर्शित करता है।
यही कारण है कि ओएस संसाधन योजनाकार सर्वर और डेस्कटॉप ऑपरेटिंग मोड के लिए भिन्न होते हैं। सर्वर मोड के लिए, सिस्टम का अधिकतम थ्रूपुट महत्वपूर्ण है, अर्थात्, कुशलता से सर्वर का उपयोग करने के लिए समय और मेमोरी का अनुकूलन। और उपयोगकर्ता के लिए, सिस्टम की प्रतिक्रिया में देरी महत्वपूर्ण है। जिस तेजी से सिस्टम क्रियाओं का जवाब देता है, उतना ही तेज लगता है, भले ही यह धीमा काम करता हो।
और अंत में, सबसे महत्वपूर्ण कारण:
यदि आवश्यकताओं और चश्मे को मिलाया जाता है, तो इसका मतलब है कि हम उन कार्यों को पूरी तरह से नहीं समझते हैं जिनके लिए हम सॉफ्टवेयर विकसित कर रहे हैं। हम सॉफ्टवेयर विकास के क्षेत्र में विषय क्षेत्र से समस्याओं को तैयार और हल करना शुरू करते हैं। इसलिए, डोमेन लॉजिक लीक हो जाता है और कोड लॉजिक को भ्रमित करता है। परिणाम कसकर युग्मित कोड है जिसे बनाए रखना मुश्किल है।
यह माइकल जैक्सन द्वारा लिखित पुस्तक प्रॉब्लम फ्रेम्स: एनालिसिंग एंड स्ट्रक्चरिंग सॉफ्टवेयर डेवलपमेंट प्रॉब्लम्स में लिखा गया था। मेरी राय में, यह सॉफ्टवेयर डेवलपर्स के लिए सबसे उपयोगी पुस्तकों में से एक है। यह उपयोगकर्ताओं की समस्याओं का विश्लेषण करने के लिए सबसे पहले सिखाता है, जिसे अच्छे सॉफ्टवेयर को हल करना चाहिए। एक सुपरफास्ट प्रोग्राम जो कम सिस्टम संसाधनों का उपभोग करता है लेकिन उपयोगकर्ता के कार्यों को हल नहीं करता है एक बुरा कार्यक्रम है। शांत लेकिन बुरा।
विनिर्देश क्या है?
एक विनिर्देश एक सॉफ्टवेयर डेवलपमेंट क्षेत्र के संदर्भ में सॉफ़्टवेयर गुणों का एक सूत्रीकरण है। यह वह जगह है जहाँ जटिलता, सिंक्रनाइज़ेशन आदि की अवधारणाएँ हैं।
विनिर्देशों को पदानुक्रम से व्यवस्थित किया जा सकता है: सार से विशिष्ट तक, जिस पर आप कोड लिख सकते हैं। यह दृष्टिकोण अक्सर सबसे प्रभावी होता है। सार विनिर्देश आसानी से वास्तुकला को दर्शाते हैं - आप मूल गुणों को देख सकते हैं, वास्तुशिल्प त्रुटियों को ढूंढ सकते हैं, आदि इसलिए, हम सॉफ्टवेयर जीवन चक्र के शुरुआती चरणों में समस्याएं पा सकते हैं और त्रुटियों को ठीक करने की लागत को काफी कम कर सकते हैं।
यह विशेष रूप से सिस्टम घटकों के बीच प्रोटोकॉल और इंटरफेस के लिए विनिर्देशों के लाभ और महत्व को ध्यान देने योग्य है, जो इन स्थितियों से बचने में मदद करेगा:

सामान्य विकास के दृष्टिकोण से क्या अंतर है?
इंजीनियरिंग दृष्टिकोण में, हम विनिर्देशों के अनुसार आवश्यक विशेषताओं के साथ सॉफ्टवेयर पूर्व-डिजाइन करते हैं। हम आवश्यकताओं से आने वाले आवश्यक गुणों के लिए विनिर्देशों की जांच करते हैं।
मैंने एक टैबलेट के रूप में तुलना की (बहुत व्यक्तिपरक):
और क्या यहां जलप्रपात विकास मॉडल के लिए आंदोलन मॉडल नहीं है?
सॉफ्टवेयर इंजीनियरिंग, यहां तक कि औपचारिक चश्मा और सिमुलेशन सहित, चुस्त दृष्टिकोण के साथ अच्छी तरह से चला जाता है।
यह माना जाता है कि विकास के लिए इंजीनियरिंग का दृष्टिकोण तेजी से चलने वाले सॉफ्टवेयर विकास के साथ असंगत है (जैसा कि कई लेखों में बताया गया है, यहां एक उदाहरण है )।
लेकिन ऐसा है नहीं। कई दृष्टिकोणों में इंजीनियरिंग दृष्टिकोण को सफलतापूर्वक लागू किया गया है, जिसमें लघु पुनरावृत्तियों वाली परियोजनाएं शामिल हैं।
पहले, खराब विकसित साधनों और समर्थन साधनों के कारण, इंजीनियरिंग दृष्टिकोण वास्तव में जलप्रपात मॉडल से निकटता से जुड़ा हुआ था।
लेकिन अब सब कुछ नाटकीय रूप से बदल गया है।
मॉडलिंग, सैट / एसएमटी-सॉल्वर्स इत्यादि के क्षेत्र में सफलताओं के लिए धन्यवाद, अब कोड की औद्योगिक मात्राओं को सत्यापित करने के लिए आवश्यक गुणों की उपस्थिति और अनावश्यक लोगों की अनुपस्थिति के लिए सिस्टम राज्यों के विशाल स्थानों की जल्दी से जांच करना संभव है।
मिश्र धातु, TLA + / TLC, Atelier B, PRISM जैसे प्रथम श्रेणी के औद्योगिक उपकरण दिखाई दिए, जिन्होंने अकादमिक / गणितीय से विशिष्टताओं को औपचारिक रूप से जाँचने और जाँचने का कार्य हस्तांतरित किया, जिसमें उच्च योग्यता और भारी प्रयासों की आवश्यकता होती है, जो पुश-बटन कार्य के लिए, अधिकांश प्रोग्रामर के लिए सुलभ है।
विनिर्देशों को अब iteratively और incrementally विकसित किया जा सकता है। मॉडल अच्छी तरह से चलने के लिए, सार से कंक्रीट तक डिज़ाइन किए गए हैं। बड़ी प्रणालियों के सिमुलेशन समय की गणना मिनटों और घंटों में की जाती है।
आवश्यकताएं विशेष रूप से आधुनिक दृष्टिकोण और उपकरणों के साथ, इसे विशेष रूप से निर्दिष्ट करना आसान है।
और आवश्यकताओं, विनिर्देशों, मॉडलों के रीफैक्टरिंग, राइटिंग कोड और उसके रीफैक्टरिंग को परिष्कृत करके आसानी से समानांतर - एक पुनरावृत्ति के भीतर जा सकते हैं।
सामान्य तौर पर, इंजीनियरिंग दृष्टिकोण अब झरना मॉडल के बराबर नहीं है, ये दो स्वतंत्र चीजें हैं।
इंजीनियरिंग दृष्टिकोण आसानी से किसी भी विकास संगठन पद्धति के साथ संयुक्त है।
हिलेल वेन के ब्लॉग से पता चलता है कि औपचारिक विनिर्देशों और मॉडलों के साथ काम करना कितना आसान है। उनके पास 10 मिनट में किसी कार्यक्रम के उपयोगकर्ता इंटरफ़ेस के तर्क को औपचारिक रूप से निर्दिष्ट करने और इसके कुछ गुणों की जांच करने का एक शानदार उदाहरण है ।
मैं विवरणों में नहीं जाऊंगा और पूरे लेख का अनुवाद करूंगा, मैं सिर्फ मिश्र धातु में विनिर्देशन दिखाऊंगा:
यूआई विनिर्देशopen util/ordering[Time]
sig Time {
state: one State
}
abstract sig State {}
abstract sig Login extends State {}
abstract sig Reports extends Login {}
one sig Logout extends State {}
one sig Students, Summary, Standards extends Reports {}
one sig Answers extends Login {}
pred transition[t: Time, start: State, end: State] {
t.state in start
t.next.state in end
}
pred logout[t: Time] { transition[t, Login, Logout] }
pred login[t: Time] { transition[t, Logout, Summary] }
pred students[t: Time] { transition[t, Reports, Students] }
pred summary[t: Time] { transition[t, Reports, Summary] }
pred standards[t: Time] { transition[t, Reports, Standards] }
pred answers[t: Time] { transition[t, Students, Answers] }
pred close_answers[t: Time] { transition[t, Answers, Students] }
fact Trace {
first.state = Summary
all t: Time - last |
logout[t] or
login[t] or
students[t] or
summary[t] or
standards[t] or
answers[t] or
close_answers[t]
}
, . , UI .
:
check {all t: Time | t.state = Answers implies
t.prev.state = Students} for 7
.
, , .
agile.
— .
, , — Alloy, .
, , ( ) .
( ) , .
, .
2. Alloy
Alloy, : , , .
, — , , - .
.
, , .
 ,
, 
 .
.
Alloy : X->Y.
( util/relation):
relation.alsmodule relation
-- :
-- set A - A,
-- one A - A
-- lone A - A
-- some A - A
-- :
-- univ - ,
--
-- iden - {A0, A0},
-- univ
-- iden = {a : univ, b: univ | a=b}
--
-- none -
-- :
-- : and, or, => (), != ( ), not
-- :
-- & -
-- A->B - .
--
-- X<:Y - Y ,
-- X
-- A in B - A B
-- ~A - A
-- A + B -
-- no A - A , A = none
-- ^A - A,
-- B , :
-- A in B,
-- {E0, E1}, {E1, E2} in B => {E0, E2} in B
-- A.B - JOIN, . :
-- {A0, B0} in A, {B0, C0, D0} in B,
-- {A0, C0, D0} in A.B
-- :
-- all X : Y | .... -
-- some X : Y | .... -
-- :
-- pred[a: A, b:B] {...}
-- : pred[a, b] a.pred[b]
--
-- -,
-- method(self : Object, args ...)
pred valid [rel : univ->univ, dom : set univ, cod : set univ] {
rel.univ in dom and rel.univ in cod
}
fun domain [rel : univ->univ] : set (rel.univ) { rel.univ }
fun codomain [rel : univ->univ] : set (univ.rel) { univ.rel }
pred total [rel: univ->univ, dom: set univ] {
all x: dom | some x.rel
}
pred partial [rel: univ->univ, dom: set univ] {
all x: dom | lone x.rel
}
pred functional [rel: univ->univ, dom: set univ] {
all x: dom | one x.rel
}
pred surjective [rel: univ->univ, cod: set univ] {
all x: cod | some rel.x
}
pred injective [rel: univ->univ, cod: set univ] {
all x: cod | lone rel.x
}
pred bijective [rel: univ->univ, cod: set univ] {
all x: cod | one rel.x
}
pred bijection [rel: univ->univ, dom, cod: set univ] {
rel.functional[dom] and rel.bijective[cod]
}
pred reflexive [rel: univ->univ, s: set univ] {
s<:iden in rel
}
pred irreflexive [rel: univ->univ] {no iden & rel}
pred symmetric [rel: univ->univ] {~rel in rel}
pred antisymmetric [rel: univ->univ] {~rel & rel in iden}
pred transitive [rel: univ->univ] {rel.rel in rel}
pred acyclic [rel: univ->univ, s: set univ] {
all x: s | x not in x.^rel
}
pred complete[rel: univ->univ, s: univ] {
all x,y:s | (x!=y => x->y in (rel + ~rel))
}
pred preorder [rel: univ->univ, s: set univ] {
rel.reflexive[s] and rel.transitive
}
pred equality [rel: univ->univ, s: set univ] {
rel.preorder[s] and rel.symmetric
}
pred partial_order [rel: univ->univ, s: set univ] {
rel.preorder[s] and rel.antisymmetric
}
pred total_order [rel: univ->univ, s: set univ] {
rel.partial_order[s] and rel.complete[s]
}
, , Alloy.
.
utils/graph, , , :
graph.alsmodule graph[node]
open relation
--
fun nodes[r: node->node]: set node {
r.domain+ r.codomain
}
-- ,
--
--
pred connected[r: node->node] {
all n1,n2 : r.nodes | n1 in n2.*(r + ~r)
}
--
pred dag [r: node->node] {
r.acyclic[r.nodes]
}
--
-- ,
--
fun roots [r: node->node] : set node {
let ns = r.nodes | -- ns -
ns - ns.^r -- ,
-- -
--
}
--
-- - ,
--
fun leaves [r: node->node] : set node {
let ns = r.nodes | -- ns -
ns - ns.^~r -- ,
-- -
--
}
— , .
:
- (1) — , , ;
- (2) — , , ;
- (3) — , ;
- (4) , — ;
- (5) . . , , , ;
- (6) , — , .
.
, , Alloy:
compgraph.alsmodule compgraph[node]
open graph[node]
open relation
pred valid [edges: node->node,
source : one node, -- 1
drain : one node -- 2
] {
edges.antisymmetric and edges.irreflexive -- 6
graph/roots[edges] = source -- 1 4
graph/leaves[edges] = drain -- 2 4
}
:
open compgraph[node] as cg -- cg -
enum node {n0, n1, n2, n3, n4}
-- ,
run cg/valid -- cg,
-- valid : relation compgraph
:
, ( ).
, .
, .
. . , .
, . :
, , . . ( , ).
, :
- (7) ( ). , , ;
- (8) , . . .
, .
, , , .
(, , ) :
:
compgraph.alsmodule compgraph[node]
open graph[node]
pred active[edges : node->node,
source: node,
n : node
] {
-- n ,
--
n in source.^edges
}
pred safe[edges : node->node,
drain : node,
n : node
] {
-- , drain,
-- n
--
-- n
--
no n.*edges & (leaves[edges] - drain)
-- ,
--
-- ,
-- , drain
drain in n.*edges
}
pred valid [edges: node->node,
source : one node, -- 1
drain : one node -- 2
] {
edges.connected --
-- (
-- ),
-- ,
-- ,
-- connected
edges.dag -- 6 8
source in edges.roots -- 1, 4 9
drain in edges.leaves -- 2, 4 8
all n : edges.roots - source |
not active[edges, source, n] -- 9
all n : edges.nodes | -- 10
active[edges, source, n] => safe[edges, drain, n]
}
.
.
, .
:
- ;
- ;
- ;
- ;
- ;
- .
. . : .
, ? ?
.
, , .
, .
, :
.
, .
:
- -> ;
- -> ;
- -> ;
- -> .
, .
, : , . - , — , / .
, : -> .
, :
, .
, Alloy , . , Alloy .
pred connect[
old_edges : node->node,
new_edges : node->node,
source : one node,
drain : one node,
from : one node,
to : one node
] {
--
from->to not in old_edges
-- from to,
--
from not in to.*old_edges
-- to ,
--
--
to in (old_edges.nodes - source)
-- to
-- ,
-- to
safe[old_edges, drain, to]
-- ,
--
--
new_edges = old_edges + from->to
}
connect .
, connect :
open compgraph[node] as cg
sig node {}
check {
-- r1, r2
all r1, r2 : node->node |
-- source, drain, from, to
all source, drain, from, to : node {
-- r1
-- source/drain /
-- r2 r1
-- connect from->to
(cg/valid[r1, source, drain] and
connect[r1, r2, source, drain, from, to])
-- , r2 + source/drain
--
--
implies cg/valid[r2, source, drain]
-- connect
--
}
} for 8
Executing "Check check$1 for 8"
Sig this/node scope <= 8
Sig this/node in [[node$0], [node$1], [node$2], [node$3],
[node$4], [node$5], [node$6], [node$7]]
Generating facts...
Simplifying the bounds...
Solver=sat4j Bitwidth=4 MaxSeq=7 SkolemDepth=4 Symmetry=20
Generating CNF...
Generating the solution...
8374 vars. 168 primary vars. 22725 clauses. 108ms.
No counterexample found. Assertion may be valid. 26904ms
Alloy . , "168 primary vars" ,  . 30 !
. 30 !
, connect .
, :
pred disconnect[
old_edges : node->node,
new_edges : node->node,
source : one node,
drain : one node,
from : one node,
to : one node
] {
--
from->to in old_edges
-- from
--
safe[new_edges, drain, from]
--
new_edges.connected
--
new_edges = old_edges - from->to
}
:
open compgraph[node] as cg
sig node {}
check {
all r1, r2 : node->node |
all source, drain, from, to : node {
(cg/valid[r1, source, drain] and
disconnect[r1, r2, source, drain, from, to])
implies cg/valid[r2, source, drain]
}
} for 8
! ! :
disconnect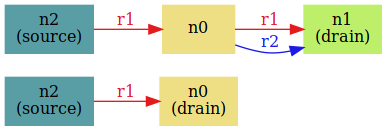
, r1, — disconnect, r2 — . , r1, r2, r2 .
, — from->to, source ( from) .
disconnect:
pred disconnect[
old_edges : node->node,
new_edges : node->node,
source : one node,
drain : one node,
from : one node,
to : one node
] {
from->to in old_edges
( safe[new_edges, drain, from] or
(from not in new_edges.nodes and
from != source))
new_edges.connected
new_edges = old_edges - from >to
}
Executing "Check check$2 for 8"
Sig this/node scope <= 8
Sig this/node in [[node$0], [node$1], [node$2], [node$3], [node$4], [node$5], [node$6], [node$7]]
Generating facts...
Simplifying the bounds...
Solver=sat4j Bitwidth=4 MaxSeq=7 SkolemDepth=4 Symmetry=20
Generating CNF...
Generating the solution...
8505 vars. 168 primary vars. 24808 clauses. 207ms.
No counterexample found. Assertion may be valid. 18369ms.
, .
, ?
, ? ?
:
--
-- ,
-- ,
--
check {
all r1,r2: node->node | all source,drain: node |
some intermediate : seq node->node {
cg/valid[r1, source, drain] and cg/valid[r2, source, drain]
=>
intermediate.first = r1 and
intermediate.last = r2 and
all i : intermediate.inds - intermediate.lastIdx {
let from = intermediate[i] |
let to = intermediate[i+1] |
some n1, n2 : node |
connect[from,to, source, drain, n1, n2]
or
disconnect[from, to, source, drain, n1, n2]
}
}
} for 3
:
Executing "Check check$3"
Sig this/node scope <= 3
Sig this/node in [[node$0], [node$1], [node$2]]
Generating facts...
Simplifying the bounds...
Solver=sat4j Bitwidth=4 MaxSeq=4 SkolemDepth=4 Symmetry=20
Generating CNF...
Generating the solution...
A type error has occured: (see the stacktrace)
Analysis cannot be performed since it requires higher-order
quantification that could not be skolemized.
?
Alloy: .
«some intermediate…», — .
.
( , ) , .
higher-order Alloy, , . , CEGIS — counter-example guided inductive synthesis.
, .
, , , :
check {
all edges, edges1 : node->node |
all source,drain, from, to : node {
(cg/valid[edges, source, drain] and
cg/valid[edges1, source, drain] and
edges1 = edges + from->to and
edges1 != edges)
=>
some n1, n2: node | connect[edges, edges1, source, drain, n1, n2]
}
} for 7
, :
connectExecuting "Check check$3 for 7"
Sig this/node scope <= 7
Sig this/node in [[node$0], [node$1], [node$2], [node$3],
[node$4], [node$5], [node$6]]
Generating facts...
Simplifying the bounds...
Solver=sat4j Bitwidth=4 MaxSeq=7 SkolemDepth=4 Symmetry=20
Generating CNF...
Generating the solution...
6471 vars. 133 primary vars. 16634 clauses. 200ms.
Counterexample found. Assertion is invalid. 116ms.
!
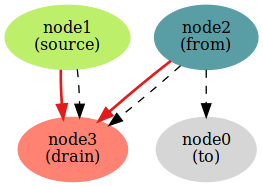
— , — . from->to.
, connect (, , ).
connect:
connectpred connect[
old_edges : node->node,
new_edges : node->node,
source : one node,
drain : one node,
from : one node,
to : one node
] {
from->to not in old_edges
from not in to.*old_edges
to in (old_edges.nodes - source)
--
active[old_edges, source, from] => safe[old_edges, drain, to]
-- to from,
-- , to ,
-- from,
--
new_edges.connected
-- ,
-- :)
new_edges = old_edges + from -> to
}
:
Executing "Check check$3 for 7"
Sig this/node scope <= 7
Sig this/node in [[node$0], [node$1], [node$2], [node$3],
[node$4], [node$5], [node$6]]
Generating facts...
Simplifying the bounds...
Solver=sat4j Bitwidth=4 MaxSeq=7 SkolemDepth=4 Symmetry=20
Generating CNF...
Generating the solution...
6513 vars. 133 primary vars. 16837 clauses. 125ms.
No counterexample found. Assertion may be valid. 291ms.
.
disconnect. , :
diconnectpred disconnect[
old_edges : node->node,
new_edges : node->node,
source : one node,
drain : one node,
from : one node,
to : one node
] {
from->to in old_edges
-- ,
--
active[old_edges, source, from] => safe[new_edges, drain, from]
-- ,
-- , :
-- (from not in new_edges.nodes and
-- from != source)
new_edges.connected
new_edges = old_edges - from->to
}
, , / , .
, , (, source->drain), connect/disconnect .
( , , ).
?
, .
, , , . .
: , ( safe/active .).
.
, .
, — , . .
, .
, .
, , ( ) .
?
Alloy .
.
, , , Python.
, ( ) .
?
Alloy Analyzer, GitHub — .
Alloy?
:
- , , - ;
- , , , assert’ , . .;
- ( );
- , , , . , , .
. Facebook, Google, Microsoft, Amazon .
, , .
agile- , .
, : .
.
.
, , , , (TLA+/TLC, B-method/Atelier B, Promela/SPIN). .
, , , . .
- Michael Jackson Problem Frames: Analysing & Structuring Software Development Problems
( !), . , . - Daniel Jackson Software Abstractions: Logic, Language, and Analysis
model finder Alloy . , . ( join, ). , . - . MODEL CHECKING.
. , , . , .
Alloy
- Pamela Zave. How to Make Chord Correct
Alloy DHT Chord, ( , ), . , .
Alloy, .
- Hillel Wayne
. , . , .
- . . , . . , . . .
, , .
Alloy
- Alloy Analyzer + Higher-Order Alloy
Alloy. - Online Tutorial
, . - Tutorial Materials
.