👐🏻 👨🏼‍🌾 👨🏾‍🎓 सुपर-लॉन्ग रेडियो टेलीस्कोप का गणितीय मॉडल 📈 ⚽️ 🕵🏼

परिचय

1937 में अमेरिकन ग्रोटो रेबर द्वारा निर्मित पहली रेडियो दूरबीनों में से एक। रेडियो टेलीस्कोप एक टिन का दर्पण था जिसमें 9.5 मीटर का व्यास लकड़ी के फ्रेम पर लगाया गया था:

1944 तक, रेबर ने मिल्की वे क्षेत्र में अंतरिक्ष रेडियो तरंगों के वितरण का पहला नक्शा तैयार किया था।

रेडियो एस्ट्रोनॉमी के विकास ने कई खोजों को जन्म दिया: 1946 में, 1951 में तारामंडल साइग्नस से रेडियो उत्सर्जन की खोज की गई थी, 1963 में - एक्सट्रागैलेक्टिक विकिरण, 1963 में, और 1965 में 7.5 सेमी की तरंग दैर्ध्य पर पृष्ठभूमि विकिरण की खोज की गई थी।

1963 में, Arecibo (प्यूर्टो रिको) में एक अद्वितीय 300-मीटर रेडियो टेलीस्कोप बनाया गया था। यह एक गतिहीन कटोरे है जो एक हिलने वाले विकिरण के साथ है, जो इलाके के एक प्राकृतिक झरने में बनाया गया है।

एकल रेडियो दूरबीनों में एक छोटा कोणीय संकल्प होता है, जो सूत्र द्वारा निर्धारित किया जाता है:

$\ Theta = \ frac {\ lambda} {d}$
जहाँ

$\ lambda$ - तरंग दैर्ध्य

ड

$ड$ - रेडियो टेलीस्कोप का व्यास।

जाहिर है, संकल्प को बेहतर बनाने के लिए, एंटीना के व्यास को बढ़ाना आवश्यक है, जो शारीरिक रूप से एक मुश्किल काम है। रेडियो इंटरफेरोमीटर के आगमन के साथ इसे हल करना संभव था।

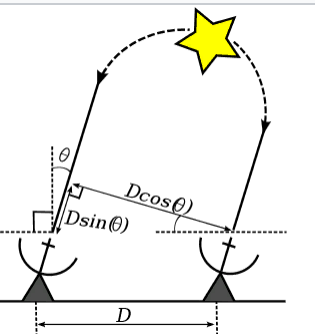
पृथ्वी के पास एक दूर के तारे द्वारा उत्सर्जित विद्युत चुम्बकीय तरंग के सामने को सपाट माना जा सकता है। सबसे सरल इंटरफेरोमीटर के मामले में, दो एंटेना से मिलकर, इन दो एंटेना पर पहुंचने वाली किरणों के मार्ग में अंतर इसके बराबर होगा:

$\ Delta = D \ cdot sin (\ Theta)$ ।
जहां:

$\ Delta$ - किरणों के मार्ग में अंतर;

ड ी

$डी$ - एंटेना के बीच की दूरी;

$\ Theta$ - किरणों के आने की दिशा और उस रेखा के बीच का कोण जिस पर एंटेना स्थित होते हैं।

पर

$\ Theta = 0$ दोनों एंटेना पर आने वाली तरंगों को चरण में अभिव्यक्त किया जाता है। एंटीपेज़ में, पहली बार लहरें दिखाई देंगी:

$\ Delta = \ frac {\ lambda} {2}, \ Theta = arcsin \ frac {\ lambda} {2D}$ ।
जहां:

$\ lambda$ - तरंग दैर्ध्य।

अगले अधिकतम पर होगा

$\ Delta = \ lambda,$ न्यूनतम पर

$\ Delta = \ frac {3 \ lambda} {2}$ आदि एक बहु पंखुड़ी विकिरण पैटर्न (डीएन) प्राप्त की जाती है, जिसमें से मुख्य लोब की चौड़ाई होती है

$\ lambda << D$ के बराबर है

$\ lambda / D$ । मुख्य लोब की चौड़ाई रेडियो इंटरफेरोमीटर के अधिकतम कोणीय संकल्प को निर्धारित करती है, यह लोब की चौड़ाई के बराबर है।

अल्ट्रा-लॉन्ग बेस रेडियो इंटरफेरोमेट्री (वीएलबीआई) एक प्रकार का इंटरफेरोमेट्री है जिसका उपयोग रेडियो एस्ट्रोनॉमी में किया जाता है जिसमें इंटरफेरोमीटर (टेलीस्कोप) के प्राप्त तत्व एक दूसरे से महाद्वीपीय दूरी पर स्थित नहीं होते हैं।

वीएलबीआई विधि आपको कई दूरबीनों द्वारा बनाई गई टिप्पणियों को संयोजित करने की अनुमति देती है, और इस तरह एक दूरबीन का अनुकरण करती है, जिसके आयाम मूल दूरबीनों के बीच अधिकतम दूरी के बराबर होते हैं। VLBI का कोणीय संकल्प सर्वश्रेष्ठ ऑप्टिकल उपकरणों के संकल्प से हजारों गुना अधिक है।

वीएलबीआई नेटवर्क की वर्तमान स्थिति

आज, कई वीएलबीआई नेटवर्क अंतरिक्ष को सुन रहे हैं:

यूरोपीय -EVN (यूरोपीय VLBI नेटवर्क), जिसमें 20 से अधिक रेडियो दूरबीन शामिल हैं;
अमेरिकन –VLBA (वेरी लॉन्ग बेसलाइन एरे), जिसमें 25 मीटर के व्यास के साथ दस टेलीस्कोप शामिल हैं;
जापानी - जेवीएन (जापानी वीएलबीआई नेटवर्क) में जापान में स्थित दस एंटेना शामिल हैं, जिनमें चार एस्ट्रोमेट्रिक एंटेना (वीईए प्रोजेक्ट - वीएलबीआई एक्सप्लोरेशन ऑफ रेडियो एस्ट्रोमेट्री) शामिल हैं;
ऑस्ट्रेलियाई - एलबीए (लॉन्ग बेसलाइन एरे);
चीनी - सीवीएन (चीनी वीएलबीआई नेटवर्क), जिसमें चार एंटेना होते हैं;
दक्षिण कोरियाई - KVN (कोरियाई वीएलबीआई नेटवर्क), जिसमें तीन 21-मीटर रेडियो दूरबीन शामिल हैं;
रूसी एक 32 मीटर के व्यास के साथ रेडियो दूरबीनों के साथ स्थायी रेडियो इंटरफेरोमेट्रिक कॉम्प्लेक्स कज़ार-केवीओ पर आधारित है, जो 1.35 सेमी से 21 सेमी तक तरंगदैर्ध्य रेंज में अत्यधिक संवेदनशील क्रायोरेडियोमीटर से सुसज्जित है। ठिकानों की लंबाई - संश्लेषित "दर्पण" का प्रभावी व्यास - दिशा में लगभग 4400 किमी है। पूर्व-पश्चिम (चित्र देखें)।

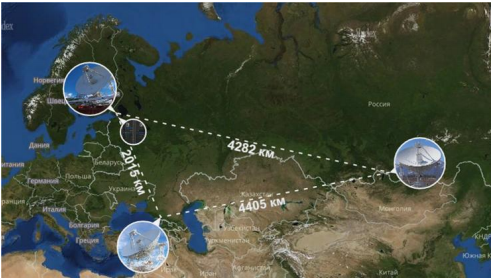
वीएलबीआई कॉम्प्लेक्स "केवज़र-केवीओ" में, हाइड्रोजन मानकों का उपयोग सभी आवृत्ति परिवर्तनों के लिए एक संदर्भ आवृत्ति स्रोत के रूप में किया जाता है, जो 1420.405 मेगाहर्ट्ज की आवृत्ति के साथ हाइड्रोजन परमाणु के ग्राउंड राज्य के हाइपरफाइन संरचना के स्तरों के बीच संक्रमण का उपयोग करते हैं, जो रेडियो खगोल विज्ञान में 21 सेमी से अधिक है।

VLBI के माध्यम से हल किए गए कार्य

खगोल भौतिकी। प्राकृतिक अंतरिक्ष वस्तुओं (क्वासर और अन्य वस्तुओं) की रेडियो छवियां दसवीं और सौवें मास (एक चाप के मिलीसेकंड) के संकल्प के साथ बनाई जा रही हैं।
एस्ट्रोमेट्रिक की पढ़ाई। समन्वय-समय प्रणालियों का निर्माण। अनुसंधान की वस्तुएं बहुत छोटे कोणीय आकार के रेडियो स्रोत हैं, जिनमें क्वासिस्टेलर रेडियो स्रोत और रेडियो आकाशगंगाओं के नाभिक शामिल हैं, जो कि उनकी महान सुदूरता के कारण, सहायक स्थिर वस्तुओं का एक नेटवर्क बनाने के लिए लगभग आदर्श वस्तुएं हैं।
आकाशीय यांत्रिकी और सौर मंडल की गतिशीलता, अंतरिक्ष नेविगेशन पर शोध। ग्रहों की सतहों पर एक बीकन की स्थापना और ग्रहों के स्वचालित स्टेशनों के बीकन को ट्रैक करना, ऐसे मापदंडों का अध्ययन करना संभव बनाता है जैसे कि ग्रह की कक्षीय गति, रोटेशन कुल्हाड़ियों की दिशा और उनके पूर्वग्रह, ग्रह-उपग्रह प्रणाली की गतिशीलता। चंद्रमा के लिए, भौतिक लिब्रेशन का निर्धारण करने और चंद्रमा-पृथ्वी प्रणालियों की गतिशीलता को निर्धारित करने की बहुत महत्वपूर्ण समस्या भी हल हो रही है।

वीएलबीआई का उपयोग कर अंतरिक्ष में नेविगेशन

1971 में चंद्र सतह पर अंतरिक्ष यात्रियों की गतिविधियों की निगरानी करना। वे रोवर चंद्र रोवर की मदद से चले गए। चंद्र मॉड्यूल के सापेक्ष इसकी स्थिति निर्धारित करने की सटीकता 20 सेमी तक पहुंच गई और मुख्य रूप से चंद्रमा के कंपन पर निर्भर करती थी (Libration - आवधिक पेंडुलम-जैसे चंद्रमा के दोलनों में इसके द्रव्यमान के केंद्र के सापेक्ष);
वीनस (VEGA परियोजना) के वातावरण में उड़ने वाले वाहनों से एयरोस्टेट जांच के वितरण और निर्वहन के लिए नेविगेशन समर्थन। शुक्र की दूरी 100 मिलियन किमी से अधिक है, ट्रांसमीटर की शक्ति केवल 1 वाट है। VEGA-1/2 की शुरूआत दिसंबर 1984 में हुई थी। 11 और 15 जून, 1985 को शुक्र के वातावरण में गुब्बारे गिराए गए थे। 46 घंटों तक अवलोकन किया गया था।

सरलीकृत VLBI नेटवर्क का संरचनात्मक आरेख

एक वास्तविक वीएलबीआई नेटवर्क पर आधारित, पायथन सॉफ्टवेयर का उपयोग करते हुए, हम प्रत्येक यूनिट या प्रक्रिया के लिए अलग-अलग मॉडल के रूप में एक सरलीकृत वीएलबीआई प्रणाली का मॉडल तैयार करते हैं। मॉडल का यह सेट बुनियादी प्रक्रियाओं का पालन करने के लिए पर्याप्त होगा। सरलीकृत VLBI नेटवर्क का संरचनात्मक आरेख चित्र में प्रस्तुत किया गया है:

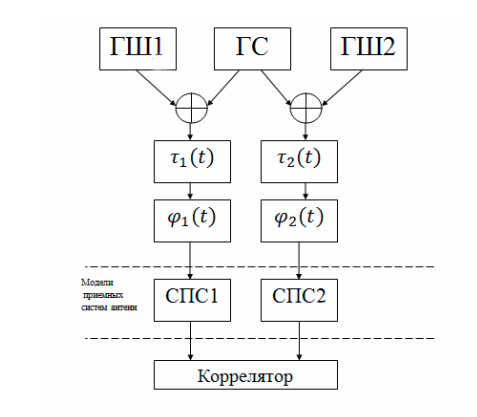
प्रणाली में निम्नलिखित घटक शामिल हैं:

जनरेटर उपयोगी चरण-संशोधित संकेत (एचएस);
शोर जनरेटर (GSh1, GSh2)। सिस्टम में दो रेडियो टेलिस्कोप (एंटेना प्राप्त करने वाले) होते हैं जिनका अपना शोर होता है। इसके अलावा, वायुमंडल के शोर और रेडियो उत्सर्जन के अन्य प्राकृतिक और कृत्रिम स्रोत नहीं हैं;
एक समय देरी इकाई पृथ्वी के रोटेशन के कारण एक रेखीय रूप से बदलती समय देरी का अनुकरण करती है;
डॉपलर प्रभाव का अनुकरण करने वाला चरण शिफ्टर;
सिग्नल रूपांतरण प्रणाली (एसपीएस), आवृत्ति में डाउन सिग्नल को स्थानांतरित करने और एक बैंड-पास फिल्टर के लिए एक स्थानीय थरथरानवाला से मिलकर;
FX correlator।

Correlator सर्किट निम्नलिखित आकृति में दिखाया गया है:

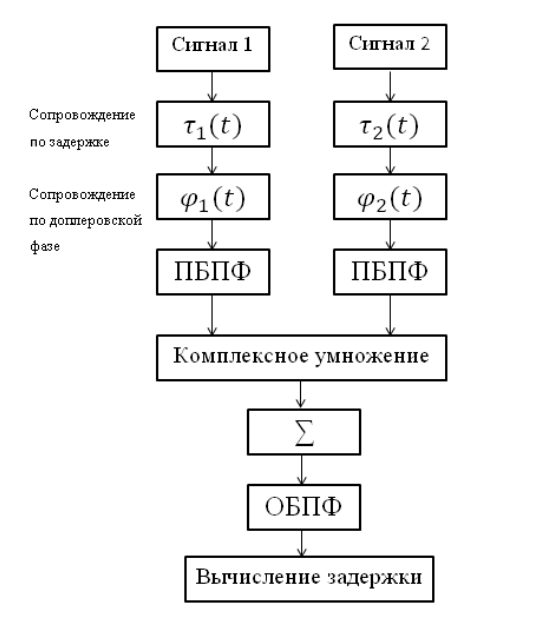
दिए गए सहसंबंधक सर्किट, जिसमें निम्नलिखित ब्लॉक शामिल हैं:

डायरेक्ट फास्ट फूरियर ट्रांसफॉर्म (PBPF) और व्युत्क्रम फूरियर ट्रांसफॉर्म (OBPF);
पहले शुरू की गई देरी के लिए क्षतिपूर्ति;
डॉपलर प्रभाव की भरपाई;
दो स्पेक्ट्रा के जटिल गुणन;
संचित कार्यान्वयन योग।

नेविगेशन सिग्नल मॉडल

वीएलबीआई माप के लिए सबसे सुविधाजनक उपग्रह नेविगेशन सिस्टम, जैसे जीपीएस और ग्लोनास के अंतरिक्ष यान के नेविगेशन सिग्नल हैं। नेविगेशन सिग्नल्स पर कई तरह की आवश्यकताएं लागू होती हैं:

आप अच्छी तरह से pseudorange को परिभाषित करने की अनुमति देते हैं;
नेविगेशन प्रणाली की स्थिति के बारे में जानकारी संचारित करना;
अन्य एनएस के संकेतों से अलग होना;
अन्य रेडियो प्रणालियों में हस्तक्षेप न करें;
प्राप्त करने और संचारित करने के लिए जटिल उपकरणों की आवश्यकता नहीं होती है।

काफी हद तक वे एक द्विआधारी (दो-स्थिति) चरण मॉड्यूलेशन - बीपीएसके (बाइनरी चरण शिफ्ट कुंजी) के साथ एक संकेत से संतुष्ट हैं, जिसे रूसी साहित्य में एफएम -2 के रूप में दर्शाया गया है। यह मॉड्यूलेशन वाहक दोलन के चरण को phase से बदलता है, जिसे निम्न रूप में दर्शाया जा सकता है:

$S (t) = A \ cdot G (t) \ cdot cos (2 \ pi ft),$

जहाँ G (t) मॉड्यूलेटिंग फ़ंक्शन है।

चरण मॉडुलन को लागू करने के लिए, दो जनरेटर का उपयोग किया जा सकता है, जिनमें से प्रत्येक एक ही आवृत्ति बनाता है, लेकिन एक अलग प्रारंभिक चरण के साथ। मॉड्यूलेटिंग फ़ंक्शन आपको सिग्नल के स्पेक्ट्रम का विस्तार करने और सैटेलाइट (रिसीवर और उपग्रह और रिसीवर के बीच की दूरी, सटीक रूप से बिना उपग्रह और घड़ी की घड़ी के बीच के अंतर के लिए सुधार के द्वारा गणना की दूरी) को मापने की अनुमति देता है।

यहां BPSK के मूल सिद्धांतों की व्याख्या करने वाली एक सूची दी गई है:

लिस्टिंग

from scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2; #f  fs = 100; #    t = arange(0,1,1/fs) #    1 / fs #      BPSK p1 = 0; p2 = pi; #     N =12#     #   bit_stream=np.random.random_integers(0, 1, N+1) #   time =[]; digital_signal =[]; PSK =[]; carrier_signal =[]; #  for ii in arange(1,N+1,1): #   if bit_stream [ii] == 0: bit = [0 for w in arange(1,len(t)+1,1)]; else: bit = [1 for w in arange(1,len(t)+1,1)]; digital_signal=hstack([digital_signal,bit ]) #  BPSK if bit_stream [ii] == 0: bit = sin (2*pi*f*t+p1); else: bit = sin (2*pi*f*t+p2); PSK=hstack([PSK,bit]) #   carrier = sin (2*f*t*pi); carrier_signal = hstack([carrier_signal,carrier]) ; time = hstack([time ,t]); t=t+1 suptitle("    (BPSK)") subplot (3,1,1); plot(time,digital_signal,'r'); grid(); subplot (3,1,2); plot (time,PSK); grid(); subplot (3,1,3); plot (time,carrier_signal); grid() show() figure() title("     (BPSK)") n = len(PSK) k = np.arange(n) T = n/fs frq = k/T frq = frq[np.arange(int(n/2))] Y = fft(PSK)/n Y = Y[range(n //2)] / max(Y[range(n // 2)]) plot(frq[75:150], abs(Y)[75:150], 'b')#    grid() #   PSK  scales = scg.periods2scales( arange(1, 40)) ax2 = scg.cws(PSK, scales=scales, figsize=(6.9,2.9)); show()

हमें मिलता है:

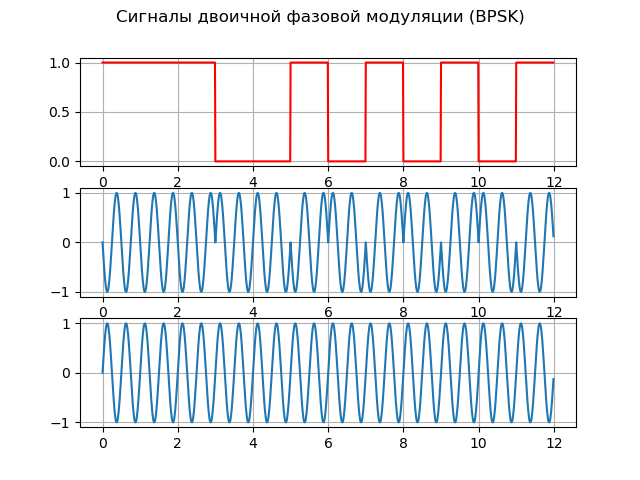
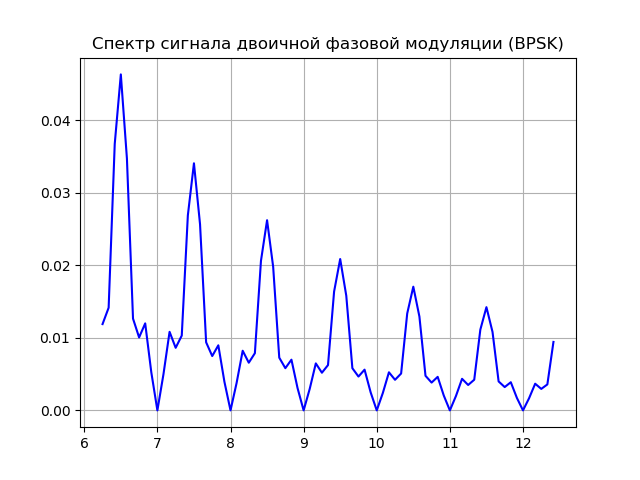
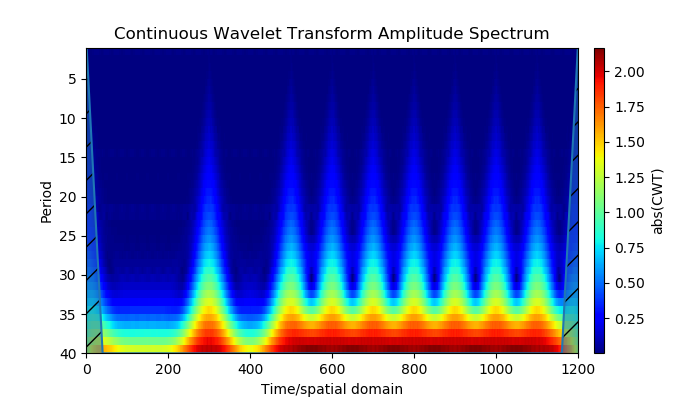
स्रोत मॉडल

उपग्रह या अंतरिक्ष यान से चरण-संग्राहक नेविगेशन हार्मोनिक संकेत का रूप है:

$x = a (2 \ pi f_ {c} t + \ sum s_ {n} cos (2 \ pi f_ {n} t)),$

वाहक आवृत्ति कहां है

$f_ {c} = $ 8.$ गीगा।

संकेत में कई नियंत्रित पैरामीटर हैं: एनटी मॉड्यूलेटिंग दोलन का आयाम

$s_ {n},$ इसकी आवृत्ति

$f_ {c}$ और वाहक दोलन का आयाम a।

एक सहसंबंध समारोह प्राप्त करने के लिए, जिसमें इसकी साइड लॉब्स जितना संभव हो दबाया जाता है और सबसे संकीर्ण सहसंबंध शिखर तक पहुंचा जाता है, हम आवृत्ति मानों को 2, 4, 8 और 16 मेगाहर्ट्ज के मान का उपयोग करके अलग-अलग करेंगे, और index के वेतनवृद्धि में 0 से 2 the तक रेंज में मामूली सूचकांक। अंतिम परिणाम के लिए एक चरण-संशोधित फ़ंक्शन के मापदंडों की खोज के लिए आपको कार्यक्रम की एक सूची देता हूं:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 fc = 8.4e9 #  #   A1 = 2*pi A2 = 0 A3 =2*pi A4 = 4*pi #   fm1 = 2e6 fm2 = 4e6 fm3 = 8e6 fm4 = 16e6 f = 20e6 #     ff = fc - f #   fco = 16e6 #     def korel(x,y): #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('   ') grid(True) plot(t*1e9 - 250, C, 'b',label="    \n    ") legend(loc='best') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =noise1 #   x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) x2 = filt(x1) y2 = filt(y1) X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1) #     ##for A1 in [pi/4,pi/2,pi]: ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)) ## korel(x,y) ##for fm in [ fm2,fm3,fm4]: ## A1=2*pi ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm*t1)) ## y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm*t2)) ## korel(x,y) #     ##for fm2 in [ fm1, fm2,fm3,fm4]: ## A1=2*pi ## A2=2*pi ## fm1=2e6 ## x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)) ## y =cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2)+A2*np.cos(2*pi*fm2*t2)) ## korel(x,y) x = cos(2*pi*fc*t1 + A1*cos(2*pi*fm1*t1)+A2*np.cos(2*pi*fm2*t1)+A3*cos(2*pi*fm3*t1)+A4*cos(2*pi*fm4*t1)) y = cos(2*pi*fc*t2 + A1*cos(2*pi*fm1*t2) +A2*cos(2*pi*fm2*t2) +A3*cos(2*pi*fm3*t2)+A4*cos(2*pi*fm4*t2)) korel(x,y)

हमें मिलता है:

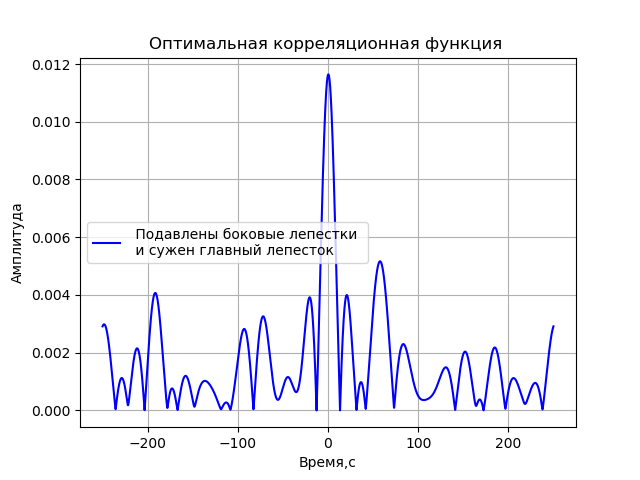
परिणामी फ़ंक्शन का रूप है:

$x = cos (2 \ pi f_ {c} t + 2 \ pi cos (2 \ pi 10 ^ {6} t) +2 \ pi cos (2 \ pi 10 ^ {8} t) +4 \ pi cos (२ \ pi १० ^ {१६} टी))। (१)$

आगे, इस फ़ंक्शन का उपयोग VLBI को अनुकरण करने के लिए किया जाएगा।

अंतरिक्ष और पृथ्वी के वातावरण से संकेत के साथ एक शोर जनरेटर सिमुलेशन हस्तक्षेप का मॉडल प्राप्त हुआ

चरण-संग्राहक नेविगेशन सिग्नल के फ़ंक्शन (1) को रेडियो इंटरफेरोमीटर के दोनों चैनलों पर लागू किया जा सकता है, लेकिन दूसरे चैनल में सिग्नल की देरी और दोनों चैनलों में शोर को ध्यान में रखना आवश्यक है जैसा कि निम्नलिखित सूची में दिखाया गया है:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  delay =1e-7 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9 #  # print(" :") No1 = No2 = 0.5 noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) title("    \n    ") plot(t1,x,label="  ") plot(t2,y,label="  c ") x=noise1;y=noise2 plot(t1,x,label="  ") plot(t2,y,label="  ") legend(loc='best') grid(True) figure() noise1_2 = np.random.uniform(-No1, No1, size = N) #     sko=np.std(noise1_2) mo= np.mean(noise1_2) sko=round(sko,2) mo=round(mo,2) title("  . :%s,:%s"%(sko,mo)) ylabel('   ') xlabel('  ') hist(noise1_2,bins='auto') show()

हमें मिलता है:

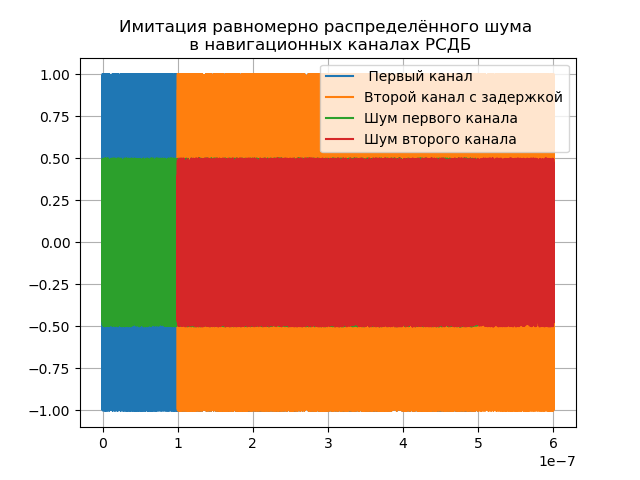
देरी देरी = 1e-7 प्रदर्शन के लिए निर्धारित है, वास्तव में यह आधार पर निर्भर करता है और चार या अधिक इकाइयों तक पहुंच सकता है।

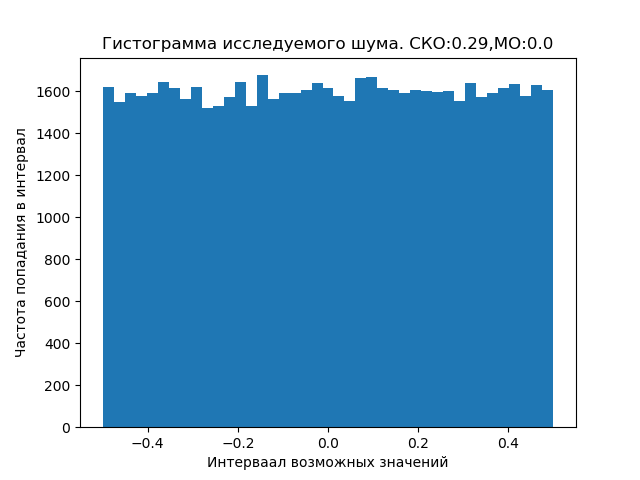
लौकिक और निकट-पृथ्वी दोनों को शोर, दिए गए वर्दी से अलग एक कानून के अनुसार वितरित किया जा सकता है, जिसके लिए विशेष अध्ययन की आवश्यकता होती है।

डॉपलर प्रभाव मॉडलिंग

इस तथ्य के कारण कि पृथ्वी का एक गोल आकार है और अपनी धुरी के चारों ओर घूमता है, अंतरिक्ष से संकेत विभिन्न देरी के साथ एंटेना पर पहुंचते हैं। इस कारण से, समय में संकेतों को स्थानांतरित करना और डॉपलर आवृत्ति को ध्यान में रखना आवश्यक है। हम लगभग इस बात पर विचार करेंगे कि विलंब एक रैखिक कानून के अनुसार भिन्न होता है:

$\ tau _ {x} (a) = a_ {x} + b_ {x} t, (2)$

जहाँ

$a_ {x} = 1..3 \ cdot 10 ^ {- 3}$ एमएस, और

$b_ {x} = 1..3 \ cdot 10 ^ {- 6}$ एमएस। डॉपलर चरण को देरी के व्युत्पन्न के रूप में पाया जाता है:

$f_ {dx} = \ frac {d \ tau (t)} {dt} = b_ {x}, (3)$

प्राप्त संकेत इस तरह दिखना चाहिए:

$\ hat {x} = x (t- \ tau _ {x}) e ^ {j2 \ pi f_ {dx} t},$
जहां x (t) अंतरिक्ष यान से विकिरणित संकेत है।

निम्नलिखित सूची में डॉपलर प्रभाव का प्रदर्शन दिखाया गया है:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real figure() title("    ") ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) plot(t1[0:150],x[0:150],label="      ") plot(t1[0:150],sx[0:150],label="      ") grid(True) legend(loc='best') figure() title("    ") ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) plot(t2[0:150],y[0:150],label="      ") plot(t2[0:150],sy[0:150],label="      ") grid(True) legend(loc='best') show()

हमें मिलता है:

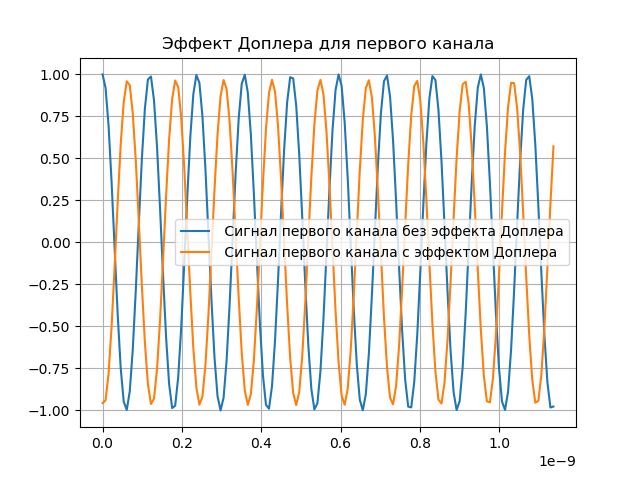
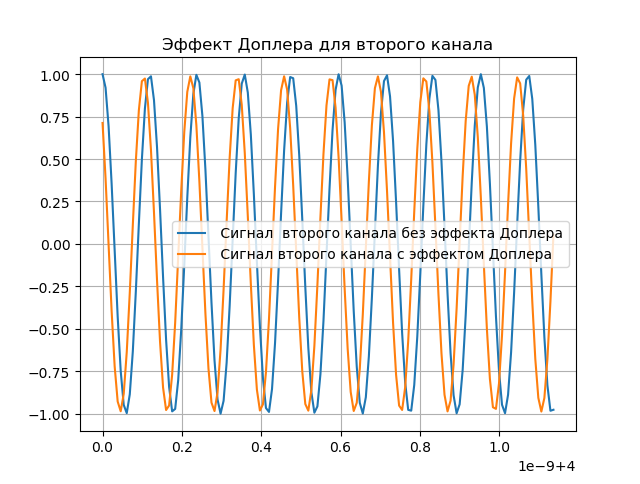
मॉडलिंग डॉपलर मुआवजा

जाहिर है, सिग्नल में किए गए बदलाव की भरपाई होनी चाहिए। इस प्रयोजन के लिए, सिस्टम में देरी और डॉपलर चरण के लिए समर्थन शामिल है। पंजीकरण प्रणाली के माध्यम से सिग्नल पास होने के बाद, देरी शुरू की गई है:

$\ tau _ {ex} (t) = a_ {x} + b_ {ex} t, (4)$

यह विचार करेगा कि देरी की गणना एक निश्चित सटीकता के साथ की जाती है, जैसे कि

$\ _ बाएं | a_ {ex} -a_ {x} \ right | <30$ एनएस

$\ _ बाएं | b_ {ex} -b_ {x} \ right | <10$ ns, अर्थात वह पहले की देरी से थोड़ा अलग होगा। यह स्पष्ट है कि देरी को पहले पेश किए गए की तुलना में विपरीत संकेत के साथ पेश किया गया है।

प्राप्त संकेत इस तरह दिखेगा:

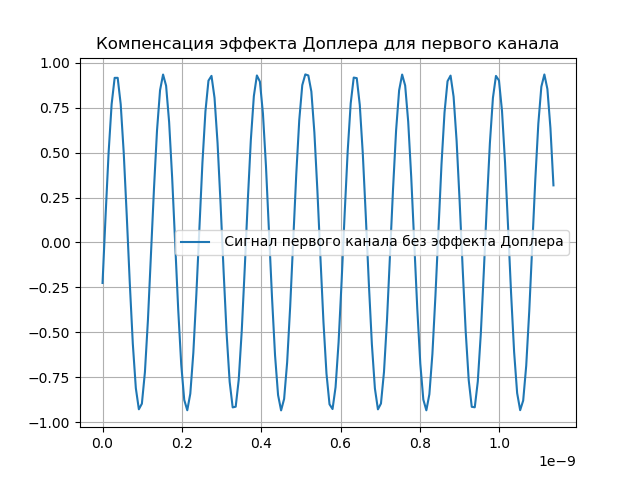
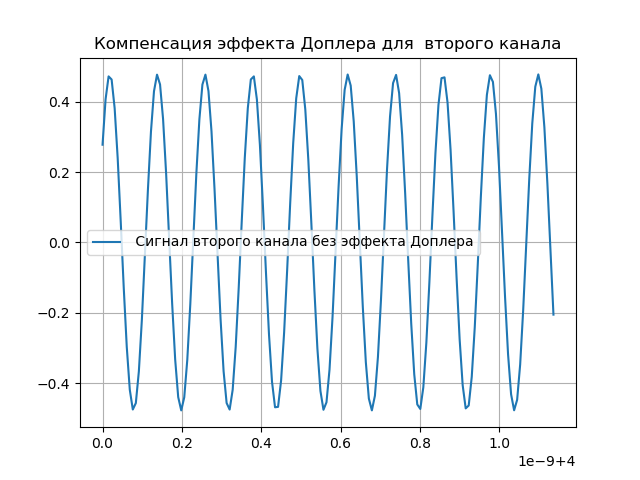
$\ hat {x} = \ tilde {x} (t + \ tau _ {ex}) e ^ {- j2 \ pi f_ {de} t}। (५)$

डॉपलर प्रभाव मुआवजा निम्नलिखित सूची में दिखाया गया है:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s.real ax = 3e-3 bx = 3e-6 taux = ax + bx*t1 x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) sx=phase_shifter1(x, t1, taux, bx ) ay = 2e-3 by = 3e-6 tauy = ay + by*t2 y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) sy= phase_shifter1(y, t2, tauy, by) def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s.real figure() title("     ") aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 tauex = aex + bex*t1 x1 = phase_shifter2(sx, t1, tauex, bex) plot(t1[0:150],x1[0:150],label="      ") grid(True) legend(loc='best') figure() title("     ") aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 tauey = aey + bey*t2 y2 = phase_shifter2(sy, t2, tauey, bey) plot(t2[0:150],y2[0:150],label="      ") grid(True) legend(loc='best') show()

हमें मिलता है:

संकेत विषम सिमुलेशन

सिग्नल पंजीकरण प्रणाली में प्रवेश करने के बाद, एक आवृत्ति रूपांतरण होता है, जिसे हेट्रोडाइनिंग भी कहा जाता है। यह एक गैर-रेखीय परिवर्तन है जिसमें दो अलग-अलग आवृत्तियों के संकेत हैं

$f_ {1}$ और

$f_ {2}$ अंतर आवृत्ति संकेत पर प्रकाश डाला गया है -

$f = \ left | f_ {1} -f_ {2} \ सही |$ स्थानीय थरथरानवाला सिग्नल की आवृत्ति जांच संकेत की आवृत्ति और उस आवृत्ति के बीच अंतर के बराबर होगी जिसे आप हस्तांतरण के माध्यम से प्राप्त करना चाहते हैं। हार्मोनिक दोलनों के एक सहायक जनरेटर का उपयोग करके हेटेरोडिंग किया जाता है - एक स्थानीय थरथरानवाला और एक गैरलाइन तत्व। गणितीय रूप से, हेट्रोडाइनिंग एक घातांक द्वारा एक संकेत का गुणन है:

$x_ {g} = \ hat {x} e ^ {j2 \ pi f_ {g} t}, (6)$
जहाँ

$f_ {g}$ - स्थानीय दोलक संकेत।

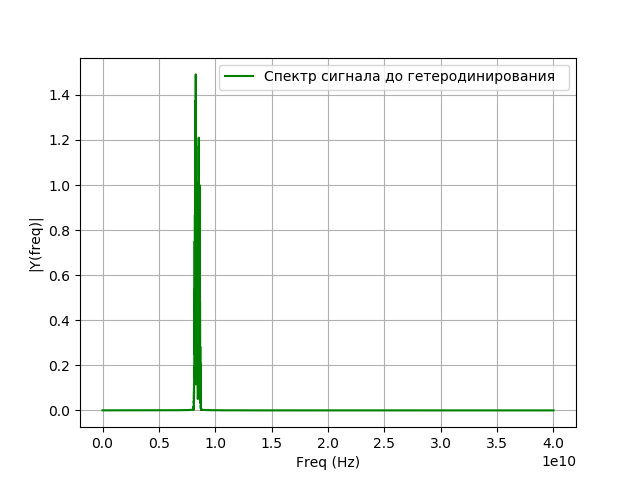
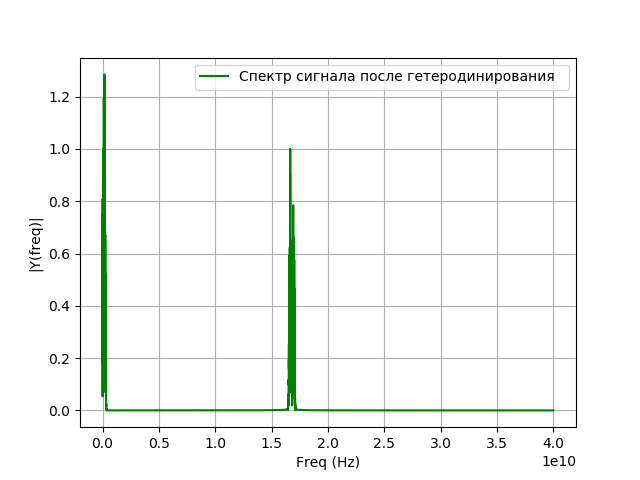
विषमता के लिए कार्यक्रम:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) a=fs;b=0;c=20000;e='g'; st='     ' spectrum_wavelet(x,a,b,c,e,st) show()

हमें मिलता है:

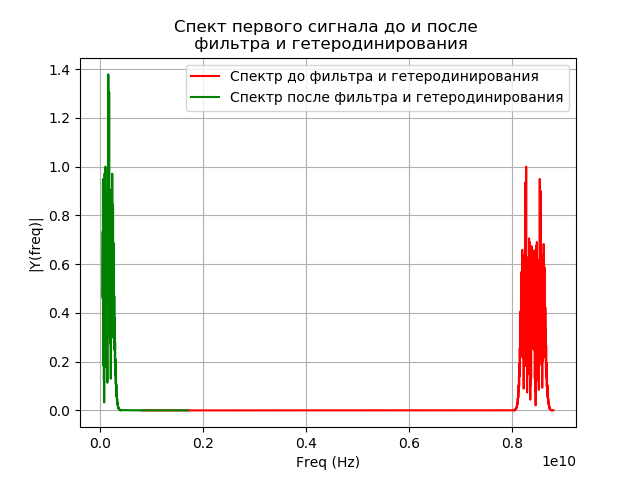
विषमता के बाद मॉडलिंग फ़िल्टरिंग

हेट्रोडाइनिंग के बाद, सिग्नल बैंडपास फिल्टर में प्रवेश करता है। फ़िल्टर Passband (पीपी)

$f_ {पास} = 32$ मेगाहर्ट्ज। फ़िल्टर की आवेग प्रतिक्रिया का संकेत सिग्नल विधि का उपयोग करके विंडो विधि द्वारा किया जाता है। फ़िरविन लाइब्रेरी फ़ंक्शन। फ़िल्टर के आउटपुट पर एक सिग्नल प्राप्त करने के लिए, फ़िल्टर का कनवल्शन और टाइम डोमेन में सिग्नल का प्रदर्शन किया जाता है। हमारे मामले के लिए अभिन्न अभिन्न रूप लेता है:

$\ check {x} (t) = \ int _ {- \ infty} ^ {+ \ infty} x_ {g} (t) h (t- {t} ’) dt, (7)$

जहां h (t) फिल्टर की आवेग प्रतिक्रिया है।

पुष्टिकरण सिग्नल का उपयोग कर पाया जाता है। पुस्तकालय फ़ंक्शन का उपयोग करें। पंजीकृत संकेत, खाते में हेट्रोडाइनिंग और फ़िल्टरिंग को एक सूत्र के रूप में प्रस्तुत किया जाता है

$\ check {x} (t) = (\ hat {x} (t) e ^ {- j2 \ pi f_ {g} t}) * h$

जहां सजा * से संकेत मिलता है।

मॉडलिंग निस्पंदन के लिए कार्यक्रम:

Listinng

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t).real z=heterodyning(x, t1) fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y q=filt(z) a=fs;b=0;c=850;e='g'; st='    ' spectrum_wavelet(q,a,b,c,e,st) show()

हमें मिलता है:

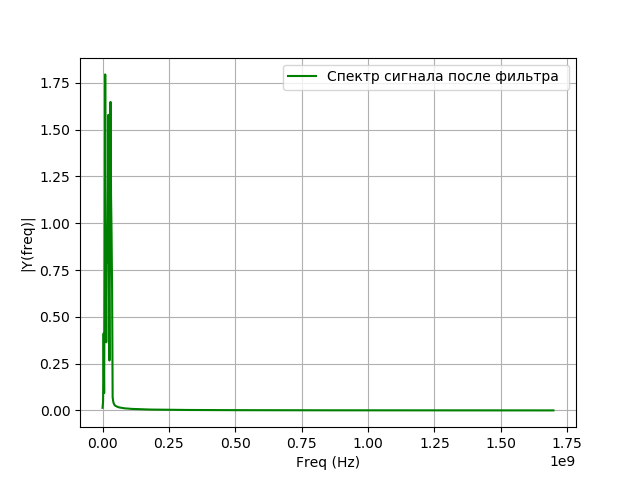
वीएलबीआई के लिए डिजिटल सिग्नल कन्वर्टर्स मुख्य रूप से एक सीमित आवेग प्रतिक्रिया (एफआईआर) के साथ फिल्टर का उपयोग करते हैं, क्योंकि उनके पास अनंत आवेग प्रतिक्रिया (IIR) के साथ फिल्टर की तुलना में कई फायदे हैं:

एफआईआर फिल्टर में आवेग प्रतिक्रिया (आईएम) समरूपता के मामले में एक सख्ती से रैखिक चरण प्रतिक्रिया हो सकती है। इसका मतलब यह है कि इस तरह के फिल्टर का उपयोग करके, चरण विकृतियों से बचा जा सकता है, जो रेडियो इंटरफेरोमेट्री के लिए विशेष रूप से महत्वपूर्ण है। अनंत आवेग प्रतिक्रिया (IIR) वाले फिल्टर में THEM की समरूपता नहीं होती है और इसमें रैखिक चरण प्रतिक्रिया नहीं हो सकती है।
एफआईआर फिल्टर गैर-पुनरावर्ती होते हैं, जिसका अर्थ है कि वे हमेशा स्थिर होते हैं। IIR फ़िल्टर की स्थिरता की हमेशा गारंटी नहीं दी जा सकती है।
फिल्टर को लागू करने के लिए सीमित संख्या में बिट्स का उपयोग करने के व्यावहारिक परिणाम एफआईआर फिल्टर के लिए काफी कम महत्वपूर्ण हैं।

उपरोक्त लिस्टिंग में, एफआई बैंडपास फ़िल्टर के मॉडल को विंडो विधि का उपयोग करके कार्यान्वित किया गया है, फ़िल्टर ऑर्डर का चयन किया गया था ताकि फ़िल्टर की आवृत्ति प्रतिक्रिया का आकार आयताकार के करीब हो। नकली फिल्टर के गुणांक की संख्या n = 100001 है, अर्थात फ़िल्टर का क्रम P = 100000 है।

प्राप्त एफआईआर फिल्टर की आवृत्ति प्रतिक्रिया और चरण प्रतिक्रिया के निर्माण के लिए कार्यक्रम:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**16 #-  t1 =linspace(0, T, N) fs = (N - 1)/T #  fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     n = 100001 #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) #  def AFC(A, n, f, deltf, min, max): plot((fftfreq (n, 1./fs)/1e9), 10*log10(abs(fft(A))), 'k') axvline((f - fco)/1e9, color = 'red', label='  ') axvline((f + fco)/1e9, color = 'red') axhline(-3, color='green', linestyle='dashdot') text(8.381, -3, repr(round(-3, 9))) xlabel(', ') ylabel(' , ') title('') grid(True) axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) grid(True) show() #  def PFC(A, n, f, deltf, min, max): plot(fftfreq(n, 1./fs)/1e9, np.unwrap(np.angle(fft(A))), 'k') axvline((f - fco)/1e9, color='red', label='  ') axvline((f + fco)/1e9, color='red') xlabel(', ') ylabel(',') title('') axis([(f - deltf)/1e9, (f + deltf)/1e9, min, max]) #  grid(True) legend(loc='best') show() AFC(h, n, f, 20e6, -30, 1) PFC(h, n, f, 20e6, -112, 0)

हमें मिलता है:

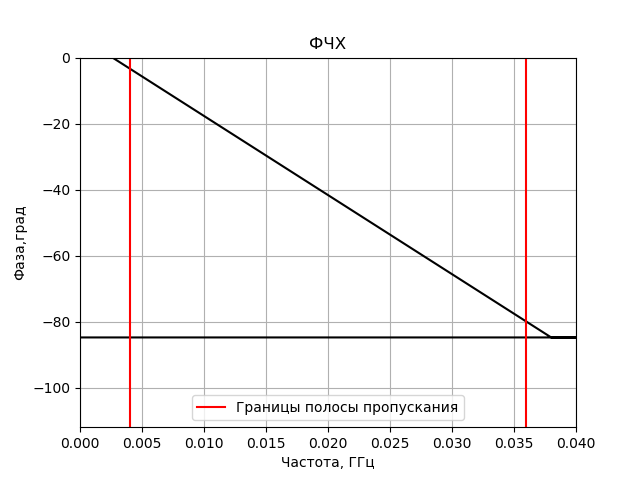
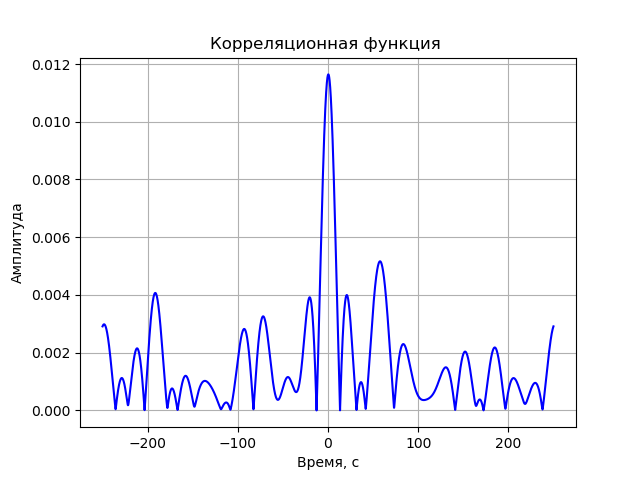
FX सहसंबंधी मॉडल

इसके बाद, प्रत्येक सिग्नल एक तेज फूरियर ट्रांसफॉर्म (FFT) से गुजरता है। FFT को scipy.fftpack से fft लाइब्रेरी फ़ंक्शन का उपयोग करके कार्यान्वित किया जाता है। परिणामी स्पेक्ट्रा जटिल संयुग्मित गुणक हैं:

$S (j \ _ omega) = S_ {1} (j \ omega) * S_ {2} (j \ omega) = (a_ {1} + jb_ {1}) * (a_ {2} -jb_ {2} ) = a_ {1} a_ {2} + b_ {1} b_ {2} + j (b_ {1} a_ {2} -a_ {1} b_ {2})$

अंतिम क्रिया FFT का विलोम है। चूंकि सहसंबंध समारोह का आयाम ब्याज का है, परिणामी संकेत को सूत्र द्वारा परिवर्तित किया जाना चाहिए:

$A = \ sqrt {re ^ {2} + im ^ {2}}$

पंजीकरण प्रणाली की विकृतियों को ध्यान में रखे बिना सहसंबंध समारोह का कार्यक्रम:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7#   N = 2**16 #-  t1 =linspace(0, T, N) delay =4 # t2 = linspace(0 + delay, T + delay, N) fc = 8.4e9#  def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N q=sqrt(z.real**2 + z.imag**2) c1=q[int(N/2):N] c2=q[0:int(N/2)] C = concatenate((c1, c2)) xlabel(',') ylabel('') title('  ') grid(True) plot(t1*1e9 - 250, C, 'b') show() x= cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) corr(x, y)

हमें मिलता है:

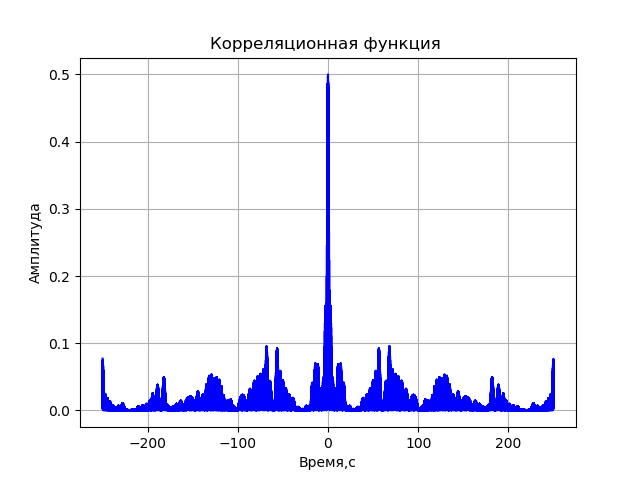
VLBI के कंप्यूटर मॉडल की पूरी सूची:

लिस्टिंग

 # coding: utf-8 from pylab import* from scipy import signal from scipy import * T = 5e-7 #   N = 2**18 #-  delay =4 # t1 =linspace(0, T, N) t2 = linspace(0 + delay, T + delay, N) fs = (N - 1)/T #  ax = 1e-3 bx = 2e-6 ay = 2e-3 by = 3e-6 aex = 1e-3 + 30e-9 bex = 2e-6 + 10e-12 aey = 2e-3 + 30e-9 bey = 3e-6 + 10e-12 taux = ax + bx*t1 tauy = ay + by*t2 tauex = aex + bex*t1 tauey = aey + bey*t2 #  # print(" :") No1 = No2 = 0 #    # print(" :") fc = 8.4e9 #  f = 20e6 #     ff = fc - f #   fco = 16e6 #     #  def phase_shifter1(x, t, tau, b): L = linspace(0, N, N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s = ((ifft(fft(x)*exp(-1j*2*pi*tau*fexp))).real)*exp(1j*2*pi*b*fc*t) return s #   def phase_shifter2(x, t, tau, b): L = linspace(0,N,N) fexp = ifftshift((L) - ceil((N - 1)/2))/T s =((ifft(fft(x)*exp(1j*2*pi*tau*fexp))).real)*exp(-1j*2*pi*b*fc*t) return s # def heterodyning(x, t): return x*exp(-1j*2*pi*ff*t) # def filt(S): p = signal.convolve(S,h) y = p[int((n - 1)/2) : int(N+(n - 1)/2)] return y def spectrum_wavelet(y,a,b,c,e,st):#   n = len(y)#   k = arange(n) T = n / a frq = k / T #    frq = frq[np.arange(int(n/2))] #    Y = fft(y)/ n # FFT    Y = Y[arange(int(n/2))]/max(Y[arange(int(n/2))]) plot(frq[b:c],abs(Y)[b:c],e,label=st) #   xlabel('Freq (Hz)') ylabel('|Y(freq)|') legend(loc='best') grid(True) def corr(y1, y2): Y1 = fft(y1) Y2 = fft(y2) # Z = Y1*Y2.conjugate() # z = ifft(Z)/N return sqrt(z.real**2 + z.imag**2) #   def graf(c, t): c1=c[int(N/2):N] c2=c[0:int(N/2)] C = concatenate((c1, c2)) xlabel(', ') ylabel('') title('  ') grid(True) plot(t*1e9 - 250, C, 'b') show() noise1 = random.uniform(-No1, No1, size = N) #   noise2 =random.uniform(-No1, No1, size = N) #   def signal_0(): x = cos(2*pi*fc*t1 + 2*pi*cos(2*pi*2*10**6*t1)+2*pi*cos(2*pi*8*10**6*t1)+4*pi*cos(2*pi*16*10**6*t1)) y = cos(2*pi*fc*t2 + 2*pi*cos(2*pi*2*10**6*t2)+2*pi*cos(2*pi*8*10**6*t2)+4*pi*cos(2*pi*16*10**6*t2)) return x,y title(" +  +   ") x,y= signal_0() x1 = heterodyning(phase_shifter1(x + noise1, t1, taux, bx), t1) plot(x1.real,label="  ") y1 = heterodyning(phase_shifter1(y + noise2, t2, tauy, by), t2) plot(y1.real,label=" ") grid(True) legend(loc='best') show() n = 100001 #  #  h = signal.firwin(n, cutoff = [((f - fco) / (fs * 0.5)), ((f + fco) / (fs *0.5))], pass_zero = False) title("- -    ") x2 = filt(x1) plot(x2.real,label="  ") y2 = filt(y1) plot(y2.real,label="  ") grid(True) legend(loc='best') show() plt.title("      \n   ") a=fs;b=400;c=4400;e='r' st="    " spectrum_wavelet(x,a,b,c,e,st) a=fs;b=20;c=850;e='g' st="    " spectrum_wavelet(x1,a,b,c,e,st) show() X2 = phase_shifter2(x2, t1, tauex, bex) Y2 = phase_shifter2(y2, t2, tauey, bey) Corr = corr(X2, Y2) graf(Corr, t1)

हमें मिलता है:

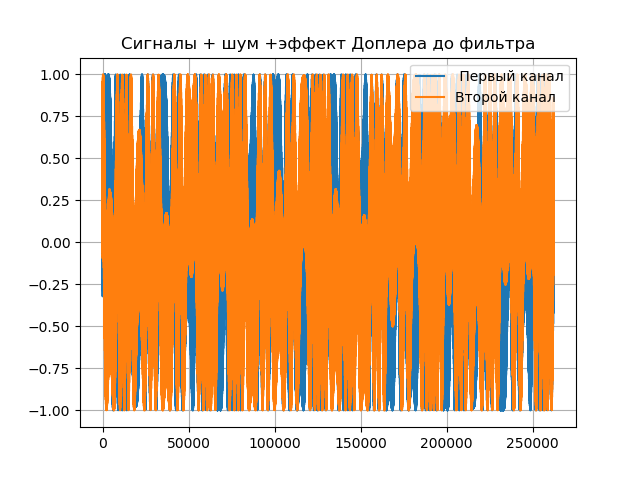
निष्कर्ष

रेडियो खगोल विज्ञान के विकास का एक संक्षिप्त इतिहास दिया गया है।
वीएलबीआई नेटवर्क की वर्तमान स्थिति का विश्लेषण किया जाता है।
वीएलबीआई नेटवर्क के माध्यम से हल की गई समस्याओं पर विचार किया जाता है।
पायथन टूल्स ने बाइनरी (दो-स्थिति) चरण मॉड्यूलेशन - बीपीएसके (बाइनरी चरण शिफ्ट कुंजी) के साथ नेविगेशन सिग्नल का एक मॉडल बनाया। मॉडल चरण मॉडुलन के तरंग विश्लेषण का उपयोग करता है।
सिग्नल स्रोतों का एक मॉडल प्राप्त किया गया है, जो किसी को मॉड्यूलेशन मापदंडों को निर्धारित करने की अनुमति देता है जो साइड लॉब्स को दबाने के लिए मानदंड और केंद्रीय पालि के अधिकतम आयाम के अनुसार इष्टतम सहसंबंध समारोह प्रदान करता है।
एक सरलीकृत वीएलबीआई नेटवर्क का एक मॉडल प्राप्त होता है, जो शोर और डॉपलर प्रभाव को ध्यान में रखता है। एक परिमित आवेग प्रतिक्रिया के साथ एक फिल्टर का उपयोग करके फ़िल्टर करने की विशेषताएं मानी जाती हैं।
सिद्धांत के एक संक्षिप्त सारांश के बाद, सभी मॉडल प्रदर्शन कार्यक्रमों से सुसज्जित हैं जो आपको मॉडल मापदंडों के प्रभाव को ट्रैक करने की अनुमति देते हैं।

सुपर-लॉन्ग रेडियो टेलीस्कोप का गणितीय मॉडल

परिचय

वीएलबीआई नेटवर्क की वर्तमान स्थिति

VLBI के माध्यम से हल किए गए कार्य

वीएलबीआई का उपयोग कर अंतरिक्ष में नेविगेशन

सरलीकृत VLBI नेटवर्क का संरचनात्मक आरेख

नेविगेशन सिग्नल मॉडल

स्रोत मॉडल

अंतरिक्ष और पृथ्वी के वातावरण से संकेत के साथ एक शोर जनरेटर सिमुलेशन हस्तक्षेप का मॉडल प्राप्त हुआ

डॉपलर प्रभाव मॉडलिंग

मॉडलिंग डॉपलर मुआवजा

संकेत विषम सिमुलेशन

विषमता के बाद मॉडलिंग फ़िल्टरिंग

FX सहसंबंधी मॉडल

VLBI के कंप्यूटर मॉडल की पूरी सूची:

निष्कर्ष

More articles: