एलेक्सी सवेटेव: इंटरनेट और सामाजिक नेटवर्क के मॉडल

"अर्थव्यवस्था के अस्तित्व का एकमात्र कारण गणितज्ञों को नए कारनामों के लिए प्रेरित करना है।"



2013 में, एलेक्सी सवेटेव ने सामाजिक नेटवर्क और इंटरनेट के मॉडल पर कई व्याख्यान दिए। मैंने इस विषय को बहुत उत्सुक और अवांछनीय रूप से भुला दिया। आइए मुद्दे को समझने की कोशिश करें। मुझे यह जानने में भी दिलचस्पी है कि इस स्थिति के बाद से स्थिति कैसे बदल गई है और इस क्षेत्र में क्या उपयोगी प्रकाशन हैं।

इंटरनेट पर और सामाजिक नेटवर्क के जीव विज्ञान में, वे गुणों का प्रदर्शन करते हैं जो व्यक्तिगत रूप से मॉडल द्वारा वर्णित हैं, लेकिन सभी एक साथ - वे किसी भी गणित को भ्रमित करते हैं। सवेटेव का दावा है कि "जो इससे निपटता है उसे नोबेल पुरस्कार मिलेगा।" भविष्य नेटवर्क के साथ काम करने की क्षमता पर निर्भर करेगा।

निम्नलिखित तीन व्याख्यान वीडियो का संकलित निचोड़ है, वीडियो स्वयं अंत में है। (पोस्ट व्याख्याता उद्धरण के साथ स्लाइड के एक सेट की तरह लग रहा है, एक एकल और चिकना पाठ में सब कुछ बांधने के लिए, मेरे पास रूसी भाषा और गणित के लिए कौशल की कमी है, लेकिन विषय बहुत महत्वपूर्ण है, इसलिए मैं इसे प्रकाशित करना चाहता हूं।)

सामाजिक नेटवर्क में निम्न शामिल हैं:

• एजेंटों
• एजेंटों के बीच संचार

कनेक्शन दो-तरफ़ा (मित्र, सह-लेखक) हो सकते हैं, और एक तरफ़ा (ग्राहक) हो सकते हैं। सामाजिक हमेशा अस्तित्व में था, लेकिन मैक्रो स्तर पर उनका अध्ययन करना केवल ऑनलाइन नेटवर्क के आगमन के साथ संभव हो गया। पिछले 10 वर्षों में मानवता ने क्वांटम छलांग लगाई है। इसने अपने आप को संपूर्ण रूप में जांचना सीखा। यह डिजीटल हो सकता है। अपने बारे में जानकारी जुटाएं।

जब "बॉन्ड स्ट्रेंथ" के गुणांकों को इंगित किया जाता है तो भारित ग्राफ़ के मॉडल का निर्माण करना उचित होगा। लेकिन चंद्रमा के रूप में हमारे लिए।

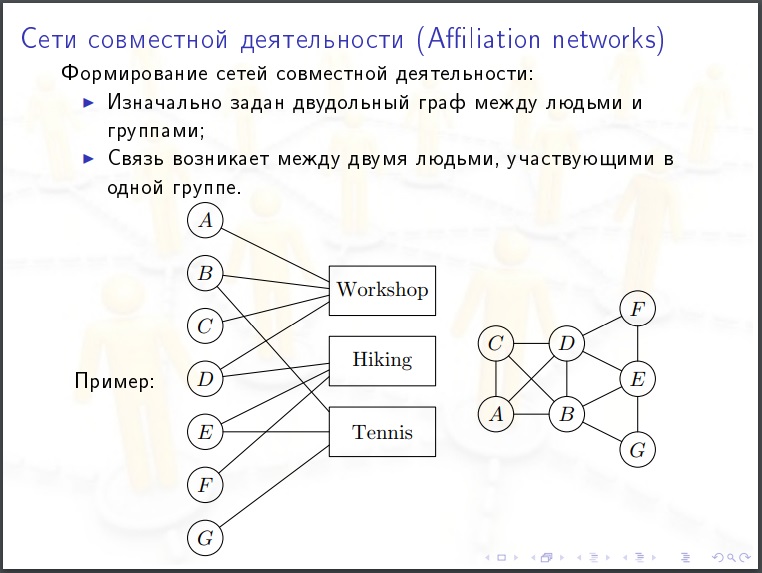
गैलरी

यह चित्रों को देखने के लिए उपयोगी है। चित्र को देखने के बाद आप जिस परिकल्पना को सामने रख सकते हैं वह स्पष्ट रूप से बेतुका हो सकता है।

सामाजिक नेटवर्क का अध्ययन करने के लिए कौन उपयोगी है

अर्थशास्त्र: एक धारणा है कि अर्थव्यवस्था में सूक्ष्म और स्थूल स्तर एक "नेटवर्क" के माध्यम से जुड़े हुए हैं
राजनीति विज्ञान: एक धारणा है कि शासन रहेगा या बदल जाएगा, इस पर निर्भर करता है कि किसके पास अधिक शक्तिशाली नेटवर्क विशेषज्ञ होंगे।



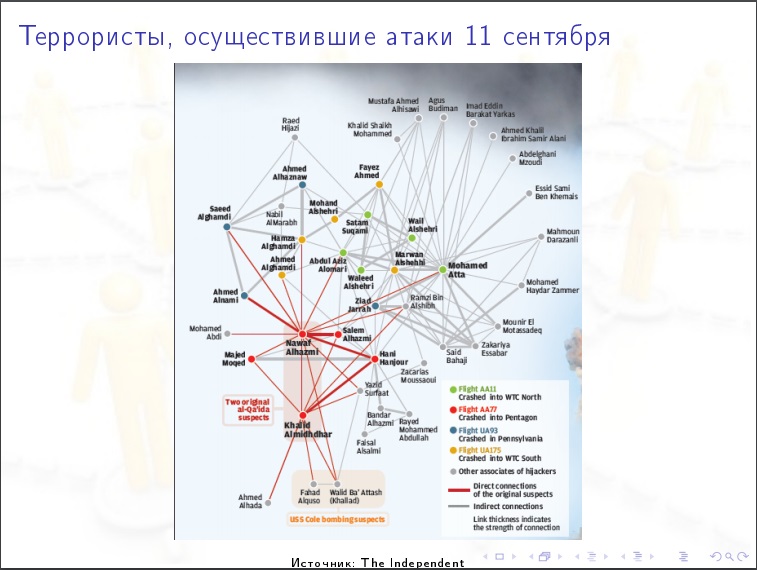सोशल मीडिया एनालिटिक्स उदाहरण।

सामाजिक नेटवर्क की संख्यात्मक विशेषताएं

• दूरी
• व्यास
• वर्टेक्स डिग्री
• वर्टेक्स डिग्री वितरण
• नोड केंद्रीयता के उपाय
• केंद्रीय वितरण
• क्लस्टरिंग गुणांक
• वर्गीकरण गुणांक

दूरी - एक शीर्ष से दूसरे तक जाने के लिए आपको कितने किनारों की आवश्यकता होती है।

व्यास ग्राफ में अधिकतम दूरी है।

एक शीर्ष की डिग्री शीर्ष पर किनारों की संख्या है।

सिक्स हैंडशेक का सिद्धांत

किसी भी सामाजिक ग्राफ में बहुत कम औसत व्यास ( छह हैंडशेक का सिद्धांत ) है। इसके अलावा, वहाँ एक बहुत घने कोर है। मैं अपने राष्ट्रपति के माध्यम से कुछ अफ्रीकी लोगों से "परिचित" हूं, जिन्होंने अफ्रीकी राष्ट्रपति से हाथ मिलाया।







स्थानीय क्लस्टरिंग गुणांक । हम एक व्यक्ति के सभी पड़ोसियों को देखते हैं, "के" टुकड़े। अधिकतम पसलियां - k (k-1) / 2। हम किनारों की वास्तविक संख्या को देखते हैं और इसे अधिकतम से विभाजित करते हैं।

वैश्विक क्लस्टरिंग कारक । "चेकमार्क" की तुलना में कितने "त्रिकोण" हैं।





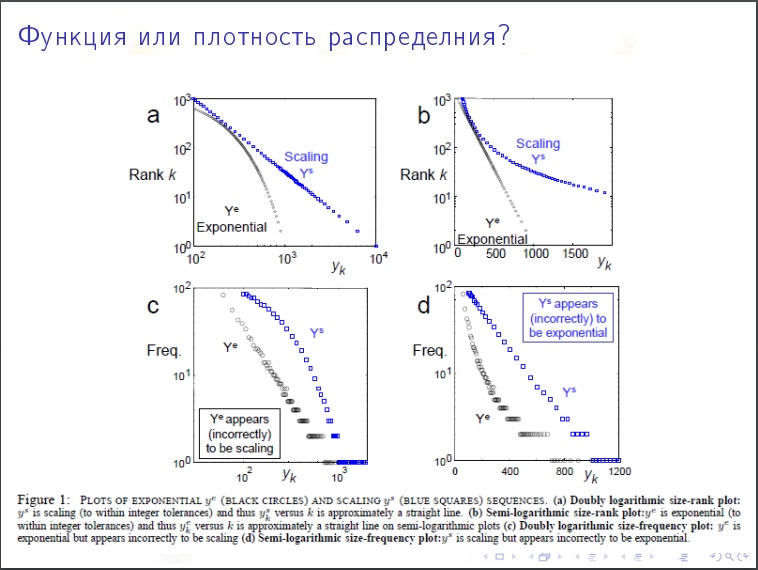
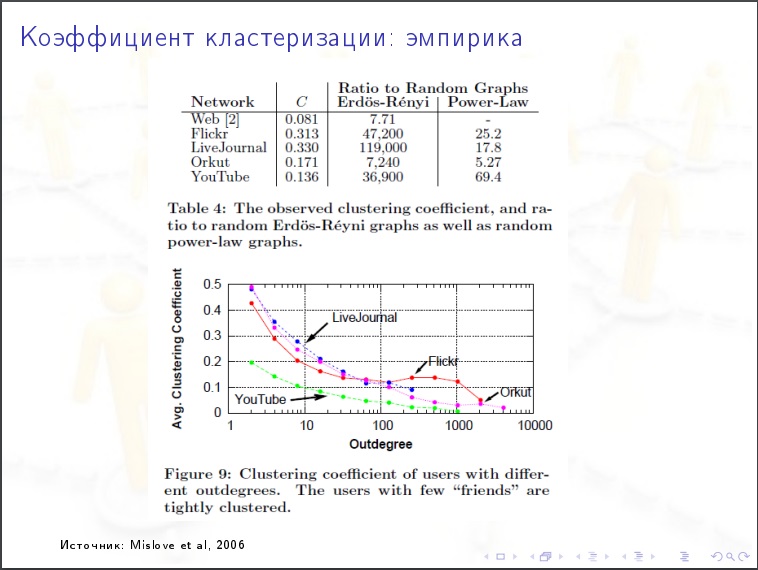वर्टेक्स का डिग्री वितरण । कितने% कोने में डिग्री 1000 से कम है? वितरण की प्रकृति घातीय या घातीय है? यह पता चला है कि इंटरनेट में एक शांत प्रकृति है।

गुणांक "2" है। वे कोने जिनकी डिग्री "x" है वह N / x ^{2 होगा} । हम जाँचते हैं कि LJ में एक अरब उपयोगकर्ता, हजार-हजार को एक हजार से हजार वर्ग में विभाजित किया जाना चाहिए। एक हज़ार हज़ार।

यह बहुत धीरे-धीरे घटने वाली चीज है।













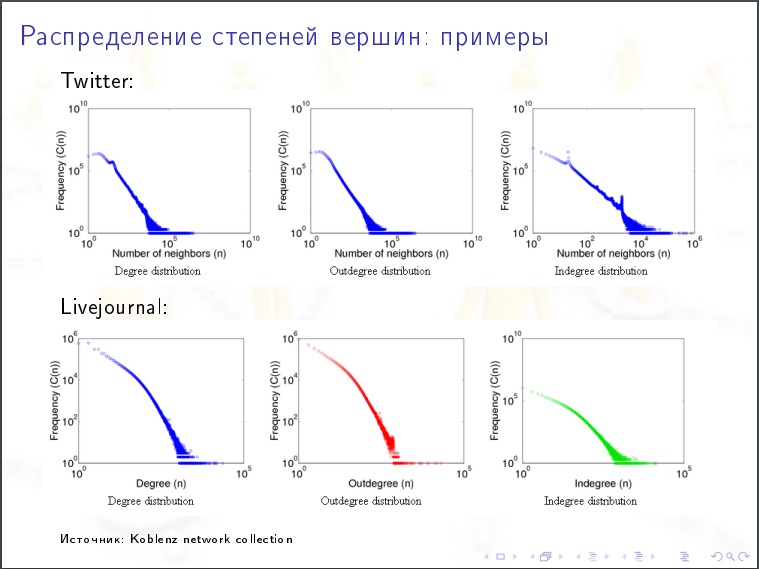
वर्गीकरण का गुणांक । मोटे तौर पर दृष्टिकोण - हम लगभग समान डिग्री के साथ चोटियों को लेते हैं, क्या वे एक दूसरे के साथ या कम के साथ जुड़े होने की अधिक संभावना है? यदि ऐसा है, तो यह मिश्रित है। विसंगति - जब बड़ी संख्या के साथ डिग्री कम होने की संभावना अधिक होती है। यह एक भोला दृष्टिकोण है। एक अधिक सही दृष्टिकोण यह है। प्रत्येक शीर्ष पर कुछ अन्य विशेषता (बैंक की कुल पूंजी) है, और इस सूचक द्वारा वर्गीकरण दिखता है।





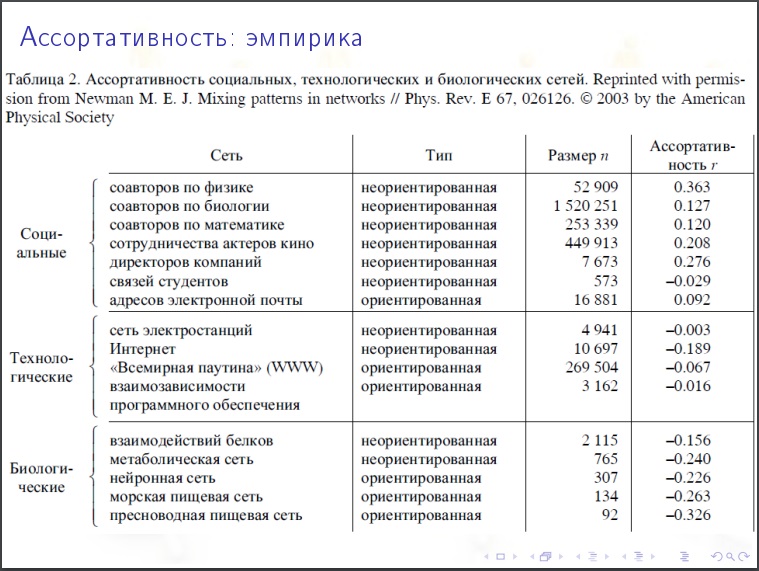
एक सामाजिक नेटवर्क के लिए नोड की केंद्रीयता । हम एक व्यक्ति को लेते हैं, हम उसके लिए निम्नलिखित मूल्य पर विचार करते हैं। हम अन्य लोगों (एन -1) (एन -2) / 2 के सभी जोड़ों के माध्यम से सॉर्ट करते हैं और प्रत्येक मामले में हम ग्राफ में निकटतम डेटिंग मार्ग पूछते हैं, क्या यह इस व्यक्ति के माध्यम से जाता है? कई छोटे रास्ते हो सकते हैं और उनमें से कुछ में हमारा व्यक्ति होता है, फिर हम उसे% देते हैं। यह सामाजिक नेटवर्क में सबसे महत्वपूर्ण विशेषता है। महामारी के प्रसार के लिए, जनता की राय। इसे ही मापने की जरूरत है।









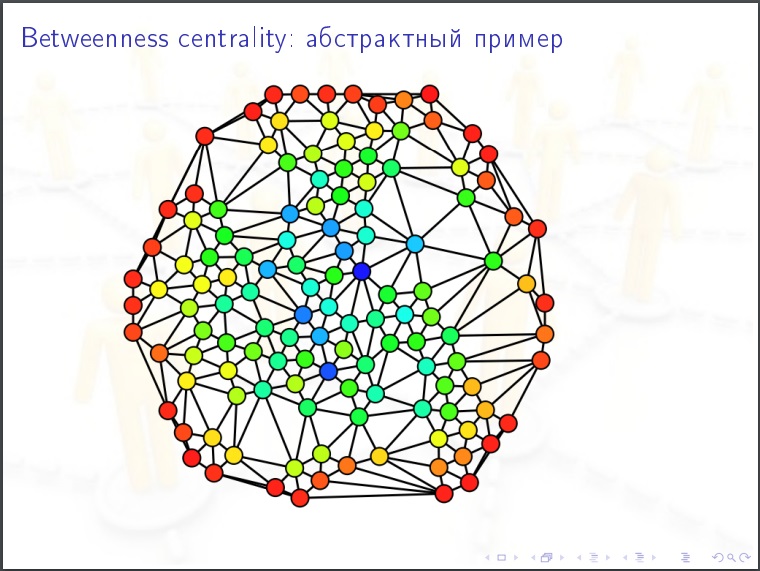
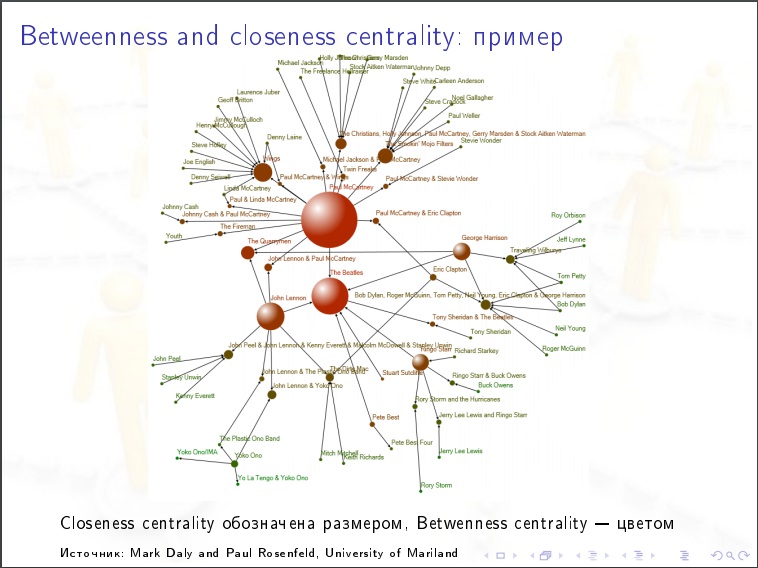
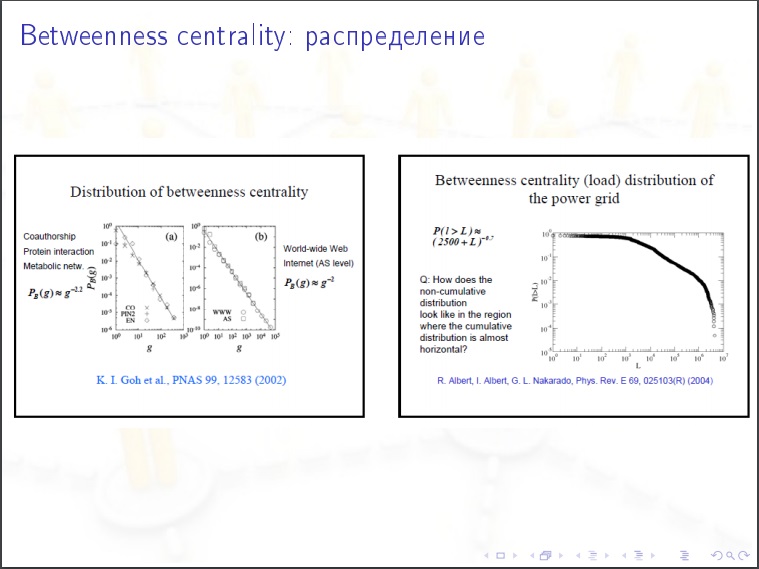
सामाजिक नेटवर्क की विशेषताएं:

• छोटे व्यास और कोने के बीच की औसत दूरी
• कोने और डिग्री की केंद्रीयता के वितरण का शक्ति कानून
• उच्च क्लस्टरिंग अनुपात
• assortative
• बारीकी से संबंधित कोर की उपस्थिति

कार्य एक मॉडल बनाना है जो पहले तीन गुणों को कवर करता है (और अधिमानतः अंतिम दो)। पहले तीन समय में इस बिंदु पर पहले से ही दुर्गम जटिलताएं हैं। 2013 के लिए, ऐसा कोई मॉडल नहीं है।

हम यादृच्छिक ग्राफ मॉडल के विवरण की ओर मुड़ते हैं जो अस्तित्व में थे।

आदर्श

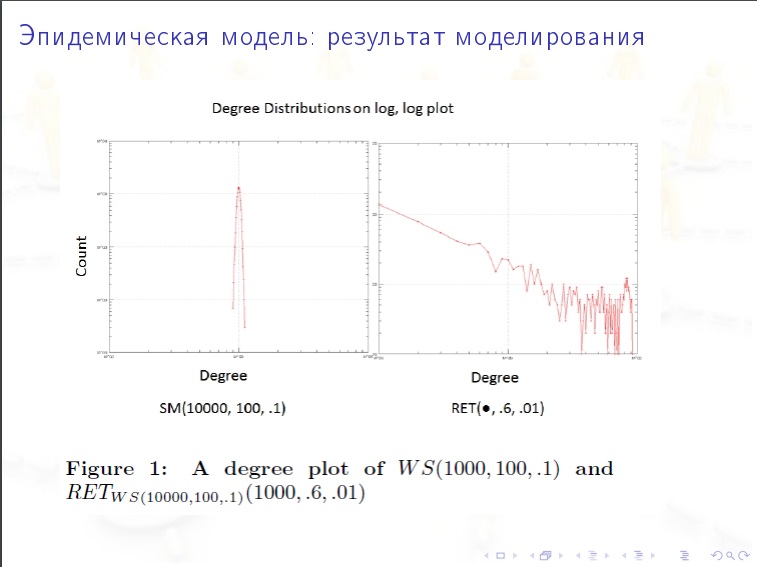
मॉडल हैं:

• तकनीकी (किनारों को अनियमित रूप से उत्पन्न किया जाता है)
• गेम-सिद्धांतवादी (जब यह किसी के लिए फायदेमंद हो)
• कोई संरचना नहीं (केवल बहुत सी परतें)
• संरचनात्मक (लंबवत मीट्रिक स्थान के बिंदु हैं या वज़न है; वहाँ कोने के सेट पर एक संरचना है)

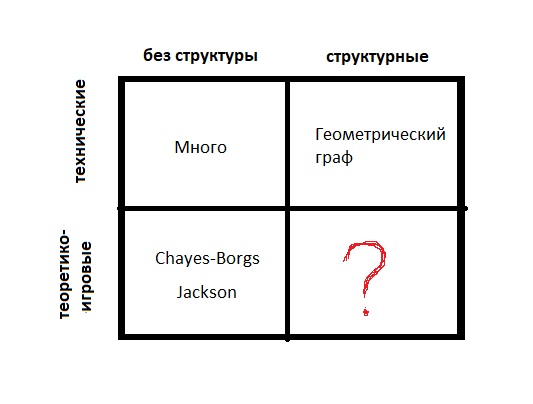
यदि आप समझते हैं कि क्या रेखांकित किया गया है, तो आपको बहुत बड़ी संख्या में मापदंडों द्वारा निर्देशित किया जा सकता है। यदि अच्छी तरह से चुने गए पैरामीटर एक अच्छा अनुमान देते हैं, तो आप अच्छी तरह से कर रहे हैं। और यहां तक ​​कि अगर सबसे अच्छा संयोजन एक बुरा परिणाम देता है और मनाया तथ्यों के अनुरूप नहीं है, तो अलविदा।

यह सब एक उद्देश्य के लिए किया जाता है - स्पैम से लड़ने के लिए।

इंटरनेट को कई स्तरों पर एक जटिल नेटवर्क के रूप में कल्पना की जा सकती है:

• तकनीकी स्तर । ऊर्ध्वाधर और किनारे नोड्स और संचार लाइनें हैं।
• हाइपरटेक्स्ट स्तर । कोने साइट या पृष्ठ हैं, और किनारे हाइपरलिंक हैं।
• सामाजिक स्तर । कोने उपयोगकर्ता हैं, और किनारे उन या उनके बीच अन्य कनेक्शन हैं: सामाजिक नेटवर्क पर दोस्ती, ब्लॉगों की सदस्यता, वितरित परियोजनाओं में सहयोग (जैसे विकिपीडिया), आदि।

जटिल नेटवर्क के लिए, कई स्थानीय और वैश्विक संख्यात्मक विशेषताओं को जाना जाता है: कोने की डिग्री का वितरण, क्लस्टरिंग गुणांक, वर्गीकरण गुणांक

यह पता चलता है कि कई विशेषताएं इंटरनेट नेटवर्क की विशेषता हैं:

• Paretto डिग्रियों का वितरण
• क्लस्टरिंग के उच्च गुणांक,
• सकारात्मक वर्गीकरण
• छोटा व्यास।

इंटरनेट नेटवर्क मॉडलिंग का अंतिम लक्ष्य समान सुविधाओं के साथ मॉडल बनाना है।

एर्दोस मॉडल - रेनी

एर्दोस - रेनी मॉडल दो बारीकी से संबंधित यादृच्छिक ग्राफ पीढ़ी मॉडल में से एक है। मॉडल का नाम गणितज्ञ पाल एर्दो और अल्फ्रेड रेनी के नाम पर रखा गया है, जो 1959 में पहली बार एक मॉडल पेश करने वाले थे। डेटिंग ग्राफ की व्याख्या की।

एन बिंदुओं पर विचार करें। संभावित किनारों - एन * (एन -1) / 2। प्रत्येक रिब के लिए हम एक यादृच्छिक परीक्षण करते हैं। रिब होने की संभावना - पी। क्या नहीं हुआ - (१-पी)। चलो "परीक्षण" चलाते हैं, हमें एक ग्राफ मिलता है। लेकिन कुछ समस्याएं हैं। प्रकट होने के लिए "दुर्लभता" संपत्ति के लिए, पी 1 / एन के आदेश पर बहुत छोटा होना चाहिए, और फिर व्यास बहुत बड़ा होगा।

कोई भी शोधकर्ता जो यह सुनता है कि एर्दोक्स-रेनी मॉडल हंसी के अनुसार इंटरनेट को एक यादृच्छिक ग्राफ के रूप में वर्णित किया गया है।

एक दिलचस्प प्रभाव यह है कि जब आप संभाव्यता की एक निश्चित सीमा को पार करते हैं, तो ग्राफ जुड़ा हुआ है।

बोलोबाशी मॉडल

यह इंटरनेट के निर्माण के लिए एक गतिशील मॉडल है। हम यह अनुमान लगाने की कोशिश कर रहे हैं कि यह धीरे-धीरे कैसे बना। विचार यह है। हम एक शीर्ष और एक किनारे के साथ एक ग्राफ लेते हैं, और फिर प्रत्येक चरण में हम यादृच्छिक रूप से खेलते हैं। हम एक शीर्ष जोड़ते हैं, उसके बाद, कुछ संभावना के साथ, यह अपने आप बंद हो जाता है, और कुछ संभावना के साथ पिछले एक से जुड़ जाता है। कुछ संभाव्यता के साथ अगला शिखर अपने आप बंद हो जाता है, और कुछ पिछले लोगों में से एक के पास जाता है। इसके अलावा, शीर्ष को मारने की संभावना हमेशा किनारों की संख्या के लिए आनुपातिक होती है। एक यादृच्छिक मूल्य बाहर खेला जाता है, और अगला ड्रा पिछले एक के परिणाम पर निर्भर करता है। ऐसा मॉडल सहज है, लेकिन गणितीय रूप से गणना करना मुश्किल है। यह मॉडल एक गैर-घातीय बिजली वितरण देता है। व्यास एक ही है।

लेकिन यह मॉडल क्लस्टरिंग के साथ काम नहीं करता है।

दो प्रतिस्पर्धी दृष्टिकोण हैं जो क्लस्टरिंग के साथ काम करते हैं।

ज्यामितीय दृष्टिकोण

धारणा छत से ली गई है। इंटरनेट का ग्राफ मीट्रिक स्पेस पर आधारित है। स्वाद, रुचियों, वरीयताओं का स्थान। लोग एक दूसरे के लिए कितने दिलचस्प हैं। राय में भावना के कितने करीब। यदि लोग करीब हैं, तो वे एक-दूसरे को संदर्भित करते हैं।

हम इस अंतरिक्ष में 10 ¹⁰ अंक लेते हैं और फेंकते हैं। बड़ी संख्या में पैरामीटर यहां दिखाई देते हैं। विशाल।

क्लस्टरिंग उत्कृष्ट है, लेकिन घटते हुए कोने घातीय हैं। विरोधाभास।

यह विधि बहुत सरल है और एल्गोरिदम "संयोग से" हैं।

गेम-बोर्ग खेल-सिद्धांत संबंधी दृष्टिकोण

क्या आप जानते हैं कि वॉन न्यूमैन के दिनों में यह घोषणा की गई थी कि खेल सिद्धांत सोवियत संघ के खिलाफ एक नई पीढ़ी का हथियार होगा?

हम मानते हैं कि लोग एक दूसरे के साथ संवाद करने के लिए निर्णय लेते हैं या नहीं।

हम बैठकें / कार्यक्रम आयोजित करते हैं। एक घटना आमंत्रित मेहमानों की एक सूची है, साथ ही साथ इसकी "तीव्रता" भी है।
लागत = तीव्रता * (निरंतर + के * (आमंत्रितों की संख्या))। मुझे इवेंट को "बेचने" के लिए संसाधन खर्च करने होंगे और मुझे प्रत्येक प्रतिभागी पर अधिक खर्च करना होगा। जन्मदिन हैं, और बढ़ोतरी हैं। गुणांक "पी" दिखाई देता है, जो जन्मदिन के लिए छोटा है और बढ़ोतरी के लिए बड़ा है। तीव्रता डेटिंग।

एक व्यक्ति तीव्रता ₁ पी, पी ₂ ... पी _{एन के} साथ कई घटनाओं का आयोजन कर सकता है। दूसरे भी ऐसा ही करते हैं।

सामाजिक संबंध स्थापित करने के लिए मेरे कार्य हैं, और अजनबी हैं।

समारोह जीतना = (उन लोगों की संख्या जिनके साथ आप काफी परिचित हो चुके हैं) - लागत

"पर्याप्त रूप से परिचित" का अर्थ है उन सभी घटनाओं की तीव्रता, जहां आप एक साथ थे, एक निश्चित सीमा मूल्य से अधिक है। और इससे कोई फर्क नहीं पड़ता कि किसने कार्यक्रम आयोजित किया।

पसलियों को अच्छे परिचितों के लिए रखा जाता है।



यह साबित होता है कि इस मॉडल में वास्तविक बंद होने के कई गुण प्राप्त होते हैं। सभी नैश संतुलन में, वास्तविक बंद गुण और यहां तक ​​कि मजबूत क्लस्टरिंग गुण भी देखे जाते हैं, जो वास्तविक इंटरनेट के ग्राफ पर भी देखे जाते हैं।



लेकिन अन्य गुणों के बारे में कुछ भी स्पष्ट नहीं है, लेकिन यह आधी परेशानी है। मुसीबत यह है कि अगर कम से कम एक नैश संतुलन है जहां कम से कम दो लोग एक दूसरे को जानते हैं, तो एक नैश संतुलन है जिसमें हर कोई हर किसी से परिचित है।





दो दृष्टिकोणों को संयोजित करने का विचार है। यह विचार करने के लिए कि लोग एक मीट्रिक स्थान में रहते हैं, और जब वे घटनाओं का आयोजन करते हैं, या किसी कार्यक्रम में भाग लेते हैं, तो लागत, तीव्रता और दहलीज अनुपात "निकटता" पर निर्भर करते हैं। यह मॉडलों की पांचवीं पीढ़ी है।

विभेदित लागत

विकल्प विभेदित लागत और विभेदित जीत बनाने के लिए हैं। कुछ को दूसरों की तुलना में आमंत्रित करना आसान होता है। एक के साथ परिचित होना दूसरे के साथ परिचित होने की तुलना में अधिक लाभदायक है।





मान लीजिए कि हम परिधि के चारों ओर समान रूप से सभी लोगों की व्यवस्था करते हैं। और जो किसी के करीब है उसे आमंत्रित करना सस्ता है। बैलेंस कैसा दिखेगा? हर कोई किसी न किसी पड़ोस को आमंत्रित करेगा, है ना? सच नहीं है। ऐसा कोई सन्तुलन नहीं है।

सबूत। मान लीजिए कि यह मौजूद है, तो एक दूसरे के करीबी लोग पहले से ही कई अलग-अलग बैठकों में आमंत्रित किए जाते हैं। फिर उसे इस प्रियजन को आमंत्रित करने की आवश्यकता नहीं है। इस संतुलन का अस्तित्व इस संतुलन के अस्तित्व का खंडन करता है।



शुद्ध संतुलन मौजूद है, यह पाया जाता है, यह एकमात्र है। प्रत्येक एक पड़ोस को आमंत्रित करता है जो कि (या वामावर्त) एक निश्चित दूरी पर और एक निश्चित लंबाई पर स्थित है।

(- यह आकाशगंगाओं का निर्माण है!)
(- यह एक सहज समरूपता है!)

निष्कर्ष

पेलेविन ने एक बार लिखा था कि "रूसी जीवन का अर्थ एक विशाल आइकोस्टेसिस के अनहेल्दी गिल्डिंग में है।" यह गणित का अर्थ है - उसी में। केवल आइकोस्टेसिस वैज्ञानिक है।



यह एक बहु-विषयक अध्ययन है। जैसा कि आप कल्पना कर सकते हैं।

सूत्रों का कहना है

पुनश्च

“एक बार जब मुझे नवलनी को क्लब में बुलाया गया, तो कुछ युवा, उत्साही लोग हैं जो उसकी मदद करते हैं। मैंने तुरंत चेतावनी दी कि मैं अप्रिय बातें कहूंगा। एक क्रांति विजयी होती है यदि गणितज्ञ जो क्रांति के लिए हैं, वे उन लोगों की तुलना में अधिक मजबूत हैं जो खिलाफ हैं। नवलनी के युवाओं को यह नहीं पता था कि उन्हें इस तरह के मॉडल कैसे बताए जाते हैं, लेकिन वे यह नहीं समझते हैं, वे यह भी नहीं जानते कि कैसे एकीकृत करना है - वे बस चलाते हैं और कहीं चिल्लाते हैं। और उनके खिलाफ सिर पर गंभीर लोगों के साथ एक मजबूत संस्थान बैठता है, जो क्रेमलिन के आदेश से कहता है कि वास्तव में और कितना गिरफ्तार किया जाना चाहिए ताकि कुछ भी न हो। वे कहते हैं: "हम विकेंद्रीकृत हैं - विशेष रूप से नवलनी का कोई मतलब नहीं है, कई महत्वपूर्ण नेता हैं।" और फिर एक गणितज्ञ आता है और मानता है कि केंद्रीयकरण इस नेटवर्क का 90% है। आप किसी को अपनी जरूरत के कुछ दिनों के लिए ब्लॉक कर देते हैं - और कोई क्रांति नहीं होती है। मठ जीतता है। ”
- एलेक्सी सवेटेव, "अगर अच्छे गणितज्ञ हैं तो क्रांति जीतती है"

पी पी एस

कौन जानता है कि सामाजिक नेटवर्क और उनके व्यावहारिक लाभों के क्षेत्र में काम करने वाले अन्य दिलचस्प लेख (लेख, व्याख्यान) कृपया साझा करें।