ग्रासहॉपर क्रिप्टोग्राफिक एल्गोरिथ्म: बस जटिल के बारे में

यह आलेख GOST R 34.12-2015 में परिभाषित ब्लॉक एन्क्रिप्शन एल्गोरिथ्म को ग्रासहॉपर के रूप में विस्तार देगा। यह किस पर आधारित है, ब्लॉक क्रिप्टोग्राफिक एल्गोरिदम का गणित क्या है, और यह एल्गोरिथ्म जावा में कैसे लागू किया जाता है।

कौन, कैसे, कब और क्यों विकसित हुआ यह एल्गोरिथ्म लेख के दायरे से बाहर रहेगा, क्योंकि इस मामले में हम बहुत कम रुचि रखते हैं, सिवाय इसके:

ग्रासहॉपर = कुज़नेत्सोव, नेचाएव और कंपनी।



चूंकि क्रिप्टोग्राफी मुख्य रूप से गणित पर आधारित है, इसलिए कि आगे की व्याख्या से बहुत सारे प्रश्न नहीं होते हैं, आपको पहले उन बुनियादी अवधारणाओं और गणितीय कार्यों का विश्लेषण करना चाहिए, जिन पर यह एल्गोरिथ्म बनाया गया है।

फ़ील्ड्स गैलोज़

गलाइस क्षेत्रों का अंकगणित बहुपद अंकगणित है, अर्थात इस क्षेत्र का प्रत्येक तत्व एक बहुपद है। किसी भी ऑपरेशन का परिणाम भी इस क्षेत्र का एक तत्व है। एक विशेष गाल्वा क्षेत्र में संख्याओं की एक निश्चित सीमा होती है। क्षेत्र की विशेषता को कुछ अभाज्य संख्या p कहा जाता है। फील्ड ऑर्डर, अर्थात्। इसके तत्वों की मात्रा विशेषता की एक निश्चित प्राकृतिक डिग्री है $$$p ^ m$ , जहां m where N. m = 1 के लिए, क्षेत्र को सरल कहा जाता है। ऐसे मामलों में जहां एम> 1, एक क्षेत्र के गठन के लिए, डिग्री मीटर की एक बहुपद बनाने की भी आवश्यकता होती है, ऐसे क्षेत्र को विस्तारित कहा जाता है। $$$Gf (p ^ m)$ - गैलोज क्षेत्र का पदनाम। बहुपद उत्पन्न करने वाला अप्रासंगिक है, अर्थात, सरल (अभाज्य संख्याओं के साथ समानता से यह 1 से विभाज्य है और शेष के बिना स्वयं)। चूंकि किसी भी जानकारी के साथ काम करना बाइट्स के साथ काम कर रहा है, और एक बाइट 8 बिट है, एक क्षेत्र के रूप में लें $$$Gf (2 ^ 8)$ और उत्पन्न बहुपद:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

हालांकि, इसके साथ शुरू करने के लिए, हम एक सरल क्षेत्र में बुनियादी संचालन का विश्लेषण करेंगे $$$Gf (2 ^ 3)$ बहुपद पैदा करने के साथ $$$f (x) = x ^ 3 + x + 1$ ।

जोड़ आपरेशन

सबसे सरल अतिरिक्त ऑपरेशन है, जो गाल्वा क्षेत्र अंकगणित में एक सरल बिटवाइज़ जोड़ मोडुलो 2 (.) है।

मैं तुरंत इस तथ्य पर ध्यान आकर्षित करता हूं कि "+" यहां और उसके बाद साइन इन करता है बिटवाइज़र एक्सओआर के संचालन को संदर्भित करता है, और सामान्य रूप में इसके अलावा नहीं।

HOR फ़ंक्शन की सत्य तालिका



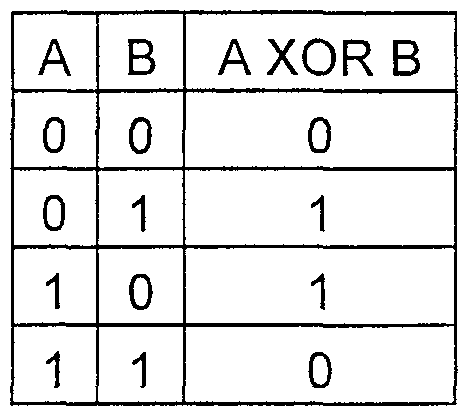
एक उदाहरण: $$$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

बहुपद रूप में, यह ऑपरेशन जैसा दिखेगा

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

गुणन क्रिया

गुणन के संचालन को करने के लिए, संख्याओं को बहुपद रूप में परिवर्तित करना आवश्यक है:

$$

$$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$$

जैसा कि आप देख सकते हैं, बहुपद रूप में संख्या एक बहुपद है जिसका गुणांक संख्या के द्विआधारी प्रतिनिधित्व में बिट्स के मान हैं।

बहुपद रूप में दो संख्याओं को गुणा करें:

$$

$$5 * 7 = (x ^ 2 + 1) * (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 =$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

गुणन परिणाम 27 का उपयोग क्षेत्र में नहीं है। $$$Gf (2 ^ 3)$ (इसमें 0 से 7 तक संख्याएँ हैं, जैसा कि ऊपर बताया गया है)। इस समस्या से निपटने के लिए, एक उत्पन्न बहुपद का उपयोग करना आवश्यक है।

यह भी माना जाता है कि x समीकरण को संतुष्ट करता है $$$f (x) = x ^ 3 + x + 1 = 0$ तो



चलो एक गुणन तालिका बनाते हैं:



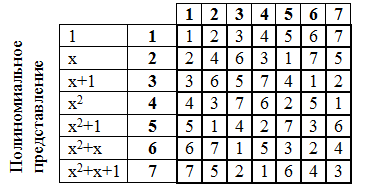
बहुत महत्व की बात यह है कि गैलोज़ क्षेत्र के तत्वों की डिग्री की तालिका है। गुणन के समान एक शक्ति में वृद्धि को बहुपद रूप में भी किया जाता है।

एक उदाहरण:

$$

$$5 ^ 2 = (x ^ 2 + 1) ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

इस प्रकार, हम डिग्री की एक तालिका संकलित करते हैं:



डिग्री तालिका चक्रीय है: सातवीं डिग्री शून्य से मेल खाती है, इसलिए आठवीं पहली से मेल खाती है, आदि। आप चाहें तो इसे चेक कर सकते हैं।

गैलोज़ के क्षेत्रों में, एक आदिम शब्द की अवधारणा है - एक क्षेत्र तत्व जिसकी डिग्री में सभी गैर-अक्षीय क्षेत्र तत्व होते हैं। यह देखा जा सकता है कि सभी तत्व इस स्थिति के अनुरूप हैं (ठीक है, 1 को छोड़कर, निश्चित रूप से)। हालांकि, यह हमेशा मामला नहीं होता है।

जिन क्षेत्रों पर हम विचार कर रहे हैं, वह है, विशेषता 2 के साथ, हमेशा 2 चुनें। आदिम सदस्य के रूप में, इसकी संपत्ति को देखते हुए, क्षेत्र के किसी भी तत्व को आदिम सदस्य की डिग्री के संदर्भ में व्यक्त किया जा सकता है।



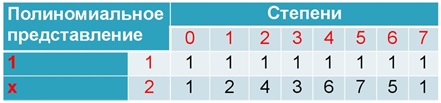
एक उदाहरण: $$$5 = 2 ^ 6.7 = 2 ^ 5$

इस संपत्ति का उपयोग करना, और डिग्री तालिका की चक्रीयता को ध्यान में रखते हुए, हम संख्याओं को फिर से गुणा करने का प्रयास करेंगे:

$$

$$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$$

परिणाम के साथ संयोग है कि हमने पहले क्या गणना की थी।

अब चलो विभाजन करते हैं:

$$

$$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$$

प्राप्त परिणाम भी सत्य है।

खैर, पूर्णता के लिए, आइए एक शक्ति को बढ़ाते हुए देखें:

$$

$$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$$

बहुपद और विभाजन के लिए इस तरह का दृष्टिकोण बहुपद का उपयोग करके वास्तविक संचालन की तुलना में बहुत सरल है, और उनके लिए एक बड़ी गुणा तालिका को स्टोर करने की आवश्यकता नहीं है, लेकिन एक आदिम क्षेत्र के सदस्य की डिग्री की एक पंक्ति।

अब वापस अपने क्षेत्र में $$$Gf (2 ^ 8)$

फ़ील्ड का शून्य तत्व एक है, पहला एक दो है, प्रत्येक 2 से 254 वें तत्व के बाद के तत्व की गणना पिछले एक के रूप में की जाती है, 2 से गुणा किया जाता है, और यदि तत्व फ़ील्ड के बाहर है, अर्थात, इसका मान इससे अधिक है $$$(2 ^ 8-1)$ फिर XOR नंबर के साथ किया जाता है $$$195_ {10}$ , यह संख्या क्षेत्र के अकाट्य बहुपद का प्रतिनिधित्व करती है $$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ , हम इस संख्या को क्षेत्र में लाते हैं $$$451-256 = $ 19$ । और 255 वां तत्व फिर से है। 1. इसलिए हमारे पास एक फ़ील्ड है जिसमें 256 तत्व हैं, यानी बाइट्स का एक पूरा सेट, और हमने इस क्षेत्र में किए जाने वाले मूल संचालन का विश्लेषण किया है।



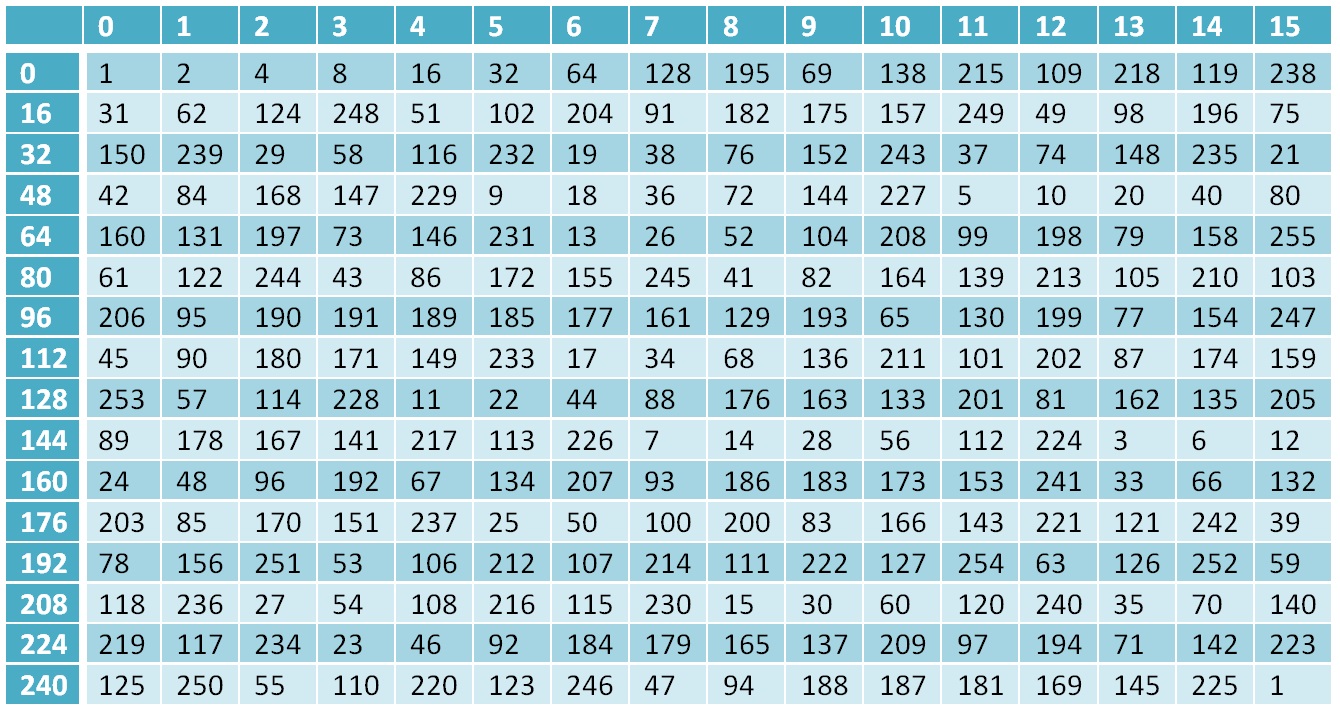
क्षेत्र के लिए दो की शक्तियों की तालिका $$$Gf (2 ^ 8)$

इसकी आवश्यकता क्यों थी - ग्रासहॉपर एल्गोरिथ्म में गणना का हिस्सा गैलोज़ मैदान में किया जाता है, और क्रमशः गणना के परिणाम इस क्षेत्र के तत्व हैं।

Feistel नेटवर्क

Feistel Network एक ब्लॉक एन्क्रिप्शन पद्धति है जो 1971 में IBM पर Horst Feistel द्वारा विकसित की गई थी। आज Feistel का नेटवर्क बड़ी संख्या में क्रिप्टोग्राफ़िक प्रोटोकॉल का आधार है।

Feistel नेटवर्क स्पष्ट-पाठ ब्लॉक के साथ संचालित होता है:

1. ब्लॉक को दो समान भागों में बांटा गया है - बाएं L और दाएं R।
2. बाईं उप-ब्लॉक L को कुंजी K: X = f (L, K) का उपयोग करके फ़ंक्शन f द्वारा बदल दिया जाता है। फ़ंक्शन के रूप में, कोई भी परिवर्तन हो सकता है।
3. परिणामी सबब्लॉक एक्स को सही सबब्लॉक आर के साथ मोडुलो 2 जोड़ा जाता है, जो अपरिवर्तित रहता है: एक्स = एक्स + आर।
4. परिणामी हिस्से आपस में जुड़े और चिपके होते हैं।

क्रियाओं के इस क्रम को Feistel cell कहा जाता है।


चित्रा 1. Feistel सेल

Feistel नेटवर्क में कई सेल होते हैं। पहली सेल के आउटपुट पर प्राप्त सबब्लॉक दूसरी सेल के इनपुट पर जाते हैं, जिसके परिणामस्वरूप दूसरी सेल से तीसरे सेल के इनपुट पर जाते हैं, और इसी तरह।

एन्क्रिप्शन एल्गोरिथ्म

अब हम उपयोग किए गए संचालन से परिचित हो गए हैं और मुख्य विषय पर आगे बढ़ सकते हैं - अर्थात्, ग्रासहॉपर क्रिप्टो-एल्गोरिदम।

एल्गोरिथ्म का आधार तथाकथित एसपी नेटवर्क है - प्रतिस्थापन-क्रमपरिवर्तन नेटवर्क। एसपी नेटवर्क पर आधारित सिफर इनपुट पर एक ब्लॉक और एक कुंजी प्राप्त करता है और प्रतिस्थापन चरणों और क्रमचय चरणों से मिलकर कई वैकल्पिक राउंड करता है। ग्रासहॉपर ने पूरे नौ राउंड किए, जिनमें से प्रत्येक में लगातार तीन ऑपरेशन शामिल हैं:

1. एक कुंजी और एक इनपुट डेटा ब्लॉक के एक गोल कुंजी या बिटवाइज़ XOR को लागू करने का संचालन;
2. गैर-रैखिक रूपांतरण, जो तालिका के अनुसार एक बाइट का दूसरे के साथ सरल प्रतिस्थापन है;
3. रैखिक परिवर्तन। प्रखंड से प्रत्येक बाइट को गॉलॉइस क्षेत्र में श्रृंखला के 148 गुणकों (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) से गुणा किया जाता है। बाइट संख्या (15 वीं से 0 वीं तक के सीरियल नंबर के लिए एक श्रृंखला प्रस्तुत की जाती है, जैसा कि चित्र में दिखाया गया है)। बाइट्स को मॉडुलो 2 के साथ जोड़ा जाता है, और ब्लॉक के सभी 16 बाइट्स को निम्न क्रम की ओर स्थानांतरित किया जाता है, और परिणामी संख्या रीड बाइट के स्थान पर लिखी जाती है।

अंतिम दसवां दौर पूरा नहीं हुआ है, इसमें केवल पहला XOR ऑपरेशन शामिल है।

ग्रासहॉपर एक ब्लॉक एल्गोरिथ्म है, यह 128 बिट्स या 16 बाइट्स लंबे डेटा ब्लॉक के साथ काम करता है। मुख्य लंबाई 256 बिट्स (32 बाइट्स) है।


चित्रा 2. डेटा ब्लॉक की एन्क्रिप्शन और डिक्रिप्शन स्कीम

आरेख संचालन के अनुक्रम को दिखाता है, जहां एस एक गैर-रैखिक परिवर्तन है, एल एक रैखिक परिवर्तन है, की गोल कुंजी हैं। सवाल तुरंत उठता है - गोल कुंजी कहां से आती हैं।

गोल कुंजी गठन

Iterative (या राउंड) कुंजियां एक मास्टर कुंजी के आधार पर कुछ परिवर्तनों द्वारा प्राप्त की जाती हैं, जिनमें से लंबाई, जैसा कि हम पहले से जानते हैं, 256 बिट्स है। यह प्रक्रिया मास्टर कुंजी को आधे हिस्से में विभाजित करने से शुरू होती है, इसलिए पहले दौर की कुंजी प्राप्त की जाती है। Feistel नेटवर्क के आठ पुनरावृत्तियों का उपयोग प्रत्येक बाद की जोड़ी को बनाने के लिए किया जाता है, प्रत्येक पुनरावृत्ति में एक स्थिरांक का उपयोग किया जाता है, जिसे एल्गोरिथ्म के रैखिक परिवर्तन को पुनरावृत्ति संख्या के मान पर लागू करके गणना की जाती है।


पुनरावृत्ति (गोल) कुंजी प्राप्त करने की योजना

यदि हम चित्र 1 को याद करते हैं, तो बायाँ उप-खंड L, मूल कुंजी का बायाँ आधा भाग है, दायाँ उप-खंड R मूल कुंजी का दाहिना आधा है, K निरंतर CE है, फ़ंक्शन f का संचालन R XOR Ci, गैर-रेखीय परिवर्तन, रैखिक परिवर्तन का अनुक्रम है।

पुनरावृति क्रम संख्या के L- परिवर्तन का उपयोग करके पुनरावृत्ति स्थिरांक सी प्राप्त किया जाता है।

इसलिए, पाठ के एक ब्लॉक को एन्क्रिप्ट करने के लिए, हमें सबसे पहले 32 पुनरावृत्त स्थिरांक की गणना करने की आवश्यकता है, फिर कुंजी के आधार पर 10 गोल कुंजी की गणना करें, और फिर चित्र 2 में दिखाए गए संचालन के अनुक्रम को निष्पादित करें।

चलो स्थिरांक की गणना करके शुरू करते हैं:
पहले कांस्टेबल $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ हालांकि, हमारे एल्गोरिथ्म में सभी परिवर्तन 16 बाइट्स के ब्लॉक के साथ किए जाते हैं, इसलिए ब्लॉक की लंबाई के साथ निरंतर को पूरक करना आवश्यक है, अर्थात् दाईं ओर 15 शून्य बाइट्स जोड़ें, हमें मिलता है

$$

$$C_1 = 01000000000000000000000000000000$$

एक श्रृंखला (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) द्वारा इसे गुणा करें:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(यह समानता गैलोज़ क्षेत्रों के संचालन में दी गई है)
चूंकि शून्य बाइट को छोड़कर सब कुछ 0 के बराबर है, और शून्य बाइट 1 से गुणा किया जाता है, हम 1 प्राप्त करते हैं और इसे संख्या के उच्च क्रम में लिखते हैं, सभी बाइट्स को निम्न क्रम में स्थानांतरित करते हुए, हम प्राप्त करते हैं:

$$

$$C_1 = 00000000000000000000000000000001$$

उसी ऑपरेशन को दोहराएं। इस बार $$$a_ {15} = 1$ , अन्य सभी बाइट्स 0 हैं, इसलिए, केवल पहला शब्द शर्तों से बना हुआ है $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ हमें मिलता है:

$$

$$C_1 = 00000000000000000000000000000194$$

हम तीसरी पुनरावृत्ति करते हैं, यहाँ दो अशाब्दिक शब्द हैं:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$= 10010100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

$$132_ {10} = 84_ {16}$$

डिग्री की तालिका के अनुसार, इसे बहुत आसान हल किया जा सकता है:

$$

$$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$$

$$

$$C_1 = 00000000000000000000000000019484$$

इसके अलावा, सब कुछ वास्तव में एक ही है, प्रत्येक निरंतर के लिए केवल 16 पुनरावृत्तियों

$$

$$C_1 = 000000000000000000000000019484DD$$

$$

$$C_1 = 0000000000000000000000019484DD10$$

$$

$$C_1 = 00000000000000000000019484DD10BD$$

$$

$$C_1 = 000000000000000000019484DD10BD27$$

$$

$$C_1 = 0000000000000000019484DD10BD275D$$

$$

$$C_1 = 00000000000000019484DD10BD275DB8$$

$$

$$C_1 = 000000000000019484DD10BD275DB87A$$

$$

$$C_1 = 0000000000019484DD10BD275DB87A48$$

$$

$$C_1 = 00000000019484DD10BD275DB87A486C$$

$$

$$C_1 = 000000019484DD10BD275DB87A486C72$$

$$

$$C_1 = 0000019484DD10BD275DB87A486C727$$

$$

$$C_1 = 00019484DD10BD275DB87A486C7276A2$$

और अंतिम स्थिरांक:

$$

$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$

अन्य स्थिरांक:

$$

$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$

$$

$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$

$$

$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$

$$

$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$

$$

$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$

$$

$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$

$$

$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$

$$

$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF8888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

अब हम ऊपर प्रस्तुत योजना के अनुसार गोल कुंजी की गणना करेंगे, एन्क्रिप्शन कुंजी लेंगे:

$$

$$K = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$EFCDAB896745230101252547698BADCFE$$

तो

$$

$$K_1 = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$K_2 = EFCDAB89674523011032547698BADCFE$$

$$$K_1$ Feistel नेटवर्क का बायां सब-ब्लॉक होगा, और $$$K_2$ - सही है।
चलो ऑपरेशन करते हैं $$$K_1 + C_1$
पहला बाइट $$$K_1$ के बराबर है $$$77_ {16} = 01110111_2$
पहला बाइट $$$C_1$ के बराबर है $$$01_ {16} = 00000001_2$

$$

$$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$$

शेष बाइट्स को उसी तरीके से परिवर्तित किया जाता है, परिणामस्वरूप $$$X (K_1, C_1) = K_1 + C_1$ :

$$

$$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE$$

अगला, हम एक nonlinear परिवर्तन करते हैं $$$S (X (K_1, C_1))$ । यह तालिका के अनुसार किया जाता है:


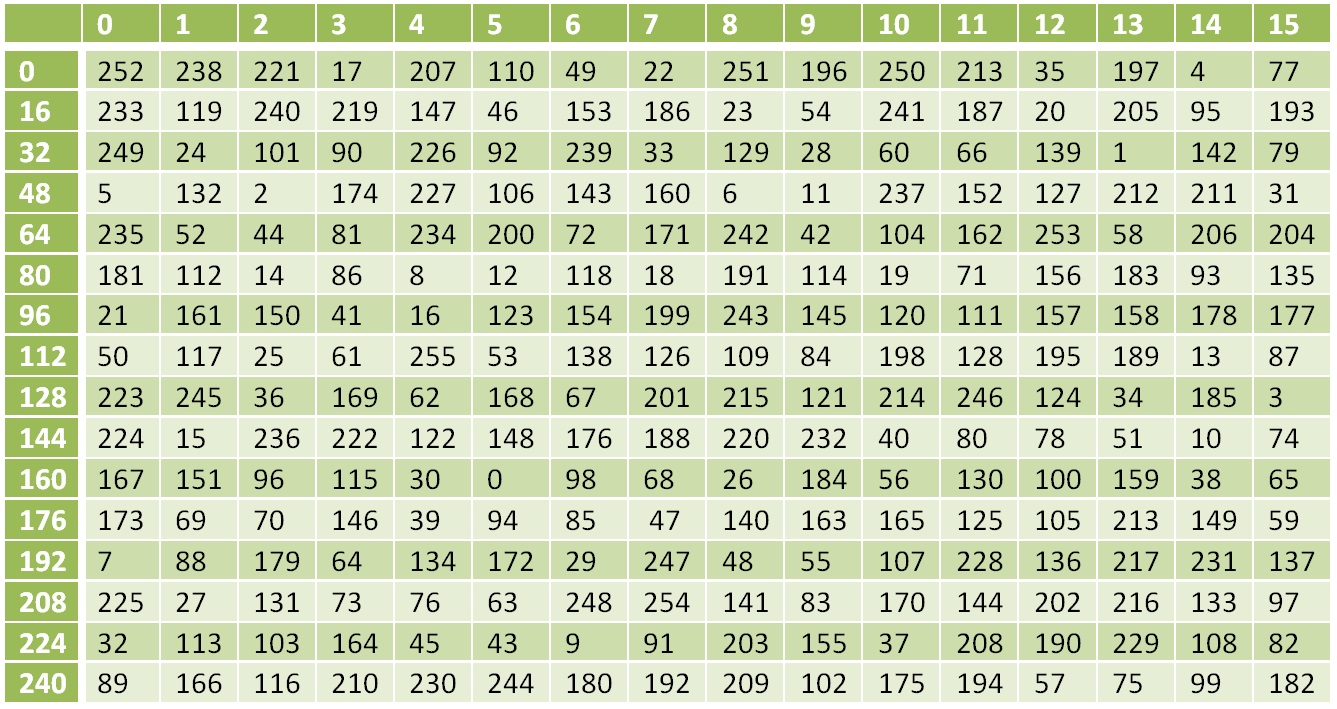नॉनलाइनर रूपांतरण तालिका

संख्या 0 को 252, 1 को 238, 17 को 119, आदि द्वारा प्रतिस्थापित किया जाता है।

$$

$$76_ {16} = 118_ {10}$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

अब एक रैखिक परिवर्तन करते हैं $$$L (S (X (K_1, C_1)))$ , पुनरावृत्त स्थिरांक की गणना करते समय इस पर विस्तार से विचार किया गया था, इसलिए यहां हम केवल अंतिम परिणाम देते हैं:

$$

$$L (S (X (K_1, C_1))) = A644615E1D0757926A5DB79D9940093D$$

Feistel सेल की योजना के अनुसार, हम XOR को सही सब-ब्लॉक के साथ करते हैं, अर्थात् $$$K_2$ :

$$

$$X (L (S (X (K_1, C_1)))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

और परिणाम पहले Feistel सेल के आउटपुट पर प्राप्त हुआ:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

यह मान आधा हो जाता है और दूसरी फिस्टल सेल के इनपुट पर जाता है, जहां दूसरा कंटीन्यू पहले से ही इस्तेमाल किया जाता है $$$C_2$ । आठ कोशिकाओं के माध्यम से जाने के बाद, हमें निम्नलिखित 2 कुंजी मिलती हैं $$$K_3$ और $$$K_4$ । हम उनके साथ Feistel नेटवर्क के आठ पुनरावृत्तियों का प्रदर्शन करेंगे, अगली कुंजी जोड़ी प्राप्त करेंगे, और इसी तरह। प्रमुख जोड़ी प्रति आठ पुनरावृत्तियों, चूंकि हमारे पास शुरुआत में पहली जोड़ी है, फिर 32 पुनरावृत्तियों को कुल मिलाकर किया जाता है, प्रत्येक अपने स्वयं के निरंतर के साथ।

शेष कुंजी:

$$

$$K_3 = 448CC78CEF6A8D2243436915534831DB$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$K_5 = ACF129F44692E5D3285E4AC468646457$$

$$

$$K_6 = 1B58DA3428E832B532645C16359407BD$$

$$

$$K_7 = B198005A26275770DE45877E7540E651$$

$$

$$K_8 = 84F98622A2912AD73EDD9F7B0125795A$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

एन्क्रिप्शन को ब्लॉक करें

हमने सभी कुंजियों की गणना की और अब अंत में हम सीधे टेक्स्ट के ब्लॉक के एन्क्रिप्शन पर जा सकते हैं और यदि आप ऊपर लिखी गई सभी चीजों को ध्यान से पढ़ते हैं, तो टेक्स्ट को एन्क्रिप्ट करना मुश्किल नहीं होगा, क्योंकि इस प्रक्रिया में उपयोग किए गए सभी ऑपरेशन और उनके अनुक्रम की विस्तार से जांच की गई है।

प्लेनटेक्स्ट ब्लॉक लें:

$$

$$T = 8899AABBCCDDEEFF0077665544332211$$

एक्स, एस, एल के संचालन के अनुक्रम को निष्पादित करें

$$

$$X (T, K_1) = FFFFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6B6E87DE8B6E87DE$$

$$

$$L (S (X (T, K_1))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$T_1 = 30081449922F4ACFA1B055E386B697E2$$

$$

$$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1, K_2))) = 7290C6A158426FB396D562087A495E28$$

$$

$$T_2 = 7290C6A158426FB396D562087A495E28$$

और इसी तरह, अंतिम परिणाम इस तरह दिखेगा:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

ब्लॉक डिक्रिप्शन

पाठ को डिक्रिप्ट करने के लिए, आपको उल्टे क्रम में उलटा संचालन का उपयोग करने की आवश्यकता है (चित्र 2 देखें)।

एक्सओआर ऑपरेशन स्वयं के विपरीत है, एस के उलट ऑपरेशन एस निम्नलिखित तालिका के अनुसार प्रतिस्थापन है:


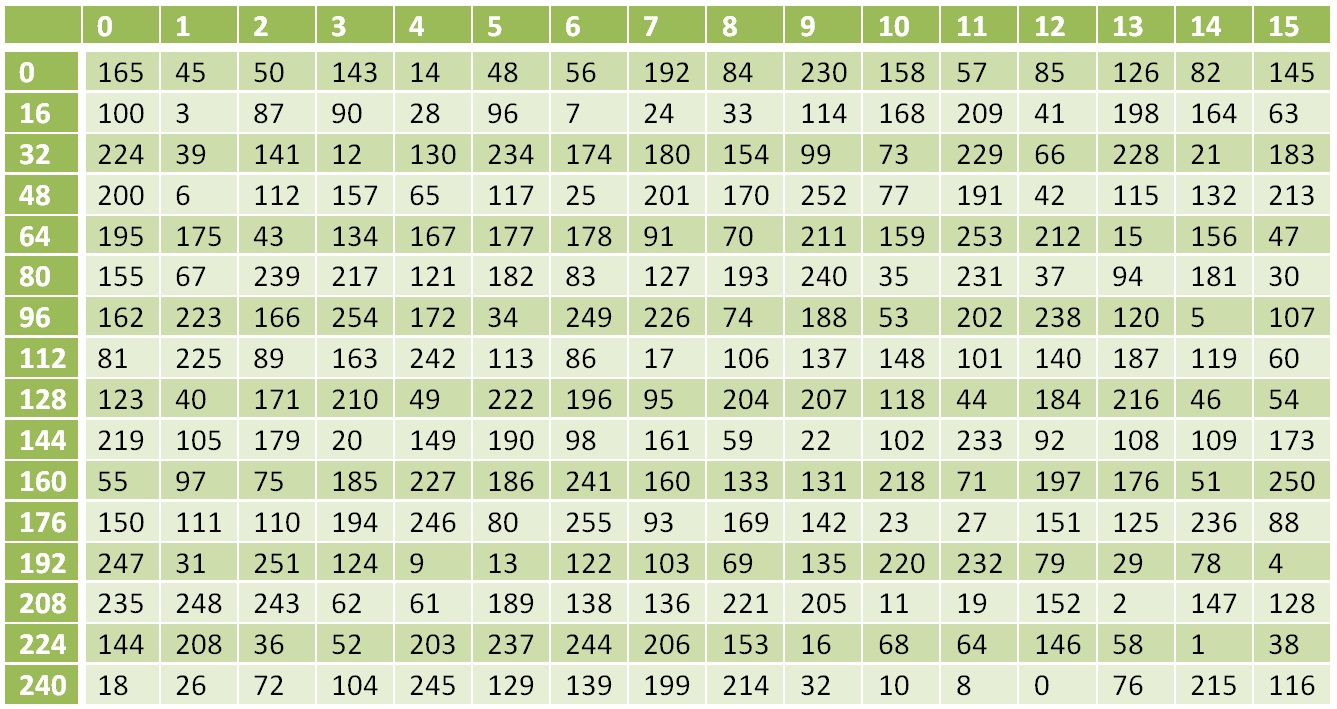उलटा नॉनलाइनियर परिवर्तन तालिका

फ़ंक्शन L का व्युत्क्रम परिवर्तन होगा:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

और वरिष्ठ स्तर की दिशा में एक बदलाव। (ऑपरेशन 16 बार दोहराएं)

जावा कार्यान्वयन

सबसे पहले, हम आवश्यक स्थिरांक परिभाषित करते हैं

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

आइए सभी मुख्य कार्य बनाएं:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

फ़ंक्शन एल को लागू करने के लिए, हमें कई सहायक कार्यों की आवश्यकता होती है, एक गैल्वेन फ़ील्ड में संख्याओं के गुणन की गणना के लिए, और एक पाली के लिए।

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

उलटा कार्य:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

खैर, और मुख्य कार्य

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

हमने पाठ को एन्क्रिप्ट करने के लिए एक डेटा ब्लॉक को एन्क्रिप्ट करना सीखा, जिसकी लंबाई ब्लॉक की लंबाई से अधिक है; मानक में वर्णित कई मोड हैं - GOST 34.13-2015:

• सरल प्रतिस्थापन मोड (इलेक्ट्रॉनिक कोडबुक, ईसीबी);
• गामा मोड (काउंटर, सीटीआर);
• आउटपुट फीडबैक (आउटपुट फीडबैक, ओएफबी) के साथ गामा मोड;
• सरल प्रतिस्थापन गियरिंग मोड (सिफर ब्लॉक चेनिंग, सीबीसी);
• सिफरटेक्स्ट (सिफर फीडबैक, सीएफबी) में फीडबैक के साथ गामा मोड;
• संदेश प्रमाणीकरण कोड (मैक) मोड।

सभी मोड में, पाठ की लंबाई हमेशा ब्लॉक की लंबाई के एक से अधिक होनी चाहिए, इसलिए पाठ को हमेशा एक एकल बिट और शून्य को ब्लॉक की लंबाई के साथ दाईं ओर गद्देदार किया जाता है।

सबसे आसान मोड सरल प्रतिस्थापन मोड है। इस मोड में, टेक्स्ट को ब्लॉक में विभाजित किया जाता है, फिर प्रत्येक ब्लॉक को बाकी हिस्सों से अलग से एन्क्रिप्ट किया जाता है, फिर सिफरटेक्स्ट के ब्लॉक को एक साथ चिपका दिया जाता है और हमें एक एन्क्रिप्टेड संदेश मिलता है। यह मोड सबसे सरल और सबसे कमजोर दोनों है और व्यवहार में लगभग कभी लागू नहीं होता है।

अन्य विधाओं पर बाद में विस्तार से विचार किया जा सकता है।