संख्याओं और उसके तत्वों की एक प्राकृतिक श्रृंखला का एक मॉडल। हीरे

   

इस काम में, बुनियादी जी ² is मॉडल को बरकरार रखा गया है, लेकिन इसकी कोशिकाओं का एक अलग संगठन स्वीकार किया जाता है (एक अन्य आंकड़ा)। 1 × 1 कोशिकाओं के साथ प्राथमिक जाली के शीर्ष पर, एक बड़े ग्रिड का प्रतिनिधित्व किया जाता है - rhombuses का एक ग्रिड, और rhombuses के केंद्रों का एक ग्रिड भी माना जाता है (SCR)। अंतिम ग्रिड को चित्रित नहीं किया गया है ताकि rhombuses के साथ पैटर्न के साथ लाइनों को अधिभार न डालें। हम उन परिभाषाओं और अवधारणाओं को नहीं दोहराएंगे जो पिछले कार्यों में विस्तार से वर्णित थे, लेकिन इन कार्यों की ओर इशारा करते हुए लिंक दें।

रचनात्मक मॉडल विवरण

कोशिकाओं के माध्यम से जी ^{2 ±} - यहां तक ​​कि जी ^{2 -} - सबमॉडल के भीतर शून्य के साथ समाप्त होने वाली संख्याओं में भी लंबे डी _आई और शॉर्ट के _आई विकर्ण में निहित मॉडल, रेखाएं खींची जाती हैं जो विमान में एक बड़े नेटवर्क का रूप लेती हैं। कोशिकाओं के लिए समवर्ती क्षेत्र सामूहिक रूप से अंतराल के बिना पूरे विमान को कवर करते हैं। प्रत्येक रोम्बस में 41 कोशिकाएँ होती हैं, जिनमें से केवल 16 ही रुचिकर होती हैं, और जब एक रोम्बस की जांच की जाती है, तो निश्चित फ्लेक्सन के साथ केवल 4 कोशिकाओं का उपयोग किया जाता है।

Rhombs की विशेषताओं में शामिल होंगे:

• रोम्बस में कोशिकाओं की संख्या;
• केंद्रीय सेल में संख्या का मूल्य;
• इसके क्षैतिज ( N _i ) और वर्टिकल ( V _i ) की संख्या;
• 1, 3, 7, 9 के साथ संख्याओं के लिए कोशिकाओं की पहचान करना;
• रोम्बस के केंद्रीय सेल में उत्पत्ति के साथ रंबल के समन्वय प्रणाली में इन कोशिकाओं के निर्देशांक।

रोम्बस केंद्रों की कोशिकाओं के माध्यम से भी रोम्बस केंद्रों की एक ग्रिड का निर्माण किया जाता है, जिनमें से नोड्स उन संख्याओं के साथ लंबे और छोटे विकर्णों के चौराहे पर स्थित होते हैं जो संख्या 5 के गुणक होते हैं।
Rhombuses वाले आंकड़े से यह स्पष्ट है कि किस तरह का ग्रिड शामिल है। रोम्बस की विशेषताओं को समझने के लिए, प्रत्येक अर्ध-समतल में रंबों के एक जोड़े के चित्र दिए गए हैं। इन रोम्बोउज़ को निचले आधे हिस्से में कोशिकाओं की संख्या और ऊपरी आधे-विमानों में इस तरह के रंबोम्स की एक और जोड़ी के साथ चिह्नित किया जाता है। तिर्यक D _{0 के} नीचे के आधे तल में rhombuses का अंकन इसके ऊपर के आधे विमान में rhombuses के अंकन से भिन्न होता है, लेकिन समान अर्ध-समतल के भीतर, सभी rhombuses का अंकन निचले और ऊपरी आधे विमानों के लिए समान होता है। अंकन का सार उन संख्याओं वाली कोशिकाओं का स्थानीयकरण है जिनके समान विभक्तीकरण होते हैं (कोशिकाओं को समान रंग से भरकर चिह्नित किया जाता है), उनके निर्देशांक x ₁ , x _{0 को} सेट करते हैं। नामित rhombuses को मौलिक कहा जाएगा, उनमें से ज़ूमिंग वाले अन्य rhombuses बन सकते हैं।

निचले आधे तल के समचतुर्भुज के केंद्र दो अंकों में समाप्त होने वाली कोशिकाएं होती हैं, जो 25 या तो क्षैतिज संख्या के साथ होती हैं 5 फ्लेक्सियन 0 के साथ और ऊर्ध्वाधर संख्या के साथ फ्लेक्सियन 0, या 75 के साथ क्षैतिज संख्या में फ्लेक्सियन 0 के साथ और ऊर्ध्वाधर संख्या के साथ फ्लेक्सियन 5। ऊपरी आधे विमान में ^{2 +} - सबमॉडल्स, सभी संख्याओं के केंद्रीय कक्षों में सभी संख्याएं दो अंकों के 25 के साथ समाप्त होती हैं। इसके अलावा, हम अपने विचार को आधा-प्लेन मोटोरोला ² तक सीमित रखते हैं ^-


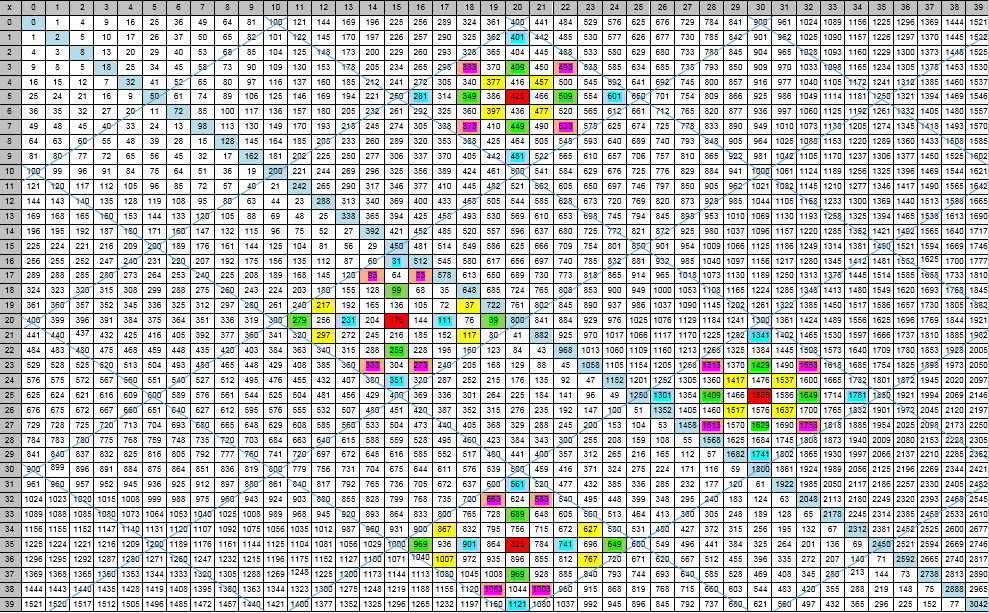_{चित्रा 1 - एक हीरे के मॉडल का दृश्य प्रतिनिधित्व}

परिभाषा 1. मौलिक समभुज, ² model - मॉडल की संरचना है, इस संख्या के दो छोटे और दो लंबे विकर्णों द्वारा सीमित है जो संख्या 10 के गुणक हैं। 10. मुख्य तत्व जो रंबल की विशेषता है, उसके केंद्र की कोशिका ( x _1c , x _0c ) है। केंद्र में N का एक संख्यात्मक मान होता है, जो कि 5 से अधिक है।

परिभाषा 2. मौलिक rhombuses के केंद्रों का सेट छोटी और लंबी विकर्णों को समेटने वाले rhombuses (SCR) के केंद्रों के नेटवर्क की नोड्स (कोशिकाएं) हैं, जिनकी संख्या 5 के गुणक हैं। rhombuses खुद को पूरी तरह से विमान को कवर करते हैं खेल ² models - मॉडल (लकड़ी की छत सिद्धांत)।

सभी rhombuses एक ही तरीके से व्यवस्थित होते हैं, और निश्चित अंत के साथ उनकी कोशिकाओं में संख्याओं को निश्चित पदों (कोशिकाओं) में रखा जाता है। यह आपको इस संख्या को आसानी से फैक्ट करने की अनुमति देता है, जब एक निश्चित समभुज में संख्या N को स्थानीय करने की समस्या को हल किया जाता है। दस क्षैतिज, जिनमें से कोशिकाएं एक रंबल और पड़ोसी रंबोम्स बनाती हैं (इसके साथ निर्देशांक अलग हैं), रंबोल की एक पट्टी कहलाएगी। क्षैतिज बैंड माना जाता है: पश्चिम-पूर्व (;); ऊर्ध्वाधर: उत्तर-दक्षिण (NW), छोटे विकर्णों के साथ: पूर्वोत्तर (NE) और लंबे विकर्णों के साथ: उत्तर-पश्चिम (NW)। एक रोम्बस से दूसरे में ऑफसेट पट्टी को इंगित करने के अलावा, संकेतित बैंड के साथ एक संकेत (ऊपर और नीचे) द्वारा पूरक किया जा सकता है।

चूंकि यह परिभाषा 2 से इस प्रकार है कि सभी rhombuses की कोशिकाओं का सेट G ² one मॉडल की सभी कोशिकाएं हैं, तो एक निश्चित rhombus से संबंधित कोशिकाओं (x _1p , x _0p ) में से एक, एक पूर्वनिर्धारित समग्र विषम प्राकृतिक संख्या (ELF) N ( x _1p , x _0p ) = N (x ₁ , x ₀ ) । इसी समय, हम मानते हैं कि सभी कोशिकाओं की जांच करने की तुलना में इस तरह के एक रोम्बस (इसके केंद्रीय सेल के निर्देशांक निर्धारित करके) (x _1c , x _0c ) को इंगित करना संभव है, यहां तक ​​कि केवल विषम विकर्णों की जांच करने के लिए खुद को सीमित करना।

इस तरह के एक रोम्बस का संकेत और उसके भीतर वांछित सेल किसी दिए गए नंबर N (x ₁ , x ₀ ) के लिए स्थानीयकरण समस्या का समाधान है। यह समस्या और इसका समाधान WFCH के निर्णय की प्राप्ति से पहले था। स्थानीयकरण समस्या का अर्थ और अंतिम लक्ष्य किसी दिए गए ELF N (x ₁ , x ₀ ) के लिए एक निश्चित rhombus में इंगित करना है , G ^{2 ±} मॉडल में सेल (x _1p , x _0p ) के निर्देशांक का मान जिसमें N के साथ एक संयोग है। (x ₁ , x ₀ ) ।

इस लेख में, हम किसी दिए गए नंबर N के संबंधित को एक विशिष्ट समभुज और उसमें एक सेल की स्थापना के लिए उपयोग करते हैं। यह तंत्र सबसे अच्छा है, लेकिन प्रस्तावित उदाहरणों में यह कार्य के साथ मुकाबला करता है। पाठकों को या तो अपनी मूल पेशकश करने के लिए आमंत्रित किया जाता है, या इस तंत्र में सुधार किया जाता है।

हमारा तंत्र लेखक द्वारा खोजी गई G ² by मॉडल की उल्लेखनीय नियमितता पर आधारित है: संख्याओं के साथ क्षैतिज रेखाओं में उपस्थिति जो पांच (और कुछ अन्य) के गुणक हैं, कोशिकाएं पाइथागोरस त्रिगुण के तत्वों के वर्गों के साथ (PFT) < g, k ₂ > = <hypotenuseuse , पैर ₁ , पैर ₂ >। सीएफटी एक और काम में चर्चा की जाएगी।

निष्कर्ष और गणना को सरल बनाने के लिए, हमें तीन समन्वय प्रणालियों की आवश्यकता है: प्लानर, जिसे पहले ही पेश किया जा चुका है , एससीआर (छवि 2) के लिए विकर्णों की अन्य संख्याओं वाला नेटवर्क और रम्बिक (तालिका 1), जिसमें शुरुआत रंबल के केंद्र की कोशिका से जुड़ी होती है।


<sub>चित्रा 2. लघु विकर्णों की संख्या (दोहराव) और
लघु विकर्णों पर हीरे के केंद्रों का वितरण

तालिका 1. एक निर्धारित rhombus के भीतर एक खोज बिंदु के निर्देशांक का निर्धारण</sub>



SCR प्रणाली में, निम्नलिखित संकेत दिए गए हैं: लघु विकर्ण n _p की संख्या, c उस पर केंद्र की क्रम संख्या है, साथ ही केंद्र में नेटवर्क-व्यापी C संख्या, n _p = 1 से शुरू होने वाले छोटे विकर्णों की अपनी संख्या (तलीय प्रणाली में 5 वीं लघु विकर्ण है) , फिर संख्या n _p = 2 (यह संख्या 10 से बढ़ जाती है, यानी 15 वें विमान K _i ) और फिर चरण 10 अन्य सभी के साथ। एससीआर के प्रत्येक K _i में rhombus केंद्रों की सभी कोशिकाओं की स्थिति भी लघु विकर्ण _के डबल नेटवर्क नंबर के c = 1 से c = 2n _p तक गिना जाता है।

उदाहरण 1 यह किसी कक्ष के नेटवर्क-व्यापी संख्या C को खोजने के लिए आवश्यक है और इस सेल में संख्या N, rhombuses के केंद्रों से गुजरने वाले लघु विकर्ण के लिए, इसके नेटवर्क नंबर n _p = 5 , और उस पर एक romombs के केंद्र c = 3 के क्रमांक संख्या को खोजने के लिए आवश्यक है। काफी बस, इस rhombus के केंद्र कोशिका के नेटवर्क निर्देशांक को फॉर्म (n _p , q) = (5, 3) में दर्शाया गया है।

1. दिए गए विकर्ण (nd) की शुरुआत में सेल के समतल x _{1 को} खोजें:
   x ₁ = x _nd = 10n _p - 5 = 50 - 5 = 45
   हमारे मामले के लिए, हमें x ₁ = x _nd = 45 मिला है ।
   
2. अब हम तुरंत वांछित केंद्र के सेल ( x _1c , x _sc ) के विमान निर्देशांक की खोज के लिए आगे बढ़ सकते हैं: x ₁ = x _nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x ₀ = 0 + 5 ( μ - 1) = 2 = 5 = 10।
   
3. रोम्बस के केंद्र ( C ) का नेटवर्क नंबर ज्ञात कीजिए।
   
   नोट। यह ज्ञात है कि संख्या x के लिए सूत्र 2C _{x + 1} ² = x (x + 1) दो में x + 1 के संयोजन की दोगुनी संख्या है।
   लघु विकर्ण n _p = 5 से पहले वाले केंद्रों की संख्या 2n _p (n _p - 1) है । फिर सूत्र द्वारा नेटवर्क केंद्र का क्रम संख्या सी दिया जाता है
   C = n _p (n _p -1) + c = 2C _{n p} ² + 3 = 5 + 4 + 3 = 23
   
4. समभुज N = x ₁ ² - x ₀ ² के केंद्र के कक्ष में संख्या N (x _1c , x _sc ) का मान ज्ञात करें - सूत्र में संकेत मुख्य विकर्ण के सापेक्ष केंद्र की स्थिति के आधार पर लिया गया है।
   हमारे मामले के लिए एन = 35 ² - 10 ² = 1125 -।
   

इस प्रकार, केंद्रों की कोशिकाओं से होकर गुजरने _वाले लघु विकर्ण के केवल नेटवर्क नंबर n _p और इस विकर्ण पर rhombus c की वर्तमान केंद्र संख्या होने से, हम rhombus के केंद्र के बारे में अन्य सभी जानकारी प्राप्त कर सकते हैं।

ब्याज एन के सभी अजीब सकारात्मक पूर्णांक हीरे की कोशिकाओं से संबंधित हैं। Flexion की अवधारणा, एक संख्या का अंतिम अंक, rhombs के भीतर अपनी स्थिति को स्थानीय बनाने की अनुमति देता है। कारक के लिए, वे संख्या N जो संख्या 1, 3, 7, 9 के साथ समाप्त होती हैं, ब्याज की हैं।

यहां तक ​​कि संख्याओं को एन के रूप में नहीं माना जाता है , क्योंकि उनके पास एक प्रमुख भाजक है। पांच के साथ समाप्त होने वाले संख्याओं में एक प्रधान भाजक 5 है, जो एन के लिए भी अस्वीकार्य है । यह इस तथ्य के संदर्भ में है कि केंद्र के बीच में एक विशिष्ट एन स्थानीयकरण करने के लिए सलाह दी जाती है, इस तथ्य के संदर्भ में कि केंद्र रोम्बस की सबसे महत्वपूर्ण विशेषता है। इस तथ्य के आधार पर कि सभी rhombuses में एक ही संरचना होती है, गुणनखंडन के लिए निर्दिष्ट संख्या N के बीच एक स्पष्ट संबंध है और कुछ inflections के साथ rhombus कोशिकाओं में और rhombus केंद्र की सेल में संख्या। ऐसे रिलेशनशिप नंबरों का डेटा टेबल में दिया गया है। 1।

हालांकि, वांछित rhombus खोजने के लिए एक विमान पर सभी rhombuses को छांटना समय या कम्प्यूटेशनल लागत में अस्वीकार्य है। इस प्रकार, इस समस्या को क्षेत्रों को स्थानीय बनाने के लिए उत्पन्न हुआ है ^{2 -} - सबमॉडल्स (आधे-विमान), ऐसे ऐसे रोम्बस शामिल हैं जिनमें प्रारंभिक संख्या एन होती है , जिन्हें कारक बनाया जाना चाहिए।

पाइथागोरस के त्रिगुण । हल करने के लिए तैयार की गई समस्या का उपयोग किया जाता है
पायथागॉरियन ट्राइएल्स पायथागॉरियन प्रमेय को संतुष्ट करने वाली संख्याओं के त्रिगुण हैं: अर्थात्, पायथागॉरियन ट्रिपल जो तथाकथित मिस्र के त्रिभुज के नियम को संतुष्ट करते हैं, अर्थात् पक्षों के साथ एक त्रिकोण जो 3, 4, 5 के गुणक हैं।
प्रत्येक क्षैतिज एक्स ₁ में रंबॉब्स के केंद्र होते हैं, एक या अधिक ऐसे पायथागॉरियन त्रिक होते हैं।

स्थानीयकरण समस्या में पहला रोम्बस लगभग इंगित किया गया है और "मिस" होने की स्थिति में, निम्नलिखित रंबों का चयन किया जाना चाहिए। इसके लिए, एससीआर के साथ आंदोलन की दिशा निर्धारित करना आवश्यक है, ताकि धीरे-धीरे अंतिम लक्ष्य तक पहुंच सकें। उदाहरण के लिए, यदि संख्याओं के वर्तमान rhombus में 4 का छोटा हिस्सा दिए गए N से कम है, तो उसमें से उत्तर-पूर्व और पूर्व के rhombuses में 4 से भी कम नंबर होते हैं, यानी ऐसे rhombs की जांच नहीं की जानी चाहिए। पश्चिमी rhombus में जाने से इसकी सभी 4 कोशिकाओं में मूल्यों में इतनी वृद्धि होती है कि पश्चिमी rhombus की एक छोटी संख्या भी पिछले rhombus की बड़ी संख्या की तुलना में बड़ी हो जाती है और इसलिए, N से अधिक है। इसलिए: समाधान: rhombus से rhombus से उत्तर-पश्चिम दिशा में बढ़ें।

यदि एन (एक्स _{1 पी} , एक्स 0 _पी ) = एन के बराबर संख्या के साथ एक सेल युक्त एक रोम्बस पाया जाता है और सेल के निर्देशांक (एक्स _{1 पी} , एक्स 0 _पी ) का निर्धारण किया जाता है, तो एफबीसीएच का समाधान मूल संबंध से निर्धारित होता है मोटोरोला ² - मॉडल का
N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p। Q

एक और उपप्रोग्रामम प्रोबिंग के लिए चुने गए रंबल के सेल बाईपास अनुक्रम का चयन और कार्यान्वयन है। यहां, एंटीक्लॉकवाइज ट्रैवर्सल ऑर्डर को अपनाया जाता है, ऊपरी बाएं सेल से शुरू होता है जिसमें आवश्यक विभक्ति के साथ संख्या होती है। डायमंड सेल N (x _1p , x _0p ) और दिए गए नंबर N (x ₁ , x ₀ ) में मूल्यों के संयोग की स्थिति में , उनके बीच का अंतर शून्य हो जाता है।

ZFBCH समाधान एल्गोरिथ्म मौलिक rhombuses और PFT का उपयोग कर

1. हम संख्या एन से जड़ को निकालते हैं । नीचे गोल।
   
2. हम जाँचते हैं कि checkN 3 से विभाज्य है। यदि विभाज्य है, तो इस मान को पहले चरण k1 पर असाइन करें, अन्यथा, 3 से विभाज्यता गुण को संतुष्ट करने के लिए, परिणाम से 1 या 2 घटाएं और इसे k1 के रूप में संग्रहीत करें। तीन एम = byN / 3 द्वारा पूरी तरह से चयनित मूल्य को विभाजित करने का परिणाम - स्केलिंग पीएफटी गुणांक को याद रखें।
   
3. हमें दूसरे चरण के _{2 के} लिए मूल्य मिलता है, मिस्र के त्रिकोण के नियम के अनुसार, के ₂ = 4 the एम।
   
4. हम कर्ण g = 5 and M का मान ज्ञात करते हैं , और x ₁ = g का मान संख्या पाँच से विभाजित किया जाना चाहिए। जैसा कि आप देख सकते हैं, कर्ण का मान हमेशा PFT के साथ क्षैतिज संख्या के बराबर होता है।
   
5. निर्देशांक x ₁ = g का पता लगाएं।
   
6. उसके बाद, हम संख्या N , N = N (mod10) के विभक्ति (अंतिम अंक) का निर्धारण करते हैं।
   
7. हम k1 के निकटतम rhombus का केंद्र पाते हैं और फिर rhombuses के बैंड में से किसी एक में आसन्न rhombuses की जांच करते हैं (एक समाधान खोजने के लिए 4 दिशाएं हैं)।
   
8. अनुच्छेद 6 में हमें किस प्रकार का विभ्रम मिलता है, इसके आधार पर, हम तालिका में प्रस्तुत किए गए वांछित कॉलम (मास्क) का उपयोग करते हैं। 1 खोज बिंदु ( x _1p , x _0p ) के निर्देशांक निर्धारित करने के लिए और इस सेल N _p में संख्या का मान _{ज्ञात} करें। प्रत्येक रोम्बस में, 41 वें सेल से केवल 4 कोशिकाओं की जाँच की जाती है।
   
9. यह स्थापित करने के बाद कि संख्या N एक विशेष ताल और उसी कक्ष के आधार पर एक सेल से संबंधित है। 1 हमें विमान निर्देशांक N: (x _1p , x _0p ) मिलता है ।
   
10. चयनित गणितीय मॉडल के गुणों का उपयोग करना
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p। Q
    हम एडिटिव से एन का गुणक प्रतिनिधित्व प्राप्त करते हैं।
    
11. इस प्रकार, एल्गोरिथ्म के आउटपुट में, हमारे पास: एन = पी । क्यू । तालिका में सूत्रों के अनुसार फ्लेक्सन एफ के मूल्य पर निर्भर करता है। 1, बिंदु (x _1p , x _0p ) के निर्देशांक _{निर्धारित} किए जाते _हैं और अंतर ∆ = N (x _1p , x _0p ) - N (x ₁ , x ₀ ) की गणना की जाती है। यदि If ∆ 0 है , तो किसी अन्य कक्ष में जाएं, यदि रोम्बस की सभी कोशिकाओं की जाँच की जाती है, तो दूसरे रंबल में।
    यदि If = 0 , तो x ₁ = x _1p , x ₀ = x _0p और p = (x ₁ - x ₀ ) , q = N / p = (x ₁ + x ₀ ) ।
    

उदाहरण 2. दिया गया: N = 1037 , 4 की क्षमता वाला एक नंबर। इसे फैक्टर करने के लिए आवश्यक है। हम दिए गए एल्गोरिथम के अनुसार कार्य करते हैं।

1. हम एन से जड़ निकालते हैं: =N = 32.202 । हम नीचे गोल करते हैं: =N = 32 ।
2. हम जाँचते हैं कि 32 3 से विभाज्य है। चूंकि 32 3 से विभाज्य नहीं है, इसलिए हम 2. घटाते हैं। इसलिए, हम मानते हैं कि पहला पैर k = ₁ = 3 = 10 = 30 है , यहाँ M = 10 = 30/3 PFT स्केलिंग कारक है।
3. हमें दूसरे चरण k ₂ = 4 = 10 = 40 के लिए मान मिलता है।
4. हम कर्ण मान g = (k ² ₁ + k ² ₂ ) ^0.5 पाते हैं, बशर्ते कि यह 5, (30 ² +40 ² ) ^0.5 = 50 से विभाजित हो ।
5. इस प्रकार, X1 = k1 = 50 और PFT फॉर्म g = 50 , k ₁ = 30, k ₂ = 40 के रूप में बदल जाता है ।
6. हम संख्या N : 10 (1037) = 1037 (mod10) = 7 की विभक्ति पाते हैं।
7. हम एन = 1037 के सबसे करीब स्थित केंद्र का पता लगाते हैं ।
   इसमें रोम्बस के केंद्रीय सेल के निर्देशांक होंगे: x ₁ = 50, x ₀ = 35 । पहला समन्वय CFT युक्त लाइन नंबर है। छोटे पैर का वर्ग 900 है, यह 40 की संख्या के साथ ऊर्ध्वाधर में समाहित है। संख्या 957 के साथ संख्या सात के साथ समाप्त होती है जो 900 के पूर्व में क्षैतिज संख्या में 49 के साथ है और 38 की संख्या के साथ ऊर्ध्वाधर में है। यह रंबल में और के साथ 4 की सबसे छोटी संख्या है। inflection 7. यहां हम तालिका के डेटा का उपयोग करते हैं। 1. समभुज का निकटतम केंद्र बाईं ओर तीन कोशिकाएं होनी चाहिए, अर्थात यह लंबवत 38 - 3 = 35 के अंतर्गत आता है, यह रोम्बस के केंद्र का दूसरा समन्वय है। रोम्बस के केंद्र की संख्या में संख्या का मान N (50, 35) = 1275 है
   
   यह एक बॉम्ब है, जिसके बॉर्डर पर पैर k ₁ और k _{2 के} वर्ग हैं। इस समभुज के भीतर, मिन एक सेल ( x ₁ = 49, x ₀ = 38 ) में सात 957 में समाप्त होने वाली संख्या है, और इस ऊर्ध्वाधर में 711 1157 में समाप्त होने वाली एक और संख्या, बड़ी संख्या 1377 और 1577 केंद्रीय सेल के बाईं ओर स्थित है, जो संख्या के साथ मेल खाता है। N = 1037 नहीं, इसलिए, केंद्रीय कक्ष 1125 में मान के साथ बाईं और उच्चतर समभुज तक बढ़ना आवश्यक है और केंद्रीय सेल के निर्देशांक के साथ ( x ₁ = 50 - 5 = 45, x ₀ = 35 = 5 = 30 ) flexion 7 के लिए चार नंबरों की जांच करें ये 87४ 10, १०२ 10, १२० and और १३ there हैं और इस रंभा में N = १०३ 10 के साथ कोई संयोग नहीं हैं), हम एक ही दिशा में rhombs के NW बैंड के साथ और भी ऊंचे उठेंगे। नए rhombus के केंद्र कक्ष का मान 975 और निर्देशांक ( x ₁ = 45 -5 = 40, x ₀ = 35 - 5 = 25 ) है। हम इस ताल में विभक्ति के लिए चार नंबरों की जाँच करते हैं। यह 737, 897, 1197 है और अंत में हम सेल में 1037 प्राप्त करते हैं ( x _1p = 39, x _0p = 22 ), हमें दिए गए N के साथ एक पूर्ण मिलान मिला ।
   
   विस्तार से, इन कार्यों को निम्नलिखित गणनाओं द्वारा दर्शाया गया है: तालिका 1 के अनुसार, हम कोशिकाओं के निर्देशांक और उनमें संख्या मानों की गणना करते हैं। उसके बाद, हम एन के गणना और दिए गए मानों के बीच अंतर पाते हैं। पहले रोम्बस में, सभी 4 कोशिकाओं की गणना की जाती है।
   
   ∆ = एन (एक्स _{1 सी} -1, एक्स 0 _सी -3) - एन (एक्स ₁ , एक्स ₀ ) = एन (49.32) - 1037 = 1377 - 1037 = 340, 0
   ∆ = एन (एक्स _{1 सी} +1, एक्स 0 _सी -3) - एन (एक्स ₁ , एक्स ₀ ) = एन (51.32) - 1037 = 1577 - 1037 = 540, 0
   ∆ = एन (एक्स _{1 सी} +1, एक्स 0 _सी +3) - एन (एक्स ₁ , एक्स ₀ ) = एन (51.38) - 1037 = 1157 - 1037 = 120, 0।
   ∆ = एन (एक्स _{1 सी} -1, एक्स 0 _सी +3) - एन (एक्स ₁ , एक्स ₀ ) = एन (49.38) - 1037 = 957 - 1037 = - 80। 0।
   इस rhombus में कोशिकाओं में संख्याओं के साथ संख्या N का कोई संयोग नहीं है।
   
   हम सेल में केंद्र (x _1c -5, x _0c -5) = (45, 30) के साथ अगले rhombus पर जाते हैं और इसमें मान N (x _1c -5, x _0c -5) = N (45, 30) - 1125 ।
   ∆ = N (x _1ts -1, x _0ts -3) - N (x ₁ , x ₀ ) = N (44.27) - 1037 = 1207 - 1037 = 170, 0
   ∆ = एन (एक्स _{1 सी} +1, एक्स 0 _सी -3) - एन (एक्स ₁ , एक्स ₀ ) = एन (46.27) - 1037 = 1387 - 1037 = 350, 0
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (46.33) - 1037 = 1027 - 1037 = - 10, 0
   ∆ = एन (एक्स _{1 सी} -1, एक्स 0 _सी +3) - एन (एक्स ₁ , एक्स ₀ ) = एन (44.33) - 1037 = 847 - 1037 = - 190। 0।
   इस rhombus में, कोशिकाओं में संख्याओं के साथ संख्या N का कोई संयोग भी नहीं है।
   
   हम सेल में केंद्र (x _1c -5, x _0c -5) = (40, 25) के साथ अगले rhombus पर जाते हैं और इसमें मान N (x _1c -5, x _0c -5) = N (40, 25) - 975
   ∆ = एन (एक्स _{1 सी} -1, एक्स 0 _सी -3) - एन (एक्स ₁ , एक्स ₀ ) = एन (39.22) - 1037 = 1037 - 1037 = 0।
   मानों का एक शून्य अंतर मिला। पूरा संयोग है। इस से यह निम्नानुसार है कि दी गई संख्या N (x ₁ , x ₀ ) = 1037 निर्देशांक (x _1p , x _0p ) = (39, 22) के साथ सेल में निहित है । आखिरकार, HFBC का समाधान मूल मॉडल ^{2 "±} - मॉडल द्वारा निर्धारित किया जाता है।
   N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = (39 - 22) (39 + 22) = p = q = 17। 61 ।
   
8. आप अलग तरह से कार्य कर सकते हैं। तालिका 6 का उपयोग करके पैरा 6 में संकेतित रोम्बस के साथ शुरू करें। 1, हम पता लगाते हैं कि क्या संख्या N एक विशेष समभुज से संबंधित है, पहले मुख्य तिरछे की ओर, क्षैतिज रूप से rhombs के केंद्रों के बीच चलती है, फिर rhombs की अगली पट्टी पर नीचे जाती है और फिर से सब कुछ दोहराती है।
9. यह स्थापित करने के बाद कि संख्या N एक निश्चित rhombus से संबंधित है (हमारे मामले में, rhombus में निर्देशांक ( x ₁ = 40, x ₀ = 25 )) एक ही तालिका के आधार पर होगा। 1 हमें निर्देशांक N : x _1p = 39 , x _2p = 22 (9 rhombs देखे गए) मिलते हैं।
10. संख्या के चयनित गणितीय मॉडल के गुणों का उपयोग करना
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p। Q
    हमें एडिटिव से एन का गुणात्मक प्रतिनिधित्व मिलता है:
    एन = (39 - 22) (39 + 22) = 17 39 61 = 1037 ।

इस प्रकार, आउटपुट पर हमारे पास N = p · q = 17 · 61 = 1037 है , अर्थात, समस्या का समाधान सफलतापूर्वक प्राप्त किया गया था।

हम भी उदाहरण 3 में समस्या के लिए एक सॉफ्टवेयर समाधान का परिणाम प्राप्त करते हैं।

उदाहरण 3 दिया गया: एन = 3808572773, 10 के संकल्प के साथ एक संख्या।

1. हम एन से जड़ निकालते हैं : =N = 61713 , 64 = 61713 ।
2. जाँच करें कि 61713 3 से विभाज्य है। चूंकि 61713 3 से विभाज्य है,
   6 + 1 + 7 + 1 + 3 = 18 को 3 से विभाजित किया जाता है, फिर पहला पैर k ₁ k ₁ = 61713 के बराबर होता है ।
3. हमें दूसरा पैर k ₂ = 4k 1/3 => 4k 2/3 = 82284 मिलता है ।
4. हम कर्ण g = 12k ₁₂ + k ₂₂ पाते हैं, बशर्ते कि यह विभाजित हो
   5 जी = g617132 + 822842 = 102855 ।
5. इस प्रकार, x ₁ = k ₁ = 61713 , और पायथागॉरियन ट्रिपल क्रमशः k ₁ = 61713, k ₂ = 82284, g = 102855 में बदल जाता है ।
6. N: (3808572773) = 3808572773(mod10) = 3 .
7. . x ₁ = 61715; x ₉ = 0 .
8. , 7, . 1, N , , , , .
9. N ( x ₁ = 62015 , x ₀ = 6085 ) N :
   x _1p = 62013; x _0p = 6086 ; ( 60 ).
10. 
    N = x ² ₁ — x ² ₀ = (x ₁ — x ₀ )(x ₁ + x ₀ ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
11. , N = p · q = 55927 · 68099 = 3808572773 , . . .