कल्पना करें कि आपको 1 से 10 तक एक समान रूप से वितरित यादृच्छिक संख्या उत्पन्न करने की आवश्यकता है। अर्थात, प्रत्येक घटना के समान संभाव्यता (10%) के साथ 1 से 10 समावेशी का पूर्णांक। लेकिन, सिक्के, कंप्यूटर, रेडियोधर्मी सामग्री, या अन्य समान स्रोतों के लिए (छद्म) यादृच्छिक संख्याओं तक पहुंच के बिना कहें। आप लोगों के पास केवल एक कमरा है।

मान लीजिए कि इस कमरे में 8500 से अधिक छात्र हैं।

सबसे सरल बात किसी से पूछना है: "अरे, एक से दस तक एक यादृच्छिक संख्या चुनें!"। आदमी जवाब देता है: "सात!"। बहुत बढ़िया! अब आपके पास एक नंबर है। हालांकि, आप आश्चर्यचकित होने लगते हैं कि क्या यह समान रूप से वितरित किया गया है।

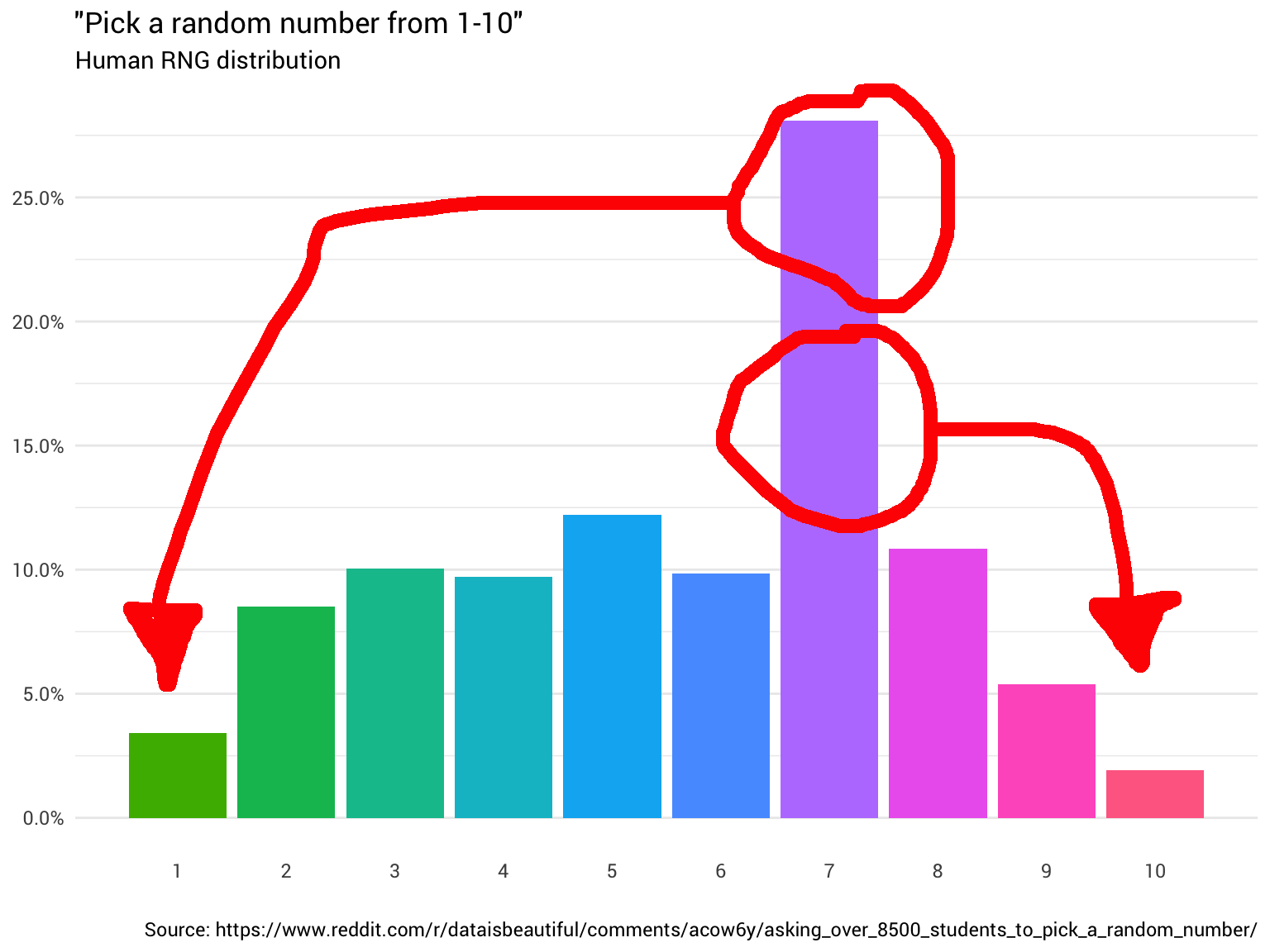
इसलिए आपने कुछ और लोगों से पूछने का फैसला किया। आप उनसे पूछते रहते हैं और उनके जवाबों को गिनते रहते हैं, भिन्नात्मक संख्याओं को पार करते हैं और उन लोगों को अनदेखा करते हैं जो सोचते हैं कि 1 से 10 तक की सीमा में 0. शामिल हैं। अंत में, आप यह देखना शुरू करते हैं कि वितरण बिल्कुल भी नहीं है:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Reddit से डेटा

आप अपना माथा पटकें। खैर, ज़ाहिर है , यह यादृच्छिक नहीं होगा। आखिरकार, आप लोगों पर भरोसा नहीं कर सकते ।

तो क्या करें?

काश मैं कुछ ऐसा फंक्शन पाता जो "मानव RNG" के वितरण को एक समान वितरण में बदल देता ...

यहां अंतर्ज्ञान अपेक्षाकृत सरल है। आपको बस वितरण के द्रव्यमान को 10% से ऊपर ले जाने की आवश्यकता है, और इसे उस स्थान पर ले जाएँ जहाँ यह 10% से कम है। ताकि चार्ट पर सभी कॉलम समान स्तर पर हों:



सिद्धांत रूप में, ऐसे फ़ंक्शन का अस्तित्व होना चाहिए। वास्तव में, कई अलग-अलग कार्य (क्रमपरिवर्तन के लिए) होने चाहिए। एक चरम मामले में, आप प्रत्येक स्तंभ को असीम रूप से छोटे ब्लॉकों में "काट" सकते हैं और किसी भी आकार (जैसे लेगो ईंटों) का वितरण कर सकते हैं।

बेशक, इस तरह के एक चरम उदाहरण थोड़ा बोझिल है। आदर्श रूप से, हम जितना संभव हो उतना प्रारंभिक वितरण रखना चाहते हैं (यानी, संभव के रूप में कुछ कतरनों और आंदोलनों को बनाने के लिए)।

ऐसे फ़ंक्शन को कैसे ढूंढें?

ठीक है, ऊपर हमारी व्याख्या रैखिक प्रोग्रामिंग की तरह लगती है। विकिपीडिया से:

रैखिक प्रोग्रामिंग (एलपी, जिसे रैखिक अनुकूलन भी कहा जाता है) सर्वश्रेष्ठ परिणाम प्राप्त करने की एक विधि है ... एक गणितीय मॉडल में जिसकी आवश्यकताओं को रैखिक संबंधों द्वारा दर्शाया जाता है ... एक रैखिक प्रोग्रामिंग समस्या का वर्णन करने के लिए मानक रूप सामान्य और सबसे सहज रूप है। इसमें तीन भाग होते हैं:

• रैखिक कार्य को अधिकतम किया जाना है
  
• निम्न प्रपत्र की समस्या सीमाएँ
  
• गैर-नकारात्मक चर

इसी तरह, पुनर्वितरण की समस्या को सूत्रबद्ध किया जा सकता है।

समस्या की प्रस्तुति

हमारे पास चर का एक सेट है $$$(x_ {i, j}$ , जिनमें से प्रत्येक एक पूर्णांक से पुनर्वितरित प्रायिकता के एक अंश को कूटबद्ध करता है $$$मैं$ (1 से 10) एक पूर्णांक तक $$$ज$ (1 से 10 तक)। इसलिए, यदि $$$(x_ {7,1} = 0.2$ , तब हमें सात से एक तक 20% उत्तरों को स्थानांतरित करना होगा।

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # एक स्पर्श: 100 x 4
 ## नाम ix से
 ## <dbl> <dbl> <गोंद> <int>
 ## 1 1 1 x (1,1) 1
 ## 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 ## 6 1 6 x (1,6) 6
 ## 7 1 7 x (1,7) 7
 ## 8 1 8 x (1,8) 8
 ## ९ १ ९ x (१.९) ९
 ## 10 1 10 x (1,10) 10
 ## # ... 90 और पंक्तियों के साथ 

हम इन चरों को सीमित करना चाहते हैं ताकि सभी पुनर्वितरित संभावनाएं 10% तक बढ़ जाएं। दूसरे शब्दों में, प्रत्येक के लिए $$$ज$ 1 से 10 तक:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0.1$$

हम आर। बाद में इन प्रतिबंधों की एक सूची के रूप में प्रतिनिधित्व कर सकते हैं, हम उन्हें एक मैट्रिक्स में बांधते हैं।

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

हमें यह भी सुनिश्चित करना चाहिए कि प्रारंभिक वितरण से संभावनाओं का पूरा द्रव्यमान संरक्षित है। तो सभी के लिए $$$ज$ 1 से 10 तक की सीमा में:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0.1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

जैसा कि पहले ही उल्लेख किया गया है, हम मूल वितरण के संरक्षण को अधिकतम करना चाहते हैं। यह हमारा उद्देश्य है :

$$

$$अधिकतम (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10}}$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

फिर हम समस्या को सॉल्वर तक lpSolve , उदाहरण के लिए, R में lpSolve पैकेज, निर्मित अवरोधों को एक मैट्रिक्स में संयोजित करना:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

निम्नलिखित पुनर्वितरण वापस आ गया है:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

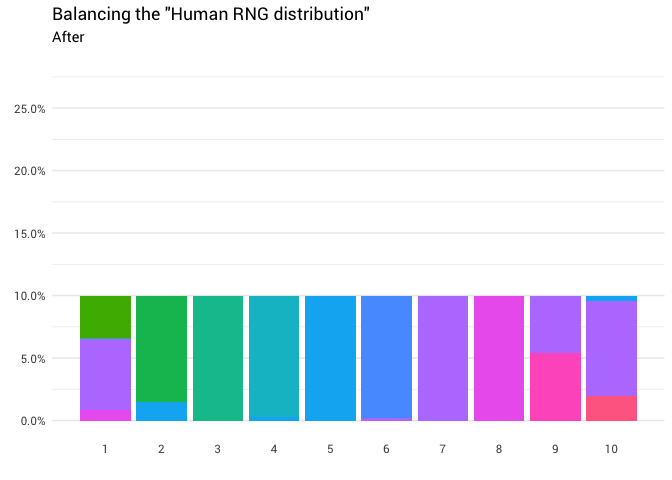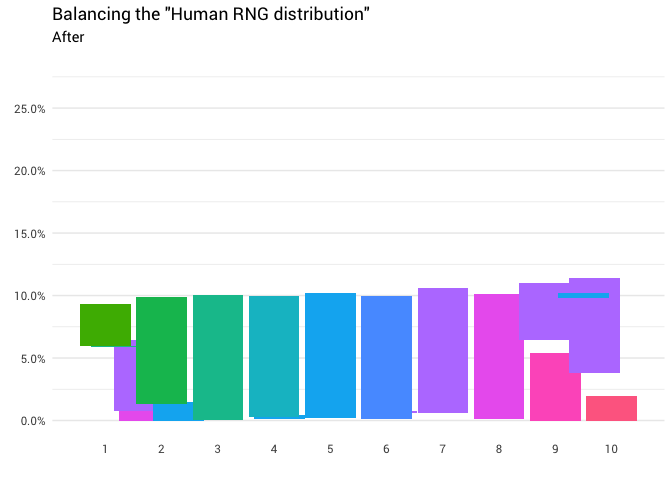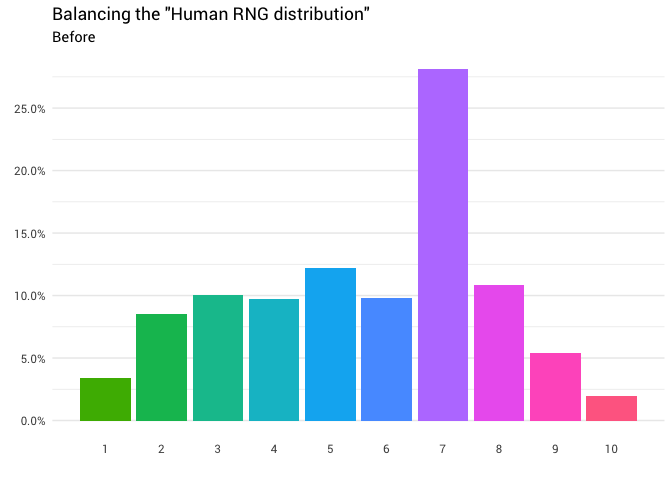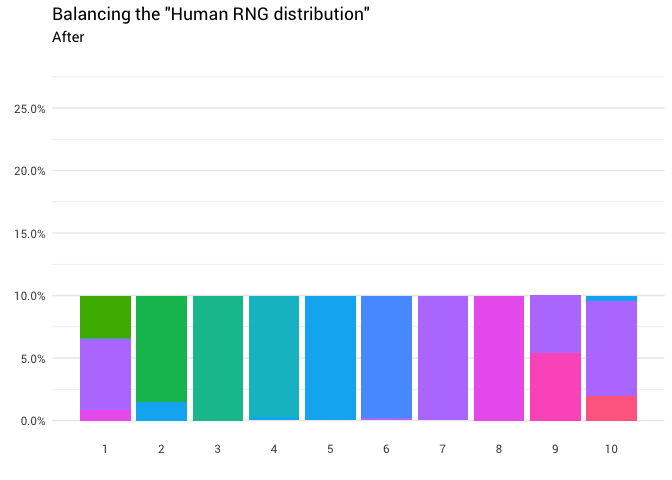
बहुत बढ़िया! अब हमारे पास पुनर्वितरण समारोह है। आइए देखें कि द्रव्यमान कैसे चलता है:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

यह चार्ट कहता है कि लगभग 8% मामलों में जब कोई आठ को एक यादृच्छिक संख्या कहता है, तो आपको उत्तर को एक इकाई के रूप में लेना होगा। शेष 92% मामलों में, वह आठ बनी हुई है।

समस्या को हल करने के लिए यह काफी सरल होगा यदि हमारे पास समान रूप से वितरित यादृच्छिक संख्याओं के जनरेटर तक पहुंच हो (0 से 1 तक)। लेकिन हमारे पास केवल लोगों से भरा एक कमरा है। सौभाग्य से, यदि आप कुछ मामूली अशुद्धियों के साथ आने के लिए तैयार हैं, तो आप लोगों को दो बार से अधिक पूछे बिना बहुत अच्छा आरएनजी बना सकते हैं।

हमारे मूल वितरण पर लौटते हुए, हमारे पास प्रत्येक संख्या के लिए निम्नलिखित संभावनाएँ हैं, जिनका उपयोग यदि आवश्यक हो, तो किसी भी संभावना को फिर से असाइन करने के लिए किया जा सकता है।

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # एक स्पर्श: 10 x 2
 ## संख्या संभावना
 ## <dbl> <chr>
 ## 1 1 3.4%
 ## 2 2 8.5%
 ## 3 3 10.0%
 ## 4 4 9.7%
 ## 5 5 12.2%
 ## 6 6 9.8%
 ## 7 7 28.1%
 ## 8 8 10.9%
 ## ९ ९ ५.४%
 ## 10 10 1.9% 

उदाहरण के लिए, जब कोई हमें एक यादृच्छिक संख्या के रूप में आठ देता है, तो हमें यह निर्धारित करने की आवश्यकता है कि यह आठ एक इकाई बन जाए या नहीं (संभावना 8%)। यदि हम किसी अन्य व्यक्ति से यादृच्छिक संख्या के बारे में पूछते हैं, तो 8.5% की संभावना के साथ वह "दो" उत्तर देगा। इसलिए यदि यह दूसरी संख्या 2 है, तो हम जानते हैं कि हमें 1 को समान रूप से वितरित यादृच्छिक संख्या के रूप में वापस करना होगा।

इस तर्क को सभी संख्याओं में विस्तारित करते हुए, हम निम्नलिखित एल्गोरिथ्म प्राप्त करते हैं:

• यादृच्छिक संख्या के लिए किसी व्यक्ति से पूछें, $$$n_1$ ।
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ या $$$10$ :
  
  • आपका रैंडम नंबर $$$n_1$
• अगर $$$n_1 = 5$ :
  
  • यादृच्छिक संख्या के लिए किसी अन्य व्यक्ति से पूछें ( $$$n2$ )
  • अगर $$$n_2 = 5$ (12.2%):
    
    • आपका यादृच्छिक नंबर 2
  • अगर $$$n_2 = 10$ (1.9%):
    
    • आपका रैंडम नंबर 4
  • अन्यथा, आपका यादृच्छिक संख्या 5 है
• अगर $$$n_1 = 7$ :
  
  • यादृच्छिक संख्या के लिए किसी अन्य व्यक्ति से पूछें ( $$$n2$ )
  • अगर $$$n_2 = 2$ या $$$5$ (20.7%):
    
    • आपका यादृच्छिक नंबर 1
  • अगर $$$n_2 = 8$ या $$$9$ (16.2%):
    
    • आपका रैंडम नंबर 9 है
  • अगर $$$n_2 = 7$ (28.1%):
    
    • आपका रैंडम नंबर 10 है
  • अन्यथा, आपका यादृच्छिक संख्या 7 है
• अगर $$$n_1 = 8$ :
  
  • यादृच्छिक संख्या के लिए किसी अन्य व्यक्ति से पूछें ( $$$n2$ )
  • अगर $$$n_2 = 2$ (8.5%):
    
    • आपका यादृच्छिक नंबर 1
  • अन्यथा, आपका यादृच्छिक संख्या 8 है

इस एल्गोरिथ्म का उपयोग करके, आप 1 से 10 तक समान रूप से वितरित यादृच्छिक संख्याओं के एक जनरेटर के करीब पाने के लिए लोगों के एक समूह का उपयोग कर सकते हैं!