तंत्रिका नेटवर्क और गहन शिक्षा, अध्याय 3, भाग 2: नियमितीकरण से रिट्रेनिंग को कम करने में मदद क्यों मिलती है?

अनुभवजन्य रूप से, हमने देखा है कि नियमितीकरण रिट्रेनिंग को कम करने में मदद करता है। यह प्रेरणादायक है - लेकिन, दुर्भाग्य से, यह स्पष्ट नहीं है कि नियमितीकरण क्यों मदद करता है। आमतौर पर लोग इसे किसी तरह से समझाते हैं: एक अर्थ में, छोटे वजन में कम जटिलता होती है, जो डेटा का एक सरल और अधिक कुशल विवरण प्रदान करती है, इसलिए उन्हें प्राथमिकता दी जानी चाहिए। हालाँकि, यह एक स्पष्टीकरण बहुत कम है, और इसके कुछ हिस्से संदिग्ध या रहस्यमय लग सकते हैं। आइए इस कहानी को सामने लाएँ और आलोचनात्मक नज़र से देखें। ऐसा करने के लिए, मान लें कि हमारे पास एक सरल डेटा सेट है जिसके लिए हम एक मॉडल बनाना चाहते हैं:


अर्थ के संदर्भ में, यहां हम वास्तविक दुनिया की घटना का अध्ययन करते हैं, और x और y वास्तविक डेटा को दर्शाते हैं। हमारा लक्ष्य एक मॉडल का निर्माण करना है जो हमें x के कार्य के रूप में y की भविष्यवाणी करने की अनुमति देता है। हम इस तरह के मॉडल को बनाने के लिए एक तंत्रिका नेटवर्क का उपयोग करने की कोशिश कर सकते हैं, लेकिन मैं कुछ सरल सुझाव देता हूं: मैं एक्स में एक बहुपद के रूप में y को मॉडल करने का प्रयास करूंगा। मैं तंत्रिका नेटवर्क के बजाय ऐसा करूंगा, क्योंकि बहुपद का उपयोग स्पष्टीकरण को विशेष रूप से स्पष्ट करता है। जैसे ही हम बहुपद के मामले से निपटेंगे, हम नेशनल असेंबली का रुख करेंगे। ऊपर दिए गए ग्राफ़ पर दस बिंदु हैं, जिसका अर्थ है कि हम एक अद्वितीय 9-क्रम बहुपद y = _{0 0} ^{9 9} + ₁ x ⁸ + ... + _{9 प्राप्त} कर सकते हैं जो वास्तव में डेटा को फिट करता है। और यहाँ इस बहुपद का ग्राफ है।


एकदम सही हिट। लेकिन हम रैखिक मॉडल y = 2x का उपयोग करके एक अच्छा अनुमान प्राप्त कर सकते हैं


कौन सा बेहतर है? कौन सा सच होने की अधिक संभावना है? जो वास्तविक दुनिया की इसी घटना के अन्य उदाहरणों के लिए बेहतर सामान्यीकृत होगा?

मुश्किल सवाल। और अंतर्निहित वास्तविक दुनिया की घटना के बारे में अतिरिक्त जानकारी के बिना उन्हें बिल्कुल जवाब नहीं दिया जा सकता है। हालांकि, आइए दो संभावनाओं को देखें: (1) 9-क्रम बहुपद के साथ एक मॉडल वास्तव में वास्तविक दुनिया की घटना का वर्णन करता है, और इसलिए, पूरी तरह से सामान्य करता है; (2) सही मॉडल y = 2x है, लेकिन हमारे पास माप त्रुटि से जुड़ा अतिरिक्त शोर है, इसलिए मॉडल पूरी तरह से फिट नहीं है।

एक प्राथमिकता, कोई यह नहीं कह सकता कि दोनों में से कौन सी संभावना सही है (या कोई तीसरा नहीं है)। तार्किक रूप से, उनमें से कोई भी सच हो सकता है। और उनके बीच अंतर nontrivial है। हां, उपलब्ध आंकड़ों के आधार पर, यह कहा जा सकता है कि मॉडलों के बीच केवल मामूली अंतर है। लेकिन मान लीजिए कि हम x के कुछ बड़े मूल्य के अनुसार y के मूल्य की भविष्यवाणी करना चाहते हैं, जो कि ग्राफ़ में दिखाए गए किसी भी व्यक्ति की तुलना में बहुत बड़ा है। यदि हम ऐसा करने की कोशिश करते हैं, तो दो मॉडलों की भविष्यवाणियों के बीच एक बड़ा अंतर दिखाई देगा, क्योंकि ⁹ वें क्रम बहुपद में x ⁹ शब्द हावी है, और रैखिक मॉडल रैखिक रहता है।

जो कुछ हो रहा है, उस पर एक बिंदु यह बताना है कि यदि संभव हो तो विज्ञान में एक सरल व्याख्या का उपयोग किया जाना चाहिए। जब हम एक सरल मॉडल पाते हैं जो कई संदर्भ बिंदुओं की व्याख्या करता है, तो हम केवल चिल्लाना चाहते हैं: "यूरेका!" आखिरकार, यह संभावना नहीं है कि दुर्घटना से एक सरल व्याख्या पूरी तरह से दिखाई देगी। हमें संदेह है कि मॉडल को घटना से जुड़े कुछ सत्य का उत्पादन करना चाहिए। इस मामले में, मॉडल y = 2x + शोर y = _{0 0 0} ⁹ + ₁ x ⁸ + ... की तुलना में बहुत सरल लगता है ... यह आश्चर्य की बात होगी यदि संयोग से सादगी उत्पन्न हुई, तो हमें संदेह है कि y = 2x + शोर कुछ व्यक्त करता है अंतर्निहित सत्य। इस दृष्टि से, 9 वां ऑर्डर मॉडल केवल स्थानीय शोर के प्रभाव का अध्ययन करता है। हालांकि 9 वां ऑर्डर मॉडल इन विशिष्ट संदर्भ बिंदुओं के लिए पूरी तरह से काम करता है, यह अन्य बिंदुओं के लिए सामान्य नहीं कर सकता है, जिसके परिणामस्वरूप शोर के साथ रैखिक मॉडल में बेहतर भविष्य कहनेवाला क्षमताएं होंगी।

आइए देखें कि तंत्रिका नेटवर्क के लिए यह दृष्टिकोण क्या है। मान लीजिए, हमारे नेटवर्क में, मुख्य रूप से कम वजन हैं, जैसा कि आमतौर पर नियमित नेटवर्क में होता है। अपने छोटे वजन के कारण, नेटवर्क का व्यवहार बहुत अधिक नहीं बदलता है जब कई यादृच्छिक इनपुट यहां और वहां बदल जाते हैं। नतीजतन, नियमित नेटवर्क डेटा में मौजूद स्थानीय शोर के प्रभावों को सीखना मुश्किल है। यह यह सुनिश्चित करने की इच्छा के समान है कि व्यक्तिगत साक्ष्य पूरे नेटवर्क के उत्पादन को बहुत प्रभावित नहीं करते हैं। इसके बजाय, नियमित नेटवर्क को उन साक्ष्य का जवाब देने के लिए प्रशिक्षित किया जाता है जो अक्सर प्रशिक्षण डेटा में पाए जाते हैं। इसके विपरीत, बड़े वजन वाले एक नेटवर्क इनपुट डेटा में छोटे बदलावों की प्रतिक्रिया में अपने व्यवहार को काफी मजबूती से बदल सकते हैं। इसलिए, एक अनियमित नेटवर्क एक जटिल मॉडल को प्रशिक्षित करने के लिए बड़े वजन का उपयोग कर सकता है जिसमें प्रशिक्षण डेटा में बहुत अधिक शोर की जानकारी होती है। संक्षेप में, नियमित नेटवर्क की सीमाएं उन्हें अपेक्षाकृत सरल मॉडल बनाने की अनुमति देती हैं, जो पैटर्न के आधार पर प्रशिक्षण डेटा में पाए जाते हैं, और वे प्रशिक्षण डेटा में शोर के कारण विचलन के लिए प्रतिरोधी हैं। एक उम्मीद है कि यह हमारे नेटवर्क को स्वयं घटना का अध्ययन करेगा, और प्राप्त ज्ञान को बेहतर ढंग से सामान्य करेगा।

उस सभी के साथ, सरल स्पष्टीकरणों को वरीयता देने का विचार आपको परेशान करना चाहिए। कभी-कभी लोग इस विचार को "ओकाम का उस्तरा" कहते हैं और उत्साह से इसे लागू करते हैं, जैसे कि यह एक सामान्य वैज्ञानिक सिद्धांत की स्थिति है। लेकिन यह, ज़ाहिर है, एक सामान्य वैज्ञानिक सिद्धांत नहीं है। जटिल लोगों को सरल स्पष्टीकरण पसंद करने के लिए कोई प्राथमिकता तार्किक कारण नहीं है। कभी-कभी अधिक जटिल स्पष्टीकरण सही होता है।

मुझे दो उदाहरणों का वर्णन करें कि कैसे अधिक जटिल स्पष्टीकरण सही निकला। 1940 के दशक में भौतिक विज्ञानी मार्सेल शेन ने एक नए कण की खोज की घोषणा की। जिस कंपनी के लिए उन्होंने काम किया, जनरल इलेक्ट्रिक, वह प्रसन्न थी, और इस घटना के प्रकाशन को व्यापक रूप से वितरित किया। हालांकि, भौतिक विज्ञानी हंस बेठे को संदेह था। बेथ ने शेन का दौरा किया और शेन के नए कण के निशान के साथ प्लेटों का अध्ययन किया। शेन ने प्लेट के बाद बीटा प्लेट दिखाई, लेकिन बेते ने उनमें से प्रत्येक पर एक समस्या पाई, जिसने इस डेटा को मना करने की आवश्यकता का संकेत दिया। अंत में, शेन ने बीटा को एक रिकॉर्ड दिखाया जो कि फिट दिखता था। बेठे ने कहा कि यह शायद एक सांख्यिकीय विचलन था। शेन: "हां, लेकिन आंकड़ों की वजह से इसके होने की संभावना यहां तक ​​कि आपके अपने फॉर्मूले से भी पांच में से एक है।" बेठे: "हालांकि, मैंने पहले ही पांच रिकॉर्ड देखे हैं।" अंत में, शेन ने कहा: "लेकिन आपने मेरे प्रत्येक रिकॉर्ड, हर अच्छी छवि को किसी अन्य सिद्धांत के साथ समझाया, और मेरी एक परिकल्पना है जो सभी रिकॉर्ड्स को एक ही बार में समझाती है, जिससे यह अनुसरण होता है कि हम एक नए कण के बारे में बात कर रहे हैं।" बेठे ने उत्तर दिया: “मेरे स्पष्टीकरण और तुम्हारे बीच एकमात्र अंतर यह है कि तुम्हारा गलत होना और मेरा सही होना। आपकी एकल व्याख्या गलत है, और मेरे सभी स्पष्टीकरण सही हैं। " इसके बाद, यह पता चला कि प्रकृति बेथ से सहमत थी, और शेन के कण वाष्पित हो गए।

दूसरे उदाहरण में, 1859 में, खगोलविद अर्बेन जीन जोसेफ ले वेरियर ने पाया कि बुध की कक्षा का आकार न्यूटन के सार्वभौमिक गुरुत्वाकर्षण के सिद्धांत के अनुरूप नहीं है। इस सिद्धांत से एक छोटे से विचलन हुआ, और फिर समस्या को हल करने के लिए कई विकल्प प्रस्तावित किए गए, जो इस तथ्य पर उबल पड़े कि न्यूटन का सिद्धांत संपूर्ण रूप से सही है, और केवल थोड़े बदलाव की आवश्यकता है। और 1916 में, आइंस्टीन ने दिखाया कि इस विचलन को सापेक्षता के अपने सामान्य सिद्धांत का उपयोग करके अच्छी तरह से समझाया जा सकता है, न्यूटनियन गुरुत्वाकर्षण से मौलिक रूप से अलग और बहुत अधिक जटिल गणित पर आधारित है। इस अतिरिक्त जटिलता के बावजूद, यह आमतौर पर आज स्वीकार किया जाता है कि आइंस्टीन का स्पष्टीकरण सही है, और न्यूटोनियन गुरुत्वाकर्षण एक संशोधित रूप में भी गलत है। यह विशेष रूप से होता है, क्योंकि आज हम जानते हैं कि आइंस्टीन का सिद्धांत कई अन्य घटनाओं की व्याख्या करता है, जिनके साथ न्यूटन के सिद्धांत में कठिनाइयां थीं। इसके अलावा, और भी आश्चर्यजनक रूप से, आइंस्टीन का सिद्धांत कई घटनाओं को सटीक रूप से भविष्यवाणी करता है जो न्यूटोनियन गुरुत्वाकर्षण ने भविष्यवाणी नहीं की थी। हालांकि, ये प्रभावशाली गुण अतीत में स्पष्ट नहीं थे। मात्र सादगी के आधार पर न्याय करना, फिर न्यूटन के सिद्धांत के कुछ संशोधित रूप अधिक आकर्षक लगेंगे।

इन कहानियों से तीन नैतिकताएं खींची जा सकती हैं। सबसे पहले, कभी-कभी यह तय करना काफी मुश्किल होता है कि दोनों में से कौन सा स्पष्टीकरण "आसान" होगा। दूसरे, भले ही हमने ऐसा निर्णय लिया हो, सादगी को बहुत सावधानी से निर्देशित किया जाना चाहिए! तीसरा, मॉडल का असली परीक्षण सादगी नहीं है, लेकिन यह व्यवहार की नई स्थितियों में नई घटनाओं की कितनी अच्छी भविष्यवाणी करता है।

यह सब देखते हुए और सावधानी बरतते हुए, हम एक अनुभवजन्य तथ्य को स्वीकार करेंगे - नियमित एनएस आमतौर पर अनियमित लोगों की तुलना में बेहतर सामान्यीकृत होते हैं। इसलिए, बाद में पुस्तक में हम अक्सर नियमितीकरण का उपयोग करेंगे। उल्लिखित कहानियों को केवल यह समझाने की आवश्यकता है कि क्यों किसी ने अभी तक पूरी तरह से सैद्धांतिक व्याख्या क्यों विकसित नहीं की है कि नियमितीकरण नेटवर्क को सामान्य बनाने में मदद क्यों करता है। शोधकर्ता उन कार्यों को प्रकाशित करना जारी रखते हैं जहां वे नियमितीकरण के लिए विभिन्न तरीकों की कोशिश करने की कोशिश करते हैं, उनकी तुलना करते हैं, जो सबसे अच्छा काम करता है उसे देखते हुए, और यह समझने की कोशिश करते हैं कि अलग-अलग दृष्टिकोण बदतर या बेहतर क्यों काम करते हैं। इसलिए नियमितीकरण को बादल की तरह माना जा सकता है। जब यह बहुत बार मदद करता है, तो हमारे पास जो कुछ भी हो रहा है उसकी पूरी तरह से संतोषजनक प्रणालीगत समझ नहीं है - केवल अधूरा हेयुरिस्टिक और व्यावहारिक नियम

यहाँ उन समस्याओं का गहरा समूह निहित है जो विज्ञान के बहुत हृदय तक जाती हैं। यह एक सामान्यीकरण मुद्दा है। नियमितीकरण हमें एक कम्प्यूटेशनल जादू की छड़ी दे सकता है जो हमारे नेटवर्क को डेटा को बेहतर बनाने में मदद करता है, लेकिन यह सामान्य समझ नहीं देता है कि सामान्यीकरण कैसे काम करता है, और इसके लिए सबसे अच्छा तरीका क्या है।

ये समस्याएं प्रेरण की समस्या पर वापस जाती हैं, जिसकी एक प्रसिद्ध व्याख्या स्कॉटलैंड के दार्शनिक डेविड ह्यूम ने " ए स्टडी ऑन ह्यूमन कॉग्निशन " पुस्तक (1748) में की थी। इंडक्शन प्रॉब्लम डेविड वाल्परट और विलियम मैक्रेडी (1977) द्वारा " मुफ्त भोजन की अनुपस्थिति पर प्रमेय " का विषय है।

और यह विशेष रूप से कष्टप्रद है, क्योंकि सामान्य जीवन में लोग अभूतपूर्व रूप से डेटा को सामान्य बनाने में सक्षम होते हैं। हाथी की कुछ छवियों को बच्चे को दिखाएं, और वह जल्दी से अन्य हाथियों को पहचानना सीख जाएगा। बेशक, वह कभी-कभी एक गलती कर सकता है, उदाहरण के लिए, एक हाथी के साथ एक राइनो को भ्रमित करें, लेकिन सामान्य तौर पर, यह प्रक्रिया आश्चर्यजनक रूप से सटीक रूप से काम करती है। अब, हमारे पास एक प्रणाली है - मानव मस्तिष्क - मुक्त मापदंडों की एक बड़ी मात्रा के साथ। और जब उसे एक या एक से अधिक प्रशिक्षण चित्र दिखाए जाते हैं, तो सिस्टम उन्हें अन्य छवियों के लिए सामान्य बनाना सीखता है। हमारा मस्तिष्क, एक अर्थ में, नियमित रूप से आश्चर्यजनक रूप से अच्छा है! लेकिन हम यह कैसे करते हैं? फिलहाल, यह हमारे लिए अज्ञात है। मुझे लगता है कि भविष्य में हम कृत्रिम तंत्रिका नेटवर्क में अधिक शक्तिशाली नियमितीकरण तकनीकों का विकास करेंगे, तकनीकें जो अंततः नेशनल असेंबली को भी छोटे डेटा सेट के आधार पर डेटा को सामान्य बनाने की अनुमति देती हैं।

वास्तव में, हमारे नेटवर्क पहले से ही बहुत बेहतर सामान्यीकरण कर रहे हैं, इससे पहले की अपेक्षा की जा सकती है। 100 छिपे हुए न्यूरॉन्स वाले नेटवर्क में लगभग 80,000 पैरामीटर हैं। हमारे पास प्रशिक्षण डेटा में केवल 50,000 छवियां हैं। यह 50,000 संदर्भ बिंदुओं पर 80,000 क्रम के बहुपद को खींचने की कोशिश के समान है। सभी संकेतों के द्वारा, हमारे नेटवर्क को बहुत पीछे हटना चाहिए। और फिर भी, जैसा कि हमने देखा है, ऐसा नेटवर्क वास्तव में बहुत अच्छी तरह से सामान्यीकृत है। ऐसा क्यों हो रहा है? यह पूरी तरह से स्पष्ट नहीं है। इसकी परिकल्पना की गई थी कि "बहुपरत नेटवर्क में ढाल वंश द्वारा सीखने की गतिशीलता आत्म-नियमन के अधीन है।" यह एक चरम भाग्य है, लेकिन यह भी एक परेशान करने वाला तथ्य है, क्योंकि हम यह नहीं समझते हैं कि ऐसा क्यों होता है। इस बीच, हम व्यावहारिक दृष्टिकोण अपनाएँगे, और जहाँ भी संभव होगा, हम नियमितीकरण का उपयोग करेंगे। यह हमारी नेशनल असेंबली के लिए फायदेमंद होगा।

मुझे पहले जो व्याख्या नहीं की थी, उसे वापस करके इस खंड को समाप्त कर दूं: L2 के नियमितीकरण से विस्थापन सीमित नहीं होता। स्वाभाविक रूप से, नियमितीकरण प्रक्रिया को बदलना आसान होगा ताकि यह विस्थापन को नियमित करे। लेकिन आनुभविक रूप से, यह अक्सर किसी भी ध्यान देने योग्य तरीके से परिणाम नहीं बदलता है, इसलिए, कुछ हद तक, पक्षपात के नियमितीकरण से निपटने के लिए, या नहीं, समझौते का विषय है। हालांकि, यह ध्यान देने योग्य है कि एक बड़ा विस्थापन बड़े भार की तरह इनपुट के लिए एक न्यूरॉन के प्रति संवेदनशील नहीं बनाता है। इसलिए, हमें बड़े ऑफ़सेट्स के बारे में चिंता करने की ज़रूरत नहीं है जो हमारे नेटवर्क को प्रशिक्षण डेटा में शोर सीखने की अनुमति देते हैं। उसी समय, बड़े विस्थापन की अनुमति देकर, हम अपने नेटवर्क को उनके व्यवहार में अधिक लचीला बनाते हैं - विशेष रूप से, बड़े विस्थापन न्यूरॉन्स की संतृप्ति को सुविधाजनक बनाते हैं, जो हम चाहेंगे। इस कारण से, हम आमतौर पर नियमितीकरण में ऑफसेट शामिल नहीं करते हैं।

अन्य नियमितीकरण तकनीक

एल 2 के अलावा कई नियमितीकरण तकनीकें हैं। वास्तव में, पहले से ही कई तकनीकों का विकास किया गया है, जो कि सभी इच्छा के साथ, मैं संक्षेप में उन सभी का वर्णन नहीं कर सका। इस खंड में, मैं संक्षेप में तीन अन्य दृष्टिकोणों का वर्णन करूंगा ताकि रिट्रेनिंग को कम किया जा सके: एल 1 को नियमित करना, छोड़ना और प्रशिक्षण सेट को कृत्रिम रूप से बढ़ाना। हम उन्हें पिछले विषयों की तरह गहराई से अध्ययन नहीं करेंगे। इसके बजाय, हम बस उन्हें जानते हैं, और साथ ही मौजूदा नियमितीकरण तकनीकों की विविधता की सराहना करते हैं।

नियमितीकरण L1

इस दृष्टिकोण में, हम वज़न के पूर्ण मूल्यों के योग को जोड़कर अनियमित लागत फ़ंक्शन को संशोधित करते हैं:

$$

$$C = C_0 + \ frac {\ lambda} {n} \ sum_w | w | {टैग {95}$$

सहज रूप से, यह एल 2 के नियमितीकरण के समान है, जो बड़े वजन के लिए जुर्माना करता है और नेटवर्क को कम वजन पसंद करता है। बेशक, एल 1 का नियमितीकरण शब्द एल 2 के नियमितीकरण की तरह नहीं है, इसलिए आपको बिल्कुल समान व्यवहार की उम्मीद नहीं करनी चाहिए। आइए समझने की कोशिश करें कि नियमितीकरण L1 के साथ प्रशिक्षित नेटवर्क का व्यवहार नियमितीकरण L2 के साथ प्रशिक्षित नेटवर्क से कैसे भिन्न है।

ऐसा करने के लिए, लागत फ़ंक्शन के आंशिक डेरिवेटिव को देखें। विभेदीकरण (95), हम प्राप्त करते हैं:

$$

$$\ frac {\ आंशिक C} {\ आंशिक w} = \ frac {\ आंशिक C_0} {\ आंशिक w} + \ frac {\ lambda} {n} \, {\ rm sgn} (w) टैग {96 }$$

जहाँ sgn (w) w का चिह्न है, अर्थात, यदि w सकारात्मक है, और -1 यदि w ऋणात्मक है, तो। इस अभिव्यक्ति का उपयोग करते हुए, हम पीछे के प्रसार को थोड़ा संशोधित करते हैं ताकि यह नियमित रूप से L1 का उपयोग करके स्टोकेस्टिक क्रमिक वंश का प्रदर्शन करे। L1- नियमित नेटवर्क के लिए अंतिम अद्यतन नियम:

$$

$$w \ rightarrow w '= w- \ frac {\ eta \ lambda} {n} \ mbox {sgn} (w) - \ eta \ frac {\ आंशिक C_0} {\ आंशिक w} {97}$$

जहां, हमेशा की तरह, /C / asw को मिनी-पैकेट के औसत मूल्य का उपयोग करके वैकल्पिक रूप से अनुमानित किया जा सकता है। नियमितीकरण नियम L2 (93) के साथ इसकी तुलना करें:

$$

$$w \ rightarrow w '= w \ left (1 - \ frac {\ eta \ lambda} {n} \ right) - \ eta \ frac {\ आंशिक C_0} {\ आंशिक w} \ टैग {98}$$

दोनों अभिव्यक्तियों में, नियमितीकरण का प्रभाव वजन कम करना है। यह सहज धारणा के साथ मेल खाता है कि दोनों प्रकार के नियमितीकरण बड़े भार को दंडित करते हैं। हालांकि, वजन अलग-अलग तरीकों से कम हो जाता है। L1 के नियमितीकरण में, वजन एक निरंतर मान से घटता है, 0. से झुकता है। L2 के नियमितीकरण में, वजन w के अनुपात में घट जाता है। इसलिए, जब कुछ वजन का एक बड़ा मूल्य होता है | w |, L1 के नियमितीकरण से वजन कम हो जाता है जितना L2 नहीं होता है। और इसके विपरीत, जब | w | L1 के छोटे, नियमितीकरण से L2 के नियमितीकरण की तुलना में वजन कम होता है। परिणामस्वरूप, L1 के नियमितीकरण से नेटवर्क वेट को उच्च महत्व के बॉन्ड की अपेक्षाकृत कम संख्या में केंद्रित किया जाता है, जबकि अन्य वेट शून्य हो जाते हैं।

मैंने पिछली चर्चा में एक समस्या को थोड़ा सुलझाया था - w = 0 होने पर आंशिक व्युत्पन्न ∂C / onew को परिभाषित नहीं किया गया है। इसकी वजह है फंक्शन | w | बिंदु w = 0 पर एक तीव्र "किंक" है, इसलिए, इसे वहां विभेदित नहीं किया जा सकता है। लेकिन यह डरावना नहीं है। हम सिर्फ w = 0 होने पर स्टोकेस्टिक क्रमिक वंश के लिए सामान्य, अनियमित नियम लागू करते हैं। वास्तव में, इसमें कुछ भी गलत नहीं है - नियमितीकरण को वज़न कम करना चाहिए, और जाहिर है कि यह वज़न को पहले से ही 0. के बराबर कम नहीं कर सकता है। अधिक सटीक रूप से, हम समीकरण (96) और (97) का उपयोग इस शर्त के साथ करेंगे कि sgn (0) = 0। यह हमें नियमितीकरण L1 के साथ स्टोचस्टिक ढाल वंश के लिए एक सुविधाजनक और कॉम्पैक्ट नियम देगा।

अपवाद [ड्रॉपआउट]

एक अपवाद पूरी तरह से अलग नियमितीकरण तकनीक है। एल 1 और एल 2 के नियमितीकरण के विपरीत, अपवाद लागत फ़ंक्शन में परिवर्तन से संबंधित नहीं है। इसके बजाय, हम नेटवर्क को ही बदल रहे हैं। मुझे इसके अपवाद के बुनियादी यांत्रिकी की व्याख्या करने से पहले कि यह क्यों काम करता है और किन परिणामों के साथ विषय में देरी करता है।

मान लीजिए कि हम एक नेटवर्क को प्रशिक्षित करने की कोशिश कर रहे हैं:


विशेष रूप से, मान लें कि हमारे पास प्रशिक्षण इनपुट x और संबंधित वांछित आउटपुट y है। आमतौर पर, हम इसे सीधे नेटवर्क पर x वितरित करके प्रशिक्षित करेंगे, और फिर ढाल के योगदान को निर्धारित करने के लिए वापस प्रचार करेंगे। एक अपवाद इस प्रक्रिया को संशोधित करता है। हम बेतरतीब ढंग से और अस्थायी रूप से नेटवर्क में छिपे हुए न्यूरॉन्स के आधे हिस्से को हटाते हैं, इनपुट और आउटपुट न्यूरॉन्स को अपरिवर्तित छोड़ देते हैं। उसके बाद, हमारे पास लगभग ऐसा नेटवर्क होगा। ध्यान दें कि बहिष्कृत न्यूरॉन्स, जिन्हें अस्थायी रूप से हटा दिया गया है, अभी भी आरेख में चिह्नित हैं:


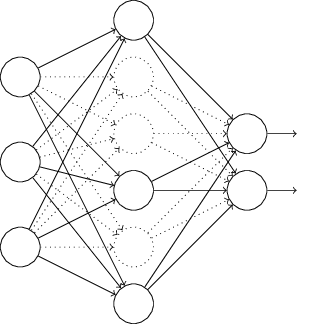
हम बदले हुए नेटवर्क पर सीधे वितरण के द्वारा x पास करते हैं, और फिर बदले हुए नेटवर्क पर भी परिणाम वितरित करते हैं। उदाहरणों के मिनी-पैकेज के साथ ऐसा करने के बाद, हम संबंधित वज़न और ऑफ़सेट को अपडेट करते हैं। फिर हम इस प्रक्रिया को दोहराते हैं, पहले बहिष्कृत न्यूरॉन्स को पुनर्स्थापित करते हैं, फिर एक और मिनी-पैकेट के लिए ढाल का मूल्यांकन करने के लिए छिपे हुए न्यूरॉन्स के एक नए यादृच्छिक सबसेट को चुनते हैं, और नेटवर्क के वजन और ऑफसेट को अपडेट करते हैं।

इस प्रक्रिया को बार-बार दोहराते हुए, हमें एक नेटवर्क मिलता है जिसने कुछ वज़न और विस्थापन सीखे हैं। स्वाभाविक रूप से, इन वज़न और विस्थापन को उन परिस्थितियों में सीखा गया था जिनमें छिपे हुए न्यूरॉन्स में से आधे को बाहर रखा गया था।और जब हम नेटवर्क को पूर्ण रूप से लॉन्च करते हैं, तो हमारे पास दो बार कई सक्रिय छिपे हुए न्यूरॉन्स होंगे। इसकी भरपाई के लिए, हम छिपे हुए न्यूरॉन्स से आने वाले वज़न को आधा कर देते हैं।

बहिष्करण प्रक्रिया अजीब और मनमाना लग सकती है। उसे नियमितीकरण में मदद क्यों करनी चाहिए? यह समझने के लिए कि क्या हो रहा है, मैं चाहता हूं कि आप कुछ समय के लिए अपवाद को भूल जाएं और एक मानक तरीके से नेशनल असेंबली का प्रशिक्षण प्रस्तुत करें। विशेष रूप से, कल्पना करें कि हम एक ही प्रशिक्षण डेटा का उपयोग करके कई अलग-अलग एनएस को प्रशिक्षित करते हैं। बेशक, नेटवर्क पहले अलग-अलग हो सकते हैं, और कभी-कभी प्रशिक्षण विभिन्न परिणाम उत्पन्न कर सकते हैं। ऐसे मामलों में, हम यह तय करने के लिए किसी तरह की औसत या मतदान योजना लागू कर सकते हैं कि कौन से आउटपुट को स्वीकार करना है। उदाहरण के लिए, यदि हमने पांच नेटवर्क को प्रशिक्षित किया है, और उनमें से तीन संख्याओं को "3" के रूप में वर्गीकृत करते हैं, तो यह संभवतः सही तीन है। और अन्य दो नेटवर्क शायद गलत हैं। इस तरह की एक औसत योजना अक्सर रिट्रीटिंग को कम करने के लिए एक उपयोगी (यद्यपि महंगा) तरीका है। कारण हैकि अलग-अलग नेटवर्क अलग-अलग तरीकों से पुन: उपयोग कर सकते हैं, और औसत इस तरह के रिट्रेनिंग को खत्म करने में मदद कर सकता है।

यह सब अपवाद से कैसे संबंधित है? स्वाभाविक रूप से, जब हम न्यूट्रॉन के विभिन्न सेटों को बाहर करते हैं, तो ऐसा लगता है जैसे हम विभिन्न एनएस को प्रशिक्षित कर रहे थे। इसलिए, बहिष्करण प्रक्रिया बहुत बड़ी संख्या में विभिन्न नेटवर्क पर औसत प्रभावों के समान है। अलग-अलग नेटवर्क अलग-अलग तरीकों से पीछे हटते हैं, इसलिए यह आशा की जाती है कि बहिष्करण के औसत प्रभाव से रिट्रेनिंग कम हो जाएगी।

बहिष्करण के लाभों की एक संबंधित अनुमानात्मक व्याख्या जल्द से जल्द काम करती हैइस तकनीक का उपयोग करना: “यह तकनीक न्यूरॉन्स के जटिल संयुक्त अनुकूलन को कम करती है, क्योंकि न्यूरॉन कुछ पड़ोसियों की उपस्थिति पर भरोसा नहीं कर सकता है। अंत में, उसे और अधिक विश्वसनीय लक्षण सीखने होंगे जो कि न्यूरॉन्स के कई अलग-अलग यादृच्छिक सबसेट के साथ मिलकर काम करने में उपयोगी हो सकते हैं। ” दूसरे शब्दों में, यदि हम एक अनुमान बनाने वाले मॉडल के रूप में हमारी नेशनल असेंबली की कल्पना करते हैं, तो एक अपवाद सबूत के व्यक्तिगत भागों के नुकसान के लिए मॉडल की स्थिरता की गारंटी देने का एक तरीका होगा। इस अर्थ में, तकनीक एल 1 और एल 2 की नियमितताओं से मिलती जुलती है, जो वजन कम करने की कोशिश करती है, और इस तरह से नेटवर्क में किसी भी व्यक्तिगत कनेक्शन के नुकसान के लिए नेटवर्क को अधिक प्रतिरोधी बनाता है।

स्वाभाविक रूप से, अपवर्जन की उपयोगिता का सही माप तंत्रिका नेटवर्क की दक्षता में सुधार करने में इसकी जबरदस्त सफलता है। में मूल कृतिजहां इस पद्धति को पेश किया गया था, यह कई अलग-अलग कार्यों के लिए लागू किया गया था। हम इस तथ्य में विशेष रूप से रुचि रखते हैं कि लेखकों ने एमएनआईएसटी से संख्याओं के वर्गीकरण के अपवाद को लागू किया, एक साधारण प्रत्यक्ष वितरण नेटवर्क का उपयोग करके जिसकी हमने जांच की थी। कागज नोट करता है कि उस समय तक, ऐसी वास्तुकला के लिए सबसे अच्छा परिणाम 98.4% सटीकता था। उन्होंने बहिष्करण के संयोजन और नियमितीकरण L2 के संशोधित रूप का उपयोग करके इसे 98.7% तक सुधार दिया। पैटर्न और भाषण मान्यता, और प्राकृतिक भाषा प्रसंस्करण सहित कई अन्य कार्यों के लिए समान रूप से प्रभावशाली परिणाम प्राप्त किए गए थे। अपवाद विशेष रूप से बड़े गहरे नेटवर्क को प्रशिक्षित करने में उपयोगी था, जहां अक्सर छंटनी की समस्या उत्पन्न होती है।

कृत्रिम रूप से प्रशिक्षण डेटा सेट का विस्तार करना

हमने पहले देखा था कि हमारी MNIST वर्गीकरण सटीकता 80 प्रतिशत तक गिर गई, जब हमने सिर्फ 1,000 प्रशिक्षण छवियों का उपयोग किया। और कोई आश्चर्य नहीं - कम डेटा के साथ, हमारा नेटवर्क लोगों द्वारा नंबर लिखने के लिए कम विकल्पों को पूरा करेगा। आइए दक्षता में परिवर्तन को देखने के लिए निर्धारित प्रशिक्षण के विभिन्न संस्करणों का उपयोग करके, 30 छिपे हुए न्यूरॉन्स के हमारे नेटवर्क को प्रशिक्षित करने का प्रयास करें। हम 10 के मिनी-पैकेट आकार, सीखने की गति, = 0.5, नियमितीकरण पैरामीटर λ = 5.0, और क्रॉस एन्ट्रोपी के साथ लागत फ़ंक्शन का उपयोग करके प्रशिक्षित करते हैं। हम डेटा के एक पूरे सेट का उपयोग करके 30 युगों के एक नेटवर्क को प्रशिक्षित करेंगे, और प्रशिक्षण डेटा की मात्रा में कमी के अनुपात में युगों की संख्या में वृद्धि करेंगे। प्रशिक्षण डेटा के विभिन्न सेटों के लिए समान वजन घटाने के कारक की गारंटी देने के लिए, हम नियमितीकरण पैरामीटर λ = 5 का उपयोग करेंगे।एक पूर्ण प्रशिक्षण सेट के साथ, और आनुपातिक रूप से डेटा वॉल्यूम में कमी के साथ इसे कम करें।


यह देखा जा सकता है कि प्रशिक्षण डेटा में वृद्धि के साथ वर्गीकरण सटीकता काफी बढ़ जाती है। यह वृद्धि वॉल्यूम में और वृद्धि के साथ जारी रहने की संभावना है। बेशक, ऊपर दिए गए ग्राफ से देखते हुए, हम संतृप्ति के करीब पहुंच रहे हैं। हालाँकि, मान लें कि हम इस ग्राफ को प्रशिक्षण डेटा की मात्रा पर एक लघुगणकीय निर्भरता के लिए फिर से तैयार करते हैं:


यह देखा जा सकता है कि अंत में चार्ट अभी भी ऊपर जाता है। इससे यह पता चलता है कि यदि हम 50,000 से अधिक के बजाय, उदाहरण के लिए, लाखों या अरबों हस्तलिखित उदाहरणों का अधिक मात्रा में डेटा लेते हैं - तो शायद हमें इतने छोटे आकार का भी बेहतर काम करने वाला नेटवर्क मिल जाएगा।

अधिक प्रशिक्षण डेटा प्राप्त करना एक महान विचार है। दुर्भाग्य से, यह महंगा हो सकता है, इसलिए व्यवहार में यह हमेशा संभव नहीं होता है। हालांकि, एक और विचार है जो लगभग काम कर सकता है - डेटा सेट को कृत्रिम रूप से बढ़ाएं। उदाहरण के लिए, मान लें कि हम MNIST से पाँच की छवि लेते हैं, और इसे थोड़ा घुमाते हैं, 15 से डिग्री:



यह स्पष्ट रूप से एक ही आंकड़ा है। लेकिन पिक्सेल स्तर पर, यह MNIST डेटाबेस में उपलब्ध छवियों से बहुत अलग है। यह मानना ​​उचित है कि इस छवि को प्रशिक्षण डाटासेट में जोड़ने से हमारे नेटवर्क को छवि वर्गीकरण के बारे में अधिक जानने में मदद मिल सकती है। इसके अलावा, हम स्पष्ट रूप से सिर्फ एक छवि जोड़ने की क्षमता तक सीमित नहीं हैं। हम MNIST से सभी प्रशिक्षण चित्रों के कुछ छोटे मोड़ बनाकर और फिर नेटवर्क की दक्षता बढ़ाने के लिए प्रशिक्षण डेटा के विस्तारित सेट का उपयोग करके अपने प्रशिक्षण डेटा का विस्तार कर सकते हैं।

यह विचार बहुत शक्तिशाली है, और इसका व्यापक रूप से उपयोग किया जाता है। आइए वैज्ञानिक कार्यों से परिणाम देखेंजिन्होंने इस विचार के कई रूपों को MNIST में लागू किया। उनके द्वारा माना जाने वाले नेटवर्क का एक आर्किटेक्चर हमारे द्वारा उपयोग किए जाने के समान था - 800 एनट्रॉन के साथ प्रत्यक्ष वितरण नेटवर्क, क्रॉस एन्ट्रॉपी के साथ लागत फ़ंक्शन का उपयोग करना। इस नेटवर्क को मानक MNIST प्रशिक्षण सेट के साथ लॉन्च करके, उन्होंने 98.4% की वर्गीकरण सटीकता प्राप्त की। लेकिन फिर उन्होंने प्रशिक्षण डेटा का विस्तार किया, न केवल ऊपर वर्णित रोटेशन का उपयोग करते हुए, बल्कि छवियों के हस्तांतरण और विरूपण भी। उन्नत डेटा पर नेटवर्क को प्रशिक्षित करने के बाद, उन्होंने इसकी सटीकता 98.9% तक बढ़ा दी। उन्होंने तथाकथित के साथ प्रयोग भी किया "लोचदार विरूपण", एक विशेष प्रकार की छवि विरूपण, जिसे हाथ की मांसपेशियों के यादृच्छिक कंपन को खत्म करने के लिए डिज़ाइन किया गया है। डेटा का विस्तार करने के लिए लोचदार विकृतियों का उपयोग करते हुए, उन्होंने 99.3% की सटीकता हासिल की। संक्षेप में, उन्होंने अपने नेटवर्क अनुभव का विस्तार किया,असली लिखावट में पाए गए उसके कई हस्तलिखित रूपांतर हैं।

इस विचार के वेरिएंट का उपयोग कई शिक्षण कार्यों के प्रदर्शन को बेहतर बनाने के लिए किया जा सकता है, न केवल लिखावट की मान्यता के लिए। सामान्य सिद्धांत उनके लिए संचालन को लागू करके प्रशिक्षण डेटा का विस्तार करना है जो वास्तविकता में आई विविधताओं को दर्शाते हैं। इस तरह की विभिन्नताएँ आसानी से सामने आती हैं। मान लीजिए हम भाषण मान्यता के लिए NS बना रहे हैं। लोग पृष्ठभूमि शोर जैसे विकृतियों के साथ भी भाषण को पहचान सकते हैं। इसलिए, आप पृष्ठभूमि शोर जोड़कर डेटा का विस्तार कर सकते हैं। हम त्वरित और धीमे भाषण को पहचानने में भी सक्षम हैं। यह प्रशिक्षण डेटा का विस्तार करने का एक और तरीका है। इन तकनीकों का हमेशा उपयोग नहीं किया जाता है - उदाहरण के लिए, शोर को जोड़कर प्रशिक्षण सेट का विस्तार करने के बजाय, उन्हें शोर फ़िल्टर लागू करके इनपुट को साफ करने के लिए अधिक कुशल हो सकता है। और फिर भी, यह प्रशिक्षण सेट के विस्तार के विचार को ध्यान में रखता है,और इसका उपयोग करने के तरीकों की तलाश करें।

व्यायाम

• जैसा कि हमने ऊपर चर्चा की है, MNIST से प्रशिक्षण डेटा को विस्तारित करने का एक तरीका प्रशिक्षण चित्रों के छोटे घुमाव का उपयोग करना है। यदि हम किसी भी कोण पर चित्रों के रोटेशन की अनुमति देते हैं तो क्या समस्या आ सकती है?

बड़ा डेटा पाचन और वर्गीकरण सटीकता की तुलना का अर्थ है

आइए एक बार फिर देखें कि प्रशिक्षण सेट के आकार के आधार पर हमारे एनएस की सटीकता कैसे भिन्न होती है:


मान लीजिए कि NS का उपयोग करने के बजाय हम संख्याओं को वर्गीकृत करने के लिए एक और मशीन लर्निंग तकनीक का उपयोग करेंगे। उदाहरण के लिए, आइए हम सदिश मशीन (एसवीएम) पद्धति का उपयोग करने का प्रयास करें, जिसे हम संक्षेप में अध्याय 1 में मिलते हैं। तब तक, यदि आप एसवीएम से परिचित नहीं हैं, तो चिंता न करें, हमें इसके विवरण को समझने की आवश्यकता नहीं है। हम एसवीएम का उपयोग स्किटिट-लर्न लाइब्रेरी के माध्यम से करेंगे। यहां बताया गया है कि प्रशिक्षण सेट के आकार के साथ एसवीएम की प्रभावशीलता कैसे भिन्न होती है। तुलना के लिए, मैंने नेशनल असेंबली के शेड्यूल और परिणामों को रखा।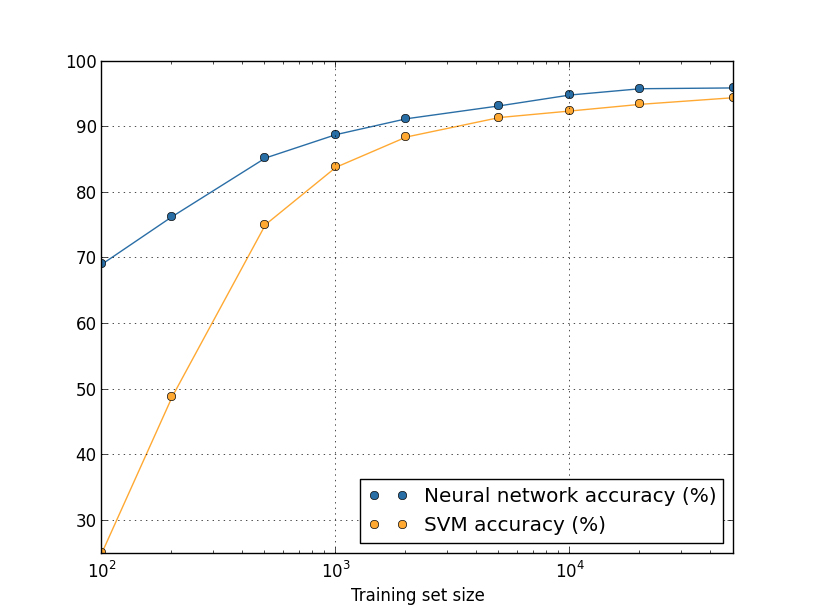


संभवत: पहली चीज जो आपकी आंख को पकड़ती है - एनएस प्रशिक्षण सेट के किसी भी आकार में एसवीएम से आगे निकल जाती है। यह अच्छा है, हालांकि यह इससे दूरगामी निष्कर्ष निकालने के लायक नहीं है, क्योंकि मैंने पूर्वनिर्धारित स्कोर-लर्न सेटिंग्स का उपयोग किया था, और हमने अपने एनएस पर काफी गंभीरता से काम किया। एक कम ज्वलंत, लेकिन अधिक दिलचस्प तथ्य, जो ग्राफ से निम्नानुसार है, अगर हम 50,000 छवियों का उपयोग करके हमारे एसवीएम को प्रशिक्षित करते हैं, तो यह 5000 चित्रों के साथ प्रशिक्षित हमारे एनएस की तुलना में बेहतर (94.48% सटीकता) काम करेगा। 93.24%)। दूसरे शब्दों में, प्रशिक्षण डेटा की मात्रा में वृद्धि कभी-कभी एमओ एल्गोरिदम के अंतर की भरपाई करती है।

कुछ और दिलचस्प हो सकता है। मान लीजिए कि हम दो एल्गोरिदम एमओ, ए और बी का उपयोग करके एक समस्या को हल करने की कोशिश कर रहे हैं। कभी-कभी ऐसा होता है कि एल्गोरिथ्म ए एक प्रशिक्षण डेटा के एक सेट पर एल्गोरिदम बी से आगे है, और एल्गोरिदम बी प्रशिक्षण डेटा के एक और सेट पर एल्गोरिदम ए से आगे है। हमने इसे ऊपर नहीं देखा - फिर रेखांकन प्रतिच्छेद करेगा - लेकिन ऐसा होता है । प्रश्न का सही उत्तर: "क्या एल्गोरिथ्म एल्गोरिथम बी से बेहतर है?" वास्तव में, यह: "आप किस प्रशिक्षण डेटासेट का उपयोग कर रहे हैं?"

यह सब ध्यान में रखा जाना चाहिए, दोनों विकास के दौरान और वैज्ञानिक पत्र पढ़ने के दौरान। कई काम मानक माप डेटा सेट पर बेहतर परिणाम निचोड़ने के लिए नई चालें खोजने पर ध्यान केंद्रित करते हैं। "हमारे सुपरफूड तकनीक ने हमें मानक तुलनात्मक सेट वाई पर एक एक्स% सुधार दिया" - इस तरह के एक अध्ययन में विहित आवेदन पत्र। कभी-कभी ऐसे बयान वास्तव में दिलचस्प होते हैं, लेकिन यह समझना सार्थक है कि वे केवल एक विशिष्ट प्रशिक्षण सेट के संदर्भ में लागू होते हैं। एक वैकल्पिक कहानी की कल्पना करें, जिसमें शुरू में तुलनात्मक सेट बनाने वाले लोगों को एक बड़ा शोध अनुदान प्राप्त हुआ। वे अतिरिक्त डेटा एकत्र करने के लिए अतिरिक्त धन का उपयोग कर सकते हैं। यह संभव है कि सुपर-डुपर तकनीक का "सुधार" एक बड़े डेटासेट पर गायब हो जाए। दूसरे शब्दों में,सुधार का सार सिर्फ एक दुर्घटना हो सकती है। इस से, निम्न नैतिकता को व्यावहारिक अनुप्रयोग के क्षेत्र में ले जाना चाहिए: हमें बेहतर एल्गोरिदम और बेहतर प्रशिक्षण डेटा दोनों की आवश्यकता है। बेहतर एल्गोरिदम की तलाश में कुछ भी गलत नहीं है, लेकिन सुनिश्चित करें कि आप इस पर ध्यान केंद्रित नहीं करते हैं, प्रशिक्षण डेटा की मात्रा या गुणवत्ता में वृद्धि करके जीतने के आसान तरीके की अनदेखी कर रहे हैं।

कार्य

• . ? . – , , , . , . - ? , .

परिणाम

हमने अपना विसर्जन रिट्रेनिंग और नियमितीकरण में पूरा किया है। निश्चित ही, हम इन समस्याओं की ओर लौटेंगे। जैसा कि मैंने पहले ही कई बार उल्लेख किया है, एनएस के क्षेत्र में रिट्रेनिंग एक बड़ी समस्या है, खासकर जब कंप्यूटर अधिक शक्तिशाली हो जाते हैं और हम अपने नेटवर्क को प्रशिक्षित कर सकते हैं। नतीजतन, रिट्रेनिंग को कम करने के लिए प्रभावी नियमितीकरण तकनीकों को विकसित करने की तत्काल आवश्यकता है, इसलिए यह क्षेत्र आज बहुत सक्रिय है।

वजन की शुरूआत

जब हम अपना NS बनाते हैं, तो हमें वज़न और ऑफसेट के शुरुआती मूल्यों का चुनाव करना होगा। अब तक, हमने उन्हें अध्याय 1 में वर्णित दिशानिर्देशों के अनुसार चुना है। मैं आपको याद दिला दूं कि हमने 0 की गणितीय अपेक्षा के साथ एक स्वतंत्र गौसियन वितरण के आधार पर वज़न और ऑफसेट को चुना था और 1 का मानक विचलन। इस दृष्टिकोण ने अच्छा काम किया है, लेकिन ऐसा लगता है कि यह मनमाना है, इसलिए यह इसके लायक है इसे संशोधित करें और सोचें कि क्या शुरुआती वजन और विस्थापन को निर्दिष्ट करने का एक बेहतर तरीका खोजना संभव है, और, शायद, हमारे एनएस को तेजी से सीखने में मदद मिलेगी।

यह पता चला है कि सामान्यीकृत गाऊसी वितरण के साथ तुलनात्मक प्रक्रिया में गंभीरता से सुधार किया जा सकता है। इसे समझने के लिए, मान लें कि हम एक नेटवर्क के साथ बड़ी संख्या में इनपुट न्यूरॉन्स के साथ काम करते हैं, कहते हैं, 1000 के साथ। और मान लें कि हमने सामान्य गॉसियन वितरण का उपयोग पहली छुपी हुई परत से जुड़े भार को आरंभ करने के लिए किया। अब तक, मैं केवल इनपुट न्यूरॉन्स को छिपी हुई परत में पहले न्यूरॉन से जोड़ने वाले तराजू पर ध्यान केंद्रित करूंगा, और बाकी नेटवर्क को अनदेखा करूंगा:


सादगी के लिए, कल्पना करें कि हम इनपुट x के साथ एक नेटवर्क को प्रशिक्षित करने का प्रयास कर रहे हैं, जिसमें आधे इनपुट न्यूरॉन्स चालू हैं, अर्थात, उनका मान 1 है, और आधा बंद है, अर्थात, उनका मान 0. है। अगला कार्य अधिक सामान्य स्थिति में काम करता है, लेकिन यह आसान है इस विशेष उदाहरण पर उसे समझेंगे। एक छिपे हुए न्यूरॉन के लिए इनपुट के भारित राशि z = w _j w _j x _j + b पर विचार करें। योग के 500 सदस्य गायब हो जाते हैं क्योंकि संबंधित एक्स _जे 0. हैं। इसलिए, z 501 सामान्यीकृत गाऊसी यादृच्छिक चर, 500 वज़न और 1 अतिरिक्त ऑफसेट का योग है। इसलिए, z मान में केवल 0 की गणितीय अपेक्षा और ≈501 √ 22.4 का एक मानक विचलन के साथ एक गाऊसी वितरण है। यह है, z में तेज चोटियों के बिना एक काफी विस्तृत गाऊसी वितरण है:


विशेष रूप से, यह ग्राफ़ दिखाता है कि z | z | काफी बड़ा है, अर्थात, z ≫ 1 या z। -1। इस मामले में, छिपे हुए न्यूरॉन्स case (z) का आउटपुट 1 या 0. के बहुत करीब होगा। इसका मतलब है कि हमारे छिपे हुए न्यूरॉन को संतृप्त किया जाएगा। और जब ऐसा होता है, जैसा कि हम पहले से ही जानते हैं, वज़न में छोटे बदलाव एक छिपे हुए न्यूरॉन की सक्रियता में छोटे बदलाव पैदा करेंगे। बदले में ये छोटे परिवर्तन, नेटवर्क में शेष न्यूट्रॉन को व्यावहारिक रूप से प्रभावित नहीं करेंगे, और हम लागत समारोह में संबंधित छोटे बदलाव देखेंगे। नतीजतन, इन वेट को धीरे-धीरे प्रशिक्षित किया जाएगा जब हम ढाल वंश एल्गोरिथ्म का उपयोग करेंगे। यह उस कार्य के समान है जिसे हमने पहले ही इस अध्याय में चर्चा की थी, जिसमें आउटपुट न्यूरॉन्स गलत मूल्यों के साथ संतृप्त होते हैं जिससे सीखने की गति धीमी हो जाती है। हम इस समस्या को बड़ी चतुराई से लागत समारोह का चयन करके हल करते थे। दुर्भाग्य से, हालांकि इससे संतृप्त आउटपुट न्यूरॉन्स के साथ मदद मिली, यह छिपे हुए न्यूरॉन्स की संतृप्ति के साथ बिल्कुल भी मदद नहीं करता है।

अब मैंने पहली छिपी हुई परत के आने वाले पैमानों के बारे में बात की। स्वाभाविक रूप से, एक ही तर्क निम्नलिखित छिपी हुई परतों पर लागू होता है: यदि बाद की छिपी हुई परतों में भार सामान्यीकृत गाऊसी वितरणों का उपयोग करके शुरू किया जाता है, तो उनकी सक्रियता अक्सर 0 या 1 के करीब होगी, और प्रशिक्षण बहुत धीरे-धीरे चलेगा।

क्या वज़न और ऑफ़सेट के लिए सबसे अच्छा इनिशियलाइज़ेशन विकल्प चुनने का एक तरीका है, ताकि हमें इस तरह की संतृप्ति न मिले, और सीखने में देरी से बच सकें? मान लीजिए कि हमारे पास आने वाले भार n की संख्या के साथ एक न्यूरॉन _है । फिर हमें 0 की गणितीय अपेक्षा और 1 / 1n के मानक विचलन के साथ यादृच्छिक गाऊसी वितरण के साथ इन वज़न को शुरू करने की आवश्यकता _है । यही है, हम गॉसियंस को संकुचित करते हैं, और न्यूरॉन की संतृप्ति की संभावना को कम करते हैं। फिर हम 0 की गणितीय अपेक्षा और 1 के मानक विचलन के साथ विस्थापन के लिए एक गाऊसी वितरण का चयन करेंगे, इस कारण से कि मैं थोड़ी देर बाद लौटूंगा। इस विकल्प को बनाने के बाद, हम फिर से यह पाते हैं कि z = w _j w _j x _j + b एक गाऊसी वितरण वाला एक यादृच्छिक चर होगा जिसमें 0 की गणितीय अपेक्षा होगी, लेकिन पहले की तुलना में अधिक स्पष्ट शिखर के साथ। मान लीजिए, पहले की तरह, कि ५०० इनपुट ० और ५०० हैं। १. तब यह दिखाना आसान है (नीचे दिए गए व्यायाम को देखें) कि z में ० की गणितीय अपेक्षा के साथ गौसियन वितरण है और √ (3/2) 1.22 का एक मानक विचलन है ... इस ग्राफ में बहुत अधिक तेज शिखर है, इतना अधिक कि स्थिति के नीचे की तस्वीर को भी थोड़ा समझा जा सकता है, क्योंकि मुझे पिछले ग्राफ की तुलना में ऊर्ध्वाधर अक्ष के पैमाने को बदलना था:


इस तरह के एक न्यूरॉन को बहुत कम संभावना के साथ संतृप्त किया जाएगा, और, तदनुसार, यह सीखने में मंदी का सामना करने की कम संभावना होगी।

व्यायाम

• पुष्टि करें कि पिछले पैराग्राफ से z = _{j j} w _j x _j + b का मानक विचलन √ (3/2) है। इसके पक्ष में विचार: स्वतंत्र यादृच्छिक चर की राशि का भिन्नता, व्यक्तिगत यादृच्छिक चर के चर के योग के बराबर है; विचरण मानक विचलन के वर्ग के बराबर है।

मैंने ऊपर उल्लेख किया है कि हम 0 की गणितीय अपेक्षा के साथ एक स्वतंत्र गौसियन वितरण के आधार पर, पहले की तरह, विस्थापन को जारी रखना जारी रखेंगे और 1. का एक सामान्य विचलन है, और यह सामान्य है, क्योंकि यह हमारे न्यूरॉन्स की संतृप्ति की संभावना को बहुत अधिक नहीं बढ़ाता है। दरअसल, अगर हम संतृप्ति की समस्या से बचने के लिए प्रबंध करते हैं तो ऑफसेट की शुरुआत ज्यादा मायने नहीं रखती है। कुछ लोग सभी ऑफरों को शून्य करने की कोशिश करते हैं, और इस तथ्य पर भरोसा करते हैं कि ढाल वंशज उपयुक्त ऑफसेट सीख सकते हैं। लेकिन चूंकि यह संभावना है कि यह कुछ को प्रभावित करेगा, इसलिए हम पहले की तरह ही आरंभिक प्रक्रिया का उपयोग करना जारी रखेंगे।

आइए MNIST से संख्याओं को वर्गीकृत करने के कार्य का उपयोग करते हुए भार को आरंभ करने के लिए पुराने और नए दृष्टिकोणों के परिणामों की तुलना करें। पहले की तरह, हम 30 छिपे हुए न्यूरॉन्स का उपयोग करेंगे, आकार 10 का एक मिनी-पैकेट, एक नियमितीकरण पैरामीटर और लैम्ब्डा = 5.0, और क्रॉस एन्ट्रोपी के साथ एक लागत फ़ंक्शन। हम धीरे-धीरे सीखने की गति को 0.5 = 0.5 से 0.1 तक कम कर देंगे, क्योंकि इस तरह से परिणाम ग्राफ पर थोड़ा बेहतर दिखाई देंगे। आप पुरानी वज़न आरंभीकरण विधि का उपयोग करके सीख सकते हैं:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

आप वेट को इनिशियलाइज़ करने के लिए नए दृष्टिकोण का उपयोग करके भी सीख सकते हैं। यह और भी सरल है, क्योंकि डिफ़ॉल्ट रूप से network2 एक नए दृष्टिकोण का उपयोग करके वज़न को आरंभ करता है। इसका अर्थ है कि हम net.large_weight_initializer () कॉल को पहले छोड़ सकते हैं:

 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

हम प्लॉट करते हैं (प्रोग्राम weight_initialization.py का उपयोग करके):


दोनों मामलों में, 96% की वर्गीकरण सटीकता प्राप्त की जाती है। परिणामस्वरूप सटीकता दोनों मामलों में लगभग समान है। लेकिन नई इनिशियलाइज़ेशन तकनीक इस बिंदु तक बहुत तेज़ी से पहुँचती है। प्रशिक्षण के अंतिम युग के अंत में, वजन को कम करने का पुराना तरीका 87% की सटीकता तक पहुंच जाता है, और नया दृष्टिकोण पहले से ही 93% है। जाहिरा तौर पर, वज़न को कम करने के लिए एक नया दृष्टिकोण बहुत बेहतर स्थिति से शुरू होता है, इसलिए हमें बहुत तेज़ी से अच्छे परिणाम मिलते हैं। यदि हम 100 न्यूरॉन्स वाले नेटवर्क के लिए परिणाम बनाते हैं तो यही घटना देखी गई है:


इस मामले में, दो घटता घटित नहीं होती हैं। हालांकि, मेरे प्रयोगों का कहना है कि यदि आप थोड़ा और युग जोड़ते हैं, तो सटीकता लगभग संयोग से शुरू होती है। इसलिए, इन प्रयोगों के आधार पर, हम यह कह सकते हैं कि भार के आरंभ में सुधार से केवल प्रशिक्षण में तेजी आती है, लेकिन समग्र नेटवर्क दक्षता में बदलाव नहीं होता है। हालाँकि, अध्याय 4 में हम एनएस के उदाहरणों को देखेंगे जिसमें 1 / ofn के माध्यम से भार के आरंभ के परिणामस्वरूप दीर्घकालिक दक्षता में काफी सुधार हुआ _है । इसलिए, यह न केवल सीखने की गति में सुधार करता है, बल्कि कभी-कभी परिणामी प्रभावशीलता भी।

तंत्रिका नेटवर्क के प्रशिक्षण को बेहतर बनाने _में मदद करता है। वजन को प्रारंभिक करने के लिए अन्य तकनीकों का प्रस्ताव किया गया है, जिनमें से कई इस मूल विचार पर आधारित हैं। मैं उन्हें यहां नहीं मानूंगा, क्योंकि 1 / worksn हमारे उद्देश्यों के लिए अच्छी तरह _से काम करता है। यदि आप रुचि रखते हैं, तो मैं योशुआ बेंगजियो द्वारा 2012 के एक पत्र में पृष्ठ 14 और 15 पर चर्चा पढ़ने की सलाह देता हूं।

कार्य

• नियमितीकरण का संयोजन और एक बेहतर वजन आरंभीकरण विधि। कभी-कभी L2 का नियमितीकरण स्वचालित रूप से वज़न को आरम्भ करने की एक नई विधि के समान परिणाम देता है। मान लें कि हम पुराने दृष्टिकोण का उपयोग वजन को कम करने के लिए करते हैं। इस बात को साबित करने वाले एक तर्क वितर्क को रेखांकित करें कि: (1) यदि λ बहुत छोटा नहीं है, तो प्रशिक्षण के पहले युग में, वज़न कम करना लगभग पूरी तरह से हावी होगा; (2) अगर ≪λ, n, तो वज़न ई ^{/λ / m} को कमजोर करेगा युग में; (3) यदि λ बहुत बड़ा नहीं है, तो जब वज़न घटकर लगभग 1 / 1n हो जाता है, तो वजन कम हो जाएगा, जहाँ n नेटवर्क में कुल वज़न की संख्या है। सिद्ध करें कि ये स्थितियाँ उन उदाहरणों में संतुष्ट हैं जिनके लिए इस खंड में रेखांकन का निर्माण किया गया है।

लिखावट मान्यता पर लौटना: कोड

आइए इस अध्याय में वर्णित विचारों को लागू करें। हम एक नया प्रोग्राम, network2.py, जो कि हम अध्याय 1 में बनाए गए network.py का एक उन्नत संस्करण है, विकसित करेंगे। यदि आपने लंबे समय तक इसका कोड नहीं देखा है, तो यह इसके माध्यम से त्वरित रूप से चलने लायक हो सकता है। ये कोड की सिर्फ 74 लाइनें हैं, और इसे समझना आसान है।

जैसा कि network.py के साथ किया जाता है, network2.py का तारा नेटवर्क क्लास है, जिसका उपयोग हम अपने एनएस का प्रतिनिधित्व करने के लिए करते हैं। हम इसी नेटवर्क परतों के आकार की सूची के साथ वर्ग उदाहरण को आरंभीकृत करते हैं, और लागत फ़ंक्शन का विकल्प, डिफ़ॉल्ट रूप से यह क्रॉस एन्ट्रॉपी होगा:

 class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost 

__In___ पद्धति की पहली जोड़ी नेटवर्क-नेटवर्क के समान है, और स्वयं द्वारा समझी जाती है। अगली दो पंक्तियाँ नई हैं, और हमें विस्तार से समझने की ज़रूरत है कि वे क्या कर रहे हैं।

चलिए default_weight_initializer पद्धति से शुरू करते हैं। वह वजन को कम करने के लिए एक नए, बेहतर दृष्टिकोण का उपयोग करता है। जैसा कि हमने देखा है, इस दृष्टिकोण में, न्यूरॉन में प्रवेश करने वाले भार को 0 की गणितीय अपेक्षा के साथ एक स्वतंत्र गाऊसी वितरण के आधार पर आरंभ किया जाता है और न्यूरॉन के आने वाले लिंक की संख्या के वर्गमूल से विभाजित 1 का मानक विचलन होता है। इसके अलावा, यह विधि 0 के माध्य से गौसियन वितरण का उपयोग करके ऑफ़सेट्स को इनिशियलाइज़ करेगी और 1 का मानक विचलन है। यहाँ कोड है:

  def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

इसे समझने के लिए, आपको यह याद रखने की आवश्यकता है कि एनपी रैखिक बीजगणित से निपटने वाला एक नम्पी पुस्तकालय है। हमने इसे कार्यक्रम की शुरुआत में आयात किया था। यह भी ध्यान दें कि हम न्यूरॉन्स की पहली परत में विस्थापन को प्रारंभिक नहीं करते हैं। पहली परत भीतर की ओर है, इसलिए ऑफसेट का उपयोग नहीं किया जाता है। वही नेटवर्क्स था।

Default_weight_initializer पद्धति के अतिरिक्त, हम एक बड़ा_weight_initializer विधि बनाएंगे। यह अध्याय 1 से पुराने दृष्टिकोण का उपयोग करके वज़न और ऑफ़सेट्स को आरंभ करता है, जहाँ 0 की गणितीय अपेक्षा के साथ एक स्वतंत्र गॉसियन वितरण के आधार पर वज़न और ऑफ़सेट आरंभ किए जाते हैं और 1 का एक मानक विचलन। बेशक, यह कोड default_weight_initializer से बहुत अलग नहीं है:

  def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

मैंने इस पद्धति को मुख्य रूप से शामिल किया क्योंकि इस अध्याय और अध्याय 1 के परिणामों की तुलना करना हमारे लिए अधिक सुविधाजनक था। मैं किसी भी वास्तविक विकल्प की कल्पना नहीं कर सकता जिसमें मैं इसका उपयोग करने की सलाह दूंगा!

__Init__ विधि की दूसरी नवीनता लागत विशेषता का आरंभीकरण होगी। यह समझने के लिए कि यह कैसे काम करता है, आइए हम उस वर्ग को देखें जिसका उपयोग हम क्रॉस-एन्ट्रापी लागत फ़ंक्शन का प्रतिनिधित्व करने के लिए करते हैं (@staticmethod निर्देश दुभाषिया को बताता है कि यह विधि ऑब्जेक्ट से स्वतंत्र है, इसलिए स्वयं पैरामीटर fn और डेल्टा विधियों के लिए पारित नहीं हुआ है)।

 class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay) 

चलिए इसका पता लगाते हैं। पहली चीज जो यहां देखी जा सकती है, वह यह है कि, हालांकि क्रॉस एन्ट्रॉपी गणितीय दृष्टिकोण से एक फ़ंक्शन है, हम इसे अजगर वर्ग के रूप में लागू करते हैं, न कि अजगर फ़ंक्शन के रूप में। मैंने ऐसा करने का फैसला क्यों किया? हमारे नेटवर्क में, मान दो अलग-अलग भूमिका निभाता है। स्पष्ट - यह एक माप है कि आउटपुट सक्रियण वांछित आउटपुट y के अनुरूप कितना अच्छा है। यह भूमिका CrossEntropyCost.fn विधि द्वारा प्रदान की गई है। (वैसे, ध्यान दें कि CrossEntropyCost.fn के अंदर np.nan_to_num को कॉल करना सुनिश्चित करता है कि Numpy शून्य के करीब संख्याओं के लघुगणक को सही ढंग से संसाधित करता है)। हालांकि, लागत नेटवर्क का उपयोग हमारे नेटवर्क में दूसरे तरीके से किया जाता है। हम अध्याय 2 से याद करते हैं कि बैकप्रॉपैगमेंट एल्गोरिथ्म को शुरू करते समय, हमें नेटवर्क error ^एल के आउटपुट एरर पर विचार करना होगा ^। आउटपुट त्रुटि का रूप लागत फ़ंक्शन पर निर्भर करता है: विभिन्न लागत कार्यों में आउटपुट त्रुटि के विभिन्न रूप होंगे। क्रॉस एन्ट्रापी के लिए, आउटपुट एरर, समीकरण (66) से निम्नानुसार होगा:

$$

$$\ डेल्टा ^ एल = ए ^ एल-वाई \ टैग {99}$$

इसलिए, मैं एक दूसरी विधि को परिभाषित करता हूं, CrossEntropyCost.delta, जिसका लक्ष्य नेटवर्क को यह बताना है कि आउटपुट त्रुटि की गणना कैसे करें। और फिर हम इन दो तरीकों को एक वर्ग में जोड़ते हैं जिसमें हमारे नेटवर्क को लागत फ़ंक्शन के बारे में जानने की जरूरत है।

समान कारण से, network2.py में एक वर्ग होता है जो एक द्विघात लागत फ़ंक्शन का प्रतिनिधित्व करता है। अध्याय 1 के परिणामों की तुलना के लिए इसे शामिल करना, क्योंकि भविष्य में हम मुख्य रूप से क्रॉस एन्ट्रॉपी का उपयोग करेंगे। कोड नीचे है। QuadraticCost.fn विधि आउटपुट a और वांछित आउटपुट y के साथ जुड़े द्विघात लागत की एक सरल गणना है। QuadraticCost.delta द्वारा दिया गया मान द्विघात मान के आउटपुट त्रुटि के लिए अभिव्यक्ति (30) पर आधारित है, जिसे हम अध्याय 2 में प्राप्त करते हैं।

 class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z) 

अब हमने network2.py और network2.py के बीच मुख्य अंतर का पता लगा लिया है। सब कुछ बहुत सरल है। अन्य छोटे परिवर्तन हैं जिनका मैं नीचे वर्णन करूंगा, जिनमें L2 के नियमितीकरण का कार्यान्वयन शामिल है। इससे पहले, चलो पूर्ण network2.py कोड को देखें। यह विस्तार से अध्ययन करने के लिए आवश्यक नहीं है, लेकिन यह मूल संरचना को समझने के लायक है, विशेष रूप से, कार्यक्रम के प्रत्येक टुकड़े को समझने के लिए टिप्पणियों को पढ़ना। निश्चित रूप से, मैं इस प्रश्न पर उतनी रोक नहीं लगाता हूँ, जितनी आप चाहते हैं! यदि आप खो जाते हैं, तो प्रोग्राम के बाद पाठ को पढ़ने का प्रयास करें, और फिर से कोड पर लौटें। सामान्य तौर पर, यहाँ यह है:

 """network2.py ~~~~~~~~~~~~~~   network.py,            .   –      , ,   .     ,    .   ,       . """ ####  #  import json import random import sys #  import numpy as np ####   ,      class QuadraticCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. """ return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): """  delta   .""" return (ay) * sigmoid_prime(z) class CrossEntropyCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. np.nan_to_num    .  ,   ``a``  ``y``      1.0,   (1-y)*np.log(1-a)  nan. np.nan_to_num ,       (0.0). """ return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): """  delta   .  ``z``    ,          delta     . """ return (ay) ####   Network class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].       ,   ``self.default_weight_initializer`` (.  ). """ self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost def default_weight_initializer(self): """            0    1,       ,       .          0    1.    ,         ,           . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def large_weight_initializer(self): """          0    1.          0    1.    ,         ,           .         1,    .       . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def feedforward(self, a): """  ,  ``a``  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, lmbda = 0.0, evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False): """     -    . ``training_data`` –   ``(x, y)``,       .       ,    ``lmbda``.    ``evaluation_data``,     ,   .         ,     ,   .      :   ,    ,   ,              .  ,      30 ,        30 ,        .     ,   . """ if evaluation_data: n_data = len(evaluation_data) n = len(training_data) evaluation_cost, evaluation_accuracy = [], [] training_cost, training_accuracy = [], [] for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch( mini_batch, eta, lmbda, len(training_data)) print "Epoch %s training complete" % j if monitor_training_cost: cost = self.total_cost(training_data, lmbda) training_cost.append(cost) print "Cost on training data: {}".format(cost) if monitor_training_accuracy: accuracy = self.accuracy(training_data, convert=True) training_accuracy.append(accuracy) print "Accuracy on training data: {} / {}".format( accuracy, n) if monitor_evaluation_cost: cost = self.total_cost(evaluation_data, lmbda, convert=True) evaluation_cost.append(cost) print "Cost on evaluation data: {}".format(cost) if monitor_evaluation_accuracy: accuracy = self.accuracy(evaluation_data) evaluation_accuracy.append(accuracy) print "Accuracy on evaluation data: {} / {}".format( self.accuracy(evaluation_data), n_data) print return evaluation_cost, evaluation_accuracy, \ training_cost, training_accuracy def update_mini_batch(self, mini_batch, eta, lmbda, n): """    ,          -. ``mini_batch`` –    ``(x, y)``, ``eta`` –  , ``lmbda`` -  , ``n`` -     .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) # backward pass delta = (self.cost).delta(zs[-1], activations[-1], y) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """  l      ,      . l = 1    , l = 2 – ,   .    ,   python      . """ for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def accuracy(self, data, convert=False): """    ``data``,      .   –        .  ``convert``  False,    –    ( )  True,   .    - ,  ``y`` -     .  ,       .           .          ?     –       ,      .   ,      .       mnist_loader.load_data_wrapper. """ if convert: results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data] else: results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data] return sum(int(x == y) for (x, y) in results) def total_cost(self, data, lmbda, convert=False): """      ``data``.  ``convert``   False,   –  (),   True,   –   . .    ,      ``accuracy``, . """ cost = 0.0 for x, y in data: a = self.feedforward(x) if convert: y = vectorized_result(y) cost += self.cost.fn(a, y)/len(data) cost += 0.5*(lmbda/len(data))*sum( np.linalg.norm(w)**2 for w in self.weights) return cost def save(self, filename): """    ``filename``.""" data = {"sizes": self.sizes, "weights": [w.tolist() for w in self.weights], "biases": [b.tolist() for b in self.biases], "cost": str(self.cost.__name__)} f = open(filename, "w") json.dump(data, f) f.close() ####  Network def load(filename): """    ``filename``.    Network. """ f = open(filename, "r") data = json.load(f) f.close() cost = getattr(sys.modules[__name__], data["cost"]) net = Network(data["sizes"], cost=cost) net.weights = [np.array(w) for w in data["weights"]] net.biases = [np.array(b) for b in data["biases"]] return net ####   def vectorized_result(j): """  10-    1.0   j     .      (0..9)     . """ e = np.zeros((10, 1)) e[j] = 1.0 return e def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

अधिक दिलचस्प परिवर्तनों में एल 2 नियमितीकरण का समावेश है। हालाँकि यह एक बड़ा वैचारिक बदलाव है, लेकिन इसे लागू करना इतना आसान है कि आप इसे कोड में नोटिस नहीं कर सकते। अधिकांश भाग के लिए, यह विभिन्न विधियों, विशेष रूप से Network.SGD के लिए lmbda पैरामीटर से गुजर रहा है। सभी काम कार्यक्रम की एक पंक्ति में किए जाते हैं, नेटवर्क में अंत से चौथा ।update_mini_batch विधि। वहाँ हम वजन घटाने को शामिल करने के लिए ढाल वंश अद्यतन नियम को बदलते हैं। परिवर्तन छोटा है, लेकिन परिणामों को गंभीरता से प्रभावित कर रहा है!

यह, वैसे, अक्सर तंत्रिका नेटवर्क में नई तकनीकों को लागू करते समय होता है। हमने नियमितीकरण पर चर्चा करते हुए हजारों शब्द खर्च किए। वैचारिक रूप से, यह एक बहुत ही सूक्ष्म और समझने में कठिन बात है। हालांकि, यह तुच्छ रूप से कार्यक्रम में जोड़ा जा सकता है! अप्रत्याशित रूप से, जटिल तकनीकों को मामूली कोड परिवर्तनों के साथ लागू किया जा सकता है।

कोड में एक और छोटा लेकिन महत्वपूर्ण बदलाव नेटवर्क हेल्ड स्टोचैस्टिक ग्रेडिएंट डिसेंट विधि के लिए कई वैकल्पिक झंडों का जोड़ है।ये झंडे या तो प्रशिक्षण की लागत और सटीकता को ट्रैक करने के लिए संभव बनाते हैं या प्रशिक्षण_डेटा या मूल्यांकन_डेटा, जो नेटवर्क वीईएमडी को प्रेषित किया जा सकता है। पहले अध्याय में, हम अक्सर इन झंडों का उपयोग करते थे, लेकिन मुझे उनके उपयोग का एक उदाहरण दें, बस एक अनुस्मारक के रूप में:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

हमने सत्यापन_डेटा को सत्यापन_डेटा के माध्यम से सेट किया। हालाँकि, हम test_data और किसी अन्य डेटा सेट पर प्रदर्शन को ट्रैक कर सकते हैं। हमारे पास चार झंडे हैं जो मूल्यांकन_दत्ता और प्रशिक्षण_दाता दोनों पर लागत और सटीकता को ट्रैक करने की आवश्यकता को निर्दिष्ट करते हैं। ये ध्वज डिफ़ॉल्ट रूप से गलत पर सेट होते हैं, हालांकि नेटवर्क की प्रभावशीलता को ट्रैक करने के लिए उन्हें यहाँ शामिल किया गया है। इसके अलावा, network2.py से Network.SGD विधि ट्रैकिंग परिणामों का प्रतिनिधित्व करने वाला एक चार-तत्व टपल देता है। आप इसे इस तरह से उपयोग कर सकते हैं:

 >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

इसलिए, उदाहरण के लिए, मूल्यांकन_कोस्ट 30 तत्वों की एक सूची होगी जिसमें प्रत्येक युग के अंत में अनुमानित डेटा की लागत शामिल होगी। तंत्रिका नेटवर्क के व्यवहार को समझने के लिए ऐसी जानकारी बेहद उपयोगी है। नेटवर्क व्यवहार को समझने के लिए ऐसी जानकारी बेहद उपयोगी है। यह, उदाहरण के लिए, समय के साथ नेटवर्क सीखने के ग्राफ को खींचने के लिए इस्तेमाल किया जा सकता है। इस तरह मैंने इस अध्याय से सभी ग्राफ बनाए। हालांकि, यदि झंडे में से एक सेट नहीं है, तो संबंधित टपल तत्व एक खाली सूची होगी।

अन्य कोड परिवर्धन में Network.save विधि शामिल होती है, जो नेटवर्क ऑब्जेक्ट को डिस्क और मेमोरी में लोड करने के कार्य को सहेजती है। बचत और लदान JSON के माध्यम से किया जाता है, न कि पायथन अचार या cPickle मॉड्यूल के लिए, जो आमतौर पर अजगर में डिस्क को बचाने और लोड करने के लिए उपयोग किया जाता है। JSON का उपयोग करने के लिए अचार या cPickle की तुलना में अधिक कोड की आवश्यकता होती है। यह समझने के लिए कि मैंने JSON को क्यों चुना, कल्पना कीजिए कि भविष्य में कुछ बिंदु पर हमने अपने नेटवर्क वर्ग को बदलने का फैसला किया ताकि सिग्माइड न्यूरॉन्स से अधिक हो। इस परिवर्तन को लागू करने के लिए, हम सबसे अधिक संभावना नेटवर्क में परिभाषित विशेषताओं को बदलेंगे।। Init__ विधि। और अगर हम सिर्फ अचार को बचाने के लिए इस्तेमाल करते हैं, तो हमारा लोड फ़ंक्शन काम नहीं करेगा। स्पष्ट क्रमांकन के साथ JSON का उपयोग करना हमारे लिए गारंटी देना आसान बनाता हैनेटवर्क ऑब्जेक्ट के पुराने संस्करणों को डाउनलोड किया जा सकता है।

कोड में कई छोटे-छोटे बदलाव हैं, लेकिन ये नेटवर्क-थ्रेड के थोड़े ही बदलाव हैं। अंतिम परिणाम 74 लाइनों के हमारे कार्यक्रम का एक बहुत अधिक कार्यात्मक कार्यक्रम 152 लाइनों का विस्तार है।

कार्य

• नियमितीकरण L1 की शुरुआत करके नीचे दिए गए कोड को संशोधित करें, और इसे 30 छिपे हुए न्यूरॉन्स वाले नेटवर्क द्वारा MNIST अंकों को वर्गीकृत करने के लिए उपयोग करें। क्या आप एक नियमितीकरण पैरामीटर चुन सकते हैं जो आपको नियमितीकरण के बिना नेटवर्क की तुलना में परिणाम में सुधार करने की अनुमति देता है?
• Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?