गणित और Numpy का उपयोग करते हुए एक सरल तंत्रिका नेटवर्क लिखना

खरोंच से तंत्रिका नेटवर्क लिखने के बारे में अगला लेख क्यों? काश, मुझे ऐसे लेख नहीं मिलते, जहाँ सिद्धांत और संहिता को खरोंच से पूरी तरह काम करने वाले मॉडल के रूप में वर्णित किया गया था। मैंने तुरंत चेतावनी दी कि बहुत सारा गणित होगा। मुझे लगता है कि पाठक रैखिक बीजगणित, आंशिक व्युत्पत्ति और कम से कम आंशिक रूप से, प्रायिकता सिद्धांत के साथ-साथ पायथन और नेम्पी की मूल बातें से परिचित है। हम पूरी तरह से जुड़े तंत्रिका नेटवर्क और MNIST से निपटेंगे।

गणित। भाग 1 (सरल)

पूरी तरह से जुड़ी हुई परत (FC लेयर) क्या है? आमतौर पर वे कहते हैं कि "एक पूरी तरह से जुड़ी हुई परत एक परत है, जिसमें से प्रत्येक न्यूरॉन पिछली परत के सभी न्यूरॉन्स से जुड़ा होता है"। यह अभी स्पष्ट नहीं है कि न्यूरॉन्स क्या हैं, वे कैसे जुड़े हुए हैं, खासकर कोड में। अब मैं एक उदाहरण के साथ इसे पार्स करने की कोशिश करूंगा। बता दें कि 100 न्यूरॉन्स की एक परत होती है। मुझे पता है कि मैंने अभी तक यह नहीं बताया है कि यह क्या है, लेकिन चलो कल्पना करते हैं कि 100 न्यूरॉन्स हैं और उनके पास एक इनपुट है जहां डेटा भेजा जाता है, और एक आउटपुट जहां वे डेटा देते हैं। और 28x28 पिक्सेल का एक ब्लैक-एंड-व्हाइट चित्र इनपुट को खिलाया जाता है - केवल 784 मान, यदि आप इसे वेक्टर में खिंचाव करते हैं। एक तस्वीर को इनपुट लेयर कहा जा सकता है। फिर, प्रत्येक "न्यूरॉन" से जुड़ने के लिए 100 न्यूरॉन्स में से प्रत्येक के लिए या, यदि आपको पसंद है, तो पिछली परत (यानी, चित्र) का मूल्य, यह आवश्यक है कि 100 न्यूरॉन्स में से प्रत्येक मूल चित्र के 784 मूल्यों को स्वीकार करता है। उदाहरण के लिए, प्रत्येक 100 न्यूरॉन्स के लिए यह तस्वीर के 784 मानों को कुछ 784 संख्याओं से गुणा करने और उन्हें एक साथ जोड़ने के लिए पर्याप्त होगा, परिणामस्वरूप, एक नंबर बाहर आता है। अर्थात्, यह एक न्यूरॉन है:

$$$ $ $ $ $ \ टेक्स्ट {न्यूरॉन आउटपुट} = \ टेक्स्ट {कुछ संख्या} _ {1} \ cdot \ text {चित्र मान} _1 ~ + \\ + ~ ... ~ + ~ \ पाठ {कुछ- वह संख्या} _ {784} \ cdot \ text {चित्र मान} _ {784} $ $ प्रदर्शन $ $

फिर यह पता चला कि प्रत्येक न्यूरॉन में 784 संख्याएँ हैं, और ये सभी संख्याएँ: (इस परत पर न्यूरॉन्स की संख्या) x (पिछली परत पर न्यूरॉन्स की संख्या) =$$ $ इनलाइन $ 100 \ times784 $ इनलाइन $ = 78,400 अंक। इन नंबरों को आमतौर पर लेयर वेट कहा जाता है। प्रत्येक न्यूरॉन अपनी संख्या दे देगा और परिणामस्वरूप हमें 100-आयामी वेक्टर मिलेगा, और वास्तव में हम लिख सकते हैं कि यह 100-आयामी वेक्टर 784-आयामी वेक्टर (हमारी मूल छवि) को आकार के एक वजन मैट्रिक्स द्वारा गुणा करके प्राप्त किया जाता है।$$ $ इनलाइन $ 100 \ times784 $ इनलाइन $ :

$$$$ प्रदर्शन $ $ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $ $ प्रदर्शन $ $

इसके अलावा, परिणामी 100 नंबरों को सक्रियण समारोह में पारित किया जाता है - कुछ गैर-रेखीय कार्य - जो प्रत्येक संख्या को अलग से प्रभावित करते हैं। उदाहरण के लिए, सिग्मोइड, हाइपरबोलिक स्पर्शरेखा, ReLU और अन्य। सक्रियण फ़ंक्शन आवश्यक रूप से गैर-रैखिक है, अन्यथा तंत्रिका नेटवर्क केवल सरल परिवर्तन सीखेंगे।



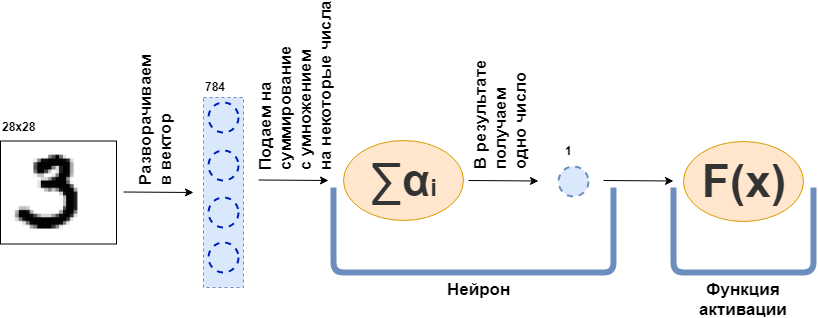
फिर, परिणामी डेटा फिर से एक पूरी तरह से जुड़े परत को खिलाया जाता है, लेकिन एक अलग संख्या में न्यूरॉन्स के साथ, और फिर सक्रियण फ़ंक्शन के लिए। ऐसा कई बार होता है। नेटवर्क की अंतिम परत वह परत है जो उत्तर का उत्पादन करती है। इस मामले में, जवाब तस्वीर में संख्या के बारे में जानकारी है।



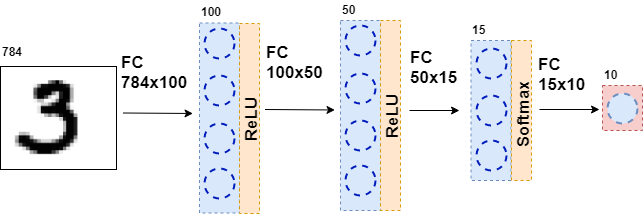
नेटवर्क के प्रशिक्षण के दौरान, यह आवश्यक है कि हमें पता हो कि चित्र में कौन सी आकृति दिखाई गई है। यही है, कि डेटासेट ऊपर चिह्नित है। फिर आप एक अन्य तत्व - त्रुटि फ़ंक्शन का उपयोग कर सकते हैं। वह तंत्रिका नेटवर्क की प्रतिक्रिया को देखती है और वास्तविक उत्तर के साथ तुलना करती है। इसके लिए, तंत्रिका नेटवर्क सीख रहा है।

समस्या का सामान्य विवरण

संपूर्ण डेटासेट एक बड़ा टेंसर है (हम एक बहुआयामी डेटा सरणी को टेंसर कहेंगे)$$ $ इनलाइन $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ right) $ इनलाइन $ जहाँ$$ $ इनलाइन $ \ boldsymbol {x} _i $ इनलाइन $ - i-th ऑब्जेक्ट, उदाहरण के लिए, एक तस्वीर, जो एक टेंसर भी है। प्रत्येक वस्तु के लिए है$$ $ इनलाइन $ y_i $ इनलाइन $ - i-th ऑब्जेक्ट पर सही उत्तर। इस मामले में, एक तंत्रिका नेटवर्क को कुछ फ़ंक्शन के रूप में दर्शाया जा सकता है जो किसी वस्तु को इनपुट के रूप में लेता है और उस पर कुछ उत्तर देता है:

$$$ $ प्रदर्शन $ $ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ प्रदर्शन $ $

अब चलिए फंक्शन पर करीब से नज़र डालते हैं$$ $ इनलाइन $ F (\ boldsymbol {x} _i) $ इनलाइन $ । चूंकि तंत्रिका नेटवर्क में परतें होती हैं, प्रत्येक व्यक्तिगत परत एक फ़ंक्शन होती है। और इसका मतलब है

$$$ $ प्रदर्शन $ $ F (\ boldsymbol {x} _i) = f_k (f_ {k-1) (\ ldots (f_1 (\ boldsymbol {x} _i)))) = \ hat (y) _i $$ प्रदर्शन $ $

यही है, बहुत पहले कार्य में - पहली परत - एक तस्वीर कुछ टेंसर के रूप में प्रस्तुत की जाती है। समारोह$$ $ इनलाइन $ f_1 $ इनलाइन $ कुछ जवाब देता है - एक टेंसर भी, लेकिन एक अलग आयाम का। इस टेंसर को आंतरिक प्रतिनिधित्व कहा जाएगा। अब यह आंतरिक प्रतिनिधित्व फ़ंक्शन के इनपुट को खिलाया जाता है$$ $ इनलाइन $ f_2 $ इनलाइन $ , जो इसका आंतरिक प्रतिनिधित्व देता है। और इतने पर, फ़ंक्शन तक$$ $ इनलाइन $ f_k $ इनलाइन $ - अंतिम परत - उत्तर नहीं देगी$$ $ इनलाइन $ \ hat {y} _i $ इनलाइन $ ।

अब, कार्य नेटवर्क को प्रशिक्षित करना है - नेटवर्क उत्तर को सही उत्तर से मिलान करने के लिए। सबसे पहले आपको यह मापने की आवश्यकता है कि तंत्रिका नेटवर्क कितना गलत है। इसे मापना एक त्रुटि कार्य है।$$ $ इनलाइन $ L (\ hat {y} _i, y_i) $ इनलाइन $ । और हम प्रतिबंध लगाते हैं:

1।$$ $ इनलाइन $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ इनलाइन $
2।$$ $ इनलाइन $ \ मौजूद है ~ dL (\ hat {y} _i, y_i) $ इनलाइन $
3।$$ $ इनलाइन $ L (\ hat {y} _i, y_i) \ geq 0 $ इनलाइन $

प्रतिबंध 2 परतों के सभी कार्यों पर लगाया गया है$$ $ इनलाइन $ f_j $ इनलाइन $ - उन सभी को अलग-अलग होने दें।

इसके अलावा, वास्तव में (मैंने इसका उल्लेख नहीं किया है) इनमें से कुछ कार्य मापदंडों पर निर्भर करते हैं - तंत्रिका नेटवर्क का वजन -$$ $ इनलाइन $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ इनलाइन $ । और पूरा विचार इस तरह के वजन को उठाना है ताकि$$ $ इनलाइन $ \ hat {y} _i $ इनलाइन $ के साथ मेल खाता है$$ $ इनलाइन $ y_i $ इनलाइन $ डेटासेट की सभी वस्तुओं पर। मैं ध्यान देता हूं कि सभी कार्यों में भार नहीं है।

तो हम कहाँ रुक गए? तंत्रिका नेटवर्क के सभी कार्य अलग-अलग हैं, त्रुटि फ़ंक्शन भी भिन्न है। ग्रेडिएंट के गुणों में से एक को याद करें - फ़ंक्शन के विकास की दिशा दिखाएं। हम इसका उपयोग करते हैं, प्रतिबंध 1 और 3, तथ्य यह है कि

$$$$ प्रदर्शन $ $ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1) (\ ldots (f_1 (\ boldsymbol {x} _i)))) = L (\ hat) {y} _i) $$ प्रदर्शन $ $

और तथ्य यह है कि मैं एक जटिल फ़ंक्शन के आंशिक डेरिवेटिव और डेरिवेटिव पर विचार कर सकता हूं। अब गणना करने के लिए आपकी जरूरत की हर चीज मौजूद है

$$$$ प्रदर्शन $ $ \ frac {\ आंशिक L (F (\ boldsymbol {x} _i))}} {\ आंशिक \ boldsymbol {\ omega_j}} $$ प्रदर्शन $ $

किसी भी i और j के लिए। यह आंशिक व्युत्पन्न दिशा दिखाता है जिसमें परिवर्तन करना है$$ $ इनलाइन $ \ boldsymbol {\ omega_j} $ इनलाइन $ विस्तार करना$$ $ इनलाइन $ एल $ इनलाइन $ । कम करने के लिए आपको पक्ष में एक कदम उठाने की आवश्यकता है$$ $ इनलाइन $ - \ frac {\ आंशिक L (F (\ boldsymbol {x} _i))}} {\ आंशिक \ boldsymbol {\ omega_j}} $ इनलाइन $ कुछ भी जटिल नहीं है।

तो नेटवर्क के प्रशिक्षण की प्रक्रिया निम्नानुसार निर्मित है: कई बार एक चक्र में हम संपूर्ण डेटासेट से गुजरते हैं (इसे एक युग कहा जाता है), प्रत्येक डेटासेट वस्तु के लिए जिसे हम मानते हैं$$ $ इनलाइन $ L (\ hat {y} _i, y_i) $ इनलाइन $ (इसे फॉरवर्ड पास कहा जाता है) और आंशिक व्युत्पन्न पर विचार करें$$ $ इनलाइन $ \ आंशिक एल $ इनलाइन $ सभी भार के लिए$$ $ इनलाइन $ \ boldsymbol {\ omega_j} $ इनलाइन $ , फिर वेट को अपडेट करें (इसे बैकवर्ड पास कहा जाता है)।

मैं ध्यान देता हूं कि मैंने अभी तक कोई विशिष्ट कार्य और परतें पेश नहीं की हैं। यदि इस स्तर पर यह स्पष्ट नहीं है कि इस सब के साथ क्या करना है, तो मैं आगे पढ़ना जारी रखने का प्रस्ताव करता हूं - अधिक गणित होगा, लेकिन अब यह उदाहरणों के साथ जाएगा।

गणित। भाग 2 (कठिन)

त्रुटि समारोह

मैं अंत से शुरू करूँगा और वर्गीकरण समस्या के लिए त्रुटि फ़ंक्शन प्राप्त करूंगा। प्रतिगमन समस्या के लिए, त्रुटि फ़ंक्शन की व्युत्पत्ति पुस्तक "डीप लर्निंग" में अच्छी तरह से वर्णित है। तंत्रिका नेटवर्क की दुनिया में विसर्जन। ”

सादगी के लिए, एक न्यूरल नेटवर्क (NN) है जो बिल्ली की तस्वीरों को कुत्ते की तस्वीरों से अलग करता है, और बिल्लियों और कुत्तों की तस्वीरों का एक सेट है, जिसके लिए एक सही उत्तर है$$ $ इनलाइन $ y_ {सत्य} $ इनलाइन $ ।

$$$ $ प्रदर्शन $ $ एनएन (चित्र | \ ओमेगा) = y_ {पूर्व} $ $ प्रदर्शन $ $

मैं जो कुछ भी करूंगा वह सभी अधिकतम संभावना विधि के समान है। इसलिए, मुख्य कार्य संभावना फ़ंक्शन को ढूंढना है। यदि हम विवरण को छोड़ देते हैं, तो ऐसा फ़ंक्शन जो तंत्रिका नेटवर्क की भविष्यवाणी और सही उत्तर की तुलना करता है, और यदि वे मेल खाते हैं, तो एक महान मूल्य देता है, यदि नहीं, तो इसके विपरीत। एक सही उत्तर की संभावना दिए गए मापदंडों के साथ ध्यान में आती है:

$$$ $ प्रदर्शन $ $ पी (y_ {पूर्व} = y_ {सच} | \ ओमेगा) $ $ प्रदर्शन $ $

और अब हम कुछ सामंत बनाएंगे, जो, ऐसा लगता है, कहीं से भी पालन नहीं करता है। तंत्रिका नेटवर्क को दो-आयामी वेक्टर के रूप में एक उत्तर दें, जिनमें से मानों का योग 1 है। इस वेक्टर के पहले तत्व को एक आत्मविश्वास माप कहा जा सकता है कि बिल्ली फोटो में है, और दूसरा तत्व विश्वास उपाय है कि कुत्ते तस्वीर में है। हाँ, यह लगभग संभावना है!

$$$ $ प्रदर्शन $ $ एनएन (चित्र | \ ओमेगा) = \ छोड़ दिया [\ start {मैट्रिक्स} p_0 \\ p_1 \\\ अंत {मैट्रिक्स} \ सही] $ $ प्रदर्शन $ $

अब संभावना समारोह को फिर से लिखा जा सकता है:

$$$ $ प्रदर्शन $ $ p (y_ {पूर्व} = y_ {सच} | \ ओमेगा) = p_ \ Omega (y_ {पूर्व}) ^ t_ {0} * (1 - p_ \ Omega (y_ {पूर्व}) ^ ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $ $ $ $ प्रदर्शित

जहाँ$$ $ इनलाइन $ t_0, t_1 $ इनलाइन $ सही वर्ग के लेबल, उदाहरण के लिए, यदि$$ $ इनलाइन $ y_ {सत्य} = बिल्ली $ इनलाइन $ तो$$ $ इनलाइन $ t_0 == 1, t_1 == 0 $ इनलाइन $ अगर$$ $ इनलाइन $ y_ {सत्य} = डॉग $ इनलाइन $ तो$$ $ इनलाइन $ t_0 == 0, t_1 == 1 $ इनलाइन $ । इस प्रकार, एक वर्ग की संभावना की भविष्यवाणी एक तंत्रिका नेटवर्क द्वारा की जानी चाहिए (लेकिन जरूरी नहीं कि इसके द्वारा भविष्यवाणी की जाए) हमेशा माना जाता है। अब इसे किसी भी वर्ग के लिए सामान्यीकृत किया जा सकता है (उदाहरण के लिए, m कक्षाएं):

$$$ $ प्रदर्शन $ $ p (y_ {पूर्व} = y_ {सत्य} | \ ओमेगा) = \ prod_0 ^ m p_i ^ {t_i} $ $ प्रदर्शन $ $

हालांकि, किसी भी डेटासेट में कई ऑब्जेक्ट्स हैं (उदाहरण के लिए, एन ऑब्जेक्ट्स)। मैं चाहता हूं कि तंत्रिका नेटवर्क प्रत्येक या अधिकांश वस्तुओं पर सही उत्तर दे। और इसके लिए आपको डेटासेट से प्रत्येक ऑब्जेक्ट के लिए ऊपर दिए गए सूत्र के परिणामों को गुणा करना होगा।

$$$ $ प्रदर्शन $ $ अधिकतम अधिकतम = = prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $ $ प्रदर्शन $ $

अच्छे परिणाम प्राप्त करने के लिए, इस फ़ंक्शन को अधिकतम करने की आवश्यकता है। लेकिन, सबसे पहले, यह कम से कम करने के लिए है, क्योंकि हमारे पास एक स्टोकेस्टिक ग्रेडिएंट वंश है और इसके लिए सभी बन्स - बस एक माइनस असाइन करें, और दूसरी बात, यह एक बहुत बड़ा काम करने के लिए मुश्किल है - यह लॉगजीथम।

$$$$ प्रदर्शन $$ CrossEntropyLoss = - \ sum \ limit_ {j = 0} ^ {N} \ sum \ limit_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p {{i, j) }) $ $ प्रदर्शन $ $

अद्भुत! परिणाम बाइनरी केस या लॉगलॉस में एंट्रॉपी या पार था। इस फ़ंक्शन को गिनना आसान है और अंतर करना भी आसान है:

$$$$ प्रदर्शन $ $ \ frac {\ आंशिक CrossEntropyLoss} {\ आंशिक p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}} $ $ प्रदर्शन $ $ प्रदर्शित करें

आपको बैकप्रॉपैगेशन एल्गोरिथ्म के लिए अंतर करने की आवश्यकता है। मैं ध्यान देता हूं कि त्रुटि फ़ंक्शन वेक्टर के आयाम को नहीं बदलता है। यदि, एमएनआईएसटी के मामले में, आउटपुट उत्तर के 10-आयामी वेक्टर है, तो व्युत्पन्न की गणना करते समय, हमें डेरिवेटिव के 10-आयामी वेक्टर मिलते हैं। एक और दिलचस्प बात यह है कि व्युत्पन्न का केवल एक तत्व शून्य नहीं होगा, जिस पर$$ $ इनलाइन $ t_ {i, j} \ neq 0 $ इनलाइन $ , वह सही उत्तर के साथ है। और किसी दिए गए ऑब्जेक्ट पर तंत्रिका नेटवर्क द्वारा अनुमानित सही उत्तर की संभावना जितनी कम होगी, उतनी ही त्रुटि फ़ंक्शन उस पर होगा।

सक्रियण सुविधाएँ

एक तंत्रिका नेटवर्क के प्रत्येक पूरी तरह से जुड़े परत के उत्पादन में, एक nonlinear सक्रियण फ़ंक्शन मौजूद होना चाहिए। इसके बिना, एक सार्थक तंत्रिका नेटवर्क को प्रशिक्षित करना असंभव है। आगे देखते हुए, एक तंत्रिका नेटवर्क की एक पूरी तरह से जुड़ी हुई परत केवल एक वजन मैट्रिक्स द्वारा इनपुट डेटा का गुणन है। रैखिक बीजगणित में, इसे एक रेखीय मानचित्र कहा जाता है - एक रैखिक कार्य। रैखिक कार्यों का संयोजन भी एक रैखिक कार्य है। लेकिन इसका मतलब यह है कि ऐसा फ़ंक्शन केवल रैखिक कार्यों को अनुमानित कर सकता है। काश, यह क्यों तंत्रिका नेटवर्क की जरूरत नहीं है।

Softmax

आमतौर पर इस फ़ंक्शन का उपयोग नेटवर्क की आखिरी परत पर किया जाता है, क्योंकि यह वेक्टर को अंतिम परत से "संभावनाओं" के वेक्टर में बदल देता है: वेक्टर का प्रत्येक तत्व 0 से 1 तक रहता है और उनका योग 1 होता है। यह वेक्टर के आयाम को नहीं बदलता है।

$$$ $ प्रदर्शन $ $ सॉफ्टमैक्स_आई = \ frac {e ^ {x_i}} {\ sum \ limit_ {j} e ^ {x_j}} $ $ प्रदर्शन $ $

अब हम व्युत्पन्न खोज पर चलते हैं। क्योंकि$$ $ इनलाइन $ \ boldsymbol {x} $ इनलाइन $ एक सदिश राशि है, और इसके सभी तत्व हमेशा हर में मौजूद होते हैं, तब व्युत्पन्न लेने पर हमें जेकबियन मिलता है:

$$$ $ प्रदर्शन $ $ J_ {सॉफ्टमैक्स} = \ _ {केस} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ "अंत" $ $ $ प्रदर्शन

अब backpropagation के बारे में। डेरिवेटिव की वेक्टर पिछली परत से आती है (आमतौर पर यह एक त्रुटि फ़ंक्शन है)$$ $ इनलाइन $ \ boldsymbol {dz} $ इनलाइन $ । मामले में$$ $ इनलाइन $ \ boldsymbol {dz} $ इनलाइन $ mnist पर एक त्रुटि फ़ंक्शन से आया,$$ $ इनलाइन $ \ boldsymbol {dz} $ इनलाइन $ - 10-आयामी वेक्टर। फिर जैकबियान का आयाम 10x10 है। पाने के लिए$$ $ इनलाइन $ \ boldsymbol {dz_ {new}} $ इनलाइन $ , जो पिछली परत के आगे बढ़ता है (यह मत भूलो कि हम अंत से नेटवर्क की शुरुआत तक जाते हैं जब त्रुटि वापस प्रचारित होती है), हमें गुणा करना होगा$$ $ इनलाइन $ \ boldsymbol {dz} $ इनलाइन $ पर$$ $ इनलाइन $ J_ {सॉफ्टमैक्स} $ इनलाइन $ (पंक्ति प्रति स्तंभ):

$$$ $ प्रदर्शन $ $ dz_ {नया} = \ boldsymbol {dz} \ गुना J_ {सॉफ्टमैक्स} $ $ प्रदर्शन $ $

आउटपुट पर, हमें डेरिवेटिव के 10-आयामी वेक्टर मिलते हैं$$ $ इनलाइन $ \ boldsymbol {dz_ {new}} $ इनलाइन $ ।

Relu

$$$$ प्रदर्शन $$ ReLU (x) = \ start {केस} x, x> 0 \\ 0, x <0 \ end {केस} $ $ प्रदर्शन $$

2011 के बाद, जब "डीप स्पार्स रेक्टिफायर न्यूरल नेटवर्क्स" नामक लेख प्रकाशित हुआ, तब ReLU का बड़े पैमाने पर इस्तेमाल किया जाने लगा। हालांकि, इस तरह के एक समारोह पहले से जाना जाता था। "सक्रियण शक्ति" की अवधारणा ReLU (अधिक विवरण के लिए, "डीप लर्निंग (तंत्रिका सीखने की दुनिया में विसर्जन)" पुस्तक देखें) के लिए लागू है। लेकिन मुख्य विशेषता जो ReLU को अन्य सक्रियण कार्यों की तुलना में अधिक आकर्षक बनाती है, वह इसकी सरल व्युत्पन्न गणना है:

$$$$ प्रदर्शन $$ d (ReLU (x)) = \ start {मामलों} 1, x> 0 \\ 0, x <0 \ end {मामलों} $ $ प्रदर्शन $ $

इस प्रकार, ReLU अन्य सक्रियण कार्यों (सिग्मोइड, हाइपरबोलिक स्पर्शरेखा, आदि) की तुलना में कम्प्यूटेशनल रूप से अधिक कुशल है।

पूरी तरह से जुड़ी हुई परत

अब एक पूरी तरह से जुड़े परत पर चर्चा करने का समय है। अन्य सभी के लिए सबसे महत्वपूर्ण है, क्योंकि यह इस परत में है कि सभी भार स्थित हैं, जो तंत्रिका नेटवर्क को अच्छी तरह से काम करने के लिए समायोजित किया जाना चाहिए। एक पूरी तरह से जुड़ी परत बस एक वजन मैट्रिक्स है:

$$$ $ प्रदर्शन $ $ W = | w_ {i, j} | $ $ प्रदर्शन $ $

वेट मैट्रिक्स को इनपुट कॉलम से गुणा करने पर एक नया आंतरिक प्रतिनिधित्व प्राप्त होता है:

$$$$ डिस्प्ले $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ डिस्प्ले $$ प्रदर्शित करता है

जहाँ$$ $ इनलाइन $ \ boldsymbol {x} $ इनलाइन $ का आकार है$$ $ इनलाइन $ इनपुट \ _shape $ इनलाइन $ , और$$ $ इनलाइन $ x_ {नया} $ इनलाइन $ -$$ $ इनलाइन $ आउटपुट \ _shape $ इनलाइन $ । उदाहरण के लिए$$ $ इनलाइन $ \ boldsymbol {x} $ इनलाइन $ - 784-आयामी वेक्टर, और$$ $ इनलाइन $ \ boldsymbol {x} _ {new} $ इनलाइन $ 100-आयामी वेक्टर है, फिर मैट्रिक्स W का आकार 100x784 है। यह पता चला है कि इस परत पर 100x784 = 78,400 वज़न है।

त्रुटि के पीछे प्रसार के साथ, इस मैट्रिक्स के प्रत्येक वजन के संबंध में व्युत्पन्न को लेने की आवश्यकता है। समस्या को सरल करें और सम्मान के साथ केवल व्युत्पन्न लें$$ $ इनलाइन $ w_ {1,1} $ इनलाइन $ । मैट्रिक्स और वेक्टर को गुणा करते समय, नए वेक्टर का पहला तत्व$$ $ इनलाइन $ \ boldsymbol {x} _ {new} $ इनलाइन $ के बराबर है$$ $ इनलाइन $ x_ {नया ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1,784} \ cdot x_ {784} $ इनलाइन $ , और व्युत्पन्न$$ $ इनलाइन $ x_ {नया ~ 1} $ इनलाइन $ पर$$ $ इनलाइन $ w_ {1,1} $ इनलाइन $ सरल होगा$$ $ इनलाइन $ x_1 $ इनलाइन $ , आपको केवल उपरोक्त राशि का व्युत्पन्न लेने की आवश्यकता है। इसी तरह अन्य सभी भारों के लिए होता है। लेकिन यह एक त्रुटि वापस प्रसार एल्गोरिथ्म नहीं है, जब तक कि यह सिर्फ डेरिवेटिव का एक मैट्रिक्स है। आपको यह याद रखने की आवश्यकता है कि अगली परत से इस तक (त्रुटि अंत से शुरू तक जाती है) 100-आयामी ग्रेडिएंट वेक्टर आती है$$ $ इनलाइन $ d \ boldsymbol {z} $ इनलाइन $ । इस वेक्टर का पहला तत्व$$ $ इनलाइन $ dz_1 $ इनलाइन $ निर्माण में "भाग लेने वाले" डेरिवेटिव के मैट्रिक्स के सभी तत्वों से गुणा किया जाएगा$$ $ इनलाइन $ x_ {नया ~ 1} $ इनलाइन $ , अर्थात् पर$$ $ इनलाइन $ x_1, x_2, ..., x_ {784} $ इनलाइन $ । इसी तरह, बाकी तत्व। यदि आप इसे रेखीय बीजगणित की भाषा में अनुवादित करते हैं, तो इसे इस तरह लिखा जाता है:

$$$$ प्रदर्शन $ $ \ frac {\ आंशिक L} {\ आंशिक W} = ((d \ boldsymbol {z}, ~ dW) = \ left (\ start {मैट्रिक्स} dz_ {1} \ cdot \ boldsymol {x} \) \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {मैट्रिक्स} \ right) _ {100} $ $ प्रदर्शन $ $

आउटपुट एक 100x784 मैट्रिक्स है।


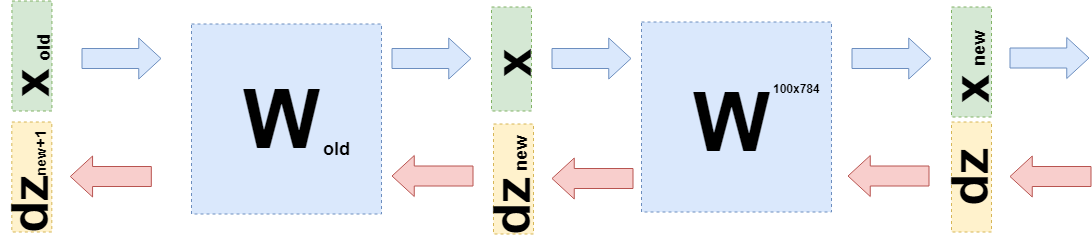
अब आपको यह समझने की आवश्यकता है कि पिछली परत को क्या स्थानांतरित करना है। इसके लिए और अब जो कुछ हुआ है, उसकी बेहतर समझ के लिए, मैं इस बात पर लिखना चाहता हूं कि इस परत पर व्युत्पन्न होने पर क्या हुआ, थोड़ी भिन्न भाषा में "क्या है गुणा" से फ़ंक्शंस (फिर से) की बारीकियों से दूर होने के लिए।

जब मैं वज़न समायोजित करना चाहता था, तो मैं इन वज़न के लिए त्रुटि फ़ंक्शन का व्युत्पन्न लेना चाहता था:$$ $ इनलाइन $ \ frac {\ आंशिक एल} {\ आंशिक डब्ल्यू} $ इनलाइन $ । यह ऊपर दिखाया गया था कि कैसे त्रुटि कार्यों और सक्रियण कार्यों के डेरिवेटिव लेने के लिए। इसलिए, हम इस तरह के एक मामले पर विचार कर सकते हैं$$ $ इनलाइन $ d \ boldsymbol {z} $ इनलाइन $ त्रुटि फ़ंक्शन और सक्रियण फ़ंक्शन के सभी डेरिवेटिव पहले से ही बैठे हैं):

$$$$ प्रदर्शन $ $ \ frac {\ आंशिक L} {\ आंशिक W} = d \ boldsymbol {z} \ cdot \ frac {\ आंशिक \ boldsymbol {x} _ {new} (W)} {\ n आंशिक रूप से} $ $ प्रदर्शन $ $

यह किया जा सकता है, क्योंकि आप विचार कर सकते हैं$$ $ इनलाइन $ \ boldsymbol {x} _ {new} $ इनलाइन $ डब्ल्यू के एक समारोह के रूप में:$$ $ इनलाइन $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} इनलाइन $ ।
आप इसे ऊपर दिए गए सूत्र में स्थानापन्न कर सकते हैं:

$$$$ प्रदर्शन $ $ \ frac {\ आंशिक L} {\ आंशिक W} = d \ boldsymbol {z} \ cdot \ frac {\ आंशिक W \ cdot \ boldsymbol {x}} {{आंशिक w} = = \ boldsymbol {$ z} \ cdot E \ cdot \ boldsymbol {x} $ $ प्रदर्शन $ $

जहाँ E एक मैट्रिक्स है जिसमें इकाइयाँ होती हैं (एक इकाई मैट्रिक्स नहीं)।

अब जब आपको पिछली परत के व्युत्पन्न को लेने की आवश्यकता है (भले ही गणना की सादगी के लिए यह पूरी तरह से जुड़ा हुआ परत भी होगा, लेकिन सामान्य स्थिति में यह कुछ भी नहीं बदलता है), तो आपको विचार करने की आवश्यकता है$$ $ इनलाइन $ \ boldsymbol {x} $ इनलाइन $ पिछली परत के एक कार्य के रूप में$$ $ इनलाइन $ \ boldsymbol {x} (W_ {पुराना}) $ इनलाइन $ :

$$$ $ प्रदर्शन $ $ \ _ शुरू {इकट्ठा} \ frac {\ आंशिक एल} {\ आंशिक W_ {पुराना}} = d \ boldsymbol {z} \ cdot \ frac {\ आंशिक \ boldsymbol {x} _ एक नया} (W) )} {\ आंशिक W_ {पुराना}} = d \ boldsymbol {z} \ cdot \ frac {\ आंशिक W \ cdot \ boldsymbol {x} (W_ {पुराना})} {\ आंशिक W_ \ _ {}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ आंशिक W \ cdot W_ {पुराना} \ _ W \ cdot ई \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ इसमें किए में भी शामिल नहीं होने में \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ टेंशन वाला शब्द अभी भी है $ $ प्रदर्शित करें

यानी$$ $ इनलाइन $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ इनलाइन $ और आपको पिछली परत पर भेजने की आवश्यकता है।

कोड

यह लेख मुख्य रूप से तंत्रिका नेटवर्क के गणित की व्याख्या करने के उद्देश्य से है। मैं कोड के लिए बहुत कम समय समर्पित करूंगा।

यह त्रुटि फ़ंक्शन का एक उदाहरण कार्यान्वयन है:

class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz 

कक्षा में सीधे और रिवर्स पास के लिए विधियां हैं। डायरेक्ट पास के समय, क्लास इंस्टेंस लेयर के अंदर डेटा को स्टोर करता है, और रिटर्न पास के समय, यह ग्रेडिएंट की गणना करने के लिए उनका उपयोग करता है। शेष परतों का निर्माण उसी तरह से किया जाता है। इसके लिए धन्यवाद, इस शैली में पूरी तरह से जुड़ा हुआ तंत्रिका लिखना संभव हो जाता है:

 class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ... 

पूर्ण कोड यहां पाया जा सकता है ।
इसके अलावा, मैं हैबे पर इस लेख का अध्ययन करने की सलाह देता हूं।

निष्कर्ष

मुझे आशा है कि मैं समझाने और दिखाने में सक्षम था कि काफी सरल गणित तंत्रिका नेटवर्क के पीछे है और यह बिल्कुल डरावना नहीं है। फिर भी, गहरी समझ के लिए, अपनी खुद की "बाइक" लिखने की कोशिश करना लायक है। सुधार और सुझाव टिप्पणियों में पढ़ने के लिए खुश हैं।