लालची दृष्टिकोण और स्लॉट मशीन। प्रोग्रामिंग चैम्पियनशिप के एमएल-ट्रैक के कार्यों का विश्लेषण

हम उन कार्यों के विश्लेषण प्रकाशित करना जारी रखते हैं जो हाल ही में चैंपियनशिप में प्रस्तावित किए गए थे। अगली पंक्ति में मशीन सीखने के विशेषज्ञों के लिए योग्यता दौर से लिए गए कार्य हैं। यह चार (बैकएंड, फ्रंटेंड, एमएल, एनालिटिक्स) का तीसरा ट्रैक है। ग्रंथों में टाइपो को सही करने के लिए एक मॉडल बनाने के लिए आवश्यक प्रतिभागियों, स्लॉट मशीनों पर खेलने के लिए एक रणनीति का प्रस्ताव, सामग्री के लिए सिफारिशों की एक प्रणाली को ध्यान में रखना और कई और कार्यक्रमों की रचना करना।

A. टाइपो

शर्त

(एपीग्राफ) (एक मंच से)
- इस बकवास की रचना किसने की?
- एस्ट्रोफिजिसिस्ट। वे लोग भी हैं।
- आपने "पत्रकार" शब्द में 10 गलतियाँ की हैं।

कई उपयोगकर्ता टाइपिंग की गलतियाँ करते हैं, कुछ की मार की वजह से, और कुछ अपनी अशिक्षा के कारण। हम यह जांचना चाहते हैं कि क्या उपयोगकर्ता वास्तव में किसी अन्य शब्द को ध्यान में रख सकता है जो उसने टाइप किया था।

औपचारिक रूप से, मान लें कि निम्न त्रुटि मॉडल होता है: उपयोगकर्ता उस शब्द से शुरू होता है जिसे वह लिखना चाहता है, और फिर बाद में इसमें कई त्रुटियां करता है। प्रत्येक गलती दूसरे प्रतिस्थापन के लिए शब्द के कुछ प्रतिस्थापन का प्रतिस्थापन है। एक त्रुटि केवल एक स्थिति में प्रतिस्थापित करने से मेल खाती है (अर्थात, यदि उपयोगकर्ता नियम "abc" → "cba" द्वारा एक ही त्रुटि करना चाहता है, तो स्ट्रिंग "abcabc" से वह या तो "cbaabc या" abccba ") प्राप्त कर सकता है। प्रत्येक त्रुटि के बाद, प्रक्रिया दोहराती है। एक ही नियम को कई बार अलग-अलग चरणों में उपयोग किया जा सकता है (उदाहरण के लिए, उपरोक्त उदाहरण में, "cbacba" को दो चरणों में प्राप्त किया जा सकता है)।

यह आवश्यक है कि उपयोगकर्ता द्वारा दी गई एक शब्द को ध्यान में रखते हुए और किसी अन्य ने लिखी गई त्रुटियों की न्यूनतम संख्या निर्धारित की हो।

निर्णय

आइए 4 से अधिक त्रुटियों के साथ सभी संभव शब्दों को सही वर्तनी से उत्पन्न करने का प्रयास करें। सबसे खराब स्थिति में, O ((L )N) ⁴ ) हो सकता है। समस्या की सीमाओं में, यह एक बड़ी संख्या है, इसलिए आपको यह पता लगाने की आवश्यकता है कि जटिलता को कैसे कम किया जाए। इसके बजाय, आप मीट-इन-द-बीच एल्गोरिथ्म का उपयोग कर सकते हैं: ऐसे शब्द उत्पन्न करें जिनमें 2 से अधिक त्रुटियां न हों, साथ ही वे शब्द जिनसे आप उपयोगकर्ता-लिखित शब्द प्राप्त कर सकते हैं, जिससे 2 से अधिक त्रुटियां न हों। ध्यान दें कि इनमें से प्रत्येक सेट का आकार 10 ⁶ से अधिक नहीं होगा। यदि उपयोगकर्ता द्वारा की गई त्रुटियों की संख्या 4 से अधिक नहीं है, तो ये सेट समाप्त हो जाएंगे। इसी तरह, हम यह सत्यापित कर सकते हैं कि त्रुटियों की संख्या 3, 2 और 1 से अधिक नहीं है।

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. कई-हथियारबंद डाकू

शर्त

यह एक संवादात्मक कार्य है।

आप खुद नहीं जानते कि यह कैसे हुआ, लेकिन आपने खुद को हॉल में स्लॉट मशीनों के साथ टोकन के पूरे बैग के साथ पाया। दुर्भाग्य से, बॉक्स ऑफिस पर, उन्होंने टोकन वापस लेने से इनकार कर दिया, और आपने अपनी किस्मत आजमाने का फैसला किया। हॉल में कई स्लॉट मशीनें हैं जिन्हें आप खेल सकते हैं। एक स्लॉट मशीन के साथ एक गेम के लिए आप एक टोकन का उपयोग करते हैं। एक जीत के मामले में, मशीन आपको एक डॉलर देती है, नुकसान के मामले में - कुछ भी नहीं। प्रत्येक मशीन में जीतने की एक निश्चित संभावना होती है (जिसे आप नहीं जानते हैं), लेकिन यह विभिन्न मशीनों के लिए अलग है। इन मशीनों के निर्माता की वेबसाइट का अध्ययन करने के बाद, आपको पता चला कि प्रत्येक मशीन के लिए जीतने की संभावना कुछ मापदंडों के साथ बीटा वितरण से विनिर्माण स्तर पर यादृच्छिक रूप से चुनी जाती है।

आप अपनी अपेक्षित जीत को अधिकतम करना चाहते हैं।

निर्णय

यह समस्या सर्वविदित है, इसे विभिन्न तरीकों से हल किया जा सकता है। जूरी के मुख्य निर्णय ने थॉम्पसन नमूनाकरण रणनीति को लागू किया, लेकिन चूंकि कार्यक्रम की शुरुआत में चरणों की संख्या ज्ञात थी, इसलिए अधिक इष्टतम रणनीतियाँ हैं (उदाहरण के लिए, यूसीबी 1)। इसके अलावा, एक भी एप्सिलॉन-लालची-रणनीति के साथ मिल सकता है: एक निश्चित संभावना के साथ and एक यादृच्छिक मशीन खेलते हैं और एक प्रायिकता के साथ (1 - best) सर्वश्रेष्ठ जीत आंकड़ों के साथ एक मशीन खेलते हैं।

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. वाक्यों का संरेखण

शर्त

एक अच्छी मशीन अनुवाद मॉडल के प्रशिक्षण के लिए सबसे महत्वपूर्ण कार्यों में से एक समानांतर मामलों का एक अच्छा मामला है। आमतौर पर, समानांतर ऑफ़र के लिए स्रोत समानांतर दस्तावेज़ हैं। यह पता चला है कि अक्सर समानांतर वाक्यों का एक निश्चित कोष बनाने के लिए, आपको उनकी लंबाई के अलावा कुछ भी जानने की आवश्यकता नहीं है। विशेष रूप से, आप नोटिस कर सकते हैं कि स्रोत भाषा में जितनी लंबी अवधि होगी, उतने लंबे समय तक इसका अनुवाद किया जा सकेगा। कुछ कठिनाई इस तथ्य में निहित है कि अनुवाद के दौरान पाठ में वाक्यों की संख्या बदल सकती है: कभी-कभी अनुवाद में दो आसन्न वाक्यों को एक में जोड़ा जा सकता है, या इसके विपरीत - एक वाक्य को दो में विभाजित किया जा सकता है। कुछ दुर्लभ मामलों में, वाक्यों को पूरी तरह से अनुवाद में छोड़ा जा सकता है, या अनुवाद में ऐसा अनुवाद दिखाई दे सकता है जो मूल में नहीं था।

अधिक औपचारिक रूप से, मान लीजिए कि समानांतर बाड़ों के लिए निम्नलिखित जेनरिक मॉडल सत्य है। प्रत्येक चरण पर, हम निम्न में से एक करते हैं:

1. रोक

प्रायिकता p _{h के साथ,} हल्स _की पीढ़ी समाप्त हो जाती है।

2. [१०३] स्किपिंग ऑफर

प्रायिकता p _{d के साथ हम} मूल पाठ में एक वाक्य लिखते हैं। हम अनुवाद के लिए कुछ भी विशेषता नहीं रखते हैं। मूल भाषा L selected 1 में वाक्य की लंबाई असतत वितरण से चुनी गई है:

।

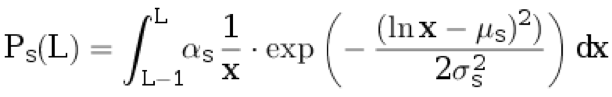
यहाँ μ _s , are _s वितरण पैरामीटर हैं, और α _s सामान्यीकरण गुणांक चुना जाता है ताकि ।

3. [0-1] सम्मिलित करें प्रस्ताव

संभाव्यता p _{i के साथ हम} अनुवाद को एक वाक्य _देते हैं। हम मूल में कुछ भी नहीं लिखते हैं। अनुवाद भाषा L selected 1 में एक वाक्य की लंबाई एक असतत वितरण से चुनी गई है:

।

यहाँ μ _t , are _t वितरण मानदंड हैं, और α _t सामान्यकरण गुणांक चुना जाता है ताकि ।

4. अनुवाद

संभाव्यता के साथ (1 - p _d - p _i - p _h ) हम वाक्य की लंबाई को मूल भाषा L _s distribution 1 में वितरण p _s (गोलाकार के साथ) से लेते हैं। अगला, हम सशर्त असतत वितरण से अनुवाद भाषा L _t the 1 में वाक्य की लंबाई उत्पन्न करते हैं:

।

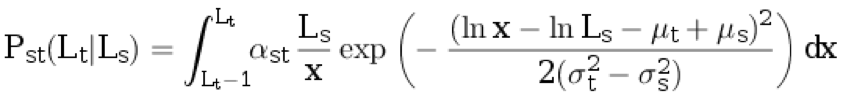
यहां, α _सेंट सामान्यीकरण गुणांक है, और शेष पैरामीटर्स पिछले पैराग्राफ में वर्णित हैं।

अगला एक और कदम है:

1. [2-1] संभाव्यता p _{विभाजन s के साथ,} मूल भाषा में उत्पन्न वाक्य दो गैर-खाली लोगों में विभाजित हो जाता है, जिससे शब्दों की कुल संख्या ठीक एक से बढ़ जाती है । संभावना है कि लंबाई L का एक वाक्य L ₁ और L _{2 के} भागों में अलग हो _{जाएगा} (यानी, L ₁ + L ₂ = L _s + 1) P _s (L ₁ ) _s P _s (L ₂ ) के समानुपाती होगा।

2. [1-2] प्रायिकता p _{विभाजित टी के साथ,} लक्ष्य भाषा में उत्पन्न वाक्य दो गैर-रिक्त वाक्यों में विभाजित हो जाता है, जिससे शब्दों की कुल संख्या ठीक एक से बढ़ जाती है। संभावना है कि लंबाई एल का एक वाक्य एल 1 और एल 2 के हिस्सों में अलग हो _{जाएगा} (यानी, एल ₁ + एल ₂ = एल _टी + 1) पी _टी (एल ₁ ) ⋅ पी _टी (एल ₂ ) के लिए आनुपातिक है।

3. 3. [1-1] (1 - p _{विभाजन s} - p _{विभाजन t} ) की संभावना के साथ, उत्पन्न वाक्यों की जोड़ी में से कोई भी क्षय नहीं होगा।

निर्णय

कार्य छिपे हुए मार्कोव मॉडल (HMM संरेखण) का उपयोग करके संरेखण का एक विशेष मामला है। मुख्य विचार यह है कि आप इस मॉडल और आगे के एल्गोरिथ्म का उपयोग करके दस्तावेजों की एक विशिष्ट जोड़ी बनाने की संभावना की गणना कर सकते हैं: इस मामले में, राज्य दस्तावेज़ उपसर्गों की एक जोड़ी है। तदनुसार, समानांतर वाक्यों की एक विशिष्ट जोड़ी के संरेखण की आवश्यक संभावना को आगे-पीछे की एल्गोरिथ्म द्वारा गणना की जा सकती है।

D. सिफारिशों का टेप

शर्त

विषम सामग्री के लिए सुझावों की एक फ़ीड पर विचार करें। यह विभिन्न प्रकार (चित्र, वीडियो, समाचार, आदि) की वस्तुओं को मिलाता है। इन वस्तुओं को आमतौर पर उपयोगकर्ता द्वारा प्रासंगिकता के लिए आदेश दिया जाता है: उपयोगकर्ता के लिए अधिक प्रासंगिक (दिलचस्प) वस्तु, सिफारिशों की सूची के शीर्ष के करीब। हालांकि, इस तरह के आदेश के साथ, परिस्थितियां अक्सर उत्पन्न होती हैं, जिसमें सिफारिशों की सूची में एक ही प्रकार की कई वस्तुएं दिखाई देती हैं। यह हमारी सिफारिशों की बाहरी विविधता को बहुत खराब करता है और इसलिए उपयोगकर्ता इसे पसंद नहीं करते हैं। एक एल्गोरिथ्म को लागू करना आवश्यक है, जो सिफारिशों की सूची के अनुसार, एक नई सूची बनाएगा जो इस समस्या से मुक्त होगा और सबसे अधिक प्रासंगिक होगा।

अनुशंसाओं की प्रारंभिक सूची को = [a ₀ , a, ..., _{n - 1} ] की लंबाई n> 0. दी गई है। संख्या के साथ एक वस्तु I में संख्या b _i 0 {0, ..., m - 1} के साथ टाइप है। इसके अतिरिक्त, संख्या I के अंतर्गत किसी वस्तु की प्रासंगिकता r (a) = 2 _{underi है} । उस सूची पर विचार करें जो प्रारंभिक एक से वस्तुओं का सबसेट चुनकर उन्हें पुन: व्यवस्थित कर रही है: x = [a ₀ , _{i 1} , ..., _{i i - 1} ] लंबाई k (0 ≤ k ≤ n)। एक सूची को स्वीकार्य कहा जाता है यदि इसमें कोई दो लगातार ऑब्जेक्ट प्रकार में मेल नहीं खाते हैं, अर्थात, b _{i j 1} b _{i j + 1} सभी j = 0, ..., k - 2 के लिए। सूची की प्रासंगिकता की गणना सूत्र द्वारा की जाती है $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$। आपको सभी मान्य के बीच अधिकतम प्रासंगिकता सूची ढूंढनी होगी।

निर्णय

सरल गणितीय गणनाओं का उपयोग करते हुए, यह दिखाया जा सकता है कि समस्या को "लालची" दृष्टिकोण द्वारा हल किया जा सकता है, अर्थात, सिफारिशों की इष्टतम सूची में, प्रत्येक आइटम में सबसे अधिक प्रासंगिक वस्तु है जो सूची की एक ही शुरुआत में मान्य है। इस दृष्टिकोण का कार्यान्वयन सरल है: हम वस्तुओं को एक पंक्ति में लेते हैं और यदि संभव हो तो उन्हें उत्तर में जोड़ते हैं। जब कोई अमान्य वस्तु सामने आती है (जिसका प्रकार पिछले एक के प्रकार के साथ मेल खाता है), तो हम इसे एक अलग कतार में रख देते हैं, जहाँ से हम इसे जल्द से जल्द प्रतिक्रिया में सम्मिलित करते हैं। ध्यान दें कि समय पर हर पल, इस कतार में सभी वस्तुओं का मिलान प्रकार होगा। अंत में, कई ऑब्जेक्ट कतार में रह सकते हैं, उन्हें प्रतिक्रिया में शामिल नहीं किया जाएगा।

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

डी। चरित्र अनुक्रमों का क्लस्टरिंग

एक परिमित वर्णमाला A = {a ₁ , a, ₂ , ..., _{K - 1} , _K = S}, एक _i , {a, b, ..., z}, S है जो रेखा का अंत है।

वर्णमाला A पर यादृच्छिक तार उत्पन्न करने की निम्न विधि पर विचार करें:

1. पहला वर्ण x ₁ वितरण P (x ₁ = a _i ) = q _i (यह ज्ञात है कि q _K = 0) के साथ एक यादृच्छिक चर है।
2. प्रत्येक अगला वर्ण सशर्त वितरण P के अनुसार पिछले एक के आधार पर उत्पन्न होता है (x _i = a _j || x _{i - 1} = a _l ) = p _jl ।
3. यदि x _i = S, पीढ़ी बंद हो जाती है और परिणाम x ₁ x ₂ ... x _{i - 1 है} ।

विभिन्न मापदंडों वाले दो वर्णित मॉडल के मिश्रण से उत्पन्न लाइनों का सेट दिया गया है। प्रत्येक पंक्ति के लिए यह आवश्यक है कि वह उस श्रृंखला का सूचकांक दे जिससे वह उत्पन्न हुई थी।

निर्णय

समस्या ईएम एल्गोरिथ्म का उपयोग करके हल की गई है : यह माना जाता है कि प्रस्तुत नमूना दो मार्कोव श्रृंखलाओं के मिश्रण से उत्पन्न होता है, जिनके मापदंडों को पुनरावृत्तियों के दौरान बहाल किया जाता है। 80% सही उत्तरों पर प्रतिबंध लगा दिया गया है ताकि समाधान की शुद्धता उन उदाहरणों से प्रभावित न हो जो दोनों श्रृंखलाओं में उच्च संभावना रखते हैं। इन उदाहरणों, इसलिए, जब ठीक से बहाल किया जाता है, तो एक श्रृंखला को सौंपा जा सकता है जो उत्पन्न प्रतिक्रिया के संदर्भ में गलत है।

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.