पोजीट-अंकगणित: अपने क्षेत्र में एक अस्थायी बिंदु को पराजित करना। भाग 1

भाग २

अनुवादक से: पोज़िट प्रारूप का विषय पहले से ही यहाँ हब पर था, लेकिन महत्वपूर्ण तकनीकी विवरण के बिना। इस प्रकाशन में, मैं आपके ध्यान में जॉन गस्टाफसन (पॉज़िट के लेखक) और पॉज़िट प्रारूप पर इसहाक योनेमोतो के लेख का अनुवाद लाता हूं।
चूंकि लेख में एक बड़ी मात्रा है, इसलिए मैंने इसे दो भागों में विभाजित किया है। लिंक की सूची दूसरे भाग के अंत में है।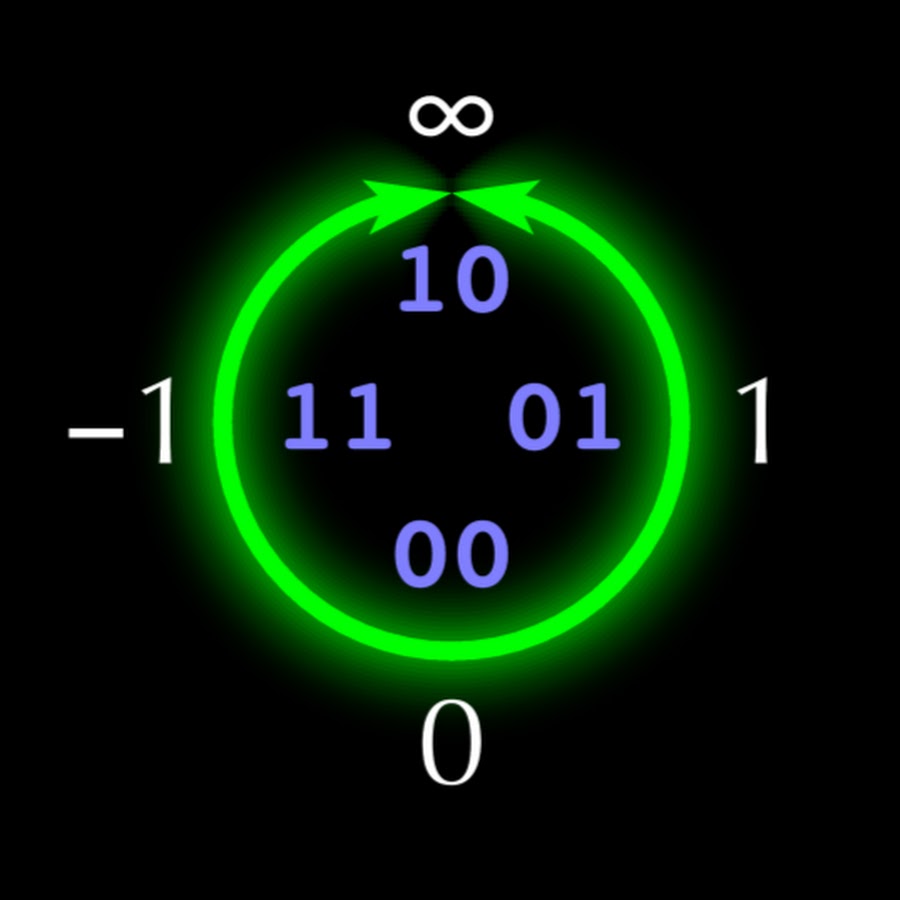



नए डेटा प्रकार, जिसे पॉज़िट कहा जाता है, को IEEE Standard 754 फ़्लोटिंग पॉइंट नंबरों के लिए सीधे प्रतिस्थापन के रूप में डिज़ाइन किया गया है। पहले के फॉर्म के विपरीत, अंकगणित, पॉज़िट मानक को अंतराल अंकगणितीय या चर-आकार वाले ऑपरेंड्स के उपयोग की आवश्यकता नहीं है, और, जैसे फ्लोट, पॉज़िट नंबरों को गोल किया जाता है, यदि परिणाम ठीक से नहीं दिखाया जा सकता है। फ्लोट प्रारूप पर उनके पास निर्विवाद फायदे हैं, जिसमें विभिन्न गतिशील रेंज, अधिक सटीकता, विभिन्न प्रणालियों पर गणना के परिणामों के बिटकॉइन संयोग, सरल हार्डवेयर और अपवादों के लिए सरल समर्थन शामिल हैं। सकारात्मक संख्याएँ अनंत या शून्य पर अतिप्रवाह नहीं करती हैं, और "संख्या नहीं" (NotNumber, NaN) क्रियाएं नहीं बिट संयोजन हैं। पॉज़िट प्रोसेसिंग यूनिट IEEE FPU से कम जटिल है। यह कम बिजली की खपत करता है और एक छोटे सिलिकॉन क्षेत्र पर कब्जा कर लेता है, इसलिए चिप एक ही हार्डवेयर संसाधनों के साथ FLOPS की तुलना में प्रति सेकंड पॉज़िट नंबर पर काफी अधिक संचालन कर सकता है। जीपीयू और डीप लर्निंग प्रोसेसर, विशेष रूप से, बिजली की खपत के प्रति वाट अधिक संचालन कर सकते हैं, जिससे उनके काम की गुणवत्ता में सुधार होगा।

विभिन्न सकारात्मक सटीकता के लिए गणना सटीकता के संदर्भ में व्यापक परीक्षण और फ्लोट की तुलना में व्यापक परीक्षण किए गए थे। कम सटीकता वाले पॉज़िट नंबर उन मामलों में "किसी न किसी गणना" के लिए सबसे अच्छा समाधान हैं जहां कम सटीकता स्वीकार्य है। उच्च-सटीक पोज़िट संख्या एक ही आकार के फ़्लोट की तुलना में उच्च परिशुद्धता प्रदान करती है; कुछ मामलों में, 32-बिट पॉज़िट सुरक्षित रूप से 64-बिट फ़्लोट को बदल सकता है। दूसरे शब्दों में, पॉज़िट अपने खेल में फ़्लोटफॉर्म को बेहतर बनाता है।

थ्योरी: अनम्स: टाइप I और टाइप II

अंकगणितीय रूपरेखा अंकुम (सार्वभौमिक संख्या, यू विविध संख्या बेर) संख्याओं का प्रतिनिधित्व करने के लिए कई रूप हैं। मूल रूप IEEE 754 का एक सुपरसेट "टाइप I" है; वह यह दर्शाने के लिए कि वास्तविक संख्या सटीक है या निकटवर्ती वास्तविक संख्याओं के बीच की सीमा में भिन्न भाग के अंत में ubit का उपयोग करती है। इस तथ्य के बावजूद कि फ्लोट की तरह, यूनम में एक चिन्ह, प्रतिपादक और भिन्नात्मक भाग है, प्रतिपादक और भिन्नात्मक भाग की लंबाई स्वचालित रूप से भिन्न होती है, उपयोगकर्ता द्वारा परिभाषित एक निश्चित मूल्य से एक बिट तक। अनम टाइप मैं अंतराल अंकगणित का प्रतिनिधित्व करने के लिए एक कॉम्पैक्ट तरीका है लेकिन चर लंबाई को अतिरिक्त प्रयास की आवश्यकता होती है। यह प्रकार एक विशेष गोलाई फ़ंक्शन का उपयोग करके फ्लोट के व्यवहार को दोहरा सकता है।

"टाइप II" यूनिवर्सल नंबर फॉर्म [4] IEEE फ्लोट के साथ संगत नहीं है, और यह प्रोजेक्टेबल रियल नंबर x पर आधारित एक साफ, गणितीय रूप से कठोर अवधारणा है। यहाँ मुख्य विचार यह है कि ऐड-ऑन कोड में हस्ताक्षर किए गए पूर्णांकों को अनुमानित रूप से वास्तविक संख्याओं में मैप किया जाता है, सकारात्मक से नकारात्मक संख्याओं पर स्विच करने की समान संपत्ति के साथ, और संख्या अक्ष पर समान क्रम के साथ। विलियम काहन का उद्धरण [5]:
"वे स्मृति स्थान को बचाते हैं क्योंकि वे संख्याओं में हेरफेर नहीं करते हैं, लेकिन मूल्यों को इंगित करते हैं। और यह बहुत तेजी से अंकगणित को संभव बनाता है। "
5-बिट अनम की संरचना को अंजीर में दिखाया गया है। 1. यदि प्रत्येक unum में n बिट्स हैं, तो "u-lattice" सर्कल के ऊपरी दाएं चतुर्थ भाग को क्रमबद्ध तरीके से भरता है। $$$2 ^ {n-3} -1$ वास्तविक संख्या $$$x_i$ (जरूरी नहीं कि तर्कसंगत)। ऊपरी बाएँ वृत्त का चतुर्थ भाग ऋणात्मक है $$$x_i$ ऊर्ध्वाधर अक्ष के सापेक्ष परिलक्षित होता है। वृत्त के निचले आधे भाग में ऐसी संख्याएँ होती हैं, जो क्षैतिज अक्ष से परावर्तित ऊपरी आधी की संख्याओं के विपरीत होती हैं, जो गुणन और विभाजन के कार्यों को जोड़ और घटाव के रूप में सममित बनाती है। टाइप I के साथ, टाइप II अनम नंबर 1 (ubit) के साथ समाप्त होता है, आसन्न सटीक बिंदुओं के बीच खुले अंतराल का प्रतिनिधित्व करता है जिसके लिए 0 के साथ अनम समाप्त होता है।


अंजीर। 1. एक अतिरिक्त कोड 4 बिट्स में पूर्णांकों के लिए मैप की गई वास्तविक वास्तविक संख्याओं की रेखा।

टाइप II अनम नंबर के पास कई आदर्श गणितीय गुण हैं, लेकिन उनके साथ अधिकांश ऑपरेशन लुक-अप तालिकाओं का उपयोग करके किए जाते हैं। यदि एन सटीक बिट्स की आवश्यकता होती है, तो तालिका (सबसे खराब स्थिति में) होगी $$$2 ^ {2 एन}$ दो तर्कों के कार्य के लिए मूल्य, लेकिन समरूपता और अन्य चाल को ध्यान में रखते हुए, तालिका को अधिक स्वीकार्य आकार में घटाया जा सकता है। तालिका का आकार इस अल्ट्राफास्ट प्रारूप के पैमाने को 20 बिट्स या आज की तकनीक के लिए कम करता है। टाइप II प्रकार अनम संख्या भी परिचालन को मर्ज करने के लिए खुद को अच्छी तरह से उधार नहीं देती है। इन कमियों ने एक प्रारूप खोजने के लिए एक प्रेरणा के रूप में कार्य किया है जो कई प्रकार के अनमोल प्रकार II संख्याओं के गुणों को बरकरार रखता है, लेकिन अधिक "हार्डवेयर अनुकूल" है और मौजूदा FPU के समान तर्क सर्किट द्वारा गणना की जा सकती है।

2. संख्या Posit और वैध

वास्तविक संख्या में गणना के लिए दो विपरीत दृष्टिकोण हैं:

• बड़ी संख्या में व्यावहारिक अनुप्रयोगों के लिए सख्त, लेकिन सस्ता और स्वीकार्य नहीं है
• गणितीय रूप से कठोर, समय और स्मृति की कीमत पर भी

पहला कथन वास्तविक अंकगणित से संबंधित है, जिसमें गोलाई त्रुटि काफी छोटी है, दूसरा कथन अंतराल अंकगणित से संबंधित है। प्रकार I और II की असमान संख्याओं को एक समान नस में भी माना जा सकता है, और यह एक कारण है कि वे "समान संख्या" हैं। हालांकि, अगर हम हमेशा प्रत्येक ऑपरेशन के बाद राउंडिंग के लिए कुछ फ़ंक्शन का उपयोग करने जा रहे हैं, तो हम बेहतर रूप से अंतिम बिट का उपयोग अंश के महत्वपूर्ण हिस्से के रूप में नहीं करते हैं और ubit के रूप में नहीं करते हैं। इस प्रकार के अंक को नंबर पॉज़िट कहा जाएगा।

न्यू ऑक्सफोर्ड अमेरिकन डिक्शनरी का उद्धरण, तीसरा संस्करण:

सकारात्मक (संज्ञा): इस कथन पर दिया गया कथन कि यह सच हो जाएगा।

हार्डवेयर कार्यान्वयन को सरल बनाने के लिए, टाइप II नंबर नियम को कमजोर करता है: सटीक उलटा मान केवल 0 के लिए मौजूद है, $$$\ pm \ infty$ और डिग्री दो। यह हमें यू-ग्रिड को भरने की अनुमति देता है ताकि अंतिम संख्या फ्लोट के समान बनी रहे, और फॉर्म होगा $$$m \ cdot2 ^ k$ जहां k और m पूर्णांक हैं। कोई खुले अंतराल नहीं हैं।

वैध, समान आकार के पॉज़िट नंबर की एक जोड़ी है, प्रत्येक को ubit में समाप्त किया जाता है। वे उन अनुप्रयोगों में उपयोग के लिए अभिप्रेत हैं, जहां संख्यात्मक अंतराल को कड़ाई से निर्धारित करना महत्वपूर्ण है, उदाहरण के लिए, जब संख्यात्मक एल्गोरिदम को डीबग करना। सामान्य अंतराल अंकगणित की तुलना में मान्य मूल्य अधिक शक्तिशाली हैं और तेजी से अत्यधिक निराशावादी अंतराल सीमाओं [2, 4] का विस्तार करने के लिए कम प्रवण हैं। हालाँकि, वे इस प्रकाशन का विषय नहीं हैं।

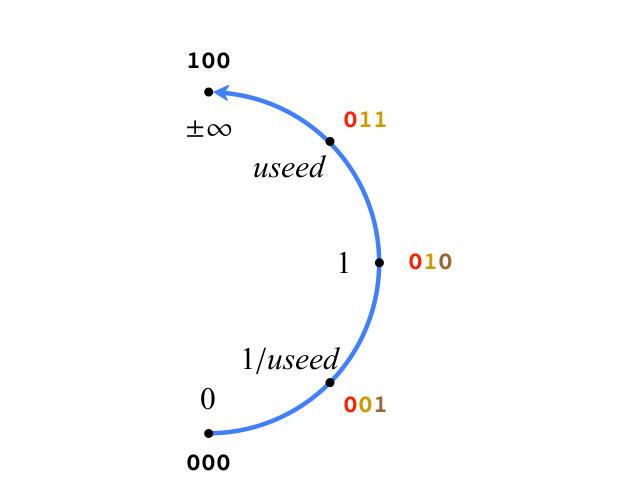
चित्रा 2 एक्स-बिट बिट्स के साथ बिट बिट पॉज़िट प्रतिनिधित्व की संरचना को दर्शाता है।


चित्रा 2. नॉनजरो मानों को पीछे करने के लिए सामान्यीकृत स्थिति प्रारूप

साइन बिट में सकारात्मक संख्याओं के लिए 0, नकारात्मक के लिए 1 होता है। नकारात्मक संख्याओं के लिए, मोड, प्रतिपादक और आंशिक भाग को डिकोड करने से पहले पूरक 2 खोजें। मोड बिट्स को समझने के लिए, तालिका 1 में दिखाए गए बाइनरी स्ट्रिंग्स पर विचार करें, जिसमें k का अर्थ है, अग्रणी अनुक्रम की लंबाई, और बिटस्ट्रीम में x का अर्थ है उदासीन अवस्था।

तालिका 1. शासन बिट्स का रन-लंबाई अर्थ k



हम अग्रणी अनुक्रम की लंबाई को संख्या मोड कहते हैं। बाइनरी तार एक निश्चित संख्या में शून्य या एक पंक्ति में शुरू होते हैं, इसके बाद विपरीत बिट या स्ट्रिंग के अंत तक पहुंच जाते हैं। मोड बिट्स को एम्बर में हाइलाइट किया जाता है, विपरीत बिट को भूरे रंग में हाइलाइट किया जाता है। अनुक्रम में समान बिट्स की संख्या m होने दें, यदि ये बिट्स शून्य हैं, तो k = -m, यदि 1, तो k = m-1। अधिकांश प्रोसेसर एक शब्द में पहली इकाई या हार्डवेयर में एक शब्द में पहला शून्य पा सकते हैं, अर्थात, डिकोडिंग लॉजिक पहले से ही उपलब्ध है। मोड का अर्थ है स्केलिंग फैक्टर के बराबर $$$उपयोग किया गया ^ k$ जहाँ $$$इस्तेमाल किया = 2 ^ {2 ^ {es}}$ । तालिका 2 उपयोग किए गए मूल्यों का एक उदाहरण दिखाता है।

तालिका 2. es फ़ंक्शन के रूप में उपयोग की जाती है



अगले बिट्स (चित्र में नीले रंग में हाइलाइट किए गए) एक्सपोनेंट ई हैं, जो एक अहस्ताक्षरित पूर्णांक को संदर्भित करता है। इसे स्थानांतरित नहीं किया जाता है, जैसा कि फ्लोट्स में किया जाता है, यह स्केलिंग टू को दर्शाता है $$$2 ^ ई$ । वहाँ प्रतिपादक बिट्स तक हो सकता है, यह निर्भर करता है कि मोड बिट्स के दाईं ओर कितने बिट्स बचे हैं। सटीकता को बदलने के लिए यह एक कॉम्पैक्ट तरीका है, निरपेक्ष मूल्य में 1 के करीब संख्या में बहुत बड़ी या बहुत छोटी संख्या की तुलना में अधिक सटीकता होती है, जो गणना में बहुत कम आम हैं।

यदि मोड और एक्सपोनेंट बिट्स के बाद बिट्स बचे हैं, तो वे फ्रैक्शनल पार्ट का प्रतिनिधित्व करते हैं, एफ, फ्लोट फॉर्मेट में फ्रैक्शनल पार्ट 1. फ की तरह, लेकिन हिडन बिट हमेशा 1. होता है। फ्लोट के विपरीत, छिपे हुए 0 के साथ कोई भी संख्या नहीं होती है।

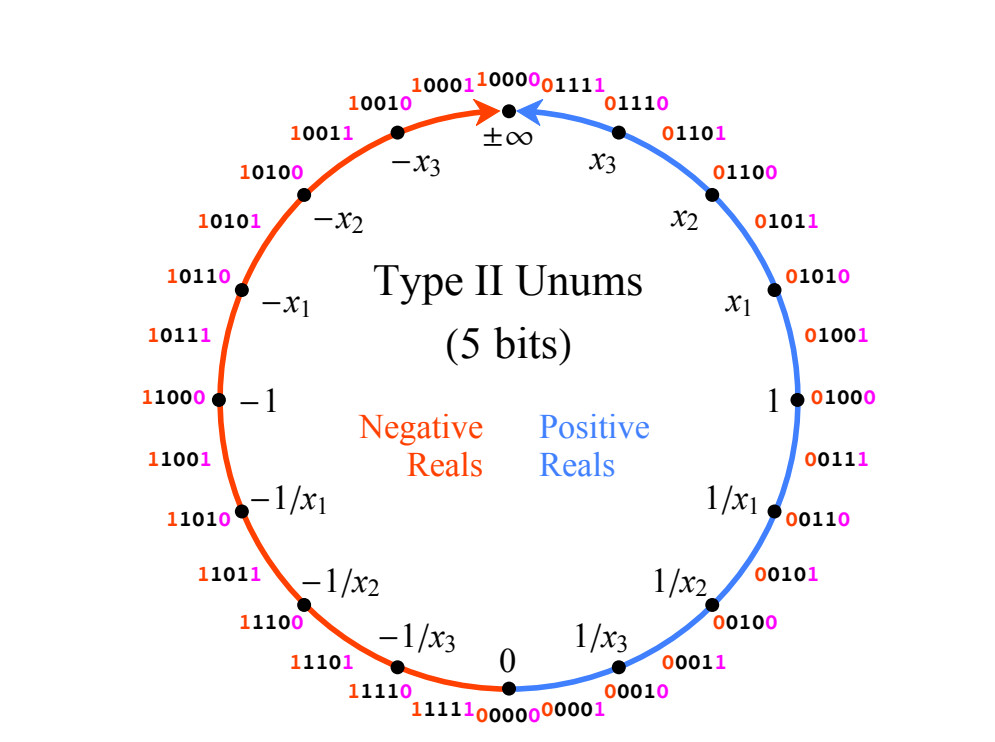
हमारे द्वारा वर्णित प्रणाली यू-ग्रिड को भरने का एक स्वाभाविक परिणाम है। आइए एक सरल 3-बिट पोजिट के साथ शुरुआत करें, स्पष्टता के लिए, अंजीर में। चित्र 3 केवल अनुमानित वास्तविक संख्याओं का सही आधा भाग दिखाता है। तो, अंजीर में संख्या। 3. प्रकार II नियम का पालन करें। केवल दो विशेष मूल्य हैं: 0 (सभी बिट्स 0 हैं) और ∞ values ​​(एक इकाई जिसके बाद सभी शून्य हैं), उनकी बिट अनुक्रम स्थितीय संकेतन का पालन नहीं करता है। चित्रा 3 में अन्य सकारात्मक मूल्यों के लिए, बिट्स ऊपर वर्णित के अनुसार रंगीन हैं। ध्यान दें कि चित्रा 3 में सभी सकारात्मक मान मोड बिट्स द्वारा प्रतिनिधित्व डिग्री कश्मीर में सटीक उपयोग किए गए मान हैं।


चित्र 3। 3-बिट पॉज़िट के सकारात्मक मूल्य

बिट्स जोड़े जाने पर Posit नंबरों की सटीकता बढ़ जाती है, और मान वहीं बने रहते हैं जब वे बिट 0 में जोड़े जाते हैं। जब 1 जोड़ा जाता है, तो सर्कल पर दो पॉज़िट मानों के बीच एक नया मान बनाया जाता है। हमें उन्हें कितना संख्यात्मक मूल्य देना चाहिए? बता दें कि मैक्सपोस सबसे बड़ा पॉजिटिव वैल्यू है और बिट स्ट्रिंग द्वारा परिभाषित सर्कल पर सबसे छोटे पॉजिटिव वैल्यू को मिनॉप करता है। चित्रा 3 में, अधिकतम उपयोग किया जाता है, और न्यूनतम 1 / उपयोग किया जाता है। प्रक्षेप नियम इस प्रकार हैं:

मैक्सपोस और max ± के बीच, नया मूल्य मैक्सपोस × उपयोग किया जाता है; 0 और minpos के बीच, नया मान minpos / उपयोग (एक नई मोड बिट के साथ) है
मौजूदा मूल्यों के बीच $$$x = 2 ^ m$ और $$$y = 2 ^ n$ , जहाँ m और n 1 से अधिक भिन्न होते हैं, नया मान उनका ज्यामितीय माध्य होगा, $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (एक नए घातांक बिट के साथ)।
अन्य मामलों में, नया मान मौजूदा x और y के बीच में स्थित है, अर्थात यह एक अंकगणितीय माध्य है, $$$(x + y) / 2$ (एक नए अंश के साथ)

एक उदाहरण के रूप में, अंजीर। 4, es = 2 के साथ 2 से 5 बिट से पॉज़िट संख्या के निर्माण को दर्शाता है, और इस प्रकार = 16 का उपयोग किया जाता है।


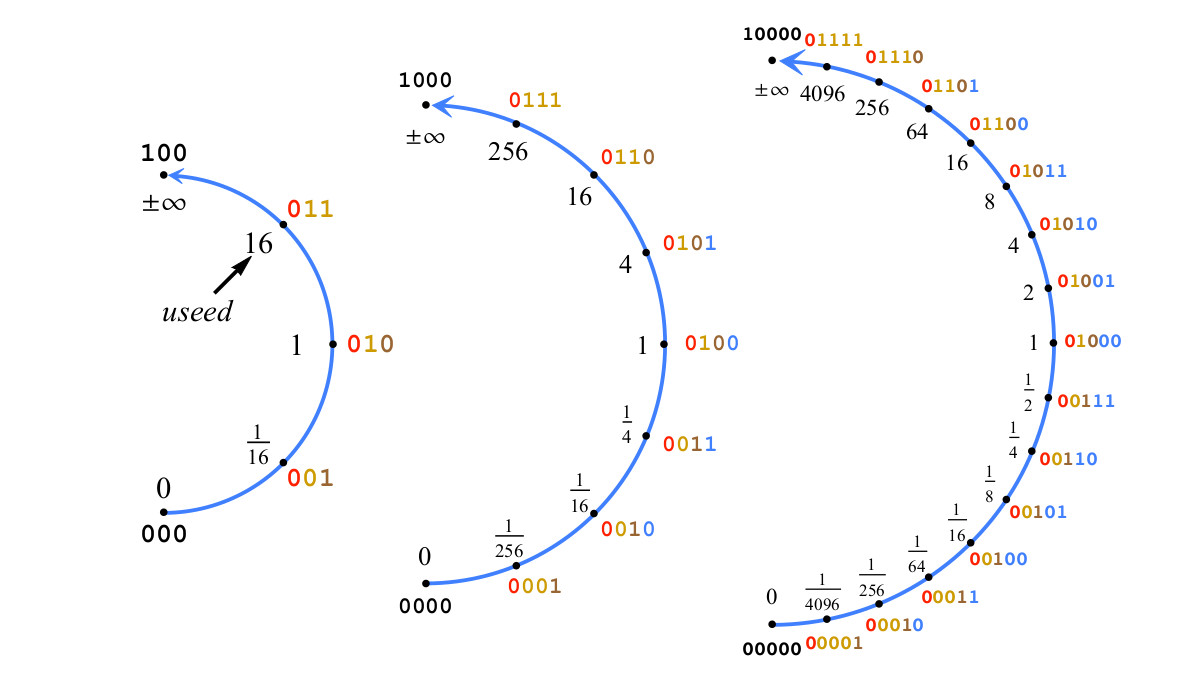अंजीर। 4. एक घातांक के दो बिट्स के साथ एक पोज़िट का निर्माण, $$$es = 2, इस्तेमाल किया = 2 ^ {2 ^ {es}} = $ 1$

अगर अंजीर में। 4 6-बिट पॉज़िट प्राप्त करने के लिए एक और बिट जोड़ें, 1/16 और 16 के बीच मानों की सीमाओं का प्रतिनिधित्व करने वाले पॉज़िट नंबरों के लिए, आंशिक भाग के बिट को जोड़ा जाएगा, न कि एक्सपोनेंट बिट। एक हस्ताक्षर किए पूर्णांक के रूप में संख्या पॉज़िट पी का प्रतिनिधित्व करने वाले बिट्स की एक स्ट्रिंग पर विचार करें, से लेकर $$$-2 ^ {n-1}$ को $$$2 ^ {n-1} -1$ । आज्ञा देना एक पूर्णांक का प्रतिनिधित्व मोड बिट्स, ई एक अहस्ताक्षरित संख्या का प्रतिनिधित्व करने वाले बिट्स, यदि मौजूद है। यदि बिट सेट एक आंशिक हिस्सा है $$$\ {f_1f_2 ... f_ {f_s} \}$ संभवत: खाली है तो चलो एक संख्या का प्रतिनिधित्व करने वाला एक मूल्य है $$$1, f_1f_2 ... f_ {f_s}$ । तब p प्रतिनिधित्व करता है

$$

$$x = \ शुरू {मामलों} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, \\ साइन (पी) \ बार उपयोग किया ^ k \ टाइम्स 2 ^ ई \ गुना f \, और \ text {कोई अन्य} p \ end {मामले}$$

मोड और es बिट्स मानक फ्लोट में घातीय बिट्स के समान कार्य करते हैं, साथ में वे दो की शक्ति के बराबर एक स्केलिंग कारक निर्धारित करते हैं, और प्रत्येक उपयोग किए गए वेतन वृद्धि का अर्थ है एक पारी $$$2 ^ {es}$ बिट। मैक्सपोस की संख्या है $$$उपयोग ^ {n-2}$ और minpos बराबर है $$$उपयोग ^ {2-n}$ । पॉज़िट संख्या को डिकोड करने का एक उदाहरण चित्र 5 में दिखाया गया है (सादगी के लिए "गैर-मानक" मूल्य के साथ,)।


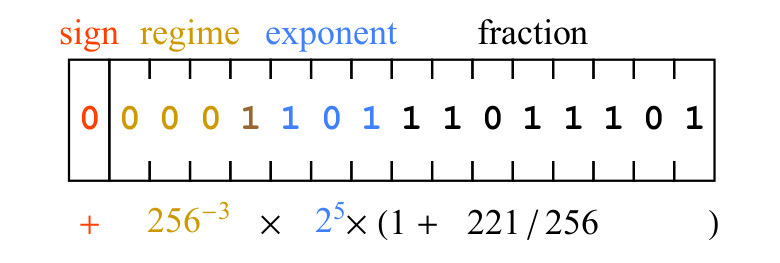अंजीर। 5. पॉज़िट बिट स्ट्रिंग और इसके गणितीय अर्थ का एक उदाहरण

संकेत 0 का एक सा मतलब है कि मूल्य सकारात्मक है। मोड 0001 के बिट्स में तीन शून्य का अनुक्रम होता है, जिसका अर्थ है कि k = -3, इसलिए, मोड के बिट्स द्वारा प्रस्तुत स्केलिंग कारक है $$$256 ^ {- 3}$ । प्रतिपादक बिट्स, 101, एक अहस्ताक्षरित बाइनरी पूर्णांक के रूप में 5 का प्रतिनिधित्व करता है, और सम्मिलन स्केलिंग कारक है $$$2 ^ 5$ । अंत में, आंशिक भाग 11011101 के टुकड़े 221 संख्या का प्रतिनिधित्व करते हैं, अर्थात, आंशिक भाग 1 + 221/256 है। चित्र 5 में बिटफील्ड के तहत लिखी गई अभिव्यक्ति। हमें परिणाम की ओर ले जाता है $$$477/134217728 \ लगभग 3.55393 \ गुना 10 ^ {- 6}$

2.2। 8-बिट पॉज़िट और न्यूरल नेटवर्क ट्रेनिंग

इस तथ्य के बावजूद कि IEEE मानक 8-बिट फ़्लोट्स को परिभाषित नहीं करता है, es = 0 के साथ 8 बिट्स की पॉज़िट संख्या कुछ उद्देश्यों के लिए उनकी उपयोगिता साबित हुई है, वे तंत्रिका नेटवर्क के निर्माण के लिए बहुत उपयोगी हैं [3, 8]। वर्तमान में, आधा परिशुद्धता (16-बिट) IEEE नंबर अक्सर इन उद्देश्यों के लिए उपयोग किया जाता है, लेकिन 8-बिट पॉज़िट संख्याओं को संभवतः 2-4 गुना तेजी से संसाधित किया जा सकता है। तंत्रिका नेटवर्क में एक महत्वपूर्ण कार्य सिग्मॉइड है, जिसमें 0 के लिए एसिम्प्टोट है $$$x \ _ से- $ infty$ और 1 के लिए $$$x \ to \ infty$ । सिग्मॉइड फ़ंक्शन का सामान्य दृश्य $$$1 / (1 + e ^ {- x})$ , और यह गणनाओं के लिए महंगा है, और पुस्तकालय से एक्सप (एक्स) फ़ंक्शन को कॉल करने के लिए और विभाजन के कारण आसानी से प्रोसेसर के सौ से अधिक चक्रों की आवश्यकता हो सकती है। पॉज़िट नंबरों के साथ, आप बस x पॉज़िट का प्रतिनिधित्व करने वाले नंबर पॉज़िट के पहले बिट को उल्टा कर सकते हैं, नंबर 2 बिट्स को दाईं ओर शिफ्ट कर सकते हैं, बिट्स को जीरो के साथ भर सकते हैं, और परिणामी पॉज़िट फ़ंक्शन, चित्र 6 में दिखाया गया है। बैंगनी, सिग्मॉइड के करीब (हरे रंग में दिखाया गया है), और यहां तक ​​कि y अक्ष को पार करते समय एक ही ढलान है।


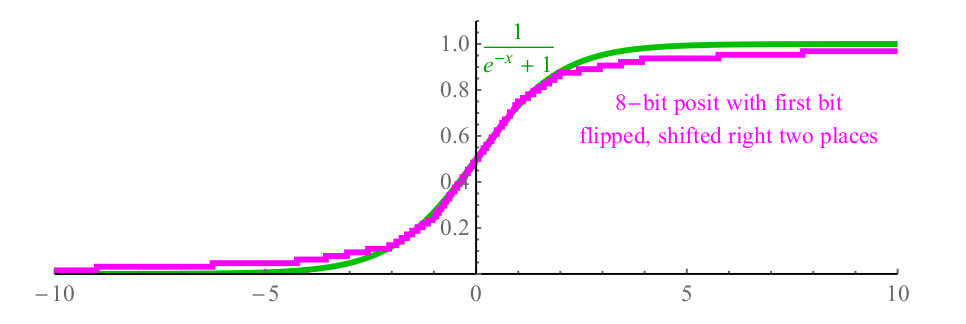अंजीर। 6. पॉज़िट प्रतिनिधित्व का उपयोग करके फास्ट सिग्मॉइड फ़ंक्शन

2.3। फ्लोट की गतिशील सीमा को प्राप्त करने और पार करने के लिए उपयोग किया जाता है

हम संख्या प्रणाली की गतिशील सीमा को न्यूनतम से सबसे बड़े धनात्मक अंतिम मान तक दशमलव क्रम से अधिकतम करने के लिए परिभाषित करते हैं। यही है, गतिशील रेंज के रूप में परिभाषित किया गया है $$$log_ {10} (अधिकतम) {log_ {10} (मिनट) = log_ {10} (अधिकतम / मिनट)$ । Es = 0 के साथ 8-बिट पोज़िट के लिए, मिनोसोल 1/64 है और अधिकतम 64 है, इसलिए डायनेमिक रेंज 3.6 दशमलव ऑर्डर है। Es = 0 के साथ परिभाषित पोजिट संख्या सुरुचिपूर्ण और सरल है, लेकिन उनके 16- और 32-बिट संस्करणों में एक ही आकार के IEEE फ्लोट की तुलना में एक छोटी गतिशील सीमा होती है। उदाहरण के लिए, 32-बिट IEEE फ़्लोट में 83 दशकों की एक डायनेमिक श्रेणी होती है, लेकिन es = 0 के साथ 32-बिट पोज़िट में केवल 18 दशकों की डायनेमिक श्रेणी होगी।

नीचे दिए गए मानों की एक तालिका है जो सकारात्मक संख्याओं को 16- और 32-बिट आकारों के लिए फ्लोट की गतिशील सीमा से अधिक करने की अनुमति देता है, और 64-, 128- और 256-बिट आकारों के लिए इसके करीब आता है।

सारणी 3. समान संख्या में बिट्स के लिए फ्लोट और पॉज़िट की डायनामिक रेंज



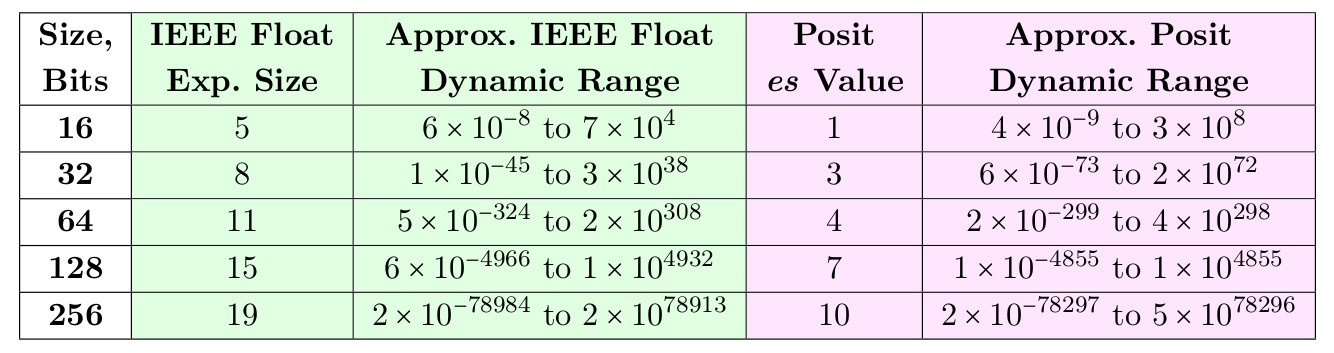
32-बिट पॉज़िट के लिए es = 3 को चुनने का एक कारण यह है कि इस मामले में वे न केवल 32-बिट फ्लोट के लिए, बल्कि 64-बिट के लिए भी एक साधारण प्रतिस्थापन के रूप में काम कर सकते हैं। इसी तरह, 16-बिट पॉज़िट के लिए 17 दशकों की गतिशील रेंज उन अनुप्रयोगों के लिए मार्ग प्रशस्त करती है जो वर्तमान में 32-बिट फ़्लोट का उपयोग करते हैं। हम दिखाते हैं कि पॉज़िट डायनेमिक रेंज और सटीकता दोनों में समान आकार में फ्लोट को बेहतर बना सकता है।

2.4। स्वरूपों की गुणात्मक तुलना फ्लोट और पॉज़िट

पोज़िट प्रारूप में कोई "NaN" नहीं है, इसके बजाय, गणना बाधित होती है, और रुकावट हैंडलर को किसी त्रुटि की रिपोर्ट करनी चाहिए या किसी तरह त्रुटि को संभालना चाहिए और गणना जारी रखनी चाहिए, लेकिन सकारात्मक संख्या एक निश्चित मान के असाइनमेंट की अनुमति नहीं देती है जो एक तार्किक त्रुटि का संकेत देती है , जो, परिभाषा से, संख्या है। यह हार्डवेयर को बहुत सरल करता है। यदि प्रोग्रामर NaN मानों का उपयोग करने की आवश्यकता देखता है, तो यह दिखाता है कि प्रोग्राम अभी तक पूरा नहीं हुआ है, और इस तरह की त्रुटियों को खोजने और समाप्त करने के लिए डीबगिंग वातावरण में मान्य संख्याओं का उपयोग किया जाना चाहिए। इसके अलावा, सकारात्मकता नहीं है $$$+ \ infty$ और $$$- \ infty$ , जैसे फ्लोट, हालांकि, मान्य नंबर खुले अंतराल का समर्थन करते हैं $$$(अधिकतम, + \ infty)$ और $$$(- \ infty, -maxpos)$ , जो किसी भी संकेत के असीमित मूल्य का प्रतिनिधित्व करना संभव बनाता है, और हस्ताक्षरित अनंत की आवश्यकता का मतलब केवल यह होगा कि सकारात्मक संख्याओं के बजाय, आपको वैध मूल्यों को लागू करने की आवश्यकता है।

सकारात्मक दृश्य में भी "नकारात्मक शून्य", नकारात्मक शून्य नहीं है, यह IEEE फ्लोट मानक में मौजूद एक और तार्किक दोष है। सकारात्मक संख्याओं के साथ, यदि a = b, तो f (a) = f (b)। IEEE 754 मानक कहता है कि संख्या व्युत्क्रम -0 है $$$- \ infty$ , और +0 के विपरीत संख्या है $$$+ \ infty$ , लेकिन यह भी कहते हैं कि -0 +0 है। इसलिए, यह समझा जाता है कि $$$- \ infty = + \ infty$ ?

फ्लोट संख्या में परिष्कृत ए = बी तुलना एल्गोरिथ्म है। यदि कोई (ए, बी) NaN है, तो तुलना का परिणाम हमेशा नकारात्मक होता है, भले ही उनका बिट प्रतिनिधित्व समान हो। यदि बिट प्रतिनिधित्व अलग है, तो अभी भी संभावना है कि ए बी के बराबर है, क्योंकि एक नकारात्मक शून्य एक सकारात्मक शून्य के बराबर है! पॉज़िक्स में, समतुल्य चेक पूर्णांक के लिए समान है: यदि बिट समान हैं, तो संख्याएं समान हैं। यदि कोई बिट अलग है, तो वे समान नहीं हैं। पोज़िट संख्याओं में एक ही संबंध (ए <b) है जो हस्ताक्षरित पूर्णांक के साथ हस्ताक्षरित पूर्णांक के रूप में है, आपको यह सुनिश्चित करना होगा कि साइन में परिवर्तन के साथ कोई अतिप्रवाह नहीं है, लेकिन आपके पास पॉज़िट की तुलना के लिए अलग मशीन निर्देश की आवश्यकता नहीं है, यदि आपके पास है हस्ताक्षरित पूर्णांक की तुलना करने के निर्देश।

पोज़िट प्रारूप में, कोई भी संख्या नहीं है, अर्थात्, कोई विशेष बिट संयोजन नहीं है जो यह दर्शाता है कि छिपा हुआ बिट 1 के बजाय 0 है । पॉज़िट एंटी-ओवरफ़्लो का उपयोग नहीं करता है, इसके बजाय, सटीकता में एक क्रमिक कमी का उपयोग किया जाता है, जो एंटी-ओवरफ़्लो की कार्यक्षमता प्रदान करता है और इसके सममित मामले, ओवरफ़्लो (सकारात्मक के विपरीत, मानक फ्लोट असममित है, और NaN मूल्यों के एक बड़े और बेकार सेट का प्रतिनिधित्व करने के लिए अपने छोटे पैटर्न का उपयोग करता है)।

फ्लोट प्रारूप में पॉज़िट पर एक लाभ है, जब हार्डवेयर विकसित होता है, तो घातांक के बिट्स की एक निश्चित व्यवस्था और आंशिक भाग उन्हें समानांतर में डीकोड करने की अनुमति देता है। प्रत्यक्ष प्रारूप में, आपको कुछ अनुक्रमों का पालन करने की आवश्यकता है, पहले मोड बिट्स को डिकोड करना, और फिर शेष बिट्स। इस प्रतिबंध के आसपास जाने का एक सरल तरीका है, फ्लोट में अपवाद हैंडलिंग की गति को बढ़ाने के लिए उपयोग की जाने वाली चाल के समान: कुछ अतिरिक्त बिट्स प्रत्येक मान से जुड़े होते हैं ताकि निर्देश को डिकोड करते समय उनमें आकार की जानकारी संग्रहीत की जा सके।

3. बिटवाइज़ कम्पेटिबिलिटी और संयुक्त ऑपरेशन

IEEE फ्लोट का एक कारण विभिन्न प्रणालियों पर समान परिणाम नहीं देता है, क्योंकि प्राथमिक कार्यों के लिए, जैसे कि $$$log(x)$ और $$$cos(x)$आईईईई को किसी भी संभावित इनपुट के लिए अंतिम बिट की सटीकता की आवश्यकता नहीं है। समर्थित अंकगणितीय परिचालनों के सभी परिणामों को सकारात्मक वातावरण को सही ढंग से पूरा करना चाहिए। (कुछ गणित पुस्तकालय प्रोग्रामर "टेबल दुविधा दुविधा" के बारे में चिंतित हैं, जो कि कुछ मूल्यों के लिए अपने सही गोलाई को निर्धारित करने के लिए बहुत महंगा हो सकता है, इसे बहुपद सन्निकटन के बजाय प्रक्षेप तालिकाओं का उपयोग करके समाप्त किया जा सकता है।) फ़ंक्शन के अंतिम बिट में गलत मान।$$$e^x$, उदाहरण के लिए, अंततः एक कंप्यूटर सिस्टम हमें बता सकता है कि 2 + 2 = 5।

आईईईई फ्लोट विभिन्न प्रणालियों पर डुप्लिकेट परिणामों का उत्पादन नहीं करता है कि अधिक मूलभूत कारण यह है कि मानक अतिप्रवाह / विरोधी अतिप्रवाह से बचने के लिए, और संचालन की सटीकता को बढ़ाने के लिए घूंघट विधियों के उपयोग की अनुमति देता है, जैसे आंतरिक रूप से घातीय और भिन्नात्मक रूप से एक अतिरिक्त कैरी बिट का भंडारण करना। भाग। पॉज़िट अंकगणित में इस तरह के छिपे हुए ट्रिक्स को प्रतिबंधित किया गया है।

IEEE 754 मानक [7] के नवीनतम (2008) संस्करण में आवश्यकताओं में एक संयुक्त गुणन-अतिरिक्त संचालन शामिल है। यह एक विवादास्पद परिवर्तन था, जिसे कई समिति सदस्यों द्वारा अनुमोदित नहीं किया गया था। संयुक्त ऑपरेशन राउंडिंग ऑपरेशन में देरी करते हैं, जब तक कि गणना में अंतिम ऑपरेशन नहीं होता है, जिसमें एक से अधिक ऑपरेशन शामिल होते हैं, सभी ऑपरेशन के बाद पूरा होता है, सटीक पूर्णांक ऑपरेशन सहित, पूरा हो जाता है। संयुक्त संचालन विस्तार योग्य सटीक अंकगणित के समान नहीं है, जो पूर्णांक की लंबाई बढ़ा सकता है जब तक कि कंप्यूटर की मेमोरी पूर्ण नहीं हो जाती।

सकारात्मक वातावरण को निम्नलिखित संयुक्त कार्यों की उपस्थिति की आवश्यकता होती है:

संयुक्त गुणा-जोड़$$$(a\times b)+c$
संयुक्त जोड़-गुणा $$$(a+b)\times c$
संयुक्त गुणन-गुणन-घटाव $$$(a\times b)-(c\times d)$
संयुक्त योग $$$\sum a_i$
संयुक्त अदिश गुणन $$$\sum a_i b_i$

ध्यान दें कि उपरोक्त सूची से सभी ऑपरेशन प्रोसेसर हार्डवेयर आवश्यकताओं के संदर्भ में संयुक्त स्केलर गुणन [6] का सबसेट हैं। स्केलर गुणा का उपयोग करके प्राप्त की जा सकने वाली सबसे छोटी गैर-शून्य संख्या है$$$minpos^2$ । कोई भी उत्पाद पूर्णांक बार होता है $$$minpos^2$ । यदि हम वैक्टर का एक अदिश उत्पाद प्राप्त करना चाहते हैं $$$\{maxpos, minpos\}$ और $$$\{maxpos, minpos\}$ एक खरोंच क्षेत्र में एक सटीक ऑपरेशन के रूप में, हमें स्टोर करने के लिए एक पूरी बड़ी आवश्यकता है $$$maxpos^2/minpos^2$ । उसको याद करो $$$maxpos=useed^{n-2}$ और $$$minpos=1/maxpos$ । इस तरह से $$$maxpos^2/minpos^2=useed^{4n-8}$ ।हस्तांतरण की बिट्स को ध्यान में रखते हुए और दो की शक्ति तक गोलाई में, हम तालिका 4 में दिए गए अनुशंसित मूल्यों को प्राप्त करते हैं।

तालिका 4. प्रत्येक सकारात्मक आकार के लिए सटीक बैटरी आकार।



कुछ मामलों में, बैटरी का आकार रजिस्टर के आकार के बराबर होता है, अन्य मामलों में, L1 या L2 कैश के बराबर एक खरोंच क्षेत्र की आवश्यकता होती है। संयुक्त संचालन सॉफ्टवेयर या हार्डवेयर किया जा सकता है, लेकिन सकारात्मक वातावरण में निष्पादन के लिए उपलब्ध होना चाहिए।