रैखिक प्रतिगमन और इसकी बहाली के लिए तरीके

स्रोत: xkcd

रैखिक प्रतिगमन डेटा विश्लेषण से संबंधित कई क्षेत्रों के लिए बुनियादी एल्गोरिदम में से एक है। इसका कारण स्पष्ट है। यह एक बहुत ही सरल और समझने योग्य एल्गोरिथ्म है, जिसने सैकड़ों नहीं, बल्कि कई दसियों के लिए इसके व्यापक उपयोग में योगदान दिया है। विचार यह है कि हम अन्य चर के सेट पर एक चर की एक रैखिक निर्भरता मान लेते हैं, और फिर इस निर्भरता को पुनर्स्थापित करने का प्रयास करते हैं।

लेकिन यह लेख व्यावहारिक समस्याओं को हल करने के लिए रैखिक प्रतिगमन लागू करने के बारे में नहीं है। यहां हम इसकी पुनर्प्राप्ति के लिए वितरित एल्गोरिदम के कार्यान्वयन की दिलचस्प विशेषताओं पर चर्चा करेंगे, जो हमने अपाचे इग्नाइट में मशीन लर्निंग मॉड्यूल लिखते समय सामना किया था। थोड़ा बुनियादी गणित, मशीन सीखने की मूल बातें, और वितरित कंप्यूटिंग आपको यह पता लगाने में मदद करेगी कि रैखिक प्रतिगमन को कैसे पुनर्स्थापित किया जाए, भले ही डेटा हजारों नोड्स में वितरित किया गया हो।

क्या बात कर रहे हो

हम रैखिक निर्भरता को बहाल करने के कार्य के साथ सामना कर रहे हैं। इनपुट के रूप में, कथित रूप से स्वतंत्र चर के कई वैक्टर दिए गए हैं, जिनमें से प्रत्येक आश्रित चर के एक निश्चित मूल्य के साथ जुड़ा हुआ है। इन आंकड़ों को दो मैट्रिक्स के रूप में दर्शाया जा सकता है:

$$

$$\ start {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ start {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

अब, चूंकि निर्भरता ग्रहण की जाती है, और इसके अलावा रैखिक है, हम अपनी धारणा को मैट्रिसेस के उत्पाद के रूप में लिखते हैं (यहां और नीचे के अंकन को सरल बनाने के लिए, यह माना जाता है कि समीकरण का मुक्त शब्द $$$x_n$, और मैट्रिक्स का आखिरी कॉलम $$$ए$इकाइयों में शामिल हैं):

$$

$$\ start {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ टाइम्स \ pm {मैट्रिक्स} x_ {शुरू 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ start {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

रेखीय समीकरणों की एक प्रणाली के समान, है ना? ऐसा लगता है, लेकिन सबसे अधिक संभावना है कि समीकरणों की ऐसी प्रणाली का कोई समाधान नहीं होगा। इसका कारण शोर है जो लगभग किसी भी वास्तविक डेटा में मौजूद है। इसके अलावा, कारण इस तरह के एक रैखिक संबंध की कमी हो सकता है, जिसे आप अतिरिक्त चर पेश करके लड़ने की कोशिश कर सकते हैं जो गैर-स्रोत पर निर्भर करते हैं। निम्नलिखित उदाहरण पर विचार करें:

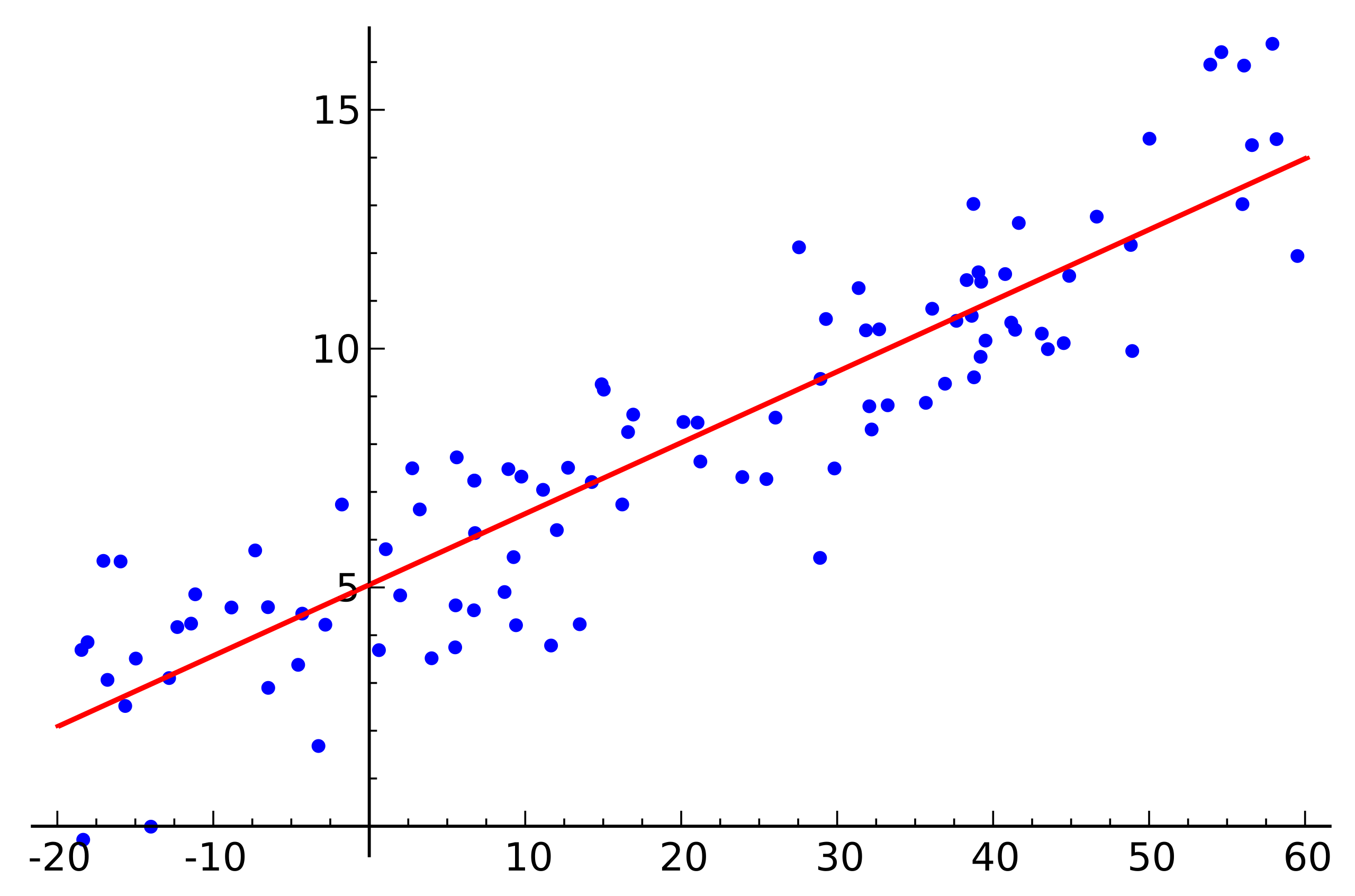स्रोत: विकिपीडिया

यह एक सरल रैखिक प्रतिगमन उदाहरण है जो अक्ष के साथ एक चर की निर्भरता को दर्शाता है $$$य$) दूसरे चर से (अक्ष के साथ) $$$x$)। समाधान के लिए इस उदाहरण के अनुरूप रैखिक समीकरणों की प्रणाली के लिए, सभी बिंदुओं को एक सीधी रेखा पर बिल्कुल झूठ होना चाहिए। लेकिन ऐसा है नहीं। लेकिन वे शोर के कारण ठीक एक सीधी रेखा पर झूठ नहीं बोलते हैं (या क्योंकि एक रैखिक निर्भरता की उपस्थिति की धारणा गलत थी)। इस प्रकार, वास्तविक डेटा से एक रैखिक निर्भरता को बहाल करने के लिए, आमतौर पर एक और धारणा पेश करना आवश्यक होता है: इनपुट डेटा में शोर होता है और इस शोर का एक सामान्य वितरण होता है । एक अन्य प्रकार के शोर वितरण के बारे में धारणा बना सकता है, लेकिन अधिकांश मामलों में यह सामान्य वितरण है जिसे बाद में चर्चा की जाएगी।

अधिकतम संभावना विधि

इसलिए, हमने यादृच्छिक रूप से वितरित शोर की उपस्थिति को मान लिया। ऐसी स्थिति में कैसे हो? इस मामले के लिए, गणित में मौजूद है और व्यापक रूप से अधिकतम संभावना विधि का उपयोग किया जाता है । संक्षेप में, इसका सार संभावना समारोह और इसके बाद के अधिकतमकरण की पसंद में निहित है।

हम सामान्य शोर के साथ डेटा से रैखिक निर्भरता की बहाली पर लौटते हैं। ध्यान दें कि माना जाता है कि रैखिक संबंध एक गणितीय अपेक्षा है $$$\ _मु$उपलब्ध सामान्य वितरण। उसी समय, संभावना है कि $$$\ _मु$एक या दूसरे मूल्य को मानता है, बशर्ते कि वेधशालाएं हों $$$x$, इस प्रकार दिखता है:

$$

$$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ _ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}} 2$$

हम अब इसके बजाय स्थानापन्न करते हैं $$$\ _मु$और $$$X$चर जो हमें चाहिए:

$$

$$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ _ [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} में; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, A_i \ _ in, b_i \ _ in B $$$

यह केवल वेक्टर खोजने के लिए बनी हुई है $$$x$जिस पर यह संभावना अधिकतम है। इस तरह के एक समारोह को अधिकतम करने के लिए, यह पहले प्रोलोगरिथम के लिए सुविधाजनक है (फ़ंक्शन का लघुगणक फ़ंक्शन के रूप में एक ही बिंदु पर इसकी अधिकतम तक पहुंच जाएगा):

$$

$$f (x) = ln (\ prod_ {i_ in [1, m]} {\ frac {1} {\ _ सिग्मा \ sqrt {2 \ pi}}; e ^ {- \ frac {(bi-a_ix) ) ^ 2} {2 \ sigma ^ 2}}} = \ sum_ {i \ _ [1, m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} में; - \ ___ {i \ _ [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

बदले में, निम्नलिखित कार्य को कम करने के लिए उबलता है:

$$

$$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$$

वैसे, इसे सबसे कम वर्ग विधि कहा जाता है। अक्सर, उपरोक्त सभी तर्क छोड़ दिए जाते हैं और इस पद्धति का उपयोग किया जाता है।

क्यूआर अपघटन

उपरोक्त फ़ंक्शन का न्यूनतम पाया जा सकता है यदि आप उस बिंदु को पाते हैं जिस पर इस फ़ंक्शन का ग्रेडिएंट शून्य के बराबर है। और ढाल इस प्रकार लिखा जाएगा:

$$

$$1 nabla f (x) = \ sum_ {i \ [1, m]} 2a_i (a_ix - b_i) = 0 $ मे$$

क्यूआर अपघटन कम से कम वर्गों में इस्तेमाल की जाने वाली न्यूनतम समस्या को हल करने के लिए एक मैट्रिक्स विधि है। इस संबंध में, हम मैट्रिक्स के रूप में समीकरण को फिर से लिखते हैं:

$$

$$A ^ T A x = A ^ Tb$$

इसलिए, हम मैट्रिक्स को बिछाते हैं $$$ए$मैट्रिसेस पर $$$क्यू$और $$$आर$और परिवर्तनों की एक श्रृंखला का प्रदर्शन करें (क्यूआर अपघटन एल्गोरिथ्म को ही यहां नहीं माना जाएगा, केवल कार्य के संबंध में इसका उपयोग):

$$

$$\ start {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ और आर ^ टी क्यू ^ टी क्यू आर एक्स = आर ^ टी क्यू ^ टी बी; \\ \ अंत {संरेखित}$$

मैट्रिक्स $$$क्यू$ऑर्थोगोनल है। इससे हम काम से छुटकारा पा सकते हैं। $$$Q Q ^ T$:

$$

$$\ start {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ और आर एक्स = क्यू ^ टी बी। \ अंत {संरेखित}$$

और अगर आप प्रतिस्थापित करते हैं $$$Q ^ T b$पर $$$z$यह निकल जाएगा $$$R x = z$। दिया है कि $$$आर$ऊपरी त्रिकोणीय मैट्रिक्स है, यह इस तरह दिखता है:

$$

$$\ start {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} और r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & ।। । & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ start {pmatrix} x_1 \\ x_2 \\ x3/3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ start {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ अंत {pmrix]$$

इसे प्रतिस्थापन विधि द्वारा हल किया जा सकता है। तत्त्व $$$x_n$की तरह है $$$z_n / r_ {nn}$पिछला आइटम $$$x_ {n-1}$की तरह है $$$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$और इसी तरह।

यहां यह ध्यान देने योग्य है कि क्यूआर अपघटन के उपयोग के माध्यम से परिणामी एल्गोरिदम की जटिलता है $$$O (2mn ^ 2)$। इसके अलावा, इस तथ्य के बावजूद कि मैट्रिक्स गुणन ऑपरेशन अच्छी तरह से समानांतर है, इस एल्गोरिथम के प्रभावी वितरित संस्करण को लिखना संभव नहीं है।

धीरे-धीरे उतरना

एक निश्चित कार्य को कम करने के बारे में बोलते हुए, यह हमेशा (स्टोकेस्टिक) ढाल वंश की विधि को याद करने के लायक है। यह एक सरल और प्रभावी न्यूनकरण विधि है जो किसी बिंदु पर किसी फ़ंक्शन के ग्रेडिएंट की गणना के आधार पर होती है और फिर इसे ढाल के विपरीत किनारे पर स्थानांतरित कर देती है। इस तरह का प्रत्येक कदम न्यूनतम के लिए समाधान लाता है। ढाल समान दिखता है:

$$

$$1 nabla f (x) = \ sum_ {i \ [1, m]} 2a_i (a_ix - b_i) $ मे$$

इस विधि को भी अच्छी तरह से वर्गीकृत किया जाता है और ढाल ऑपरेटर के रैखिक गुणों के कारण वितरित किया जाता है। ध्यान दें कि उपरोक्त सूत्र में, स्वतंत्र शब्द योग के संकेत के अंतर्गत हैं। दूसरे शब्दों में, हम सभी सूचकांकों के लिए स्वतंत्र रूप से ढाल की गणना कर सकते हैं $$$मैं$पहले से $$$k$इसके साथ समानांतर में, सूचकांकों के लिए ग्रेडिएंट की गणना करें $$$k + 1$को $$$एम$। फिर परिणामी ग्रेडिएंट्स जोड़ें। जोड़ का परिणाम उसी तरह होगा जैसे हमने पहले से सूचकांकों के लिए ग्रेडिएंट की तुरंत गणना की $$$एम$। इस प्रकार, यदि डेटा को डेटा के कई हिस्सों के बीच वितरित किया जाता है, तो प्रत्येक भाग पर ग्रेडिएंट की स्वतंत्र रूप से गणना की जा सकती है, और फिर इन गणनाओं के परिणामों को अंतिम परिणाम प्राप्त करने के लिए संक्षेपित किया जा सकता है:

$$

$$\ nabla f (x) = \ sum_ {i_ in P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ _ P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ _ P_k} में। 2a_i (a_ix - b_i)$$

कार्यान्वयन के संदर्भ में, यह MapReduce प्रतिमान में फिट बैठता है। ग्रेडिएंट डिसेंट के प्रत्येक चरण में, ग्रेडिएंट की गणना के लिए एक कार्य प्रत्येक डेटा नोड को भेजा जाता है, फिर गणना किए गए ग्रेडिएंट्स को एक साथ एकत्र किया जाता है, और परिणाम को बेहतर बनाने के लिए उनके योग का उपयोग किया जाता है।

कार्यान्वयन की सादगी और MapReduce प्रतिमान में निष्पादित करने की क्षमता के बावजूद, ग्रेडिएंट वंश में भी अपनी कमियां हैं। विशेष रूप से, अभिसरण प्राप्त करने के लिए आवश्यक कदमों की संख्या अन्य अधिक विशिष्ट तरीकों की तुलना में काफी बड़ी है।

LSQR

एलएसक्यूआर समस्या को हल करने का एक और तरीका है, जो रैखिक रिग्रेशन को फिर से संगठित करने और रैखिक समीकरणों के सिस्टम को हल करने के लिए उपयुक्त है। इसकी मुख्य विशेषता यह है कि यह मैट्रिक्स विधियों और एक पुनरावृत्ति दृष्टिकोण के लाभों को जोड़ती है। इस विधि के कार्यान्वयन को SciPy लाइब्रेरी और MATLAB दोनों में पाया जा सकता है। इस पद्धति का विवरण यहां नहीं दिया जाएगा (यह एलएसक्यूआर लेख में पाया जा सकता है : विरल रैखिक समीकरणों और विरल कम से कम वर्गों के लिए एक एल्गोरिथ्म )। इसके बजाय, वितरित वातावरण में निष्पादन के लिए एलएसक्यूआर को अनुकूलित करने के लिए एक दृष्टिकोण का प्रदर्शन किया जाएगा।

एलएसक्यूआर विधि बिडियोऑनलाइज़ेशन प्रक्रिया पर आधारित है। यह एक पुनरावृत्त प्रक्रिया है, जिसमें से प्रत्येक पुनरावृत्ति में निम्न चरण होते हैं:


लेकिन इस तथ्य पर आधारित है कि मैट्रिक्स $$$ए$क्षैतिज रूप से विभाजित, फिर प्रत्येक पुनरावृत्ति को दो चरणों के रूप में दर्शाया जा सकता है MapReduce। इस प्रकार, प्रत्येक यात्रा के दौरान डेटा स्थानांतरण को कम करना संभव है (केवल वैक्टर अज्ञात की संख्या के बराबर लंबाई के साथ):



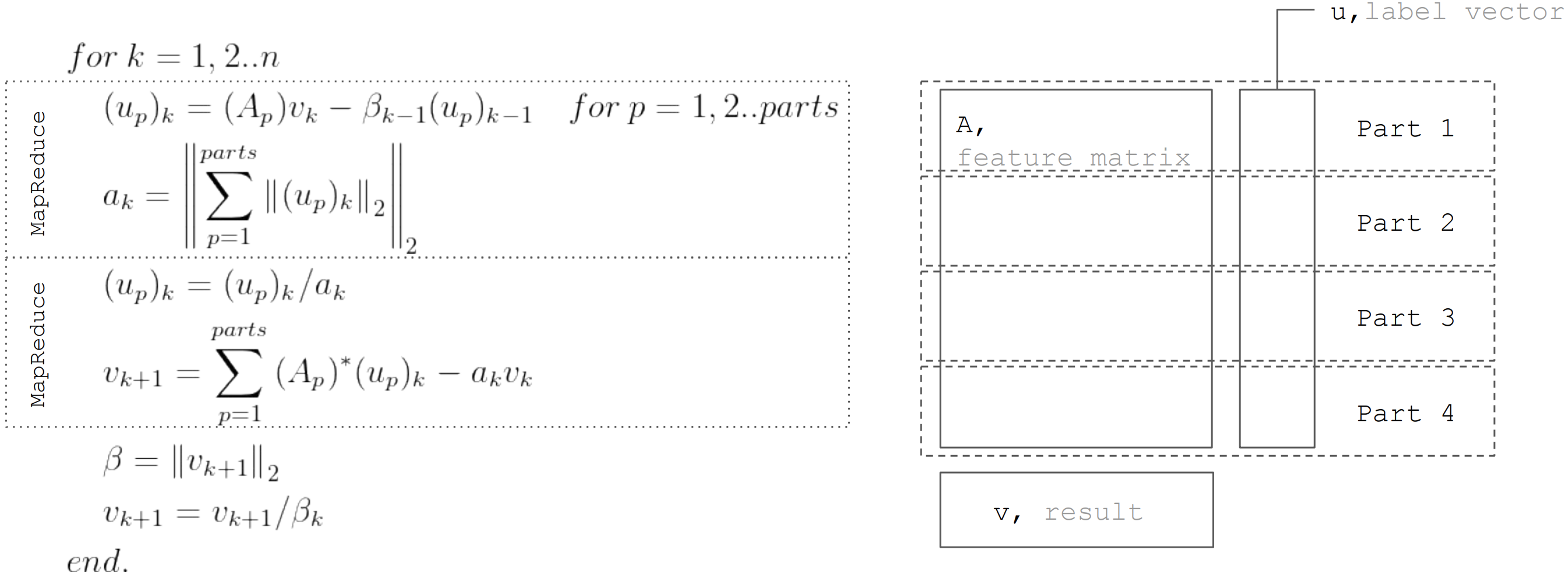अपाचे इग्नाइट एमएल में रैखिक प्रतिगमन को लागू करते समय इस दृष्टिकोण का उपयोग किया जाता है।

निष्कर्ष

कई रैखिक प्रतिगमन पुनर्प्राप्ति एल्गोरिदम हैं, लेकिन उन सभी को किसी भी स्थिति में लागू नहीं किया जा सकता है। तो क्यूआर अपघटन छोटे डेटा सरणियों पर सटीक समाधान के लिए महान है। धीरे-धीरे वंश को लागू किया जाता है और आप जल्दी से एक अनुमानित समाधान ढूंढ सकते हैं। और एलएसक्यूआर पिछले दो एल्गोरिदम के सर्वोत्तम गुणों को जोड़ती है, क्योंकि इसे वितरित किया जा सकता है, क्रमिक वंश की तुलना में तेजी से परिवर्तित होता है, और एक अनुमानित समाधान खोजने के लिए, क्यूआर अपघटन के विपरीत एल्गोरिथ्म के एक शुरुआती पड़ाव की भी अनुमति देता है।