कैसे सही ढंग से बहुपद रंग करने के लिए

बहुपद केवल अमूर्त मामलों में व्यायाम नहीं हैं। वे अप्रत्याशित स्थानों में संरचनाओं का पता लगाने के लिए महान हैं।

2015 में, एक पूर्व कवि जो गणितज्ञ बन गए, जून हो ने लगभग 50 साल पहले तैयार की गई समस्या को हल करने में मदद की। यह जटिल गणितीय वस्तुओं, " मैट्रोइड्स ", और ग्राफ़ (अंकों और खंडों के संयोजन) के साथ जुड़ा हुआ था। और यह बहुपदों से भी जुड़ा था - गणित के पाठों से हमें परिचित अभिव्यक्तियाँ, जिनमें विभिन्न डिग्री तक उठाए गए चरों के योग शामिल हैं।

स्कूल में कुछ बिंदु पर, आप संभवतः बहुपद में कोष्ठक के उद्घाटन के माध्यम से गए थे। उदाहरण के लिए, आपको याद हो सकता है कि x ² + 2xy + y ² = (x + y) ² । एक सुविधाजनक बीजीय चाल, लेकिन यह काम में कहाँ आ सकता है? यह पता चलता है कि बहुपद छिपी संरचनाओं को प्रकट करने में पूरी तरह से मदद करते हैं - और हो ने अपने प्रमाण में इस तथ्य का सक्रिय रूप से उपयोग किया है। यहाँ एक सरल पहेली है जो इसे दर्शाती है।

मान लीजिए कि हमें एक स्क्वायर टेबल पर खिलाड़ियों की दो टीमों को बैठने की जरूरत है। धोखाधड़ी को रोकने के लिए, आपको यह सुनिश्चित करने की आवश्यकता है कि खिलाड़ी अपनी टीम के अन्य खिलाड़ियों के बगल में न बैठें। बैठने की कितनी विधियाँ हैं?

चलो लाल और नीले रंग की टीम के बैठने के साथ शुरू करते हैं। मान लीजिए कि लाल खिलाड़ी चार्ट में सबसे ऊपर बैठता है:



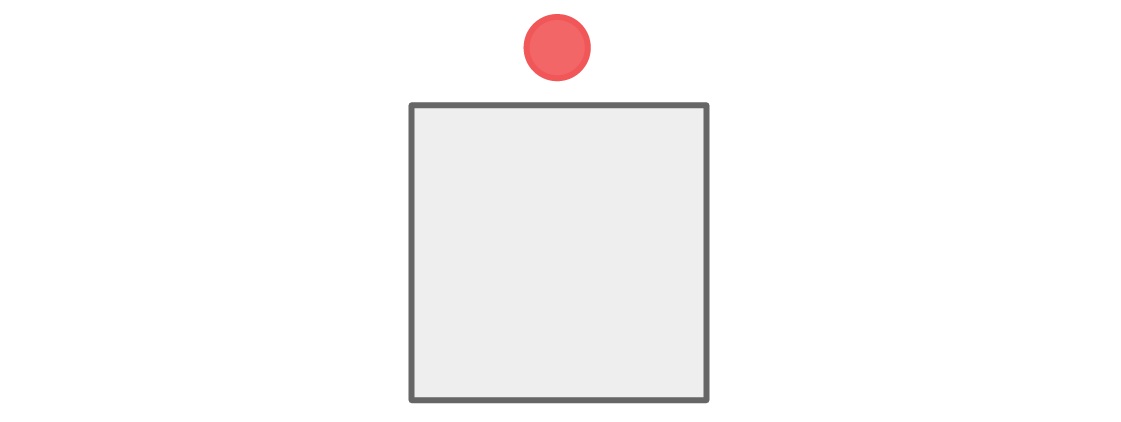
शीर्ष स्थान के पास दो स्थान हैं - दाएं और बाएं - और नियम को संतुष्ट करने के लिए, इन स्थानों पर नीले खिलाड़ियों का कब्जा होना चाहिए।



नीचे का स्थान दो नीले रंग के निकट है, इसलिए लाल खिलाड़ी को वहां बैठना चाहिए।



कोई भी खिलाड़ी अपनी टीम के सदस्य के बगल में नहीं बैठा है, और हमारी स्थिति पूरी हो गई है।

हम शीर्ष पर नीले खिलाड़ी के साथ भी शुरुआत कर सकते हैं। इसी तरह के विचार निम्नलिखित व्यवस्था की ओर ले जाते हैं:



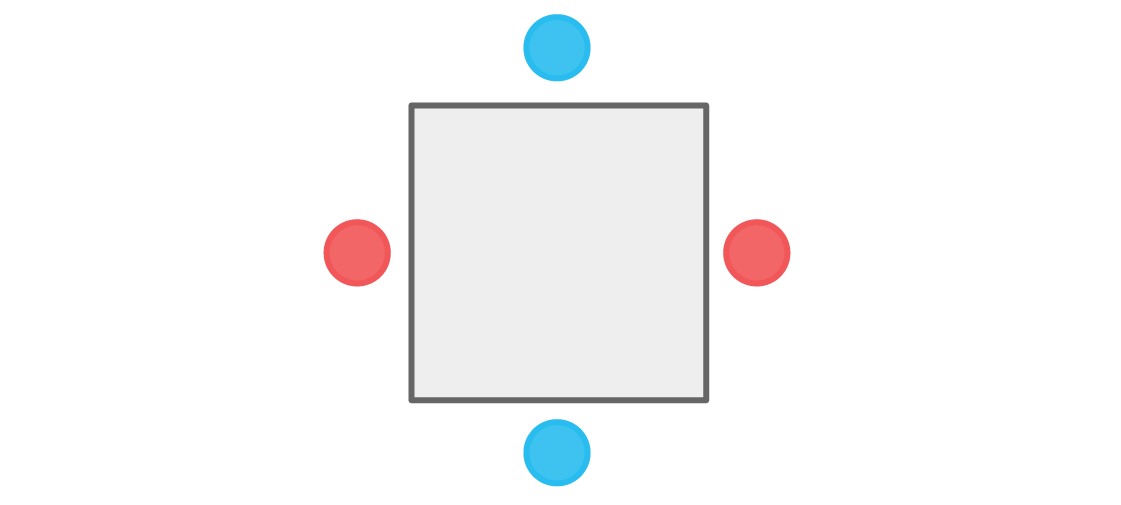
फिर से, कोई भी खिलाड़ी अपनी टीम के अन्य सदस्यों के बगल में नहीं बैठता है। हमारी स्थिति पूरी हो गई है, और बैठने की ऐसी व्यवस्था स्वीकार्य है। वास्तव में, बैठने की ऐसी दो व्यवस्थाएँ हैं। जैसे ही हम शीर्ष स्थान का रंग चुनते हैं, बाकी सभी पूरी तरह से परिभाषित होते हैं।

यह पता लगाने का एक तरीका है कि इन सभी आरेखों को चित्रित किए बिना केवल दो संभावित बैठने की व्यवस्था है। चलो ऊपर से शुरू करते हैं: हमारे पास दो विकल्प हैं, लाल और नीला। इस विकल्प के बाद, बाईं और दाईं सीटों के लिए एक विकल्प (एक अलग रंग) रहता है। और निचली सीट के लिए केवल एक ही विकल्प बचा है - वह रंग जिसके साथ हमने शुरू किया था। "गणना के मूलभूत सिद्धांत" का उपयोग करते हुए, हम जानते हैं कि अवसरों की कुल संख्या प्रत्येक विकल्पों के लिए अवसरों की संख्या को गुणा करने का परिणाम है। यह हमें 2 × 1 × 1 × 1 = 2 अंकुर देता है, जैसा कि हमने अपने आरेखों से निर्धारित किया है।

अब तीसरे कमांड को तीसरे रंग के साथ जोड़ें। कल्पना कीजिए कि हमारे पास लाल, नीले और पीले खिलाड़ी हैं। बैठने की कितनी व्यवस्था की जा सकती है, बशर्ते कि पड़ोसी स्थान अलग-अलग रंगों के हों? सभी संभावनाओं की छवि के लिए आपको आरेखों का एक पूरा वैगन खींचना होगा, इसलिए आइए इसके बजाय गणना करने का प्रयास करें।

शीर्ष स्थान के लिए, हमारे पास अब तीन रंगों का विकल्प है। इस विकल्प के बाद, हम बाईं और दाईं ओर के स्थानों के लिए दो शेष रंगों में से कोई भी चुन सकते हैं।

वर्ग के नीचे क्या होगा? यह घोषणा करने का प्रलोभन है कि अंतिम सीट के लिए केवल एक विकल्प होगा, क्योंकि यह बाईं और दाईं दोनों सीटों के बगल में है। लेकिन क्या आप इस तर्क में दोष महसूस करते हैं?



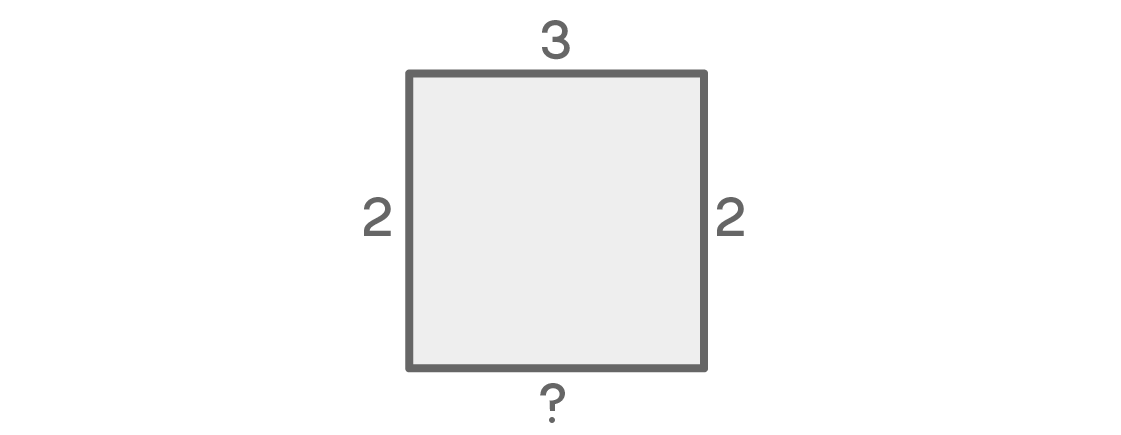
दरअसल, यदि बाएं और दाएं स्थानों में अलग-अलग रंग हैं, तो नीचे की जगह के लिए केवल एक विकल्प होगा। यदि बाईं ओर, उदाहरण के लिए, यह नीला है और दाईं ओर लाल है, तो नीचे पीला होना चाहिए। लेकिन क्या होगा अगर बाएं और दाएं रंग समान हैं? इस मामले में, नीचे की जगह के लिए दो विकल्पों का विकल्प होगा। यह अंतिम विकल्प पिछले वाले पर निर्भर करता है, जो हमारी गणना को जटिल बनाता है।

हमें दो अलग-अलग मामलों पर विचार करना होगा: जब रंग बाईं ओर और दाईं ओर मेल खाता है, और जब वे अलग होते हैं।

यदि बाईं ओर और दाईं ओर के रंग मेल खाते हैं, तो प्रत्येक स्थान के लिए संभावनाओं की संख्या इस तरह दिखाई देती है:



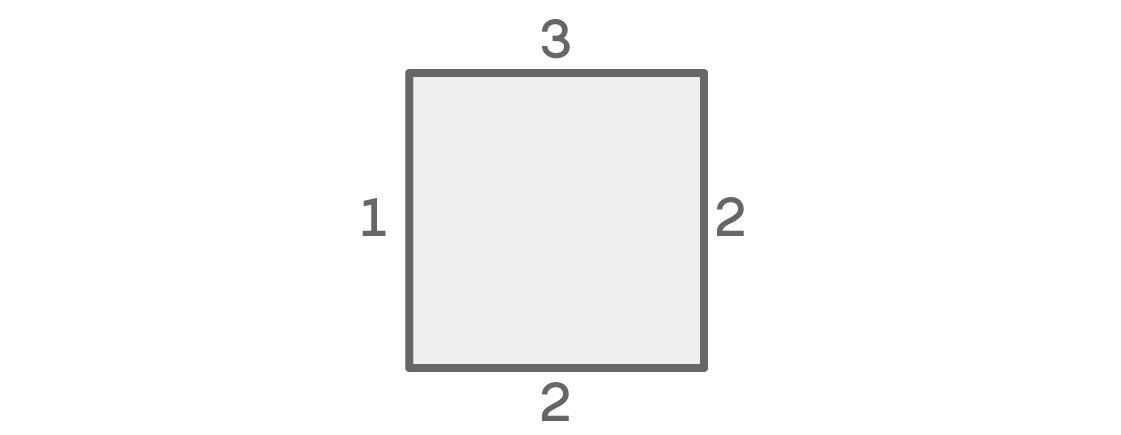
ऊपरी सीट के लिए, हमारे पास तीन विकल्प हैं। दाहिने के लिए दो बाएं हैं। चूंकि हम मानते हैं कि बाएं और दाएं स्थानों का रंग समान है, इसलिए हमारे पास बाईं ओर केवल एक ही विकल्प है: दाएं जैसा ही रंग। अंत में, चूंकि रंग बाईं और दाईं ओर समान है, इसलिए हम निचली सीट के लिए शेष दो रंगों में से किसी एक को चुन सकते हैं। नतीजतन, हमें 3 × 2 × 1 × 2 = 12 संभव बैठने की व्यवस्था मिलती है।

अब उन संभावनाओं को देखते हैं जब दाएं और बाएं रंग अलग होते हैं:



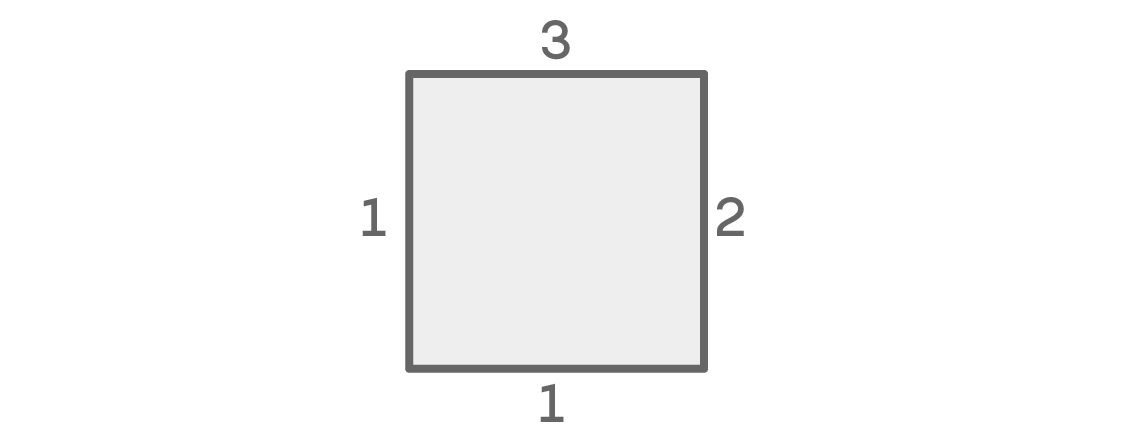
हमारे पास फिर से शीर्ष के लिए तीन और सही जगह के लिए दो विकल्प हैं। बाएं स्थान पर फिर से एक विकल्प है, लेकिन एक अलग कारण के लिए: यह हमारी स्थिति के अनुसार, शीर्ष, पड़ोसी और समान के समान नहीं हो सकता। और, चूंकि दाएं और बाएं रंग अलग-अलग हैं, केवल एक विकल्प नीचे की जगह (शीर्ष के समान) के लिए रहता है। यह मामला 3 × 2 × 1 × 1 = 6 संभावित व्यवस्था देता है।

चूंकि ये दो विकल्प सभी संभावनाओं को कवर करते हैं, हम उन्हें जोड़ते हैं और 12 + 6 = 18 संभव बैठने की व्यवस्था करते हैं।

तीसरे रंग को जोड़ने से हमारा काम जटिल हो जाता है, लेकिन हमारी मेहनत को पुरस्कृत किया जाएगा। अब हम इस रणनीति का उपयोग विभिन्न रंगों के 4, 5 या किसी भी संख्या q के लिए कर सकते हैं।

रंगों की संख्या के बावजूद, हमारे पास हमेशा दो मामले होंगे: बाएं और दाएं समान या अलग-अलग रंग होंगे। मान लीजिए हमारे पास q रंगों का विकल्प है। यहां प्रत्येक पक्ष के लिए विकल्पों की संख्या दर्शाने वाला एक चार्ट है, जिसमें दाएं और बाएं रंग समान हैं:



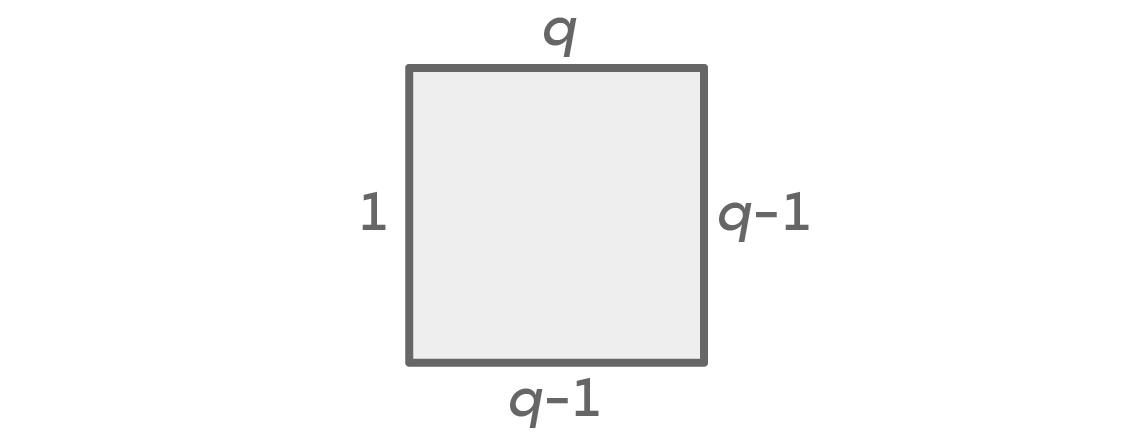
पहले हमारे पास ऊपरी सीट के लिए q रंग हैं, और दाईं ओर q-1 है। चूंकि हमने यह मान लिया था कि बाईं और दाईं ओर के रंग समान हैं, हमारे पास बाएं रंग के लिए केवल एक ही विकल्प है। यह निचले स्थान के लिए q-1 विकल्प छोड़ता है, क्योंकि यह बाएं और दाएं स्पॉट के लिए चुने गए किसी भी रंग के अलावा हो सकता है। गणना का मूल सिद्धांत हमें q × (q - 1) × 1 × (q - 1) = q (q - 1) ^{2 अतिरिक्त} लेआउट देता है।

यदि बाएँ और दाएँ स्थान अलग-अलग रंग के हैं, तो हम इस तरह से संभावनाओं की गणना कर सकते हैं:



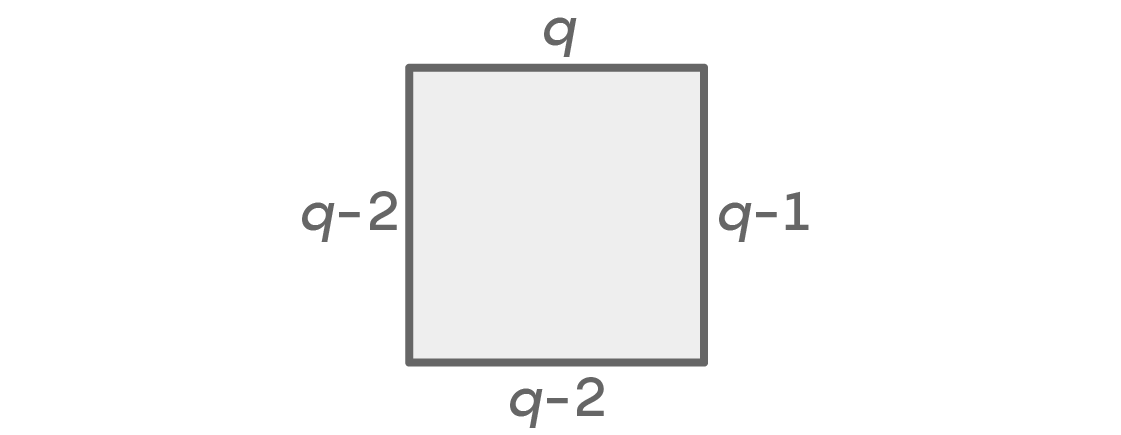
एक बार फिर, हमारे पास शीर्ष के लिए q विकल्प हैं और सही स्थानों के लिए q-1 है। बाईं ओर वही रंग नहीं हो सकता जो शीर्ष और दाएं स्थानों के लिए चुना गया है, इसलिए q-2 विकल्प हैं। नीचे कोई रंग हो सकता है, केवल उन दो को छोड़कर जो हमने बाएँ और दाएँ का उपयोग किया था, जो फिर से q-2 विकल्प देता है। हम सम q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² संभावित बैठने की व्यवस्था में प्राप्त करते हैं। चूंकि ये दो स्थितियां सभी विकल्पों को कवर करती हैं, हम, पहले की तरह, उन्हें जोड़ते हैं और संभव व्यवस्थाओं की कुल संख्या प्राप्त करते हैं: q (q - 1) ² + q (q - 1) (q - 2) ² ।

इस तरह की अभिव्यक्ति इस सवाल का एक अजीब जवाब की तरह लग सकता है: "वर्ग तालिका में विभिन्न टीमों के लिए बैठने की कितनी अलग व्यवस्था है, जैसे कि एक ही टीम के दो सदस्य कंधे से कंधा मिलाकर नहीं बैठेंगे?" हालाँकि, इस बहुपद में हमारी समस्या के बारे में बहुत सारी जानकारी है। वह न केवल हमें एक मात्रात्मक उत्तर देता है, बल्कि हमारे कार्य की संरचना को भी प्रकट करता है।

इस तरह के एक बहुपद को " गुणसूत्र बहुपद " कहा जाता है क्योंकि यह सवाल का जवाब देता है: नेटवर्क (या ग्राफ) के रंग को रंगने के लिए कितने तरीके मौजूद हैं जैसे कि किसी भी पड़ोसी के जोड़े में अलग-अलग रंग होते हैं?

प्रारंभ में, हमारी समस्या तालिका के चारों ओर बैठने से संबंधित थी, लेकिन हम इसे ग्राफ के शीर्षों को रंगने के बारे में आसानी से एक प्रश्न में बदल सकते हैं। टेबल पर लोगों के बजाय:



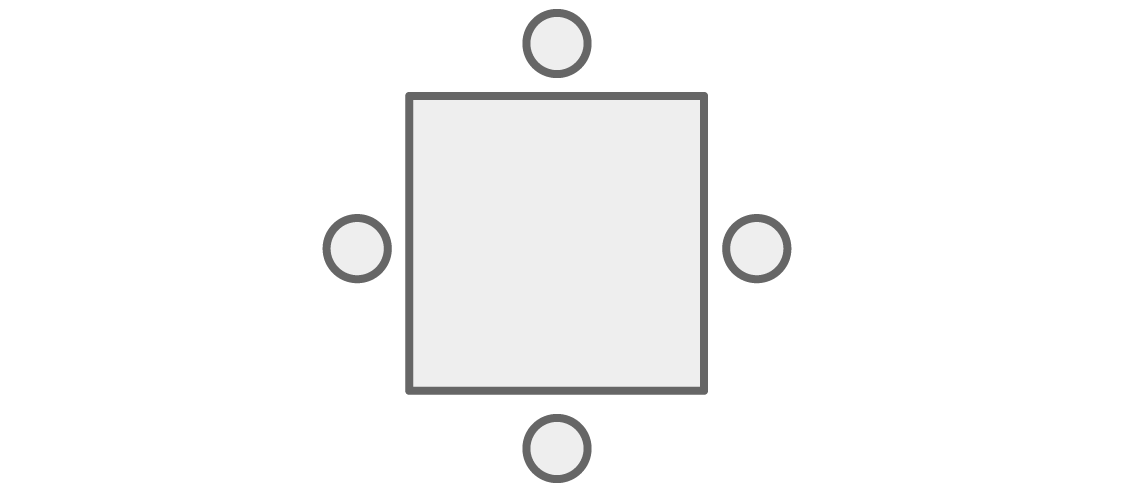
जब हम बगल में बैठे होते हैं तो हम उन्हें किनारों से जुड़ी चोटियों के रूप में कल्पना करेंगे:



अब, ग्राफ के कोने के किसी भी रंग को वर्ग के चारों ओर लोगों के बैठने के रूप में दर्शाया जा सकता है, जहां "मेज के बगल में बैठें" का मतलब है कि ग्राफ पर "एक आम बढ़त है"।

अब, एक ग्राफ के रूप में हमारी समस्या का सुधार करने के बाद, हम रंगीन बहुपद में लौटते हैं। हम इसे P (q) कहते हैं।

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

इस बहुपद की एक उल्लेखनीय संपत्ति यह है कि यह किसी भी संभावित रंगों के लिए रंग के प्रश्न का उत्तर देता है। उदाहरण के लिए, तीन रंगों के साथ एक प्रश्न का उत्तर देने के लिए, हम q = 3 डालते हैं, और हम प्राप्त करते हैं:

पी (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

यह उत्तर हमें तीन टीमों के मामले में मिला है। और अगर हम q = 2 डालते हैं:

पी (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + ² = 0 = 2

परिचित लग रहा है? यह हमारी पहली पहेली का जवाब है, जिसमें दो टीमें हैं। हम चार, पांच, या यहां तक ​​कि 10 अलग-अलग टीमों के लिए उत्तर पा सकते हैं, केवल q: P (4) = 84, P (5) = 260, और P (10) = 6 570 के लिए वांछित मान को प्रतिस्थापित कर रहे हैं। रंगीन बहुपद ने समस्या की मूल संरचना को पकड़ा। हमारी गिनती की रणनीति को संक्षेप में बताकर।

हम अपने बहुपद P (q) = q (q - 1) ² + q (q - 1) (q - 2) ² पर बीजगणितीय संक्रियाएं करके संरचना के अधिक विवरणों को प्रकट कर सकते हैं:

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² +4q + 4)
= q (q - 1) (q ² +3q + 3)

हमने योग के प्रत्येक भाग से फैक्टर q (q - 1) निकाला और एक समान रूप में बहुपद को कम करते हुए समान शब्द जोड़े। और इस रूप में, बहुपद हमें इसकी "जड़ों" की मदद से संरचना के बारे में बता सकता है।

एक बहुपद की जड़ें इनपुट मान हैं, जिस पर यह आउटपुट पर शून्य के बराबर हो जाता है। कारक के रूप में जड़ों को ढूंढना आसान है: चूंकि बहुपद को कई गुणा भागों के रूप में व्यक्त किया जाता है, किसी भी मूल्य पर जिसमें से एक कारक शून्य के बराबर होता है पूरे उत्पाद को रीसेट करता है।

उदाहरण के लिए, हमारे बहुपद पी (q) = q (q - 1) (q ² - 3q + 3) का एक कारक (q - 1) है। यदि हम q = 1 लेते हैं, तो यह कारक गुणन के पूरे परिणाम की तरह शून्य के बराबर हो जाता है। अर्थात, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. इसी प्रकार, P (0) = 0 × (-1) × 3 = 0 इसलिए, q = 1 और q = 0 हमारी बहुपद की जड़ें हैं। (आपको कारक में रुचि हो सकती है (q ² - 3q + 3)। चूँकि यह किसी वास्तविक q के लिए शून्य के बराबर नहीं है, यह हमारे गुणात्मक बहुपद को नई जड़ें नहीं देता है)।

ये जड़ें हमारे ग्राफ के ढांचे के भीतर समझ में आती हैं। यदि हमारे पास एक ही रंग का विकल्प है, तो प्रत्येक शीर्ष समान रंग होना चाहिए। ग्राफ़ को रंग देना संभव नहीं है, ताकि सभी आसन्न कोने अलग-अलग रंग के हों। इसका ठीक यही अर्थ है कि q = 1 हमारे रंगीन बहुपद की जड़ है। यदि पी (1) = 0, तो ग्राफ को रंगने के लिए बिल्कुल शून्य तरीके हैं ताकि पड़ोसी लंबवत समान रंग न हों। शून्य संख्या वाले रंगों के संस्करण के लिए भी यही सच है, पी (0) = 0. हमारे रंगीन बहुपद की जड़ें हमारे ग्राफ की संरचना के बारे में बताती हैं।

बीजगणित के माध्यम से संरचना को देखने की क्षमता और भी स्पष्ट हो जाती है अगर हम अन्य रेखांकन पर विचार करें। आइए एक त्रिकोणीय ग्राफ देखें:



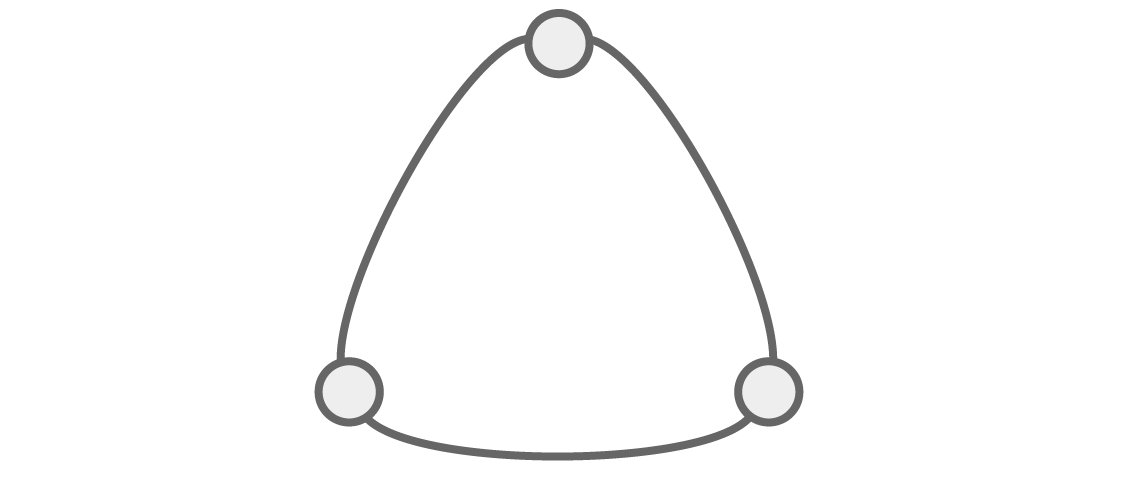
इस ग्राफ q को रंगों के साथ रंगने के कितने तरीके हैं ताकि पड़ोसी लंबवत समान रंग न हों?

हमेशा की तरह, पहले दो पड़ोसी कोने के लिए q और q-1 विकल्प हैं। और चूंकि अंतिम शीर्ष पहले दो से सटे हुए हैं, इसलिए उन दोनों से रंग में अंतर होना चाहिए, जो हमें क्यू -2 विकल्पों के साथ छोड़ देता है। यह हमें इस त्रिकोणीय ग्राफ के लिए गुणात्मक बहुपद देता है: P (q) = q (q - 1) (q - 2)।

कारक के रूप में, यह रंगीन बहुपद हमें कुछ दिलचस्प बताता है: इसकी जड़ q = 2 है। और यदि पी (2) = 0, तो इस ग्राफ को दो रंगों के साथ रंगना असंभव होना चाहिए ताकि इसमें एक ही रंग के दो आसन्न कोने न हों। क्या ऐसा है?

कल्पना कीजिए कि हम इस त्रिकोण में एक सर्कल में चल रहे हैं, रास्ते में चोटियों को रंग रहे हैं। यदि हमारे पास केवल दो रंग हैं, तो हमें उन्हें प्रत्येक शीर्ष के बाद वैकल्पिक करने की आवश्यकता है: यदि पहला लाल है, तो दूसरा नीला होगा, जिसका अर्थ है कि तीसरा फिर से लाल होना चाहिए। लेकिन पहले और तीसरे शिखर आसन्न हैं, और वे दोनों लाल नहीं हो सकते। दो रंग पर्याप्त नहीं हैं, जैसा कि बहुपद की भविष्यवाणी की गई है।

इसी तरह के एक वैकल्पिक तर्क का उपयोग करते हुए, हम एक महत्वपूर्ण सामान्यीकरण पर आ सकते हैं: विषम संख्या वाले किसी भी बंद लूप के रंगीन बहुपद का मूल 2 के बराबर होना चाहिए। यदि आप दो रंगों को वैकल्पिक करते हैं और विषम लंबाई के पाश के साथ चलते हैं, तो पहला और अंतिम रंगीन शीर्ष समान रंग होगा। । लेकिन जैसे ही यह एक लूप है, वे आसन्न होंगे। रंग भरना संभव नहीं है।

उदाहरण के लिए, हम विभिन्न तकनीकों का उपयोग यह निर्धारित करने के लिए कर सकते हैं कि पांच कोने वाले लूप के लिए रंगीन बहुपद इस तरह दिखता है: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q। इसे बाहर फैक्टर करने पर हमें P (q) = q (q - 1) (q - 2) (q2 - 2q + 2) मिलता है। जैसा कि अपेक्षित था, यह पता चलता है कि q = 2 मूल है, और P (2) = 0. दिलचस्प बात यह है कि जैसे ही हम रेखांकन और उनके बहुपदों के बीच यह संबंध पाते हैं, दोनों दिशाओं में विचार काम करने लगते हैं। बहुपद हमें रेखांकन की संरचना के बारे में जानकारी दे सकते हैं, और रेखांकन हमें बहुपद की संरचना के बारे में बता सकते हैं।

यह संरचना की खोज थी जिसने जून हो को रीड के 40 साल की परिकल्पना को गुणात्मक बहुपद के बारे में साबित करने के लिए प्रेरित किया। परिकल्पना में कहा गया है कि यदि हम गुणात्मक बहुपद के गुणांक को क्रम से दर्शाते हैं, तो उनके संकेतों को अनदेखा करते हुए, निम्नलिखित शर्त पूरी की जाएगी: किसी भी गुणांक का वर्ग कम से कम दो पड़ोसी लोगों का उत्पाद होना चाहिए। उदाहरण के लिए, हमारे पांच-वर्टिकल लूप, पी (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q के लिए वर्णक्रमीय बहुपद में, हम देखते हैं कि 5 ² × 1 × 10, 10 ² ≥ 5 × 10 और 10 ² it 10 × 4. इस से, उदाहरण के लिए, यह इस प्रकार है कि प्रत्येक बहुपद में वर्णक्रमीय नहीं हो सकता है: रेखांकन के साथ जुड़े रंगीन बहुपद एक गहरी संरचना है। इसके अलावा, इन बहुपद और अन्य डोमेन के बीच संबंध ने रीड की परिकल्पना के सबूत के कई साल बाद हो और उनके सह-लेखकों को रोथ परिकल्पना से संबंधित एक बहुत व्यापक प्रश्न का उत्तर देने की अनुमति दी।

शायद बहुपत्नी को उनके सबसे खराब रूप के लिए जाना जाता है - बीजगणितीय अभिव्यक्तियों के औपचारिक हेरफेर में सार अभ्यास के रूप में। लेकिन बहुपद और उनके गुण - जड़ें, गुणांक, विभिन्न रूप - अप्रत्याशित स्थानों में संरचनाओं को प्रकट करने में मदद करते हैं, जो हमारे चारों ओर हर चीज में बीजगणित के साथ संबंध बनाते हैं।

अभ्यास

1. एक पूरा ग्राफ एक ग्राफ है, जिसमें से प्रत्येक जोड़ी के कोने एक किनारे से जुड़े होते हैं। पाँच सिरों के एक पूर्ण ग्राफ के रंगीन बहुपद का पता लगाएं।


2. अगले ग्राफ के लिए रंगीन बहुपद का पता लगाएं (सरल रेखांकन के वर्णक्रमीय बहुपद के बारे में जानकारी का उपयोग करें)।




3. एक ग्राफ को दो तरफा कहा जाता है यदि इसके कोने को दो समूहों, ए और बी में विभाजित किया जा सकता है, ताकि ए से कोने केवल कोने बी से सटे हों, और कोने बी केवल कोने से कोने तक सटे हैं। मान लीजिए कि जी में एक क्रोमेटिक बहुपद पी है। (क्यू)। क्या संपत्ति P (q) आपको यह निष्कर्ष निकालने की अनुमति देती है कि ग्राफ G दो तरफा है?