इंटरनेट पर धीरे-धीरे वंश एल्गोरिथ्म के वर्णन के साथ कई लेख हैं। एक और होगा।
8 जुलाई, 1958 को, द न्यूयॉर्क टाइम्स ने लिखा : “एक मनोवैज्ञानिक एक कंप्यूटर के भ्रूण को दिखाता है जिसे पढ़ने और समझदार बनने के लिए डिज़ाइन किया गया है। नौसेना द्वारा विकसित ... 704 कंप्यूटर, जिसकी लागत $ 2 मिलियन थी, पचास प्रयासों के बाद बाएं और दाएं के बीच अंतर करना सीखा ... नेवी के अनुसार, वे इस सिद्धांत का उपयोग पर्सेप्ट्रॉन क्लास की पहली सोच मशीन के निर्माण के लिए करते हैं, जिसे पढ़ और लिख सकते हैं; विकास को $ 100,000 की कुल लागत के साथ एक वर्ष में पूरा करने की योजना बनाई गई है ... वैज्ञानिकों का अनुमान है कि बाद में पेरीसेप्ट्रोन लोगों को पहचानने और उन्हें नाम से बुलाने में सक्षम होंगे, तुरंत मौखिक और लिखित भाषण का एक भाषा से दूसरी भाषा में अनुवाद करेंगे। श्री रोसेनब्लैट ने कहा कि सिद्धांत रूप में "दिमाग" का निर्माण करना संभव है जो असेंबली लाइन पर खुद को पुन: उत्पन्न कर सकता है और जो अपने स्वयं के अस्तित्व के बारे में पता होगा "(एस। निकोलेंको की पुस्तक से अनुवादित और अनुवादित," डीप लर्निंग, तंत्रिका नेटवर्क की दुनिया में विसर्जन ")।
आह, इन पत्रकारों को पता है कि कैसे साज़िश करना है। यह समझने के लिए बहुत दिलचस्प है कि वास्तव में Perceptron वर्ग की एक सोच मशीन क्या है।
बाइनरी (बाइनरी) वस्तुओं का वर्गीकरण, पेरेसेप्ट्रोन वर्ग के कृत्रिम न्यूरॉन
यहाँ हमारा कृत्रिम न्यूरॉन है, यह वस्तुओं को दो वर्गों में विभाजित करता है (वस्तुओं का द्विआधारी वर्गीकरण करता है):

तो हमारे पास है:
- इनपुट: नमूना वस्तु - एम-आयामी अंतरिक्ष वेक्टर एक्स = ( एक्स 1 , । । । , एक्स मीटर )
- भार गुणांक डब्ल्यू = ( डब्ल्यू 1 , । । । , डब्ल्यू मीटर ) नमूना वस्तु की प्रत्येक विशेषता के लिए एक (एक आयामी वेक्टर भी)
- अंदर: योजक S U M = w 1 x 1 + । । । + w m x m = s u m m j = 1 w j x j - न्यूरॉन इनपुट का भारित योग
- अगला: सक्रियण $(X,w)=Φ(SUM)
- अभी और आगे: क्वांटाइज़र (दहलीज) - ([थीटा]
- सक्रियण + थ्रेशोल्ड - न्यूरॉन इनपुट (वस्तु विशेषताओं) के भारित योग के आधार पर किसी वस्तु के वर्ग लेबल की भविष्यवाणी। यह हिस्सा न्यूरॉन की विशिष्ट वास्तुकला को परिभाषित करता है।
- आउटपुट: ऑब्जेक्ट क्लास लेबल (दो में से एक) \ hat {y} = \ {1, -1 \}\ hat {y} = \ {1, -1 \}
वर्गीकरण - क्योंकि एक न्यूरॉन एक कक्षा को एक वस्तु, बाइनरी ( बाइनरी ) को असाइन करता है - क्योंकि केवल दो संभव वर्ग हैं।
y [एक ढक्कन के साथ खेल] - हम वस्तु के लिए अनुमानित (गणना की गई) वर्ग मूल्य को निरूपित करेंगे x
य [एक ढक्कन के बिना नियमित खेल] - एक वस्तु के लिए सही (ज्ञात) वर्ग मान x प्रशिक्षण सेट से।
अर्थ x (यहाँ और नीचे x और w - ये यूनिट वैल्यू नहीं हैं, लेकिन वैक्टर) ऑब्जेक्ट से ऑब्जेक्ट, वेट गुणांक तक भिन्न होते हैं w (एक बार चयनित) अपरिवर्तित रहें। प्रत्येक वस्तु के लिए निर्धारित प्रशिक्षण के लिए x क्लास लेबल ज्ञात य । प्रशिक्षण स्तर पर, आपको वजन चुनने की आवश्यकता है w ताकि मॉडल सही मूल्य पैदा करे y (के साथ मेल खाना य ) प्रशिक्षण सेट में वस्तुओं की अधिकतम संख्या के लिए। इस तरह से प्रशिक्षित एक न्यूरॉन की उपयोगिता की धारणा इस उम्मीद पर आधारित है कि यह चयनित गुणांकों के साथ सही मूल्य का उत्पादन करेगा। y नई वस्तुओं के लिए x सही वर्ग मूल्य य जिसके लिए यह पहले से ज्ञात नहीं है।
एक न्यूरॉन के इनपुट के भारित योग का सहज अर्थ यह है कि ऑब्जेक्ट की सभी विशेषताएं (प्रत्येक संकेत न्यूरॉन के इनपुट में से एक है) ऑब्जेक्ट के वर्गीकरण के परिणाम को प्रभावित करते हैं, लेकिन सभी संकेत समान रूप से प्रभावित नहीं होते हैं। किस हद तक - वजन का निर्धारण; एक निश्चित भारांक गुणांक को शून्य करने से कुल राशि के अनुरूप विशेषता का योगदान कम हो जाता है, अर्थात्। यह ऑब्जेक्ट से फीचर को हटाने के लिए टैंनामाउंट है।
अनुकूली रैखिक न्यूरॉन ADALINE
ADALINE न्यूरॉन (अनुकूली रैखिक न्यूरॉन) इस सक्रियण समारोह के साथ एक साधारण कृत्रिम न्यूरॉन है:
$(X,w)=Φ(SUM)=SUM
Phi(x(i),w)= Phi( summj=1wjx(i)j)= summj=1wjx(i)j
इसके बाद सुपरस्क्रिप्ट मैं कोष्ठक में निरूपित करेगा मैं प्रशिक्षण सेट का तत्व x(i) या सही वर्ग मूल्य y(i) या अनुमानित वर्ग मूल्य haty(i) उसके लिए।
हम कह सकते हैं कि इस तरह के न्यूरॉन में केवल एक सक्रियण फ़ंक्शन नहीं होता है और इनपुट की भारित राशि का मूल्य क्वांटाइज़र (थ्रेशोल्ड) के इनपुट को खिलाया जाता है। लेकिन एकरूपता के लिए यह विचार करना अधिक सुविधाजनक होगा कि भारित राशि का मूल्य सक्रियण के रूप में लिया जाता है।
थ्रेसहोल्ड (क्वांटाइज़र) - एक वर्ग लेबल की भविष्यवाणी करता है:
\ hat {y} ^ {(i)} = \ left \ {\ {शुरू {मैट्रिक्स} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x) ^ {(i)}, w) <\ थीटा एंड एंड {मैट्रिक्स} \ राइट।
यदि सक्रियण मान कुछ थ्रेशोल्ड मान the [थीटा] से अधिक है, तो क्वांटाइज़र ऑब्जेक्ट को "1" लेबल प्रदान करता है, यदि सक्रियण मान थ्रेशोल्ड से कम है, तो ऑब्जेक्ट लेबल -1 प्राप्त करता है।
यहां हम समस्या को पहले सन्निकटन में बना सकते हैं : हमें न्यूरॉन के मापदंडों का चयन करने की आवश्यकता है
- वजन कारक wj,j=1,..,m
- और दहलीज θ [थीटा]
ताकि वर्ग मूल्य य , जो प्रशिक्षण नमूने की वस्तुओं को न्यूरॉन असाइन करता है, कक्षाओं के वास्तविक मूल्यों के साथ मेल खाता है य समान तत्वों के लिए (या, कम से कम, बहुमत के लिए सही अर्थ दिया)।
हम थ्रेशोल्ड फ़ंक्शन को थोड़ा रूपांतरित करते हैं, क्लास के लिए केस लेते हैं y=1 और दहलीज को विषमता के बाईं ओर स्थानांतरित करें:
startइकट्ठा Phi(x(i),w) ge theta hfill summj=1wjx(i)j ge theta hfill− theta+ summj=1wjx(i)j ge0 hfillएकत्र
लक्षित w0=− थीटा और x0=1
startइकट्ठाw0x(i)0+ summj=1wjx(i)j ge0,w0=− theta,x0=1 hfill summj=0wjx(i)j ge0,x0=1 hfill endएकत्रित
जैसा कि हम देखते हैं, हम एक अलग पैरामीटर of से छुटकारा पाने में कामयाब रहे, इसे एक नए वजन गुणांक की आड़ में पेश किया w0 योग के संकेत के तहत, वस्तु के विवरण में जोड़ते समय एक नई डमी इकाई का संकेत x0=1 ।
हम नई संकेतन को ध्यान में रखते हुए समस्या के सूत्रीकरण को ठीक करेंगे।
कार्य ' : न्यूरॉन के मापदंडों का चयन करें - भार कारक wj,j=0,..,m ।
x0=1 (साइन-स्थिरांक) - काल्पनिक न्यूरॉन ( विस्थापन न्यूरॉन )
इस जगह से शुरू होकर, हम संकेत संख्या और वजन 0 c, 1 नहीं। वेक्टर के बारे में w हम कहेंगे कि यह (m + 1) के बारे में है, और आयामी नहीं है। वेक्टर x संदर्भ के आधार पर, हम विचार कर सकते हैं (m + 1) -dimensional (सूत्रों में अधिकांश भाग के लिए), लेकिन याद रखें कि वास्तव में यह m- आयामी है।
क्यों एक न्यूरॉन ( हमारे मामले में, हालांकि यह एक न्यूरॉन नहीं है, लेकिन एक वस्तु या सिर्फ एक इनपुट का संकेत है, लेकिन एक बहुपरत नेटवर्क के मामले में यह एक न्यूरॉन में बदल जाता है और आमतौर पर इसे इस तरह कहा जाता है ) काल्पनिक है - यह अभी स्पष्ट है। क्यों वह विस्थापन भी बाद में स्पष्ट हो जाएगा।
राशि के साथ सक्रियण अब इस तरह दिखेगा:
Phi(x(i),w)= Phi( summj=0wjx(i)j)= summj=0wjx(i)j,x(i)0=1 foralli
दहलीज अब हमेशा 0 (शून्य) है (वास्तविक मान पैरामीटर पर ले जाया गया w0 ):
\ hat {y} ^ {(i)} = \ left \ {\ {शुरू {मैट्रिक्स} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^) {(i)}, w) <0 \ end {मैट्रिक्स} \ सही।
एक बार फिर हम इस समस्या को दूसरे शब्दों में कहते हैं (समस्या का ज्यामितीय अर्थ)
यदि हम सक्रियण फ़ंक्शन के सूत्र को ध्यान से देखते हैं, तो हम देखेंगे कि यह (m + 1) -डिमेन्शनल स्पेस में पैरामीट्रिक हाइपरप्लेन है, जबकि पहले m डायमेंशंस में सैंपल एलिमेंट्स के पॉइंट्स के साथ कोएक्सिस्ट करता है, और (m + 1) - ई-आयाम फ़ंक्शन के मूल्यों का स्थान है, जो तत्वों से अलग है।
अब, यदि हम सक्रियण मान को शून्य (थ्रेशोल्ड मान) के बराबर करते हैं, तो यह भी एक हाइपरप्लेन होगा, केवल पहले से ही एम-डायनामिक स्पेस में, यानी। पूरी तरह से तत्व मान अंतरिक्ष में x । यह हाइपरप्लेन तत्वों को अलग कर देगा। x दो अलग-अलग समूहों में।
आमतौर पर इस जगह में वे कहते हैं कि हमारा काम पैरामीटर मानों का चयन करना है w , यानी। तत्वों के अंतरिक्ष में एक एम-आयामी हाइपरप्लेन का निर्माण करना ताकि प्रशिक्षण के तत्व "1" वर्ग के वास्तविक मूल्य के साथ निर्धारित हों, और विमान के एक तरफ के तत्व और दूसरे पर सच्चे वर्ग "-1" वाले तत्व हों।
उन लोगों के लिए जो यहां लिखे गए हैं, जो बिल्कुल नहीं समझते हैं, पर पढ़ें - अब हम सभी देखेंगे, यह पहली बार है। दूसरे, हम यह भी देखेंगे कि समस्या का ऐसा बयान, हालांकि मान्य है, पूरी तरह से पूरा नहीं हुआ है।
एक आयामी स्थान (एम = 1)
यह वह जगह है जहाँ कोड दिखाई देने लगता है। हम सभी ग्राफ़ का निर्माण हमेशा की तरह मैटलपोटलिब लाइब्रेरी के साथ करते हैं, लेकिन यहाँ मैं ग्राफ के क्षेत्र को समायोजित करने के लिए एक लाइन में सीबोर्न लाइब्रेरी का उपयोग करता हूँ, क्योंकि मुझे पसंद है कि वह इसे कैसे करती है, लेकिन सिद्धांत रूप में आप उसके बिना कर सकते हैं।
हम बहुत सारे 1-आयामी अंक लेते हैं और उनके उत्तर देते हैं:
import numpy as np import math
यहां हमारे पास ए 1 एक्स का प्रत्येक आई-वें तत्व है - यह प्रशिक्षण नमूने का आई-थ एलीमेंट (आई-थ पॉइंट) है (अधिक सटीक रूप से, इसकी पहली और एकमात्र विशेषता): x(i)=(X1[i]) । x(i)1=X1[i]
सरणी y का प्रत्येक i-th तत्व सही उत्तर है, एक एकल विशेषता X1 [i] के साथ प्रशिक्षण नमूने के i-th तत्व के अनुरूप एक वास्तविक लेबल है।
हम केवल 5 अंक लेते हैं, पहले दो को कक्षा "-1" को सौंपा गया है, शेष तीन को कक्षा "1" को सौंपा गया है।
लाइन पर इन बिंदुओं को ड्रा करें:
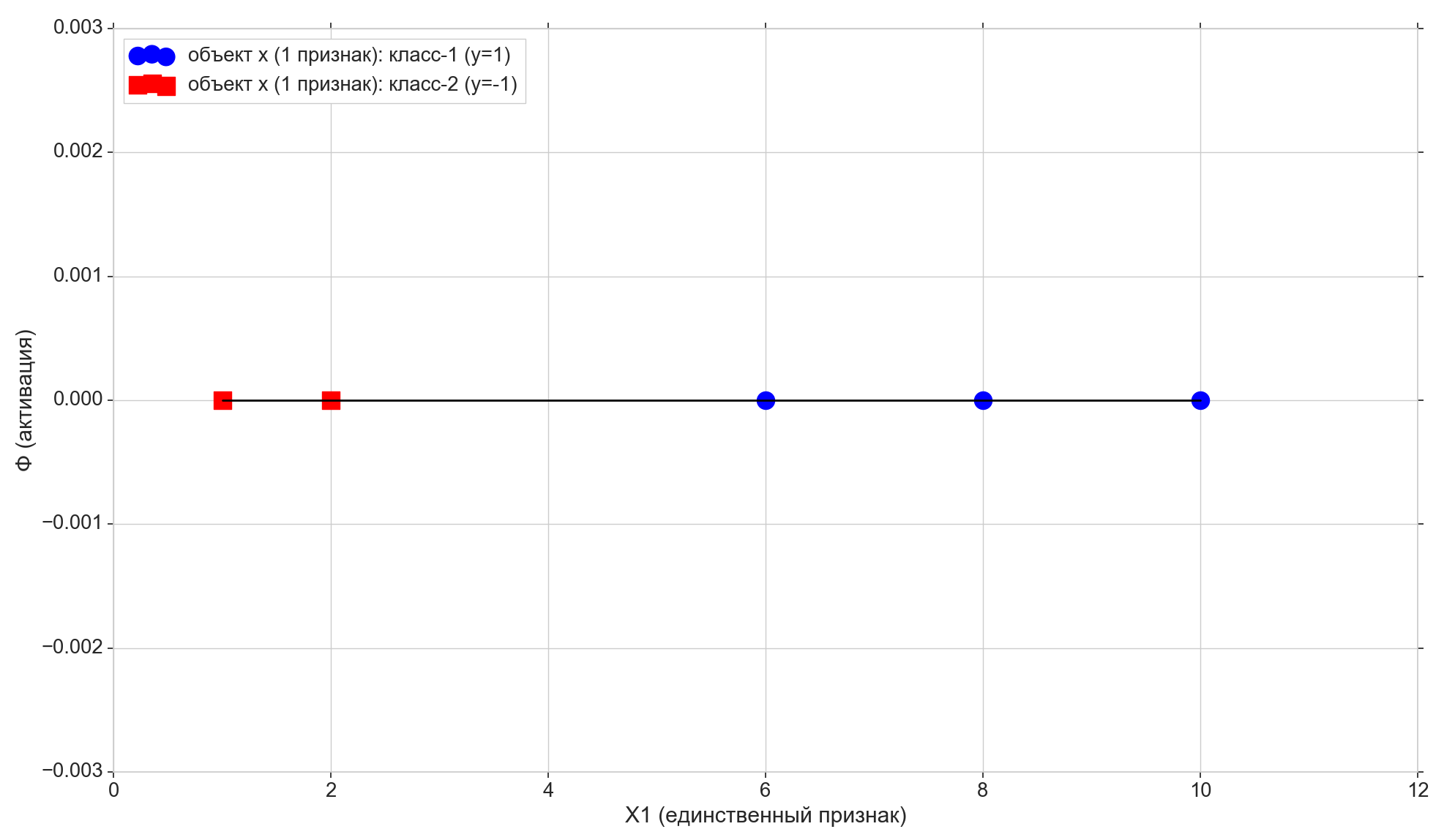
अब सक्रियण फ़ंक्शन को देखें:
Phi=w0+w1x1
जैसा कि आप देख सकते हैं, यह विमान पर एक साधारण पैरामीट्रिक रेखा है (2-आयामी में, अर्थात (m + 1) -दिमीय स्थान)
- क्षैतिज अक्ष पर हमारे पास तत्वों के बिंदु हैं (वे भी विशेषता X1 के मान हैं)
- प्रत्येक तत्व के लिए ऊर्ध्वाधर - सक्रियण मूल्यों पर
- पैरामीटर w1 - झुकाव का कोण सेट करता है,
- और w0 - ऊर्ध्वाधर अक्ष के साथ बदलाव (यहां कतरनी न्यूरॉन का उत्तर)।
w0 = -1.1 w1 = 0.4

यह भी याद रखें कि एक छोटे रूपांतरण के बाद, हमारी सक्रियता सीमा शून्य हो गई। इस प्रकार, यदि सक्रियण रेखा पर ith तत्व का प्रक्षेपण शून्य से कम है, तो हम कक्षा -1 को तत्व को सौंपते हैं ( y=−1 ), यदि यह शून्य से अधिक है, तो हम "1" वर्ग को असाइन करते हैं () y=1 )।
बैंगनी डॉट - अक्ष के साथ सक्रियण रेखा का चौराहा Phi=0 , अलग-अलग वर्गों से तत्वों को अलग करते हुए, यह 1-आयामी (यानी m-आयामी) फ़ीचर स्पेस में निर्मित हाइपरप्लेन (1-आयामी स्पेस के लिए, बिंदु हाइपरप्लेन है)। जैसा कि आप देख सकते हैं, तत्वों को समूहों में विभाजित करने के लिए, यह पर्याप्त है, लेकिन कक्षाओं को समूहों को आवंटित करने के लिए, यह अब पर्याप्त नहीं है। तत्वों को कक्षाएं आवंटित करने के लिए, हमें 2-डी में निर्मित प्रत्यक्ष (2-आयामी हाइपरप्लेन) सक्रियण की आवश्यकता होती है (यानी, (m + 1) -d) स्थान "संकेत + सक्रियण": ऊर्ध्वाधर से सक्रियण विचलन की दिशा अक्ष तत्वों के समूहों के लिए वर्ग का निर्धारण करेगा, क्योंकि यह इस बात पर निर्भर करता है कि सक्रियण पर तत्वों के अनुमान शून्य से अधिक या कम हैं या नहीं।
बदलते हुए पैरामीटर्स w0 और w1 हम अलग-अलग सक्रियण लाइनें प्राप्त करेंगे। हमें ऐसी सक्रियण रेखा बनाने की आवश्यकता है, अर्थात मापदंडों का ऐसा संयोजन खोजें w जिस पर सक्रियण रेखा पर प्रशिक्षण नमूने के पहले दो बिंदुओं का प्रक्षेपण शून्य से नीचे है (उनके लिए, मूल्य y=y=−1 ), और शेष 3 बिंदुओं का प्रक्षेपण शून्य से ऊपर (उनके लिए) होगा y=y=1 )।
यह बिल्कुल स्पष्ट है कि हमारे विशेष मामले में ऐसी लाइन के निर्माण में कुछ भी जटिल नहीं है, इसके अलावा, ऐसी लाइनें आम तौर पर एक अनंत संख्या में बनाई जा सकती हैं। लेकिन हम इसे इस तरह से बनाने की कोशिश करेंगे कि कुछ इष्टतमता मानदंड संतुष्ट हो (यह भविष्य की भविष्यवाणियों की गुणवत्ता को प्रभावित कर सकता है), साथ ही एल्गोरिदम को बहुआयामी मामले में विस्तारित करने की क्षमता होनी चाहिए।
यहां हम यह भी ध्यान दें कि हमने विशेष रूप से बिंदुओं के प्रारंभिक सेट को चुना है ताकि इसे इस तरह की रेखा से विभाजित किया जा सके (1-ई के लिए: पहले समूह के सभी तत्व छोटे हैं, दूसरे समूह के सभी तत्व कुछ निश्चित मूल्य से बड़े हैं), अर्थात कई प्रशिक्षण बिंदु रैखिक रूप से वियोज्य हैं ।
कक्षा {1, -1} के अनुरूप ग्राफ में दो और क्षैतिज रेखाएँ जोड़ें, और उन पर तत्वों को प्रोजेक्ट करें।

वर्ग "-1" परियोजना के साथ अंक नीचे की रेखा पर Phi=−1 , वर्ग "1" परियोजना के साथ शीर्ष पंक्ति के अंक Phi=1 ।
आइए हम एक और छोटी बारीकियों पर ध्यान दें। हम सक्रियण मूल्यों को ऊर्ध्वाधर अक्ष के साथ प्लॉट करते हैं, सक्रियण मानों का स्थान निरंतर है। लेकिन क्लासिफायरिफ़ायर (थ्रेशोल्ड के माध्यम से सक्रियण फ़ंक्शन) का परिणाम दो तत्वों {-1, 1} का एक असतत सेट है, न कि निरंतर पैमाना। यहां हम कक्षाओं का एक असतत सेट लेते हैं य और इसे एक सक्रियण पैमाने पर रखा Phi इसलिए कि असतत वर्ग मान सक्रियण पैमाने पर साधारण बिंदु बन जाते हैं - सक्रियण मूल्यों के विशेष मामले जिन्हें यह सीधे स्वीकार कर सकता है या उनके करीब पहुंच सकता है। कड़ाई से बोलते हुए, हम शुरू में वर्गों के रूप में संख्यात्मक मूल्यों को नहीं ले सकते थे, लेकिन स्ट्रिंग लेबल "वर्ग -1" और "वर्ग -2", जिस स्थिति में हमें सक्रियण पैमाने पर संख्यात्मक मानों के लिए स्ट्रिंग लेबल का मिलान करना होगा। इसलिए, हमारे मामले में, वर्गों "-1" और "1" के मूल्यों को क्लास लेबल के रूप में नहीं लिया जाना चाहिए क्योंकि वे हैं, लेकिन सक्रियण पैमाने पर चिह्नित कक्षाओं के मानचित्रण के रूप में।
त्रुटि मीट्रिक दर्ज करने का समय आ गया है

यह स्वीकार करना स्वाभाविक है कि चयनित तत्व के लिए सक्रियण मान जितना अधिक होता है, उसी तत्व के वर्ग मूल्य के लिए, इस तत्व के लिए सक्रियण वर्ग बेहतर होता है। इस प्रकार, चयनित तत्व के लिए त्रुटि के लिए, आप बिंदुओं के बीच की दूरी ले सकते हैं - सक्रियण रेखा पर तत्व का ऊर्ध्वाधर प्रक्षेपण और इसके ज्ञात (सत्य) वर्ग की क्षैतिज रेखा पर तत्व का प्रक्षेपण। ग्राफ पर: त्रुटियां - ऊर्ध्वाधर नारंगी रेखाएं।
लागत (नुकसान) समारोह
हमारे पास प्रत्येक व्यक्तिगत आइटम के लिए एक त्रुटि मीट्रिक है। हम संपूर्ण सक्रियण रेखा के लिए इसे एक गुणवत्ता मीट्रिक प्राप्त कर सकते हैं। उदाहरण के लिए, यह स्वीकार करना काफी स्वाभाविक है कि प्रशिक्षण नमूने के सभी तत्वों की त्रुटियों का योग जितना छोटा होगा, हमने एक सक्रियण रेखा बनाई है। प्रत्येक व्यक्तिगत तत्व के लिए, त्रुटि न्यूनतम नहीं होगी, लेकिन संपूर्ण प्रशिक्षण नमूने के रूप में, आप कुछ समझौता कर सकते हैं।
लेकिन आप त्रुटियों का एक सरल योग नहीं ले सकते हैं, लेकिन चुकता त्रुटियों का योग ( चुकता त्रुटियों का योग, चुकता त्रुटियों का योग, एसएसई )। यह काफी स्पष्ट है कि, सामान्य त्रुटियों के योग के मामले में, सक्रियण रेखा के करीब तत्वों की सही कक्षाओं के साथ अंक हैं, छोटा द्विघात त्रुटियों का योग होगा, लेकिन द्विघात त्रुटि के मामले में, सबसे दूरस्थ तत्वों को अधिक गंभीर दंड मिलेगा।
वास्तव में, हमारे यहां क्या रुचियां दूर के तत्वों के लिए जुर्माना का आकार नहीं है, लेकिन यह तथ्य कि द्विघात फ़ंक्शन का न्यूनतम है और हर जगह अलग-अलग है (सामान्य योग में न्यूनतम होगा, लेकिन इस न्यूनतम पर यह अलग नहीं होगा), देखें कि यह क्यों आवश्यक है। थोड़ा बाद में।
तो:
- त्रुटि - सक्रियण हाइपरप्लेन के लिए क्लास लेबल मूल्य से दूरी
- एसएसई - प्रशिक्षण नमूने के सभी तत्वों की द्विघात त्रुटियों का योग
- लागत समारोह जे(डब्ल्यू) - चयनित सक्रियण लाइन के लिए गुणवत्ता मीट्रिक। मूल्य जितना कम होगा, सक्रियता उतनी ही बेहतर होगी।
मान के एक फ़ंक्शन के रूप में लें 1 2सेअधिक SSE, एक रैखिक न्यूरॉन के लिए सामान्य मामले में, यह इस तरह दिखेगा:
\ शुरू {इकट्ठा} जे (डब्ल्यू) = {1 \ 2 ओवर} एसएसई = {1 \ 2 ओवर} \ योग _ {i = 1} ^ {n} (\ Phi (\ sum _ {j = 0}) ^ {m} w_ {j} x_ {j} ^ {(i)}) - y ^ {(i)}) ^ {2} = {1 \ over 2} \ sum _ {i = 1} ^ {n} ({योग _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} - y ^ {(i)}) ^ {2} \ end {इकट्ठा}
( 1 2सेअधिक पहली जगह में, यह एसएसई के साथ हस्तक्षेप नहीं करता है, और, दूसरी बात, सुविधा के लिए - यह खूबसूरती से कम हो जाएगा)
यहां मैं - तत्व संख्या, और एन - प्रशिक्षण सेट में तत्वों की संख्या। मैं आपको याद दिला दूं y(i) - सच्चा वर्ग मैं प्रशिक्षण नमूने का तत्व, अर्थात्। अग्रिम में प्रसिद्ध सही उत्तर।
जैसा कि हम याद करते हैं, सक्रियण रेखा की स्थिति मापदंडों द्वारा निर्धारित की जाती है - भार कारक w इसलिए वेक्टर w हानि फ़ंक्शन के पैरामीटर के रूप में कार्य करता है।
1-आयामी मामले के लिए
J(w)=1 2SSE=1 2 sumni=1(w0+w1x(i)1−y(i))2
अर्थ x और य अग्रिम में जाना जाता है (यह एक प्रशिक्षण सेट है), इसलिए वे तय हो गए हैं। हम मापदंडों का चयन करते हैं w , यानी। w0 और w1 ताकि मूल्य जे(डब्ल्यू) यह कम से कम निकला। मान के रूप में ग्राफ को प्लॉट करने का प्रयास करते हैं जे(डब्ल्यू) मापदंडों पर निर्भर करता है w0 और w1

सामान्य तौर पर, यह पहले से ही यहां दिखाई देता है कि नुकसान फ़ंक्शन में न्यूनतम है, और जहां यह लगभग स्थित है। लेकिन चलो एक और चाल करते हैं और एक ही ग्राफ बनाते हैं, केवल एक लघुगणकीय ऊर्ध्वाधर पैमाने के साथ ।

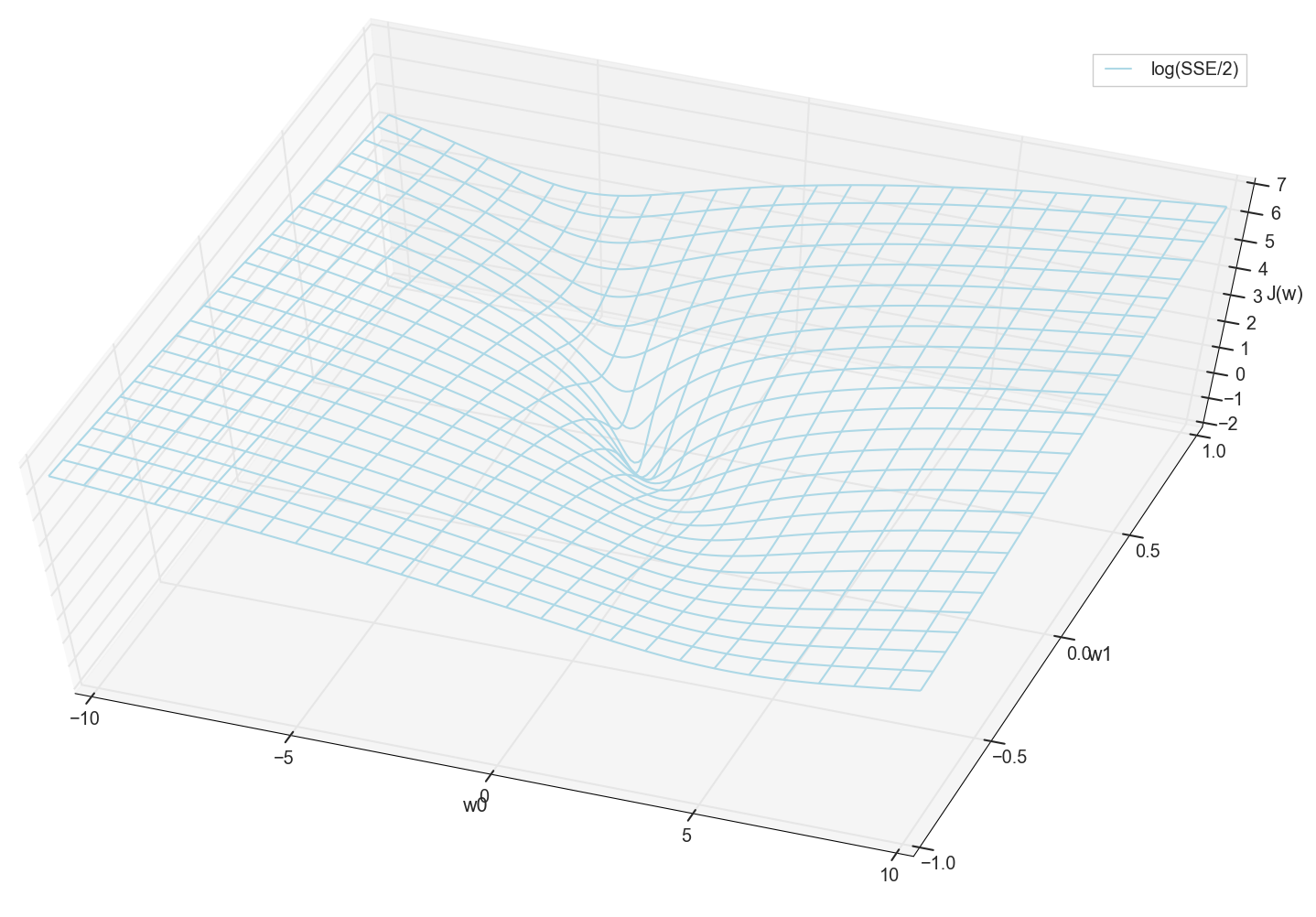
मैं आपके बारे में नहीं जानता, लेकिन व्यक्तिगत रूप से, जब मैंने पहली बार इस चार्ट को देखा, तो मुझे आत्मज्ञान का अनुभव हुआ। यह प्राकृतिक गुहा तंत्रिका नेटवर्क पर एक लोकप्रिय लेख से बहुआयामी पहाड़ियों का केवल एक आलंकारिक दृश्य नहीं है, यह एक वास्तविक ग्राफ है।
हमारा कार्य ऐसे मूल्यों का चयन करना है w0 और w1 इस गड्ढे की तह तक जाने के लिए। हमें वज़न के मूल्य मिलते हैं - हमें एक प्रशिक्षित न्यूरॉन मिलता है।
चूँकि हम सभी एक ही तरह से एक ग्राफ तैयार करते हैं और व्यक्तिगत रूप से इसका न्यूनतम निरीक्षण करते हैं, इसलिए कोई भी हमें "मैन्युअल रूप से" ग्रिड पर एक सरल गणना द्वारा अपने निर्देशांक खोजने के लिए मना नहीं करेगा:

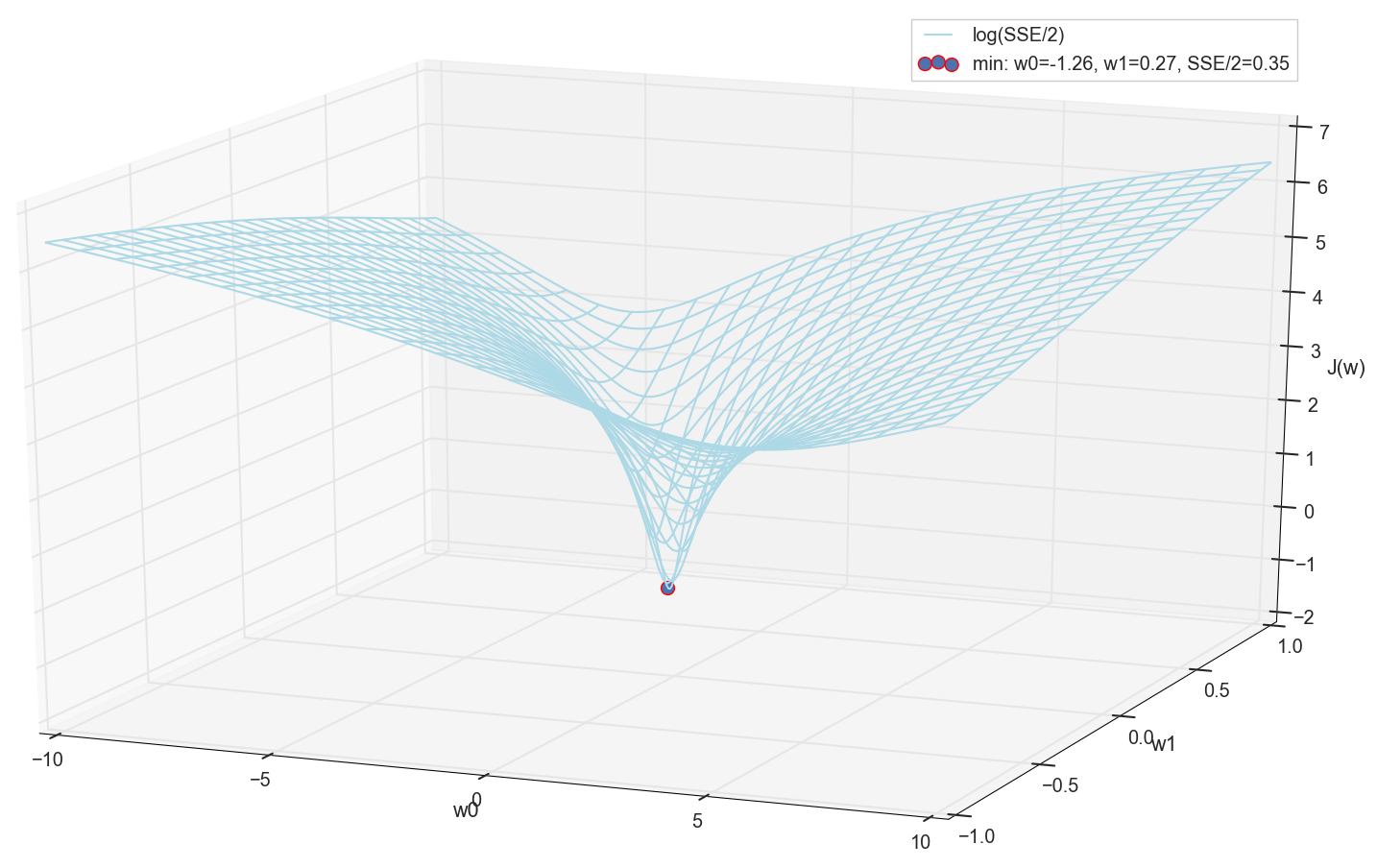
ये मूल्य हैं: w0=−1.26 और w1=0.27 एसएसई के वर्ग त्रुटियों का योग 0.69 है, लागत समारोह J(w)=SSE/2=0.35 (अधिक सटीक: 0.3456478371758288)
आइए देखें कि इन मापदंडों के साथ सक्रियण कैसा दिखता है:

मेरे लिए, यह बिल्कुल सामान्य है। एक शून्य सीमा के साथ सक्रियण का प्रतिच्छेदन बिंदु विभिन्न वर्गों से तत्वों को अलग करता है, और सक्रियण ही उन्हें सही मान प्रदान करता है। इसी समय, सक्रियता कुछ इष्टतम स्थिति में प्रतीत होती है।
आगे बढ़ने से पहले, हम फिर से ग्रिड पर ग्राफ की प्रशंसा करते हैं:
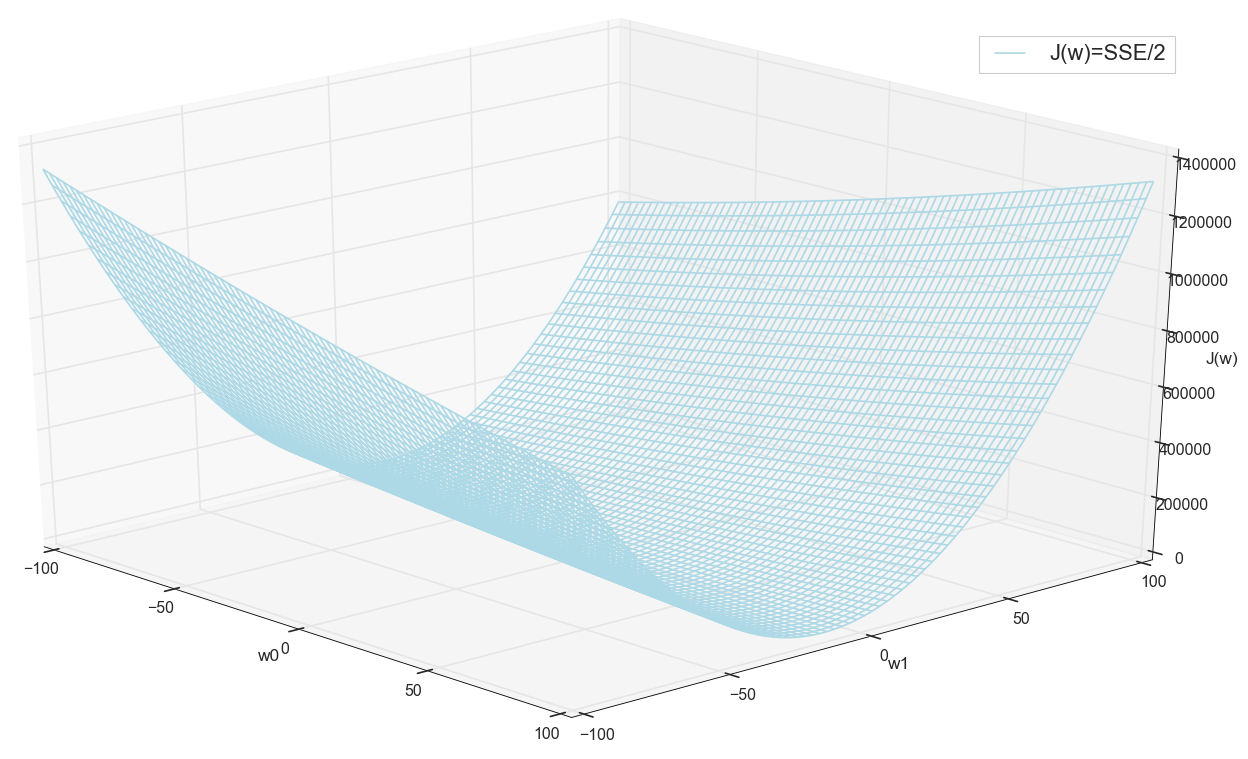
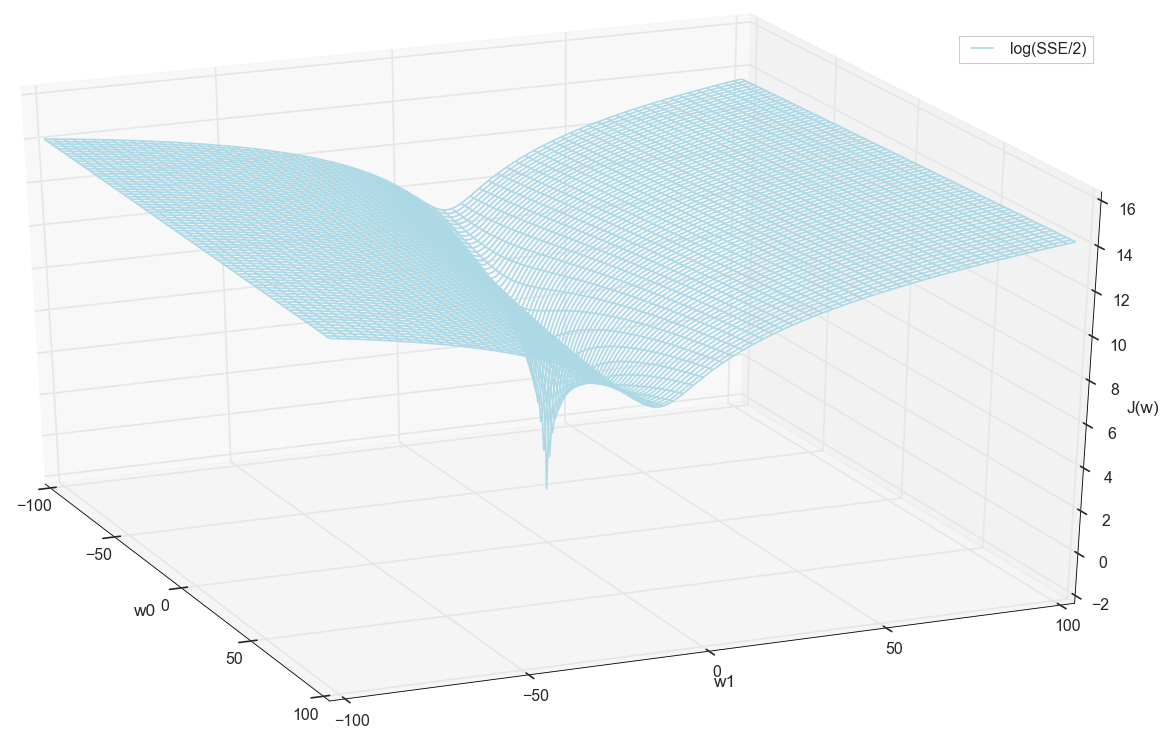
ऐसा लगता है कि आस-पास कोई और शेर नहीं है जिसने सोचा होगा।
न्यूनतम खोज
तो, हमें वेट मिला - न्यूनतम त्रुटि मान के निर्देशांक। यह प्रशिक्षण नमूने पर भार का इष्टतम मूल्य होगा। आमतौर पर, यह वही है जो हमें चाहिए, हम कह सकते हैं कि न्यूरॉन प्रशिक्षित है। शायद यह पूरा हो सकता है?
एक न्यूनतम के लिए खोजें: ग्रिड द्वारा खोजें
- पहली नज़र में विकल्प काफी काम कर रहा है (जैसा कि हम देखते हैं)
- आपको उस क्षेत्र को पहले से जानना होगा जहां न्यूनतम की तलाश करें (आप काफी बड़ी सीमाएं ले सकते हैं, फिर खोज क्षेत्र को संकीर्ण कर सकते हैं - यह केवल आंख से है)
- सटीकता बढ़ाने के लिए, आपको कदम कम करने की आवश्यकता है → और भी अधिक अंक (समाधान: आप खोज क्षेत्र को पुनरावृत्त कर सकते हैं)
- बहुत अधिक अंक (2d के लिए यह ठीक हो सकता है, लेकिन बहुआयामी मामलों के लिए हम संसाधनों में बहुत तेज़ी से भागते हैं)
- MNIST के लिए (28x28 = 784 पिक्सेल - समान संख्या में इनपुट, समान भार वाले कारक प्लस ऑफ़सेट, 100 कदम प्रति आयाम की ग्रिड): 100 ^ 785 = 10 ^ 1570।
इसलिए, यदि हम प्रत्येक माप के लिए 100 बिंदुओं के ग्रिड पर प्रत्यक्ष गणना द्वारा न्यूनतम खोज करके 28x28 = 784 पिक्सल की छवि में एकल न्यूरॉन (एक तंत्रिका नेटवर्क भी नहीं) को प्रशिक्षित करना चाहते हैं, तो हमें 10 से 1570 संयोजनों को छांटना होगा। यह भंडारण और खोज के लिए काफी है (ब्रह्मांड के दृश्य भाग में केवल 10 ^ 80 परमाणु हैं, ब्रह्मांड लगभग 4 * 10 ^ 17 सेकंड = 4 * 10 ^ 26 नैनोसेकंड के लिए मौजूद है)।
आइए तेजी से एक विकल्प खोजने की कोशिश करें।
न्यूनतम खोज: लगातार कदम वंश
चलो नुकसान फ़ंक्शन के ग्राफ को देखें जे(डब्ल्यू) विमान पर: ठीक करें w0 , परिवर्तन w1
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
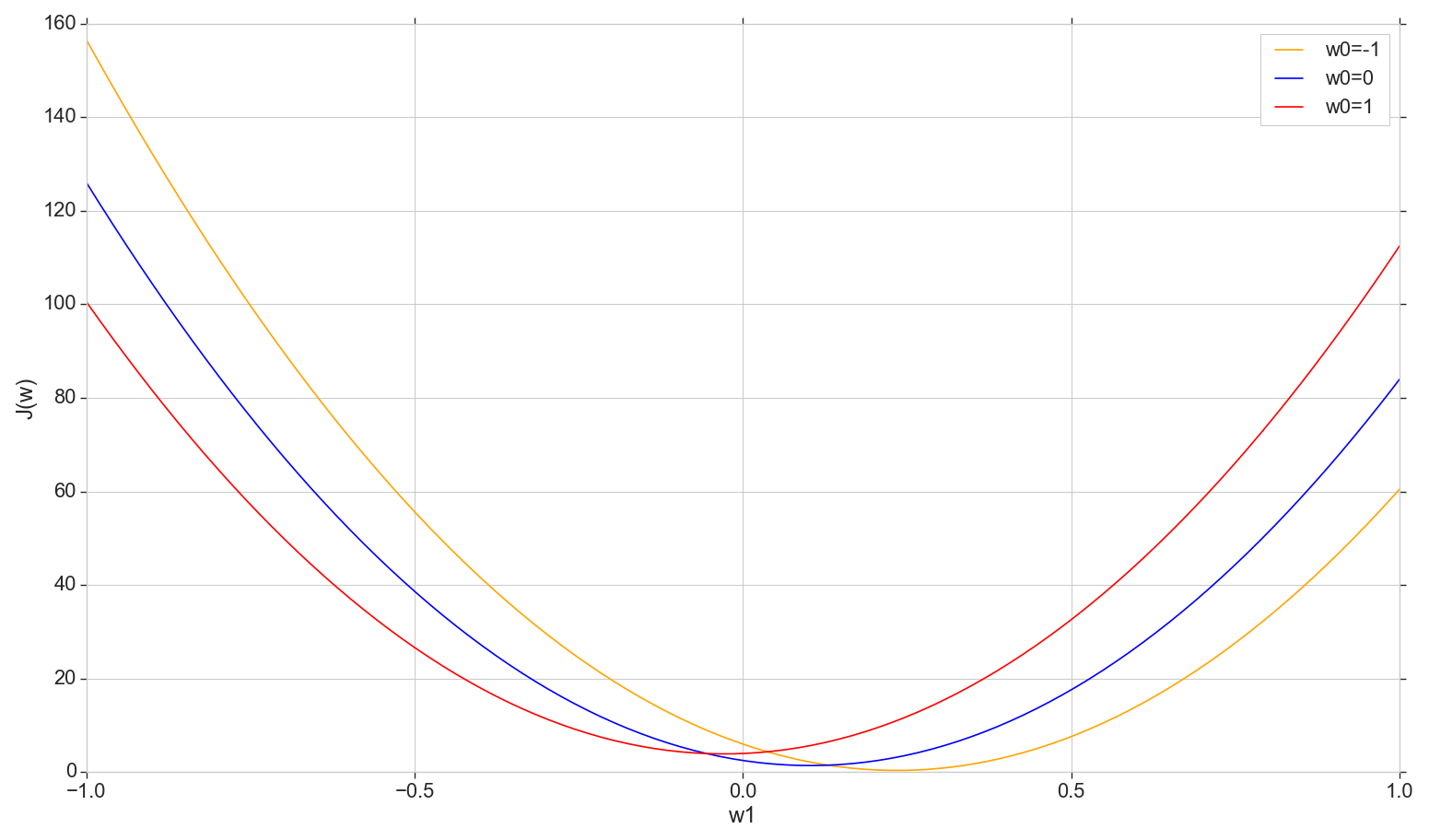
यह एक साधारण परबोला है (अधिक सटीक रूप से, परवल का एक परिवार - वे किस तरह के मूल्य के आधार पर थोड़ा अलग होंगे, इस पर निर्भर करता है w0 )। न्यूनतम परबोला खोजने के लिए, सभी बिंदुओं के माध्यम से सॉर्ट करना आवश्यक नहीं है। हम क्षैतिज अक्ष पर एक मनमाना बिंदु चुन सकते हैं और कुछ कदम के साथ न्यूनतम की ओर बढ़ सकते हैं।
एक निरंतर पिच विकल्प पर विचार करें
- यदि चरण बहुत बड़ा है, तो आप छूट सकते हैं, और न्यूनतम तक नहीं पहुँच सकते (कदम कम किया जा सकता है)
- यदि बहुत छोटा है, तो बहुत अधिक चरण होंगे (इससे अधिक हो सकता है)
- किसी भी स्थिति में, हम सटीक न्यूनतम हासिल नहीं करेंगे, लेकिन हम न्यूनतम त्रुटिपूर्ण सटीकता के पास कदम बदलकर मनमानी सटीकता के साथ इसे प्राप्त कर सकते हैं (कदम स्थिर होना बंद हो जाता है)
- हम वंश की दिशा नहीं जानते हैं (यह एल्गोरिदम को हल करना संभव है: बढ़ती त्रुटियों की ओर कदम न करें)
- सीमा खोजने के साथ समस्या हल हो गई है (आप कहीं से भी नीचे जा सकते हैं - जितनी जल्दी या बाद में हम वैसे भी नीचे जाएंगे)
- सिद्धांत रूप में, विकल्प काम कर रहा है, लेकिन शायद एक बेहतर विकल्प है?
नोट: जब मैंने व्याख्यान देने के लिए वंश के इस तरह के विकल्प के बारे में बात की, तो एक छात्र ने पूछा कि आपको चरणों में स्थानांतरित करने की आवश्यकता क्यों है यदि आप सूत्र का उपयोग करके तुरंत न्यूनतम परबोला पा सकते हैं? सबसे पहले, मैंने इस भावना में कुछ उत्तर दिया कि हम अब पुनरावृत्ति विकल्प पर विचार करने में रुचि रखते हैं, ताकि बाद में हम न केवल एक परवलय के साथ, बल्कि अन्य स्थितियों में भी इसका उपयोग कर सकें। इसके अलावा, वास्तव में, हमें इस खंड पर विशेष रूप से कम से कम एक पैराबोला की आवश्यकता नहीं है - हम न्यूनतम एक आयाम में नहीं, बल्कि सभी आयामों में इस तरह से आगे बढ़ेंगे कि प्रत्येक नए पुनरावृत्ति पर एक नया कदम इस परवलय के साथ न हो, लेकिन एक शिफ्ट मूल्य के साथ एक नया टुकड़ा के साथ parabola w0 । लेकिन बाद में सोचते हुए, मैंने सोचा कि, सिद्धांत रूप में, कुछ भी गलत नहीं है अगर हम हर स्लाइस में कदमों में नहीं, बल्कि वर्तमान स्लाइस के न्यूनतम पर तुरंत रोल करें। इसलिए, समय के बाद, माप द्वारा माप, हमें अभी भी एक वैश्विक न्यूनतम पर स्लाइड करना है, और यह कदमों की तुलना में तेज लगता है। एक एकल न्यूरॉन के लिए, यह काम करना चाहिए, न कि केवल एक पैराबोला के साथ। लेकिन मैंने अभी तक इस सिद्धांत का परीक्षण करने के लिए समय बर्बाद करना शुरू नहीं किया है, इसलिए यहां हम बस आगे बढ़ते हैं - मैंने क्रमिक वंश के बारे में बात करने का वादा किया।
एक न्यूनतम के लिए खोजें: ढाल वंश
सामान्य तौर पर, हम कदम नीचे जाते हैं, लेकिन हम इसे अधिक स्मार्ट तरीके से करते हैं। हम कदम का चयन करने के लिए लागत वक्र के व्युत्पन्न का उपयोग करते हैं (यहां, लागत वक्र नहीं , बल्कि लागत वक्र )।
- हमारे पास कई आयाम हैं और उनमें से प्रत्येक का अपना वक्र है: हम सब कुछ ठीक करते हैं wj सिवाय wk ।
- J(wk) इसमें एक त्रुटि वक्र होगा k वें आयाम
- उनमें से सभी (हमारे मामले में) परवल हैं, लेकिन, आम तौर पर बोलना, यह केवल महत्वपूर्ण है कि वे हर जगह भिन्न होते हैं और न्यूनतम होते हैं
- प्रत्येक माप में कदम को समायोजित करने के लिए, हम इस माप के संबंध में त्रुटि फ़ंक्शन के आंशिक व्युत्पन्न का उपयोग करेंगे (एक अलग गुणांक) wk )।
- ऐसे आंशिक व्युत्पन्न के वेक्टर को एक ढाल कहा जाता है ।
यह सब अच्छा है, लेकिन व्युत्पन्न कहां से आता है? अब इसका पता लगाते हैं।
व्युत्पन्न का ज्यामितीय अर्थ
मेरे लिए, लंबे समय तक व्युत्पन्न इसकी गणना के लिए विशेष सूत्र और नियमों का एक सेट बना रहा, साथ ही वृद्धि, कमी और चरम के बारे में कुछ। यह याद रखना उचित होगा कि वास्तव में व्युत्पन्न क्या है।
व्युत्पन्न कार्य y(x) इस बिंदु पर x0 फ़ंक्शन की वृद्धि के अनुपात की सीमा है Deltay वेतन वृद्धि के लिए Deltax जब एक तर्क बढ़ाना Deltax शून्य पर चलना:
y '(x_0) = \ lim \ _ \ Delta x \ to 0} {\ Delta y \ over \ Delta x}, \ Delta y = y (x_0 + \ Delta x) - y (x_0)

चित्र में बिंदी M(x0,y(x0))=(x0,y0) वह बिंदु है जिस पर हम व्युत्पन्न का निर्धारण करना चाहते हैं। बिंदु N(x0+ Deltax,y(x0+ Deltax))=(x0+ Deltax,y0+ Deltay) - तर्क को बढ़ाकर प्राप्त किया गया बिंदु Deltax । सीधे एमएन - इन दो बिंदुओं से गुजरने वाले सेक्रेटरी।
बिंदु ए - धर्मनिरपेक्षता का प्रतिच्छेदन एमएन क्षैतिज अक्ष के साथ y=0 ।
दो समकोण त्रिभुजों पर विचार करें: एक त्रिभुज त्रिकोणएनपीएम सेक्शन सेक्रेटरी के साथ एमएन कर्ण और त्रिकोण के रूप में त्रिकोणएमबीए धुरी के लिए secant की निरंतरता के साथ y=0 - खंड एएम कर्ण के रूप में। ग्राफ और स्कूल ज्यामिति पाठ्यक्रम से यह स्पष्ट है कि कोण कोणNMP और कोणMAB बराबर हैं, और इसलिए उनके स्पर्शक समान हैं:
tan angleMAB= tan angleNMP=MB overAB==NP overMP= Deltay over Deltax
तस्वीर में जोड़ें: एमडी - बिंदु पर प्रारंभिक वक्र के स्पर्शरेखा एम एक धुरी पार करता है y=0 बिंदु पर डी । त्रिकोण त्रिकोणMBD - कर्ण के साथ एक समकोण त्रिभुज - कैसेट अनुभाग, खंड एमडी ।
हम वेतन वृद्धि का लक्ष्य रखते हैं Deltax शून्य करने के लिए:
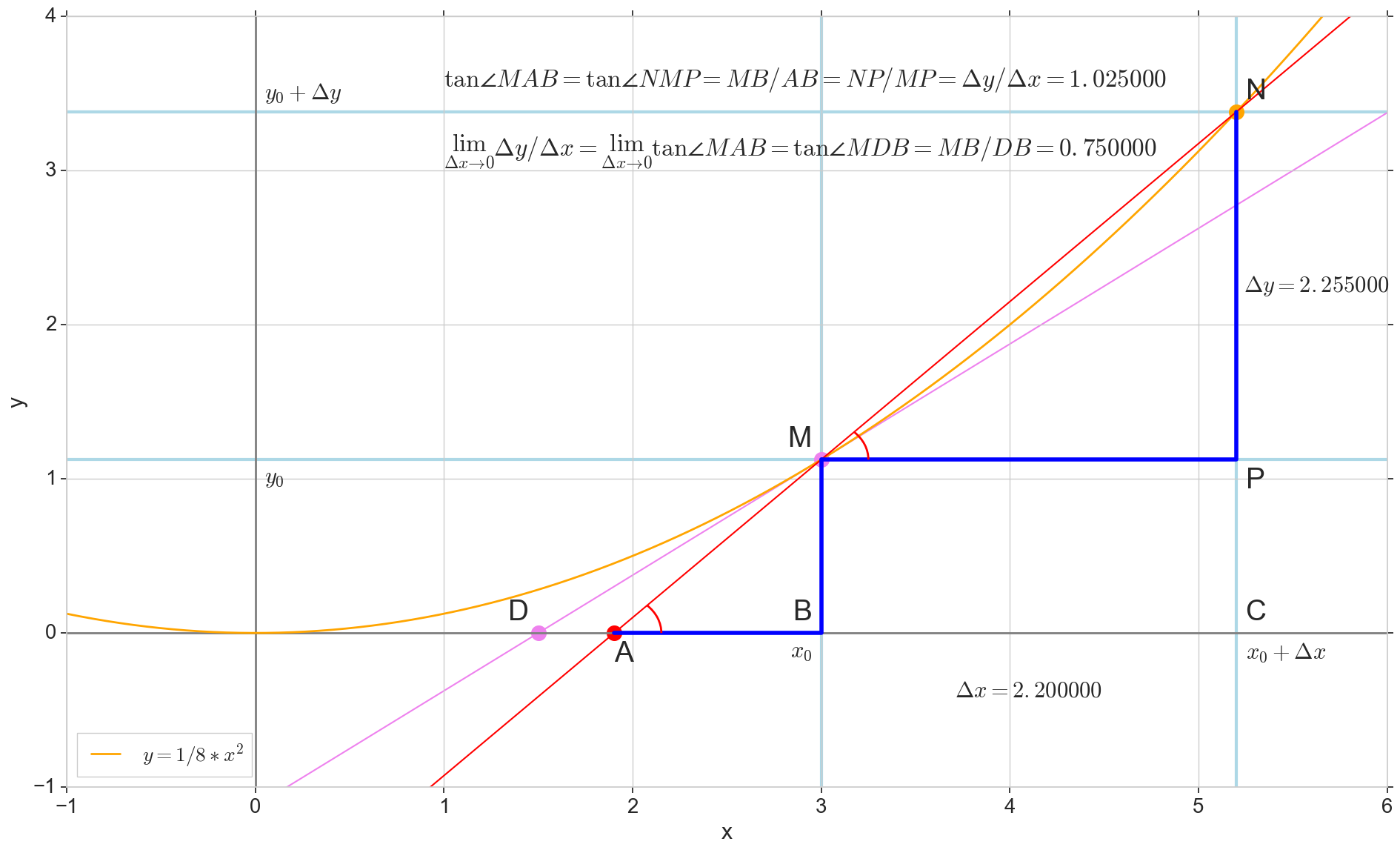
बिंदु एन बात पर चलते हुए एम फ़ंक्शन द्वारा, डॉट ए एक बिंदु पर रेंगना डी अक्ष के साथ य , विभाजन एमएन एक स्पर्शरेखा में बदल जाता है एमडी स्पर्श बिंदु के साथ एम । स्रोत त्रिकोण त्रिकोणएनपीएम पैरों के साथ Deltax और Deltay एक बिंदु पर सिकुड़ता है, लेकिन एक त्रिकोण जैसा है त्रिकोणएमबीए एक त्रिकोण में बदल जाता है त्रिकोणMBD न केवल मैक्रोस्कोपिक आयामों को संरक्षित करना, बल्कि कोणों की समानता भी कोणMAB और कोणNMP ।
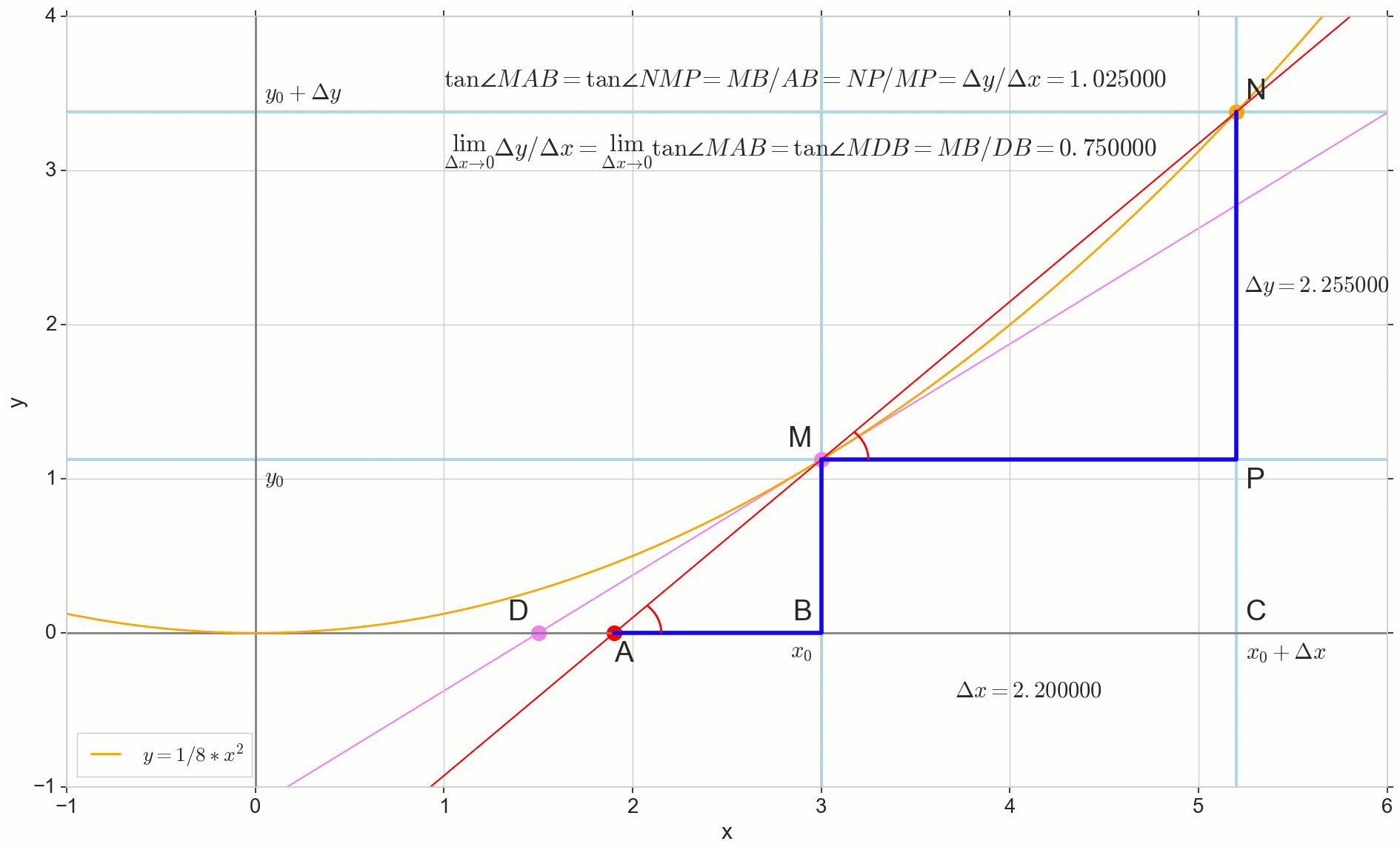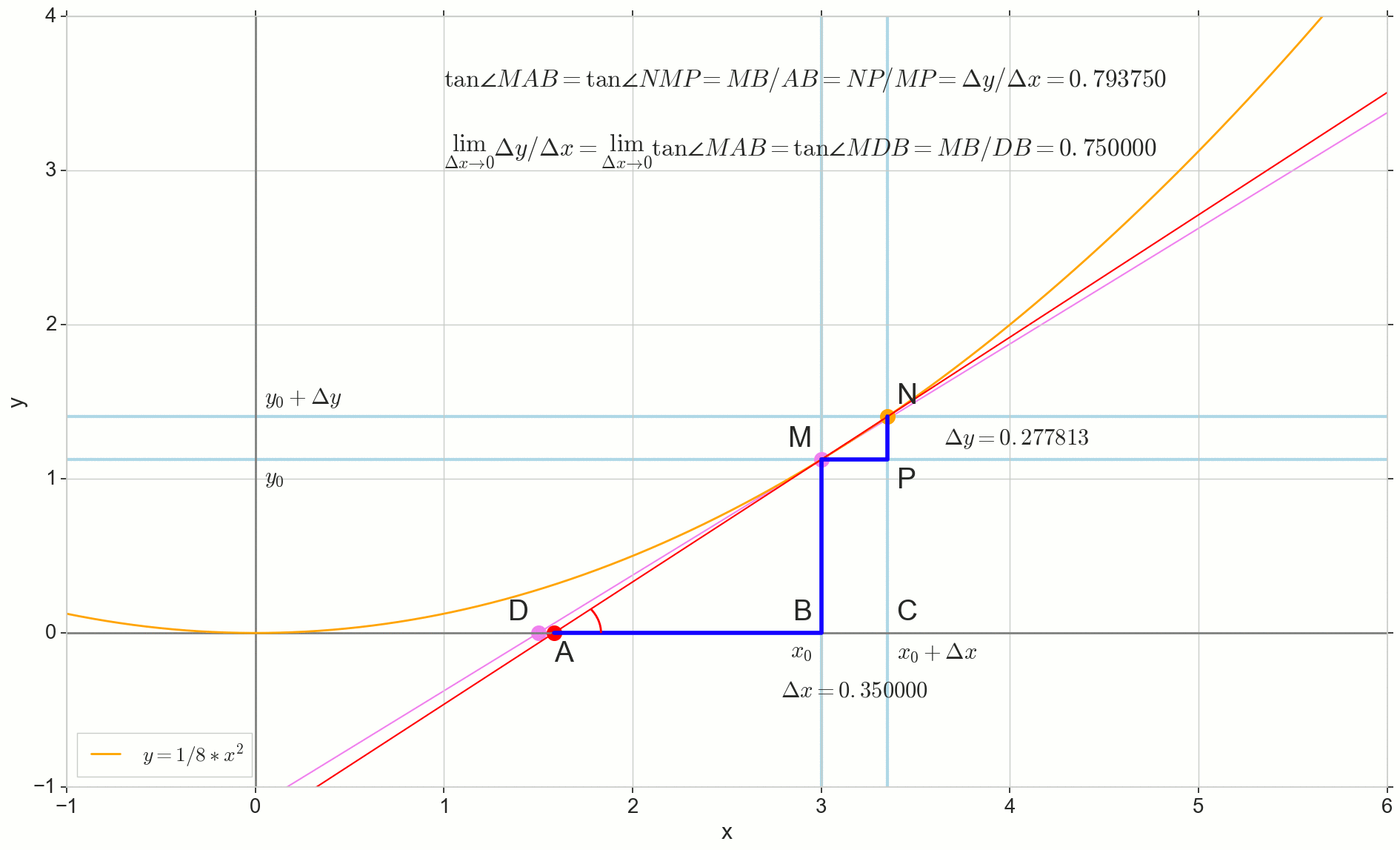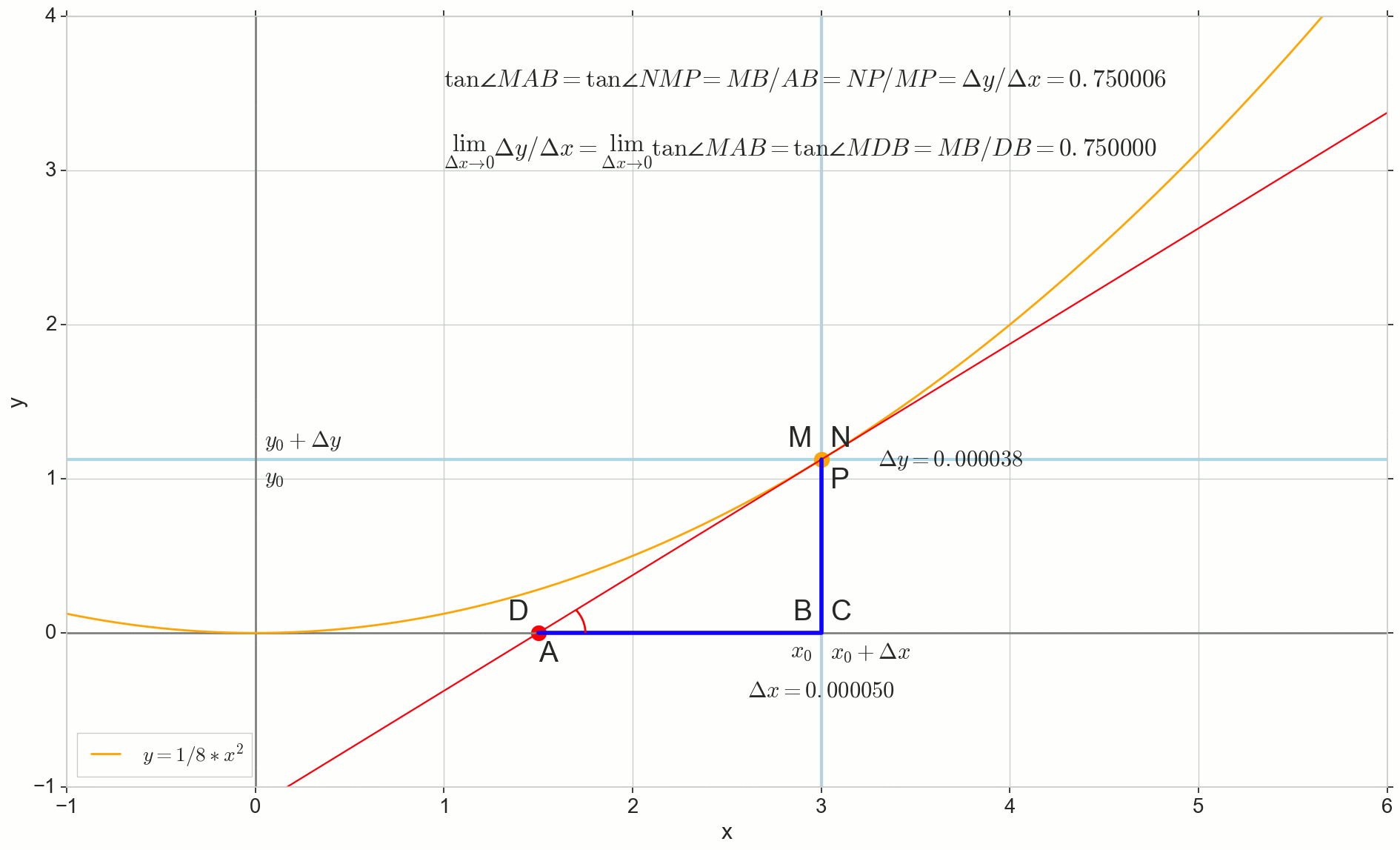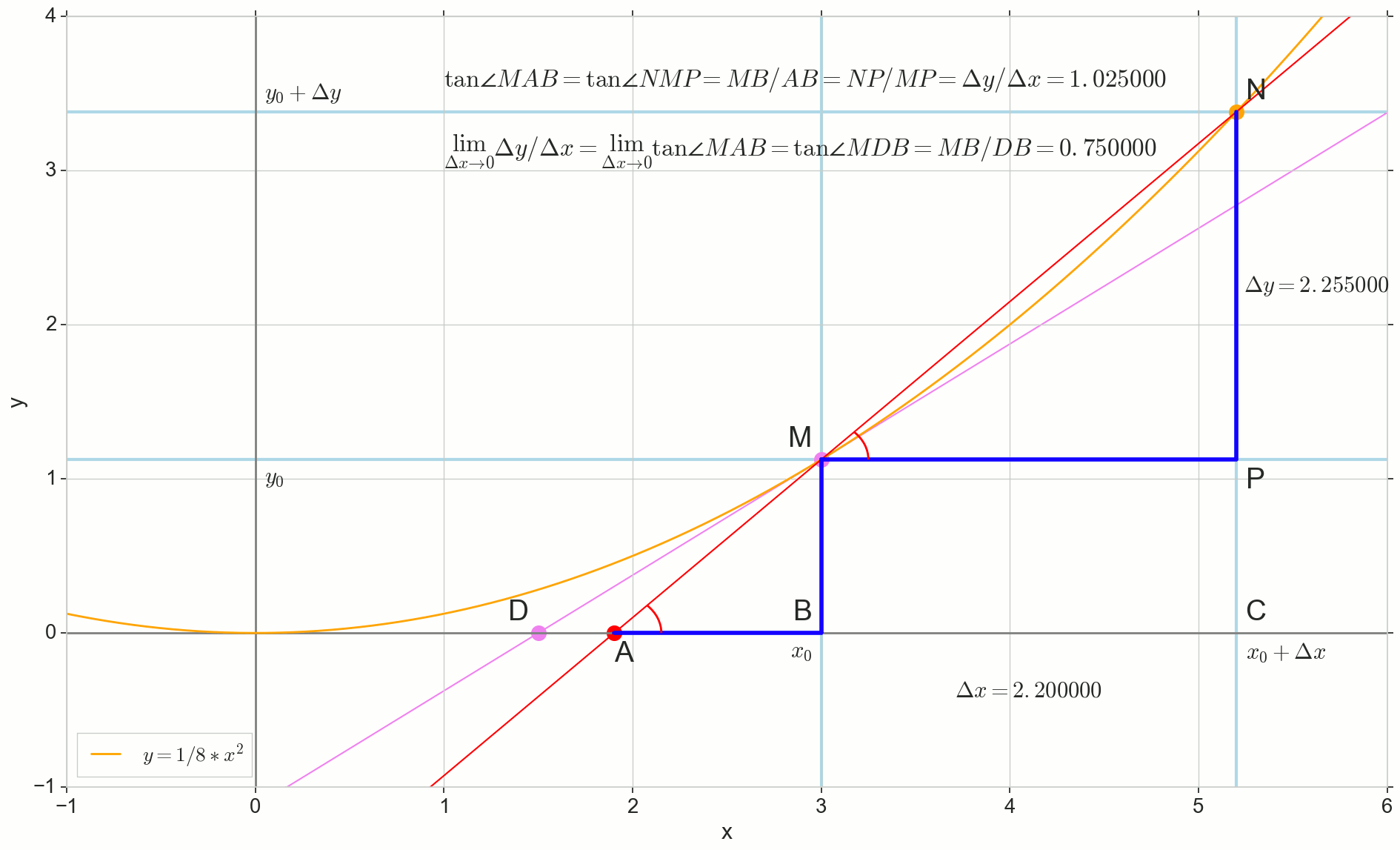
कितनी बढ़ोत्तरी Deltax , असीम रूप से शून्य के निकट, कभी शून्य तक नहीं पहुंचेगा, इसलिए बिंदु एन सटीक स्थान पर कभी नहीं एम , बिंदु ए बात तक नहीं पहुँचेंगे डी त्रिकोण त्रिकोणएमबीए में नहीं बदलेगा त्रिकोणMBD । , , «» lim ।
△MBA — △MBD , :
limΔx→0ΔyΔx=limΔx→0tan∠NMP=limΔx→0tan∠MAB=limΔx→0MBAB=MBDB=tan∠MDB
:
limΔx→0ΔyΔx=tan∠MDB
, , :
y′(x0)=limΔx→0ΔyΔx=tan∠MDB
, y=0 । .
, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).
:
- x0 y=0
- — y(x0) — x0 y=0 y=0
- «» , ,
- — : — , —
- ( , , , Δy )
, , :

— , — x0 , — . — — . — y=0 , — .

, , , , . ( , ) (: y=0 , ).

( ): , (: y=0 , ).
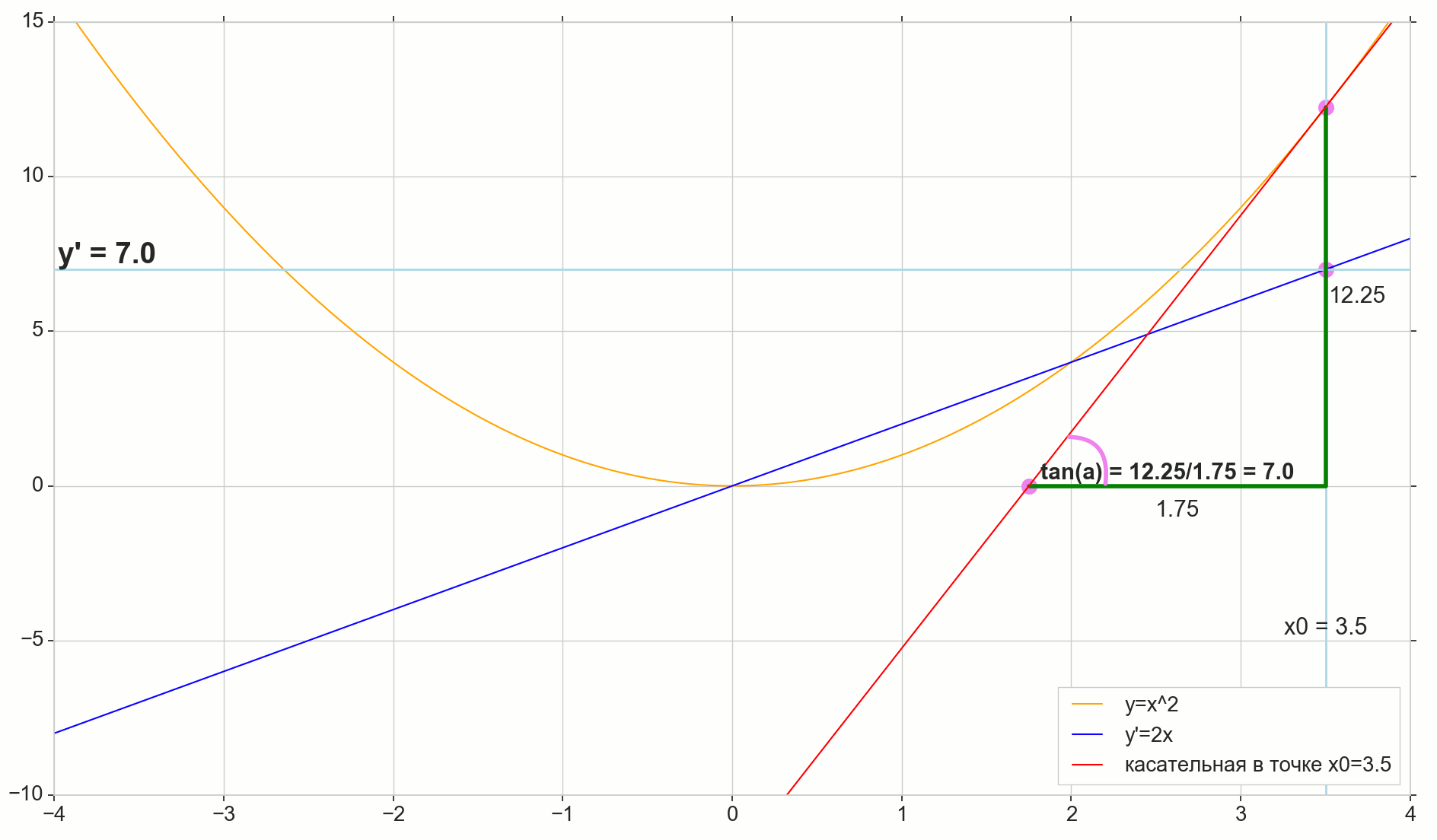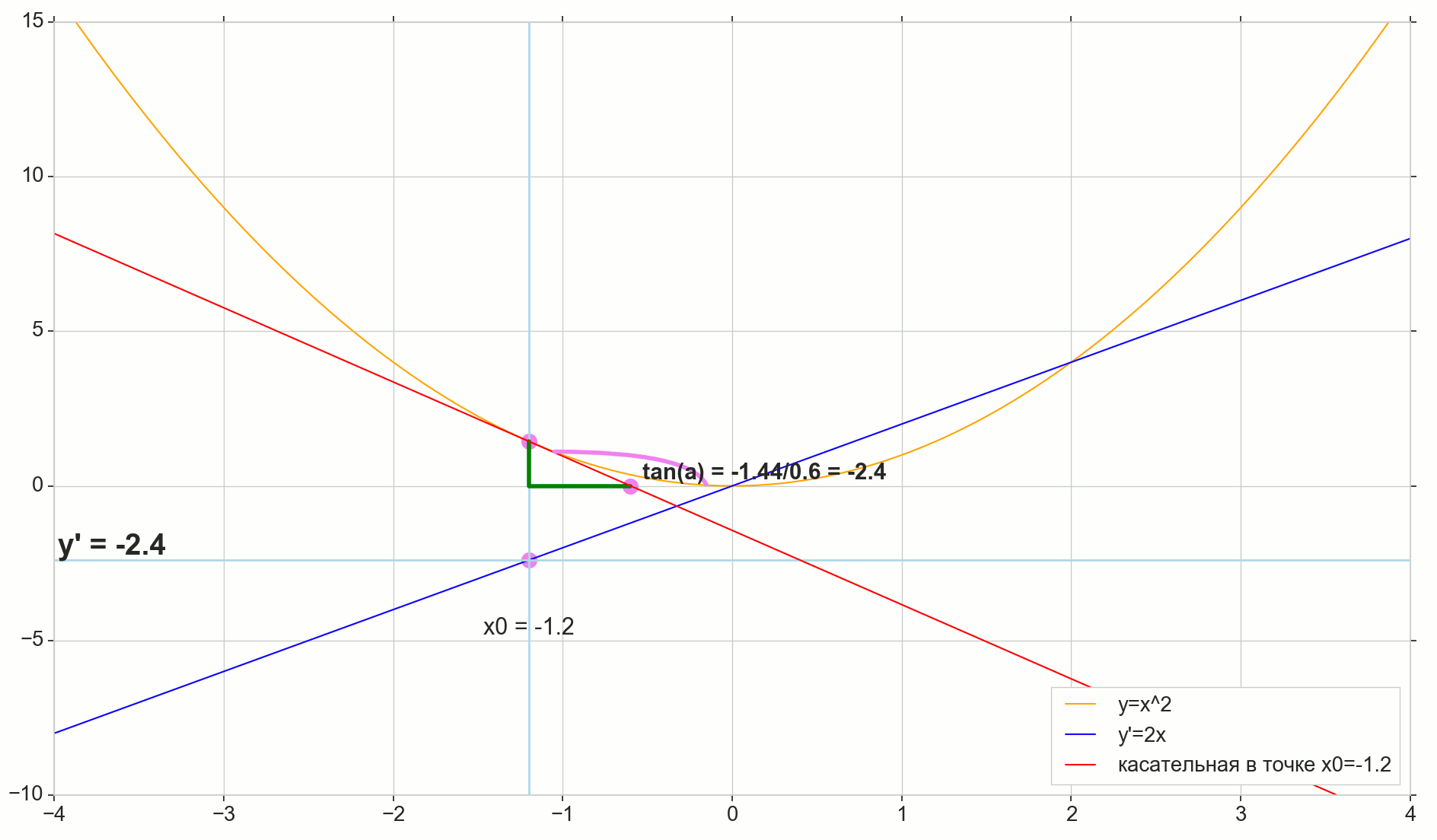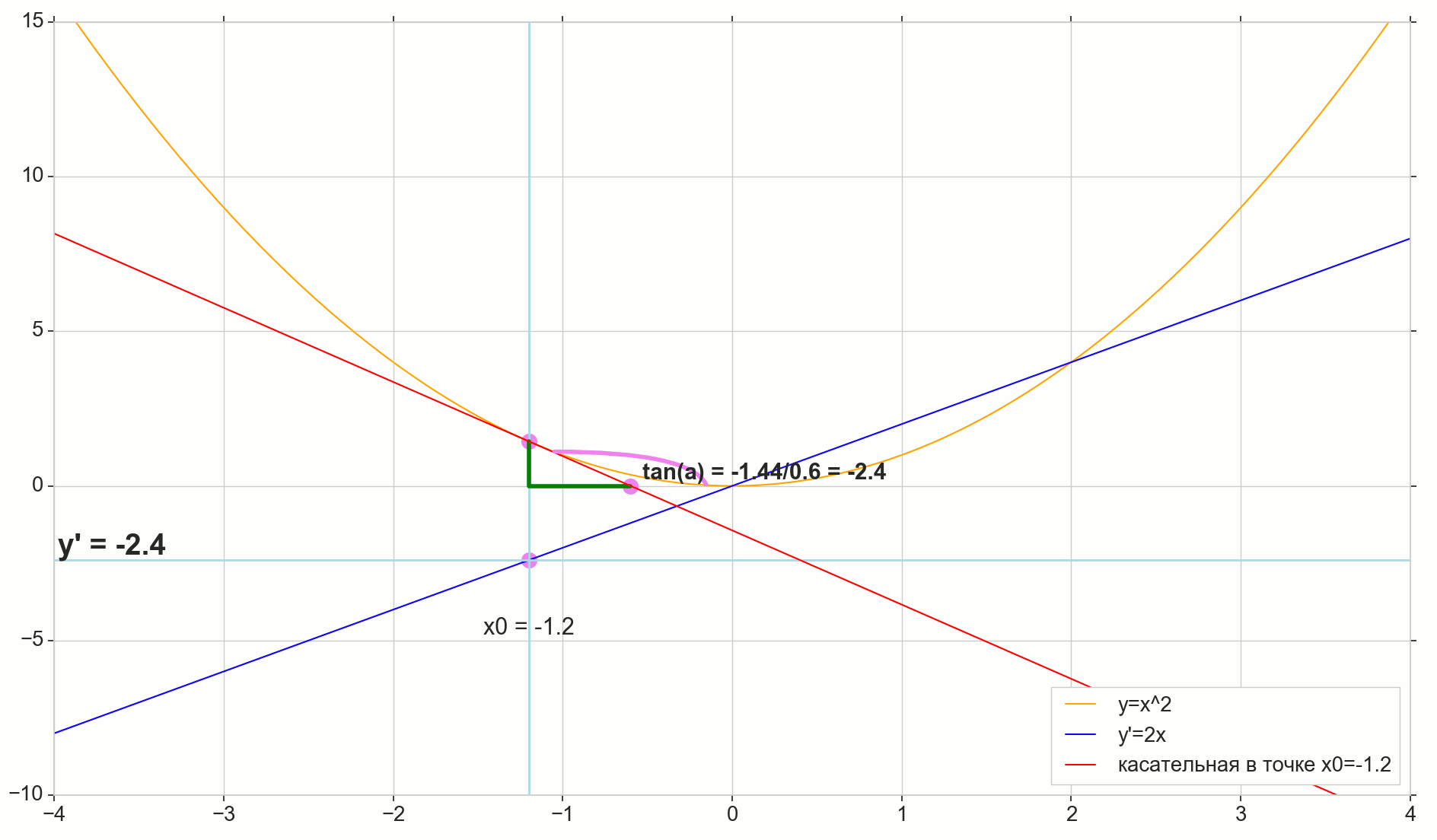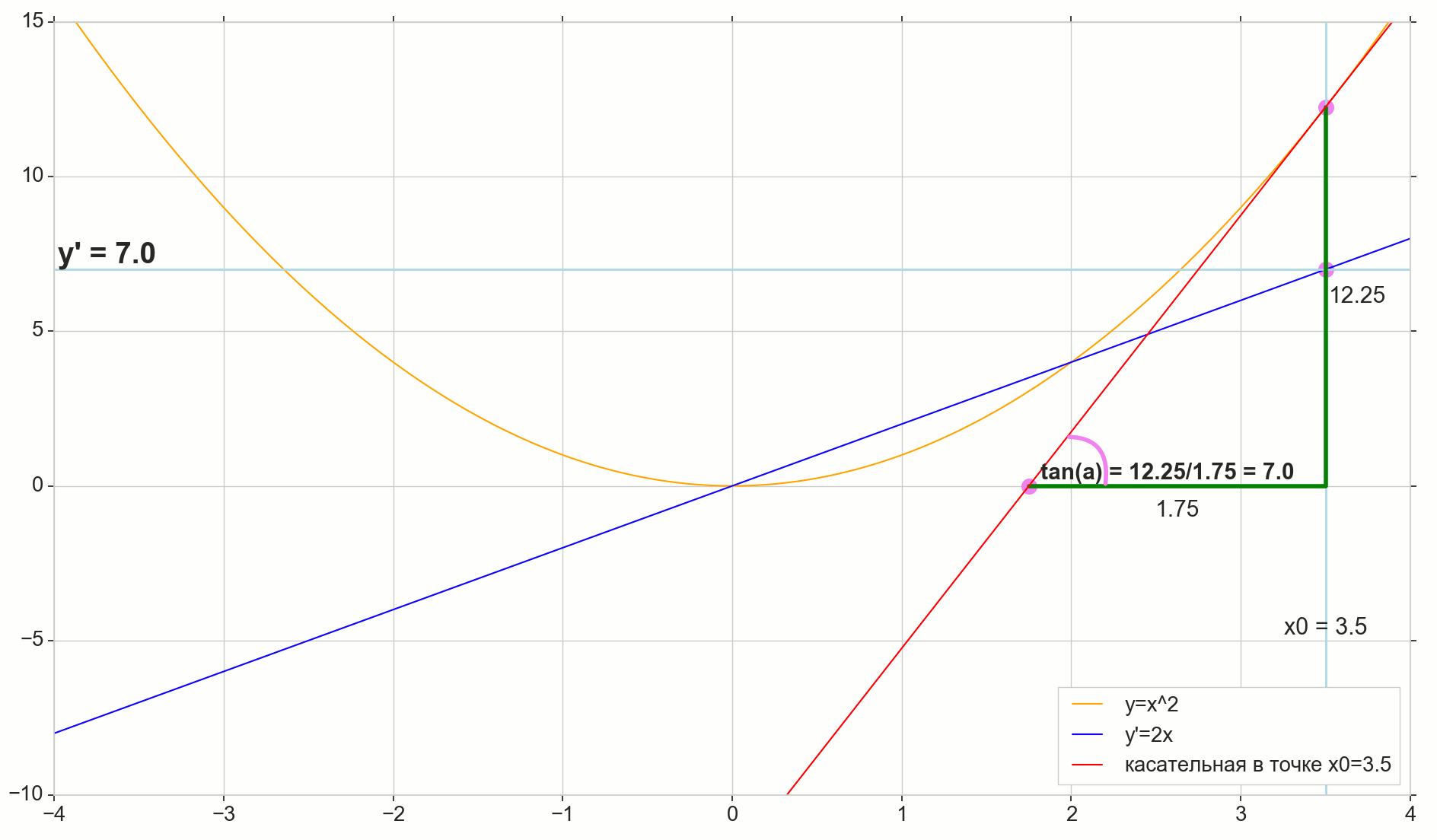
, : (), «»/«» , . — . , , ? .
J(w) । , , , .
J(w)=12SSE=12n∑i=1(m∑j=0wjx(i)j−y(i))2
∂J(w)∂wk=∂∂wk12n∑i=1(m∑j=0wjx(i)j−y(i))2=12n∑i=1∂∂wk(m∑j=0wjx(i)j−y(i))2=12n∑i=12(m∑j=0wjx(i)j−y(i))∂∂wk(m∑j=0wjx(i)j−y(i))=122n∑i=1(m∑j=0wjx(i)j−y(i))∂∂wk((w0x(i)0+...+wkx(i)k+...+wmx(i)m)−y(i))=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
, : , , , ( ) . , wk ( , ), . , , , 1/2 SSE .
:
∂J(w)∂wk=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
— ( ∇ [], , .. []):
∇J(w)=(∂J(w)∂w0,...,∂J(w)∂wm),w=(w0,...,wm)
:
w:=w+Δw,Δw=−η∇J(w)
k - :
wk:=wk+Δwk,Δwk=−η∂J(w)∂wk
:
, , , . , .
1- :
Φ(x,w)=w0+w1x1
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1−y(i))x(i)0=n∑i=1(w0+w1x(i)1−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1−y(i))x(i)1
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1−y(i))x(i)1
, . .
( w1 )
w0=1 , J(w1)
X ( ) y w0 और w1 ( ):
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
w1 -1.5 1.5.
, ( , , ):
plt.subplot(3,1,1)

, , δJ(w)δw1 — :
grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left')

Δw1(w1) (, Δw1 w1 , .. , ):
eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right')

plt.show()

- : ,
- : — «» ( , «» ),
- : — ( ), η [] ( ),
: , 1000 .
, ,
w — - - . w0=1 , w1=0.9 । η=0.001 ( , ) 12:
:
w1 J(w1,w0=1) :
Δw1(w1)
plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u' , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange')

, , ( ), . , , , .
: , , , «» , — , .
- — w1 , —
- , w1
- — : , —
- , —
- , ( ), , ( ) — , —
- ( , — ).
- : — , —
- ? — . .
- . w1 , . , «»/«» . , , . , , , « ». , : w1=0.9 200, , , , 1. , , , . — η । , 200 1. η=0.001 , w1=0.9 200*0.001=0.2 ( -1, -0.2) — .
- J(w1=0.9)=92.43 , 12 (, ) J(w1=0.03)=8.54
- , ,
, . , . , ( , ). η , .
: , , , .
, , , .
η
- η [] — ()
- ,
- «»: , , ,
- , J(w)
- : wk , η , wk
η=0.01

. , . 3- , 3- , , .. , .. . , , [] .
η J(w) η

: , , . , — , , .
:

:

.
η । , , .

, .
:
, ( ) w , , . , , , . , , .
,
, .
, :

— :
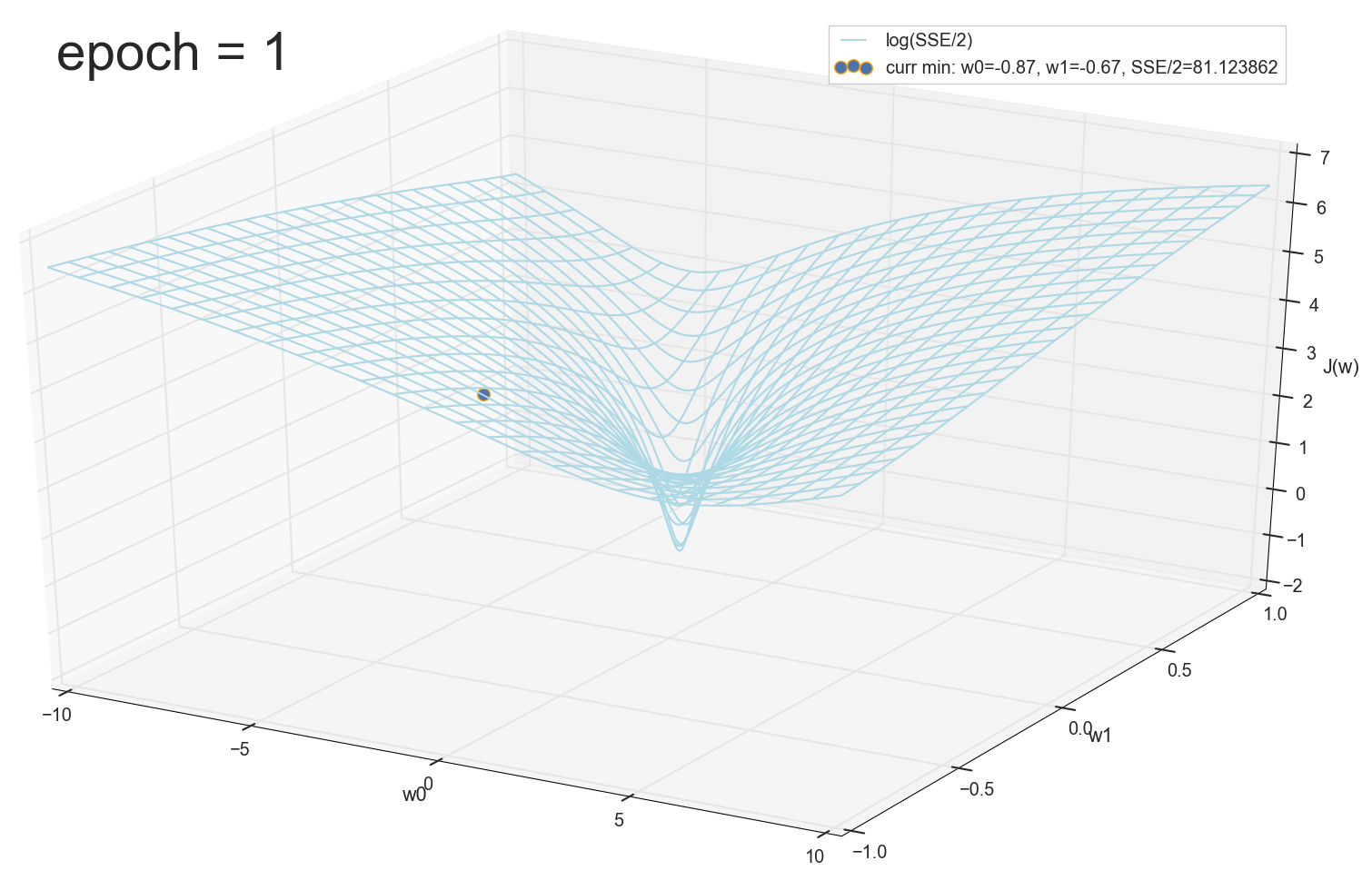
12 — , :

50 :

1767 — , :

, 62000 :

:
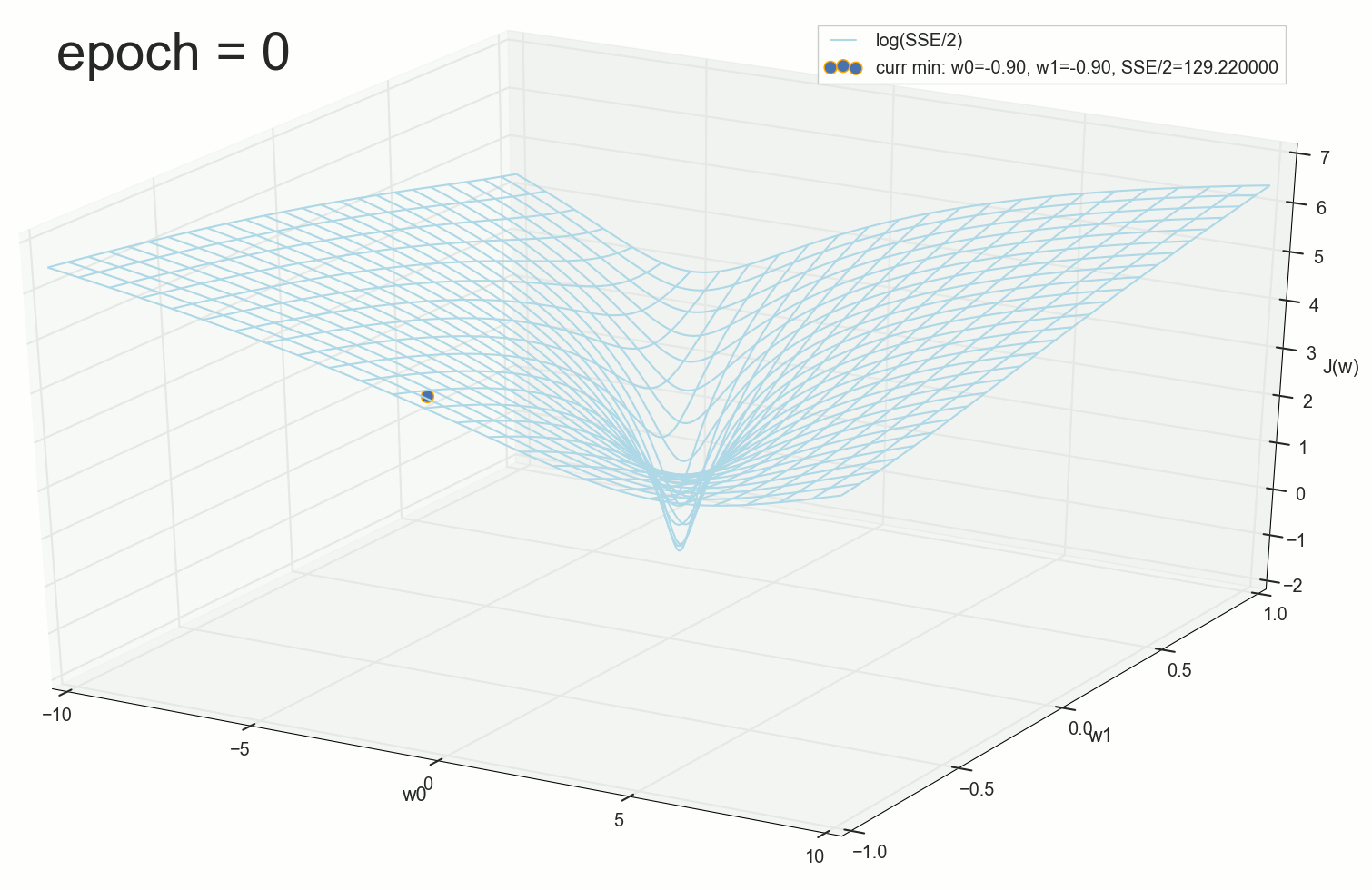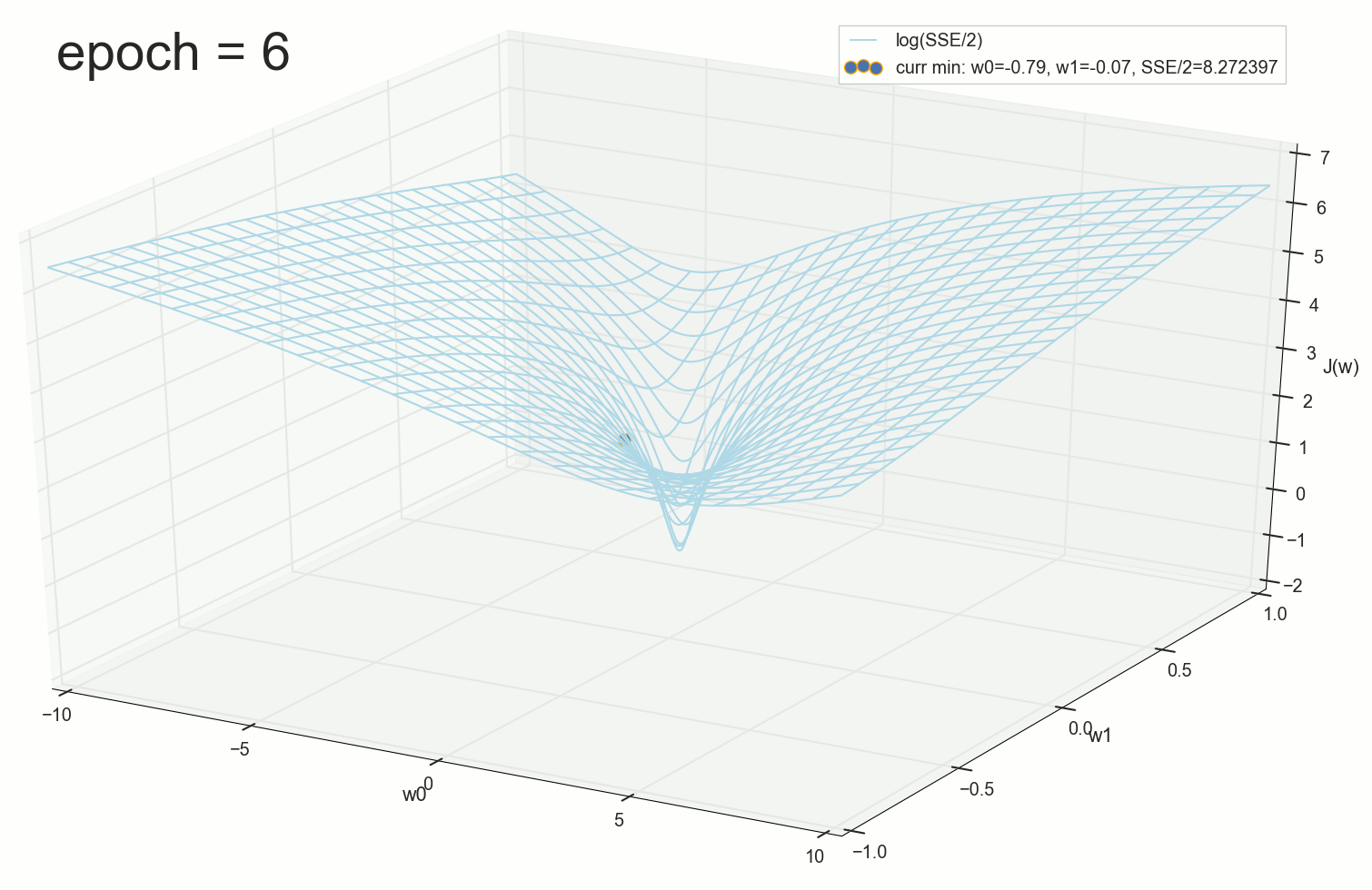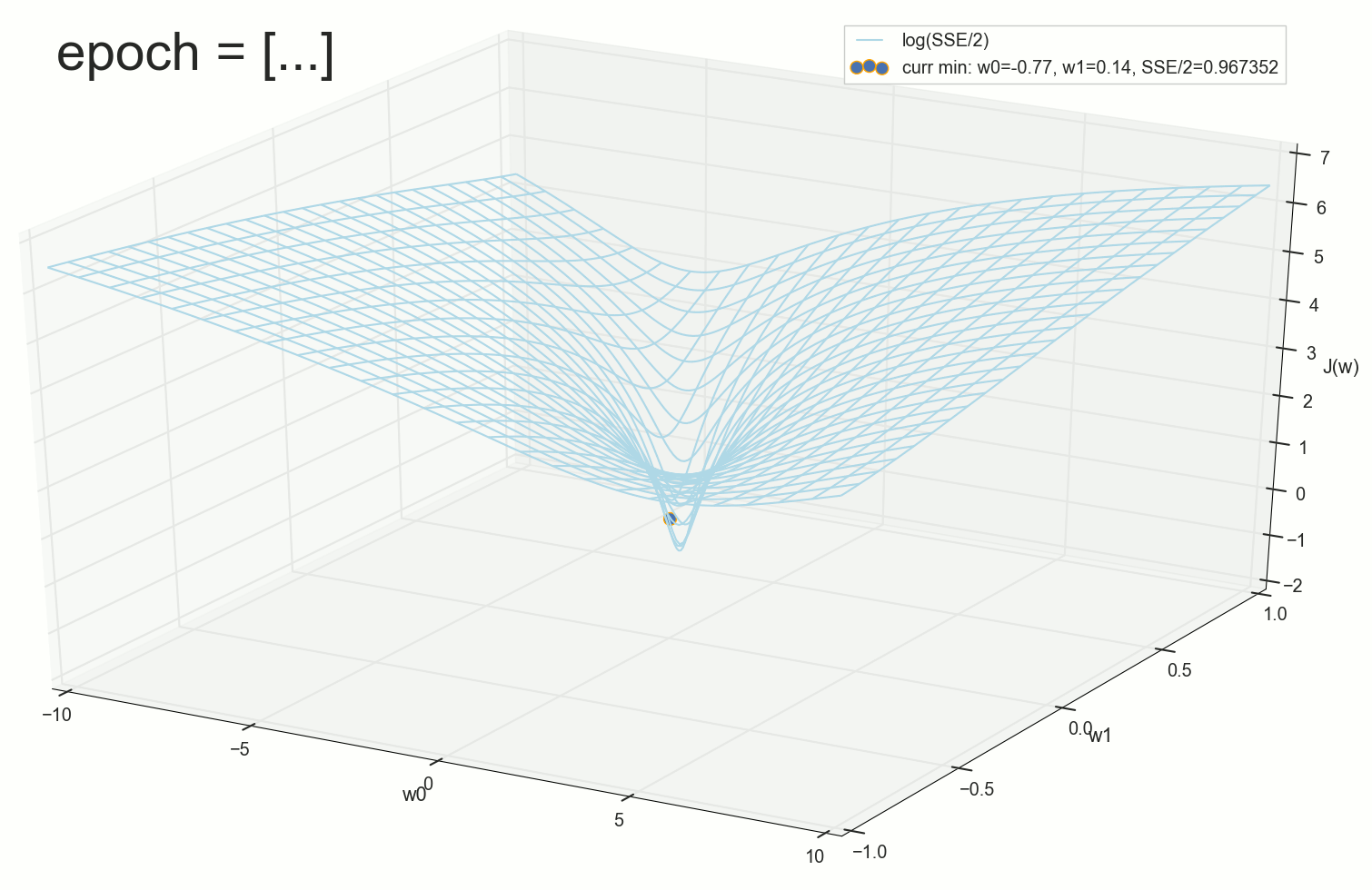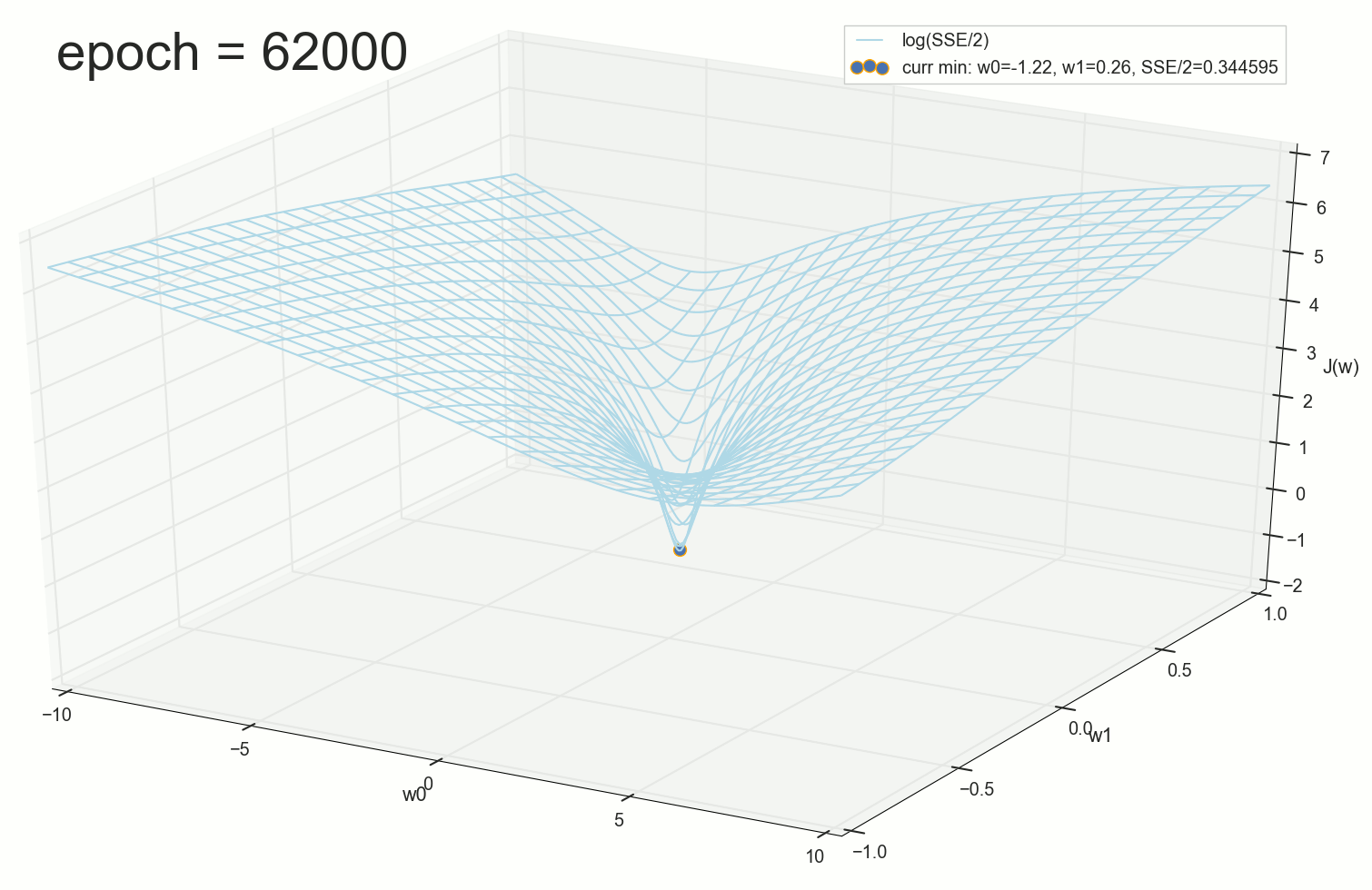
. , : , , . , , , , , , . , , - .
, , - , - : , , , , , — . , , , , , , , — . ?
, . :
, , ( ). : , . , , .
. , .
. , , . , — .

— :

11- : , ; :

12- : , , :

50- : , 12-

1766: . J(w)=0.3456480221 — , , ( J(w)=0.3456478372 : 6- , , )

1767: J(w)=0.34564503 — , ( 6- , ). w0=−1.184831 । w1=0.258455 ( w0 2- : w0=−1.27 । w1=0.26 )

62000: J(w)=0.3445945 — , ( 2- ). :

:
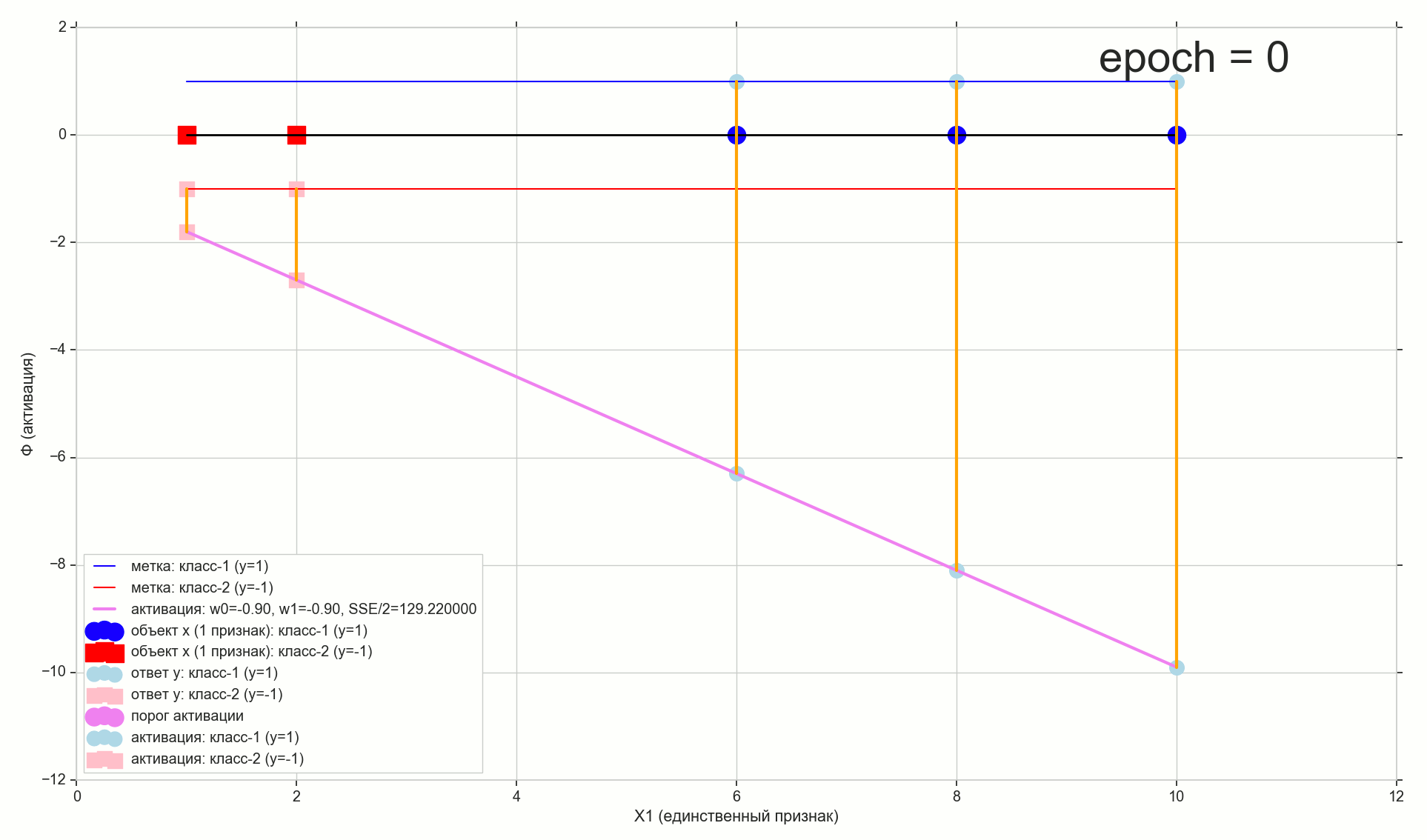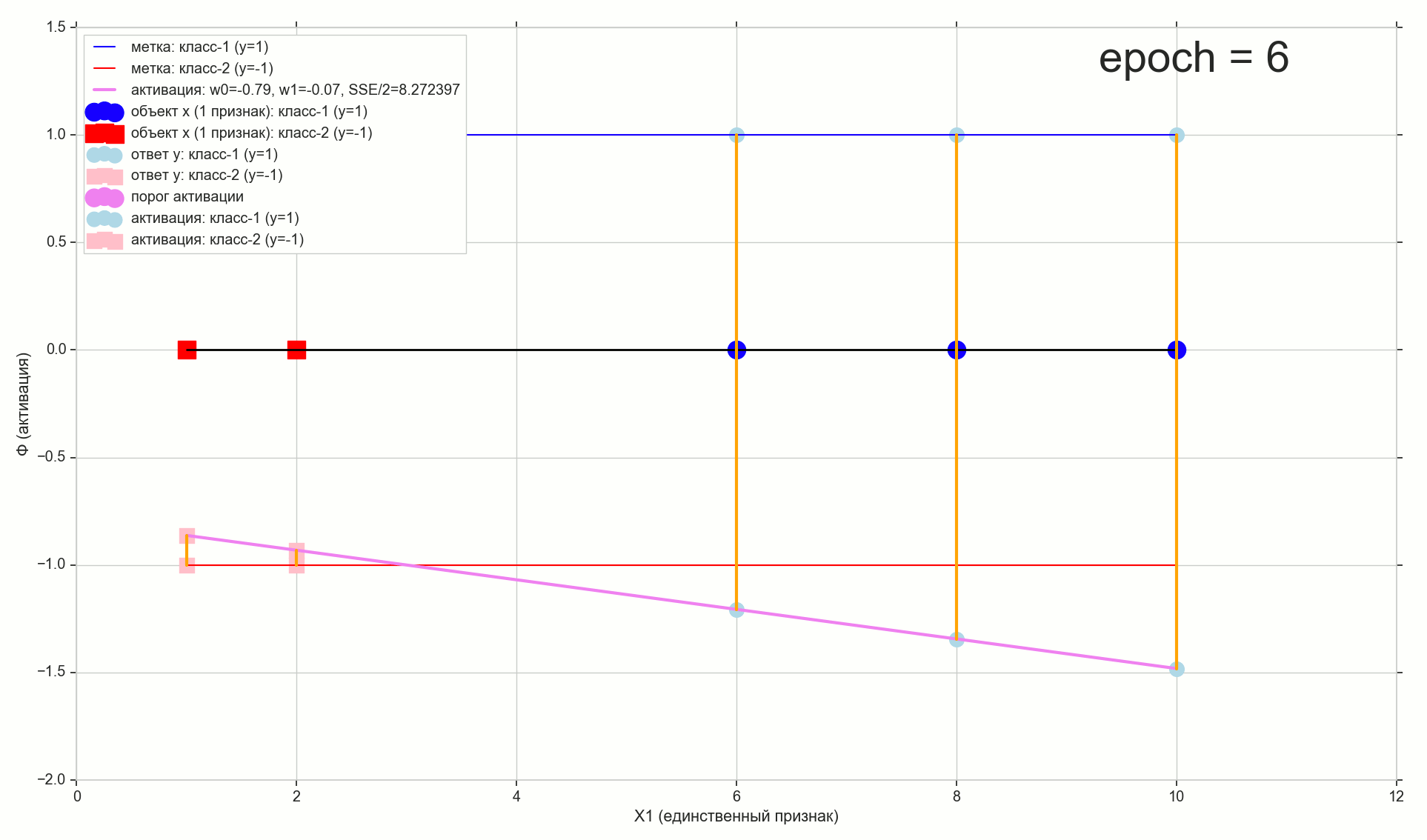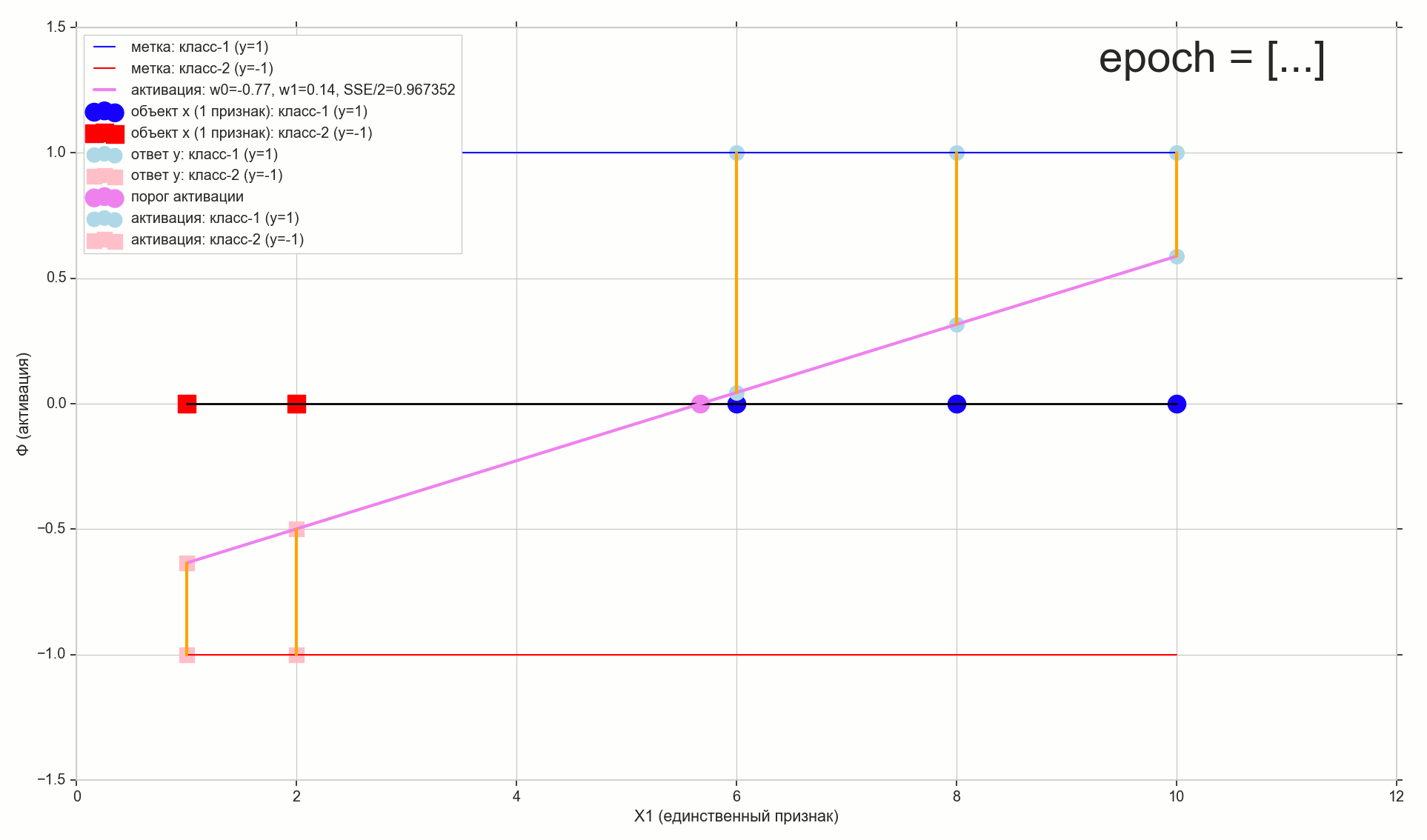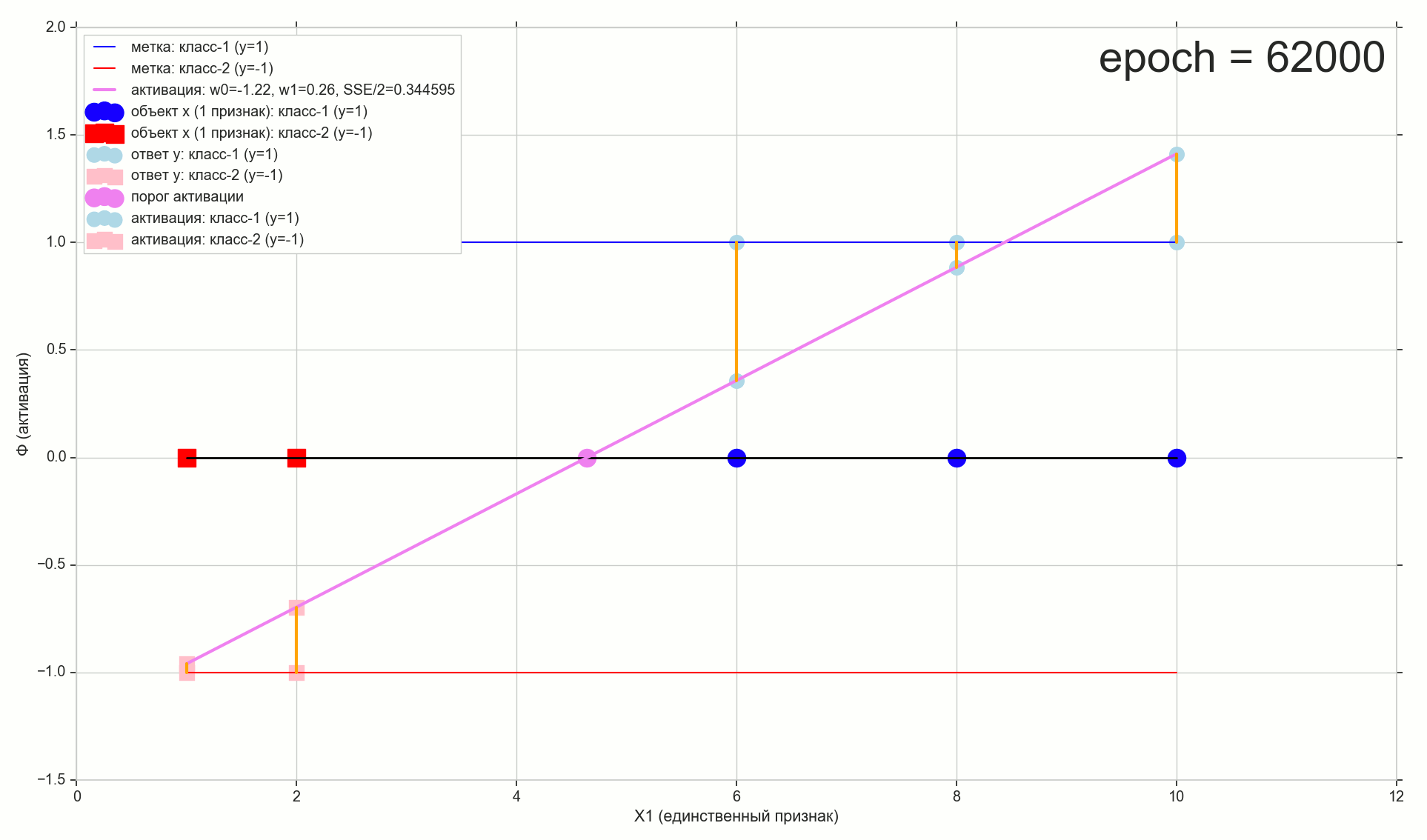
. , , , , .
- η=0.001 , 10-12- ( )
- , , , (1767)
- — 60
- —
— ( , 1767): w0=−1.184831 । w1=0.258455 ।
.
t(1)=(t(1)1)=(1.4) ( , t(i) — ). , .. , , ˆy=−1 , .. .
SUM=w0+w1∗t(1)1=−1.18+0.26∗1.4=−0.816
Φ(SUM)=SUM=−0.816
Φ(SUM)=−0.816<0⟹ˆy=−1
, .
: t(2)=(t(2)1)=(7)
Φ(SUM)=SUM=−1.18+0.26∗7=0.64⩾0⟹ˆy=1
ˆy=1 , .. . .
, ( «» ) 12 . , !
(m=2)
, , , . . , , .
— ( ). 2- .
- x=(x1,x2) ( , , )
- y={−1,1} ( , )
plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1')

, .
Φ(x,w)=w0+w1x1+w2x2
, — , , 1- , 3-:

:

:

— :

() Φ(w)=0 (-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).
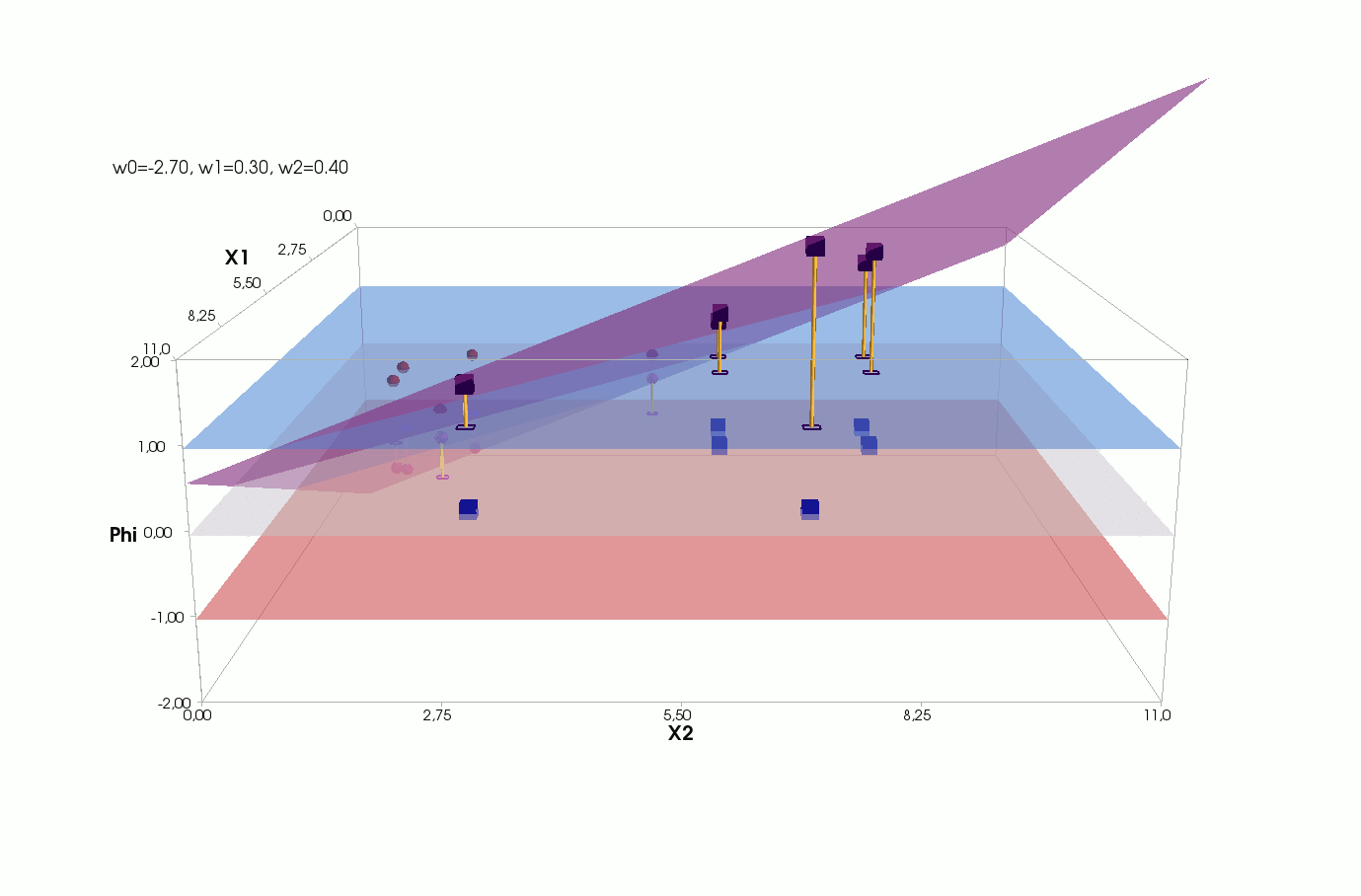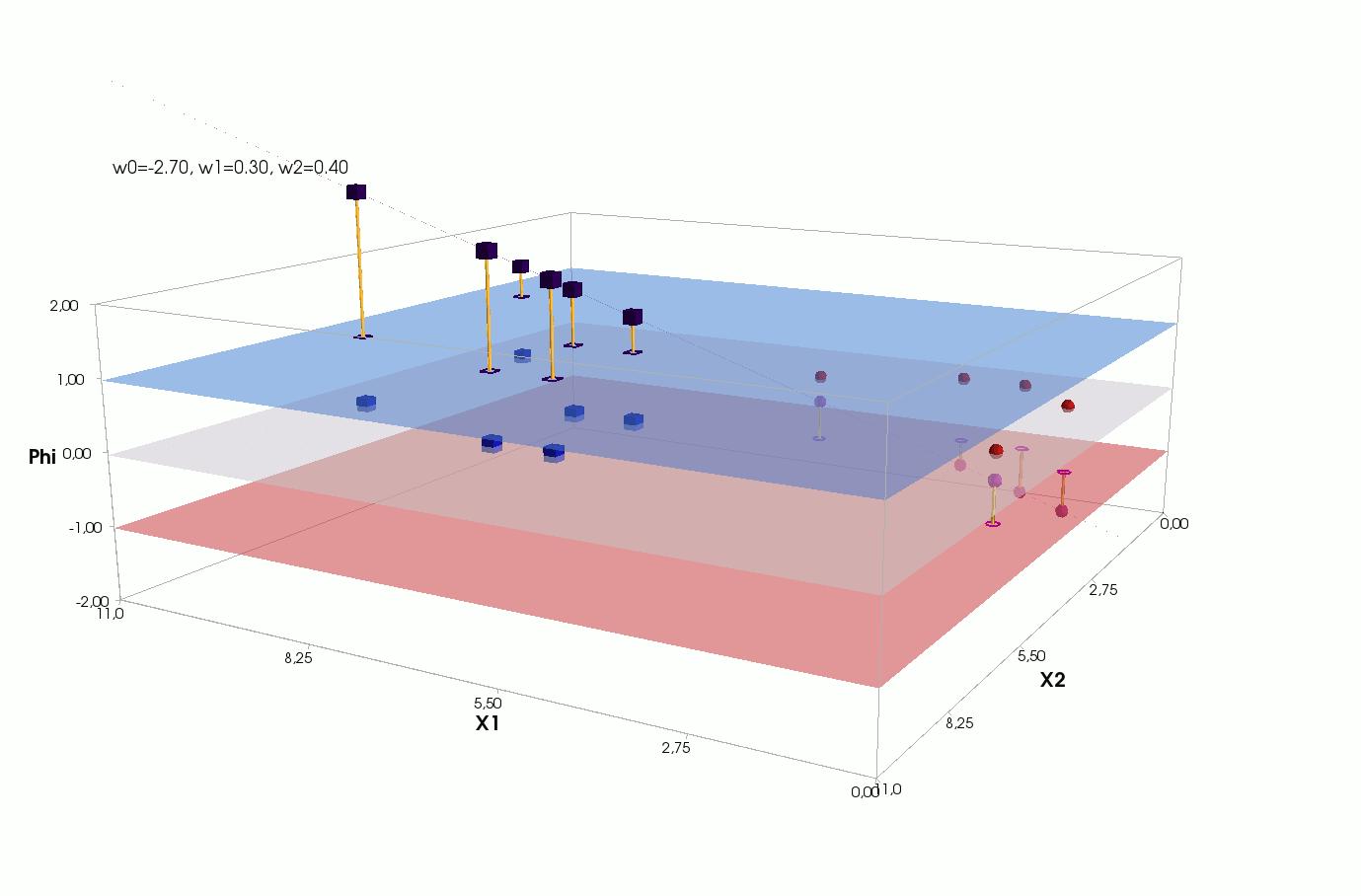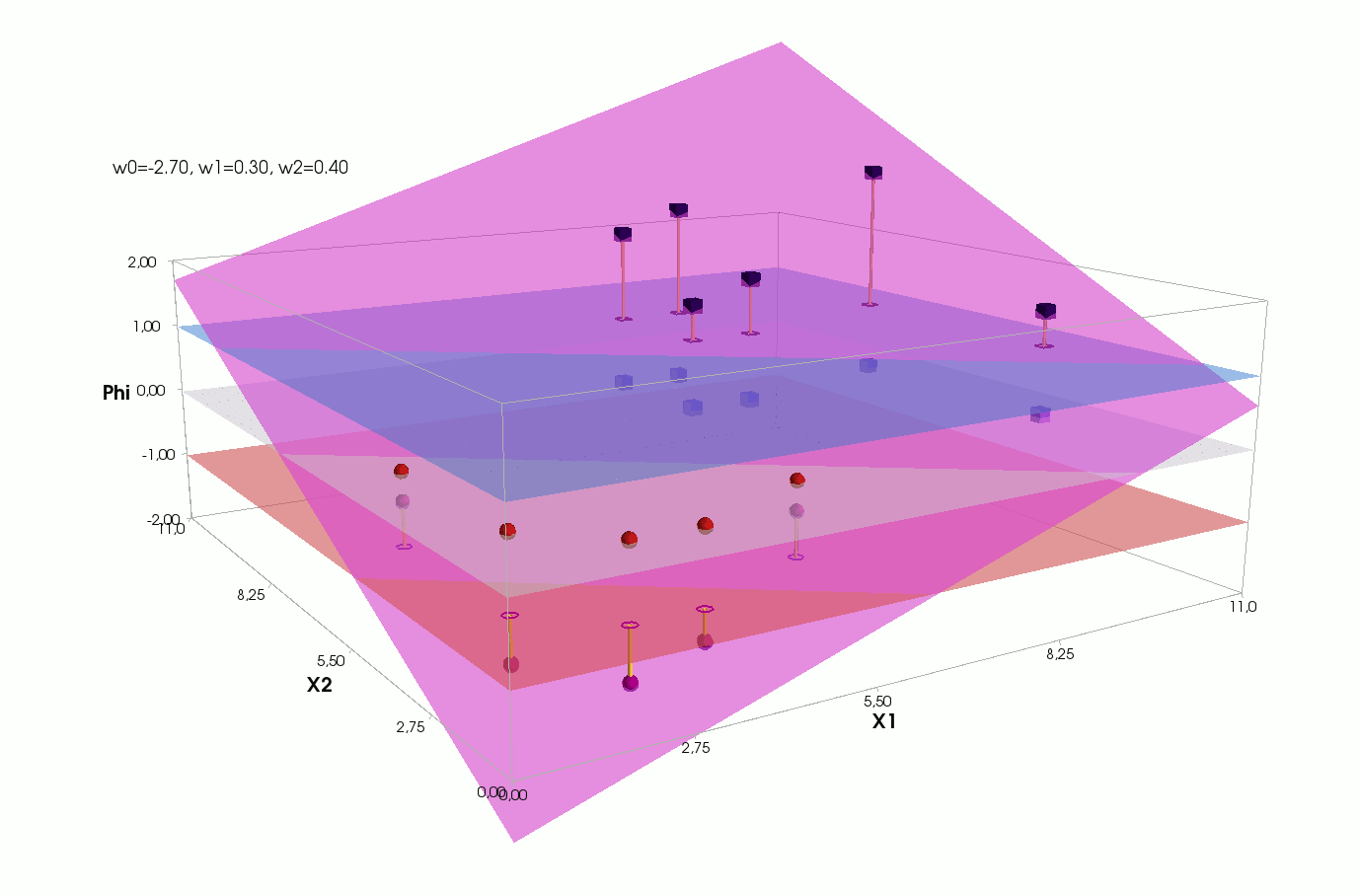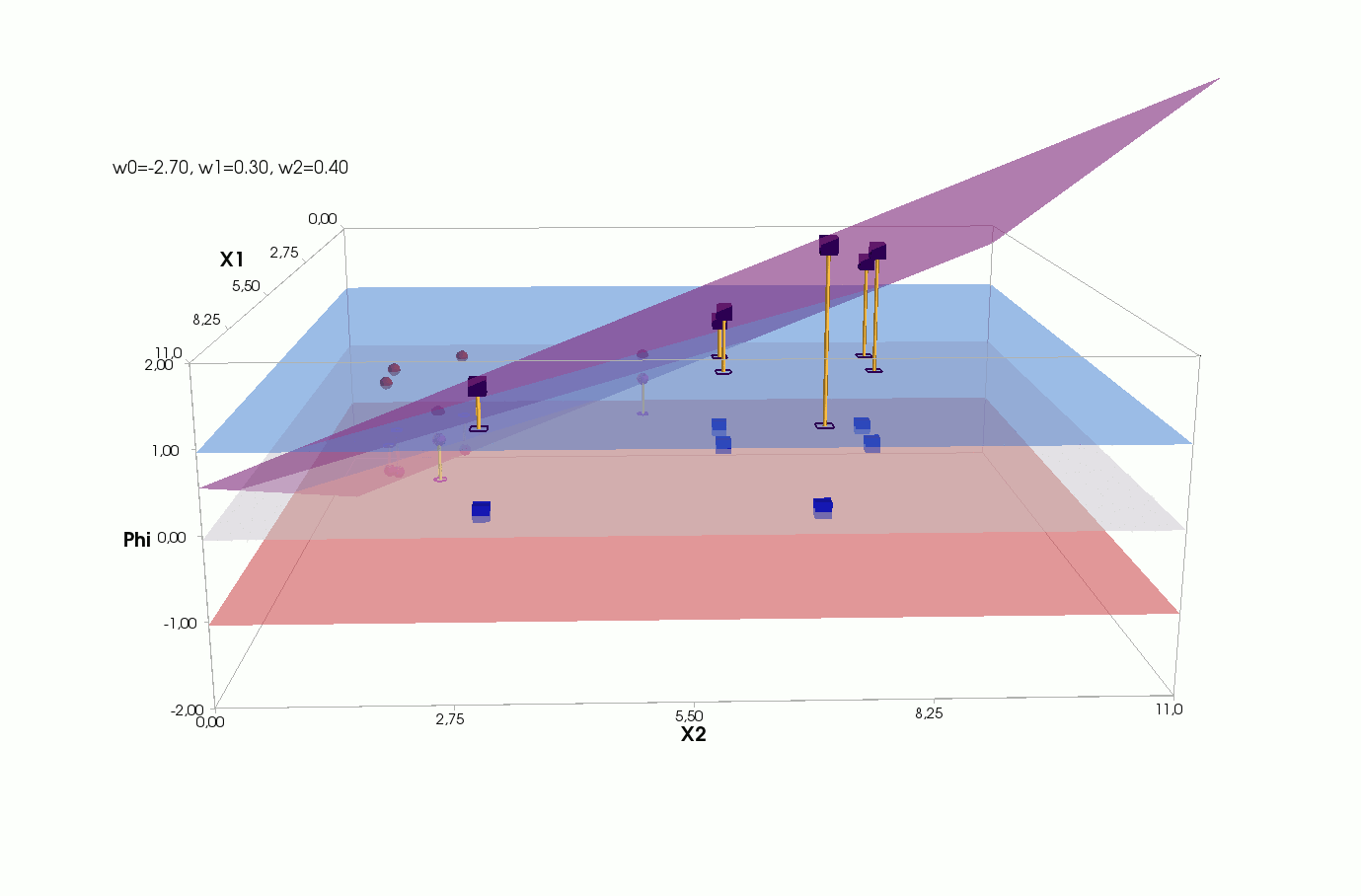
J(w)=12SSE=12n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))2
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .
2- . , , 1- 2-.
∇J(w)=(∂J(w)∂w0,∂J(w)∂w1,∂J(w)∂w1),w=(w0,w1,w2)
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
∂J(w)∂w2=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
Δw2=−η∂J(w)∂w2=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
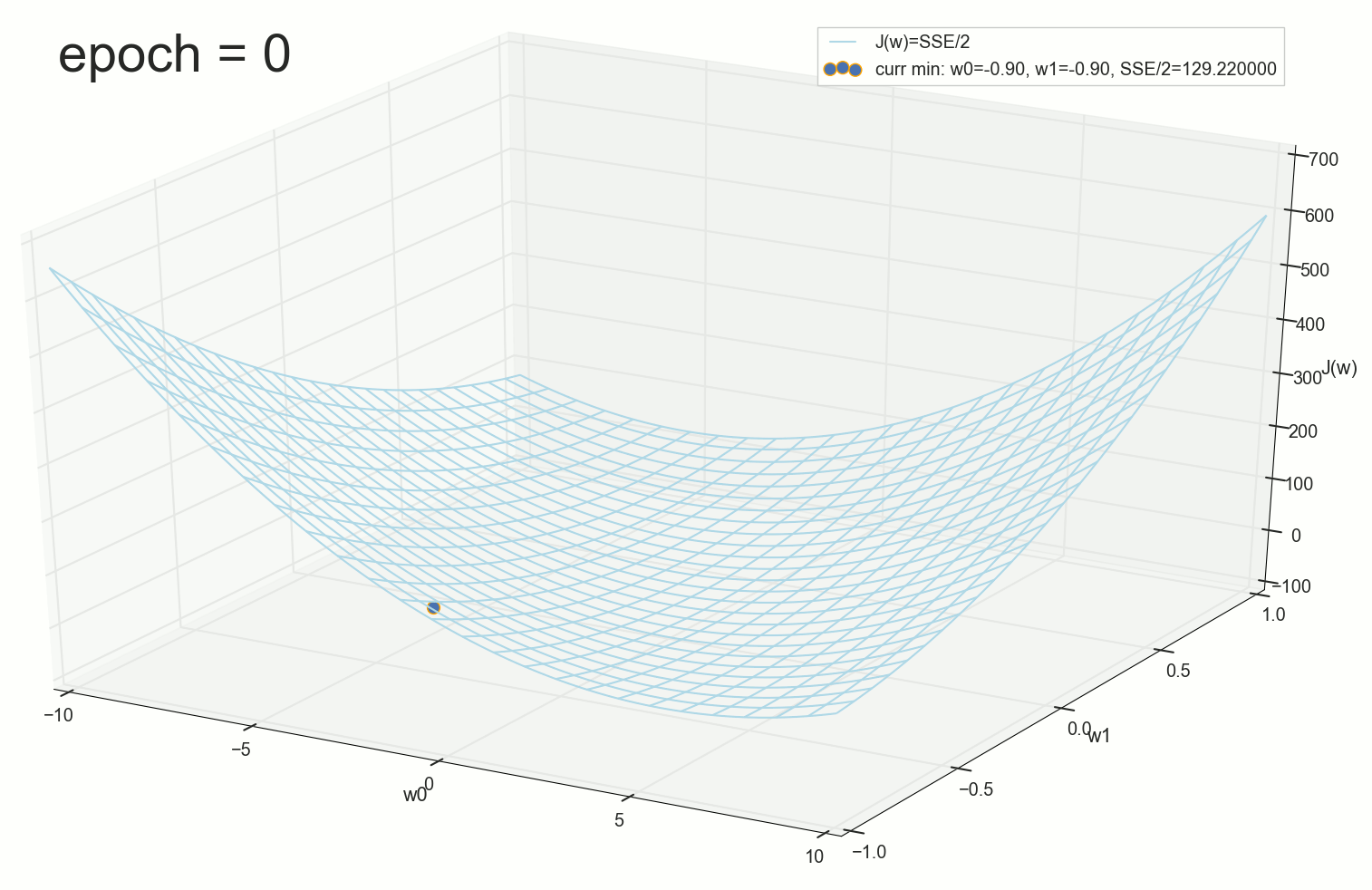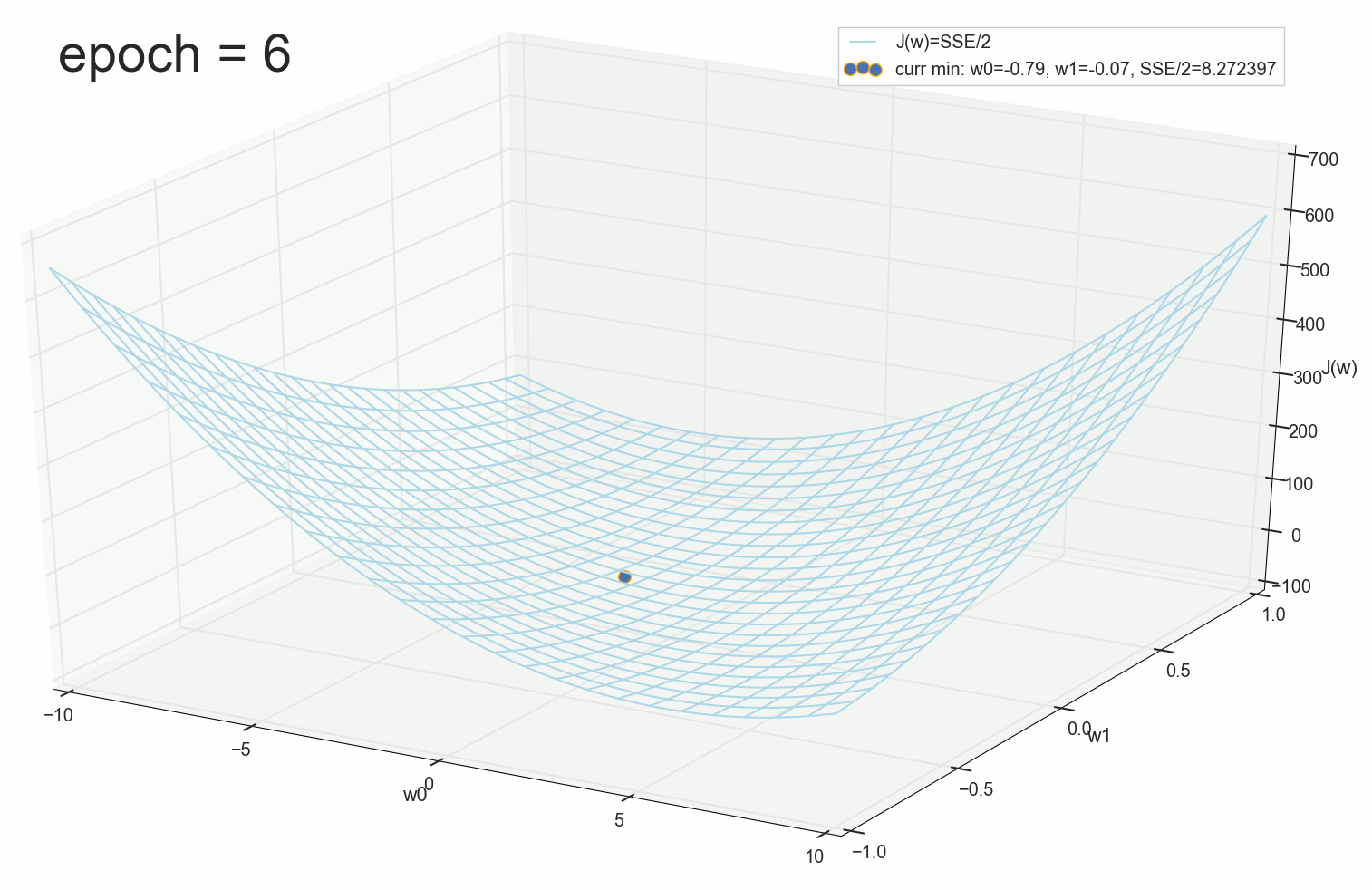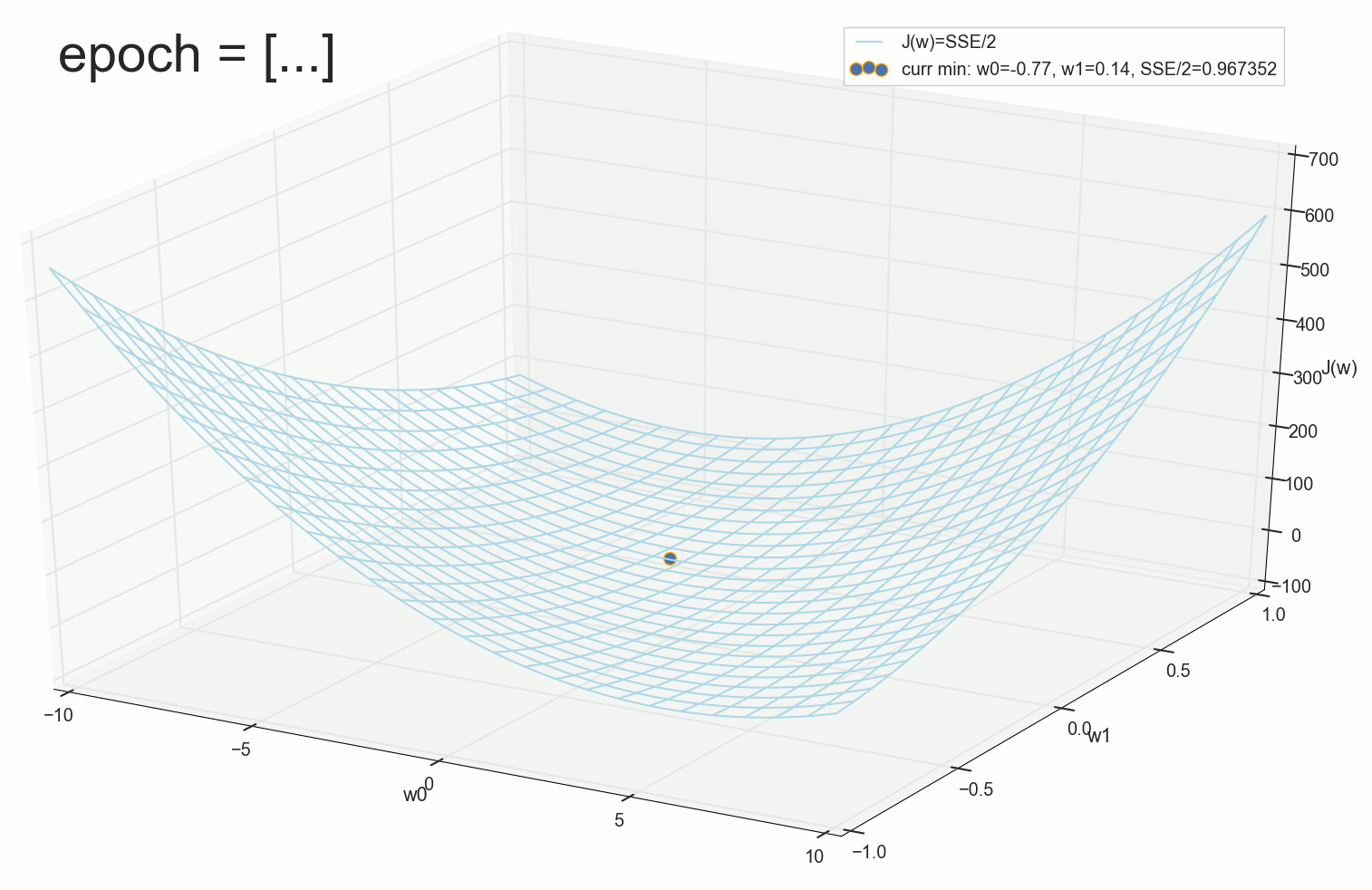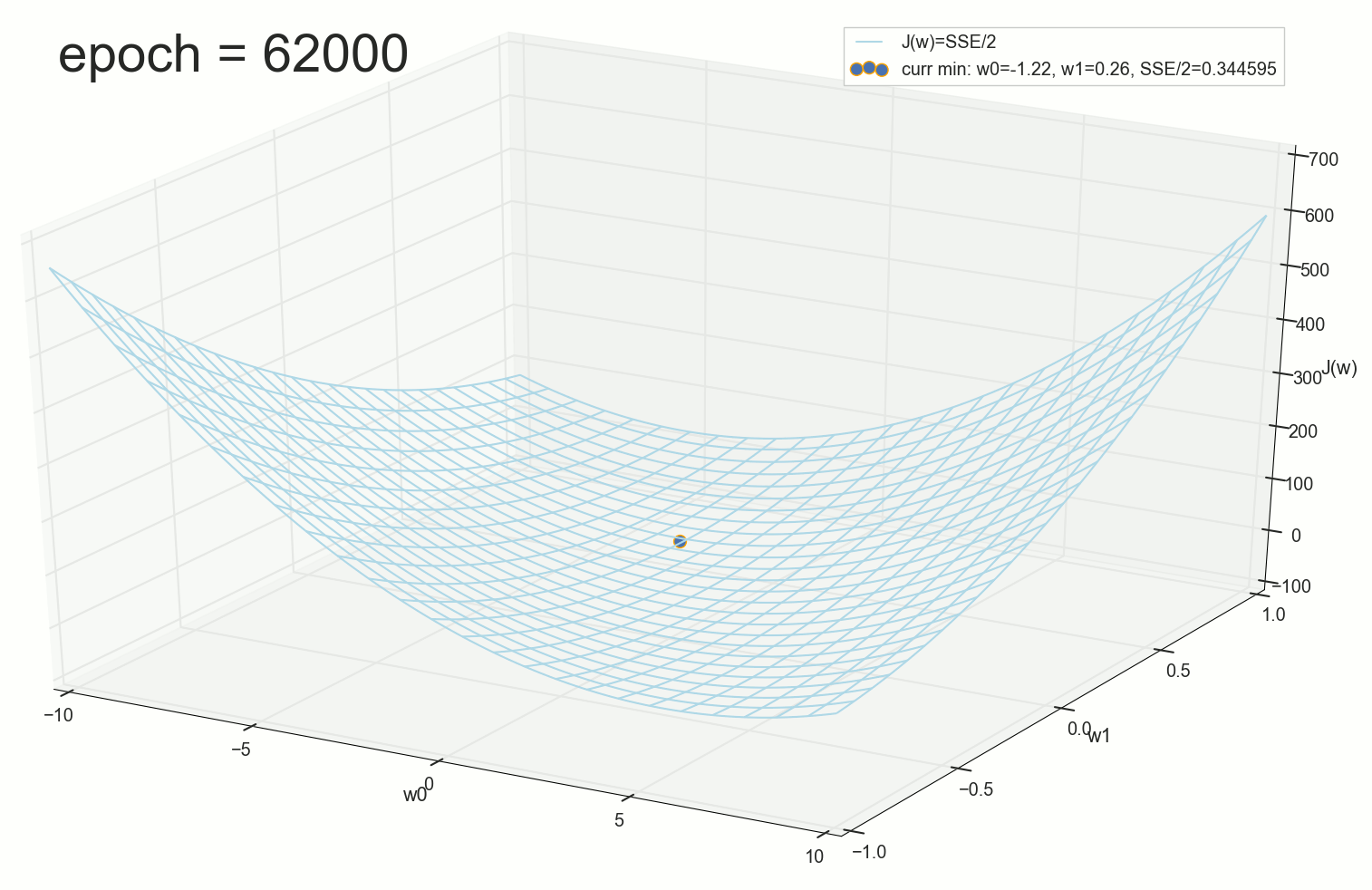
3- ( 3- ), η=0.001 , w0=−0.9 । w1=−0.9 । w2=−0.9 ।
— , , :


:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , w0 ।
कोड
matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .
import numpy from mayavi import mlab
, Mayavi , . , , , .
Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :
env QT_API=pyqt python3 gradient-2d.py
— J(w)
def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum()
12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .
निष्कर्ष
ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .
«Python » ( scikit-learn) , - .
ADALINE .
-, — , : , , , .
-, () , , , ( , , y ) — , scikit-learn.
PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .