ब्राउज़र में कॉस्मोलॉजी और क्वांटम में उतार-चढ़ाव

आइए हम एक विशुद्ध रूप से व्यावहारिक लक्ष्य निर्धारित करें - एक अंतहीन कैनवास को लागू करने और इसे माउस के साथ स्केल करने की क्षमता के साथ। इस तरह के एक कैनवास, उदाहरण के लिए, एक चित्रमय संपादक में एक चलती समन्वय प्रणाली के रूप में काम कर सकता है। हमारे विचार का कार्यान्वयन इतना जटिल नहीं है, लेकिन इसे समझने की प्रक्रिया मौलिक गणितीय और भौतिक वस्तुओं के साथ जुड़ी हुई है, जिसे हम विकसित होने पर विचार करेंगे।

समस्या का बयान

अपने कैनवास से, हम केवल दो कार्य करना चाहते हैं: माउस और माउस की गति, साथ ही स्क्रॉल करते समय ज़ूम करना। हमारे परिवर्तनों के क्षेत्र एक ब्राउज़र का चयन करेंगे। हथियार, इस मामले में, चुनने के लिए नहीं है।

स्टेट मशीन

इस तरह की प्रणालियों के व्यवहार को उनके राज्यों के बीच संक्रमण से आसानी से वर्णित किया जाता है, अर्थात्। राज्य मशीन $$$\ delta: S \ rightarrow S$ जहाँ $$$\ डेल्टा$ - राज्यों के बीच संक्रमण समारोह, अपने आप में कई राज्यों को प्रदर्शित करता है।

हमारे मामले में, राज्य आरेख इस तरह दिखता है:

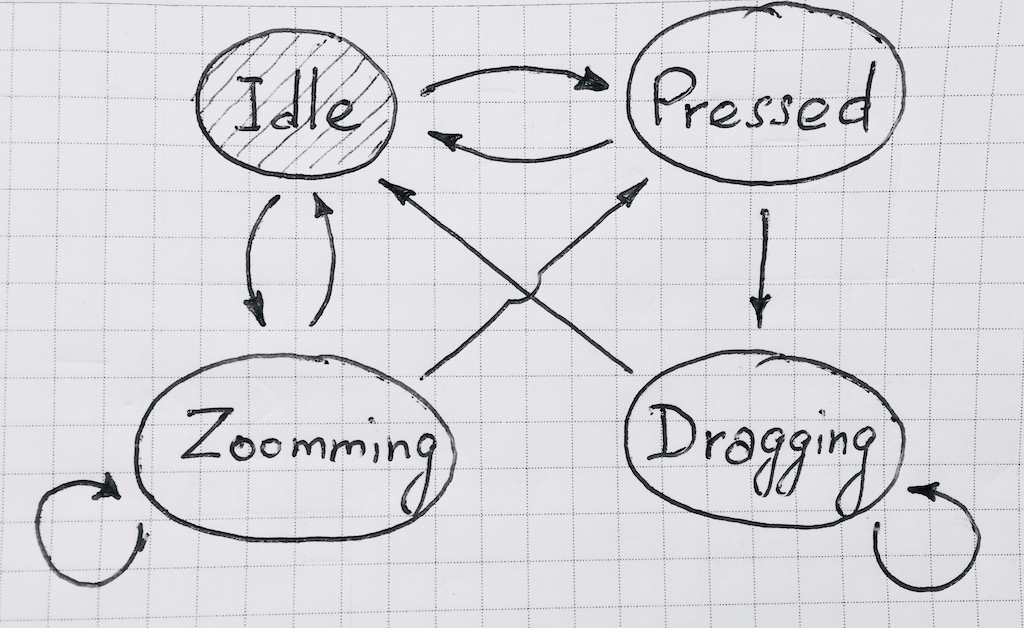
संक्रमण फ़ंक्शन को लागू करते समय, यह घटना-निर्भर बनाने के लिए सुविधाजनक है। यह भविष्य में स्पष्ट हो जाएगा। इसी तरह, मशीन की स्थिति में परिवर्तन की सदस्यता लेने में सक्षम होना सुविधाजनक है।

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; }; 

हम थोड़ी देर के लिए कार्यान्वयन को स्थगित कर देंगे और हमारे कार्य को पूरा करने वाले ज्यामितीय परिवर्तनों को उठाएंगे।

अपडेट

यदि कैनवास को स्थानांतरित करने के साथ मुद्दा इतना स्पष्ट है कि हम उस पर ध्यान नहीं देंगे, तो स्ट्रेचिंग पर अधिक विस्तार से विचार किया जाना चाहिए। सबसे पहले, हमें इसकी आवश्यकता है कि खिंचाव एक एकल बिंदु स्थिर छोड़ देता है - माउस कर्सर। प्रतिवर्ती स्थिति को भी संतुष्ट होना चाहिए, अर्थात उपयोगकर्ता क्रियाओं के रिवर्स अनुक्रम को कैनवास को उसकी मूल स्थिति में लाना चाहिए। इसके लिए क्या ज्यामिति उपयुक्त है? हम अपने आप में विमान के बिंदु परिवर्तन के कुछ समूह पर विचार करेंगे $$$\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , जो आम तौर पर नए चर की शुरूआत द्वारा व्यक्त किया जाता है $$$x ', y'$ पुराने कार्यों के रूप में परिभाषित:

गणित में द्वैत के सिद्धांत के अनुसार, ऐसे परिवर्तनों को समन्वय प्रणाली में बदलाव के साथ-साथ बाद में तय किए गए स्थान के साथ ही एक परिवर्तन के रूप में व्याख्या की जा सकती है। दूसरी व्याख्या हमारे उद्देश्यों के लिए सुविधाजनक है।

ज्यामिति की एक आधुनिक समझ पूर्वजों की समझ से अलग है। एफ। क्लेन के अनुसार, - ज्यामिति कुछ परिवर्तन समूहों के संबंध में आक्रमणकारियों का अध्ययन करती है। तो, आंदोलनों के एक समूह में $$$डी$ अपरिवर्तनीय दो बिंदुओं के बीच की दूरी है $$$d ((x_ {1}, y_ {1}), (x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ / 1) } - y_ {2}) ^ 2}$ । इसमें समानांतर हाइफ़नेशन शामिल है $$$T _ {(x, y)}$ वेक्टर पर $$$(x, y)$ रोटेशन $$$R _ {\ phi}$ एक कोण पर उत्पत्ति के सापेक्ष $$$\ phi$ और प्रतिबिंब $$$M_ {l}$ किसी लाइन के सापेक्ष $$$ल$ । इस तरह के आंदोलनों को प्राथमिक कहा जाता है। दो आंदोलनों की संरचना हमारे समूह की है और कभी-कभी प्राथमिक रूप से नीचे आती है। इसलिए, उदाहरण के लिए, सीधी रेखाओं के सापेक्ष दो लगातार दर्पण प्रतिबिंब $$$ल$ और $$$एन$ एक निश्चित कोण पर एक निश्चित केंद्र के चारों ओर एक चक्कर दें (अपने लिए जांचें):

निश्चित रूप से आपने पहले से ही अनुमान लगाया था कि इस तरह के आंदोलनों का एक समूह $$$डी$ यूक्लिडियन ज्यामिति बनाता है। हालांकि, स्ट्रेचिंग दो बिंदुओं के बीच की दूरी को संरक्षित नहीं करता है, लेकिन उनके संबंध। इसलिए, आंदोलनों का एक समूह, हालांकि इसे हमारी योजना में शामिल किया जाना चाहिए, लेकिन केवल एक उपसमूह के रूप में।

ज्यामिति जो हमें सूट करती है, एक खिंचाव समूह पर आधारित है $$$पी$ जिसमें, उपरोक्त आंदोलनों के अलावा, होमोसेटी को जोड़ा जाता है $$$S_ {k}$ गुणांक द्वारा $$$k$ ।

खैर, आखिरी। रिवर्स तत्व समूह में मौजूद होना चाहिए। और इसलिए एक तटस्थ है $$$ई$ (या एकल) जो कुछ भी नहीं बदलता है। उदाहरण के लिए

अब हम समूह-सैद्धांतिक भाषा में, माउस कर्सर बिंदु को छोड़ते हुए, स्ट्रेचिंग का वर्णन कर सकते हैं:

आंदोलन को व्यक्त करें $$$T _ {(x, y)}$ और $$$S_ {k}$ और कोड में एक वेक्टर के कार्यों के रूप में उनकी रचना

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z); 

ध्यान दें कि अब तक हम निरंतर परिवर्तनों के समूह के साथ काम कर रहे हैं। हालांकि, कंप्यूटर निरंतर मात्रा के साथ काम नहीं करता है, इसलिए, पॉइंकेयर का पालन करते हुए, हम एक सतत समूह को असतत संचालन के अनंत समूह के रूप में समझेंगे। अब जब हमने ज्यामिति का पता लगा लिया है, तो हमें गति की सापेक्षता की ओर मुड़ जाना चाहिए।

कोस्मॉलॉजी ऑफ कैनवस। मॉड्यूलर ग्रिड

एक सदी से, मानवता के रूप में, ब्रह्मांड का विस्तार ज्ञात है। दूर की वस्तुओं - आकाशगंगाओं और क्वासरों का अवलोकन करते हुए, हम विद्युत चुम्बकीय स्पेक्ट्रम के बदलाव को लंबी तरंगों की ओर पंजीकृत करते हैं - तथाकथित ब्रह्माण्ड संबंधी रेडशिफ्ट। कोई भी माप पर्यवेक्षक, अवलोकन और माप के साधनों को जोड़ता है जिसके संबंध में हम अपना माप करते हैं। उपकरणों को मापने के बिना, प्रकृति में अपरिवर्तनीय संबंधों को स्थापित करना असंभव है, अर्थात, ब्रह्मांड की ज्यामिति को निर्धारित करने के लिए। हालांकि, रेखागणित बिना किसी अवलोकन के अपना अर्थ खो देता है। इसलिए हमारे कार्य में आकाशगंगाओं जैसी भूमिकाओं का होना अच्छा है, जिसके प्रकाश के संबंध में हम अपने कैनवास की गति के सापेक्षता का निर्धारण कर सकते हैं। इस तरह की संरचना एक आवधिक जाली हो सकती है, जो प्रत्येक बार द्विगुणित होती है जब अंतरिक्ष दो बार विस्तारित होता है।

चूंकि जाली आवधिक है, इसलिए मॉड्यूलर बीजगणित को अपनाना सुविधाजनक है। इस प्रकार, हम एक समूह के रूप में कार्य करेंगे $$$पी$ टोरस पर भी $$$T ^ 2 = S ^ 1 \ _ S ^ 1$ । चूंकि मॉनिटर स्क्रीन एक निरंतर विमान नहीं है, लेकिन एक पूर्णांक जाली है $$$\ mathbb {Z} ^ 2$ (हम अब उपेक्षा करते हैं कि यह परिमित है), फिर समूह की कार्रवाई $$$पी$ पूर्णांक टोरस पर विचार किया जाना चाहिए $$$\ mathbb {Z} _ {p} ^ 2$ जहाँ $$$पी$ - चौकोर के किनारे का आकार $$$पी \ _ पी $$ :

इस प्रकार, एक बार और मूल के पास अपने टोरस को ठीक करने के लिए, हम इस पर सभी आगे की गणना करेंगे। फिर मानक कैनवास पुस्तकालय विधियों का उपयोग करके इसे प्रचारित करें। यहाँ एक पिक्सेल चाल की तरह दिखता है:

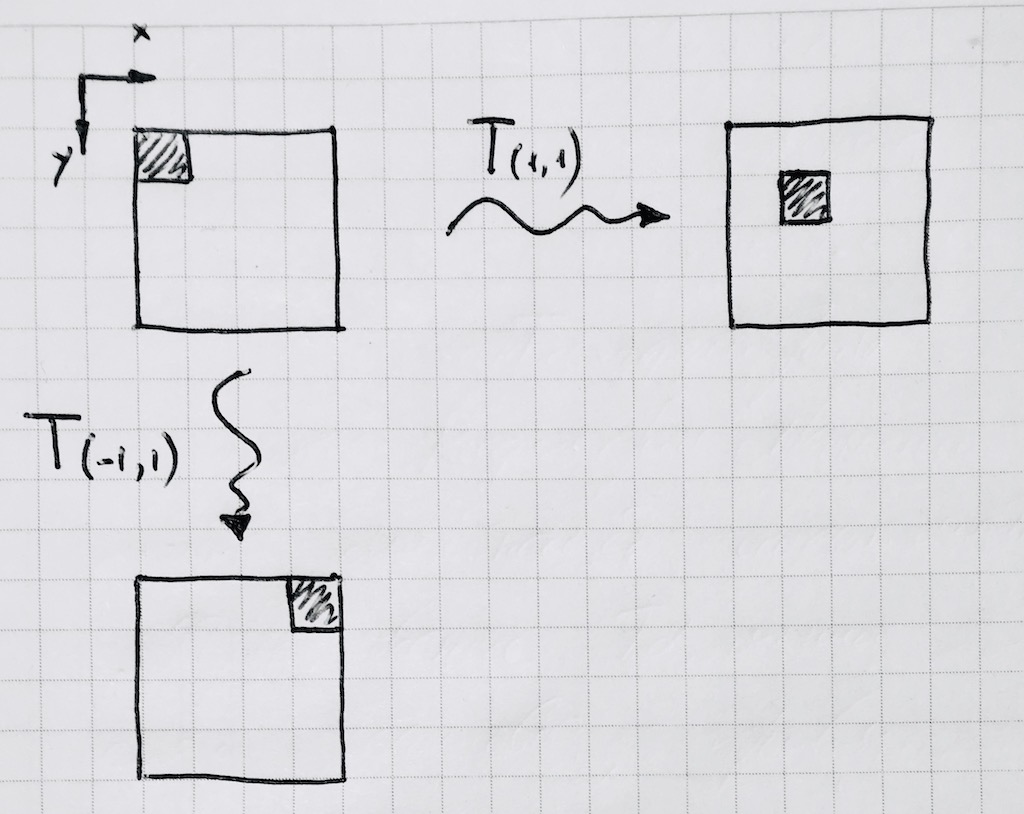
जाहिर है, मॉड्यूल एक्स% पी लेने का मानक संचालन हमारे लिए उपयुक्त नहीं है, क्योंकि यह तर्क के नकारात्मक मूल्यों को नकारात्मक लोगों में अनुवाद करता है, लेकिन पूर्णांक की धार पर कोई भी नहीं है। अपना कार्य लिखें $$$x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p; 

अब अंतिम राज्य मशीन पर वापस और

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } } 

अगला, एक संक्रमण योजना को परिभाषित करें, एक कैनवास बनाएं और

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm); 

फिर आपको रेंडरिंग फ़ंक्शन का निर्धारण करना चाहिए, आवश्यक प्रारंभिक मान सेट करें और राज्य के परिवर्तन की सदस्यता लें। कोड के सबसे दिलचस्प हिस्से पर विचार करें:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); }); 

सबसे पहले, हम गुणांक k द्वारा विस्तार नहीं करते हैं, लेकिन कुछ अनुपात nk / k द्वारा। यह इस तथ्य के कारण है कि एक निश्चित बिंदु पर हमारी मैपिंग का चरण $$$(ए, बी)$ के रूप में व्यक्त किया

या, प्रारंभिक मूल्यों के सापेक्ष $$$x_ {1}, y_ {1}$

जाहिर है उत्पाद $$$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ वहाँ पुनरावृत्ति कदम का एक nonlinear कार्य है और या तो बहुत जल्दी शून्य में परिवर्तित हो जाता है, या छोटे प्रारंभिक विचलन के साथ अनंत तक भाग जाता है।

हम चर जी का परिचय देते हैं, जो हमारे कैनवास को दोगुना करने का एक उपाय है। जाहिर है, यह एक निश्चित अंतराल पर निरंतर मूल्य लेता है। रैखिकता प्राप्त करने के लिए $$$k_ {i} ^ *$ हम सजातीय प्रतिस्थापन का उपयोग करते हैं

फिर पहले और अंतिम को छोड़कर, सभी सदस्यों के काम कम हो जाएंगे:

इसके अलावा, चरण जंप जी विस्तार दर को इस तरह से कम कर देता है कि भग्न संरचना जो हमारे सामने हमेशा लीन हो जाती है। इस प्रकार, हम ब्रह्माण्ड के विस्तार के हबल शक्ति कानून का एक अनुमानित रूपांतर प्राप्त करते हैं।

यह हमारे मॉडल की सटीकता की सीमाओं को समझने के लिए बनी हुई है।

क्वांटम उतार-चढ़ाव। 2-एडिक नंबर फ़ील्ड

माप की प्रक्रिया को समझने से वास्तविक संख्या की अवधारणा पैदा हुई। हाइजेनबर्ग का अनिश्चितता सिद्धांत इसकी सीमाओं की ओर इशारा करता है। एक आधुनिक कंप्यूटर वास्तविक संख्याओं के साथ काम नहीं करता है, लेकिन मशीन शब्दों के साथ, जिसकी लंबाई प्रोसेसर की क्षमता से निर्धारित होती है। मशीन शब्द 2-एडिक संख्याओं का एक क्षेत्र बनाते हैं $$$\ mathbb {Q_ {2}}$ और के रूप में चिह्नित कर रहे हैं $$$\ mathbb {F_ {2} ^ {n}}$ जहाँ $$$एन$ - शब्द की लंबाई। इस मामले में माप प्रक्रिया को गणना प्रक्रिया से बदल दिया जाता है और गैर-आर्किमिडीयन मीट्रिक से संबद्ध किया जाता है:

इस प्रकार, हमारे मॉडल में गणना की सीमा है। IEEE_754 मानक में सीमाएँ वर्णित हैं। कुछ बिंदु पर शुरू, हमारा आधार आकार सटीकता की सीमा से आगे बढ़ जाएगा और मॉड्यूल लेने का संचालन छद्म-यादृच्छिक अनुक्रम जैसी दिखने वाली त्रुटियों को उत्पन्न करना शुरू कर देगा। यह केवल लाइन हटाकर सत्यापित किया जाता है

 if (g < min || g > max) return; 

हमारे मामले में अंतिम सीमा की गणना अर्ध-अनुभवजन्य विधि द्वारा की जाती है, क्योंकि हम कई मापदंडों के साथ काम करते हैं।

निष्कर्ष

इस प्रकार, पहली नज़र में दूर से प्रतीत होता है, सिद्धांत ब्राउज़र में कैनवास पर जुड़े हुए हैं। कार्रवाई, माप और गणना की अवधारणाएं एक-दूसरे के साथ निकटता से संबंधित हैं। उनके संयोजन का मुद्दा अभी भी हल नहीं हुआ है।