जटिल संख्या के साथ खेलना

नमस्ते!

एक और निबंध। इस बार चलो जटिल संख्याओं के साथ खेलते हैं, सूत्र और उनके दृश्य के साथ।

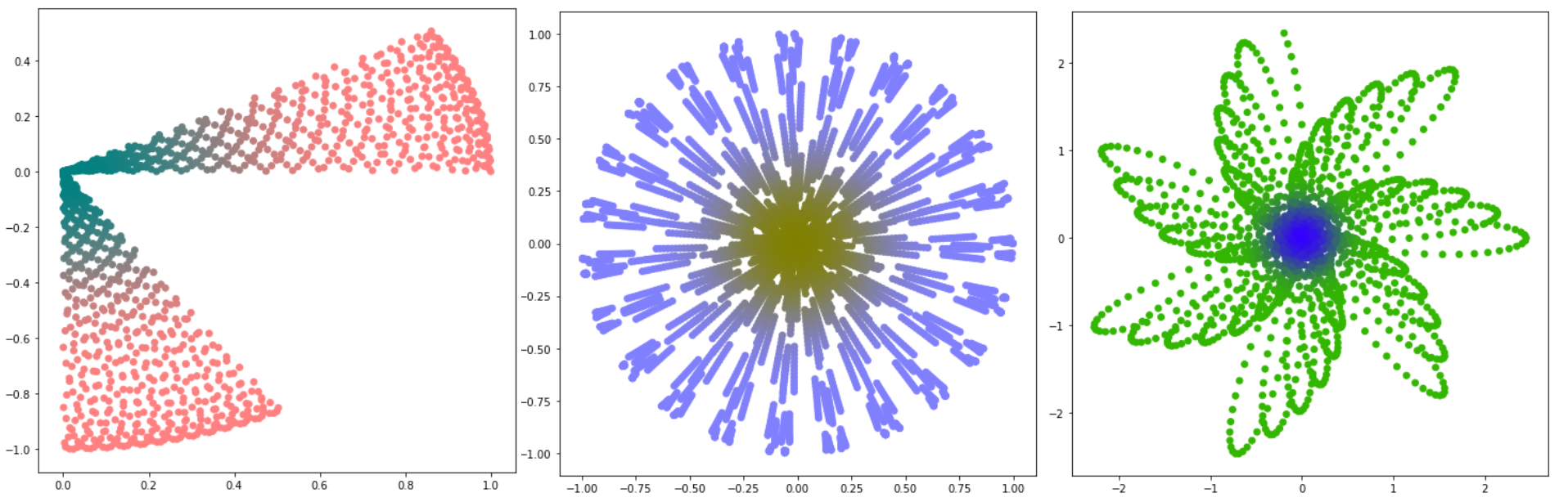
विचार

एक जटिल संख्या एक वास्तविक संख्या का एक निश्चित विस्तार है, वास्तव में एक वेक्टर जिसके लिए स्वयंसिद्धों का एक पूरा सेट परिभाषित किया गया है। किसी भी जटिल (और इसलिए वास्तविक) संख्या के रूप में लिखा जा सकता है $$$z = a + bi$जहां एक वास्तविक हिस्सा है, बी काल्पनिक हिस्सा है, मैं समीकरण का मूल है $$$x ^ {2} = - 1$। इसके लिए कई ऑपरेशन परिभाषित हैं, जो वास्तविक संख्या के लिए परिभाषित हैं, उदाहरण के लिए, $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$। दिलचस्प है, यदि आप उनके साथ विभिन्न ऑपरेशन करते हैं, एक शक्ति को बढ़ाते हैं, गुणा करते हैं, आदि, और फिर लेते हैं $$$रे (z)$(वास्तविक भाग) अक्ष के लिए बैल, और $$$इम (z)$(काल्पनिक भाग) ओए अक्ष के लिए, आप मज़ेदार चित्र प्राप्त कर सकते हैं।

वैसे, मैं स्वयं निम्नलिखित सभी सूत्रों के साथ आया हूं।

विज़ुअलाइज़ेशन फ़ंक्शन

नियमित। फ़ंक्शन, जो इस पुनरावृत्ति फ़ंक्शन के अनुसार फ़ील्ड पर सब कुछ आकर्षित करता है:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

हमारे सभी कार्य दो मापदंडों ए और बी पर निर्भर करते हैं। इसके अलावा, हम बी इनसर्ट इन विस (), और ए फ़ंक्शन के वैश्विक पैरामीटर हैं।

कर्ल समारोह

$$

$$f (A, B) = Bsin (B) * e ^ {iBcos (A)}$$

अजगर में उसकी घोषणा:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

और दौड़ो

 A = 121.5 vis(A, func_1, step=0.1) 

और ए = 121.5 के लिए परिणाम:



और ए = 221.5 के लिए:



ध्यान दें कि ये संख्या एक चिकनी कई गुना और इस संदर्भ में अर्थहीन अन्य चतुर शब्दों पर किसी निश्चित अभिन्न की गणना से पालन नहीं करती है। ये वास्तव में यादृच्छिक संख्याएं हैं, और अभी भी अलग-अलग ए की अनंतता है, जिसके परिणामस्वरूप सौंदर्य प्राप्त होता है।

पेंट करने की जरूरत है

हम एक रंग समारोह घोषित करते हैं (ऐसा फ़ंक्शन जो निर्देशांक में तीन संख्याओं का एक समूह लौटाता है):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

यादृच्छिक पैरामीटर A चुनें, इसे 149 होने दें:

 vis(149, func_1, step=0.1, c=color_1) 

गीत समारोह

गीज़ का वर्णन इस प्रकार है:

$$

$$f (A, B) = cos (B) पाप (B) * B * e ^ {iBcos (A) 2$$

पायथन घोषणा:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

ए = 106 के लिए इसका परिणाम:

फोकेशिया फ़ंक्शन

$$

$$f (A, B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

शीर्षकहीन कार्य

$$

$$f (A, B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

सौंदर्य का सूत्र

$$

$$f (A, B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

अभी के लिए बस इतना ही।