पायथन में टेन्सरफ्लो का उपयोग करके उपग्रह चित्रों को वर्गीकृत करने के लिए तंत्रिका नेटवर्क

यह लैंडसैट 5 उपग्रह से मल्टीस्पेक्ट्रल छवियों को वर्गीकृत करने के लिए एक कदम-दर-चरण निर्देश है। आज, कई क्षेत्रों में भू-स्थानिक सहित जटिल समस्याओं को हल करने के लिए एक उपकरण के रूप में गहन शिक्षा हावी है। मुझे आशा है कि आप उपग्रह डेटासेट से परिचित हैं, विशेष रूप से, लैंडसैट 5 टीएम। यदि आप मशीन लर्निंग एल्गोरिदम से थोड़ा परिचित हैं, तो यह इस मैनुअल को सीखने में आपकी सहायता करेगा। और जो लोग नहीं समझते हैं, उनके लिए यह जानना पर्याप्त होगा कि, वास्तव में, मशीन लर्निंग किसी अन्य गुण (मान या लेबल, लक्ष्य चर Y) के साथ एक वस्तु के कई विशेषताओं (विशेषताओं X का एक सेट) के बीच संबंध स्थापित करने में शामिल है। हम मॉडल को कई ऑब्जेक्ट्स के साथ फ़ीड करते हैं, जिसके लिए लक्ष्य संकेतक / ऑब्जेक्ट की श्रेणी (लेबल डेटा) की विशेषताओं और मूल्य को ज्ञात किया जाता है और इसे प्रशिक्षित किया जाता है ताकि यह नए डेटा के लिए लक्ष्य चर Y के मूल्य का अनुमान लगा सके (बिना चिह्नित)।

उपग्रह इमेजरी के साथ मुख्य समस्या क्या है?

उपग्रह चित्रों में वस्तुओं के दो या अधिक वर्ग (उदाहरण के लिए, इमारतें, खाली बहुत सारे और गड्ढे) मूल्य के समान वर्णक्रमीय लक्षण हो सकते हैं, इसलिए, पिछले बीस वर्षों में उनका वर्गीकरण एक मुश्किल काम रहा है।

इस वजह से, एक शिक्षक के साथ और उसके बिना क्लासिक मशीन लर्निंग मॉडल का उपयोग करना संभव है, लेकिन उनकी गुणवत्ता आदर्श से बहुत दूर होगी। उनमें हमेशा एक जैसी कमियां होती हैं। एक उदाहरण पर विचार करें:



यदि आप एक ऊर्ध्वाधर रेखा को एक क्लासिफायर के रूप में उपयोग करते हैं और इसे एक्स अक्ष के साथ स्थानांतरित करते हैं, तो घरों की छवियों को वर्गीकृत करना आसान नहीं होगा। डेटा वितरित किया जाता है ताकि उन्हें एक ऊर्ध्वाधर रेखा का उपयोग करके कक्षाओं में अलग करना असंभव हो (ऐसे मामलों में यह कहा जाता है कि "विभिन्न वर्गों की वस्तुएं रैखिक रूप से अलग नहीं होती हैं")। लेकिन इसका मतलब यह नहीं है कि घरों को वर्गीकृत नहीं किया जा सकता है!



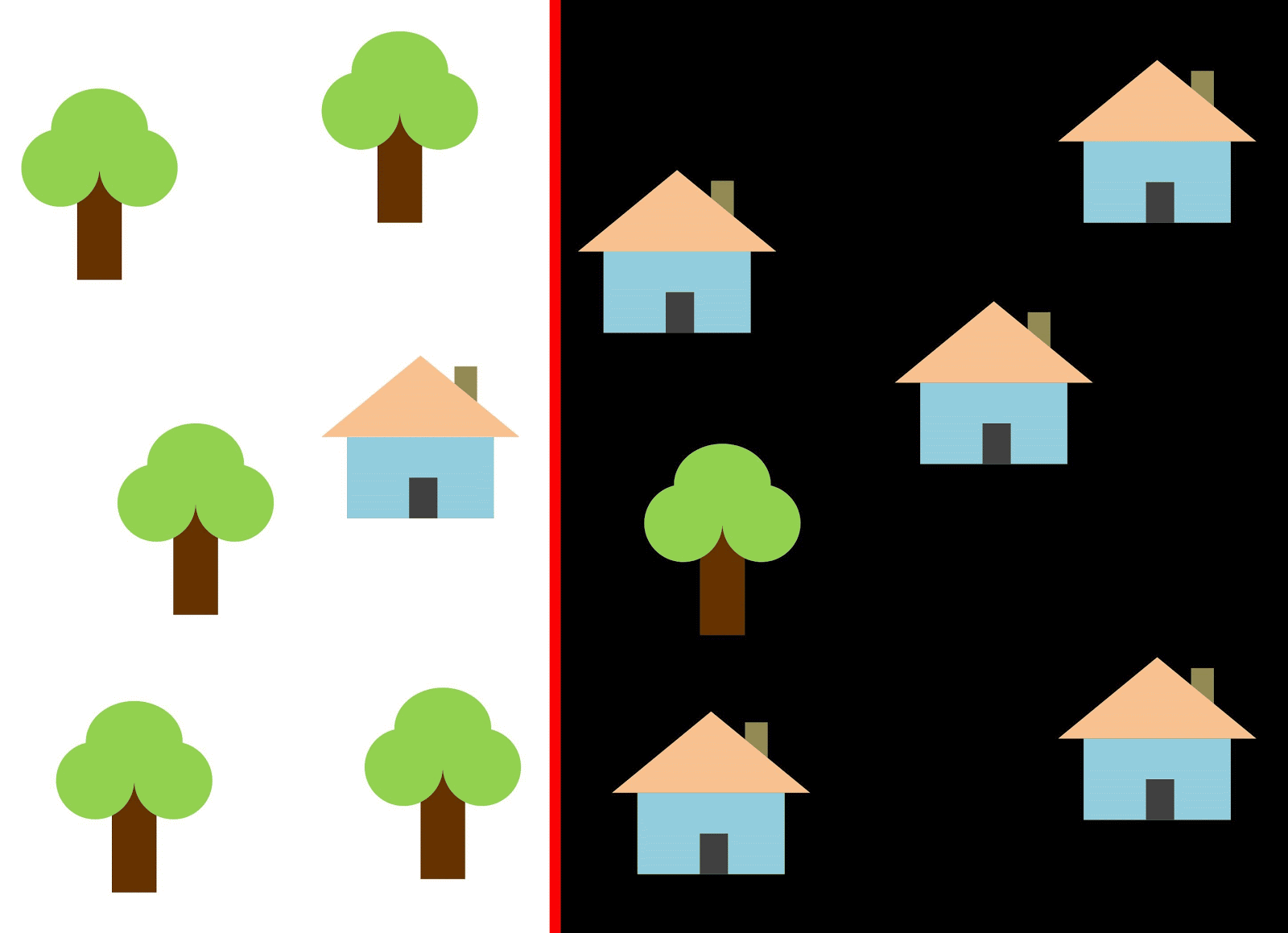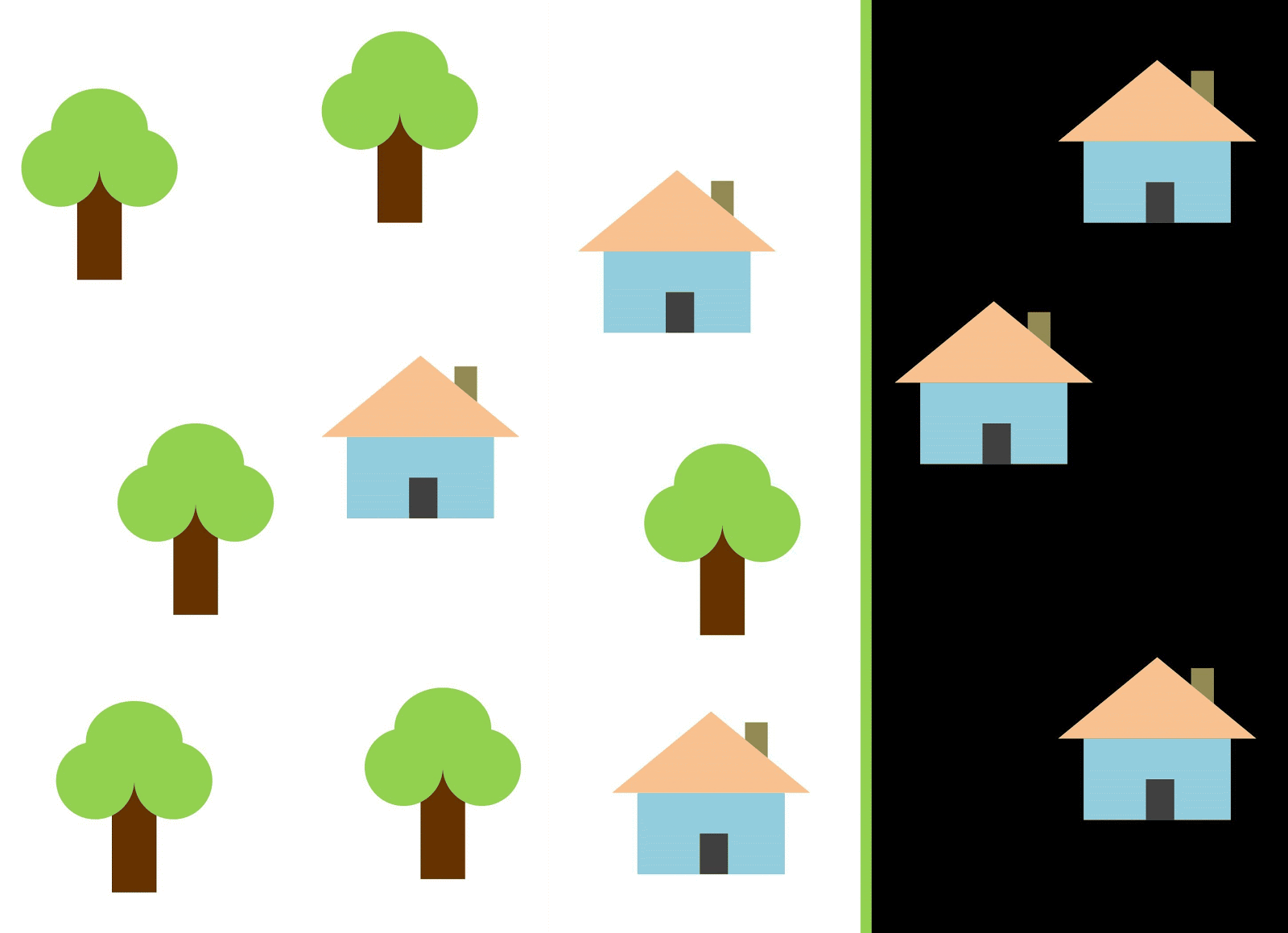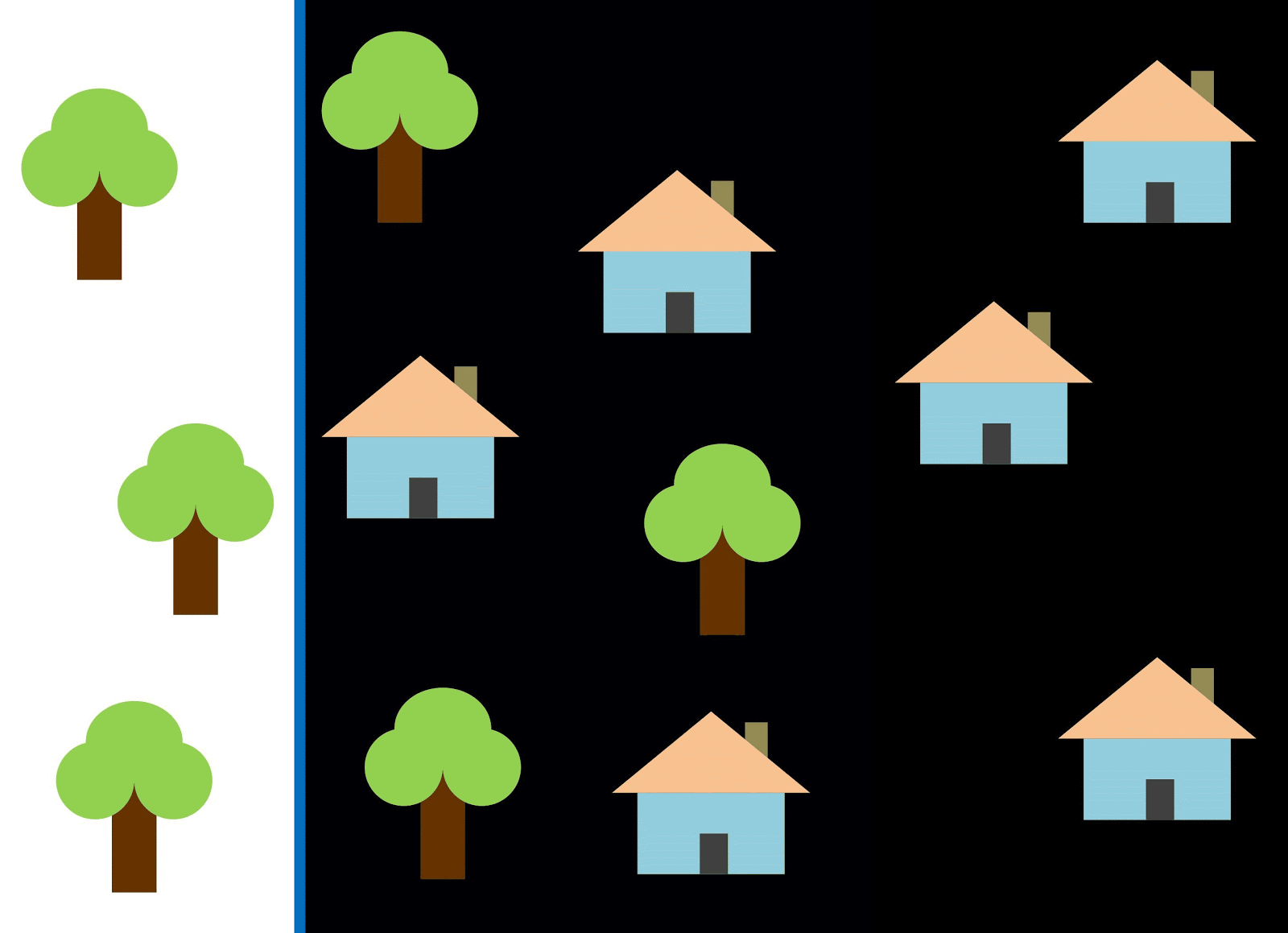
दो वर्गों को अलग करने के लिए लाल रेखा का उपयोग करते हैं। इस मामले में, क्लासिफायर ने अधिकांश घरों की पहचान की, लेकिन एक घर को उसकी कक्षा को नहीं सौंपा गया था, और तीन और पेड़ों को गलती से "घरों" को सौंपा गया था। एक भी घर को याद नहीं करने के लिए, आप नीली रेखा के रूप में क्लासिफायर का उपयोग कर सकते हैं। फिर घर पर सब कुछ कवर किया जाएगा, अर्थात हम कहते हैं कि रिकॉल मीट्रिक (पूर्णता) अधिक है। हालांकि, सभी वर्गीकृत मूल्य घरों के रूप में नहीं निकले, यानी एक ही समय में हमें सटीक मीट्रिक का कम मूल्य मिला। यदि हम ग्रीन लाइन का उपयोग करते हैं, तो घरों के रूप में वर्गीकृत सभी चित्र वास्तव में घर होंगे, अर्थात, क्लासिफायर उच्च सटीकता दिखाएगा। इस मामले में, पूर्णता कम होगी, क्योंकि तीन घरों के लिए बेहिसाब होगा। ज्यादातर मामलों में, हमें सटीकता और पूर्णता के बीच समझौता करना होगा।

घरों और पेड़ों की यह समस्या इमारतों, खाली पड़े ढेरों और गड्ढों की समस्या के समान है। उपग्रह इमेजरी वर्गीकरण मैट्रिक्स की प्राथमिकता कार्य के आधार पर भिन्न हो सकती है। उदाहरण के लिए, यदि आपको यह सुनिश्चित करने की आवश्यकता है कि सभी निर्मित क्षेत्रों को अपवाद के बिना इमारतों के रूप में वर्गीकृत किया गया है, और आप समान हस्ताक्षर वाले अन्य वर्गों के पिक्सल की उपस्थिति के साथ तैयार हैं, जो इमारतों के रूप में भी वर्गीकृत किया जाएगा, तो आपको एक उच्च पूर्णता के साथ एक मॉडल की आवश्यकता होगी। और अगर आपके लिए अन्य कक्षाओं के पिक्सल को जोड़ने के बिना, एक इमारत को वर्गीकृत करना अधिक महत्वपूर्ण है, और आप मिश्रित प्रदेशों के वर्गीकरण को छोड़ने के लिए तैयार हैं, तो उच्च सटीकता के साथ एक वर्गीकरण का चयन करें। घरों और पेड़ों के मामले में, सामान्य मॉडल लाल रेखा का उपयोग करेगा, सटीकता और पूर्णता के बीच संतुलन बनाए रखेगा।

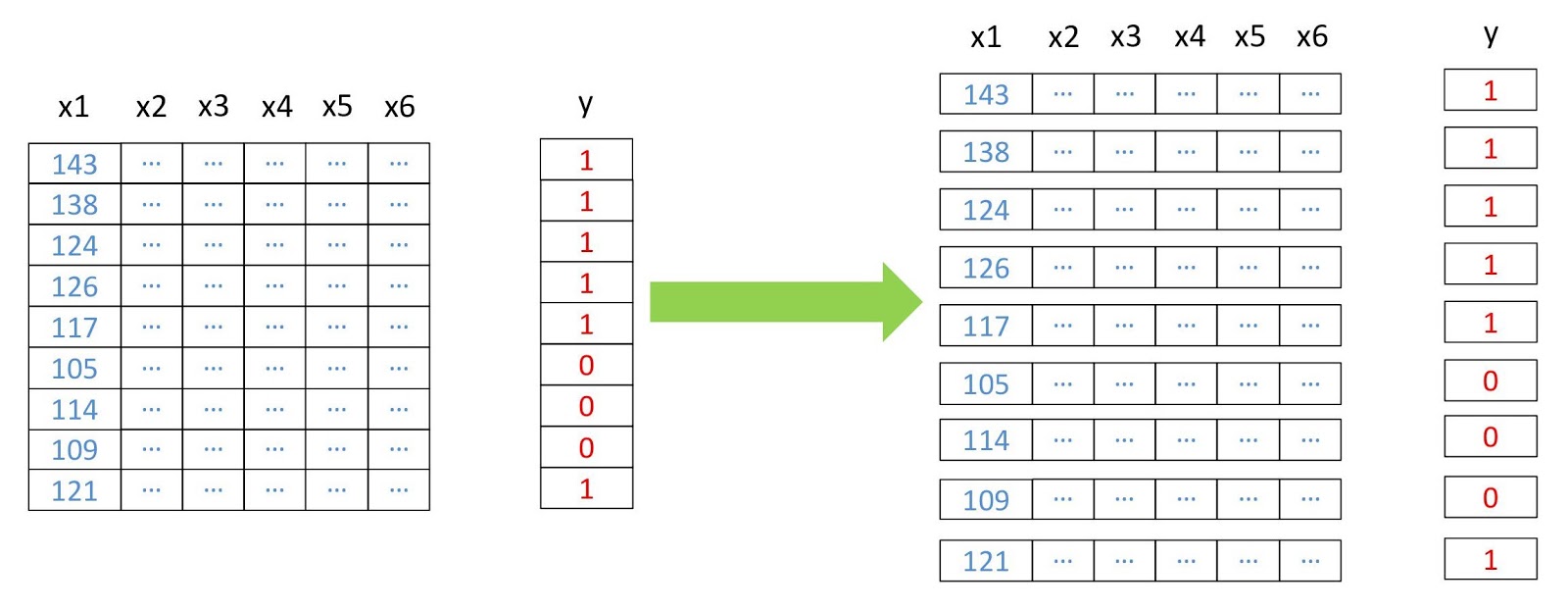
डेटा का इस्तेमाल किया

संकेत के रूप में, हम लैंडसैट 5 टीएम से छवि के छह पर्वतमाला (बैंड 2 - बैंड 7) के मूल्यों का उपयोग करेंगे, और द्विआधारी विकास वर्ग की भविष्यवाणी करने का प्रयास करेंगे। प्रशिक्षण और परीक्षण के लिए, बैंगलोर के लिए 2011 के लिए लैंडसैट 5 के साथ मल्टीस्पेक्ट्रल डेटा (छवियों और एक बाइनरी बिल्डिंग क्लास के साथ एक परत) का उपयोग किया जाएगा। और भविष्यवाणी के लिए हैदराबाद में 2005 में प्राप्त मल्टीस्पेक्ट्रल लैंडसैट 5 डेटा का उपयोग किया जाएगा।
चूंकि हम शिक्षण के लिए टैग किए गए डेटा का उपयोग करते हैं, इसलिए इसे शिक्षक के साथ शिक्षण कहा जाता है।



मल्टीस्पेक्ट्रल प्रशिक्षण डेटा और विकास के साथ संबंधित बाइनरी परत।

एक तंत्रिका नेटवर्क बनाने के लिए, हम पायथन - Google टेन्सरफ्लो लाइब्रेरी का उपयोग करेंगे। हमें इन पुस्तकालयों की भी आवश्यकता होगी:

1. pyrsgis - GeoTIFF को पढ़ने और लिखने के लिए।
   
2. scikit-learn - डेटा प्रीप्रोसेसिंग और सटीकता मूल्यांकन के लिए।
   
3. सुन्न - सरणियों के साथ बुनियादी संचालन के लिए।
   

और अब, आगे की हलचल के बिना, चलो कोड लिखते हैं।

सभी तीन फ़ाइलों को एक निर्देशिका में रखें, स्क्रिप्ट में इनपुट फ़ाइलों का पथ और नाम लिखें, और फिर जियोटीफ़ फ़ाइलों को पढ़ें।

import os from pyrsgis import raster os.chdir("E:\\yourDirectoryName") mxBangalore = 'l5_Bangalore2011_raw.tif' builtupBangalore = 'l5_Bangalore2011_builtup.tif' mxHyderabad = 'l5_Hyderabad2011_raw.tif' # Read the rasters as array ds1, featuresBangalore = raster.read(mxBangalore, bands='all') ds2, labelBangalore = raster.read(builtupBangalore, bands=1) ds3, featuresHyderabad = raster.read(mxHyderabad, bands='all') 

pyrsgis पैकेज से raster मॉड्यूल GeoPIFF जियोलोकेशन डेटा और डिजिटल नंबर (DN) मानों को अलग-अलग NumPy सरणियों के रूप में पढ़ता है। यदि आप विवरण में रुचि रखते हैं, तो यहां पढ़ें।

अब हम रीड डेटा का आकार प्रदर्शित करते हैं।

 print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape) 

परिणाम:

 Bangalore multispectral image shape: 6, 2054, 2044 Bangalore binary built-up image shape: 2054, 2044 Hyderabad multispectral image shape: 6, 1318, 1056 

जैसा कि आप देख सकते हैं, बैंगलोर की छवियों में बाइनरी लेयर (बिल्डिंग के अनुरूप) में समान पंक्तियाँ और कॉलम हैं। बैंगलोर और हैदराबाद में मल्टीस्पेक्ट्रल छवियों में परतों की संख्या भी मेल खाती है। मॉडल यह तय करना सीखेगा कि कौन से पिक्सेल भवन से संबंधित हैं और जो सभी 6 स्पेक्ट्रा के लिए संबंधित मूल्यों के आधार पर नहीं हैं। इसलिए, मल्टीस्पेक्ट्रल छवियों में एक ही क्रम में सूचीबद्ध विशेषताओं (रेंज) की समान संख्या होनी चाहिए।

अब हम सरणियों को दो-आयामी में बदलते हैं, जहां प्रत्येक पंक्ति एक अलग पिक्सेल का प्रतिनिधित्व करती है, क्योंकि अधिकांश मशीन लर्निंग एल्गोरिदम के संचालन के लिए यह आवश्यक है। हम इसे pyrsgis पैकेज से convert मॉड्यूल का उपयोग करके करेंगे।


डेटा पुनर्गठन योजना।

 from pyrsgis.convert import changeDimension featuresBangalore = changeDimension(featuresBangalore) labelBangalore = changeDimension (labelBangalore) featuresHyderabad = changeDimension(featuresHyderabad) nBands = featuresBangalore.shape[1] labelBangalore = (labelBangalore == 1).astype(int) print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape) 

परिणाम:

 Bangalore multispectral image shape: 4198376, 6 Bangalore binary built-up image shape: 4198376 Hyderabad multispectral image shape: 1391808, 6 

सातवीं पंक्ति में, हमने 1. के मान के साथ सभी पिक्सेल निकाले। यह बिना जानकारी (NoData) के पिक्सेल के साथ समस्याओं से बचने में मदद करता है, जिसमें अक्सर बेहद उच्च या निम्न मान होते हैं।
अब हम डेटा को प्रशिक्षण और सत्यापन नमूनों में विभाजित करेंगे। यह आवश्यक है ताकि मॉडल परीक्षण डेटा को न देखे और नई जानकारी के साथ ही काम करे। अन्यथा, मॉडल को वापस ले लिया जाएगा और केवल प्रशिक्षण डेटा पर अच्छा काम करेगा।

 from sklearn.model_selection import train_test_split xTrain, xTest, yTrain, yTest = train_test_split(featuresBangalore, labelBangalore, test_size=0.4, random_state=42) print(xTrain.shape) print(yTrain.shape) print(xTest.shape) print(yTest.shape) 

परिणाम:

 (2519025, 6) (2519025,) (1679351, 6) (1679351,) test_size=0.4 

इसका मतलब है कि डेटा को 60/40 के अनुपात में प्रशिक्षण और सत्यापन में विभाजित किया गया है।
तंत्रिका नेटवर्क सहित कई मशीन लर्निंग एल्गोरिदम को सामान्यीकृत डेटा की आवश्यकता होती है। इसका मतलब है कि उन्हें एक निश्चित सीमा के भीतर वितरित किया जाना चाहिए (इस मामले में, 0 से 1 तक)। इसलिए, इस आवश्यकता को पूरा करने के लिए, हम लक्षणों को सामान्य करते हैं। यह न्यूनतम मूल्य निकालने और फिर इसे प्रसार (अधिकतम और न्यूनतम मूल्यों के बीच का अंतर) से विभाजित करके किया जा सकता है। चूंकि लैंडसैट डेटासेट आठ-बिट है, न्यूनतम और अधिकतम मान 0 और 255 (2 256 = 256 मान) होंगे।

ध्यान दें कि सामान्यीकरण के लिए डेटा के आधार पर न्यूनतम और अधिकतम मूल्यों की गणना करना हमेशा बेहतर होता है। कार्य को सरल बनाने के लिए, हम डिफ़ॉल्ट रूप से आठ-बिट श्रेणी का पालन करेंगे।

प्रारंभिक प्रसंस्करण का एक और चरण द्वि-आयामी से तीन-आयामी तक संकेतों के मैट्रिक्स का परिवर्तन है, जिससे मॉडल प्रत्येक पंक्ति को एक अलग पिक्सेल (एक अलग सीखने की वस्तु) के रूप में मानता है।

 # Normalise the data xTrain = xTrain / 255.0 xTest = xTest / 255.0 featuresHyderabad = featuresHyderabad / 255.0 # Reshape the data xTrain = xTrain.reshape((xTrain.shape[0], 1, xTrain.shape[1])) xTest = xTest.reshape((xTest.shape[0], 1, xTest.shape[1])) featuresHyderabad = featuresHyderabad.reshape((featuresHyderabad.shape[0], 1, featuresHyderabad.shape[1])) # Print the shape of reshaped data print(xTrain.shape, xTest.shape, featuresHyderabad.shape) 

परिणाम:

 (2519025, 1, 6) (1679351, 1, 6) (1391808, 1, 6) 

सब कुछ तैयार है, चलो हमारे मॉडल को केरस के साथ इकट्ठा करें । आरंभ करने के लिए, चलो अनुक्रमिक मॉडल का उपयोग करते हैं, एक के बाद एक परतें जोड़ते हैं। हमारे पास एक इनपुट लेयर होगी जिसमें रेंज की संख्या के बराबर नोड्स ( nBands ) होंगे - हमारे मामले में 6. हैं। हम 14 नोड्स और ReLu सक्रियण ReLu साथ एक छिपी हुई परत का भी उपयोग करेंगे। अंतिम परत में softmax सक्रियण softmax साथ एक बाइनरी बिल्डिंग क्लास को परिभाषित करने के लिए दो नोड्स होते हैं, जो एक श्रेणीबद्ध परिणाम प्रदर्शित करने के लिए उपयुक्त है। सक्रियण कार्यों के बारे में यहाँ और पढ़ें।

 from tensorflow import keras # Define the parameters of the model model = keras.Sequential([ keras.layers.Flatten(input_shape=(1, nBands)), keras.layers.Dense(14, activation='relu'), keras.layers.Dense(2, activation='softmax')]) # Define the accuracy metrics and parameters model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics=["accuracy"]) # Run the model model.fit(xTrain, yTrain, epochs=2) 

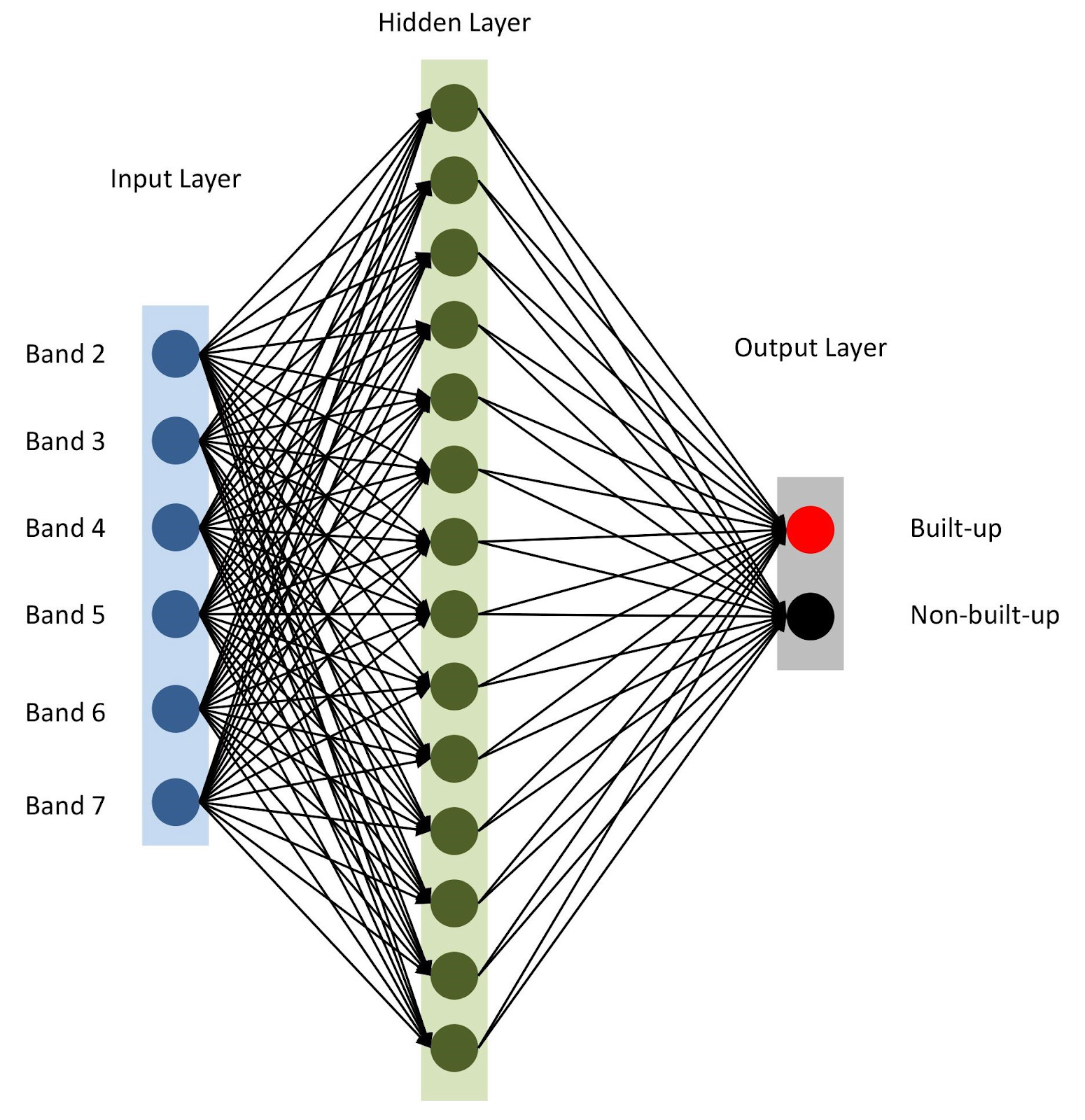तंत्रिका नेटवर्क वास्तुकला

जैसा कि लाइन 10 में उल्लेख किया गया है, हम मॉडल ऑप्टिमाइज़र के रूप में adam निर्दिष्ट करते हैं (कई अन्य हैं )। इस स्थिति में, हम क्रॉस एन्ट्रापी को एक हानि फ़ंक्शन के रूप में उपयोग करेंगे (एन। categorical-sparse-crossentropy - इसके बारे में अधिक यहां लिखा गया है )। मॉडल की गुणवत्ता का आकलन करने के लिए, हम accuracy मीट्रिक का उपयोग करेंगे।

अंत में, हम xTrain और yTrain पर दो युगों (या पुनरावृत्तियों) के लिए अपने मॉडल का प्रशिक्षण शुरू करेंगे। डेटा और प्रसंस्करण शक्ति के आकार के आधार पर इसमें कुछ समय लगेगा। संकलन के बाद आप यहां देखेंगे:



आइए सत्यापन डेटा के लिए मूल्यों की भविष्यवाणी करें जिन्हें हम अलग-अलग संग्रहीत करते हैं और विभिन्न सटीकता मैट्रिक्स की गणना करते हैं।

 from sklearn.metrics import confusion_matrix, precision_score, recall_score # Predict for test data yTestPredicted = model.predict(xTest) yTestPredicted = yTestPredicted[:,1] # Calculate and display the error metrics yTestPredicted = (yTestPredicted>0.5).astype(int) cMatrix = confusion_matrix(yTest, yTestPredicted) pScore = precision_score(yTest, yTestPredicted) rScore = recall_score(yTest, yTestPredicted) print("Confusion matrix: for 14 nodes\n", cMatrix) print("\nP-Score: %.3f, R-Score: %.3f" % (pScore, rScore)) 

softmax फ़ंक्शन प्रत्येक वर्ग के लिए प्रायिकता मान के लिए अलग कॉलम बनाता है। हम केवल प्रथम श्रेणी ("एक इमारत है") के लिए मूल्यों का उपयोग करते हैं, जैसा कि ऊपर दिए गए कोड की छठी पंक्ति से देखा जा सकता है। मशीन सीखने की अन्य शास्त्रीय समस्याओं के विपरीत, भू-स्थानिक विश्लेषण मॉडल के काम का मूल्यांकन इतना सरल नहीं है। सामान्यीकृत कुल त्रुटि पर भरोसा करना अनुचित होगा। एक सफल मॉडल की कुंजी स्थानिक लेआउट है। इस प्रकार, भ्रम की मैट्रिक्स, सटीकता और पूर्णता मॉडल की गुणवत्ता का अधिक सही विचार दे सकती है।


तो कंसोल त्रुटि मैट्रिक्स, सटीकता और पूर्णता प्रदर्शित करता है।

जैसा कि आप भ्रम मैट्रिक्स से देख सकते हैं, हजारों पिक्सेल हैं जो इमारतों से संबंधित हैं, लेकिन अलग-अलग वर्गीकृत हैं, और इसके विपरीत। हालाँकि, कुल डेटा वॉल्यूम में उनकी हिस्सेदारी बहुत बड़ी नहीं है। परीक्षण डेटा की सटीकता और पूर्णता 0.8 की सीमा से अधिक थी।

आप छिपी हुई परतों की इष्टतम संख्या, प्रत्येक छिपी परत में नोड्स की संख्या, साथ ही वांछित सटीकता को प्राप्त करने के लिए युगों की संख्या का पता लगाने के लिए अधिक समय बिता सकते हैं और कई पुनरावृत्तियों का प्रदर्शन कर सकते हैं। आवश्यकतानुसार, सुदूर संवेदन सूचकांकों जैसे NDBI या NDWI का उपयोग सुविधाओं के रूप में किया जा सकता है। वांछित सटीकता प्राप्त करते समय, नए डेटा के आधार पर विकास की भविष्यवाणी करने के लिए मॉडल का उपयोग करें और परिणाम को GeoTIFF में निर्यात करें। ऐसे कार्यों के लिए, आप मामूली बदलाव के साथ एक समान मॉडल का उपयोग कर सकते हैं।

 predicted = model.predict(feature2005) predicted = predicted[:,1] #Export raster prediction = np.reshape(predicted, (ds.RasterYSize, ds.RasterXSize)) outFile = 'Hyderabad_2011_BuiltupNN_predicted.tif' raster.export(prediction, ds3, filename=outFile, dtype='float') 

कृपया ध्यान दें कि हम अनुमानित संभावनाओं के साथ GeoTIFF का निर्यात करते हैं, न कि उनके थ्रेशोल्ड-बिनाराइज्ड संस्करण के साथ। बाद में जीआईएस वातावरण में, हम टाइप फ़्लोट की एक परत का थ्रेसहोल्ड मान सेट कर सकते हैं, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।


हैदराबाद ने मल्टीस्पेक्ट्रल डेटा के आधार पर मॉडल द्वारा निर्मित परत का अनुमान लगाया।

मॉडल सटीकता पहले से ही सटीक और याद के साथ मापा गया है। आप एक नई भविष्यवाणी की गई परत पर पारंपरिक जांच (उदाहरण के लिए, कप्पा गुणांक का उपयोग करके) भी कर सकते हैं। उपग्रह चित्रों के वर्गीकरण के साथ उपरोक्त कठिनाइयों के अलावा, अन्य स्पष्ट सीमाओं में वर्ष के अलग-अलग समय पर और विभिन्न क्षेत्रों में ली गई छवियों के आधार पर पूर्वानुमान की असंभवता शामिल है, क्योंकि उनके पास अलग-अलग वर्णक्रमीय हस्ताक्षर होंगे।

इस आलेख में वर्णित मॉडल में तंत्रिका नेटवर्क के लिए सबसे सरल वास्तुकला है। अधिक जटिल मॉडल के साथ बेहतर परिणाम प्राप्त किया जा सकता है, जिसमें दृढ़ तंत्रिका नेटवर्क शामिल हैं। इस तरह के वर्गीकरण का मुख्य लाभ मॉडल के प्रशिक्षण के बाद इसकी मापनीयता (प्रयोज्यता) है।

उपयोग किए गए डेटा और सभी कोड यहां हैं ।