Geekly articles weekly

एक बोरिंग NumPy ट्यूटोरियल

मेरा नाम व्याचेस्लाव है, मैं एक पुराना गणितज्ञ हूं और कई वर्षों से मैंने एरे के साथ काम करते समय साइकिल का उपयोग नहीं किया है ...

वास्तव में जब से मैंने NumPy में वेक्टर ऑपरेशन की खोज की है। मैं आपको उन NumPy कार्यों से परिचित कराना चाहता हूं जो मैं अक्सर डेटा और छवियों के सरणियों को संसाधित करने के लिए उपयोग करता हूं। लेख के अंत में, मैं दिखाऊंगा कि कैसे आप पुनरावृत्तियों (= बहुत तेज़) के बिना छवियों को समझाने के लिए NumPy टूलकिट का उपयोग कर सकते हैं।

के बारे में मत भूलना

import numpy as np

और चलो!


सामग्री

सुन्न क्या है?
ऐरे सृजन
तत्वों, स्लाइस तक पहुंच
सरणी का आकार और उसका परिवर्तन
एक्सिस पुनर्व्यवस्था और ट्रांसपोज़ेशन
ऐरे में शामिल हों
डाटा क्लोनिंग
सरणी तत्वों पर गणितीय संचालन
मैट्रिक्स गुणन
एग्रीगेटर्स
एक निष्कर्ष के बजाय - एक उदाहरण

सुन्न क्या है?


यह एक ओपन सोर्स लाइब्रेरी है जो एक बार SciPy प्रोजेक्ट से अलग हो गई है। NumPy, Numeric और NumArray का वंशज है। NumPy LAPAC पुस्तकालय पर आधारित है, जो कि फोरट्रान में लिखा गया है। NumPy के लिए एक गैर-पायथन विकल्प मतलाब है।

इस तथ्य के कारण कि NumPy फोरट्रान पर आधारित है, यह एक तेज़ पुस्तकालय है। और इस तथ्य के कारण कि यह बहुआयामी सरणियों के साथ वेक्टर संचालन का समर्थन करता है, यह बेहद सुविधाजनक है।

मूल संस्करण (मूल संस्करण में बहुआयामी सरणियों) के अलावा, NumPy में विशेष कार्यों को हल करने के लिए पैकेज का एक सेट शामिल है, उदाहरण के लिए:

  • numpy.linalg - रैखिक बीजगणित के संचालन को लागू करता है (मूल संस्करण में वैक्टर और मैट्रिसिस का एक सरल गुणन);
  • numpy.random - यादृच्छिक चर के साथ काम करने के लिए कार्य करता है;
  • numpy.fft - प्रत्यक्ष और व्युत्क्रम फूरियर रूपांतरण को लागू करता है।

इसलिए, मैं विस्तार से विचार करने का प्रस्ताव करता हूं केवल कुछ न्यूमप फीचर्स और उनके उपयोग के उदाहरण, जो आपके लिए यह समझने के लिए पर्याप्त होंगे कि यह टूल कितना शक्तिशाली है!

<शीर्ष>


ऐरे सृजन


एक सरणी बनाने के कई तरीके हैं:

  1. सूची को सरणी में बदलें:

     A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
  2. सरणी कॉपी करें (प्रतिलिपि और गहरी प्रतिलिपि आवश्यक !!!):

     B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
  3. किसी दिए गए आकार का एक शून्य या एक सरणी बनाएं:

     A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]]) 

     B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])

    या किसी मौजूदा सरणी के आयाम लें:

     A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]]) 

     A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])

  4. दो-आयामी वर्ग सरणी बनाते समय, आप इसे एक इकाई विकर्ण मैट्रिक्स बना सकते हैं:

     A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
  5. चरण चरण से (सहित) से (शामिल नहीं) से संख्याओं की एक सरणी बनाएँ:

     From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])

    डिफ़ॉल्ट रूप से, = 0 से, चरण = 1, इसलिए एक पैरामीटर के साथ एक संस्करण को इस रूप में व्याख्या की जाती है:

     A = np.arange(5) A Out: array([0, 1, 2, 3, 4])

    या दो के साथ - जैसे कि और से:

     A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])

ध्यान दें कि विधि संख्या 3 में, सरणी के आयामों को एक पैरामीटर (आकार का एक प्रकार) के रूप में पारित किया गया था। दूसरे नंबर के तरीके नंबर 3 और नंबर 4 में, आप इच्छित प्रकार के सरणी तत्वों को निर्दिष्ट कर सकते हैं:

 A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]]) 

 B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])

Astype विधि का उपयोग करके, आप सरणी को एक अलग प्रकार में डाल सकते हैं। वांछित प्रकार को एक पैरामीटर के रूप में दर्शाया गया है:

 A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')

सभी उपलब्ध प्रकार sctypes शब्दकोश में पाए जा सकते हैं:

 np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}


<शीर्ष>


तत्वों, स्लाइस तक पहुंच


सरणी के तत्वों तक पहुंच पूर्णांक सूचकांकों द्वारा की जाती है, उलटी गिनती 0 से शुरू होती है:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5

यदि आप नेस्टेड-डायमेंशनल सरणियों की एक प्रणाली के रूप में एक बहुआयामी सरणी की कल्पना करते हैं (एक रैखिक सरणी, जिनमें से तत्व रैखिक सरणियां हो सकते हैं), तो यह स्पष्ट हो जाता है कि आप सूचकांकों के अधूरे सेट का उपयोग करके सबरेज़ का उपयोग कर सकते हैं:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])

इस प्रतिमान को देखते हुए, हम एक तत्व तक पहुंच के उदाहरण को फिर से लिख सकते हैं:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5

सूचकांकों के अधूरे सेट का उपयोग करते समय, लापता सूचक को संबंधित अक्ष के साथ सभी संभावित सूचकांकों की सूची द्वारा प्रतिस्थापित किया जाता है। आप इसे ":" सेट करके स्पष्ट रूप से कर सकते हैं। एक सूचकांक के साथ पिछले उदाहरण को इस प्रकार फिर से लिखा जा सकता है:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])

आप किसी अक्ष या कुल्हाड़ियों के साथ एक सूचकांक छोड़ सकते हैं; यदि अक्ष अनुक्रमण के साथ कुल्हाड़ियों द्वारा पीछा किया जाता है, तो ":" होना चाहिए:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])

सूचकांक नकारात्मक पूर्णांक मान ले सकते हैं। इस मामले में, गिनती सरणी के अंत से है:

 A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4

आप एकल अनुक्रमणिका का उपयोग नहीं कर सकते, लेकिन प्रत्येक अक्ष के साथ अनुक्रमणिका की सूची:

 A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])

या सूचकांक "से: टू: स्टेप" के रूप में होता है। इस डिज़ाइन को एक स्लाइस कहा जाता है। सभी तत्वों को इंडेक्स से शुरू होने वाले सूचकांकों की सूची के अनुसार चुना जाता है, टू इंडेक्स में कदम कदम के साथ शामिल नहीं है:

 A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])

इंडेक्स स्टेप का डिफ़ॉल्ट मान 1 है और इसे छोड़ दिया जा सकता है:

 A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])

फ्रॉम एंड टू और वैल्यूज़ में डिफ़ॉल्ट वैल्यूज़ हैं: 0 और इंडेक्स एक्सिस के साथ एरे का साइज़ क्रमशः:

 A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3]) 

 A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])

यदि आप डिफ़ॉल्ट रूप से (इस अक्ष पर सभी सूचकांकों) का उपयोग करना चाहते हैं और चरण 1 से भिन्न है, तो आपको कॉलन के दो जोड़े का उपयोग करने की आवश्यकता है ताकि दुभाषिया चरण के रूप में एकल पैरामीटर की पहचान कर सके। निम्न कोड दूसरी धुरी के साथ "विस्तार" करता है, लेकिन पहले के साथ नहीं बदलता है:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]

अब इसे करते हैं

 print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]

जैसा कि आप देख सकते हैं, बी के माध्यम से हमने ए में डेटा बदल दिया है। यही कारण है कि वास्तविक कार्यों में प्रतियां का उपयोग करना महत्वपूर्ण है। उपरोक्त उदाहरण इस तरह दिखना चाहिए:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]

NumPy एक बूलियन इंडेक्स सरणी के माध्यम से कई सरणी तत्वों तक पहुंचने की क्षमता भी प्रदान करता है। सूचकांक सरणी को अनुक्रमित के आकार से मेल खाना चाहिए।

 A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])

जैसा कि आप देख सकते हैं, इस तरह का निर्माण एक फ्लैट सरणी देता है जिसमें अनुक्रमित सरणी के तत्व शामिल होते हैं जो सच्चे अनुक्रमित के अनुरूप होते हैं। हालाँकि, अगर हम ऐरे के तत्वों तक ऐसी पहुँच का उपयोग उनके मूल्यों को बदलने के लिए करते हैं, तो ऐरे के आकार को संरक्षित किया जाएगा:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]

लॉजिकल ऑपरेशंस तार्किक_और, लॉजिकल_ओर और लॉजिकल_नोट को बूलियन सरणियों को अनुक्रमित करने पर परिभाषित किया गया है और तार्किक संचालन और, या, और तत्वपूर्ण नहीं किया जाता है:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]

तार्किक_ और तार्किक_ दो ऑपरेंड लेते हैं, तार्किक_ एक लेते हैं। आप ऑपरेटरों का उपयोग कर सकते हैं और; | और किसी भी संख्या के साथ क्रमशः निष्पादित करने के लिए ~ और, या, और नहीं, क्रमशः:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]

जो केवल I1 का उपयोग करने के बराबर है।

एक संचालक के रूप में सरणी के नाम के साथ एक तार्किक स्थिति लिखकर मूल्यों के एक सरणी के रूप में इसी अनुक्रमणिका तार्किक सरणी को प्राप्त करना संभव है। अनुक्रमणिका के बूलियन मूल्य की गणना संबंधित सरणी तत्व के लिए अभिव्यक्ति की सच्चाई के रूप में की जाएगी।

I तत्वों की अनुक्रमणिका खोजें जो 3 से अधिक हैं, और 2 से कम और 4 से अधिक मान वाले तत्व शून्य पर रीसेट हो जाएंगे:

 A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]

<शीर्ष>


सरणी का आकार और उसका परिवर्तन


एक बहुआयामी सरणी को अधिकतम लंबाई के एक आयामी सरणी के रूप में दर्शाया जा सकता है, बहुत अंतिम अक्ष की लंबाई के साथ टुकड़ों में कट जाता है और अक्षों के साथ परतों में बिछाया जाता है, जो बाद के साथ शुरू होता है।

स्पष्टता के लिए, एक उदाहरण पर विचार करें:

 A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]

इस उदाहरण में, हमने 24 तत्वों की लंबाई के साथ एक आयामी सरणी से 2 नए सरणियों का गठन किया। एरे बी, आकार 4 से 6. यदि आप मूल्यों के क्रम को देखते हैं, तो आप देख सकते हैं कि दूसरे आयाम के साथ लगातार मूल्यों की श्रृंखलाएं हैं।

सरणी C में 4, 3 बाय 2, निरंतर मान अंतिम अक्ष पर चलते हैं। श्रृंखला में दूसरी धुरी के साथ ब्लॉक हैं, जिसके संयोजन से पंक्ति बी के दूसरे अक्ष के साथ एक पंक्ति होगी।

और यह देखते हुए कि हमने प्रतियां नहीं बनाई हैं, यह स्पष्ट हो जाता है कि ये एक ही डेटा सरणी के प्रतिनिधित्व के विभिन्न रूप हैं। इसलिए, आप आसानी से और जल्दी से डेटा को बदले बिना सरणी के आकार को बदल सकते हैं।

सरणी (अक्षों की संख्या) के आयाम का पता लगाने के लिए, आप ndim फ़ील्ड (संख्या) का उपयोग कर सकते हैं, और प्रत्येक अक्ष के साथ आकार का पता लगाने के लिए - आकार (टपल)। आकार की लंबाई से भी आयाम को पहचाना जा सकता है। किसी सरणी में तत्वों की कुल संख्या जानने के लिए, आप आकार मान का उपयोग कर सकते हैं:

 A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24

ध्यान दें कि ndim और आकार विशेषताएँ हैं, न कि विधियाँ!

सरणी को एक-आयामी देखने के लिए, आप ravel फ़ंक्शन का उपयोग कर सकते हैं:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])

कुल्हाड़ियों या आयाम के साथ आकार बदलने के लिए, आकार विधि का उपयोग करें:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])

यह महत्वपूर्ण है कि तत्वों की संख्या संरक्षित है। अन्यथा, एक त्रुटि उत्पन्न होगी:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)

यह देखते हुए कि तत्वों की संख्या स्थिर है, किसी भी अक्ष के साथ आकार जब पुनर्भरण को अन्य अक्षों के साथ लंबाई मानों से गणना की जा सकती है। एक अक्ष के साथ आकार -1 निर्दिष्ट किया जा सकता है और फिर इसकी गणना स्वचालित रूप से की जाएगी:

 A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)

आप ravel के बजाय reshape का उपयोग कर सकते हैं:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)

छवि प्रसंस्करण के लिए कुछ सुविधाओं के व्यावहारिक अनुप्रयोग पर विचार करें। अनुसंधान के एक उद्देश्य के रूप में हम एक तस्वीर का उपयोग करेंगे:



आइए इसे पायथन का उपयोग करके डाउनलोड करने और कल्पना करने की कोशिश करें। इसके लिए हमें OpenCV और Matplotlib की आवश्यकता है:

 import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()

परिणाम इस प्रकार होगा:



डाउनलोड बार पर ध्यान दें:

 I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)

OpenCV बीजीआर प्रारूप में छवियों के साथ काम करता है, और हम आरजीबी से परिचित हैं। हम निर्माण का उपयोग करके OpenCV फ़ंक्शन तक पहुंचने के बिना रंग अक्ष के साथ बाइट क्रम को बदलते हैं
"[:,:, :: :: 1]"।

प्रत्येक अक्ष पर छवि को 2 गुना कम करें। हमारी छवि में कुल्हाड़ियों के साथ भी आयाम हैं, क्रमशः प्रक्षेप के बिना कम किया जा सकता है:

 I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()



सरणी के आकार को बदलते हुए, हमें 2 नए अक्ष मिले, प्रत्येक में 2 मान, वे मूल छवि के विषम और यहां तक ​​कि पंक्तियों और स्तंभों से बने फ्रेम के अनुरूप हैं।
गरीब गुणवत्ता Matplotlib के उपयोग के कारण है, क्योंकि वहां आप अक्षीय आयाम देख सकते हैं। वास्तव में, थंबनेल की गुणवत्ता है:



<शीर्ष>


एक्सिस पुनर्व्यवस्था और ट्रांसपोज़ेशन


डेटा इकाइयों के एक ही क्रम के साथ सरणी के आकार को बदलने के अलावा, कुल्हाड़ियों के क्रम को बदलने के लिए अक्सर आवश्यक होता है, जो स्वाभाविक रूप से डेटा ब्लॉकों के क्रमचय की अनुमति देगा।

इस तरह के परिवर्तन का एक उदाहरण मैट्रिक्स का ट्रांसपोज़ेशन है: इंटरचेंजिंग रो और कॉलम।

 A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]

इस उदाहरण में, एटी निर्माण का उपयोग मैट्रिक्स ए को स्थानांतरित करने के लिए किया गया था। ट्रांसपोज ऑपरेटर अक्ष आदेश को निष्क्रिय करता है। तीन कुल्हाड़ियों के साथ एक और उदाहरण पर विचार करें:

 C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]

इस छोटी प्रविष्टि में एक लंबा प्रतिपक्ष है: np.transpose (A)। यह अक्ष क्रम को बदलने के लिए एक अधिक बहुमुखी उपकरण है। दूसरा पैरामीटर आपको स्रोत सरणी के अक्ष संख्याओं का एक टपल निर्दिष्ट करने की अनुमति देता है, जो परिणामी सरणी में उनकी स्थिति के क्रम को निर्धारित करता है।

उदाहरण के लिए, छवि के पहले दो अक्षों को पुनर्व्यवस्थित करें। चित्र को पलटना चाहिए, लेकिन रंग अक्ष को अपरिवर्तित छोड़ दें:

 I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()



इस उदाहरण के लिए, एक अन्य स्वेपैक्स उपकरण का उपयोग किया जा सकता है। यह विधि मापदंडों में निर्दिष्ट दो अक्षों को परस्पर जोड़ती है। ऊपर दिए गए उदाहरण को इस तरह लागू किया जा सकता है:

 I_ = np.swapaxes(I, 0, 1)

<शीर्ष>


ऐरे में शामिल हों


मर्ज किए गए सरणियों में कुल्हाड़ियों की समान संख्या होनी चाहिए। ऐरे को एक नई अक्ष के गठन के साथ, या एक मौजूदा के साथ जोड़ा जा सकता है।

नई अक्ष के निर्माण के साथ संयोजन के लिए, मूल सरणियों में सभी अक्षों के समान आयाम होने चाहिए:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])

जैसा कि आप उदाहरण से देख सकते हैं, ऑपरेंड एरेज़ नई ऑब्जेक्ट की सब-किरण बन गए और नए अक्ष के साथ पंक्तिबद्ध हो गए, जो क्रम में सबसे पहले है।

किसी मौजूदा अक्ष के साथ सरणियों को संयोजित करने के लिए, उनके पास सभी अक्षों पर समान आकार होना चाहिए, जिसमें शामिल होने के लिए चयनित एक को छोड़कर, और उनके पास मनमाने आकार हो सकते हैं:

 A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])

पहली या दूसरी धुरी के साथ संयोजन के लिए, आप क्रमशः vstack और hstack विधियों का उपयोग कर सकते हैं। हम इसे छवियों के उदाहरण के साथ दिखाते हैं। vstack ऊंचाई में समान चौड़ाई की छवियों को जोड़ती है, और hsstack एक ही चौड़ाई में एक ही ऊंचाई की छवियों को जोड़ती है:

 I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()





कृपया ध्यान दें कि इस खंड के सभी उदाहरणों में, शामिल किए गए सरणियों को एक पैरामीटर (टपल) द्वारा पारित किया जाता है। ऑपरेंड की संख्या कोई भी हो सकती है, लेकिन जरूरी नहीं कि वह केवल 2 ही हो।

सरणियों को संयोजित करते समय मेमोरी में क्या होता है, इस पर भी ध्यान दें:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]

चूंकि एक नया ऑब्जेक्ट बनाया जाता है, इसलिए इसमें डेटा को मूल सरणियों से कॉपी किया जाता है, इसलिए नए डेटा में परिवर्तन मूल को प्रभावित नहीं करते हैं।

<शीर्ष>


डाटा क्लोनिंग


Np.repeat (A, n) ऑपरेटर सरणी A के तत्वों के साथ एक-आयामी सरणी लौटाएगा, जिनमें से प्रत्येक को n बार दोहराया जाएगा।

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]

इस रूपांतरण के बाद, आप सरणी की ज्यामिति का पुनर्निर्माण कर सकते हैं और एक अक्ष में डुप्लिकेट डेटा एकत्र कर सकते हैं:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]

यह विकल्प केवल स्टैक ऑपरेटर के साथ सरणी के संयोजन से भिन्न होता है, केवल उसी अक्ष की स्थिति में जिसके साथ एक ही डेटा स्थित है। उपरोक्त उदाहरण में, यह अंतिम अक्ष है, यदि आप स्टैक का उपयोग करते हैं - पहला:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]

कोई फर्क नहीं पड़ता कि डेटा क्लोन कैसे किया जाता है, अगला कदम धुरी को स्थानांतरित करना है जिसके साथ समान मान धुरी के साथ किसी भी स्थिति में खड़े होते हैं:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]

यदि हम तत्वों की पुनरावृत्ति का उपयोग करके किसी भी अक्ष को "स्ट्रेच" करना चाहते हैं, तो विस्तार योग्य (ट्रांसपोज़ का उपयोग करके) के बाद समान मान वाले अक्ष को रखा जाना चाहिए, और फिर इन दो अक्षों (रिशेप का उपयोग करके) को मिलाएं। पंक्तियों को डुप्लिकेट करके एक ऊर्ध्वाधर अक्ष के साथ एक छवि को खींचने के साथ एक उदाहरण पर विचार करें:

 I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1] #    I1 = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1)[:, 0, :, 0] #      I2 = np.repeat(I1, 2) #   I3 = I2.reshape(I1.shape[0], I1.shape[1], I1.shape[2], -1) I4 = np.transpose(I3, (0, 3, 1, 2)) #    I5 = I4.reshape(-1, I1.shape[1], I1.shape[2]) #   print('I0', I0.shape) print('I1', I1.shape) print('I2', I2.shape) print('I3', I3.shape) print('I4', I4.shape) print('I5', I5.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I5) plt.show() Out: I0 (1280, 1920, 3) I1 (640, 960, 3) I2 (3686400,) I3 (640, 960, 3, 2) I4 (640, 2, 960, 3) I5 (1280, 960, 3)



<शीर्ष>


सरणी तत्वों पर गणितीय संचालन


यदि A और B एक ही आकार के सरणियाँ हैं, तो उन्हें एक शक्ति में गुणा, घटाया, विभाजित और जोड़ा जा सकता है। इन ऑपरेशनों को तत्व-वार किया जाता है, परिणामी सरणी ज्यामिति में मूल सरणियों के साथ मेल खाएगी, और प्रत्येक तत्व मूल सरणियों से तत्वों की एक जोड़ी पर संबंधित ऑपरेशन का परिणाम होगा:

 A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]

आप सरणी और संख्या पर ऊपर से कोई भी ऑपरेशन कर सकते हैं। इस स्थिति में, एरे के सभी तत्वों पर भी ऑपरेशन किया जाएगा:

 A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]

यह देखते हुए कि एक बहुआयामी सरणी को एक फ्लैट सरणी (पहली अक्ष) के रूप में माना जा सकता है, जिनके तत्व सरणियाँ (अन्य अक्ष) हैं, इस मामले में सरणियों ए और बी पर विचार किए गए संचालन करना संभव है जब बी का ज्यामिति पहले अक्ष के साथ एक निश्चित मान के साथ ए के उपग्रहों की ज्यामिति से मेल खाता है। । दूसरे शब्दों में, समान संख्या में कुल्हाड़ियों और आकारों के साथ ए [i] और बी। इस मामले में, ए [i] और बी में से प्रत्येक एरे पर परिभाषित संचालन के लिए ऑपरेंड होगा।

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]

इस उदाहरण में, सरणी B को सरणी A की प्रत्येक पंक्ति के साथ संचालन के अधीन किया जाता है। यदि आपको अन्य अक्ष के साथ उप-डिग्री को गुणा / विभाजित / जोड़ने / घटाने / बढ़ाने की आवश्यकता है, तो आपको वांछित अक्ष को उसके पहले स्थान पर रखने के लिए ट्रांसपोज़ेशन का उपयोग करना होगा, और फिर उसे अपने स्थान पर वापस करना होगा। उपरोक्त उदाहरण पर विचार करें, लेकिन सरणी A के स्तंभों के वेक्टर B द्वारा गुणा के साथ:

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]

(, , , , , , ..) NumPy . :

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]

NumPy .

<>



. dot(A, B). , :

  • (), ;
  • ( ) , ;
  • , ( );
  • ( ) , ;
  • , — ;
  • , ( );
  • , ( ).

: , — , .

:

 #  A = 2 B = 3 print(np.dot(A, B), '\n') #    A = np.array([2., 3., 4.]) B = 3 print(np.dot(A, B), '\n') #  A = np.array([2., 3., 4.]) B = np.array([-2., 1., -1.]) print(np.dot(A, B), '\n') #    A = np.array([[2., 3., 4.], [5., 6., 7.]]) B = 2 print(np.dot(A, B), '\n') Out: 6 [ 6. 9. 12.] -5.0 [[ 4. 6. 8.] [10. 12. 14.]]

, :
 #  ( 2)   ( 1) A = np.ones((5, 6)) B = np.ones(6) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') #  ( 2) A = np.ones((5, 6)) B = np.ones((6, 7)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') #   A = np.ones((5, 6, 7, 8)) B = np.ones((1, 2, 3, 8, 4)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') Out: A: (5, 6) B: (6,) result: (5,) A: (5, 6) B: (6, 7) result: (5, 7) A: (5, 6, 7, 8) B: (1, 2, 3, 8, 4) result: (5, 6, 7, 1, 2, 3, 4)

, dot tensordot :

 A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)

, — ( ).

<>



— NumPy . , , , , - - . , , .

, . , :

 A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]

mean average . . .

:

 A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]

sum — .

:

  • : sum nansum — nan;
  • : prod nanprod;
  • : average mean (nanmean), nanaverage ;
  • : median nanmedian;
  • : percentile nanpercentile;
  • : var nanvar;
  • ( ): std nanstd;
  • : min nanmin;
  • : max nanmax;
  • , : argmin nanargmin;
  • , : argmax nanargmax.

argmin argmax (, nanargmin, nanargmax) , .

, . argmin argmax , - ravel().

, NumPy, : np.aggregator(A, axes) A.aggregator(axes), aggregator , axes — .

 A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]

<>


—


.

.



, :



. ( ), , :

 def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J

, :

 I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)

:





;





;





.

, . . . : NumPy .

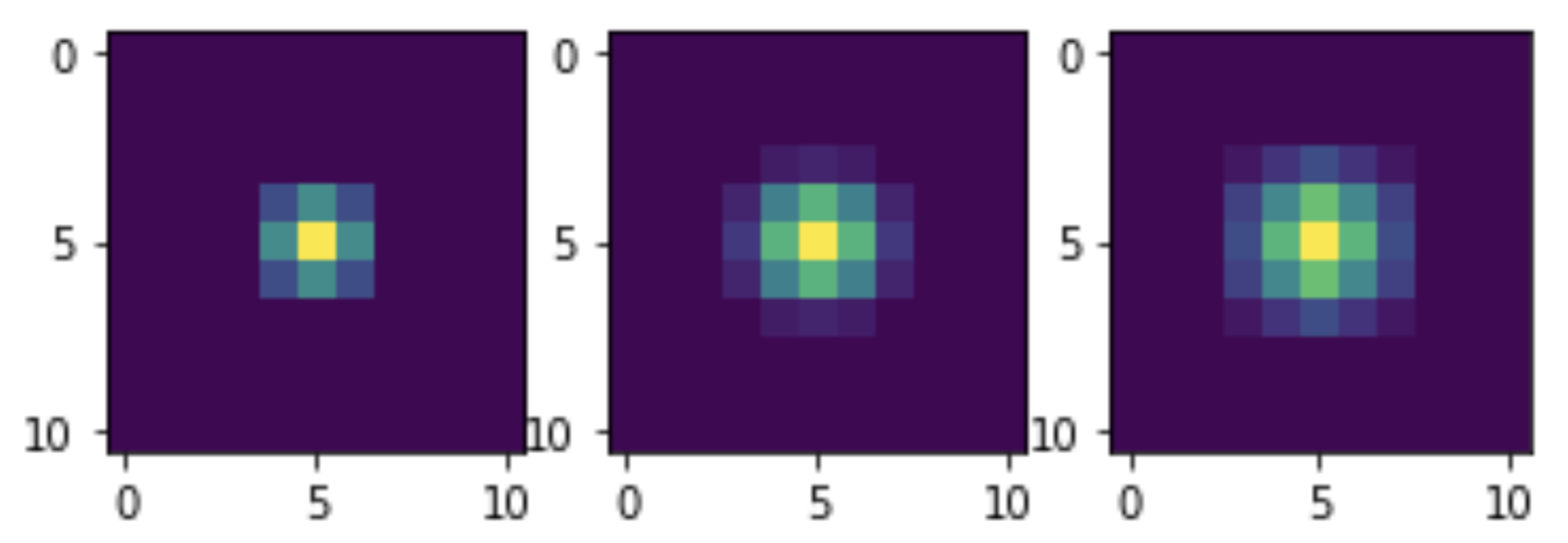
, . . , 255, . :

 M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()



NumPy, , !

<>

Source: https://habr.com/ru/post/hi469355/

More articles:


All Articles