Arend - HoTT- आधारित आश्रित प्रकार की भाषा (भाग 1)

इस पोस्ट में, हम Arend पर निर्भर प्रकारों के साथ नव जारी JetBrains भाषा के बारे में बात करेंगे (भाषा गेटिंग किराए के नाम पर है )। यह भाषा पिछले कुछ वर्षों में JetBrains रिसर्च द्वारा विकसित की गई है। हालांकि एक साल पहले रिपॉजिटरी को सार्वजनिक रूप से github.com/JetBrains पर उपलब्ध कराया गया था, लेकिन Arend की पूरी रिलीज़ केवल इस साल जुलाई में हुई।

हम यह बताने की कोशिश करेंगे कि अर्नेंड कैसे निर्भर प्रकारों के आधार पर औपचारिक गणित की मौजूदा प्रणालियों से अलग है, और अब क्या कार्यक्षमता इसके उपयोगकर्ताओं के लिए उपलब्ध है। हम मानते हैं कि इस लेख के पाठक आम तौर पर आश्रित प्रकारों से परिचित होते हैं और उन्होंने कम से कम एक भाषा को आश्रित प्रकारों के आधार पर सुना है: एजडा, इदरिस, कोक, या लीन। हालाँकि, हम पाठक से एक उन्नत स्तर पर निर्भर प्रकारों की अपेक्षा नहीं करते हैं।

सरलता और संक्षिप्तता के लिए, Arend और homotopy प्रकारों के बारे में हमारी कहानी सरलतम सॉर्टिंग एल्गोरिथ्म के Arend पर कार्यान्वयन के साथ होगी - इस उदाहरण के साथ भी, आप Arend और Agda और Coq के बीच अंतर महसूस कर सकते हैं। आश्रित प्रकारों के लिए समर्पित Habré पर पहले से ही कई लेख हैं। आइए Agda पर क्विकॉर्ट विधि का उपयोग करके छंटाई सूचियों के कार्यान्वयन के बारे में ऐसा एक लेख है । हम आवेषण छँटाई के लिए एक सरल एल्गोरिथ्म लागू करेंगे। इस मामले में, हम Arend भाषा के निर्माण पर ध्यान केंद्रित करते हैं, न कि छँटाई एल्गोरिथ्म पर।

अतः, अर्नेंड और अन्य भाषाओं पर निर्भर प्रकारों के साथ मुख्य अंतर तार्किक सिद्धांत है, जिस पर यह आधारित है। Arend हाल ही में खोजे गए V. Vvvodsky homotopy type theory ( HoTT ) के रूप में उपयोग करता है। विशेष रूप से, Arend HoTT की भिन्नता पर आधारित है जिसे "रिक्ति के साथ प्रकार सिद्धांत" कहा जाता है। स्मरण करो कि Coq आगमनात्मक निर्माणों (पथरी के प्रेरक निर्माणों) के तथाकथित कलन पर आधारित है, जबकि अगाडा और इदरिस मार्टिन-लोफ प्रकार के सिद्धांत पर आधारित हैं। तथ्य यह है कि Arend HoTT पर आधारित है, इसके सिंटैक्टिक कंस्ट्रक्शन और टाइप चेकिंग एल्गोरिथ्म (टाइपचेकर) के संचालन को महत्वपूर्ण रूप से प्रभावित करता है। हम इस लेख में इन विशेषताओं पर चर्चा करने जा रहे हैं।

आइए भाषा के बुनियादी ढांचे की स्थिति का संक्षेप में वर्णन करने का प्रयास करें। Arend के लिए IntelliJ IDEA के लिए एक प्लगइन है, जिसे सीधे IDEA प्लगइन्स के रिपॉजिटरी से इंस्टॉल किया जा सकता है। सिद्धांत रूप में, प्लगइन स्थापित करना Arend के साथ पूरी तरह से काम करने के लिए पर्याप्त है, फिर भी आपको कुछ भी डाउनलोड और इंस्टॉल करने की आवश्यकता नहीं है। टाइप चेकिंग के अलावा, Arend plugin IDEA उपयोगकर्ताओं के लिए परिचित कार्यक्षमता प्रदान करता है: कोड का हाइलाइटिंग और संरेखण, विभिन्न रिफ्लेक्टरिंग और टिप्स हैं। Arend के कंसोल संस्करण का उपयोग करने का विकल्प भी है। स्थापना प्रक्रिया का अधिक विस्तृत विवरण यहां पाया जा सकता है ।

इस लेख में कोड उदाहरण Arend Standard Library पर आधारित हैं, इसलिए हम इसके सोर्स कोड को रिपॉजिटरी से डाउनलोड करने की सलाह देते हैं। डाउनलोड करने के बाद, सोर्स डायरेक्टरी को आयात प्रोजेक्ट कमांड का उपयोग करके IDEA प्रोजेक्ट के रूप में आयात किया जाना चाहिए। Arend में, होमोटोपी प्रकार के सिद्धांत और रिंग सिद्धांत के कुछ वर्गों को पहले ही औपचारिक रूप दिया जा चुका है। उदाहरण के लिए, मानक पुस्तकालय में सभी आवश्यक रिंग-प्रमेय गुणों के प्रमाणों के साथ तर्कसंगत संख्या Q की रिंग का कार्यान्वयन है।

विस्तृत भाषा प्रलेखन , जिसमें इस लेख में शामिल कई बिंदुओं को अधिक विस्तार से समझाया गया है, सार्वजनिक डोमेन में भी है। आप टेलीग्राम चैनल में सीधे Arend Developers से सवाल पूछ सकते हैं।

1. HoTT / Arend का अवलोकन

होमोटोपी प्रकार का सिद्धांत (या संक्षेप में, HoTT) एक प्रकार का अंतरंग प्रकार का सिद्धांत है जो शास्त्रीय मार्टिन-लोफ प्रकार के सिद्धांत (MLTT, जिस पर Agda आधारित है) और आगमनात्मक निर्माण पथरी (CIC, जिस पर Coq आधारित है) से भिन्न होता है, उसी के साथ बयानों और सेटों में तथाकथित उच्च समरूपता स्तर के तथाकथित प्रकार होते हैं।

इस लेख में हमने अपने आप को HoTT की नींव को विस्तार से समझाने का लक्ष्य निर्धारित नहीं किया है - इस सिद्धांत के विस्तृत विवरण के लिए, पूरी पुस्तक को फिर से बेचना आवश्यक होगा ( यह पोस्ट देखें)। हम केवल ध्यान दें कि HoTT के स्वयंसिद्धों पर आधारित एक सिद्धांत, एक अर्थ में, शास्त्रीय मार्टिन-लोफ प्रकार के सिद्धांत की तुलना में बहुत अधिक सुरुचिपूर्ण और दिलचस्प है। इस प्रकार, कई स्वयंसिद्ध शब्द जिन्हें पहले अतिरिक्त रूप से पोस्ट किया जाना था (उदाहरण के लिए, कार्यात्मक विलक्षणता) को HoTT में प्रमेय के रूप में सिद्ध किया गया है। इसके अलावा, HoTT में, कोई आंतरिक रूप से बहुआयामी होमोटोपी क्षेत्रों को परिभाषित कर सकता है और यहां तक ​​कि अपने कुछ होमोटॉप समूहों को भी गिन सकता है।

हालाँकि, HoTT के ये पहलू मुख्य रूप से गणितज्ञों के लिए दिलचस्प हैं, और इस लेख का उद्देश्य यह बताना है कि कैसे HoTT- आधारित Arend की अगुडा / MLTT और Coq / CIC के साथ अनुकूलता की तुलना किसी भी प्रोग्रामर संस्थाओं के लिए सरल और परिचित के उदाहरण के रूप में की गई है, जो सूचियों का आदेश देती हैं। इस लेख को पढ़ते समय, यह HoTT को एक अधिक विकसित स्वयंसिद्ध के साथ एक प्रकार के गहन प्रकार के सिद्धांत के रूप में व्यवहार करने के लिए पर्याप्त है, जो सार्वभौमिक और समानता के साथ काम करते समय सुविधा देता है।

1.1 आश्रित प्रकार, करी - हावर्ड पत्राचार, ब्रह्मांड

याद रखें कि निर्भर प्रकारों वाली भाषाएं सामान्य डेटा प्रकारों के अलावा सामान्य डेटा प्रकारों से भिन्न होती हैं, जैसे कि सूचियाँ या प्राकृतिक संख्याएँ, ऐसे प्रकार होते हैं जो पैरामीटर मान पर निर्भर होते हैं। इस प्रकार के सबसे सरल उदाहरण किसी दिए गए लम्बाई के एन या संतुलित वृक्षों के वैक्टर हैं जो किसी गहराई के घ के हैं। इस प्रकार के कुछ और उदाहरणों का उल्लेख यहाँ किया गया है।

याद रखें कि करी - हावर्ड पत्राचार तर्क के बयानों पर निर्भर प्रकारों के रूप में व्याख्या करने की अनुमति देता है। इस पत्राचार का मुख्य विचार यह है कि एक खाली प्रकार एक गलत कथन से मेल खाता है, और आबादी वाले प्रकार एक सच्चे कथन के अनुरूप हैं। प्रकार तत्वों को इसी तार्किक कथन के प्रमाण के रूप में सोचा जा सकता है। उदाहरण के लिए, किसी भी तत्व जैसे पूर्णांक को इस तथ्य के प्रमाण के रूप में माना जा सकता है कि पूर्णांक मौजूद हैं (अर्थात पूर्णांक का प्रकार आबादी है)।

विभिन्न प्रकार के विभिन्न प्राकृतिक निर्माण अलग-अलग तार्किक संयोजनों के अनुरूप हैं:

• प्रकार ए × बी के उत्पाद को कभी-कभी जोड़ी ए बी का प्रकार कहा जाता है क्योंकि इस प्रकार को आबादी और अगर दोनों प्रकार के ए और बी आबादी वाले हैं, तो यह निर्माण तार्किक "और" से मेल खाता है।
• ए + बी प्रकार के योग हास्केल में, इस प्रकार को या तो ए बी कहा जाता है क्योंकि इस प्रकार को आबादी और अगर ए या बी प्रकारों में से एक आबादी है, तो यह निर्माण एक तार्किक "या" से मेल खाता है।
  
• कार्यात्मक प्रकार ए → बी। इस प्रकार का कोई भी फ़ंक्शन ए के तत्वों को बी के तत्वों में परिवर्तित करता है। इस प्रकार, ऐसा फ़ंक्शन ठीक उसी प्रकार मौजूद होता है, जब टाइप ए के तत्व का अस्तित्व टाइप बी के तत्व के अस्तित्व से होता है। इसलिए, यह निर्माण निहितार्थ से मेल खाता है।
  

मान लीजिए कि अब हमें A का एक निश्चित प्रकार A और प्रकार B का परिवार दिया गया है, जो A के एक तत्व के द्वारा परिमाणित है। आइए हम निर्भर प्रकारों पर अधिक जटिल निर्माणों के उदाहरण दें।

• आश्रित कार्य प्रकार Π (a: A) (B a)। यह प्रकार सामान्य कार्यात्मक प्रकार A → B के साथ मेल खाता है यदि B, A के प्रकार से स्वतंत्र है Π (a: A) (B) प्रकार A के प्रकार A के तत्व को किसी भी तत्व में परिवर्तित करता है। इस प्रकार, इस तरह के एक फ़ंक्शन मौजूद है यदि और केवल अगर, किसी के लिए : ए, एक तत्व बी मौजूद है। इसलिए, यह निर्माण सार्वभौमिक क्वांटिफायर से मेल खाता है onds। आश्रित कार्यात्मक प्रकार के लिए, Arend सिंटैक्स \Pi (x : A) -> B a , और इस प्रकार के शब्द का निर्माण लंबोदर अभिव्यक्ति \lam (a : A) => f a. उपयोग से किया जा सकता \lam (a : A) => f a.
• निर्भर जोड़े का प्रकार is (a: A) (B) है। यह प्रकार सामान्य प्रकार के ए × बी जोड़े के साथ मेल खाता है यदि बी ए से स्वतंत्र है। प्रकार Σ (ए: ए) (बी) एक तत्व के मौजूद होने पर सटीक रूप से आबादी है: ए और ए प्रकार बी का एक तत्व। इस प्रकार, यह प्रकार अस्तित्व मात्रा ∃ से मेल खाता है। Arend में निर्भर जोड़े के प्रकार को \Sigma (a : A) (B a) द्वारा दर्शाया जाता है, और इसे (निर्भर) जोड़ी के निर्माणकर्ता (a, b) उपयोग से निर्मित होने वाली शर्तों से जोड़ा जाता है।
  
• समानता का प्रकार a = a 'है, जहाँ a और' a 'कुछ प्रकार के दो तत्व हैं। ए ऐसा प्रकार आबाद है यदि a और' बराबर हैं, और अन्यथा खाली है। जाहिर है, इस प्रकार के तर्क में समानता की भविष्यवाणी का एक एनालॉग है।

इस बिंदु पर, हम पाठक को उन स्रोतों का उल्लेख करते हैं जिनमें करी - हावर्ड पत्राचार की अधिक विस्तार से जांच की जाती है (उदाहरण के लिए, एक व्याख्यान पाठ्यक्रम या यहां या यहां लेख)।

टाइप थ्योरी में विचार किए गए सभी अभिव्यक्तियों में कुछ प्रकार होना चाहिए। चूँकि इस सिद्धांत के ढांचे में प्रकारों को निरूपित करने वाले भावों पर भी विचार किया जाता है, इसलिए उन्हें एक निश्चित प्रकार को सौंपा जाना चाहिए। सवाल यह है कि यह किस प्रकार का होना चाहिए?

मन में आने वाला पहला भोला-भाला निर्णय है, सभी प्रकार के एक औपचारिक प्रकार को टाइप करने के लिए असाइन किया जाता है, जिसे ब्रह्मांड कहा जाता है (इसे इसलिए कहा जाता है क्योंकि इसमें सभी प्रकार सामान्य हैं)। यदि हम इस ब्रह्मांड का उपयोग करते हैं, तो उपर्युक्त राशि और प्रकार के उत्पाद, हस्ताक्षर \Type → \Type → \Type को प्राप्त करेंगे \Type → \Type → \Type _ \Type → \Type → \Type , और आश्रित उत्पाद के अधिक जटिल निर्माण और आश्रित राशि को हस्ताक्षर Π (A : \Type) → ((A → \Type) → \Type) ।

इस बिंदु पर, यह सवाल उठता है कि किस प्रकार का \Type ब्रह्मांड खुद होना चाहिए? यह कहने की एक भोली कोशिश कि ब्रह्मांड का \Type , परिभाषा के अनुसार, \Type _ \Type ही गिरार्ड विरोधाभास की ओर जाता है, इसलिए एक एकल ब्रह्मांड के बजाय \Type ब्रह्मांड का एक अनंत पदानुक्रम मानते हैं , अर्थात्। ब्रह्मांडों की नेस्टेड श्रृंखला \Type 1 < \Type 2 < … , जिसका स्तर प्राकृतिक संख्याओं द्वारा गिना जाता है, और परिभाषा के अनुसार ब्रह्मांड का \Type i , ब्रह्मांड \Type (i+1) । ऊपर वर्णित प्रकार के निर्माणों के लिए, अधिक जटिल हस्ताक्षर भी पेश करने होंगे।

इस प्रकार, प्रकार सिद्धांत में ब्रह्मांड की आवश्यकता होती है ताकि किसी भी अभिव्यक्ति का एक निश्चित प्रकार हो। प्रकार के सिद्धांत की कुछ किस्मों में, ब्रह्मांडों का उपयोग दूसरे उद्देश्य के लिए किया जाता है: प्रकारों की किस्मों के बीच अंतर करने के लिए। हम पहले ही देख चुके हैं कि सेट और कथन विशेष प्रकार के मामले हैं। इससे पता चलता है कि यह सिद्धांत में बयानों के लिए एक अलग प्रोप ब्रह्मांड और सेट के लिए सेट _i ब्रह्मांडों की एक अलग पदानुक्रम को लागू करने के लिए समझ में आता है। यह कैलकुलस ऑफ इंडक्टिव कंस्ट्रक्शंस में इस्तेमाल किया जाने वाला दृष्टिकोण है, जिस सिद्धांत पर Coq प्रणाली आधारित है।

1.2 सरल आगमनात्मक प्रकार और पुनरावर्ती कार्यों के उदाहरण

सरलतम आगमनात्मक प्रकार के डेटा के आर्न्ड पर परिभाषाओं पर विचार करें: बूलियन प्रकार, प्राकृतिक संख्या प्रकार और बहुरूपी सूची। नए प्रेरक प्रकारों को पेश करने के लिए Arend \data कीवर्ड का उपयोग करता है।

\data Empty -- ,

\data Bool
| true
| false

\data Nat
| zero
| suc Nat

\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)

जैसा कि आप ऊपर दिए गए उदाहरणों से देख सकते हैं, \data कीवर्ड के बाद, आपको आगमनात्मक प्रकार और उसके निर्माणकर्ताओं की सूची निर्दिष्ट करनी होगी। उसी समय, डेटा प्रकार और कंस्ट्रक्टर्स के कुछ पैरामीटर हो सकते हैं। मान लें कि उदाहरण में List प्रकार में एक पैरामीटर A nil लिस्ट कंस्ट्रक्टर के कोई पैरामीटर नहीं हैं, और कंस्ट्रक्टर: -: के दो पैरामीटर हैं (जिनमें से एक टाइप A , और दूसरा टाइप List A )। ब्रह्मांड \Set में ऐसे प्रकार होते हैं जो \Set होते हैं (सेट की परिभाषा अगले भाग में दी जाएगी)। \infixr आपको कंस्ट्रक्टर के लिए infix संकेतन का उपयोग करने की अनुमति देता है: -: और, इसके अलावा, Arend पार्सर को बताता है कि ऑपरेटर: -: प्राथमिकता 5 के साथ एक सही-सहयोगी ऑपरेशन है।

Arend में, सभी कीवर्ड एक बैकस्लैश चरित्र ("\"), LaTeX से प्रेरित कार्यान्वयन से शुरू होते हैं। बस ध्यान दें कि Arend में शाब्दिक नियम बहुत उदार हैं: Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left और even n:Nat - ये सभी शाब्दिक शब्द Arend में मान्य पहचानकर्ताओं के उदाहरण हैं। अंतिम उदाहरण दिखाता है कि पहचानकर्ता और बृहदान्त्र वर्णों के बीच रिक्त स्थान को याद रखना Arend उपयोगकर्ता के लिए कितना महत्वपूर्ण है। ध्यान दें कि Arend आइडेंटिफ़ायर में इसे यूनिकोड वर्णों का उपयोग करने की अनुमति नहीं है (विशेष रूप से, आप सिरिलिक का उपयोग नहीं कर सकते हैं)।

\func को परिभाषित करने के लिए Arend \func कीवर्ड का उपयोग करता है। इस निर्माण का सिंटैक्स निम्नानुसार है: \func कीवर्ड के बाद, आपको फ़ंक्शन का नाम, उसके पैरामीटर और रिटर्न वैल्यू का प्रकार निर्दिष्ट करना होगा। किसी फ़ंक्शन को परिभाषित करने में अंतिम तत्व उसका शरीर है।

यदि स्पष्ट रूप से उस अभिव्यक्ति को निर्दिष्ट करना संभव है जिसमें दिए गए फ़ंक्शन की गणना की जानी है, तो फ़ंक्शन के शरीर को इंगित करने के लिए, टोकन => का उपयोग किया जाता है। उदाहरण के लिए, एक प्रकार का नकार कार्य की परिभाषा पर विचार करें।

 \func Not (A : \Type) : \Type => A -> Empty 

फ़ंक्शन का वापसी प्रकार हमेशा स्पष्ट रूप से निर्दिष्ट करने के लिए आवश्यक नहीं है। ऊपर दिए गए उदाहरण में, Arend स्वतंत्र रूप से टाइप Not लगाने में सक्षम होगा, और हम कोष्ठक के बाद ": \Type " अभिव्यक्ति को छोड़ सकते हैं।

जैसा कि अधिकांश औपचारिक गणित प्रणालियों में, उपयोगकर्ता को \Type ब्रह्मांड के लिए एक स्पष्ट भविष्य कहनेवाला स्तर निर्दिष्ट करने की आवश्यकता नहीं होती है, और जिन परिभाषाओं में सार्वभौमिक रूप से एक पूर्वानुमान स्तर को निर्दिष्ट किए बिना उपयोग किया जाता है उन्हें बहुरूपी माना जाता है।

अब एक फ़ंक्शन को परिभाषित करने का प्रयास करें जो सूची की लंबाई की गणना करता है। इस तरह के फ़ंक्शन को पैटर्न मिलान के माध्यम से पहचानना आसान है। इसके लिए Arend \elim कीवर्ड का उपयोग करता है। इसके बाद, आपको उन चर को निर्दिष्ट करना होगा जिनके द्वारा तुलना की जाती है (यदि एक से अधिक ऐसे चर हैं, तो उन्हें अल्पविराम से लिखा जाना चाहिए)। यदि तुलना सभी स्पष्ट मापदंडों के लिए की जाती है, तो चर के साथ \elim छोड़ा जा सकता है। यह तुलना के बिंदुओं के एक ब्लॉक के बाद होता है, एक दूसरे से एक ऊर्ध्वाधर पट्टी द्वारा अलग किया जाता है "" | इस ब्लॉक में प्रत्येक आइटम फॉर्म की एक अभिव्यक्ति है «, » => «» ।

 \func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs) 

ऊपर के उदाहरण में, length फ़ंक्शन का पैरामीटर ए घुंघराले ब्रेसिज़ से घिरा हुआ है। Arend में इन कोष्ठकों का उपयोग निहित तर्क देने के लिए किया जाता है, अर्थात तर्क है कि उपयोगकर्ता किसी फ़ंक्शन को कॉल करते समय या एक प्रकार का उपयोग करके छोड़ सकता है। ध्यान दें कि Arend में आप एक पैटर्न के साथ मिलान करते समय कंस्ट्रक्टर्स को नामित करने के लिए infix संकेतन का उपयोग नहीं कर सकते हैं, इसलिए नमूना उदाहरण में उपसर्ग संकेतन का उपयोग किया जाता है।

जैसे कि Coq / Agda, Arend में सभी कार्यों को पूरा करने की गारंटी दी जानी चाहिए (यानी, Arend में समाप्ति की जाँच मौजूद है)। लंबाई फ़ंक्शन की परिभाषा में, यह चेक सफल है, क्योंकि एक पुनरावर्ती कॉल सख्ती से पहले स्पष्ट तर्क को कम करता है। यदि ऐसी कोई कमी नहीं होती है, तो Arend एक त्रुटि संदेश देगा।

 \func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad 

Arend परिपत्र निर्भरता और पारस्परिक रूप से पुनरावर्ती कार्यों की अनुमति देता है जिसके लिए पूर्ण जाँच भी की जाती है। ए। एबेल के लेख के आधार पर इस चेक के एल्गोरिदम को लागू किया गया है। इसमें आपको उन स्थितियों का अधिक विस्तृत विवरण मिलेगा जो पारस्परिक रूप से पुनरावर्ती कार्यों को संतुष्ट करना चाहिए।

१.३ स्टेटमेंट से कैसे भिन्न होते हैं?

हमने पहले लिखा था कि प्रकार के उदाहरण सेट और स्टेटमेंट हैं। इसके अलावा, हमने Arend में coses को निरूपित करने के लिए keywords \Type और \Set का उपयोग किया। इस खंड में, हम और अधिक विस्तार से समझाने की कोशिश करेंगे कि कैसे स्टेटमेंट्स इन्टीरियर टाइप थ्योरी (MLTT, CIC, HoTT) की किस्मों के संदर्भ में अलग-अलग होते हैं, और साथ ही साथ यह भी समझाते हैं कि Arend में कीवर्ड्स \Prop , \Set और \Type क्या अर्थ होते हैं।

स्मरण करो कि शास्त्रीय मार्टिन-लोफ सिद्धांत में सेट और कथनों में प्रकारों का पृथक्करण नहीं है। विशेष रूप से, सिद्धांत रूप में केवल एक संचयी ब्रह्मांड है (जिसे या तो सेट इन एग्डा, या टाइप इन इदरिस, या सॉर्ट इन लीन) में दर्शाया गया है। यह दृष्टिकोण सबसे सरल है, लेकिन ऐसी परिस्थितियां हैं जिनमें इसकी कमियां प्रकट होती हैं। मान लीजिए कि हम "ऑर्डर की गई सूची" प्रकार को एक आश्रित जोड़ी के रूप में लागू करने की कोशिश कर रहे हैं जिसमें एक सूची और उसके आदेश का प्रमाण शामिल है। यह पता चला है कि "शुद्ध" एमएलटीटी के ढांचे में, समान तत्वों से मिलकर आदेशित सूचियों की समानता को साबित करना संभव नहीं होगा, जो कि एक ही समय में आदेश के प्रमाण के संदर्भ में भिन्न होते हैं। ऐसी समानता होना बहुत स्वाभाविक और वांछनीय होगा, इसलिए इसे साबित करने की असंभवता को एमएलटीटी में एक सैद्धांतिक दोष माना जा सकता है।

आगाडा में, इस समस्या को आंशिक रूप से अनैतिकता के तथाकथित एनोटेशन की मदद से हल किया जाता है ( स्रोत देखें, जिसमें सूची उदाहरण पर अधिक विस्तार से चर्चा की गई है)। ये एनोटेशन, हालांकि, MLTT सिद्धांत से एक निर्माण नहीं हैं, न ही वे प्रकारों पर पूर्ण-निर्मित निर्माण हैं (यह एक प्रकार के एनोटेशन के साथ चिह्नित करना असंभव है जो फ़ंक्शन तर्क में उपयोग नहीं किया जाता है)।

सीआईसी में, सीआईसी पर आधारित, दो अलग-अलग ब्रह्मांड हैं जो एक दूसरे में Prop : Prop (बयानों का ब्रह्मांड) और Set (सेटों का ब्रह्मांड), जो Type ब्रह्मांडों के व्यापक पदानुक्रम में डूबे हुए हैं। Prop और Set बीच मुख्य अंतर यह है कि चर पर कई प्रतिबंध हैं जिनका प्रकार Prop में Coq से संबंधित है। उदाहरण के लिए, उनका उपयोग गणनाओं में नहीं किया जा सकता है, और उनके लिए नमूने के साथ तुलना केवल अन्य कथनों के साक्ष्य के अंदर ही संभव है। दूसरी ओर, Prop ब्रह्मांड से संबंधित प्रकार के सभी तत्व असंगत प्रमाण के स्वयंसिद्ध में समान हैं, Coq.Logic.ProofIrrelevance में कथन देखें। इस स्वयंसिद्ध का उपयोग करके, हम ऊपर उल्लिखित आदेश सूचियों की समानता को आसानी से साबित कर सकते हैं।

अंत में, बयानों और ब्रह्मांडों के लिए Arend / HoTT दृष्टिकोण पर विचार करें। मुख्य अंतर यह है कि HoTT असंगत साक्ष्य के स्वयंसिद्ध के साथ फैलता है। यही है, HoTT में कोई विशेष स्वयंसिद्ध नहीं है जो यह बताता है कि बयानों के सभी तत्व समान हैं। लेकिन HoTT में, एक प्रकार, परिभाषा के अनुसार , एक बयान है अगर यह साबित किया जा सकता है कि इसके सभी तत्व एक दूसरे के बराबर हैं। हम एक प्रकार से एक विधेय को परिभाषित कर सकते हैं जो सच है यदि प्रकार एक कथन है:

 \func isProp (A : \Type) => \Pi (aa' : A) -> a = a' 

प्रश्न उठता है: इस विधेय को किस प्रकार संतुष्ट करते हैं, अर्थात् कथन हैं? यह सत्यापित करना आसान है कि यह खाली और सिंगलटन प्रकारों के लिए सही है। उन प्रकारों के लिए जहां कम से कम दो अलग-अलग तत्व हैं, यह अब सच नहीं होगा।

बेशक, हम चाहते हैं कि सभी आवश्यक तार्किक संयोजनों को बयानों पर परिभाषित किया जाए। धारा 1.1 में, हमने पहले से ही चर्चा की कि वे किस प्रकार प्रकार-सिद्धांत निर्माण का उपयोग करके निर्धारित किए जा सकते हैं। हालाँकि, निम्न समस्या है: हमने जो भी ऑपरेशन दर्ज किए हैं, वे सभी isProp संपत्ति को बनाए रखने के लिए isProp हैं। प्रकार के उत्पाद और (निर्भर) कार्यात्मक प्रकार के निर्माण इस संपत्ति को बनाए रखते हैं, जबकि प्रकार और निर्भर जोड़े के योग का निर्माण नहीं है। इस प्रकार, हम वजूद और अस्तित्व की मात्रा का उपयोग नहीं कर सकते।

इस समस्या को एक नए निर्माण की मदद से हल किया जा सकता है, जिसे तथाकथित प्रपोज़ल ट्रंकेशन HoTT में जोड़ा जाता है । यह डिज़ाइन आपको किसी भी प्रकार को एक बयान में बदलने की अनुमति देता है। इसे एक औपचारिक ऑपरेशन के रूप में माना जा सकता है, जो इस प्रकार के निवासियों को समान करने वाले सभी शब्दों को समान बनाता है। यह ऑपरेशन कुछ हद तक Agda की अपरिपक्वता के एनोटेशन के समान है, हालांकि, उनके विपरीत, यह हस्ताक्षर \Type -> \Prop साथ प्रकारों पर एक पूर्ण ऑपरेशन है।

बयानों का अंतिम महत्वपूर्ण उदाहरण किसी प्रकार के दो तत्वों की समानता है। यह पता चला है कि सामान्य मामले में समानता का प्रकार a = a' कथन होना आवश्यक नहीं है। प्रकार जिनके लिए यह एक है उन्हें सेट कहा जाता है:

 \func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a') 

सामान्य प्रोग्रामिंग भाषाओं में पाए जाने वाले सभी प्रकार इस विधेय को संतुष्ट करते हैं, अर्थात् उन पर समानता एक कथन है। उदाहरण के लिए, प्राकृतिक संख्याओं, पूर्णांक, सेटों के उत्पादों, सेटों की संख्याओं, सेटों के कार्यों, सेटों की सूचियों और सेटों से निर्मित अन्य प्रेरक डेटा प्रकारों के लिए यह सही है। इसका मतलब यह है कि यदि हम केवल ऐसे परिचित निर्माणों में रुचि रखते हैं, तो हम मनमाने प्रकारों के बारे में नहीं सोच सकते हैं जो इस विधेय को संतुष्ट नहीं करते हैं। Coq में पाए जाने वाले सभी प्रकार सेट हैं ।

यदि आप होमोटॉपी प्रकार के सिद्धांत से निपटना चाहते हैं तो टाइप सेट उपयोगी नहीं हैं। अभी के लिए, हम केवल एन-आयामी क्षेत्र की परिभाषा वाले मानक पुस्तकालय मॉड्यूल के लिए पाठक को संदर्भित करते हैं, एक प्रकार का एक उदाहरण जो एक सेट नहीं है।

Arend के पास क्रमशः विशेष ब्रह्माण्ड \Prop और \Set , जिसमें कथन और सेट शामिल हैं। यदि हम पहले से ही जानते हैं कि टाइप ए \Prop (या \Set ) ब्रह्मांड में समाहित है, तो Arend में संबंधित isProp (या isSet ) isSet के प्रमाण को पूर्व में निर्मित Path.inProp axiom का उपयोग करके प्राप्त किया जा सकता है (हम इस axiom का उपयोग करने का एक उदाहरण देते हैं) खंड 2.3 में)।

 \func inProp {A : \Prop} : \Pi (aa' : A) -> a = a' 

हम पहले ही नोट कर चुके हैं कि प्रकारों पर सभी प्राकृतिक निर्माणों को isProp संपत्ति बरकरार नहीं isProp है। उदाहरण के लिए, दो या अधिक निर्माणकर्ताओं के साथ आगमनात्मक डेटा प्रकार इसे कभी संतुष्ट नहीं करते हैं। जैसा कि ऊपर उल्लेख किया गया है, हम किसी भी प्रकार के बयान में बदल जाने वाले प्रोपोज़ल ट्रंकेशन निर्माण का उपयोग कर सकते हैं।
Arend लाइब्रेरी में, प्रोपोज़ल ट्रंकेशन के मानक कार्यान्वयन को Logic.TruncP कहा जाता है। हम एक प्रकार के तार्किक "या" को Arend में टाइप के योग को परिभाषित करते हुए परिभाषित कर सकते हैं:

 \data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/" 

Arend में, प्रोपोज़ली ट्रंकेटेड इंडक्टिव टाइप को परिभाषित करने के लिए एक और सरल और अधिक सुविधाजनक तरीका है। ऐसा करने के लिए, डेटा प्रकार को परिभाषित करने से पहले बस \truncated कीवर्ड जोड़ें। उदाहरण के लिए, Arend मानक पुस्तकालय में एक तार्किक "या" की परिभाषा निम्नानुसार दी गई है।

 \truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B 

भविष्य में काट-छाँट किए गए प्रकारों के साथ आगे के काम कोक में Prop ब्रह्मांड को सौंपे गए प्रकारों से मिलते जुलते हैं। उदाहरण के लिए, एक वैरिएबल का पैटर्न मिलान जिसका प्रकार एक कथन है केवल एक ऐसी स्थिति में अनुमति दी जाती है जहां अभिव्यक्ति के प्रकार को परिभाषित किया जा रहा है। इस प्रकार, फ़ंक्शन को परिभाषित करना हमेशा आसान होता Or-to-|| नमूने के साथ तुलना के माध्यम से, लेकिन यह उलटा कार्य करता है, केवल अगर टाइप ए `Or` बी एक बयान है (जो कि काफी दुर्लभ है, उदाहरण के लिए, जब प्रकार A और B दोनों बयान और एक दूसरे के परस्पर अनन्य हैं)।

 \func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight 

यह भी याद रखें कि Coq में ब्रह्मांडों के तंत्र की ख़ासियत यह है कि अगर कुछ परिभाषा को Prop ब्रह्मांड को सौंपा गया था, तो किसी भी तरह से गणना में इसका उपयोग करना संभव नहीं होगा। इस कारण से, खुद कोक डेवलपर्स प्रपोजल कंस्ट्रक्शन के उपयोग की अनुशंसा नहीं करते हैं , लेकिन यदि संभव हो तो उन्हें सेट के ब्रह्मांड से एनालॉग्स के साथ बदलने की सलाह देते हैं। एरेन्ड ब्रह्मांडों के तंत्र में यह कमी नहीं है, अर्थात, कुछ स्थितियों में गणना में बयानों का उपयोग करना संभव है। हम इस तरह की स्थिति का एक उदाहरण देंगे जब हम सूची के एल्गोरिथ्म के कार्यान्वयन पर चर्चा करेंगे।

Arend में 1.4 कक्षाएं

चूंकि हमारा लक्ष्य सरलतम सॉर्टिंग एल्गोरिथ्म को लागू करना है, इसलिए यह अपने आप को परिचित करने के लिए उपयोगी है ताकि अरमान मानक पुस्तकालय में उपलब्ध ऑर्डर किए गए सेटों के कार्यान्वयन के साथ खुद को परिचित कराया जा सके।

Arend में, कक्षाओं का उपयोग संचालन और स्वयंसिद्धों को एनकैप्सुलेट करने के लिए किया जाता है जो गणितीय संरचनाओं को परिभाषित करते हैं, और विरासत के उपयोग से इन संरचनाओं के बीच संबंधों को उजागर करने के लिए भी। कक्षाएं भी नाम स्थान हैं, जिसके अंदर निर्माण और सिद्धांतों को स्थान देना सुविधाजनक है जो अर्थ में उपयुक्त हैं।

बेस क्लास, जिसमें से सभी ऑर्डर क्लासेस को Arend विरासत में मिला है, BaseSet क्लास है, जिसमें होस्ट सेट के लिए पदनाम E अलावा कोई भी सदस्य नहीं है (यानी, वह सेट जिस पर BaseSet वंशज BaseSet पहले से ही विभिन्न ऑपरेशन हैं)। मानक एरेन्ड लाइब्रेरी से इस वर्ग की परिभाषा पर विचार करें।

 \class BaseSet (E : \Set) -- ,     

उपरोक्त परिभाषा में, वाहक E एक वर्ग पैरामीटर घोषित किया E । कोई पूछ सकता है कि, निम्नलिखित परिभाषा से BaseSet की उपरोक्त परिभाषा में कोई अंतर है, जिसमें वाहक ई को एक वर्ग के रूप में परिभाषित किया गया है?

 \class BaseSet' --      | E : \Set 

थोड़ा अप्रत्याशित उत्तर यह है कि Arend में इस अर्थ में दो परिभाषाओं में कोई अंतर नहीं है कि Arend में कोई भी क्लास पैरामीटर (यहां तक ​​कि निहित), वास्तव में इसका क्षेत्र है। इस प्रकार, BaseSet कार्यान्वयन के लिए, कोई व्यक्ति xE का उपयोग फ़ील्ड ई के उपयोग के लिए कर सकता है। BaseSet परिभाषा के उपरोक्त वेरिएंट के बीच अभी भी एक अंतर है, लेकिन यह अधिक सूक्ष्म है, हम अगले उदाहरण में इसकी अधिक विस्तार से जांच करेंगे जब हम कक्षा के उदाहरणों पर चर्चा करेंगे ( वर्ग उदाहरण)।

किसी सूची को छाँटने की क्रिया तभी समझ में आती है जब सूची में किसी प्रकार के ऑब्जेक्ट पर एक रेखीय क्रम निर्दिष्ट किया जाता है, इसलिए हम पहले एक सख्त आंशिक रूप से सेट की गई परिभाषा और एक रैखिक क्रमबद्ध सेट पर विचार करते हैं।

 \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y } 

प्रकार के सिद्धांत के दृष्टिकोण से, अरिंद में वर्गों को अनुमानों और निर्माणकर्ताओं के लिए अधिक सुविधाजनक वाक्यविन्यास के साथ सिग्मा प्रकारों के एनालॉग के रूप में माना जा सकता है। , Arend- -, .

, . , . , StrictPoset <-irreflexive <-transitive , E < — . , (, , ) , .

, , . , Arend , , . , . , , , , . :

 \class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y) 

Dec , Dec E , E , E , E .

 \data Dec (E : \Prop) | yes E | no (Not E) 

, , Dec ( decidable) Order.LinearOrder . Dec , , , trichotomy , , E , <. , Dec Comparable Java.

 \class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} --   | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} } 

Dec Dec , , , , . Dec , .

, Dec ( ). Dec , Arend ( Dec LinearOrder, DecSet ), , (diamond inheritance).

: , ( , ).

Dec Order.LinearOrder IDEA ( [Ctrl]+[H]), , .



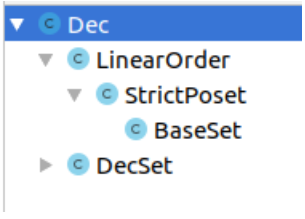
Arend ( IDEA BaseSet ). , .

1.5 , , .

StrictPoset Nat. Arend , . -, , , - ( ), .

: . .

 data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z') 

\func \lemma . , , , . , \lemma , \Prop .

x'<y' — -, x' < y' . - (.. , , ).

(instance) StrictPoset . Arend . \new . « ».

 \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

StrictPoset { … } \new : - StrictPoset . - , , , \new . \new C { … } C { … } . C, C. , , NatOrder StrictPoset .

, . , StrictPoset Nat StrictPoset { | E => Nat } . , NatOrder StrictPoset , ( ).

NatOrder \cowith ( - ).

 \func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

, , \instance.

 \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Arend , Haskell. NatOrder \instance \cowith , StrictPoset ( ).

, BaseSet - E ( ), , E . .

, Arend . Arend , , ( , « » \classifying \field , Arend ). :

• Arend . , X StrictPoset , List X List XE .
  
• Arend .

, . , \instance StrictPoset , Nat Int ( NatOrder IntOrder ).

, x < y , x, y , , x, y . Arend , NatOrder.< , — IntOrder.< .

, . Arend , < StrictPoset , E. , Arend x<y StrictPoset ( ), E . , < .

, Arend. , \use \coerce . Arend — , , . - , \where .

. fromNat .

 \data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n } 

\use \coerce \func , . , , (, , ).

: HoTT JetBrains Research.