मुझे एक दिलचस्प पहेली आई: वास्तव में, संख्या और धनात्मक पूर्णांक n दिए गए हैं। पुस्तकालयों का उपयोग किए बिना किसी संख्या की nth रूट की गणना करें।
इनपुट डेटा: संख्या वास्तविक, गैर-नकारात्मक, 1000 से अधिक नहीं है, 6 दशमलव स्थानों की सटीकता के साथ निर्दिष्ट है। संख्या n प्राकृतिक है, 10 से अधिक नहीं है।
आउटपुट: प्रोग्राम को एक एकल संख्या का उत्पादन करना चाहिए: कम से कम 5 दशमलव स्थानों की सटीकता के साथ समस्या का जवाब।
स्वाभाविक रूप से, एक पेंसिल के साथ एक मसौदे में इसे हल करना दिलचस्प था, और फिर इसे संपादक में आकर्षित करें और संकलन करने का प्रयास करें। पुस्तकालयों का उपयोग किए बिना, googling, टिप्स और भी बहुत कुछ। यदि आप यह पहली बार तय करते हैं, तो पहले सामान्य वर्गमूल को खोजने के लिए एक प्रोग्राम लिखने का प्रयास करें। यदि आपको कार्य कठिन लगता है, तो लगभग समान ही हल करें, लेकिन सरल। तब आपका डर दूर हो जाएगा और किसी न किसी तरह की समझ पैदा होगी।
शुरुआत के लिए, मैं लाइब्रेरी फंक्शन का उपयोग किए बिना वर्गाकार रूट की गणना करने का एक उदाहरण दूंगा। अनुक्रमिक Iteration एल्गोरिथ्म। यह बड़ी संख्याओं के लिए भी बहुत जल्दी परिवर्तित हो जाता है।
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
आप यहां कोड चला सकते हैं:
CLICKएल्गोरिथ्म के लघुगणक जटिलता? या कोई और? :)
अब आप कार्य के जटिल संस्करण पर आगे बढ़ सकते हैं। इस मामले में, समाधान अधिक सामान्यीकृत है।
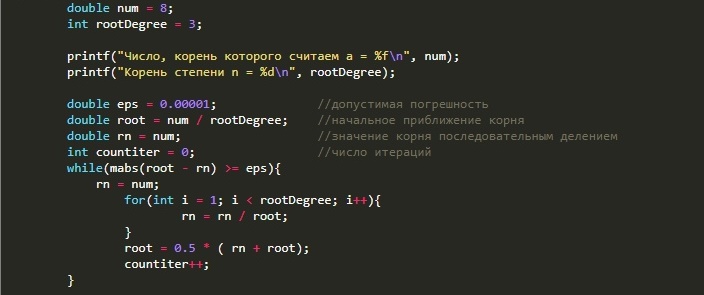
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
आप यहां कोड चला सकते हैं:
CLICKइस समाधान में, मैं अपेक्षाकृत अच्छे प्रारंभिक सन्निकटन के विचार का उपयोग करता हूं। फिर अनुक्रमिक विभाजन nth डिग्री की जड़ का दूसरा सन्निकटन है। इसके बाद, दो मौजूदा लोगों के औसत से एक नया अनुमान माना जाता है। लगातार, एल्गोरिथ्म पूर्व निर्धारित त्रुटि के साथ वांछित रूट में परिवर्तित होता है। यह एक साधारण पुनरावृत्ति विधि की तरह है।
यह घुटने पर लिखा गया पहला काम करने वाला एल्गोरिथम है। हमें अभी भी त्वरण की जटिलता और संभावनाओं को प्रतिबिंबित करने की आवश्यकता है। वैसे, आपकी राय में इस एल्गोरिदम के त्वरण की क्या विशेषताएं लागू की जा सकती हैं?
मुझे लगता है कि एक सवाल होगा: "अगर यह सब कुछ सौ साल पहले पुस्तकालयों में लागू किया गया था तो क्यों?"
उत्तर: व्यक्तिगत रूप से, मैं हमेशा एल्गोरिदम के बारे में सोचना पसंद करता था जो पहले से ही मानक पुस्तकालयों में लागू होते हैं। उन्हें स्वयं विकसित करने की कोशिश करें (अच्छी तरह से, या कुछ प्रकार की धीमी गति से चलने वाली पैरोडी और असफलता विकसित करने के लिए)। यह मस्तिष्क को बहुत अच्छी तरह से प्रशिक्षित करता है। इसलिए, मेरी राय में, "पहिया को फिर से मजबूत करना" बहुत उपयोगी है। और यह आंतरिक संरचना के किसी भी विचार के बिना, हमेशा तैयार सब कुछ का उपयोग करने के लिए स्पष्ट रूप से हानिकारक है।