लेख अपनी अवधि को कम करने के संदर्भ में एक प्रभावी बॉन्ड पोर्टफोलियो बनाने के लिए एक कार्यक्रम विकसित करने के अनुभव पर चर्चा करेगा। शायद मैं मूल नहीं होगा और उन सभी के लिए जो बांड में निवेश करते हैं, इष्टतम वजन निर्धारित करने के मुद्दों को लंबे समय से हल किया गया है, लेकिन फिर भी, मुझे उम्मीद है कि वर्णित दृष्टिकोण और प्रदान किया गया प्रोग्राम कोड किसी के लिए उपयोगी होगा।

इसमें थोड़ी मात्रा में गणित की उपस्थिति के कारण लेख किसी को जटिल लग सकता है। लेकिन अगर आपने पहले ही निवेश शुरू करने का फैसला कर लिया है, तो आपको इस तथ्य के लिए तैयार रहने की जरूरत है कि गणित अक्सर वित्तीय वास्तविकता में पाया जाता है और यह और भी जटिल है।

कार्यक्रम का स्रोत कोड और अनुकूलन के लिए एक उदाहरण पोर्टफोलियो GitHub पर उपलब्ध है।

अद्यतन: जैसा कि वादा किया गया था, ने एक सरल वेब सेवा बनाई जो कोड की नकल या संकलन के बिना सभी को कार्यक्रम उपलब्ध कराती है।
लिंक
एक ही स्थान पर उपयोग के लिए निर्देश।
यदि कुछ काम नहीं करता है या आपको कुछ ठीक करने की आवश्यकता है - टिप्पणियों में लिखें।

इसलिए, हमारे पास बांडों का एक प्रभावी पोर्टफोलियो बनाने का काम है।

भाग 1. पोर्टफोलियो की अवधि का निर्धारण

गैर-प्रणालीगत जोखिमों (जिसके लिए पोर्टफोलियो में विविधता है) को कम करने के दृष्टिकोण से, किसी विशेष मुद्दे, जारीकर्ता (यदि ओएफजेड तक सीमित नहीं है), कागज व्यवहार आदि के मापदंडों पर विचार करके प्रतिभूतियों का चुनाव किया गया था। (इस तरह के विश्लेषण के दृष्टिकोण प्रत्येक निवेशक के लिए काफी व्यक्तिगत हैं और इस लेख में विचार नहीं किया गया है)।

कई प्रतिभूतियों का चयन करना जो निवेश के लिए सबसे बेहतर हैं, एक स्वाभाविक प्रश्न उठता है: आपको प्रत्येक मुद्दे के कितने टुकड़ों को खरीदने की आवश्यकता है? यह पोर्टफोलियो के अनुकूलन का कार्य है ताकि पोर्टफोलियो के जोखिम कम से कम हों।

अवधि को एक अनुकूलित पैरामीटर के रूप में माना जाना स्वाभाविक है। इस प्रकार, कार्य पोर्टफोलियो में प्रतिभूतियों के वजन का निर्धारण करना है, जैसे कि पोर्टफोलियो की अवधि कुछ निश्चित पोर्टफोलियो उपज के लिए न्यूनतम होगी। यहाँ आपको कुछ आरक्षण करने की आवश्यकता है:

1. बॉन्ड पोर्टफोलियो की अवधि इसके घटक प्रतिभूतियों द्वारा निर्धारित की जाती है। ये अवधि ज्ञात हैं (वे सार्वजनिक डोमेन में हैं)। पोर्टफोलियो की अवधि इसमें शामिल प्रतिभूतियों की अधिकतम अवधि के बराबर नहीं है (ऐसी गिरावट है)। व्यक्तिगत प्रतिभूतियों की अवधि और संपूर्ण पोर्टफोलियो की अवधि के बीच संबंध रैखिक नहीं है, अर्थात। अपने घटक बॉन्ड की भारित औसत अवधि के बराबर नहीं है (यह सत्यापित करने के लिए, यह अवधि फॉर्मूला (नीचे (1) देखें) पर विचार करने के लिए पर्याप्त है) और उदाहरण के लिए, दो पेपरों से युक्त एक सशर्त पोर्टफोलियो की भारित औसत अवधि की गणना करने का प्रयास करें, इस तरह की अभिव्यक्ति में अवधि के लिए सूत्र का प्रतिस्थापन। प्रत्येक पेपर में, आउटपुट पर हमें पोर्टफोलियो की अवधि के लिए एक सूत्र नहीं मिलता है, लेकिन एक तरह का "बकवास", दो छूट दरों और असंगत नकदी प्रवाह के रूप में वजन)।
2. अवधि के विपरीत, पोर्टफोलियो रिटर्न इसमें शामिल उपकरणों के रिटर्न पर निर्भर करता है। यानी एक निश्चित आय के साथ कई उपकरणों में पैसा रखकर, हम प्रत्येक साधन में निवेश की मात्रा के लिए सीधे आनुपातिक रिटर्न प्राप्त करेंगे (और यह एक जटिल दर के लिए काम करता है, और सिर्फ एक साधारण के लिए नहीं)। सुनिश्चित करें कि यह और भी आसान है।
3. उपज की परिपक्वता ( YTM ) को बॉन्ड यील्ड दर के रूप में उपयोग किया जाता है। यह आमतौर पर अवधि की गणना करने के लिए उपयोग किया जाता है। हालांकि, पूरे पोर्टफोलियो की परिपक्वता के लिए उपज बल्कि मनमाना है, क्योंकि सभी प्रतिभूतियों की परिपक्वता अलग है। पोर्टफोलियो बनाते समय, इस विशेषता को इस अर्थ में ध्यान में रखा जाना चाहिए कि पोर्टफोलियो की समीक्षा की जानी चाहिए, किसी भी उपकरण से कम नहीं, जहां से यह बना है, संचलन से बाहर चला जाता है।

तो, पहला कार्य पोर्टफोलियो की अवधि की सही गणना है। ऐसा करने का तात्कालिक तरीका है: पोर्टफोलियो के लिए सभी भुगतानों का निर्धारण करना, उपज की परिपक्वता की गणना करना, भुगतानों की छूट, इन भुगतानों की शर्तों द्वारा प्राप्त मूल्यों को गुणा करना और जोड़ना। ऐसा करने के लिए, आपको पूरे पोर्टफोलियो के लिए सभी उपकरणों के भुगतान कैलेंडर को एक ही भुगतान कैलेंडर में संयोजित करने की आवश्यकता है, उपज को परिपक्वता की गणना करने के लिए एक अभिव्यक्ति लिखें, इसकी गणना करें, प्रत्येक भुगतान के लिए इसे छूट दें, इसकी नियत तारीख से गुणा करें, जोड़ें ... सामान्य तौर पर, एक बुरा सपना। दो पेपरों के लिए भी ऐसा करना एक बहुत ही श्रमसाध्य कार्य है, भविष्य में नियमित रूप से पोर्टफोलियो की पुनर्गणना का उल्लेख नहीं करना है। यह तरीका हमें शोभा नहीं देता।

इसलिए, एक अलग, तेज तरीके से पोर्टफोलियो की अवधि निर्धारित करने के लिए एक अवसर की तलाश करना आवश्यक है। एक स्वीकार्य विकल्प वह होगा जो आपको ज्ञात साधन अवधि द्वारा पोर्टफोलियो की अवधि निर्धारित करने की अनुमति देता है। अवधि सूत्र के अध्ययन से पता चला है कि इस तरह का एक रास्ता है और यहां मैं इसे विस्तार से देना चाहूंगा (यदि कोई गणना के गणितीय विवरणों में दिलचस्पी नहीं रखता है, तो आप सूत्र के साथ कुछ पैराग्राफों को सुरक्षित रूप से छोड़ सकते हैं और उदाहरण के लिए सीधे जा सकते हैं)।

एक ऋण साधन की अवधि को निम्नानुसार परिभाषित किया गया है:

$$$$ प्रदर्शन $ $ \ _ {समीकरण} D = \ frac {\ _ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~ (1) \ _ अंत {समीकरण} $ $ प्रदर्शन $ $

जहां:

• t _i , i-th भुगतान का समय है;
• $$$ इनलाइन $ \ start {समीकरण} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {समीकरण} $ इनलाइन $ - i-th रियायती भुगतान;
• सीएफ _मैं - आई-वें भुगतान;
• आर डिस्काउंट रेट है।

हम छूट गुणांक k = (1 + r) का परिचय देते हैं और रियायती भुगतान P की राशि को k के कार्य के रूप में मानते हैं:

$$$$ प्रदर्शन $ $ \ _ {समीकरण} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~ ~~~~ (2) \ अंत {समीकरण} $ $ प्रदर्शन $ $

K के संबंध में P को विभेदित करने पर , हम प्राप्त करते हैं

$$$$ प्रदर्शन $ $ \ _ {समीकरण} पी '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {{}} sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~ (3) \ end {समीकरण} $ $ $ $ प्रदर्शन

उत्तरार्द्ध को देखते हुए, बांड की अवधि के लिए अभिव्यक्ति रूप लेती है

$$$$ प्रदर्शन $$ \ start {समीकरण} D = -k \ frac {P ’(k)} {P (k)} ~~~~~~~~~~~~ (4) \ end {समीकरण} $ $ प्रदर्शन $ $

उसी समय, हम याद करते हैं कि बांड के मामले में छूट दर r के रूप में, परिपक्वता (YTM) के लिए उपज का उपयोग किया जाता है।

प्राप्त अभिव्यक्ति एक बंधन के लिए मान्य है, लेकिन हम बांड के एक पोर्टफोलियो में रुचि रखते हैं। आइए हम पोर्टफोलियो की अवधि निर्धारित करने के लिए आगे बढ़ते हैं।

हम निम्नलिखित संकेतन प्रस्तुत करते हैं:

• P _i , i-th बॉन्ड की कीमत है;
• z _i - पोर्टफोलियो में i-th बॉन्ड की प्रतिभूतियों की संख्या;
• k _i - पोर्टफोलियो में i-th बॉन्ड का छूट गुणांक;
• $$$ इनलाइन $ \ start {समीकरण} P_p = \ sum_ {i} {z_iP_i} \ end {समीकरण} $ इनलाइन $ - पोर्टफोलियो मूल्य;
• $$$ इनलाइन $ \ शुरू {समीकरण} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} अंत {समीकरण} $ इनलाइन $ - पोर्टफोलियो में आई-वें बॉन्ड का वजन; स्पष्ट आवश्यकता$$ $ इनलाइन $ \ start {समीकरण} \ sum_ {i} w_i = 1 \ end {समीकरण} $ इनलाइन $ ;
• $$$ इनलाइन $ \ start {समीकरण} k_p = \ sum_ {i} w_ik_i \ end {समीकरण} इनलाइन $ - पोर्टफोलियो छूट गुणांक;

भिन्नता की रैखिकता के कारण, निम्नलिखित सत्य है:

$$$$ प्रदर्शन $ $ \ _ {समीकरण} P'_p (k) = \ left (\ sum_ {i} z_iP_i (k) \ right) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~ (5) \ अंत {समीकरण} $ $ प्रदर्शन $ $

इस प्रकार, खाते (4) और (5) को ध्यान में रखते हुए, पोर्टफोलियो की अवधि के रूप में व्यक्त किया जा सकता है

$$$ $ प्रदर्शन $ $ \ शुरू {समीकरण} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ _ sum_ / j} z_jP'_j} {\ _ sum_ {j} z_jP_j} \ right) ~~~~~~~~~~~~~~ (6) \ end {समीकरण} $ $ प्रदर्शन $ $

(4) से यह स्पष्ट रूप से अनुसरण करता है$$ $ इनलाइन $ \ start {समीकरण} P'_j = - \ frac {D_jP_j} {k_j} \ end {समीकरण} $ इनलाइन $ ।
इस अभिव्यक्ति को (6) में प्रतिस्थापित करते हुए, हम पोर्टफोलियो की अवधि के लिए निम्नलिखित सूत्र पर आते हैं:

$$$ $ प्रदर्शन $ $ \ शुरू {समीकरण} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ _ sum_ {j} \ frac {D_j} {k_j} z_jP_j}} {\ _ sum_ {j} z_jP_j} \ right) = \ बाएँ (\ sum_ {i} w_ik_i \ right) \ बाएँ (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~ (7) \ _ अंत {समीकरण} $ $ प्रदर्शन $ $

शर्तों के तहत जब प्रत्येक उपकरण की परिपक्वता की अवधि और उपज ज्ञात होती है (और हम याद करते हैं, हम सिर्फ ऐसी स्थितियों में हैं), अभिव्यक्ति (7) अपने बांड की अवधि के आधार पर एक पोर्टफोलियो की अवधि निर्धारित करने के लिए वांछित सूत्र है। यह केवल दिखने में जटिल लगता है, लेकिन वास्तव में यह पहले से ही एमएस एक्सेल के सरलतम कार्यों की मदद से व्यावहारिक उपयोग के लिए तैयार है, जो अब हम एक उदाहरण के साथ करेंगे।

उदाहरण

सूत्र (7) के अनुसार पोर्टफोलियो की अवधि की गणना करने के लिए, हमें इनपुट डेटा की आवश्यकता होती है जिसमें पोर्टफोलियो में शामिल प्रतिभूतियों का वास्तविक सेट, उनकी अवधि और परिपक्वता के लिए उपज शामिल है। जैसा कि ऊपर उल्लेख किया गया है, यह जानकारी सार्वजनिक रूप से उपलब्ध है, उदाहरण के लिए, बांड के खंड विश्लेषण में वेबसाइट rusbonds.ru पर। स्रोत डेटा को एक्सेल प्रारूप में डाउनलोड किया जा सकता है।

एक उदाहरण के रूप में, प्रतिभूतियों के एक पोर्टफोलियो पर विचार करें जिसमें 9 बांड शामिल हैं। रस्बंड से डाउनलोड की गई मूल डेटा तालिका में निम्न रूप हैं।



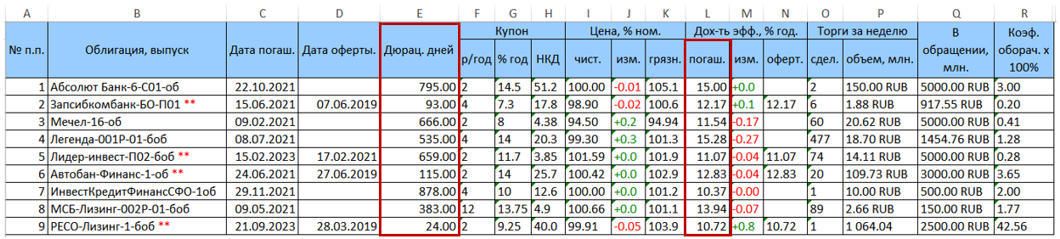
एक अवधि (स्तंभ ई) के साथ हमारे लिए ब्याज के दो कॉलम और परिपक्वता के लिए उपज (कॉलम एल = वाईटीएम) को लाल रंग में हाइलाइट किया गया है।

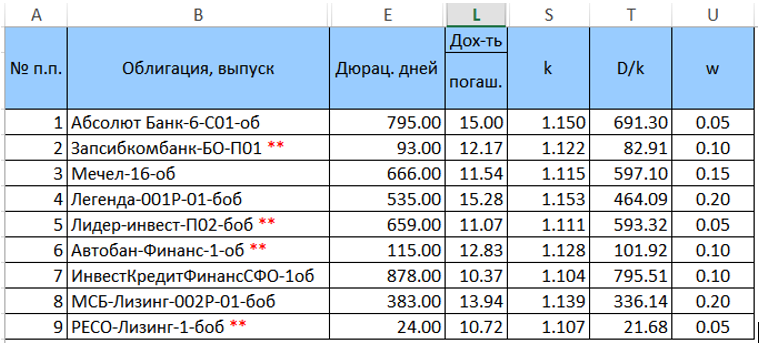
हम इस पोर्टफोलियो में बॉन्ड्स के लिए वेट सेट करते हैं (अब तक एक अनियंत्रित तरीके से, लेकिन इतना है कि उनकी राशि एकता के बराबर है) और k = (1 + YTM / 100) और D / k = ("कॉलम E" / k) की गणना करें। परिवर्तित तालिका (बिना अतिरिक्त कॉलम के) दिखेगी



अगला, हम उत्पाद की गणना करते हैं$$ $ इनलाइन $ \ start {समीकरण} w_j \ frac {D_j} {k_j} \ end {समीकरण} $ इनलाइन $ और$$ $ इनलाइन $ \ start {समीकरण} w_ik_i \ end {समीकरण} $ इनलाइन $ और उन्हें योग करें, और परिणामी मात्राओं को एक-एक करके गुणा करें। इस गुणन का परिणाम किसी दिए गए वज़न के वितरण के लिए वांछित अवधि होगी।



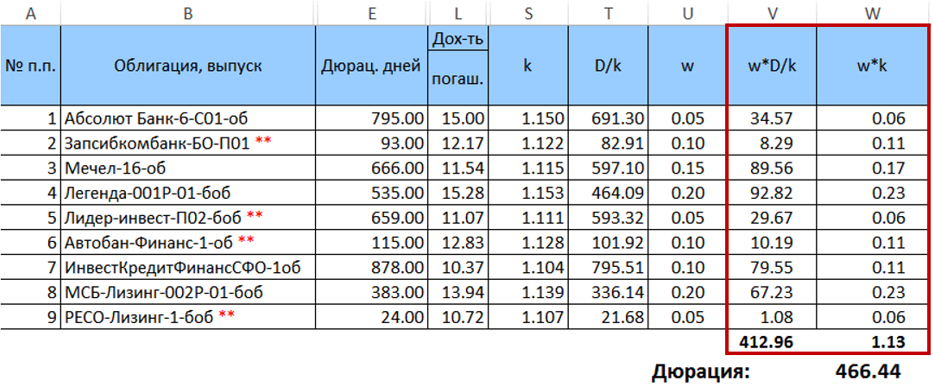
तो, पोर्टफोलियो की वांछित अवधि 466.44 दिन है। यह ध्यान रखना महत्वपूर्ण है कि इस विशेष मामले में, सूत्र द्वारा गणना की गई अवधि (7) एक ही भार (विचलन <0.5 दिन) के साथ गणना की गई भारित औसत अवधि से बहुत अलग है। हालांकि, यह अंतर वज़न के फैलाव में वृद्धि के साथ बढ़ता है। यह पेपर अवधि के प्रसार में वृद्धि के साथ भी बढ़ेगा।

जब हमने पोर्टफोलियो की अवधि की गणना के लिए सूत्र प्राप्त कर लिया है, तो अगला कदम प्रतिभूतियों के वजन का निर्धारण करना है ताकि किसी निश्चित समय पर पोर्टफोलियो की अनुमानित अवधि कम से कम हो। हम अगले भाग पर जाते हैं - पोर्टफोलियो ऑप्टिमाइज़ेशन।

भाग 2. बॉन्ड पोर्टफोलियो ऑप्टिमाइज़ेशन

मैट्रिक्स के साथ अभिव्यक्ति (7) एक द्विघात रूप है

$$$ $ प्रदर्शन $ $ \ शुरू {समीकरण} ए = \ बाएं \ {के_आई \ फ्राक {डी_जे} {के_ज} \ राइट \} = \ शुरू {pmatrix} D_1 & \ ldots & k_1 \ fd {D_n} {k_n} \ _ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {समीकरण} $ $ $ $ प्रदर्शन

तदनुसार, मैट्रिक्स रूप में, पोर्टफोलियो की अवधि के लिए अभिव्यक्ति (7) निम्नानुसार लिखी जा सकती है:

$$$$ प्रदर्शन $$ \ start {समीकरण} D_p = w ^ TAw ~~~~~~~~~~~~~ (8) \ end {समीकरण} $ $ प्रदर्शन $ $

जहां w पोर्टफोलियो में बॉन्ड वेट का कॉलम वेक्टर है। जैसा कि ऊपर बताया गया है, वेक्टर w के तत्वों का योग एकता के बराबर होना चाहिए। दूसरी ओर, अभिव्यक्ति $$$k_p = \ sum_ {i} w_i k_i$ (जो, संक्षेप में, एक साधारण स्केलर उत्पाद है ( w , k ) , जहां k बॉन्ड डिस्काउंट गुणांक का वेक्टर है) पोर्टफोलियो के लक्ष्य छूट दर के बराबर होना चाहिए, और इसलिए लक्ष्य पोर्टफोलियो रिटर्न सेट किया जाना चाहिए।

इस प्रकार, बॉन्ड पोर्टफोलियो को अनुकूलित करने का कार्य रैखिक बाधाओं के साथ द्विघात फ़ंक्शन (8) को कम करना है।

कई चर के एक समारोह के सशर्त चरम को खोजने की शास्त्रीय विधि लैग्रेंज गुणक विधि है। हालांकि, यह विधि यहां लागू नहीं है, यदि केवल इसलिए कि मैट्रिक्स ए निर्माण से पतित है (लेकिन केवल इस कारण से नहीं; हम यहां लैग्रेग विधि की प्रयोज्यता के विवरण को छोड़ देते हैं ताकि लेख को अत्यधिक गणितीय सामग्री से अधिभार न डालें)।

एक आसान और सस्ती विश्लेषणात्मक पद्धति को लागू करने में असमर्थता संख्यात्मक विधियों का उपयोग करने की आवश्यकता होती है। एक द्विघात फ़ंक्शन के अनुकूलन की समस्या सर्वविदित है और इसमें सार्वजनिक पुस्तकालयों में कई लंबे समय से विकसित कुशल एल्गोरिदम हैं।

इस विशेष समस्या को हल करने के लिए, ALGLIB पुस्तकालय और इसमें लागू द्विघात अनुकूलन एल्गोरिदम, QP-Solvers , minqp पैकेज में शामिल थे, का उपयोग किया गया था।

सामान्य रूप से द्विघात अनुकूलन समस्या इस प्रकार है:

फ़ंक्शन को कम करने के लिए एन-डायमेंशनल वेक्टर डब्ल्यू को खोजने की आवश्यकता है

$$$$ प्रदर्शन $ $ \ _ {समीकरण} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~ (9) \ end {समीकरण} $ $ प्रदर्शन $ $

दिए गए प्रतिबंधों के साथ
1) एल ) डब्ल्यू ≤ यू ;
2) सीडब्ल्यू * डी ;
जहाँ w, l, u, d, b n-आयामी वास्तविक मूल्यवान वैक्टर हैं, Q द्विघात भाग का सममितीय मैट्रिक्स है, और संकेत * का अर्थ किसी भी संबंध से है ≥ = u।
जैसा कि (8) से देखा जा सकता है, हमारे उद्देश्य फ़ंक्शन में रैखिक हिस्सा b ^t w शून्य के बराबर है। हालांकि, मैट्रिक्स ए सममित नहीं है, जो, हालांकि, फ़ंक्शन को बदले बिना इसे सममित रूप में लाने के लिए नहीं रोकता है। ऐसा करने के लिए, केवल ए की अभिव्यक्ति के बजाय रखो$$ $ इनलाइन $ \ start {समीकरण} \ frac {A ^ T + A} {2} \ end {समीकरण} $ इनलाइन $ । चूंकि सूत्र (9) में गुणांक शामिल है $$$\ frac {1} {2}$ तो हम क्यू के रूप में हम स्वीकार कर सकते हैं $$$ए ^ टी + ए$ ।

वैक्टर एल और यू के निर्देशांक वांछित वेक्टर की सीमाओं को निर्दिष्ट करते हैं और सीमा में निहित होते हैं [-1,1]। चूंकि हम बॉन्ड की कम बिक्री को नहीं मानते हैं, इसलिए हमारे मामले में वैक्टर के निर्देशांक सभी से कम नहीं हैं। नीचे दिए गए उदाहरण कार्यक्रम में, सादगी के लिए, वेक्टर एल को शून्य माना जाता है, और वेक्टर यू के गुणांक सभी 0.3 हैं । हालांकि, कुछ भी हमें कार्यक्रम को बेहतर बनाने और बाधा वाले वैक्टर को अधिक अनुकूलन बनाने से रोकता है।

मैट्रिक्स सी हमारे मामले में दो लाइनों से मिलकर बनेगा: 1) छूट गुणांक, जो, जब स्केल (जो (वी , के ) वजन) से गुणा हो जाता है , तो पोर्टफोलियो पर वापसी की लक्ष्य दर देनी चाहिए; 2) इकाइयों से मिलकर एक तार। इसकी सीमा तय करना आवश्यक है $$$\ sum_ {i} w_i = 1$ ।

इस प्रकार, हमारे कार्य के लिए अभिव्यक्ति Cw * d इस तरह दिखेगा:

$$$ $ प्रदर्शन $ $ \ _ शुरू {समीकरण} \ वाम \ {शुरू {सरणी} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {सरणी} \ सही। ~~~~~~~~~~~~~ (10) \ अंत {समीकरण} $ $ प्रदर्शन $ $

अब हम इष्टतम पोर्टफोलियो के लिए खोज के सॉफ़्टवेयर कार्यान्वयन की ओर मुड़ते हैं। ALGLIB में द्विघात अनुकूलक का आधार वस्तु है $$$\ tt \ small न्यूनतम $$

alglib::minqpstate state; 

ऑप्टिमाइज़र को इनिशियलाइज़ करने के लिए, इस ऑब्जेक्ट को कार्य आयाम पैरामीटर n के साथ minqpcreate फ़ंक्शन में दिया जाता है

 alglib::minqpcreate(n, state); 

अगला सबसे महत्वपूर्ण बिंदु अनुकूलन एल्गोरिथ्म (सॉल्वर) का विकल्प है। द्विघात अनुकूलन के लिए ALGLIB पुस्तकालय तीन सॉल्वर प्रदान करता है:

• QP-BLEIC सबसे सार्वभौमिक एल्गोरिदम है जिसे बहुत बड़ी नहीं (50 से अधिक तक प्रलेखन की सिफारिशों के अनुसार) रैखिक बाधाओं की संख्या (फॉर्म Cw * d ) की समस्याओं को हल करने के लिए डिज़ाइन किया गया है। इसी समय, यह बड़े आयाम के कार्यों पर प्रभावी हो सकता है (जैसा कि प्रलेखन का दावा है - n = 10000 तक)।
• QuickQP एक बहुत ही कुशल एल्गोरिदम है, खासकर जब एक उत्तल फ़ंक्शन को अनुकूलित किया जाता है। हालाँकि, दुर्भाग्य से, यह रैखिक बाधाओं के साथ काम नहीं कर सकता है - केवल सीमा स्थितियों (प्रपत्र l≤w≤u ) के साथ।
• घने-औल - बहुत बड़े आयामों और प्रतिबंधों की एक बड़ी संख्या के मामले के लिए अनुकूलित। लेकिन, प्रलेखन के अनुसार, छोटे एल्गोरिदम के कार्यों और प्रतिबंधों की संख्या अन्य एल्गोरिदम का उपयोग करके अधिक कुशलता से हल की जाएगी।

उपरोक्त विशेषताओं को देखते हुए, यह स्पष्ट है कि QP-BLEIC solver हमारे कार्य के लिए सबसे उपयुक्त है।

इस एल्गोरिदम का उपयोग करने के लिए ऑप्टिमाइज़र को निर्देश देने के लिए, आपको फ़ंक्शन को कॉल करना होगा $$$\ tt \ small minqpsetalgobleic$ । ऑब्जेक्ट स्वयं और स्टॉपिंग मानदंड इस फ़ंक्शन को पास किए जाते हैं, जिस पर हम अधिक विस्तार से नहीं जाएंगे: यहां पर दिए गए कार्यक्रम में, डिफ़ॉल्ट मानों का उपयोग किया जाता है। फ़ंक्शन कॉल निम्नानुसार है:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

सॉल्वर के आगे आरंभीकरण में शामिल हैं:

• द्विघात भाग के मैट्रिक्स का स्थानांतरण Q - $$$\ tt \ small अल्गलिब :: minqpsetquadraticterm (स्थिति, qpma):$
• रैखिक भाग के वेक्टर का संचरण (हमारे मामले में, शून्य वेक्टर) - $$$\ tt \ small एल्जीलिब :: minqpsetlinearterm (राज्य, बी);$
• सीमा स्थिति वैक्टर l और u का स्थानांतरण - $$$\ tt \ small अल्ग्लीब :: minqpsetbc (स्थिति, bndl, bndu।)$
• रैखिक ट्रांसमिशन - $$$\ tt \ small एल्जीलिब :: minqpsetlc (राज्य, सी, सीटी);$
• सदिश स्थान के समन्वय पैमाने को निर्धारित करना $$$\ tt \ small एल्जीलिब :: minqpsetscale (राज्य, s);$

चलो प्रत्येक आइटम पर रहते हैं:
वैक्टर और मैट्रिसेस निर्दिष्ट करने के लिए, ALGLIB पुस्तकालय विशेष प्रकार की वस्तुओं (पूर्णांक और वास्तविक-मूल्यवान) का उपयोग करता है: $$$\ tt \ small अल्जीब :: पूर्णांक \ _1 डी \ _अरे$ । $$$\ tt \ small alglib :: असली \ _1d \ _array$ । $$$\ tt \ small अल्ग्लीब :: पूर्णांक \ _2d \ _array$ । $$$\ tt \ small एल्जीलिब :: वास्तविक \ _2d \ _array$ । मैट्रिक्स तैयार करने के लिए, हमें एक प्रकार की आवश्यकता है $$$\ tt \ small वास्तविक \ _2d \ _array$ । कार्यक्रम में, पहले एक मैट्रिक्स बनाएं ( $$$\ tt \ small alglib :: वास्तविक \ _2d \ _array ~ qpma$ ), और फिर सूत्र के अनुसार $$$Q = A ^ T + A$ इससे हम मैट्रिक्स Q का निर्माण करते हैं ( $$$\ tt \ small alglib :: वास्तविक \ _2d \ _array ~ qpmq$ )। ALGLIB में मैट्रिक्स आयाम सेट करना एक अलग कार्य है $$$\ tt \ small setlength (एन, एम)$ ।

मेट्रिसेस के निर्माण के लिए, हमें छूट गुणांक ( k _i ) के वेक्टर और इन गुणांक में अवधि के संबंध की आवश्यकता है ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

मेट्रिसेस के निर्माण को लागू करने वाला कोड स्निपेट निम्नलिखित सूची में दिखाया गया है:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

रैखिक भाग के वेक्टर, जैसा कि पहले ही संकेत दिया गया है, हमारे मामले में शून्य है, इसलिए इसके साथ सब कुछ सरल है:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

वेक्टर सीमा की स्थिति एक फ़ंक्शन द्वारा प्रेषित होती है। इस समस्या को हल करने के लिए, बहुत सरल सीमा शर्तें लागू की जाती हैं: प्रत्येक पेपर का वजन शून्य से कम नहीं होना चाहिए (हम नकारात्मक स्थिति की अनुमति नहीं देते हैं) और 30% से अधिक नहीं होनी चाहिए। यदि वांछित है, तो प्रतिबंध जटिल हो सकते हैं। कार्यक्रम के साथ प्रयोगों से पता चला कि इस सीमा में एक साधारण बदलाव भी परिणामों को बहुत प्रभावित कर सकता है। इस प्रकार, निचली सीमा में वृद्धि और / या ऊपरी एक में कमी से अंतिम पोर्टफोलियो का अधिक विविधीकरण होता है, क्योंकि अनुकूलन के दौरान एक सॉल्वर परिणामी वेक्टर से कुछ प्रतिभूतियों को बाहर कर सकता है (उन्हें 0% का वजन असाइन करें) उपयुक्त नहीं है। यदि आप तराजू की निचली सीमा निर्धारित करते हैं, कहते हैं, 5% है, तो सभी कागजात को पोर्टफोलियो में शामिल करने की गारंटी है। हालांकि, इस तरह की सेटिंग्स पर गणना की गई अवधि, निश्चित रूप से उस स्थिति से अधिक होगी जब ऑप्टिमाइज़र पेपर को बाहर कर सकता है।

तो, सीमा की स्थिति दो वैक्टर द्वारा निर्धारित की जाती है और सॉल्वर को हस्तांतरित की जाती है:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

इसके बाद, अनुकूलक को सिस्टम द्वारा निर्दिष्ट रैखिक बाधाओं (10) को पारित करने की आवश्यकता होती है। ALGLIB में, यह फ़ंक्शन का उपयोग करके किया जाता है $$$\ tt \ small एल्जीलिब :: minqpsetlc (राज्य, सी, सीटी)$ , जहां c सिस्टम के बाएं और दाएं पक्षों का मैट्रिक्स संयोजन है (10), अर्थात मैट्रिक्स देखें $$$(C ~~ d)$ , और ct संबंधों का सदिश है (यानी, ≥, =, या ≥ के रूप के पत्राचार)। हमारे मामले में, ct = (0,0), जो सिस्टम की दोनों पंक्तियों (10) के अनुपात '=' से मेल खाती है।

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

ALGLIB लाइब्रेरी के लिए प्रलेखन, आशावादी शुरू करने से पहले चर के पैमाने को निर्धारित करने की अत्यधिक अनुशंसा करता है। यह विशेष रूप से महत्वपूर्ण है यदि चर इकाइयों में मापा जाता है, जिनमें से परिवर्तन परिमाण के आदेशों से भिन्न होता है (उदाहरण के लिए, जब कोई समाधान खोज रहा है, तो टन को सौवें या हज़ारवें और इकाइयों में मीटर में बदला जा सकता है; समस्या को टन मीटर की जगह में हल किया जा सकता है); जो परित्याग के मानदंडों को प्रभावित करता है। हालांकि, एक आरक्षण है कि चर के समान स्केलिंग के साथ, स्केल सेट करना आवश्यक नहीं है। विचाराधीन कार्यक्रम में, हम अभी भी दृष्टिकोण की अधिक कठोरता के लिए पैमाने का कार्य करते हैं, खासकर जब से यह करना बहुत सरल है।

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

अगला, हम अनुकूलक को एक प्रारंभिक बिंदु निर्धारित करते हैं। सामान्य तौर पर, यह कदम वैकल्पिक भी है, और कार्यक्रम सफलतापूर्वक स्पष्ट रूप से परिभाषित प्रारंभिक बिंदु के बिना कार्य के साथ मुकाबला करता है। इसी तरह, कठोरता के कारणों के लिए, हम शुरुआती बिंदु निर्धारित करते हैं। हम स्मार्ट नहीं होंगे: शुरुआती बिंदु सभी बॉन्ड के लिए एक ही भार के साथ बिंदु होगा।

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

यह उस चर को निर्धारित करने के लिए बना रहता है जिसमें ऑप्टिमाइज़र पाया गया समाधान और स्थिति चर वापस कर देगा। फिर आप अनुकूलन चला सकते हैं और परिणाम को संसाधित कर सकते हैं

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

विशेष रूप से, कार्यक्रम के रनटाइम को प्रयोगों में नहीं मापा गया था, लेकिन सब कुछ बहुत तेज़ी से काम करता है। इसी समय, यह स्पष्ट है कि एक निजी निवेशक 10-15 से अधिक बॉन्ड के पोर्टफोलियो का अनुकूलन करने की संभावना नहीं है।

निम्नलिखित पर ध्यान देना भी महत्वपूर्ण है। ऑप्टिमाइज़र वज़न के वेक्टर को ठीक से लौटाता है। गणना की गई अवधि को प्राप्त करने के लिए, आपको सीधे सूत्र (8) का उपयोग करना होगा। कार्यक्रम यह कर सकता है। इस प्रयोजन के लिए, वैक्टर और मैट्रिस को गुणा करने के दो कार्य विशेष रूप से जोड़े गए थे। हम उन्हें यहां नहीं देंगे। जो लोग खुद चाहते हैं, उन्हें आसानी से प्रकाशित स्रोत कोड में मिल जाएंगे।

वह सब है। सभी के लिए ऋण उपकरणों में एक प्रभावी निवेश।

PS यह समझना कि किसी और के कोड में चुनना सबसे आकर्षक व्यवसाय नहीं है, और कई लोग जो निवेश करना चाहते हैं, उनके लिए यह बिल्कुल भी विशेष नहीं है, मैं इस कार्यक्रम को बाद में एक साधारण वेब सेवा में शिफ्ट करने की कोशिश करूंगा, जिसका उपयोग हर कोई कर सकता है, गणित की जानकारी की परवाह किए बिना। और प्रोग्रामिंग।