🥞 🈺 🚕 सेलुलर ऑटोमेटा के लिए नियम 30 की समस्याओं को हल करने के लिए $ 30,000

मेरे ब्लॉग में मूल अनुवाद

स्टीवन वोल्फ्राम लाइव प्रतियोगिता प्रसारण (अंग्रेजी में)

प्रतियोगिता वेबसाइट

आइए हम पाठकों को समझाते हैं कि "नियम 30" का अर्थ क्या है - यह एक प्राथमिक सेलुलर ऑटोमेटन है ( विकी देखें), जिसका राज्य (पुराने के आधार पर कोशिकाओं के एक नए स्तर के निर्माण के लिए नियम) को द्विआधारी संख्या प्रणाली में 0-0-0-1-1-1 के रूप में सेट किया गया है -1-0, जिसे दशमलव संकेतन में 30 के रूप में व्याख्या किया जा सकता है।

तो यह सब कहां से शुरू हुआ? - "नियम 30"

यह कैसे हो सकता है कि कुछ अविश्वसनीय रूप से सरल कुछ अविश्वसनीय रूप से जटिल पैदा करता है ? मुझे नियम ३० से परिचित हुए लगभग ४० साल हो चुके हैं , लेकिन यह अभी भी मुझे हैरान करता है और मुझे प्रसन्न करता है। लंबे समय के लिए यह विज्ञान के इतिहास में मेरी व्यक्तिगत पसंदीदा खोज बन गया , पिछले कुछ वर्षों में इसने मेरे पूरे विश्वदृष्टि को बदल दिया है और मुझे विज्ञान, प्रौद्योगिकी, दर्शन और बहुत कुछ के लिए नए प्रकार की समझ पैदा की है ।

लेकिन इतने सालों के बाद भी, नियम 30 के बारे में अभी भी कई बुनियादी अवधारणाएं हैं जो हमारे लिए अप्राप्य हैं। और इसलिए मैंने तय किया कि इन बुनियादी पैटर्न के मूल सेट की पहचान करने की प्रक्रिया को प्रोत्साहित करने के लिए हर संभव प्रयास करने का समय है।

इसलिए, आज मैं आवेदकों को नियम 30 के बारे में तीन मुख्य सवालों के जवाब देने के लिए कुल पुरस्कार के रूप में $ 30,000 प्रदान करता हूं।

नियम 30 अत्यंत सरल है:

काले और सफेद कोशिकाओं (कोशिकाओं) की पंक्तियों का एक क्रम होता है और, काले और सफेद कोशिकाओं की एक विशिष्ट पंक्ति को देखते हुए, नीचे की पंक्ति में कोशिकाओं के रंगों को निर्धारित किया जाता है, प्रत्येक कोशिका को व्यक्तिगत रूप से और उसके निकटवर्ती कोशिकाओं को देखते हुए, फिर निम्नलिखित प्रतिस्थापन प्रतिस्थापन नियम उन पर लागू होते हैं, अर्थात्:

कोड
RulePlot[CellularAutomaton[30]]

[वीडियो देखें, जो कुछ मिनटों में सेलुलर ऑटोमेटा और नियम 30 का सार बताता है - अनुवादक का नोट]

यदि आप एक काले सेल से शुरू करते हैं तो क्या होगा? [ सफेद कोशिकाओं की एक पंक्ति को लिया जाता है, दोनों तरफ और एक काले सेल पर अनंत, फिर ऊपर दिखाए गए नियम इस पंक्ति पर लागू होते हैं, एक नई पंक्ति प्राप्त की जाती है, आदि - अनुवादक का नोट ] मान लीजिए (जैसा कि मैंने पहले खुद किया था) नियम काफी सरल है, और जो टेम्पलेट अपने काम के आधार पर प्राप्त किया जाता है, वह तदनुसार सरल भी होना चाहिए। हालाँकि, यदि आप एक प्रयोग करते हैं, तो आप देखेंगे कि एल्गोरिथ्म के पहले 50 चरणों के बाद क्या होता है:

कोड

RulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]

स्वाभाविक रूप से, हम मान सकते हैं कि एल्गोरिथ्म के परिणामस्वरूप, बहुत सरल गणितीय वस्तु प्राप्त की जाएगी। हालाँकि, यहाँ पहले 300 चरणों के बाद क्या होता है:

नियम 30 के पहले 300 चरण - विस्तार करने के लिए क्लिक करें

नियम 30 के पहले 300 चरण - विस्तार करने के लिए क्लिक करें

इससे पता चलता है कि एक निश्चित पैटर्न है - पिरामिड के बाईं ओर । लेकिन एक ही समय में, इस टेम्प्लेट के कई पहलू ऐसे दिखते हैं जैसे कोई चीज़ यादृच्छिक रूप से बनाई गई हो ।

यह समझ से बाहर है कि इस तरह का एक सरल नियम अंततः इस तरह के जटिल प्रणाली व्यवहार को जन्म दे सकता है। इसके आधार पर, मैं इस निष्कर्ष पर पहुंचा हूं कि सभी संभावित कंप्यूटर प्रोग्रामों के कंप्यूटिंग ब्रह्मांड में , यह व्यवहार काफी सामान्य है, और भी अधिक लगभग हर जगह पाया जाता है।

इस परिकल्पना के आधार पर, मैंने पूरी तरह से नए प्रकार के विज्ञान के गठन के लिए एक दृष्टिकोण विकसित किया - सरल एल्गोरिदम के संचालन को देखने के सिद्धांतों पर आधारित।

धीरे-धीरे, अधिक सबूत इन सिद्धांतों को जमा कर रहे थे।

हालाँकि, आइए हम नियम 30 पर लौटते हैं और विस्तार से विचार करते हैं कि यह हमें क्या करने की अनुमति देता है और इसका क्या उपयोग है? इस एल्गोरिथ्म के व्यवहार के बारे में वास्तव में क्या कहा जा सकता है? यह तुरंत स्पष्ट है कि यहां तक कि सबसे स्पष्ट प्रश्नों के उत्तर कठिन हो जाते हैं।

दशकों तक जिसके बाद भी कोई जवाब नहीं मिला, मैंने फैसला किया कि यह नियम 30 के बारे में कुछ विशिष्ट प्रश्न पूछने का समय था, जबकि इस क्षेत्र को गंभीर नकद पुरस्कारों से प्रेरित किया गया था।

मैंने पहले से ही 2007 में ऐसा ही कुछ करने की कोशिश की, एक विशिष्ट ट्यूरिंग मशीन के बारे में मूल प्रश्न का उत्तर देने के लिए एक पुरस्कार की स्थापना की । और इस मामले में, परिणाम सकारात्मक था और इंतजार करने में देर नहीं लगी। कुछ ही महीनों बाद, यह पुरस्कार जीता गया - हमेशा के लिए स्थापित होने वाला जो संभव सार्वभौमिक ट्यूरिंग मशीनों में से सबसे सरल है, और कम्प्यूटेशनल तुल्यता के सामान्य सिद्धांत को भी बहुत आश्वस्त करता है, जिसे मैंने व्यक्तिगत रूप से पहले विकसित किया था।

नियम 30 प्रतियोगिता एक बार फिर खुद को एक प्रमुख कार्य को हल करने का लक्ष्य निर्धारित करती है, अर्थात्: नियम 30 का व्यवहार कितना जटिल है ? प्रत्येक कार्य इस क्षेत्र में अपने तरीके से और विशेष रूप से एक प्रश्न बनता है। नियम 30 की तरह, वे सभी अपनी मूल सेटिंग में भ्रामक रूप से सरल हैं। फिर भी, उनमें से किसी का समाधान एक बड़ी उपलब्धि होगी, जो अंततः कंप्यूटिंग ब्रह्मांड के गठन के गुणों के मूल सिद्धांतों को रोशन करने में मदद करेगा, जो नियम 30 की बारीकियों से परे जाते हैं।

मैं 35 से अधिक वर्षों से इनमें से प्रत्येक मुद्दे पर काम कर रहा हूं। और इस बार मैंने कम से कम इन समस्याओं में से एक को हल करने के लक्ष्य के साथ लगातार गणितीय या कम्प्यूटेशनल सोच के ढांचे के भीतर सही विचार खोजने की कोशिश की। अब मैं इस प्रक्रिया को पूरे विश्व समुदाय के लिए खोलना चाहता हूं। हालांकि, मुझे यह जानने में दिलचस्पी होगी कि इन मुद्दों को हल करने में क्या हासिल किया जा सकता है, और इस मामले में किन तरीकों का इस्तेमाल किया जा सकता है।

नियम 30 - हल करने के लिए कार्य

नियम 30 के तहत प्रतिस्पर्धी कार्यों के लिए, मैं नियम 30 के एल्गोरिथ्म की प्रमुख विशेषताओं में से एक को प्राथमिकता देता हूं, अर्थात्: इसके केंद्रीय स्तंभ की कोशिकाओं के गठन की स्पष्ट यादृच्छिकता । एक काले सेल से शुरू करें, फिर इस कॉलम में कोशिकाओं के रंग मूल्यों के अनुक्रम पर एक नज़र डालें और आप इस निष्कर्ष पर पहुंचेंगे कि वे यादृच्छिक हैं:

कोड

ArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]

लेकिन वे किस मायने में "वास्तव में यादृच्छिक" हैं ? और क्या यह धारणा साबित हो सकती है? प्रतियोगिता के ढांचे के भीतर सेट किए गए प्रत्येक कार्य की अपनी यादृच्छिकता मानदंड का उपयोग किया जाता है, और उसके बाद यह पूछता है कि क्या अनुक्रम इस मानदंड के अनुसार यादृच्छिक है।

कार्य 1: क्या केंद्रीय स्तंभ हमेशा गैर-आवधिक रहता है?

नियम 30 के केंद्रीय स्तंभ की शुरुआत पर विचार करें:

कोड

ArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]

यह पता लगाना मुश्किल नहीं है कि इस कॉलम में मानों को दोहराया नहीं गया है - यह आवधिक नहीं है। लेकिन चुनौती यह है कि क्या केंद्रीय स्तंभ कभी भी समय-समय पर बनेंगे? नियम 30 को लॉन्च करने से, हम देखते हैं कि अनुक्रम पहले अरब चरणों में भी आवधिक नहीं हो जाता है। इसे कुछ के लिए स्थापित करने और साबित करने के लिए क्या करने की आवश्यकता है।

यहां वह लिंक है जहां इस क्रम के पहले मिलियन और पहले अरब मूल्य स्थित हैं ( वोल्फ्राम डेटा वेयरहाउस )।

कार्य 2: कोशिका का प्रत्येक रंग (काला या सफेद) औसत रूप से केंद्र स्तंभ में समान रूप से होने की संभावना है?

जब हम नियम 30 एल्गोरिथ्म के केंद्रीय स्तंभ में अधिक चरणों में क्रमिक रूप से काले और सफेद कोशिकाओं की संख्या की गणना करते हैं तो यह हमें मिलता है:

The number of black and of white cells in the center column of rule 30

The number of black and of white cells in the center column of rule 30

कोड

Dataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]

परिणाम निश्चित रूप से काले और सफेद कोशिकाओं के बराबर हैं। यहां समस्याग्रस्त (समस्या का प्रश्न) यह प्रश्न है कि क्या यह संबंध चक्र में बढ़ती संख्या के साथ 1 में परिवर्तित होता है ।

कार्य 3: केंद्रीय स्तंभ के nth सेल की गणना के लिए कम से कम O ( n ) संचालन की आवश्यकता होती है?

केंद्र स्तंभ में nth सेल को खोजने के लिए, आप हमेशा n चरणों के लिए नियम 30 चला सकते हैं, नीचे की आकृति में चुने गए हीरे के अंदर सभी कोशिकाओं के मूल्यों की गणना करते हुए:

कोड

With[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]

लेकिन अगर आप इसे सीधे करते हैं, तो यह होगा

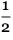n ² अलग सेल अपडेट, इसलिए, आवश्यक कंप्यूटिंग शक्ति O ( n ² ) के रूप में बढ़ जाती है। इस समस्या का सवाल यह है कि क्या सभी मध्यवर्ती गणनाओं के बिना nth सेल के मूल्य की गणना के लिए एक अधिक (या सबसे) सबसे तेज़ तरीका है - या, विशेष रूप से, O ( n ) संचालन से कम में ।

वह संख्याएँ जो पाई बनाती हैं

नियम 30 कंप्यूटिंग ब्रह्मांड का एक उत्पाद है: एक नई बौद्धिक संरचना के साथ संभावित सरल कार्यक्रमों के अध्ययन पर आधारित एक प्रणाली, जो कंप्यूटिंग के प्रतिमान द्वारा प्रदान की जाती है। हालाँकि , नियम ३० की प्रतियोगिता में मैंने जिन कार्यों को परिभाषित किया था, उनमें गणित के एनालॉग हैं, जो सदियों से हैं ।

संख्या पाई में संख्याओं के मूल्यों पर विचार करें। इन नंबरों का व्यवहार नियम 30 एल्गोरिदम के केंद्रीय कॉलम में डेटा की पीढ़ी के समान है। अर्थात्, उन्हें गणना करने के लिए एक दिया एल्गोरिथम है, और एक बार तैयार होने के बाद, वे किसी भी कार्य के लिए लगभग यादृच्छिक लगते हैं।

कोड

N[Pi, 85]

बस एनालॉग को थोड़ा करीब बनाने के लिए, आधार संख्या के साथ संख्या प्रणाली में पाई के पहले कुछ अंक यहां दिए गए हैं:

कोड

BaseForm[N[Pi, 25], 2]

और यहाँ नियम 30 के केंद्र स्तंभ में पहले कुछ बिट्स हैं:

कोड

Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]

मज़े के लिए, आप उन्हें दशमलव में बदल सकते हैं:

कोड

N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]

बेशक, पाई के अंकों की गणना के लिए प्रसिद्ध एल्गोरिदम नियम 30 के केंद्रीय स्तंभ में कोशिकाओं को बनाने के लिए अपेक्षाकृत सरल नियम की तुलना में अधिक जटिल हैं। तो, हम पाई में अंकों के बारे में क्या जानते हैं?

सबसे पहले, हम जानते हैं कि वे दोहराए नहीं जाते हैं। यह 18 वीं शताब्दी के 60 के दशक में वापस साबित हो गया था, जब यह दिखाया गया था कि पाई एक अपरिमेय संख्या है , क्योंकि केवल वही संख्याएँ जिनमें संख्याओं को दोहराया जाता है वे परिमेय संख्याएँ हैं। ( 1882 में, यह भी दिखाया गया था कि पाई ट्रान्सेंडैंटल है, अर्थात यह बहुपद की जड़ों के माध्यम से व्यक्त नहीं किया जा सकता है)।

तो समस्या 2 के निर्माण के साथ किस तरह की सादृश्यता तैयार की जा सकती है? क्या हम जानते हैं कि पाई के अंकों के अनुक्रम में , एक ही आवृत्ति के साथ अलग-अलग अंक होते हैं? आज तक , 100 ट्रिलियन से अधिक द्विआधारी अंकों की गणना की गई है - और मापा अंकों की आवृत्तियां बहुत करीब हैं (पहले 40 ट्रिलियन बाइनरी अंकों में पाई, इकाइयों का अनुपात शून्य से लगभग 0.99999998064 है)। लेकिन जब सीमा की गणना करते हैं, तो क्या आवृत्तियां बिल्कुल समान होंगी? वैज्ञानिक कई सदियों से यह सवाल पूछ रहे हैं, लेकिन अभी तक गणित इसका जवाब नहीं दे पाया है।

परिमेय संख्याओं के लिए, अंकों के अनुक्रम, जिनकी वे रचना करते हैं, आवधिक होते हैं, और एक संख्या में इन संख्याओं की घटना की सापेक्ष आवृत्तियों को निर्धारित करना आसान है। हालांकि, अन्य सभी के अंकों के अनुक्रम के लिए "प्रकृति द्वारा निर्मित (स्वाभाविक रूप से निर्मित)" संख्याएं, ज्यादातर मामलों में, व्यावहारिक रूप से कुछ भी ज्ञात नहीं है कि संख्या में शामिल अंकों की आवृत्तियों क्या होती हैं। यह मानना तर्कसंगत होगा कि वास्तव में पाई के अंक (साथ ही नियम 30 के केंद्रीय स्तंभ) इस अर्थ में " सामान्य " हैं कि न केवल प्रत्येक व्यक्तिगत अंक, बल्कि किसी दिए गए लंबाई के अंकों का कोई भी ब्लॉक समान अधिकतम आवृत्ति के साथ मिलता है। और, जैसा कि 1930 के दशक के इस विषय पर काम करता है, सामान्य संख्याओं के "डिजिटल निर्माण (मॉडल) का निर्माण" करना काफी संभव है। लगातार पूर्णांकों के अंकों को मिलाकर प्राप्त चम्पारणोन स्थिरांक उपरोक्त तर्क का एक उदाहरण है (इसे किसी भी सामान्य संख्या के आधार पर लगातार पूर्णांकों के कार्यों के मानों को मिलाकर प्राप्त किया जा सकता है):

कोड

N[ChampernowneNumber[10], 85]

यह ध्यान दिया जाना चाहिए कि यहां बिंदु यह है कि मानक गणितीय कार्यों के संयोजन द्वारा गठित "स्वाभाविक रूप से निर्मित" संख्याओं के लिए, एक भी खोजा गया उदाहरण नहीं मिला है जहां संख्याओं का कोई नियमित अनुक्रम पाया जाएगा। स्वाभाविक रूप से, अंत में, यह प्रावधान "नियमितता" से अभिप्राय है, जो इस बात पर निर्भर करता है कि कुछ स्तर पर यह कार्य एक प्रकार की डिजिटल-टू-एनालॉग खोज है जो अलौकिक बुद्धि के लिए है । हालांकि, इसका कोई सबूत नहीं है कि यह संभव नहीं है, उदाहरण के लिए, वर्ग जड़ों के कुछ जटिल संयोजन को खोजने के लिए जो कुछ बहुत स्पष्ट नियमितता के साथ संख्याओं का एक क्रम होगा।

तो, आखिरकार, पाई के लिए समस्या 3 के एनालॉग पर विचार करें? नियम 30 के विपरीत, जहां एक क्रम में तत्वों की गणना करने का स्पष्ट तरीका एक समय में एक कदम है, पाई के अंकों की गणना के लिए पारंपरिक तरीकों में एक सटीक संख्या के रूप में पाई के लिए सबसे अच्छा सन्निकटन शामिल हैं। 1910 में रामानुजन द्वारा आविष्कृत मानक ("विचित्र") श्रृंखला के साथ और 1989 में चुडनोव्स्की भाइयों द्वारा सुधार किया गया था, इस श्रृंखला के पहले कुछ सदस्य निम्नलिखित अनुमान देते हैं:

Standard series

कोड

Style[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]

तो nth अंक को खोजने के लिए कितने ऑपरेशन की आवश्यकता है? पंक्ति में आवश्यक शब्दों की संख्या O ( n ) है। लेकिन प्रत्येक स्थिति की गणना एन- डिजिट सटीकता के साथ की जानी चाहिए, जिसके लिए कम से कम हे ( एन ) अलग कम्प्यूटेशनल संचालन की आवश्यकता होती है, जिसका अर्थ है कि सामान्य कम्प्यूटेशनल वर्कलोड ओ ( एन ) से अधिक होगा।

1990 के दशक तक, यह मान लिया गया था कि पिछले सभी लोगों की गणना के बिना पाई के एनटी अंक की गणना करने का कोई तरीका नहीं है। लेकिन 1995 में, साइमन प्लफ ने खोजा कि वास्तव में गणना करना संभव है, हालांकि कुछ संभावना के साथ, पिछले अंकों की गणना के बिना एनटी अंक। और यद्यपि कोई यह सोचता है कि यह आपको n (O) संचालन से कम में nth अंक प्राप्त करने की अनुमति देगा, इस तथ्य कि आपको n- अंकों की सटीकता के साथ गणना करने की आवश्यकता है, जिसका अर्थ है कि कम से कम O ( n) ) संचालन।

परिणाम, उपमा और अंतर्ज्ञान

कार्य 1: क्या केंद्रीय स्तंभ हमेशा गैर-आवधिक रहता है?

नियम 30 प्रतियोगिता के तीन पुरस्कारों में से, यह वह है जिसमें इस मुद्दे को हल करने में अधिकांश प्रगति पहले ही हासिल की जा चुकी है। चूंकि यह अभी भी अज्ञात है कि क्या नियम 30 का केंद्रीय स्तंभ आवधिक हो जाएगा, 1986 में एरिका जेन ने दिखाया कि कोई भी दो स्तंभ आवधिक नहीं हो सकते। और वास्तव में यह ऐसा है, और एक व्यक्ति इस तथ्य के पक्ष में भी तर्क दे सकता है कि एक कॉलम दूसरे कॉलम में अलग-अलग कोशिकाओं के संयोजन में आवधिक नहीं हो सकता है ।

स्तंभों की जोड़ी का प्रमाण नियम 30 की एक विशेषता का उपयोग करता है। नियम की संरचना पर विचार करें:

कोड

RulePlot[CellularAutomaton[30]]

केवल यह कहना संभव है कि कोशिकाओं के प्रत्येक ट्रिपल के लिए नियम इसके द्वारा केंद्रीय सेल के रंग को निर्धारित करता है, लेकिन नियम 30 के लिए, आप नियम को प्रभावी रूप से पक्ष में भी निष्पादित कर सकते हैं: दाईं ओर और ऊपर सेल को ध्यान में रखते हुए, आप बाईं ओर सेल के रंग को विशिष्ट रूप से निर्धारित कर सकते हैं। इसका मतलब है कि यदि आप दो निकटवर्ती कॉलम लेते हैं, तो आप बाईं ओर पूरे टेम्पलेट को पुनर्स्थापित कर सकते हैं :

कोड

GraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - qr + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]

हालाँकि, यदि स्तंभों की आवधिक संरचना होती है, तो यह तुरंत होगा कि बहाल टेम्पलेट भी आवधिक होना चाहिए। इसलिए, उदाहरण के लिए, निर्माण द्वारा, कम से कम प्रारंभिक शर्तें निश्चित रूप से आवधिक नहीं हैं, और इसलिए दोनों कॉलम आवधिक नहीं हो सकते हैं। यदि स्तंभ समीप नहीं हैं, और यदि दोनों स्तंभों में सभी कोशिकाओं का पता नहीं है, तो यह कथन सही है। हालांकि, इस प्रावधान को केंद्रीय स्तंभ जैसे एकल स्तंभ के लिए वितरित करने का कोई ज्ञात तरीका नहीं है, और इस प्रकार यह नियम 30 के तहत प्रतियोगिता के पहले कार्य को हल नहीं करता है।

तो, इसे हल करने के लिए क्या इस्तेमाल किया जा सकता है? यदि यह पता चला है कि केंद्रीय स्तंभ अंततः आवधिक है, तो आप इसकी गणना कर सकते हैं। हम जानते हैं कि यह पहले अरब चरणों के लिए आवधिक नहीं है, लेकिन हम कम से कम यह मान सकते हैं कि खरबों चरणों के साथ एक संक्रमण प्रक्रिया हो सकती है, जिसके बाद यह आवधिक हो जाती है।

क्या आपको लगता है कि यह विश्वसनीय है? रोगी होते हैं - और सैद्धांतिक रूप से ( ट्यूरिंग मशीन को रोकने की शास्त्रीय समस्या के रूप में) वे मनमाने ढंग से लंबाई के भी हो सकते हैं। यहां हम कुछ उदाहरण देखते हैं - खोज के दौरान मिले - नियम 4 संभावित रंगों (सामान्य कोड 150898) के साथ। मान लें कि हमने इसे 200 चरणों में चलाया, और, जैसा कि आप देख सकते हैं, केंद्रीय स्तंभ पूरी तरह से यादृच्छिक होगा:

Rule 150898

कोड

ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]

500 चरणों के बाद, पूरा टेम्पलेट पूरी तरह से यादृच्छिक दिखता है:

Rule 150898

कोड

ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]

यहां आप देख सकते हैं कि केंद्रीय स्तंभ के पास पहुंचने पर, कुछ आश्चर्यजनक होता है: 251 चरणों के बाद, केंद्रीय स्तंभ एक निश्चित मूल्य (या कम से कम अगले एक लाख से अधिक चरणों में तय) के लिए पुनर्जन्म होता है:

Rule 150898

कोड

Grid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]

क्या नियम 30 में समान संक्रमण हो सकता है? नियम 30 से पैटर्न पर विचार करें, और उन लोगों का चयन करें जहां बाईं ओर विकर्णों की आवधिकता है:

कोड

steps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];

diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];

transientdiagonalrule30 = %;

transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;

decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];

transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];

transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];

smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];

Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]

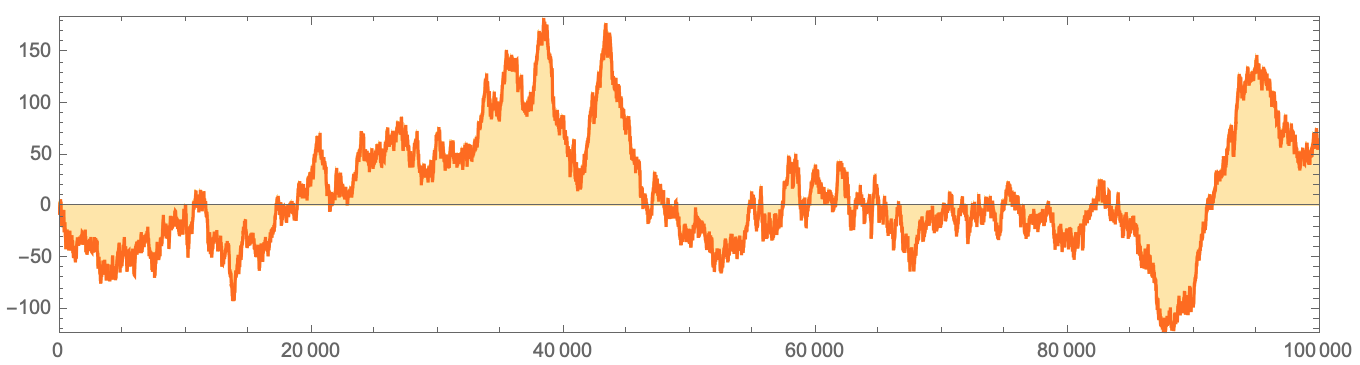
जाहिर है, यहां एक सीमा है जो विकार के बाईं ओर के क्रम को दाईं ओर अलग करती है। और, कम से कम पहले 100,000 कदम या तो, ऐसा लगता है कि सीमा प्रत्येक चरण पर बाईं ओर औसतन 0.252 कदमों से चलती है - कुछ यादृच्छिक विचलन के साथ :

कोड

data = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];

ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]

लेकिन हम अंततः यह कैसे पता लगा सकते हैं कि ये उतार-चढ़ाव किस बिंदु पर महत्वपूर्ण होंगे, इतना कि वे बाईं ओर के आदेश को केंद्र स्तंभ को पार करने के लिए मजबूर करते हैं और, शायद, पूरे टेम्पलेट को आवधिक भी बनाते हैं? उपलब्ध आंकड़ों को देखते हुए, यह अनुमान असंभव प्रतीत होता है, जबकि मैं बिल्कुल नहीं कह सकता कि यह कैसे निर्धारित किया जा सकता है।

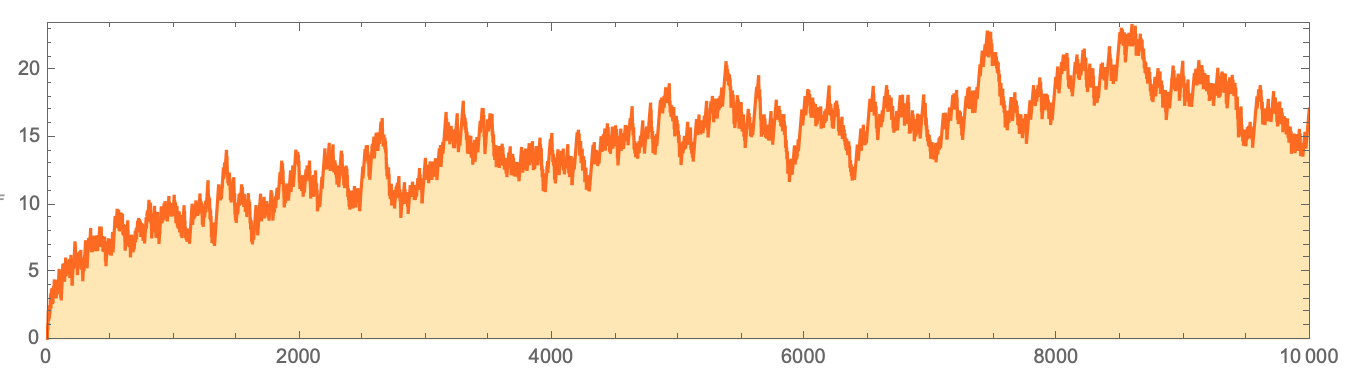
यह, निश्चित रूप से, वास्तव में ऐसा मामला है जो असाधारण रूप से लंबे "ग्राहकों" के साथ सिस्टम के अस्तित्व को दिखाता है। अब primes के वितरण पर विचार करें और LogIntegral की गणना करें [ n ] - प्राइमपी [ n ]

कोड

DiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]

हां, उतार-चढ़ाव हैं, लेकिन इस चित्रण में ऐसा लग रहा है कि यह अंतर हमेशा सकारात्मक क्षेत्र में होगा। और यह, उदाहरण के लिए, रामानुजन चर्चा कर रहे थे, लेकिन अंत में यह पता चला कि ऐसा नहीं है । शुरुआत में, जहां वह असफल रहा, उस समय की सीमा, खगोलीय रूप से बड़ी ( स्काइव नंबर 10 ^{10 ^{10 ⁹⁶⁴}} ) थी। और यद्यपि किसी ने अभी तक n का एक स्पष्ट मान नहीं पाया है जिसके लिए अंतर नकारात्मक है, यह ज्ञात है कि n = 10 ^{317 तक} यह मौजूद होना चाहिए (और अंततः अंतर नकारात्मक होगा)।

मैंने राय बनाई है कि नियम 30 के केंद्रीय कॉलम में कुछ भी नहीं होता है, लेकिन अभी तक हमारे पास कोई सबूत नहीं है कि यह असंभव है, यह तर्क नहीं दिया जा सकता है।

यह ध्यान दिया जाना चाहिए कि यह धारणा बनाना संभव है कि यद्यपि नियम 30 के केंद्रीय स्तंभ में नियमितता को प्रकट करके आवधिकता साबित करना मौलिक रूप से संभव है, गैर-आवधिकता के लिए कुछ भी नहीं किया जा सकता है। यह ज्ञात है कि ऐसे पैटर्न हैं जिनके केंद्रीय स्तंभ गैर-आवधिक हैं, हालांकि वे बहुत नियमित हैं। ऐसे उदाहरणों का मुख्य वर्ग नेस्टेड टेम्पलेट हैं। यहाँ, उदाहरण के लिए, नियम 161 से एक बहुत ही सरल चित्रण है, जिसमें केंद्र स्तंभ में सफेद कोशिकाएँ होती हैं जब n = 2 ^k :

Rule 161

कोड

GraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]

और यहाँ एक और अधिक जटिल उदाहरण है (दो पड़ोसियों के लिए 2-रंग नियम 69540422 से) , जिसमें केंद्रीय स्तंभ एक थ्यू - मोर्स अनुक्रम है - थ्यूमोरसे [ एन ]:

Thue-Morse sequence

कोड

GraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]

हम अनुमान लगा सकते हैं कि प्रतिस्थापन के अनुक्रमिक अनुप्रयोग द्वारा थ्यू - मोर्स अनुक्रम उत्पन्न होता है:

कोड

RulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]

यह पता चला है कि इस क्रम में nth शब्द Mod [ DigitCount [ n , 2, 1], 2] के रूप में सेट है - यह ऑब्जेक्ट कभी भी आवधिक नहीं होगा।

क्या ऐसा हो सकता है कि नियम 30 के केंद्रीय स्तंभ को प्रतिस्थापन द्वारा उत्पन्न किया जा सकता है? यदि ऐसा है, तो मैं इस तथ्य से चकित हो जाऊंगा (हालांकि बहुत जटिल प्रतिस्थापन प्रणालियां दिखाई देने पर प्राकृतिक उदाहरण प्रतीत होंगे ), लेकिन फिर से, जब तक कि इसका कोई सबूत नहीं है।

यह ध्यान दिया जाना चाहिए कि नियम 30 से सभी प्रतिस्पर्धी कार्यों को एक एल्गोरिथ्म के निर्माण में माना जाता है जो अनंत संख्या में कोशिकाओं पर चलता है। , n , , ( )? , 2 ⁿ — , , . n =5:

Graph

Graph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]

n =5 n =11:

Grid

Row[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]

, , , , . , 2 ⁿ ( , , ).

, n 30 , , 2 ⁿ . , ( ):

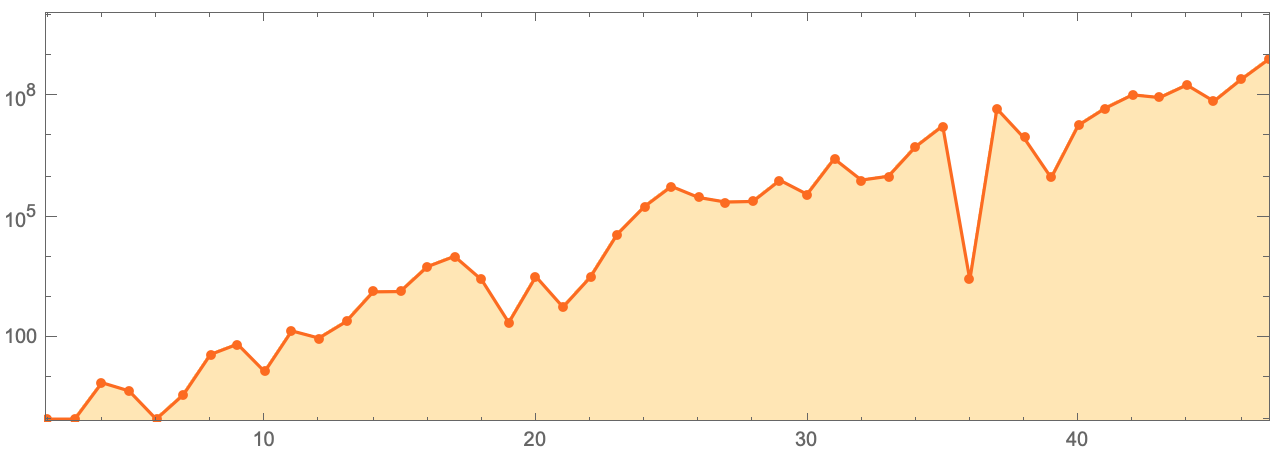
ListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]

, , n 2 ^{0.63 n} . , , . , , ? .

2: ?

10000 30:

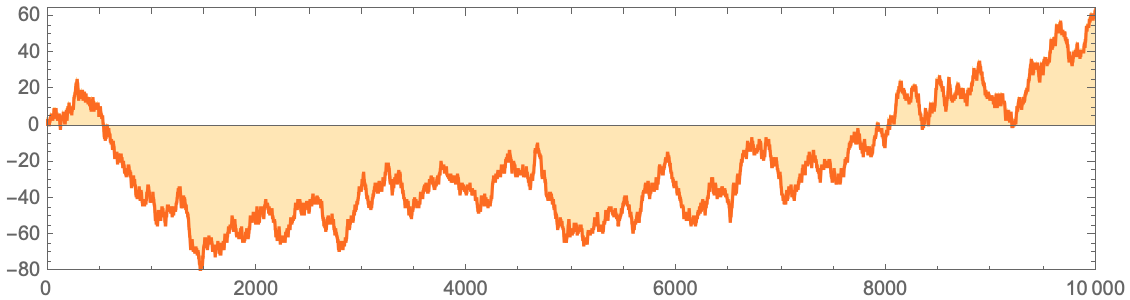
RListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]

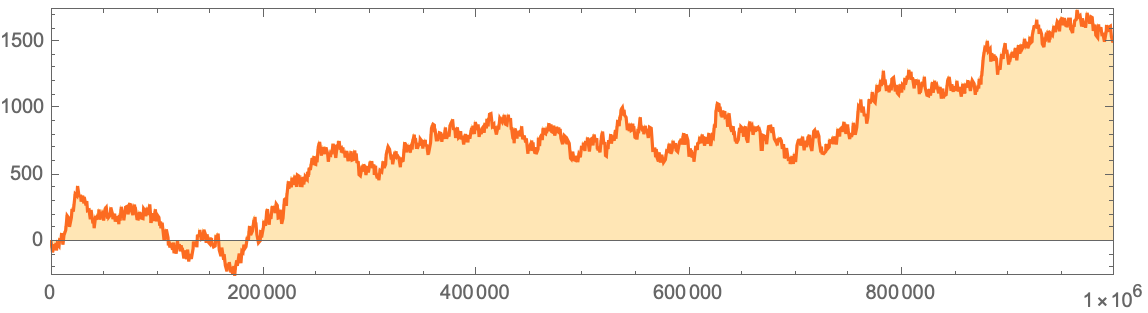
ListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]

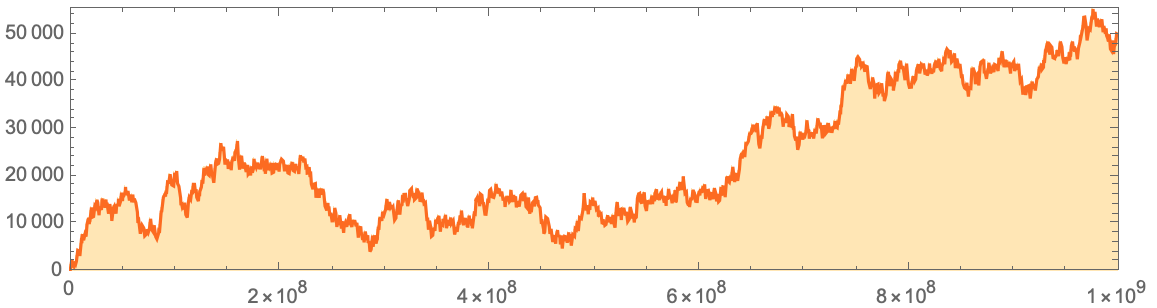
data=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]

, , 1 () 0 (), , , , , , , .

. 10 000 :

Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]

, 1? …

, :

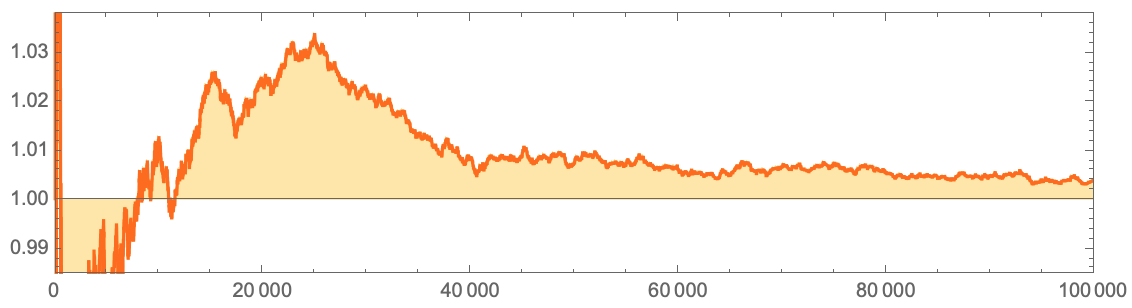
Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]

, , . 1 , :

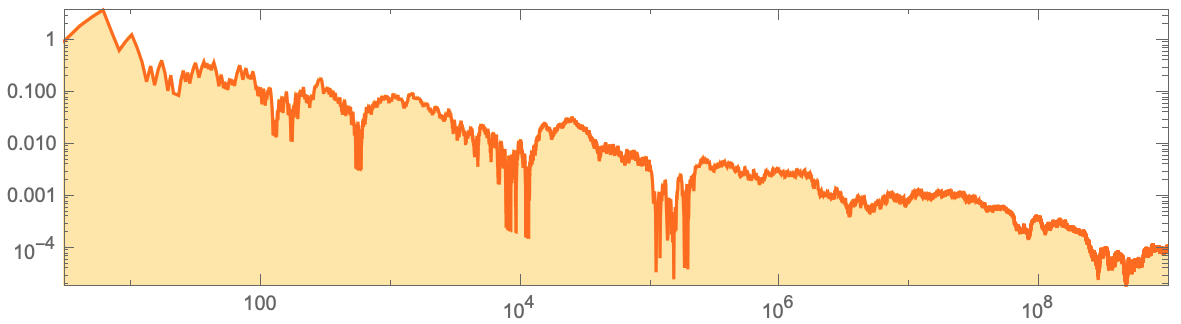
accdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];

diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];

data=diffratio[accdata];

ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]

, ? . , . , , , , .

, , 30, .

, , k . , 2 ^k . , - , , , , 30 k ( ).

, . , , k =22, 2 ^k , , :

ListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]

, , . , – , , .

— — , , , , , , 30, , , , , .

30 , , « », , , , , , . , «»: 30, , , , , , , , 30.

, . 30, , - , , , 30, , , - .

. 30 , , . , , 30 - ( ), , , , 30. 200 :

ListLinePlot[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {200, {0, 200}}], Mesh -> All,
AspectRatio -> 1/4, Frame -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.0085]}],
PlotTheme -> "Detailed", PlotStyle -> Directive[{
Hue[0.1, 1, 0.99]}], ImageSize -> 575]

, :

Grid[{Table[
Histogram[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {10^n, {0, 20}}], {.01},
Frame -> True,
FrameTicks -> {{None,
None}, {{{0, "0"}, .2, .4, .6, .8, {1, "1"}}, None}},
PlotLabel -> (StringTemplate["`` steps"][10^n]),
ChartStyle -> Directive[Opacity[.5], Hue[0.09, 1, 1]],
ImageSize -> 208,
PlotRangePadding -> {{0, 0}, {0, Scaled[.06]}}], {n, 4, 6}]},
Spacings -> .2]

, , , 0 1.

1900- . , , FractionalPart [ hn ] n h . , FractionalPart [ h ⁿ ] h ( ), — FractionalPart [(3/2) ⁿ ] — . (, , 16- , , 2- FractionalPart [16 x _{n -1} + r [ n ]], r [ n ] n .)

3: n- O( n ) ?

, 150 :

Row[{ArrayPlot[CellularAutomaton[150, {{1}, 0}, 30], Mesh -> All,
ImageSize -> 315],
ArrayPlot[CellularAutomaton[150, {{1}, 0}, 200], ImageSize -> 300]}]

, ( ), , :

ArrayPlot[{Table[Mod[IntegerExponent[t, 2], 2], {t, 80}]},
Mesh -> All, ImageSize -> Full]

n- ? , , : Mod [ IntegerExponent [ n , 2], 2]. , n , , .

, « »? , n , Log [2, n ] . , , O(log n ) .

- 30? , n- , 30 n ² , , . , -, , , — , , , , , .

« » (, , . .), , , , , (, , 3D- . .), .

, 1980- , , , , , , , .

, 3 30 , , . ( O( n ) ; O( n ^α ) α <2, , , O(log ^β ( n )) — , , .)

3 , , n- , O( n ), 150 .

O ( n )? () , « »? , — — , , .

, . , , , n , , , n , (, «», O(log n ) .

, . , , , , Wolfram Language . « ». , , Wolfram Language , .

, 30 , 3 , , , , , , n- , O( n ) , .

, , . , , . , , , , , — , O(log n ) , n .

, P NP . , 30 ( P LOGTIME ), , , , . , , , n n , O( n ² ) , , P (« »), , , , , NP. («») , , , , 2 ⁿ .

, 2 ⁿ , , . , NP- , , , NP . 30 NP-? , , ( - , 30 NP).

30 . : 30 , , 30, «» , , , , .

, 256 110 ( , ), 110 , , , . , , , «» 110 .

Rule 110

SeedRandom[23542345]; ArrayPlot[
CellularAutomaton[110, RandomInteger[1, 600], 400],
PixelConstrained -> 1]

30, , — , «» , . , , 30 , , , , .

, , , , , 30. , , (, ) , , . , , — , . , .

, , 3. , , , , n- ?

, 30 . , 2 ^{m ²} m × m , , . , , , O( n ² ) ( ). , O( n ) ? .

, 1 , , - O( n ) — , « ». , ( , 2 ), , , .

- , , , ? , , .

. «» , , , . 30 - . ( — — 30 Wolfram Language, « !» ).

: « - , , ». ? , , , - . . , — , . , , , — - «» 30.

, 30. , 30 - . , , , - 30 , , , , — 30, , , , .

. , 3 2 6 :

Digits of successive powers

Row[Riffle[
ArrayPlot[#, ImageSize -> {Automatic, 275}] & /@ {Table[
IntegerDigits[3^t, 2, 159], {t, 100}],
Table[IntegerDigits[3^t, 6, 62], {t, 100}]}, Spacer[10]]]

, 6 . ( 2 ). , , .

s- n . s- 3 ⁿ , «» ( b — , 2 6) Mod [ Quotient [3 ⁿ , b ^s ], b]. ? , 3 ⁿ n , : , , 3 ⁿ , log( n ). , , , . , 30, , - , .

3 n - 30 , , O( n ), , n , . , r [ n ] , r [ n ] «O-» n , , MaxLimit [ r [ n ]/ n , n →∞ ]<∞.

, ( - ), . , r [ n ] n , , , - , , r [ n ] . , - n ( - ), r [ n ] . , , , r [ n ] O( n ).

30

, ( , ).

Wolfram Language t 30 :

c[t_] := CellularAutomaton[30, {{1}, 0}, {t, {{0}}}]

c [ t ].

1: ?

\!\(
\*SubscriptBox[\(\[NotExists]\), \({p, i}\)]\(
\*SubscriptBox[\(\[ForAll]\), \(t, t > i\)]c[t + p] == c[t]\)\)

NotExists[{p, i}, ForAll[t, t > i, c[t + p] == c[t]]]

p i t , t > i , [ t + p ] c [ t ].

2: ?

\!\(\*UnderscriptBox[\(\[Limit]\), \(t\*
UnderscriptBox["\[Rule]",
TemplateBox[{},
"Integers"]]\[Infinity]\)]\) Total[c[t]]/t == 1/2

DiscreteLimit[Total[c[t]]/t, t -> Infinity] == 1/2

c [ t ]/ t t →∞ 1/2.

3: n- O( n ) ?

machine[ m ] , m (, TuringMachine [...]), machine[ m ][ n ] { v , t }, v — , t — (, ). :

समस्या 3

\!\(
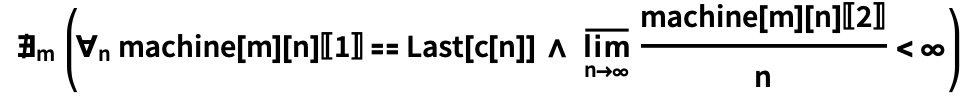
\*SubscriptBox[\(\[NotExists]\), \(m\)]\((
\*SubscriptBox[\(\[ForAll]\), \(n\)]\(\(machine[m]\)[n]\)[[1]] ==
Last[c[n]]\ \[And] \
\*UnderscriptBox[\(\[MaxLimit]\), \(n -> \[Infinity]\)]
\*FractionBox[\(\(\(machine[m]\)[n]\)[[
2]]\), \(n\)] < \[Infinity])\)\)

« m, , machine[ m ] n c [ n ] , n , ». ( m , «» ).

, , , , . 3 ( ), , 1 2, . 3 ( ), , 1 . : 1 , , 3 .

1 , , , , , 2. , 2 - 3. , , O( n ) — , , 3, , .

, , ?

1 , , , 30 - , . , 1 , . , , - , .

( , ), 2, 3 , — , , , . , 3 , , (, , ), O( n ) .

, - . , n n- . . , - , . , , n n . , . , « » . , n , . , , O( n ) .

: ? « », / ( ).

, , ( )? , , , , «» , -, ( ) , .

, , . , , , . , () .

, , , , : « ». , , , .

, — - . - n , . . — (« » . .). , , , .

— , , . , ( FindEquationalProof ). , () .

, , , — , . — , .

, . Wolfram|Alpha (, ) , . , .

, , - , , , , .

? , «» , . Wolfram Language , . Wolfram Language, .

« »? , , - . . - , , «» , , - ( ), . , , «» — , .

?

, ? . . , . - , . . - , , .

, , «» — , — , « ». , 2,3 2007 .

— , , 30, , . . - ( , , ). , , ( ) , , .

n — 30 n , n . Wolfram Language . , 0,4 100 000 :

CellularAutomaton[30, {{1}, 0}, {100000, {{0}}}]; // Timing

, 30 Xor [ p , Or [ q , r ]], . , CellularAutomaton :

मॉड्यूल

Module[{a = 1},
Table[BitGet[a, a = BitXor[a, BitOr[2 a, 4 a]]; i - 1], {i,
100000}]]; // Timing

. . , , 30, , 30 , , , : .

. , , «» . 30 — . , , , .

— , , . , , 30, .

, , 30, . 45° , 30, , . ; . ?

? ? - ? , , , , , .

? 30, . , , , , , . , - , , , , , , - .

– , «» . ( , - ). , , , , « » :

आवधिक पैटर्न में एक 'एकल दोष'

GraphicsRow[(ArrayPlot[
CellularAutomaton[30,
MapAt[1 - #1 &, Flatten[Table[#1, Round[150/Length[#1]]]], 50],
100]] &) /@ {{1, 0}, {1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0}, {1,
0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0}}]

, , , . ? , « » ?

, (, ), , - 30?

« 30». , «» ? 30 , ? «» ?

, , 30, , , , 30, . 256 ( ) , , :

Row[Riffle[
Labeled[ArrayPlot[CellularAutomaton[#, {{1}, 0}, {150, All}],
PixelConstrained -> 1, Frame -> False],
Style[Text[StringTemplate["rule ``"][#]], 12],
LabelStyle -> Opacity[.5]] & /@ {45, 73}, Spacer[8]]]

, . , . , , . , , , « 30», .

« 30». 30 ( 1), , — , .

2, 30, , .

3 . n- O( n ^γ ) γ <2 ( - )? , n- , O(log( n )) ? O(log( n )) ? ? . ?

, 30. 30, (, , 110) , 30.

, NP-, 30 , , NP-? , . , , , « », 30?

?

2007 2,3 , — , , , . , . 30? . 40 , - ( , !). , , (, ) .

, - ( ), , , , , , , . ( ), , , .

, « » ( , ), . , . , (« » . .). . , - « », , , …

, . , , . , , . , .

, 30 40 , - .

स्टीफन वुल्फराम के पोस्ट का अनुवाद " नियम 30 पुरस्कारों की घोषणा "।
मैं प्रकाशन और अनुवाद तैयार करने में मदद के लिए पीटर टेनिशेव के प्रति अपनी गहरी कृतज्ञता व्यक्त करता हूं ।

Wolfram Language?
« Wolfram » ( ).

सेलुलर ऑटोमेटा के लिए नियम 30 की समस्याओं को हल करने के लिए $ 30,000 - स्टीफन वोल्फ्राम से एक प्रतियोगिता

तो यह सब कहां से शुरू हुआ? - "नियम 30"

नियम 30 - हल करने के लिए कार्य

कार्य 1: क्या केंद्रीय स्तंभ हमेशा गैर-आवधिक रहता है?

कार्य 2: कोशिका का प्रत्येक रंग (काला या सफेद) औसत रूप से केंद्र स्तंभ में समान रूप से होने की संभावना है?

कार्य 3: केंद्रीय स्तंभ के nth सेल की गणना के लिए कम से कम O ( n ) संचालन की आवश्यकता होती है?

वह संख्याएँ जो पाई बनाती हैं

परिणाम, उपमा और अंतर्ज्ञान

कार्य 1: क्या केंद्रीय स्तंभ हमेशा गैर-आवधिक रहता है?

2: ?

3: n- O( n ) ?

30

1: ?

2: ?

3: n- O( n ) ?

?

?

More articles: