यूलर-पॉइसन अभिन्न। गणना के तरीकों पर विवरण

लेख में, विस्तार से, सबसे छोटे विवरण के नीचे, यूलर-पॉइसन इंटीग्रल लेने के तीन तरीकों पर विचार किया गया है। विधियों में से एक में, एक सहायक कमी सूत्र प्राप्त होता है। कुछ जटिल इंटीग्रल्स को खोजने के लिए, एक कटौती फ़ार्मुलों का उपयोग कर सकते हैं जो एक को इंटीग्रैंड की डिग्री को कम करने की अनुमति देता है और चरणों की एक सीमित संख्या में संबंधित इंटीग्रल्स की गणना करता है।

यह अभिन्न गौसियन फ़ंक्शन से लिया गया है: $$$I = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx}$
बहुत ही रोचक गणितीय तरीका है। मूल अभिन्न को खोजने के लिए, पहले इस अभिन्न के वर्ग की तलाश करें, और फिर परिणाम से मूल निकालें। क्यों? हां, क्योंकि ध्रुवीय निर्देशांक में जाना इतना आसान और दर्द रहित है। इसलिए, गौसियन अभिन्न के वर्ग पर विचार करें:
$$$I ^ 2 = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} \ int \ limit_0 ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limit_0 ^ "infty { \ int \ limit_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}}} dxdy$
हम देखते हैं कि हमें किसी फ़ंक्शन का दोहरा अभिन्न हिस्सा मिलता है $$$g \ बाएँ ({x, y} \ दाएँ) = \ exp \ बाएँ [{- \ बाएँ ({x ^ 2 + y ^ 2} \ दाएँ)} \ दाएँ]$ । इस सतह के अंत में अभिन्न कार्टेशियन समन्वय प्रणाली में क्षेत्र तत्व है $$$dS = dxdy$ ।
अब ध्रुवीय समन्वय प्रणाली की ओर चलते हैं:

$$

$$\ start {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ left। \ start {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ right | \ से x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ से x ^ 2 + y ^ 2 = r ^ 2 \\ \ अंत {सरणी}$$

यहां यह ध्यान दिया जाना चाहिए कि r 0 से + because तक भिन्न हो सकता है, क्योंकि एक ही सीमा के भीतर एक्स विविध। लेकिन कोण to 0 से π / 2 तक भिन्न होता है, जो कार्टेशियन समन्वय प्रणाली की पहली तिमाही में एकीकरण क्षेत्र का वर्णन करता है। स्रोत में प्रतिस्थापित, हम प्राप्त करते हैं:

$$

$$\ start {array} {l} I ^ 2 = \ int \ limit_0 ^ \ infty {\ int \ limit_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}} } dxdy = \ int \ limit_0 ^ {\ frac {\ _ pi} {2}} {\ int \ limit_0 ^ \ infty {e ^ {- r ^ 2}}} rd \ varphi dr = int \ limit_0 ^ {\ _ frac {\ pi} {2}} {d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limit_0 ^ {\ frac {\ _ p}} {2}} {{ d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ left ({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limit_0 ^ {\ _ frac {\ pi} {2}} {d \ varphi} \ left ({\ _ बाईं; {- e ^ {- r ^ 2}} \ right | _0 ^ \ _ \ _} \ right) = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({- e ^ {- \ infty} - \ बाएँ ({) - e ^ 0} (दाईं ओर)} \ right) = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} / 2 } \ बाईं ({\ _ बाएं। \ varphi \ right। _0 ^ {\ frac {\ pi} {2}}} \ right) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac \ _ \ _ pi} {4} \ से I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {सरणी}$$

इंटीग्रल की समरूपता और सकारात्मक रेंज के मूल्यों के कारण, हम यह निष्कर्ष निकाल सकते हैं

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ _ \ _ \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

आइए जानें कुछ और उपाय? यह दिलचस्प है! :)

फ़ंक्शन पर विचार करें $$$g \ बाएँ (t \ दाएँ) = \ बाएँ ({1 + t} \ दाएँ) e ^ {- t}$
अब चलो स्कूल के गणित को याद करते हैं और डेरिवेटिव और सीमाओं का उपयोग करते हुए एक फ़ंक्शन का एक सरल अध्ययन करते हैं। ऐसा नहीं है कि हम यहां जटिल सीमाओं पर विचार करेंगे (आखिरकार, वे उन्हें स्कूल में पास नहीं करते हैं), हम सिर्फ इस बात पर चर्चा करते हैं कि फ़ंक्शन का क्या होगा यदि इसका तर्क शून्य या अनंत हो जाता है, इस प्रकार हम असममित व्यवहार का अनुमान लगाएंगे, जो हमेशा गणित में बहुत महत्वपूर्ण है। यह जो हो रहा है उसका गुणात्मक मूल्यांकन जैसा है।

$$

$$\ स्टार्ट {एरे} {एल} जी \ लेफ्ट (टी \ राइट) = \ लेफ्ट ({1 + टी} \ राइट) ई ^ {- टी} \\ जी '\ लेफ्ट (टी \ राइट) = ई ^ { - t} - \ left ({1 + t} \ right) e ^ {- t} = - te ^ {- t} \\ g '\ बाएँ (t \ right) = 0 \ से t = 0 \\ \ बाएं [\ start {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ left (t \ right) - {\ rm {बढ़ता है}} \\ t> 0 \ to - te ^ {- t} <0 \ to g \ left (t \ right) - {\ rm {कम हो जाती है}} \\ \ end {array} \ right। \\ g \ बाएँ (0 \ दाएँ) = \ बाएँ ({1 + 0} \ दाएँ) e ^ {- 0} = 1 \\ g \ बाएँ ({- 1} \ दाएँ) = \ बाएँ ({1 -) 1} (दाएं) e ^ {- \ बाएं ({- 1} \ दाएँ)} = 0 \\ g \ बाएं (\ infty \ right) = \ बाएं ({1 + \ infty} \ right) e ^ {- \ infty} = 0 \\ \ end {सरणी}$$

यह अंतराल (-∞; + and) पर एकता और अंतराल [-1; +;) पर शून्य से ऊपर है।

हम चर के निम्नलिखित परिवर्तन करते हैं $$$t = \ pm x ^ 2$
और हम प्राप्त करते हैं:

$$

$$t = \ pm x ^ 2 \ _ to \ left \ {\ शुरू करना {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ बाएं ({1 + x ^ 2} \ सही) e ^ {- x ^ 2} <1 \\ \ end {सरणी} \ सही। \ _ से \ _ \ _ \ _ शुरू {सरणी} {l} 0 <\ बाएँ ({1 - x ^ 2} \ सही) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ अंत {सरणी} \ सही।$$

पहली असमानता में, हम भिन्नता (0,1) को सीमित करते हैं, और दूसरे में, अंतराल (0; +;), हम दोनों असमानताओं को n की शक्ति तक बढ़ाते हैं, क्योंकि असमानताओं को सकारात्मक शब्दों के साथ किसी भी सकारात्मक डिग्री तक उठाया जा सकता है। हमें मिलता है:

$$

$$\ start {array} {* {20} c} {\ left \ {\ {start {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ अंत {सरणी} \ सही।} & {\ वाम \ _ \ _ शुरू {सरणी} {एल} ई ^ {- nx ^ 2} <\ frac {1} {{\ _ बाएं ({1 + x ^ 2} \ सही) ^ n}} \\ x> 1 \\ \ अंत {सरणी} \ सही।} \\ \ अंत {सरणी} $$$

असमानताओं को प्रदर्शित करने के लिए n = 1 के लिए ग्राफ बनाते हैं

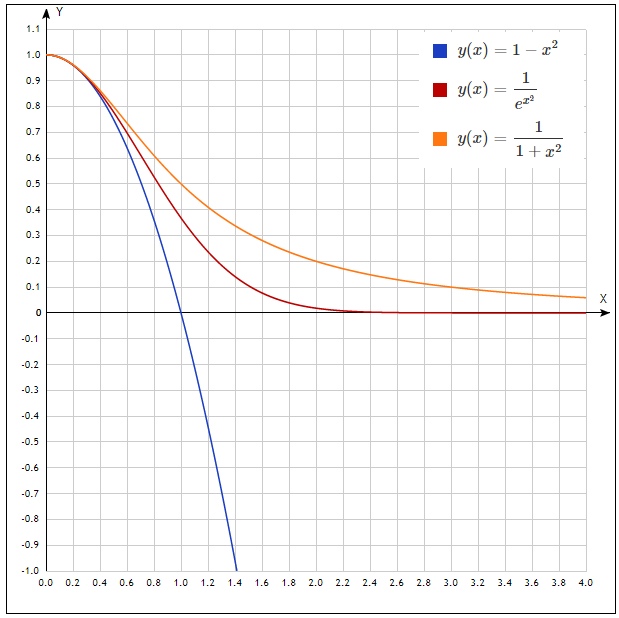
अब हम संबंधित प्रणालियों में इंगित सीमाओं के भीतर असमानताओं को एकीकृत करने का प्रयास करते हैं। और तुरंत एक असमानता में सब कुछ मिलाएं:

$$

$$\ int \ limit_0 ^ 1 {\ बाएँ ({1 - x ^ 2} \ right) ^ n dx} <\ int \ limit_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ _ infty {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ राइट) ^ n}} dx}$$

फिर से, यदि आप रेखांकन देखें, तो यह असमानता सच है।

एक छोटे से प्रतिस्थापन को देखते हुए, यह देखना आसान है:

$$

$$\ int \ limit_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ left [\ start {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ _ \ _ क्रेक {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ right] = \ frac {1} {{sqrt n}} \ int \ limit_0 ^ \ infty {e ^ {} { 2} dp} = \ frac {1} {{\ sqrt n}} I$$

यानी बीच में उस बड़ी असमानता में, हमारे पास यूलर-पॉइसन अभिन्न हैं, और अब हमें उन अभिन्न लोगों को खोजने की जरूरत है जो इस असमानता की सीमाओं पर खड़े हैं।

बाईं सीमा से अभिन्न का पता लगाएं:

$$

$$\ start {array} {l} \ int \ limit_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ start {array} {* {20} c} \ start {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ _ {सरणी} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ से t = \ arcsin 0 = 0 \\ \ end {सरणी} \\ \ अंत {सरणी}} \ सही] = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limit \ _0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {सरणी}$$

इसकी गणना और मूल्यांकन करने के लिए, आइए पहले एक सामान्य अभिन्नता का पता लगाएं। अब मैं आपको दिखाऊंगा कि किसी दिए गए अभिन्न के लिए कमी के फार्मूले को कैसे प्राप्त किया जाए (गणित में, ऐसे फॉर्मूले से उनका मतलब है डिग्री कम करना)।

$$

$$\ शुरू {सरणी} {l} \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n tdt} = \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = = \\ = \ left [{\ _ start {array} {* {} 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {DV = d \ बाएँ ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ left। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} t \ left ({1 - \ cos ^ 2 t} \ right) dt} = \\ = \ left। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} tdt} - \ बाएँ ({n - 1} \ दाएँ) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n tdt} \\ \ end {सरणी}$$

$$

$$\ start {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} tdt} - \ बाएँ ({n - 1} \ सही) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n tdt} \\ \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n ttt } + \ छोड़ दिया ({n - 1} \ सही) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n tdt} = \ बाएँ। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} tdt} \\ n \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt = \ left। {a cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ {n - 2} tdt}} \\ \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ n tdt = \ frac {1} {n} \ left। {<cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limit_ \ अल्फा ^ \ बीटा {\ cos ^ { n - 2} tdt}} \\ \ end {सरणी}$$

अब, अगर कमी सूत्र का उपयोग करते हुए हम एक ही अभिन्न पर विचार करते हैं, लेकिन हमारी सीमा 0 से using / 2 तक है, तो हम कुछ सरलीकरण कर सकते हैं:

$$

$$\ start {array} {l} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ left। {[cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limit_0 ^ {\ _ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ _ frac {1} {n} \ left। {[cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ left ({\ _ frac) / 1 } {{n - 2}} \ छोड़ दिया। {\ cos ^ {n - 3} t \ sin t} \ __ _ ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ _ frac {{n - 3}} {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5 }} {{n - 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right)} \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ बाएँ ({\ frac {{n - 7}} {{n - 6}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} सही )} \ राइट)} \ राइट) = ... \\ \ एंड {सरणी}$$

जैसा कि हम देखते हैं, आप इसे अनंत तक कम कर सकते हैं (एन पर निर्भर करता है)। हालांकि, एक सूक्ष्मता है। सूत्र इस बात पर निर्भर करता है कि n एक सम संख्या है या नहीं।
इसके लिए, हम दो मामलों पर विचार करते हैं।

$$

$$\ _ {सरणी} {l} n = 10: \\ \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ _ \ _ \ _ \ _ \ _ \ _ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ left ({frac {1) } {2} + \ _ frac {1} {2} \ cos 2t} \ right) dt} = = \\ = \ frac {{9 \ _ cdot 7 \ cdot 5 \ cdot 3}}} {{10 \ _ \ _ 8 \ _ 6 \ cdot 4}} \ बाएँ। {बायाँ ({\ _ frac {1} {2} t + \ _ frac {1} {2} \ _ \ _ 2t} \ right)} \ _ \ _ | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ सी-डॉट 7 \ सी-डॉट 5 \ सी-डॉट 3}} {{10 \ सी-डॉट 8 \ सी-डॉट 6 \ सी-डॉट 4}} \ सी-डॉट \ frac {\ pi} {4} = \ frac {{9 \ सी-डॉट 7 \ सी-डॉट 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{बाईं ओर (n) (1} \ सही) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {सरणी}$$

$$

$$\ start {सरणी} {l} n = 9: \\ \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ _ \ _ 6 \ _ \ _ \ _ 4 \ cdot 2}} {{9 \ _ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {8 \ _ \ _ cdot 6 \ _ cdot 4 \ cdot 2}} {{9 \ "cdot 7 \ cdot 5 \ cdot 3}} छोड़ दिया। {बायां ({\ _ sint} \ right)} \ right | _0 ^ {\ _ frac {\ pi} {2}} = \\ = \ frac {{8 \ _ \ _ 6 \ _ कूटना 4 \ _ \ _ 2}}} {} {९ \ _डॉइट c \ _डॉइट ५ \ _कॉस्ट ३ \ _डॉइट १}} = = फ्राक {{\ _ बाएं ({n - १} \ _ सही) !!}} {{n !!}} \\ \ end {व्यू}$$

N कहाँ है !! - दोहरा तथ्य। N के दोहरे तथ्य को n द्वारा निरूपित किया जाता है !! और अंतराल में सभी प्राकृतिक संख्याओं के उत्पाद के रूप में परिभाषित किया गया है [1, n] समान समता वाले n

इस तथ्य के कारण कि n के किसी भी मान के लिए 2n + 1 एक विषम संख्या है, हम अपनी असमानता की बाईं सीमा के लिए प्राप्त करते हैं:

$$

$$\ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ _ बाईं ({2n} \ right) !!}}} {{बाईं ओर} !! ({2n + 1} \ सही) !!}}$$

सही सीमा से अभिन्न का पता लगाएं:
(यहाँ हम वही कमी सूत्र का उपयोग करते हैं जो पहले सिद्ध किया गया था)

$$

$$\ शुरू {सरणी} {l} \ int \ limit_0 ^ \ infty {\ frac {1} {{बाएं ({1 + x ^ 2} \ राइट) ^ n}} dx = \ बाएँ [\ start {सरणी } {l} x = \ tan t \ to \ start {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ t से = \ frac {\ pi} तक। {2}} \\ \ end {सरणी} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}} = \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ right]} = \\ = \ int \ limit_0 ^ {\ frac {\ _ pi} {२} } {\ cos ^ {2n - 2} tdt} = \ left [{\ left ({2n - 2} \ right) - {\ rm {सम}}}} सही] = \ frac {{\ n (2n) - 3} (दाएं) !!}} {{\ _ बाएं ({2n - 2} \ दाएं) !!}}} \ cdot \ frac {\ pi} {2} \\ \ end {सरणी}$$

असमानता के बाएँ और दाएँ पक्ष का अनुमान लगाने के बाद, हम असमानता के बाएँ और दाएँ पक्षों की सीमाओं का मूल्यांकन करने के लिए कुछ परिवर्तन करते हैं, बशर्ते कि n to की ओर रुख करे:

$$

$$\ _ {सरणी} {l} \ frac {{\ _ बाईं ({2n} \ right) !!}}} {{बाएं ({2n + 1} \ ")}}} <\ frac {1} {!! {\ sqrt n}} \ cdot I <\ frac {{\ _ बाईं ({2n - 3} \ दाहिनी) !!}} {{\ _ बाईं ({2n - 2} \ right) !!}} \ cdot \ frac !! {{pi} {2} \\ \ sqrt n \ _ cdot \ frac {{\ _ बाएँ ({2n \ _ \ _)}}}} {{\ _ बाईं ({2n + 1} \ right) !!}} <I !! <\ sqrt n \ cdot \ frac {{\ _ बाईं ({2n - 3} \ right) !!}} {{\ _ बाईं ({2n - 2} \ ") !!}} \ cdot \ frac {\ pi} !! {2} \\ \ end {सरणी}$$

असमानता के दोनों किनारों को स्क्वायर करें:

$$

$$n \ cdot \ frac {{\ _ बाएँ ({\ _ बाएं ({2n} \ दाएँ) !!} \ दाएँ) ^ 2}}} {{बाएं ({2 छोड़ दिया ({2n + 1} \ ") !! } \ right) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ _ बाएं ({\ _ बाएं ({2n - 3} \ दाएं) !!} \ "दाएं) ^ 2}} {{बाएं () {बाएं ({2n - 2} \ सही) !!} \ सही) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

अब थोड़ा विषयांतर करते हैं। 1655 में, जॉन वालिस (एक गणितीय गणितज्ञ, गणितीय विश्लेषण के अग्रदूतों में से एक।) ने संख्या का निर्धारण करने के लिए एक सूत्र प्रस्तावित किया π। जे। वालिस उसके पास आया, एक सर्कल के क्षेत्र की गणना करता है। यह उत्पाद बहुत धीरे-धीरे परिवर्तित होता है, इसलिए, वालिस सूत्र संख्या की व्यावहारिक गणना के लिए बहुत कम उपयोग करता है। लेकिन यह हमारी अभिव्यक्ति का मूल्यांकन करने के लिए बहुत अच्छा है :)

$$

$$\ pi = \ mathop {\ lim} {सीमाएं {{\ _ to \ infty} \ frac {1} {n} \ left [{\ frac {{\ _ बाईं ({2n} \ right)}}} {{!! \ बाएं ({2n - 1} \ सही) !!}}} \ सही] ^ 2$$

अब हम अपनी असमानता को बदल देते हैं ताकि हम देख सकें कि वालिस फॉर्मूला को कहां स्थान दिया जाए:

$$

$$\ start {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {{वाम ({\ _ बाएं ({2n} \ दाएँ) !!} \ दाएँ) ^ 2}} {{\ _ बाएं ({\ _ बाएं ({2n - 1} \ _ दाएं) !!} \ "दाएं) ^ 2} !! } <I ^ 2 <\ frac {1} {{\ _ frac {1} {n} \ cdot \ frac {{\ _ बाईं ({\ _ बाईं ({2n - 2} \ ") !!} \ right) ^ 2 !! }} {{\ _ बाएं ({\ _ बाएं ({2n - 3} \ दाएँ) !!} \ दाएँ) ^ 2}}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {[लिम} \ लिमिट_ {एन \ _ टू इनफेंटि} \ लेफ्ट [{\ फ्राक {{एन ^ 2}} {{\ लेफ्ट ({2 एन + 1} \ राइट) ^ 2}}} \ राइट] \ cdot \ मैथॉप {\ लिम} \ लिमिट_ {एन \ _ टू इनफेंटि} \ लेफ्ट [{\ फ्राक {1} {एन} \ सीडॉट \ फ्राक {{\ _ लेफ्ट ({2 लेफ्ट ({2 एन} \ राइट)}}} राइट !! ) ^ 2}} {{\ _ बाईं ({\ _ बाईं ({2n - 1} \ सही) !!} \ सही) ^ 2}}}} \ "] <I ^ 2 <\ frac {1} {{\ _ mathop {\ _} \ limit_ {n \ _ to infty} \ left [{\ _ frac {1} {n} \ cdot \ frac {{\ _ बाईं ({\ n बाईं ({2n - 2} \ ") !!} !! दाएँ) ^ 2}} {{\ _ बाएं ({2 बाएँ ({2n - 3} \ दाएँ) !!} \ दाएँ) ^ 2}}}} \ दाएँ]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ _ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ _ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ _ मैं = \ frac {{\ sqrt \ pi}} {2} \\ \ end {सरणी}$$

यह वालिस सूत्र से इस प्रकार है कि बाएं और दाएं दोनों भाव the / 4 को n → is कहते हैं
इस तथ्य के कारण कि फ़ंक्शन exp [-x the] सम है, हम सुरक्षित रूप से मान लेते हैं

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ _ \ _ \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

पहली बार, एक आयामी गाऊसी अभिन्न की गणना 1729 में यूलर द्वारा की गई थी, फिर पॉइसन ने इसकी गणना करने का एक सरल तरीका खोजा। इस संबंध में, इसे यूलर - पॉइसन अभिन्न कहा जाता था।

आइए गौसियन अभिन्न की गणना करने का प्रयास करें। इसे विभिन्न रूपों में लिखा जा सकता है। आखिरकार, चर के नाम पर कुछ भी नहीं बदलता है जिसके द्वारा एकीकरण होता है।

$$

$$\ start {array} {l} I = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- z ^ 2} dz} \\ \ end {सरणी}$$

आप त्रि-आयामी कार्टेशियन से गोलाकार निर्देशांक पर जा सकते हैं और गॉस के अभिन्न अंग पर विचार कर सकते हैं।

$$

$$\ बाईं \ {\ _ शुरू करें {सरणी} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ अंत {सरणी} \ सही। \ x से 2 + y ^ 2 + z ^ 2 = r ^ 2$$

इस परिवर्तन के याकूब की गणना इस प्रकार की जा सकती है:

$$

$$\ start {array} {l} J = \ left | {{शुरू {सरणी} {* {20} c} {\ frac {{आंशिक x}} {{\ आंशिक r}}}} & {\ frac {{आंशिक x}} {{आंशिक \ _}} } & {\ _ frac {{आंशिक x}} {{\ आंशिक \ varphi}}} \\ {\ frac {{आंशिक y}}} {{आंशिक r}}} & {\ _ frac {{आंशिक पक्ष }} {{\ आंशिक \ "थीटा}}} और {\ frac {{आंशिक y}} {{\ आंशिक \ varphi}}}} \\ {\ frac {{आंशिक पक्ष}} {{\ आंशिक r}} } & {\ _ frac {{\ _ आंशिक z}}} {{\ _ \ _ आंशिक \}}} & {\ frac {{आंशिक z}} {{\ _ \ _ आंशिक \ _}}}} \\ \ अंत {सरणी}} \ _ सही | = \ _ बाएं | {\ _ {सरणी} {* {20} c} {\ sin \ theta \ cos \ varphi} और {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi, \\ {/ sin \ theta \ sin \ varphi} & {r \ cos \ theta \ sin \ varphi} और {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} और {r \ sin \ " थीटा} और 0 \\ \ अंत {सरणी}} \ सही | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ शुरू {सरणी} {l} मैं ^ 3 = \ int \ limit_ {- \ infty} ^ \ infty {\ int \ limit_ {- \ infty} ^ \ infty {\ int \ limit_ {- \ infty} \ _ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ limit_0 ^ {2 \ pi} {\ int \ limit_0 ^ \ pi {\ int \ __ ^ ^ \ infty { e ^ {- r ^ 2} Jdrd \ थीटा d} \ varphi =}} \\ = \ int \ limit_0 ^ {2 \ pi} {d \ varphi} \ int \ limit_0 ^ \ pi / \ sin \ थीटा d \ _ थीटा} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {सरणी}$$

हम आंतरिक रूप से शुरू करते हुए, क्रमिक रूप से अभिन्न गणना करते हैं।

$$

$$\ start {array} {l} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ left [\ start {array} {l} u = r \ to du = dr \\ DV = re ^ {- r ^ 2} dr \ से v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {सरणी} \ सही] = \\ = \ left। {बायाँ ({- \ _ frac {1} {2} re ^ {- r ^ 2}} \ right)} \ right | _0 ^ \ infty + \ frac {1} {2} \ int \ limit_0 ^ \ infty | {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limit_0 ^ \ pi {\ sin \ theta d \ theta} = \ left। {बाएं ({- \ cos \ theta} \ right)} \ right | _0 ^ \ pi = \ left ({- \ cos \ pi} \ right) - \ बाएं ({- \ cos 0} \ right) = 1 + 1 = 2 \\ \ int \ limit_0 ^ {2 \ pi} {d \ varphi} = \ left। \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {सरणी}$$

फिर परिणामस्वरूप हम प्राप्त करते हैं:

$$

$$\ start {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ से I ^ 3 = \ pi I \ _ to I ^ 2 = \ pi \ i = = \ sqrt \ pi \\ I = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {सरणी}$$

यूलर-पॉइसन इंटीग्रल का उपयोग प्रायः प्रायिकता सिद्धांत में किया जाता है।

मुझे उम्मीद है कि किसी के लिए यह लेख उपयोगी होगा और कुछ गणितीय तकनीकों को समझने में मदद करेगा :)