सीयूडीए पर नवियर-स्टोक्स समीकरण और द्रव सिमुलेशन

हाय, हैब्र। इस लेख में, हम एक असंगत तरल पदार्थ के लिए नवियर-स्टोक्स समीकरण से निपटेंगे, संख्यात्मक रूप से इसे हल करेंगे, और एक सुंदर सिमुलेशन बनायेंगे जो CUDA पर समानांतर कंप्यूटिंग द्वारा काम करता है। मुख्य लक्ष्य यह दिखाना है कि आप मॉडलिंग तरल पदार्थ और गैसों की समस्या को हल करते समय गणित को समीकरण में अंतर्निहित कैसे लागू कर सकते हैं।




नोट: यदि आप मोबाइल डिवाइस से Habr पढ़ रहे हैं, और आप सूत्र नहीं देखते हैं, तो साइट के पूर्ण संस्करण का उपयोग करें

एक असंगत द्रव के लिए नवियर-स्टोक्स समीकरण

$$

$${\ आंशिक {\ bf \ vec {u}} \ over {\ आंशिक t}} = - - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} {{1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

मुझे लगता है कि हर कोई कम से कम एक बार इस समीकरण के बारे में सुनता है, कुछ, शायद विश्लेषणात्मक रूप से इसके विशेष मामलों को भी हल करते हैं, लेकिन सामान्य शब्दों में यह समस्या अब तक अनसुलझी है। बेशक, हम इस लेख में सहस्राब्दी समस्या को हल करने का लक्ष्य निर्धारित नहीं करते हैं, हालांकि हम अभी भी इसके लिए पुनरावृत्ति विधि को लागू कर सकते हैं। लेकिन शुरुआत के लिए, आइए इस सूत्र में संकेतन देखें।

परंपरागत रूप से, नवियर-स्टोक्स समीकरण को पांच भागों में विभाजित किया जा सकता है:

• $$$\ आंशिक {\ bf \ vec {u}} \ over \ आंशिक t$ - एक बिंदु पर द्रव वेग के परिवर्तन की दर को दर्शाता है (हम अपने सिमुलेशन में प्रत्येक कण के लिए इस पर विचार करेंगे)।
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {}}}$ - अंतरिक्ष में द्रव की गति।
• $$$- {1 \ over \ rho} \ nabla {\ bf p}$ क्या कण पर दबाव डाला गया है (यहां) $$$\ rho$ - द्रव घनत्व गुणांक)।
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - माध्यम की चिपचिपाहट (यह जितना बड़ा होता है, उतना ही मजबूत तरल अपने हिस्से पर लागू होने वाले बल का प्रतिरोध करता है), $$$\ n$ - चिपचिपापन गुणांक)।
• $$$\ bf \ vec {F}$ - बाहरी बल जो हम द्रव पर लागू करते हैं (हमारे मामले में, बल बहुत विशिष्ट भूमिका निभाएगा - यह उपयोगकर्ता द्वारा किए गए कार्यों को प्रतिबिंबित करेगा।

इसके अलावा, चूंकि हम एक असंगत और सजातीय द्रव के मामले पर विचार करेंगे, हमारे पास एक और समीकरण है: $$${{\ _ nabla \ cdot \ bf \ vec {u}} = 0}$ । पर्यावरण में ऊर्जा निरंतर है, कहीं नहीं जाती है, कहीं से नहीं आती है।

उन सभी पाठकों को वंचित करना गलत होगा जो वेक्टर विश्लेषण से परिचित नहीं हैं, इसलिए, एक ही समय में और संक्षेप में उन सभी ऑपरेटरों के माध्यम से जाते हैं जो समीकरण में मौजूद हैं (हालांकि, मैं दृढ़ता से यह याद रखने की सलाह देता हूं कि व्युत्पन्न, अंतर और वेक्टर क्या हैं, क्योंकि वे सभी को रेखांकित करते हैं। नीचे क्या चर्चा की जाएगी)।

हम नबला ऑपरेटर के साथ शुरू करते हैं, जो इस तरह के एक वेक्टर है (हमारे मामले में, यह दो-घटक होगा, क्योंकि हम तरल पदार्थ को दो-आयामी स्थान में मॉडल करेंगे):

$$

$$\ n नाला = {\ _ {pmatrix} {\ आंशिक \ ओवर \ आंशिक x}, {\ आंशिक \ ओवर \ आंशिक y} \ अंत {pmatrix}}$$

नबला ऑपरेटर एक वेक्टर अंतर ऑपरेटर है और इसे स्केलर फ़ंक्शन और वेक्टर वेक्टर दोनों पर लागू किया जा सकता है। स्केलर के मामले में, हमें फ़ंक्शन (इसके आंशिक डेरिवेटिव के वेक्टर) का ग्रेडिएंट मिलता है, और वेक्टर के मामले में, कुल्हाड़ियों के साथ आंशिक डेरिवेटिव का योग। इस ऑपरेटर की मुख्य विशेषता यह है कि इसके माध्यम से आप वेक्टर विश्लेषण के मुख्य संचालन - ग्रेड ( ग्रेडिएंट ), div ( विचलन ), रोट ( रोटर ) को व्यक्त कर सकते हैं $$$\ n नबला ^ 2$ ( लाप्लास ऑपरेटर )। यह तुरंत ध्यान देने योग्य है कि अभिव्यक्ति $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {}} $$ नहीं करने के लिए नहीं $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {}} $$ - नबला संचालक के पास कम्यूटिटी नहीं है।

जैसा कि हम बाद में देखेंगे, इन अभिव्यक्तियों को एक असतत स्थान पर ले जाते समय विशेष रूप से सरल किया जाता है, जिसमें हम सभी गणनाओं को अंजाम देंगे, इसलिए यदि आप इस सब के साथ क्या करें, इस बारे में बहुत स्पष्ट नहीं हैं, तो चिंतित न हों। कार्य को कई भागों में विभाजित करने के बाद, हम क्रमिक रूप से उनमें से प्रत्येक को हल करेंगे और यह सब हमारे पर्यावरण के लिए कई कार्यों के अनुक्रमिक अनुप्रयोग के रूप में प्रस्तुत करेंगे।

नवियर-स्टोक्स समीकरण का संख्यात्मक समाधान

कार्यक्रम में हमारे तरल पदार्थ का प्रतिनिधित्व करने के लिए, हमें समय पर मनमाने ढंग से प्रत्येक द्रव कण की स्थिति का गणितीय प्रतिनिधित्व प्राप्त करने की आवश्यकता है। इसके लिए सबसे सुविधाजनक तरीका एक समन्वय विमान के रूप में अपने राज्य को संग्रहीत करने वाले कणों का एक वेक्टर क्षेत्र बनाना है:



हमारे दो-आयामी सरणी के प्रत्येक सेल में, हम एक समय में कण वेग को संग्रहीत करेंगे $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ start {pmatrix} x, y \ end {pmrrix}$ , और कणों के बीच की दूरी को निरूपित किया जाता है $$$\ डेल्टा x$ और $$$\ डेल्टा y$ क्रमशः। कोड में, यह हमारे लिए प्रत्येक समीकरण के गति मान को बदलने के लिए पर्याप्त होगा, कई समीकरणों के एक सेट को हल करता है।

अब हम ग्रेडिएंट, डाइवरेज और लाप्लास ऑपरेटर को हमारे समन्वय ग्रिड के रूप में लेते हैं। $$$i, j$ - सरणी में सूचकांक, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y))$ - वेक्टर से संबंधित घटकों को लेते हुए):

यदि हम ऐसा मानते हैं तो हम वेक्टर ऑपरेटरों के असतत फार्मूले को और सरल बना सकते हैं $$$\ डेल्टा x = \ डेल्टा y = १$ । यह धारणा एल्गोरिदम की सटीकता को बहुत प्रभावित नहीं करेगी, हालांकि, यह प्रति पुनरावृत्ति संचालन की संख्या को कम करती है, और आम तौर पर आंखों के लिए अभिव्यक्ति को अधिक सुखद बनाती है।

कण आंदोलन

ये कथन तभी काम करते हैं, जब हम वर्तमान में विचार के तहत निकटतम कणों को पा सकते हैं। उन्हें खोजने के साथ जुड़े सभी संभावित लागतों को कम करने के लिए, हम उनके आंदोलन को ट्रैक नहीं करेंगे, लेकिन जहां कण पुनरावृत्ति की शुरुआत से आगे आने वाले समय में आंदोलन के प्रक्षेपवक्र का अनुमान लगाते हैं (दूसरे शब्दों में, वेग वेक्टर समय को बदलने से घटाते हैं) वर्तमान स्थिति)। सरणी के प्रत्येक तत्व के लिए इस तकनीक का उपयोग करते हुए, हम यह सुनिश्चित करेंगे कि किसी भी कण में "पड़ोसी" होगा:



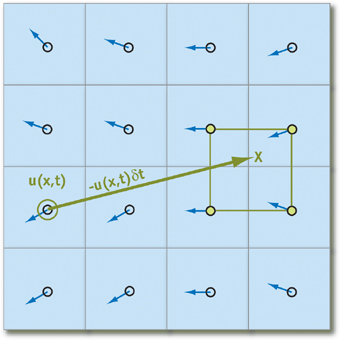
लगा रहे हैं $$$q$ - एक सरणी तत्व जो कण की स्थिति को संग्रहीत करता है, हम समय के साथ इसकी स्थिति की गणना के लिए निम्न सूत्र प्राप्त करते हैं $$$\ डेल्टा टी$ (हम मानते हैं कि त्वरण और दबाव के रूप में सभी आवश्यक मापदंडों की गणना पहले ही की जा चुकी है):

$$

$$q ({{\ _ vec {\ bf x}}, t + \ delta t}) = q ({{\ _ bf \ vec {x}} - {\ bf \ vec {u}} \ "डेल्टा =}, t)$$

हम तुरंत ध्यान दें कि पर्याप्त रूप से छोटे के लिए $$$\ डेल्टा टी$ और हम सेल की सीमा से बाहर कभी नहीं जा सकते हैं, इसलिए उपयोगकर्ता को कणों को देने के लिए सही गति चुनना बहुत महत्वपूर्ण है।

सेल की सीमा से टकराने या गैर-पूर्णांक निर्देशांक के मामले में सटीकता की हानि से बचने के लिए, हम चार निकटतम कणों के राज्यों के बिलिनियर प्रक्षेप को अंजाम देंगे और इसे बिंदु पर सही मान के रूप में लेंगे। सिद्धांत रूप में, ऐसी विधि व्यावहारिक रूप से अनुकरण की सटीकता को कम नहीं करेगी, और साथ ही इसे लागू करना काफी सरल है, इसलिए हम इसका उपयोग करेंगे।

चिपचिपापन

प्रत्येक तरल में एक निश्चित चिपचिपाहट होती है, उसके भागों पर बाहरी बलों के प्रभाव को रोकने की क्षमता (शहद और पानी एक अच्छा उदाहरण होगा, कुछ मामलों में उनकी चिपचिपाहट गुणांक परिमाण के एक क्रम से भिन्न होती है)। चिपचिपापन सीधे तरल द्वारा अधिग्रहित त्वरण को प्रभावित करता है, और नीचे सूत्र द्वारा व्यक्त किया जा सकता है, अगर संक्षिप्तता के लिए हम थोड़ी देर के लिए अन्य शर्तों को छोड़ देते हैं:

$$

$${\ आंशिक \ vec {\ bf u} \ over \ आंशिक t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

। इस स्थिति में, गति के लिए पुनरावृत्ति समीकरण निम्न रूप लेता है:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf का vec {u }$$

हम इस समानता को थोड़ा बदल देंगे, इसे रूप में लाएंगे $$$\ bf A \ vec {x} = \ vec {b}$ (रैखिक समीकरणों की एक प्रणाली का मानक रूप):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + delta t) = {u ({\ bf \ vec [x}}}, t )}$$

जहाँ $$$\ bf I$ पहचान मैट्रिक्स है। समीकरणों की कई समान प्रणालियों को हल करने के लिए हमें बाद में जैकोबी पद्धति को लागू करने के लिए ऐसे परिवर्तनों की आवश्यकता है। हम बाद में भी इस पर चर्चा करेंगे।

बाहरी ताकतें

एल्गोरिथ्म का सबसे सरल चरण है, माध्यम से बाहरी बलों का अनुप्रयोग। उपयोगकर्ता के लिए, यह माउस या इसके आंदोलन के साथ स्क्रीन पर क्लिक के रूप में परिलक्षित होगा। बाहरी बल को निम्नलिखित सूत्र द्वारा वर्णित किया जा सकता है, जिसे हम मैट्रिक्स के प्रत्येक तत्व के लिए लागू करते हैं ( $$$\ vec {\ bf G}$ - गति वेक्टर $$$x_p, y_p$ - माउस स्थिति $$$x, y$ - वर्तमान सेल के निर्देशांक, $$$आर$ - कार्रवाई की त्रिज्या, स्केलिंग पैरामीटर):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} या r r} \ n)$$

एक आवेग वेक्टर को आसानी से माउस की पिछली स्थिति और वर्तमान एक (यदि वहाँ एक था) के बीच अंतर के रूप में गणना की जा सकती है, और यहां आप अभी भी रचनात्मक हो सकते हैं। यह एल्गोरिथ्म के इस हिस्से में है कि हम रंगों को एक तरल, इसकी रोशनी आदि के साथ जोड़ सकते हैं। बाहरी बलों में गुरुत्वाकर्षण और तापमान भी शामिल हो सकते हैं, और हालांकि इस तरह के मापदंडों को लागू करना मुश्किल नहीं है, हम इस लेख में उन पर विचार नहीं करेंगे।

दबाव

नवियर-स्टोक्स समीकरण में दबाव वह बल है जो कणों को किसी भी बाहरी बल को लागू करने के बाद उन्हें उपलब्ध सभी जगह को भरने से रोकता है। तुरंत, इसकी गणना बहुत कठिन है, लेकिन हेल्महोल्त्ज़ अपघटन प्रमेय को लागू करके हमारी समस्या को बहुत सरल किया जा सकता है ।

हम कहते हैं $$$\ bf \ vec {W}$ विस्थापन, बाहरी बलों और चिपचिपाहट की गणना के बाद प्राप्त वेक्टर क्षेत्र। इसमें नॉनज़रो डाइवर्जेंस होगा, जो तरल की अपूर्णता की स्थिति का विरोध करता है ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ), और इसे ठीक करने के लिए, दबाव की गणना करना आवश्यक है। हेल्महोल्त्ज़ अपघटन प्रमेय के अनुसार, $$$\ bf \ vec {W}$ दो क्षेत्रों के योग के रूप में प्रतिनिधित्व किया जा सकता है:

$$

$$\ bf \ vec {W} = \ vec {u} + \ nabla p$$

जहाँ $$$\ bf यू$ - यह वेक्टर क्षेत्र है जिसे हम शून्य विचलन के साथ देख रहे हैं। इस लेख में इस समानता का कोई प्रमाण नहीं दिया जाएगा, लेकिन अंत में आप एक विस्तृत विवरण के साथ एक लिंक पा सकते हैं। हम स्केलर प्रेशर फ़ील्ड की गणना के लिए निम्न सूत्र प्राप्त करने के लिए अभिव्यक्ति के दोनों किनारों पर नाबला ऑपरेटर को लागू कर सकते हैं:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ n nabla ^ 2 p = \ nabla ^ 2 p$$

ऊपर लिखा अभिव्यक्ति दबाव के लिए पॉइसन समीकरण है। हम इसे पूर्वोक्त जैकोबी विधि द्वारा भी हल कर सकते हैं, और इस तरह नवियर-स्टोक्स समीकरण में अंतिम अज्ञात चर खोज सकते हैं। सिद्धांत रूप में, रैखिक समीकरणों की प्रणालियों को विभिन्न और परिष्कृत तरीकों से हल किया जा सकता है, लेकिन हम अभी भी उनमें से सबसे सरल पर ध्यान केंद्रित करेंगे, ताकि इस लेख को और अधिक बोझ न डालें।

सीमा और प्रारंभिक शर्तें

परिमित डोमेन पर बनाए गए किसी भी अंतर समीकरण को सही ढंग से निर्दिष्ट प्रारंभिक या सीमा शर्तों की आवश्यकता होती है, अन्यथा हमें शारीरिक रूप से गलत परिणाम प्राप्त होने की बहुत संभावना है। समन्वय ग्रिड के किनारों के पास तरल पदार्थ के व्यवहार को नियंत्रित करने के लिए सीमा की स्थिति स्थापित की जाती है, और प्रारंभिक शर्तें उन मापदंडों को निर्दिष्ट करती हैं जो कार्यक्रम शुरू होने के समय कणों के पास होती हैं।

प्रारंभिक शर्तें बहुत सरल होंगी - शुरू में द्रव स्थिर है (कण वेग शून्य है), और दबाव भी शून्य है। दिए गए सूत्रों द्वारा गति और दबाव के लिए सीमा की स्थिति निर्धारित की जाएगी:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ over 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ over 2 \ डेल्टा x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ over \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ _ \ _ डेल्टा y} = 0$$

इस प्रकार, किनारों पर कणों का वेग किनारों पर वेग के विपरीत होगा (जिससे वे किनारे से पीछे हट जाएंगे), और दबाव सीमा के बगल में मूल्य के बराबर है। इन ऑपरेशनों को सरणी के सभी बाउंडिंग तत्वों पर लागू किया जाना चाहिए (उदाहरण के लिए, एक ग्रिड आकार है $$$N \ गुना M$ , तो हम आकृति में नीले रंग में चिह्नित कोशिकाओं के लिए एल्गोरिदम लागू करते हैं):

डाई

अब हमारे पास क्या है, आप पहले से ही बहुत सारी दिलचस्प चीजें ले सकते हैं। उदाहरण के लिए, एक तरल में डाई के प्रसार का एहसास करने के लिए। ऐसा करने के लिए, हमें बस एक और स्केलर फ़ील्ड बनाए रखने की आवश्यकता है, जो सिमुलेशन के प्रत्येक बिंदु पर पेंट की मात्रा के लिए जिम्मेदार होगा। डाई को अद्यतन करने का सूत्र गति के समान है, और इसे इस प्रकार व्यक्त किया जाता है:

$$

$${\ आंशिक d \ over \ आंशिक t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$$

सूत्र में $$$एस$ डाई के साथ क्षेत्र को फिर से भरने के लिए जिम्मेदार (संभवतः उपयोगकर्ता क्लिक करता है) के आधार पर, $$$ड$ सीधे बिंदु पर डाई की मात्रा है, और $$$गामा$ - प्रसार गुणांक। इसे हल करना मुश्किल नहीं है, क्योंकि सूत्रों की व्युत्पत्ति पर सभी बुनियादी काम पहले से ही किए गए हैं, और यह कुछ प्रतिस्थापन बनाने के लिए पर्याप्त है। आरजीबी प्रारूप में पेंट को रंग के रूप में कोड में लागू किया जा सकता है, और इस मामले में कई वास्तविक मूल्यों के साथ संचालन के लिए कार्य कम हो जाता है।

vorticity

Vorticity समीकरण नवियर-स्टोक्स समीकरण का प्रत्यक्ष हिस्सा नहीं है, लेकिन यह एक तरल में डाई की गति के प्रशंसनीय सिमुलेशन के लिए एक महत्वपूर्ण पैरामीटर है। इस तथ्य के कारण कि हम एक असतत क्षेत्र पर एक एल्गोरिथ्म का उत्पादन कर रहे हैं, साथ ही साथ फ़्लोटिंग-पॉइंट मानों की सटीकता में नुकसान के कारण, यह प्रभाव खो गया है, और इसलिए हमें अंतरिक्ष में प्रत्येक बिंदु पर अतिरिक्त बल लागू करके इसे पुनर्स्थापित करने की आवश्यकता है। इस बल के वेक्टर के रूप में नामित किया गया है $$$\ bf \ vec {T}$ और निम्न सूत्रों द्वारा निर्धारित किया जाता है:

$$

$$\ bf \ omega = \ nabla \ टाइम्स \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ टाइम्स \ omega) \ डेल्टा x$$

$$$\ _ ओमेगा$ रोटर को वेग सदिश पर लागू करने का परिणाम है (इसकी परिभाषा लेख की शुरुआत में दी गई है), $$$\ vec \ eta$ - पूर्ण मानों के अदिश क्षेत्र का ढाल $$$\ _ ओमेगा$ । $$$\ vec \ psi$ एक सामान्यीकृत वेक्टर का प्रतिनिधित्व करता है $$$\ vec \ eta$ , और $$$\ epsilon$ एक स्थिर है जो नियंत्रित करता है कि हमारे द्रव में कितने बड़े भंवर होंगे।

रेखीय समीकरणों के सिस्टम को हल करने के लिए जैकोबी विधि

नवियर-स्टोक्स समीकरणों का विश्लेषण करने में, हम समीकरणों की दो प्रणालियों के साथ आए - एक चिपचिपाहट के लिए और दूसरा दबाव के लिए। वे एक पुनरावृत्त एल्गोरिथ्म द्वारा हल किए जा सकते हैं, जिसे निम्नलिखित पुनरावृत्त सूत्र द्वारा वर्णित किया जा सकता है:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ Alpha b_ {i, j}} \ over \ beta}$$

हमारे लिए $$$x$ - सरणी तत्व एक अदिश या वेक्टर क्षेत्र का प्रतिनिधित्व करते हैं। $$$k$ - पुनरावृत्ति संख्या, हम इसे कम करने और उत्पादकता बढ़ाने के लिए गणना या इसके विपरीत की सटीकता बढ़ाने के लिए इसे समायोजित कर सकते हैं।

हमारे द्वारा प्रतिस्थापित चिपचिपाहट की गणना करने के लिए: $$$x = b = \ bf \ vec {u}$ । $$$\ अल्फा = {1 \ over \ nu \ delta t}$ । $$$\ बीटा = 4+ \ अल्फा$ , यहाँ पैरामीटर है $$$\ बीटा$ - भार का योग। इस प्रकार, हमें एक क्षेत्र के मूल्यों को स्वतंत्र रूप से पढ़ने और उन्हें दूसरे में लिखने के लिए कम से कम दो वेक्टर वेग क्षेत्रों को संग्रहीत करने की आवश्यकता है। औसतन, जैकोबी विधि द्वारा वेग क्षेत्र की गणना के लिए, 20-50 पुनरावृत्तियों को अंजाम देना आवश्यक है, जो कि सीपीयू पर गणना करने पर काफी होता है।

दबाव समीकरण के लिए, हम निम्नलिखित प्रतिस्थापन करते हैं: $$$x = p$ । $$$b = \ nabla \ bf \ cdot \ vec {W}$ । $$$\ अल्फा = -1$ । $$$\ बीटा = 4$ । नतीजतन, हमें मूल्य मिलता है $$$p_ {i, j} \ delta t$ बिंदु पर। लेकिन चूंकि इसका उपयोग केवल वेग क्षेत्र से घटाए गए ढाल की गणना करने के लिए किया जाता है, अतिरिक्त परिवर्तनों को छोड़ा जा सकता है। दबाव क्षेत्र के लिए, 40-80 पुनरावृत्तियों को करना सबसे अच्छा है, क्योंकि छोटी संख्या के साथ विसंगति ध्यान देने योग्य हो जाती है।

एल्गोरिदम कार्यान्वयन

हम C ++ में एल्गोरिथ्म को लागू करेंगे, हमें कुडा टूलकिट की भी आवश्यकता है (आप इसे एनवीडिया वेबसाइट पर स्थापित करने के लिए कैसे पढ़ सकते हैं), साथ ही साथ एसएफएमएल भी । हमें एल्गोरिथ्म को समानांतर करने के लिए CUDA की आवश्यकता है, और SFML का उपयोग केवल एक विंडो बनाने और स्क्रीन पर एक चित्र प्रदर्शित करने के लिए किया जाएगा (सिद्धांत रूप में, यह ओपनजीएल में लिखा जा सकता है, लेकिन प्रदर्शन का अंतर महत्वहीन होगा, लेकिन कोड 200 अन्य लाइनों से बढ़ जाएगा)।

कोडा टूलकिट

सबसे पहले, हम कार्यों को समानांतर बनाने के लिए कोडा टूलकिट का उपयोग करने के बारे में थोड़ी बात करेंगे। एनवीडिया द्वारा एक अधिक विस्तृत मार्गदर्शिका प्रदान की जाती है, इसलिए यहां हम खुद को केवल सबसे आवश्यक तक ही सीमित रखते हैं। यह भी माना जाता है कि आप संकलक को स्थापित करने में सक्षम थे, और आप त्रुटियों के बिना एक परीक्षण परियोजना बनाने में सक्षम थे।

एक फ़ंक्शन बनाने के लिए जो जीपीयू पर चलता है, आपको पहले यह घोषित करने की आवश्यकता है कि हम कितने कर्नेल का उपयोग करना चाहते हैं, और कर्नेल के कितने ब्लॉक हमें आवंटित करने की आवश्यकता है। इसके लिए, कोडा टूलकिट हमें एक विशेष संरचना प्रदान करता है - dim3 , इसके सभी x, y, z मानों को डिफ़ॉल्ट रूप से सेट करके 1. फ़ंक्शन को कॉल करते समय इसे एक तर्क के रूप में निर्दिष्ट करके, हम आवंटित कर्नेल की संख्या को नियंत्रित कर सकते हैं। चूंकि हम द्वि-आयामी सरणी के साथ काम कर रहे हैं, इसलिए हमें कंस्ट्रक्टर में केवल दो फ़ील्ड सेट करने की आवश्यकता है: x और y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

जहाँ size_x और size_y सरणी के आकार को संसाधित किया जा रहा है। हस्ताक्षर और फ़ंक्शन कॉल निम्नानुसार हैं (ट्रिपल कोण ब्रैकेट्स को कुडा संकलक द्वारा संसाधित किया जाता है):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

फ़ंक्शन में ही, आप ब्लॉक सूत्र के माध्यम से दो आयामी सरणी के सूचकांक को पुनर्स्थापित कर सकते हैं और इस ब्लॉक में कर्नेल नंबर निम्न सूत्र का उपयोग कर सकते हैं:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

यह ध्यान दिया जाना चाहिए कि वीडियो कार्ड पर निष्पादित फ़ंक्शन को __global__ टैग के साथ चिह्नित किया जाना चाहिए, और शून्य भी लौटाया जाना चाहिए, इसलिए अक्सर गणना परिणामों को तर्क के रूप में लिखा जाता है और वीडियो कार्ड की स्मृति में पूर्व-आवंटित किया जाता है।

CudaMalloc और CudaFree वीडियो कार्ड पर मेमोरी को मुक्त करने और आवंटित करने के लिए जिम्मेदार हैं। हम पॉइंटर्स पर मेमोरी क्षेत्र में काम कर सकते हैं जो वे वापस लौटते हैं, लेकिन हम मुख्य कोड से डेटा तक नहीं पहुंच सकते हैं। गणना परिणामों को वापस करने का सबसे आसान तरीका मानक मेम्ची के समान, कोडमैकेसी का उपयोग करना है , लेकिन वीडियो कार्ड से मुख्य मेमोरी और इसके विपरीत डेटा की प्रतिलिपि बनाने में सक्षम है।

SFML और विंडो रेंडर

इस सभी ज्ञान के साथ, हम आखिरकार सीधे कोड लिखने के लिए आगे बढ़ सकते हैं। शुरू करने के लिए, चलो main.cpp फ़ाइल बनाएँ और वहाँ प्रस्तुत विंडो के लिए सभी सहायक कोड रखें:


मुख्य समारोह की शुरुआत में लाइन

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

एक निरंतर लंबाई के साथ एक आयामी सरणी के रूप में एक RGBA छवि बनाता है। हम इसे अन्य मापदंडों (माउस पोजीशन, फ्रेम के बीच का अंतर) के साथ कंप्यूटफिल्ड फंक्शन में पास करेंगे। उत्तरार्द्ध, साथ ही कई अन्य कार्यों को कर्नेल.यू में घोषित किया गया है और GPU पर निष्पादित कोड को कॉल करें। आप एसएफएमएल वेबसाइट पर किसी भी फ़ंक्शन पर प्रलेखन पा सकते हैं, फ़ाइल कोड में सुपर-दिलचस्प कुछ भी नहीं हो रहा है, इसलिए हम लंबे समय तक वहां नहीं रुकते हैं।

GPU कम्प्यूटिंग

Gpu के तहत कोड लिखना शुरू करने के लिए, पहले एक कर्नेल। Cu फ़ाइल बनाएं और उसमें कई सहायक कक्षाएं परिभाषित करें: Color3f, Vec2, config, SystemConfig :


विधि नाम के सामने __host__ विशेषता का अर्थ है कि कोड को CPU पर निष्पादित किया जा सकता है, __device__ , इसके विपरीत, GPU के तहत कोड एकत्र करने के लिए कंपाइलर को बाध्य करता है। कोड दो-घटक वैक्टर, रंग के साथ काम करने के लिए आदिम घोषित करता है, मापदंडों के साथ कॉन्फ़िगर करता है जिसे रनटाइम में बदला जा सकता है, साथ ही कई स्थिर बिंदुओं को सरणियों के लिए, जिसे हम गणना के लिए बफ़र्स के रूप में उपयोग करेंगे।

cudaInit और cudaExit को भी बहुत मामूली रूप से परिभाषित किया गया है:


आरंभीकरण समारोह में, हम दो-आयामी सरणियों के लिए मेमोरी आवंटित करते हैं, उन रंगों की एक सरणी निर्दिष्ट करते हैं जिनका उपयोग हम तरल को चित्रित करने के लिए करेंगे, और साथ ही डिफ़ॉल्ट मानों को कॉन्फ़िगरेशन में सेट करेंगे। CudaExit में, हम सिर्फ सभी बफ़र्स को मुक्त करते हैं। विरोधाभासी के रूप में यह लगता है, दो आयामी सरणियों के भंडारण के लिए, यह एक आयामी सरणियों का उपयोग करने के लिए सबसे अधिक फायदेमंद है, जिस तक पहुंच निम्नलिखित अभिव्यक्ति के साथ किया जाएगा:

 array[y * size_x + x]; // equals to array[y][x] 

हम कण विस्थापन समारोह के साथ प्रत्यक्ष एल्गोरिदम का कार्यान्वयन शुरू करते हैं। फ़ील्ड ओल्डफ़िल्ड और न्यूफ़िल्ड (वह फ़ील्ड जहाँ डेटा आता है और जहाँ उन्हें लिखा जाता है), सरणी का आकार, साथ ही समय डेल्टा और घनत्व गुणांक (तरल में डाई के विघटन में तेजी लाने और मध्यम को विशेष रूप से संवेदनशील नहीं बनाने के लिए संवेदनशील बनाने के लिए स्थानांतरित किया जाता है) उपयोगकर्ता कार्रवाई)। मध्यवर्ती मूल्यों की गणना के माध्यम से बिलिनियर प्रक्षेप समारोह को शास्त्रीय तरीके से कार्यान्वित किया जाता है :


यह चिपचिपाहट प्रसार समारोह को कई भागों में विभाजित करने का निर्णय लिया गया था: कम्प्यूट्यूटिफ्यूजन को मुख्य कोड से कहा जाता है, जो फैलाना और गणना को पूर्व निर्धारित समय की गणना करता है , और फिर सरणी को स्वैप करता है जहां से हम डेटा लेते हैं और जहां हम इसे लिखते हैं। समानांतर डेटा प्रोसेसिंग को लागू करने का यह सबसे आसान तरीका है, लेकिन हम दोगुनी मेमोरी खर्च कर रहे हैं।

दोनों कार्यों में जैकोबी पद्धति की विविधताएं हैं। JacobiColor और jacobiVelocity का शरीर तुरंत जाँच करता है कि वर्तमान तत्व सीमा पर नहीं हैं - इस मामले में, हमें उन्हें सीमा और प्रारंभिक स्थितियों के खंड में वर्णित सूत्रों के अनुसार सेट करना होगा।


बाहरी बल के उपयोग को एक ही फ़ंक्शन के माध्यम से लागू किया जाता है - applyForce , जो एक तर्क के रूप में माउस की स्थिति, डाई के रंग, साथ ही साथ कार्रवाई की त्रिज्या लेता है। इसकी मदद से, हम कणों को गति दे सकते हैं, साथ ही उन्हें पेंट भी कर सकते हैं। भ्राता प्रतिपादक आपको क्षेत्र को बहुत तेज नहीं बनाने की अनुमति देता है, और साथ ही निर्दिष्ट त्रिज्या में काफी स्पष्ट है।


Vorticity की गणना पहले से ही एक अधिक जटिल प्रक्रिया है, इसलिए हम इसे computeVorticity और applyVorticity में लागू करते हैं, हम यह भी ध्यान देते हैं कि उनके लिए दो ऐसे वेक्टर ऑपरेटरों को curl (रोटर) और absGradient (निरपेक्ष क्षेत्र मूल्यों का ढाल) के रूप में परिभाषित करना आवश्यक है। अतिरिक्त भंवर प्रभावों को निर्दिष्ट करने के लिए, हम गुणा करते हैं $$$य$ ढाल वेक्टर के घटक पर $$$-1$ , और फिर लंबाई द्वारा विभाजित करके इसे सामान्य करें (यह जांचने के लिए भूलकर कि वेक्टर नॉनजरो है):


एल्गोरिथ्म में अगला चरण स्केलर दबाव क्षेत्र की गणना और वेग क्षेत्र पर इसके प्रक्षेपण होगा। ऐसा करने के लिए, हमें 4 कार्यों को लागू करने की आवश्यकता है: डायवर्जेंसी , जो गति विचलन, जैकोबायप्योर पर विचार करेगी , जो दबाव के लिए जैकोबी विधि को लागू करती है, और कम्प्यूट्रेटइम्प्लिमेंट के साथ कंप्यूटसेप्टर , इटैलिक फील्ड गणना करते हुए:


प्रक्षेपण दो छोटे कार्यों में फिट बैठता है - परियोजना और दबाव के लिए इसे ढाल कहा जाता है। इसे हमारे सिमुलेशन एल्गोरिदम का अंतिम चरण कहा जा सकता है:


प्रक्षेपण के बाद, हम सुरक्षित रूप से छवि को बफर और विभिन्न पोस्ट-इफेक्ट्स तक पहुंचाने के लिए आगे बढ़ सकते हैं। पेंट फ़ंक्शन कण फ़ील्ड से RGBA सरणी में रंगों की प्रतिलिपि बनाता है। ApplyBloom फ़ंक्शन भी लागू किया गया था, जो तरल को हाइलाइट करता है जब कर्सर को उस पर रखा जाता है और माउस बटन दबाया जाता है। अनुभव से, यह तकनीक उपयोगकर्ता की आंखों के लिए तस्वीर को अधिक सुखद और दिलचस्प बनाती है, लेकिन यह बिल्कुल भी आवश्यक नहीं है।

पोस्ट-प्रोसेसिंग में, आप उन स्थानों को भी हाइलाइट कर सकते हैं जहां द्रव की गति सबसे अधिक होती है, गति वेक्टर के आधार पर रंग बदलते हैं, विभिन्न प्रभाव जोड़ते हैं, आदि, लेकिन हमारे मामले में हम खुद को एक प्रकार की न्यूनतम तक सीमित कर लेंगे, क्योंकि इसके साथ भी छवियां बहुत आकर्षक हैं (विशेष रूप से गतिशीलता में) :


और अंत में, हमारे पास अभी भी एक मुख्य कार्य है जिसे हम main.cpp - computeField से कहते हैं। यह एल्गोरिथम के सभी टुकड़ों को एक साथ जोड़ता है, वीडियो कार्ड पर कोड को कॉल करता है, और जीपीयू से सीपीयू तक के डेटा को भी कॉपी करता है। इसमें गति वेक्टर की गणना और डाई रंग की पसंद भी शामिल है, जिसे हम लागू करते हैं :

निष्कर्ष

इस लेख में, हमने नवियर-स्टोक्स समीकरण को हल करने के लिए एक संख्यात्मक एल्गोरिथ्म का विश्लेषण किया और एक अपूर्ण तरल पदार्थ के लिए एक छोटा सिमुलेशन प्रोग्राम लिखा। शायद हम सभी पेचीदगियों को नहीं समझते थे, लेकिन मैं आशा करता हूं कि सामग्री आपके लिए दिलचस्प और उपयोगी हो, और कम से कम द्रव मॉडलिंग के क्षेत्र में एक अच्छे परिचय के रूप में सेवा की।

इस लेख के लेखक के रूप में, मैं ईमानदारी से किसी भी टिप्पणी और परिवर्धन की सराहना करूंगा, और इस पोस्ट के तहत आपके सभी सवालों के जवाब देने की कोशिश करूंगा।

अतिरिक्त सामग्री

आप इस लेख में मेरे जीथूब भंडार में सभी स्रोत कोड पा सकते हैं। सुधार के किसी भी सुझाव का स्वागत है।

मूल सामग्री जो इस लेख के लिए आधार के रूप में कार्य करती है, आप एनवीडिया की आधिकारिक वेबसाइट पर पढ़ सकते हैं। यह शेडर्स की भाषा में एल्गोरिथ्म के कुछ हिस्सों के कार्यान्वयन के उदाहरण भी प्रस्तुत करता है:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

हेल्महोल्ट्ज़ अपघटन प्रमेय का प्रमाण और द्रव यांत्रिकी पर भारी मात्रा में अतिरिक्त सामग्री इस पुस्तक में पाई जा सकती है (अंग्रेजी, खंड 1.2 देखें):
चोरिन, एजे और जेई मार्सडेन। 1993. द्रव यांत्रिकी का गणितीय परिचय। तीसरा संस्करण। स्प्रिंगर।

एक अंग्रेजी बोलने वाले YouTube का चैनल, गणित से संबंधित गुणवत्ता की सामग्री बनाना, और विशेष रूप से (अंग्रेजी) में अंतर समीकरणों को हल करना। मदद करने के लिए बहुत वर्णनात्मक वीडियो आप गणित और भौतिकी में बहुत सी बातें का सार समझ में:
3Blue1Brown - यूट्यूब
अंतर समीकरण (3Blue1Brown)

इसके अलावा धन्यवाद WhiteBlackGoose सहायता के लिए इस लेख के लिए सामग्री तैयार करने में।

---

और अंत में, एक छोटा सा बोनस - कार्यक्रम में लिया गया कुछ सुंदर स्क्रीनशॉट:


डायरेक्ट स्ट्रीम (डिफ़ॉल्ट सेटिंग्स)


व्हर्लपूल (एप्लायर्स में बड़ा त्रिज्या)


वेव (उच्च vorticity + प्रसार)

इसके अलावा, लोकप्रिय मांग से, मैंने सिमुलेशन के साथ एक वीडियो जोड़ा: