ग्रोवर एल्गोरिथम और डेटा खोज

हाय, हब्रोज़ितेली! हमने हाल ही में क्रिस बर्नहार्ड की पुस्तक क्वांटम कम्प्यूटिंग फॉर रियल आईटी को सौंप दिया है। यहाँ उन्होंने "ग्रोवर के एल्गोरिथ्म और डेटा खोज" पुस्तक का एक अंश साझा करने का निर्णय लिया

हम बड़े डेटा के युग में प्रवेश कर रहे हैं। विशाल डेटासेट्स को कुशलता से खोजना वर्तमान में कई बड़ी कंपनियों के लिए एक जलती हुई चिंता है। ग्रोवर का एल्गोरिथ्म सैद्धांतिक रूप से डेटा पुनर्प्राप्ति को तेज करने में सक्षम है।

लव ग्रोवर ने 1996 में अपने एल्गोरिथ्म का आविष्कार किया। Deutsch और साइमन के एल्गोरिदम की तरह, क्वेरी जटिलता के संदर्भ में शास्त्रीय एल्गोरिदम की तुलना में इसकी निष्पादन गति अधिक है। हालांकि, हम oracles के बिना वर्तमान डेटा पुनर्प्राप्ति एल्गोरिथ्म को लागू करने में सक्षम नहीं होंगे जो अपने प्रश्न पूछ सकते हैं। हमें एक एल्गोरिथ्म का निर्माण करना चाहिए जो ओरेकल का काम करता है। लेकिन इससे पहले कि हम ग्रोवर एल्गोरिदम के कार्यान्वयन के बारे में बात करना शुरू करें, आइए देखें कि यह क्या करता है और कैसे।

ग्रोवर एल्गोरिथम

कल्पना कीजिए कि आपके पास चार प्लेइंग कार्ड हैं। उन्हें उलटा कर दिया जाता है। आप जानते हैं कि उनमें से एक कीड़े का एक इक्का है और आपको इसे खोजने की आवश्यकता है। आपको कितने कार्ड फ्लिप करने होंगे जब तक आपको पता नहीं है कि कीड़े का इक्का कहाँ है?

यदि आप भाग्यशाली हैं, तो आपको पहली कोशिश में वांछित कार्ड मिलेगा, यदि आप भाग्यशाली नहीं हैं, तो आप तीन कार्ड फ्लिप कर सकते हैं, और उनमें से एक भी कीड़े का एक इक्का नहीं होगा। सबसे खराब स्थिति में, तीन कार्डों को चालू करने से, आपको यह पता चलेगा कि अंतिम कार्ड उस कीड़े का इक्का है जिसे आप ढूंढ रहे हैं। इसलिए, हम यह पता लगा सकते हैं कि इक्का एक से तीन कार्डों में फ़्लिप करके कहाँ है। औसतन, आपको 2.25 कार्ड फ्लिप करने की आवश्यकता है।

यह उन कार्यों में से एक है जो ग्रोवर के एल्गोरिथ्म को हल करता है। एल्गोरिथ्म का वर्णन शुरू करने से पहले, हम समस्या का सुधार करते हैं। हमारे पास चार बाइनरी अनुक्रम हैं: 00, 01, 10 और 11. हमारे पास एक फ़ंक्शन च है जो इन अनुक्रमों में से तीन के लिए 0 और चौथे अनुक्रम के लिए 1 देता है। हमें आउटपुट मान के अनुरूप बाइनरी अनुक्रम को खोजने की आवश्यकता है। 1. उदाहरण के लिए, हम निम्नलिखित परिणाम प्राप्त कर सकते हैं: f (00) = 0, f (01) = 0, f (10) = 1 और f (11) = 0. अब समस्या है यह पता लगाना है कि परिणाम को प्राप्त करने के लिए फ़ंक्शन को कितनी बार गणना की जानी चाहिए f (10) = 1. यहां हमने केवल कार्यों के साथ ताश के पत्तों की जगह समस्या का सुधार किया है, इसलिए इस प्रश्न का उत्तर पहले से ही ज्ञात है: पहले की तरह, औसत पर फ़ंक्शन की गणना करना आवश्यक होगा। २.२५ बार।

सभी जटिलता क्वेरी एल्गोरिदम के साथ, हम एक ओरेकल - एक गेट का निर्माण करते हैं जो एक फ़ंक्शन को एनकैप्सुलेट करता है। हमारे उदाहरण के लिए ओरेकल, जहां केवल चार बाइनरी अनुक्रम हैं, अंजीर में दिखाया गया है। 9.1।

ग्रोवर एल्गोरिथ्म के लिए चेन अंजीर में दिखाया गया है। 9.2।

एल्गोरिथ्म दो चरणों को पूरा करता है। सबसे पहले, प्रायिकता आयाम का संकेत फ़्लिप किया जाता है, उस स्थान से जुड़ा हुआ जिसे हम खोजने की कोशिश कर रहे हैं। दूसरा इस संभावना आयाम को पुष्ट करता है। आइए देखें कि श्रृंखला यह कैसे करती है।


हैडमार्ड वाल्वों के माध्यम से संचरण के बाद, दो ऊपरी चतुर्भुज राज्य प्राप्त करते हैं


और निचली कक्षा में एक राज्य है

संयुक्त राज्य के रूप में लिखा जा सकता है


चौकियां तब गेट एफ से गुजरती हैं। यह उस स्थान के लिए तीसरी कक्षा में 0 और 1 में प्रवेश करती है जिसे हम खोजने की कोशिश कर रहे हैं। हमारे मामले के लिए एफ (10) = 1 हमें मिलता है



इसे फिर से लिखा जा सकता है



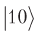
नतीजतन, हम दो ऊपरी क्वैब प्राप्त करते हैं, निचले के साथ भ्रमित नहीं होते हैं, लेकिन संभावना के आयाम वांछित स्थान का संकेत देते हुए संकेत को बदल देगा।

यदि हम इस चरण में ऊपरी दो क्वैबिट को मापते हैं, तो हमें चार स्थानों में से एक मिलता है, और सभी चार संभावित उत्तर समान रूप से संभावित हैं। हमें एक और कदम उठाने की जरूरत है - संभावना के आयाम को बढ़ाने के लिए। उनके औसत के सापेक्ष संख्याओं के अनुक्रम को उल्टा करके प्रवर्धन किया जाता है। यदि संख्या औसत से ऊपर है, तो यह फ़्लिप करती है और औसत से नीचे हो जाती है। यदि संख्या औसत से नीचे है, तो यह फ़्लिप हो जाता है और औसत से ऊपर हो जाता है। प्रत्येक मामले में, औसत से दूरस्थता बनाए रखी जाती है। समझाने के लिए, हम चार संख्याओं का उपयोग करते हैं: 1, 1, 1, और -1। उनका योग 2 है, और औसत 2/4, या 1/2 है। फिर हम अनुक्रम में संख्याओं के माध्यम से छंटनी शुरू करते हैं। पहली संख्या १ है। यह औसत से १/२ ऊपर है। तख्तापलट के बाद, यह औसत से 1/2 कम होना चाहिए। इस स्थिति में, यह 0. में बदल जाएगा। संख्या -1 औसत से नीचे 3/2 है। तख्तापलट के बाद, यह औसत से 3/2 ऊपर हो जाना चाहिए, अर्थात 2 में बदल जाना चाहिए।

वर्तमान में दो ऊपरी खदानों में एक राज्य है


औसत के सापेक्ष एम्पलीट्यूड को चालू करते हुए, हम प्राप्त करते हैं ।
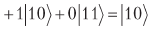
माप पूरा करने के बाद, हम निश्चित रूप से 10 प्राप्त करेंगे, अर्थात, औसत के सापेक्ष एक क्रांति हमें वही देती है जिसकी हमें आवश्यकता है। हमें बस यह सुनिश्चित करना है कि एक गेट है या, एक ही चीज क्या है, एक ऑर्थोगोनल मैट्रिक्स जो औसत के सापेक्ष क्रांति का वर्णन करता है। ऐसा मैट्रिक्स मौजूद है:


ऊपरी दो बटेरों पर वाल्व की कार्रवाई के परिणामस्वरूप, हम प्राप्त करते हैं


इस उदाहरण में, जहां हमारे पास केवल दो qubits हैं, हमें केवल एक बार oracle का उपयोग करना चाहिए। हमारे लिए एकमात्र प्रश्न पूछना पर्याप्त है। केस n = 2 के लिए, ग्रोवर एल्गोरिदम एक प्रश्न के बाद सटीक उत्तर देता है, जबकि शास्त्रीय मामले में, औसतन 2.25 प्रश्न पूछे जाने की आवश्यकता है।

यह विचार मनमानी संख्या के n qubits के मामले तक फैला हुआ है। हम संभावना आयाम के संकेत को मोड़कर शुरू करते हैं, जो वांछित स्थान से मेल खाती है। तब हम औसत के सापेक्ष क्रांति करते हैं। हालांकि, इस मामले में, आयाम का प्रवर्धन दो qubits के साथ स्थिति में उतना महत्वपूर्ण नहीं होता है। उदाहरण के लिए आठ संख्याएँ लीजिए, जिनमें से सात 1 हैं और एक -1 है। उनका योग 6 है, और औसत 6/8 है। एक पलटने के बाद, औसत 1 1/2 हो जाएगा, और -1 -1 10/4 हो जाएगा। नतीजतन, तीन qubit की उपस्थिति में, आयाम के प्रवर्धन के बाद एक qubit को मापने, हम दूसरों की तुलना में अधिक संभावना के साथ वांछित स्थान प्राप्त करेंगे। समस्या यह है कि गलत उत्तर प्राप्त करने का एक महत्वपूर्ण मौका है। हमें सही उत्तर प्राप्त करने की उच्च संभावना की आवश्यकता है - हमें मापने से पहले आयाम को और अधिक बढ़ाना होगा। समाधान श्रृंखला के माध्यम से सभी qubits को वापस स्थानांतरित करना है। हम फिर से वांछित स्थान के साथ जुड़े संभावना आयाम के चिह्न को फ्लिप करते हैं और औसत के सापेक्ष फिर से फ्लिप करते हैं।

सामान्यीकृत मामले पर विचार करें। हमें m संभावित स्थानों में से कुछ में खोजने की आवश्यकता है। शास्त्रीय तरीके से इसे खोजने के लिए, सबसे खराब स्थिति में हमें मी - 1 प्रश्न पूछना होगा। प्रश्नों की संख्या मी के अनुपात में बढ़ती है। ग्रोवर ने एक सूत्र की गणना की जो यह निर्धारित करता है कि एक सही उत्तर की अधिकतम संभावना प्राप्त करने के लिए उसकी श्रृंखला को कितनी बार उपयोग करने की आवश्यकता है। यह सूत्र जो संख्या देता है वह आनुपातिक रूप से बढ़ता है । 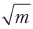यह द्विघात त्वरण है।

ग्रोवर एल्गोरिथम अनुप्रयोग

एल्गोरिथ्म के कार्यान्वयन के साथ कई समस्याएं हैं। सबसे पहले, द्विघात त्वरण का मूल्यांकन जटिलता अनुरोध के सापेक्ष किया जाता है। ओरेकल का उपयोग करने के लिए, आपको इसे बनाने की आवश्यकता है, और यदि आप इस कार्य को उचित देखभाल के साथ नहीं करते हैं, तो ऑरेकल द्वारा निष्पादित चरणों की संख्या एल्गोरिथ्म को सहेजने वाले चरणों की संख्या से आगे निकल जाएगी, और परिणामस्वरूप, एल्गोरिथ्म शास्त्रीय एक के बजाय तेजी से धीमा हो जाएगा। एक अन्य समस्या यह है कि, त्वरण का निर्धारण करने से, हम मानते हैं कि डेटा सेट अव्यवस्थित है। यदि डेटा सेट में एक विशिष्ट संरचना है, तो आप अक्सर एक क्लासिक एल्गोरिथ्म पा सकते हैं जो इस संरचना का उपयोग करता है और बहुत तेजी से समाधान खोजता है। अंतिम समस्या त्वरण से संबंधित है। द्विघात त्वरण घातीय त्वरण से अधिक कुछ नहीं है, जिसे हमने अन्य एल्गोरिदम में देखा था। क्या अधिक प्राप्त करना संभव है? आइए इन मुद्दों पर गौर करें।

ऑरेकल के कार्यान्वयन और डेटा सेट में संरचना की उपस्थिति से जुड़ी दोनों समस्याएं उचित हैं और बताती हैं कि ज्यादातर मामलों में ग्रोवर एल्गोरिथ्म में डेटाबेस की खोज के लिए व्यावहारिक अनुप्रयोग नहीं है। लेकिन कुछ स्थितियों में, डेटा में एक संरचना होने से एक ओरेकल बनाना संभव हो जाता है जो उच्च दक्षता के साथ कार्य करता है। ऐसी स्थितियों में, एल्गोरिथ्म क्लासिक एल्गोरिदम से आगे निकल सकता है। अधिक से अधिक सफलता प्राप्त करने की संभावना के सवाल का जवाब पहले ही दिया जा चुका है। यह साबित होता है कि ग्रोवर का एल्गोरिथ्म इष्टतम है। क्वांटम त्वरण से अधिक समस्या के समाधान में सक्षम कोई क्वांटम एल्गोरिथ्म नहीं है। द्विघात त्वरण, हालांकि घातीय के रूप में प्रभावशाली नहीं है, फिर भी कुछ लाभ प्रदान करता है। बड़े डेटा सेट के साथ काम करते समय, कोई भी स्पीडअप मूल्यवान हो सकता है।

यह संभावना है कि ग्रोवर एल्गोरिदम खोज के लिए मुख्य आवेदन नहीं मिलेगा, जैसा कि ऊपर प्रस्तुत किया गया था, लेकिन इसकी विविधताओं के लिए। विशेष रूप से, आयाम को बढ़ाने का विचार काम में आ सकता है।

हमने केवल कुछ एल्गोरिदम की जांच की, लेकिन शोर और ग्रोवर एल्गोरिदम को सबसे महत्वपूर्ण माना जाता है। इन दो में निहित विचारों के आधार पर कई अन्य एल्गोरिदम हैं। अब हम क्वांटम एल्गोरिदम से क्वांटम कंप्यूटिंग के आवेदन के अन्य क्षेत्रों पर अपना ध्यान केंद्रित करते हैं।