रैखिक प्रतिगमन और ग्रेडिएंट वंश

X और Y संकेतक दें, जिनकी मात्रात्मक अभिव्यक्ति है, एक निश्चित विषय क्षेत्र में अध्ययन किया जाता है।

इसके अलावा, यह मानने का हर कारण है कि सूचक Y संकेतक X पर निर्भर करता है। यह स्थिति एक वैज्ञानिक परिकल्पना दोनों हो सकती है और प्राथमिक सामान्य ज्ञान पर आधारित हो सकती है। उदाहरण के लिए, किराने की दुकानों को लें।

द्वारा अस्वीकार करें:

एक्स - बिक्री क्षेत्र (वर्ग एम।)

वाई - वार्षिक कारोबार (मिलियन पी।)

स्पष्ट रूप से, उच्च व्यापार क्षेत्र, उच्च वार्षिक कारोबार (हम एक रैखिक संबंध मानते हैं)।

कल्पना करें कि हमारे पास कुछ n स्टोर्स (रिटेल स्पेस और वार्षिक टर्नओवर) पर डेटा है - हमारे डेटासेट और k रिटेल स्पेस (X), जिसके लिए हम वार्षिक टर्नओवर (Y) - हमारे कार्य की भविष्यवाणी करना चाहते हैं।

हम अनुमान लगाते हैं कि Y का हमारा मान X के रूप में निर्भर करता है: Y = a + b * X

हमारी समस्या को हल करने के लिए, हमें गुणांक a और b चुनना होगा।

सबसे पहले, हम एक और बी यादृच्छिक मान सेट करते हैं। उसके बाद, हमें नुकसान फ़ंक्शन और अनुकूलन एल्गोरिथ्म को निर्धारित करने की आवश्यकता है।

ऐसा करने के लिए, हम रूट माध्य वर्ग हानि फ़ंक्शन ( MSELoss ) का उपयोग कर सकते हैं। इसकी गणना सूत्र द्वारा की जाती है:



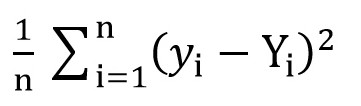
जहाँ y [i] = a + b * x [i] के बाद a = रैंड () और b = रैंड (), और Y [i] x [i] के लिए सही मान है।
इस स्तर पर, हमारे पास मानक विचलन (ए और बी का एक निश्चित कार्य) है। और यह स्पष्ट है कि, इस फ़ंक्शन का मूल्य जितना छोटा होता है, उतने ही सटीक रूप से पैरामीटर a और b को उन मापदंडों के संबंध में चुना जाता है जो खुदरा अंतरिक्ष के क्षेत्र और इस कमरे में कारोबार के बीच सटीक संबंध का वर्णन करते हैं।

अब हम ढाल वंश का उपयोग करना शुरू कर सकते हैं (बस नुकसान फ़ंक्शन को कम करने के लिए)।

धीरे-धीरे उतरना

इसका सार बहुत सरल है। उदाहरण के लिए, हमारे पास एक फ़ंक्शन है:

y = x*x + 4 * x + 3 

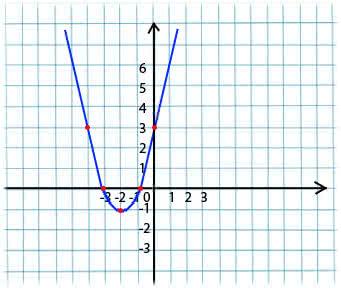
हम फ़ंक्शन की परिभाषा के डोमेन से x का एक मनमाना मान लेते हैं। कल्पना करें कि यह बिंदु X1 = -4 है।

इसके बाद, हम इस फ़ंक्शन के एक्स के संबंध में व्युत्पन्न को बिंदु X1 पर ले जाते हैं (यदि फ़ंक्शन कई वेरिएबल्स पर निर्भर करता है (उदाहरण के लिए, ए और बी), तो हमें प्रत्येक वेरिएबल के लिए आंशिक डेरिवेटिव लेने की आवश्यकता है)। y '(X1) = -4 <0

अब हमें x: x2 = X1 - lr * y '(X1) के लिए एक नया मान मिलता है। एलआर (सीखने की दर) पैरामीटर आपको चरण आकार निर्धारित करने की अनुमति देता है। इस प्रकार हम प्राप्त करते हैं:

यदि किसी दिए गए बिंदु X1 <0 पर आंशिक व्युत्पन्न (फ़ंक्शन कम हो जाता है), तो हम स्थानीय न्यूनतम के बिंदु पर चले जाते हैं। (x2 X1 से बड़ा होगा)

यदि किसी दिए गए बिंदु X1> 0 (फ़ंक्शन बढ़ता है) पर आंशिक व्युत्पन्न होता है, तो हम अभी भी स्थानीय न्यूनतम के बिंदु पर जा रहे हैं। (एक्स 2 एक्स 1 से कम होगा)

इस एल्गोरिथ्म को चलने के द्वारा, हम न्यूनतम दृष्टिकोण करेंगे (लेकिन उस तक नहीं पहुंचेंगे)।

व्यवहार में, यह सब बहुत सरल लगता है (हालांकि, मैं यह कहना नहीं चाहता कि कौन सा गुणांक a और b दुकानों के साथ उपरोक्त मामले के लिए सबसे उपयुक्त है, इसलिए हम डेटासेट बनाने के लिए फॉर्म y = 1 + 2 * x की निर्भरता लेते हैं, और फिर हमारे मॉडल को प्रशिक्षित करते हैं। यह डेटासेट):
(यहां कोड लिखा है )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

कोड संकलित करने के बाद, आप देख सकते हैं कि ए और बी के प्रारंभिक मूल्य क्रमशः 1 और 2 के आवश्यक मूल्यों से दूर थे, और अंतिम मूल्य बहुत करीब हैं।

मैं थोड़ा स्पष्ट कर दूंगा कि a_grad और b_grad को इस तरह क्यों माना जाता है।
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) । एफ के आंशिक व्युत्पन्न के संबंध में एक -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error होगा -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error । B के संबंध में F का आंशिक व्युत्पन्न -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error । हम error और x_train बाद से माध्य मान (mean()) y_train हैं और y_train मानों के सरणियाँ हैं, ए और बी स्केलर हैं।

लेख में प्रयुक्त सामग्री:

towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html