शीर्षक "आपके लिए लेख पढ़ें।" जनवरी - जून 2019

नमस्कार, हेब्र! हम चैनल #article_essense से ओपन डेटा साइंस समुदाय के सदस्यों के वैज्ञानिक लेखों की समीक्षाओं को प्रकाशित करना जारी रखते हैं। यदि आप उन्हें हर किसी से पहले प्राप्त करना चाहते हैं - समुदाय में शामिल हों!

आज के लिए लेख:

1. तंत्रिका साधारण विभेदक समीकरण (टोरंटो विश्वविद्यालय, 2018)
2. सेमी-अनसुप्राइज़्ड लर्निंग विथ डीप जेनरेटिव मॉडल्स: अल्ट्रा-स्पार्स लेबल्स (यूनिवर्सिटी ऑफ़ ऑक्सफ़ोर्ड, द एलन ट्यूरिंग इंस्टीट्यूट, लंदन, 2019) का उपयोग करके क्लस्टरिंग और वर्गीकरण।
3. अनलिमिटेड एंड मितीगेटिंग अल्गोरिथमिक बायस लर्नड लेटेंट स्ट्रक्चर (मैसाचुसेट्स इंस्टीट्यूट ऑफ टेक्नोलॉजी, हार्वर्ड यूनिवर्सिटी, 2018)
4. मानव प्राथमिकताओं से गहन सुदृढ़ीकरण सीखना (OpenAI, DeepMind, 2017)
5. छवि मान्यता के लिए रैंडमली वायर्ड न्यूरल नेटवर्क की खोज करना (फेसबुक एआई रिसर्च, 2019)
6. Photofeeler-D3: डेटिंग फोटो रेटिंग के लिए मतदाता मॉडलिंग के साथ एक तंत्रिका नेटवर्क (Photofeeler Inc., 2019)
7. मिक्समैच: सेमी-सुपरवाइज्ड लर्निंग (Google रीसर्च, 2019) के लिए एक समग्र दृष्टिकोण
8. मैट्रिक लर्निंग (हीडलबर्ग यूनिवर्सिटी, 2019) के लिए एंबेडिंग स्पेस को विभाजित और जीतें

1. तंत्रिका साधारण विभेदक समीकरण

लेखक: रिकी टीक्यू चेन, यूलिया रुबानोवा, जेसी बेटेनकोर्ट, डेविड डुवेनॉड (टोरंटो विश्वविद्यालय, 2018)
→ मूल लेख
समीक्षा के लेखक: जॉर्ज इग्नाटोव (सुस्त a2dy2n7okhtp में)
एनआईपीएस बेस्ट पेपर अवार्ड

लेख के लेखकों ने उल्लेख किया कि रेसनेट जैसे नेटवर्क अंतर समीकरणों को हल करने के लिए यूलर विधि के समान हैं। यदि ऐसा है, तो तुरंत विचार को अधिकतम क्यों न लाया जाए: अंतर समीकरण के रूप में एक तंत्रिका नेटवर्क की कल्पना करें और प्राप्त करें

• परतों की एक मनमानी संख्या के साथ एक नेटवर्क, जिसे प्रशिक्षण और अनुमान के दौरान किसी भी समय बदला जा सकता है। अधिक परतें -> अधिक सटीक और चिकनी रूपांतरण (और इसके विपरीत)।
• मापदंडों की एक छोटी संख्या, इसलिए, कम स्मृति लागत।

एनालॉग्स के माध्यम से एनओडीई:

1. $$$h_n = f_n (h_ {n-1}, W) + h_ {n-1}$ - यह है कि कैसे रेजनेट-जैसे नेटवर्क में परत n से आउटपुट की परिभाषा डब्ल्यू, पैरामीटर की तरह दिखती है।
2. $$$h_n = f (h_ {n-1}, t = n, W) + h_ {n-1$ - यह एक NODE की तरह दिखने वाला नेटवर्क होगा, बशर्ते कि n एक असतत मात्रा हो।
3. $$$h_n \ sim a f (t_n) + h_ {n-1}$ । $$$f (t) = dh (t) / dt$ - यूलर की विधि।
4. $$$dh (t) / dt = f (h (t), t, W)$ - ता-दा! ODE- संचालित तंत्रिका नेटवर्क।

हम इसे किसी भी ब्लैक-बॉक्स ODEsolver के साथ हल करते हैं, ग्रेजुएट्स को आसन्न सेंसिटिव मेथड (पोंट्रीइन एट अल, 1962) का उपयोग करके फेंक देते हैं। इसकी पूर्ण भिन्नता के कारण, NODE को पारंपरिक तंत्रिका नेटवर्क के साथ जोड़ा जा सकता है। लेखकों ने पाइटोरेक पर कोड पोस्ट किया।

लेख 3 अनुप्रयोगों पर चर्चा करता है:

1. रेसनेट जैसी वास्तुकला (एमएनआईएसटी पर) के साथ तुलना। 3 गुना कम मापदंडों का उपयोग करते हुए एनओडीई लगभग कोई बदतर काम नहीं करता है।
2. NODE के माध्यम से सामान्यीकृत प्रवाह को ओवरराइड करना - निरंतर सामान्यीकृत प्रवाह (सिंथेटिक डाटासेट)। नया मॉडल रैखिक से कंप्यूटिंग लागत (n_hidden_units ^ 3) को कम करता है।
3. अनियमित टिप्पणियों (सिंथेटिक डेटासेट) के साथ अस्थायी घटनाओं की मॉडलिंग। सर्पिल प्रक्षेपवक्र के एक डेटासेट से उत्पन्न किया गया था, जिसमें यादृच्छिक रूप से नमूने अंक के साथ छिड़का गया था: नमक: गाऊसी शोर के कारण। इसने सामान्य आरएनएन और एनओडीई का परीक्षण किया और दूसरा फिर से बेहतर साबित हुआ।

छोटे प्रिंट में:

• मिनीबैच प्रशिक्षण किसी प्रकार के कम्प्यूटेशनल ओवरहेड का कारण बनता है, लेकिन लेखकों का तर्क है कि व्यवहार में यह लगभग अदृश्य है।
• दो नए हाइपरपैरमीटर दिखाई देते हैं: ODE को हल करते समय नेटवर्क की गहराई और त्रुटि सहिष्णुता।
• अद्वितीय बने रहने के लिए ODE समाधान के लिए, नेटवर्क में कम वजन होना चाहिए और Lipshitz nonlinearities, जैसे कि tanh या relu का उपयोग करना चाहिए।

हब्र पर अधिक विस्तृत अवलोकन के लिए लिंक।

2. डीप जेनरेटिव मॉडल्स के साथ अर्ध-अनसुनीकृत लर्निंग: अल्ट्रा-स्पार्स लेबल का उपयोग करके क्लस्टरिंग और वर्गीकरण।

लेख लेखक: मैथ्यू विलेट्स, स्टीफन रॉबर्ट्स और क्रिस्टोफर होम्स
(यूनिवर्सिटी ऑफ ऑक्सफोर्ड, द एलन ट्यूरिंग इंस्टीट्यूट, लंदन, 2019)
→ मूल लेख
लेखक की समीक्षा करें: एलेक्स चिरोन (स्लेरोन शेरोन 8bit में)

लेखक वर्गीकरण की समस्या के लिए एक अर्ध-अनसुलझी स्थिति पर विचार करते हैं, जब चयन पूर्वाग्रह के कारण मार्कअप में मौजूद कक्षाओं का हिस्सा बिल्कुल भी लेबल नहीं किया गया था, और इतने पर ज्ञात डेटा वर्गों के अनुसार लेबल नहीं किया गया था। यह अतिरिक्त समस्याएं पैदा करता है, क्योंकि अधिकांश मॉडल आमतौर पर या तो अर्ध-पर्यवेक्षित / पर्यवेक्षित मोड (वर्गीकरण) या असुरक्षित मोड (क्लस्टरिंग) में काम करते हैं, और इस मामले में हमें दोनों विकल्पों पर विचार करने की आवश्यकता है। इसके अलावा, अर्ध-पर्यवेक्षित एल्गोरिदम का उपयोग इस तथ्य को जन्म दे सकता है कि असंगत डेटा को गलत कक्षाओं के निकटता के कुछ मीट्रिक के अनुसार सौंपा जाएगा। इस तरह के डेटा का एक काल्पनिक उदाहरण ट्यूमर स्कैन का एक सेट है। हमने डेटा का हिस्सा लिया और इस हिस्से पर मौजूद सभी प्रकार के ट्यूमर को चिह्नित किया, लेकिन यह पता चला कि शेष डेटा में अन्य प्रकार के ट्यूमर मौजूद थे, और मार्कअप में ज्ञात प्रजातियों की परिवर्तनशीलता पूरी तरह से परिलक्षित नहीं हुई थी।

लेखक गहरे जेनेरिक मॉडल से प्रेरित थे (छिपे हुए चर की एक परत के साथ इस तरह के मॉडल का सबसे सरल उदाहरण एक वैरिएबल ऑटो-एनकोडर है, उर्फ ​​VAE): पिछले कामों में, ऐसे मॉडल सफलतापूर्वक अर्ध-पर्यवेक्षित मामले (एम 2, एडीजीएम) और क्लस्टरिंग (दोनों) VDE, GM-VAE)।

एक ही समय में 2 समस्याओं का समाधान क्यों नहीं किया जाता है (अर्ध-पर्यवेक्षित सीखने पर शायद ही कभी चिह्नित वर्गों और अनपेक्षित कक्षाओं पर अनप्लग किए गए), सीखे गए अव्यक्त चर के स्थान को सामान्य रखते हुए और उपरोक्त मॉडल से विचारों को मिलाते हुए? यह विचार है कि लेख में प्रस्तावित जीएम-डीजीएम / एजीएम-डीजीएम मॉडल को रेखांकित करता है।

अर्ध-पर्यवेक्षित मामले में एम 2 मॉडल पर विचार करें। इसे ऐसा कहा जाता है, क्योंकि M1 के तहत, निर्माता ने z के परिणामी अव्यक्त निरूपण के लिए VAE और कुछ क्लासिफायरियर (svm) के अनुक्रमिक प्रशिक्षण को निहित किया, लेकिन M2 को पहले से ही छिपे हुए चर चर की परत में जोड़कर VAE से प्राप्त किया जाता है, जो कभी-कभी देखे गए वर्ग के लिए जिम्मेदार होता है।
$$$p _ {\ the थी} (x, y, z) = p _ {\ थीटा} (x | y, z) p (y) p (z)$ । $$$q _ {\ pi} (z, y | x) = q _ {\ pi} (z | y, x) q _ {\ pi} (y | x)$
जहाँ $$$q _ {\ phi} (y | x) = बिल्ली (\ pi _ {\ phi} (x))$ । $$$q _ {\ phi} (z | x, y) = N (z। \ mu _ {\ phi} (x, y), \ सिग्मा _ {\ phi} (x, y))$
यहाँ q एक एनकोडर है, पी एक डिकोडर है, भाग है $$$q _ {\ phi} (y | x)$ - सीधे प्रशिक्षित क्लासिफायर।

असुरक्षित / अर्ध-अनसुचित मामले के लिए, M2 काम नहीं करता है - पोस्टीरियर पतन होता है, वर्गीकरण भाग q_phi (y | x) एक प्राथमिकता वितरण p (y) तक ढह जाता है। जीएम-वीएई के लेखक ने अपने लेख में व्यवहार में एम 2 की निष्क्रियता भी दिखाई और कहा कि अक्सर एम 2 को लागू करते समय, एच 1 डिकोडर की पहली परत गाऊसी के मिश्रण के समान होती है।

इस अवलोकन के आधार पर, जीएम-वीएई क्लस्टरिंग के लिए एक गाऊसी मिश्रण को क्लस्टर करने के लिए छिपे हुए चर की एक स्पष्ट परत का उपयोग करता है, जिसे इस लेख के लेखकों द्वारा भी दोहराया जाता है। इस प्रकार, जीएम-डीजीएम मॉडल, जो अर्ध-अनसुनी मोड में सफल संचालन की अनुमति देता है, एक संशोधन है। VAE एक छिपे हुए परत में गौसियंस के मिश्रण का उपयोग करते हुए, वर्ग y के एक चर के आधार पर, ELBO की गिनती और अधिकतम करने के लिए दो शब्दों के उपरोक्त कार्य के साथ।

लेख के लेखकों ने फैशन-एमएनआईएसटीईटी के एक अर्ध-अनसुनी संस्करण पर एक प्रयोग किया: उन्होंने पहली 5 कक्षाओं के लेबल हटा दिए, शेष 5 वर्गों ने 5% लेबल छोड़ दिए, जबकि उन्हें M2 के मुकाबले 53% के मुकाबले 77.2% की कुल सटीकता प्राप्त हुई। क्लस्टरिंग के लिए मॉडल का उपयोग करने की संभावना भी दिखाई गई (जो आश्चर्य की बात नहीं है, क्योंकि यह लगभग जीएम-वीएई है)।

3. सीखा हुआ अव्यक्त संरचना के माध्यम से एल्गोरिथ्म पूर्वाग्रह को उजागर और कम करना

लेखक: अलेक्जेंडर अमिनी, अवा सोलेइमानी, विल्को श्वार्टिंग, संगीता एन भाटिया, डेनिएला रस (मैसाचुसेट्स इंस्टीट्यूट ऑफ टेक्नोलॉजी, हार्वर्ड यूनिवर्सिटी, 2019)
→ मूल लेख
लेखक की समीक्षा करें: एलेक्स चिरोन (स्लेरोन शेरोन 8bit में)

हाल ही में, मीडिया में अधिक से अधिक बार आप उन समाचारों को पा सकते हैं जो डेटा में पूर्वाग्रह के विषय पर छूते हैं, विशेष रूप से व्यक्तियों से संबंधित एल्गोरिदम के बारे में - उनकी प्रयोज्यता के विकास के साथ, उन श्रेणियों और लोगों के समूह पर एक मजबूत नकारात्मक प्रभाव का जोखिम जो अपर्याप्त (या अत्यधिक) हैं। डेटासेट में प्रस्तुत किया गया। नवीनतम उदाहरणों में से एक एक अध्ययन है जिसने गहरे रंग के रंग के साथ पैदल चलने वालों का पता लगाने में कम सटीकता दिखाई (मानक BDD100K और MSCOCO डेटासेट, लिंक पर वस्तु का पता लगाने के संदर्भ में)। बायसे को खत्म करने के लिए बुनियादी दृष्टिकोण:

1. रेज़मैपलिंग का उपयोग करते हुए क्लास बैलेंसिंग (छिपे हुए डेटा संरचना की प्राथमिक समझ की आवश्यकता है)।
2. निष्पक्ष डेटा की पीढ़ी (उदाहरण के लिए, त्वचा टन की एक विस्तृत विविधता के साथ व्यक्तियों को उत्पन्न करने के लिए GAN का उपयोग)।
3. क्लस्टरिंग और बाद में फिर से शुरू करना।
4. आप अभी भी प्रतीक्षा कर सकते हैं जब तक कि चेहरे की आईबीएम विविधता विभेदकों को अकादमिकियों में नहीं लाया जाता है।

लेख के लेखक वीएई और नमूने के संशोधन की पेशकश करते हैं, अव्यक्त चर जेड के वितरण को ध्यान में रखते हैं, जो प्रशिक्षण चरण में डेटा में पूर्वाग्रह के प्रभाव को कम कर सकते हैं।
तो, DB-VAE के पीछे मुख्य विचार हैं:

• एक वर्गीकरण समस्या पर विचार करें जिसमें हमारे पास एक प्रशिक्षण डेटासेट {(x, y)} है, x m- आयामी विशेषताएँ हैं, y d- आयामी लेबल हैं, और हमारा कार्य मानचित्रण X-> Y को अनुमानित करना है।
• वीएई को लें, लेकिन आयाम 2k के छिपे हुए चर z के वेक्टर z के अलावा हम एनकोडर को मजबूर करेंगे (मैं यहां 2 को याद करता हूं क्योंकि हम औसत और भिन्नता के साथ काम कर रहे हैं) आयाम d के एक वेक्टर को सीखने के लिए भी, जो कि उपरोक्त लेबल के लिए जिम्मेदार है। इस मामले में, डिकोडर केवल वेक्टर z को इनपुट के रूप में स्वीकार करता है। इस प्रकार, हमें अर्ध-पर्यवेक्षित सीखने का एक हिस्सा मिलता है, जहां मॉडल के भाग को इनपुट को फिर से बनाना सीखा जाता है, और एक विशिष्ट समस्या (वर्गीकरण) को हल करना है।
• हम संयुक्त नुकसान के कारण मॉडल के प्रशिक्षण को नियंत्रित करते हैं, VAE नुकसान (पुनर्निर्माण + केएल विचलन) के लिए मानक और एक सहायक समस्या (उदाहरण के लिए, द्विआधारी वर्गीकरण समस्या के लिए क्रॉस-एंट्रोपी) के लिए नुकसान का संयोजन।
• इस तथ्य पर विशेष रूप से ध्यान दिया जाता है कि आपको डेटा पर प्रशिक्षण को नियंत्रित करने की आवश्यकता है जिसे आप डिबिसिंग नहीं करना चाहते हैं (अर्थात डिकोडर से इसे बैकप्रॉप न करें)।

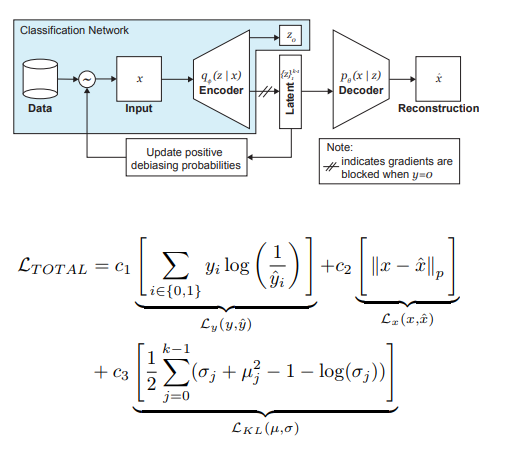
अश्वेतों के दर्द को खत्म करने में सबसे महत्वपूर्ण भूमिका प्रशिक्षण चरण में अनुकूली नमूने द्वारा निभाई जाती है। हम दुर्लभ (कुछ छिपे हुए, स्पष्ट रूप से पहचाने गए कारकों के नमूने के दृष्टिकोण से) का चयन करना चाहते हैं, इसलिए हम छिपे हुए चर z के अंतरिक्ष के प्रत्येक आयाम के लिए हिस्टोग्राम की ओर मुड़ते हैं, जिसके उत्पाद पूरे स्थान पर डेटा के वितरण Q (z) का अनुमान लगा सकते हैं। एक नया बैच बनाते समय, हम Q (z | X) वितरण W (z (x) | X) के 'व्युत्क्रम' को ध्यान में रखेंगे, जो बैच में एक उदाहरण चुनने की संभावना को निर्धारित करता है (अल्फा एक हाइपरपैरमीटर है जो डिबासिंग की डिग्री निर्धारित करता है), Q (z |) को अपडेट करते हुए। X) हर युग में। जैसा कि आप देख सकते हैं, डेबिसिंग पूर्व-चयनित नहीं है, बल्कि सीखा अव्यक्त चर पर आधारित है।

एक प्रयोग के रूप में, लेखकों ने द्विआधारी वर्गीकरण (फोटो में चेहरा खोजने) की समस्या को हल किया। प्रशिक्षण के लिए, हमने एक डेटासेट एकत्र किया, जिसमें CelebA के साथ 200 हजार लोग और Imagenet के साथ 200 हजार गैर-लोग शामिल थे, जिन्होंने छवियों को 64x64 में बदल दिया। जैसा कि पहले उल्लेख किया गया है, प्रशिक्षण के दौरान, चेहरे के बिना फोटो के लिए डिकोडर से बैकप्रोगैगेशन अवरुद्ध किया गया था (y = 0)। प्रशिक्षण के बाद, उन्हें पायलट Parliaments Benchmark (PPB) (दक्षिण अफ्रीका, रवांडा, सेनेगल, स्वीडन, फ़िनलैंड, आइसलैंड) के संसदों के 1270 फ़ोटो पर मान्य किया गया था: सभी अल्फा - 0 के लिए, श्रेणियों में पहचान सटीकता अंधेरे पुरुष, अंधेरे महिला, प्रकाश महिला की तुलना में बढ़ गई। बिना डिबिसिंग के विकल्प।

4. मानव वरीयताओं से गहन सुदृढीकरण सीखने

लेखक: पॉल क्रिस्टियानो, जान लेइक, टॉम बी। ब्राउन, मिलन मार्टिक, शेन लेग, डारियो अमोडी (ओपनएआई, डीपमाइंड, 2017)
→ मूल लेख
लेखक की समीक्षा करें: दिमित्री निकुलिन (दनिकु स्लैक में)

यह लेख पुराने विचार को गहन सुदृढीकरण सीखने (आरएल) के संदर्भ में कैसे लागू किया जाए, इसके बारे में है। विचार: आइए एक व्यक्ति से एक एजेंट के व्यवहार का मूल्यांकन करने के लिए कहें, और इसके आधार पर हम इनाम समारोह सीखेंगे। समस्या यह है कि गहरी आरएल बहुत प्रचंड है, और मानव समय महंगा है। लेख हैक का एक सेट प्रदान करता है जो आपको उचित मूल्यों के लिए मानव घंटे को कम करने की अनुमति देता है।

रिवार्ड फ़ंक्शन जोड़े (अवलोकन, क्रिया) पर एक फ़ंक्शन है। यह तंत्रिका नेटवर्क के कलाकारों की टुकड़ी की भविष्यवाणी के औसत से निर्धारित होता है। आरएल एल्गोरिदम का उपयोग किया गया (अटारी और टीआरपीओ के लिए मुजोको के लिए लेख A2C में) का मानना ​​है कि यह औसत एक सच्चा इनाम है, और इस पर प्रशिक्षित हैं। इस प्रकार, लेख इस पहनावा के प्रशिक्षण के मुद्दे पर केंद्रित है।

पहनावा मानव मूल्यांकन पर प्रशिक्षित है। प्रत्येक रेटिंग को निम्नानुसार संरचित किया गया है। एक व्यक्ति को एजेंट के दो वीडियो 1-2 सेकंड लंबे दिखाए जाते हैं। वह ऐसी जोड़ी को 4 तरीकों से रेट कर सकता है: लेफ्ट बेहतर है / राइट बेहतर है / बहुत समान / असंगत है। यदि किसी व्यक्ति ने "असंगत" कहा है, तो इस तरह के मूल्यांकन को दूर फेंक दिया जाता है। अन्यथा, ट्रिपल (σ¹, σ², μ) को याद किया जाता है, जहां agent इसी वीडियो में एजेंट का प्रक्षेपवक्र है (यानी, जोड़े की सूची (अवलोकन, अधिनियम)), और μ जोड़ी है (1, 0), (0, 1) ) या (½, ½)। इसके अलावा, यह माना जाता है कि प्रक्षेपवक्र के लिए इनाम की भविष्यवाणी प्रत्येक जोड़ी (प्रेक्षण, अधिनियम) के लिए भविष्यवाणियों के योग के बराबर है। अंत में, हम केवल softmax_cross_entropy_with_logits का अनुकूलन करते हैं।

यह माना जाता है कि 10% संभावना वाला व्यक्ति एक यादृच्छिक उत्तर का चयन करता है, और प्रशिक्षण नमूना का निर्माण करते समय इसे ध्यान में रखा जाता है। लेख की धारा २.२.३ कुछ और तरकीबें देती है और सभी सूत्रों को लिखती है।

किसी व्यक्ति को प्रदर्शन के लिए क्लिप के जोड़े निम्नानुसार चुने गए हैं: बड़ी संख्या में क्लिप का नमूना लिया जाता है, उन पर पहनावा का फैलाव माना जाता है और उच्च फैलाव वाली क्लिप के यादृच्छिक जोड़े लोगों को दिखाए जाते हैं। लेखकों का कहना है कि मैं जानकारी के मूल्य के अनुसार चुनना चाहूंगा, लेकिन यह भविष्य का काम है।

लेखकों ने अटारी और मुजोको पर परीक्षण चलाए, जिसमें वास्तविक मानव रेटिंग (काम पर रखे गए ठेकेदार) और सिंथेटिक (रेटिंग्स सच्चे इनाम समारोह के अनुसार उत्पन्न होते हैं), और साथ ही उनकी तुलना सामान्य आरएल के साथ की जाती है। लगभग समान संख्या में रेटिंग के साथ, सिंथेटिक और वास्तविक परीक्षण समान रूप से काम करते हैं। इसके अलावा, आश्चर्यजनक रूप से, नियमित रूप से आरएल (जो सच इनाम समारोह देखता है) जरूरी नहीं कि बेहतर काम करे।

अंत में, सामान्य अर्थों में बहुत अधिक इनाम पाने के लिए एजेंट को प्रशिक्षित करने की कोशिश करने के अलावा, लेख दो अन्य कार्यों का भी उदाहरण देता है: मुजपो में हूपर बैकफ्लिप करता है, और अटारी एंडुरो में मशीन अन्य कारों से आगे नहीं निकलती है, लेकिन उनके समानांतर यात्रा करती है। यह दोनों समस्याओं को हल करने के लिए निकला।

निष्कर्ष में: उदाहरण इस लेख को पुन: पेश करने का प्रयास बताता है। यह प्रयास सफल रहा, लेकिन खाली समय में 8 महीने का काम हुआ और शुद्ध समय के 220 घंटे, जिनमें से आधे सरल संस्करण को डिबग करने के लिए चले गए।

5. छवि पहचान के लिए रैंडमली वायर्ड न्यूरल नेटवर्क की खोज

लेखक: स्काईंग ज़ी, अलेक्जेंडर किरिलोव, रॉस गिरिश, कैमिंग हे (फेसबुक एआई रिसर्च, 2019)
→ मूल लेख
लेखक की समीक्षा करें: ईगोर पैन्फिलोव (सुस्त टाटके 1जा में)

परिचय:

काम तंत्रिका नेटवर्क की वास्तुकला पैदा करने का मुद्दा उठाता है। वर्तमान में, कई आर्किटेक्चरल ट्रिक्स ज्ञात हैं (LSTM, इंसेप्शन, रेसनेट, डेंसनेट), जो कई कार्यों की गुणवत्ता में सुधार कर सकते हैं, लेकिन वे मॉडल से पहले एक निश्चित मजबूत वास्तुशिल्प का भी परिचय देते हैं। उल्लिखित समाधानों के बजाय, Google अपनी तंत्रिका वास्तुकला खोज (NAS) के साथ आगे बढ़ रहा है, जहां एक विशिष्ट कार्य के लिए वास्तुकला खोज RL - NASNet, AmoebaNet के माध्यम से पूर्वनिर्धारित मॉड्यूल से की जाती है।

लेखकों का तर्क है कि दोनों दृष्टिकोण जहां डिजाइन आदमी द्वारा निर्धारित किए गए हैं और एनएएस वास्तुकला से पहले बहुत सख्त परिचय देते हैं। इसे कम करने के प्रयास में, वे तंत्रिका नेटवर्क के पैरामीट्रिक जनरेटिव दृष्टिकोण का उपयोग करने का प्रयास करते हैं, जहां तत्वों के तारों (कनेक्शन) को बेतरतीब ढंग से किया जाता है। यह पता चला है कि ए। ट्यूरिंग, एम। मिंस्की, एफ। रोसेनब्लट जैसे वैज्ञानिकों द्वारा 1940 के दशक से यादृच्छिक तारों के दृष्टिकोण का पता लगाया गया है। एक और तर्क के रूप में, लेखक याद करते हैं कि तंत्रिका विज्ञान के अध्ययनों में यह पता चला था कि एक प्रजाति के जीवों में न्यूरोनल कनेक्शन की संरचना भिन्न होती है (निश्चित स्तर तक विस्तार की, निश्चित रूप से)। यह कीड़े और मानव शिशुओं दोनों के लिए सच है। सामान्य तौर पर, तंत्रिका नेटवर्क की प्रक्रियात्मक पीढ़ी का विचार दिलचस्प और आशाजनक लगता है, जो कि काम के बारे में है।

विधि:

चलो एक ग्राफ दृष्टिकोण के माध्यम से तंत्रिका नेटवर्क वास्तुकला की प्रक्रियात्मक पीढ़ी की प्रक्रिया को संशोधित करने का प्रयास करते हैं। प्रारंभिक चरण निम्नानुसार हैं:

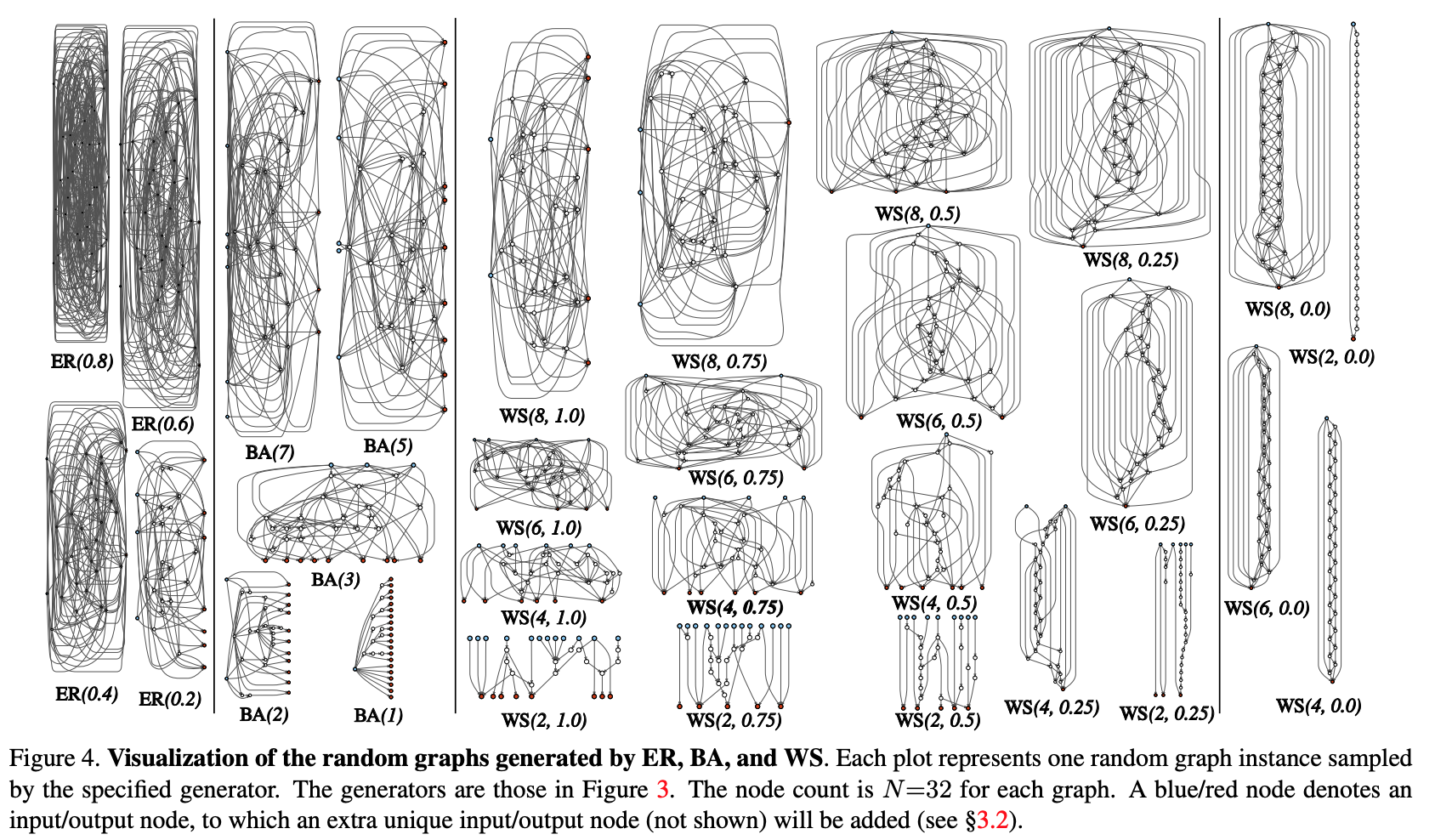
1. एक मानकीकृत परिवार से एक स्टोकेस्टिक ग्राफ उत्पन्न होता है। क्लासिक विधियों का उपयोग किया जाता है: एर्डोस-रेनी (ईआर), बाराबासी-अल्बर्ट (बीए), और वाट्स-स्ट्रोगेट्ज़ (डब्ल्यूएस)।
2. ग्राफ एक तंत्रिका नेटवर्क में बदल जाता है:
   
   • ग्राफ के सभी किनारों को डेटा टेंसरों के निर्देशित वाहक माना जाता है;
   • ग्राफ़ के प्रत्येक शीर्ष के लिए, जो ऑपरेशन करता है उसका प्रकार निर्धारित किया जाता है: (I) प्रशिक्षित भार के साथ संक्षेप में एकत्रीकरण, (II) परिवर्तन - ReLU + कनवल्शन + बीएन, (III) वितरण - प्रत्येक आउटपुट किनारे पर टेंसर का स्थानांतरण;
   • पिछले उपखंड के परिणामों के अनुसार, कई इनपुट और आउटपुट कोने हो सकते हैं, लेकिन मैं ग्राफ़ में 1 प्रविष्टि बिंदु और 1 आउटपुट बिंदु रखना चाहता हूं। ऐसे नोड्स अलग से बनाए जाते हैं। इनपुट एक बस टेंसर की एक कॉपी को ग्राफ के सभी इनपुट वर्टिकल में फैला देता है, आउटपुट एक को सभी आउटपुट वर्जन के अनवीटेड एवरेज को मानता है। चरण 1 और 2 के परिणामस्वरूप, वास्तव में, एक पूरा नेटवर्क नहीं बनता है, लेकिन केवल एक मॉड्यूल (जैसे कि conv_1, ... लोकप्रिय) में से एक है। convolutional एनकोडर)। तंत्रिका नेटवर्क को पूरी तरह से प्राप्त करने के लिए:
3. कई मॉड्यूल श्रृंखला में बनाए और जुड़े हुए हैं। नेटवर्क मापदंडों की संख्या को कम करने के लिए, मॉड्यूल के सभी इनपुट वर्टिकल में परिवर्तन 2x2 के स्ट्राइड के साथ किए जाते हैं। अगले मॉड्यूल में संक्रमण में चैनलों की संख्या 2 गुना बढ़ जाती है। एक विशिष्ट कार्य पर प्रयोगों का संचालन करने के लिए:
4. नेटवर्क के आउटपुट में, वर्गीकरण के लिए एक सिर जोड़ा जाता है।

परिणाम:

इमेजनेट पर वर्गीकरण समस्या पर विधि का परीक्षण किया गया था। उत्पन्न न्यूरल नेटवर्क की गुणवत्ता SotA आर्किटेक्चर के बराबर हो गई, हाल ही में Google के DeepBrain AmoebaNet से थोड़ा सा हार गया: (मापदंडों की तुलनात्मक संख्या के साथ)।

हमने जाँच की कि परिणामी ग्राफ से यदि हम एक यादृच्छिक वर्टेक्स / एज निकाल दें तो क्या होगा। मीट्रिक - क्रमशः उत्पादन किनारों / इनपुट कोने की आसन्न संख्या के आधार पर गुणवत्ता में कमी। सामान्य तौर पर, गुणवत्ता गिर रही है, लेकिन महत्वपूर्ण नहीं है।

लेखकों ने यह भी जांचा कि क्या इस आर्किटेक्चर के साथ ट्रांसफर लर्निंग काम करता है। COCO डिटेक्शन कार्य में, FPN के साथ बैकबस्टर फास्टर आर-सीएनएन को एक उत्पन्न और पूर्व-प्रशिक्षित नेटवर्क के साथ बदल दिया गया था। परिणामों से पता चला कि मॉडल की गुणवत्ता ResNeXt-50 / -101 की तुलना में खराब नहीं है। लेकिन यहां तक ​​कि तथ्य यह है कि हस्तांतरण सीखने शुरू हो रहा है बहुत मनोरंजक है।

6. फ़ोटोग्राफ़र-डी 3: डेटिंग फोटो रेटिंग के लिए मतदाता मॉडलिंग के साथ एक तंत्रिका नेटवर्क

लेख के लेखक: अगस्त्य कालरा और बेन पीटरसन (फ़ोटोग्राफ़र इंक।, 2019)
→ मूल लेख
लेखक की समीक्षा करें: एलेक्स चिरोन (स्लेरोन शेरोन 8bit में)

लेखक Photofeeler-D3 का सुझाव देते हैं: 3 दिशाओं / लक्षणों में डेटिंग साइटों से तस्वीरों का मूल्यांकन करने के लिए एक नेटवर्क आर्किटेक्चर - एक व्यक्ति कितना स्मार्ट लगता है, भरोसेमंद और आकर्षक (प्रभामंडल प्रभाव की उपेक्षा करें!)। यह कार्य द गार्जियन के एक सर्वेक्षण के आधार पर हुआ, जिसके अनुसार 90% लोग एक संभावित उपग्रह के फोटो के मूल्यांकन के आधार पर भविष्य की तारीख तय करते हैं।

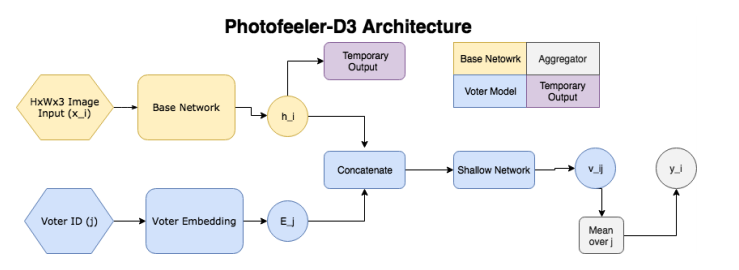
तो, नेटवर्क में निम्नलिखित ब्लॉक होते हैं:

1. ( ) — (GAP ), 10 ( ) — temporary output.
2. ( , voter model) - (voter), , temporary output , , 10 v_ij (( 10 [0;1]). v_ij [0.05, 0.15, 0.25...0.95].
3. , 200 , .

, , , , . Facial Beauty Prediction (FBP) SCUT-FBP Hot-Or-Not, , Photofeeler, . : +100k , 1.2 , (200 ) 200 (50 ). , 600px. 10000 8000 . , 0 3, [0,1] ( , ).

:

1. (backbone , , etc) (20000 train, 3000 val, 2311 test), xception 600x600.
2. , (temporary output) KL- ( , , 10 [0,1]).
3. voter model one-hot .
4. voter' , 2 .
5. trait' 2 , .:
   
   • ~80% , London Faces , prettyscale.com hotness.ai (81 53 52).
   • FBP (SCUT-FBP Hot-Or-Not) , SOTA.
   • , , 10

7. MixMatch: A Holistic Approach to Semi-Supervised Learning

: D. Berthelot, N. Carlini, IJ Goodfellow, N. Papernot, A. Oliver and Colin Raffel (Google Reasearch, 2019)
→
: ( JanRocketMan)

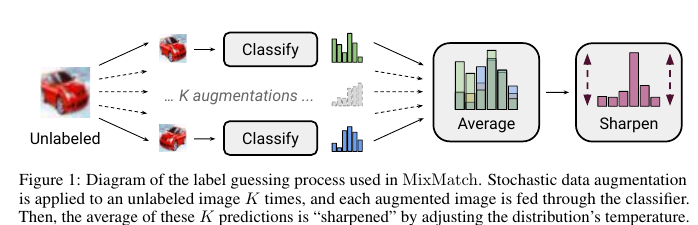
MeanTeacher Mixup- SOT- Semi-Supervised Learning (SSL) . , SSL consistency regularization. , ( ) "" , . Mean Teacher ( — c EMA ), — Mixup ( ). , . :

1. unsupervised , .
   "" p.
2. "" , one-hot. : $$$p_{new} = p^{1 / T} / sum(p^{1 / T}, dim=1)$ । T , , , ( ), .
3. , . , SVHN, STL CIFAR10.

CIFAR10 90% accuracy 250 . — VAT, 60%. SVHN - 96% 250- , VAT Mean Teacher 90.

STL10 90% 1 , - CCGAN, 80. , :

1. , ( );
2. GridSearch- ;
   c. SSL SVHN .

8. Divide and Conquer the Embedding Space for Metric Learning

: Artsiom Sanakoyeu, Vadim Tschernezki, Uta Buchler and Bjorn Ommer (Heidelberg University, 2019)
→
: ( Alexander Denisenko)

— , . , , – , , , ..

, :

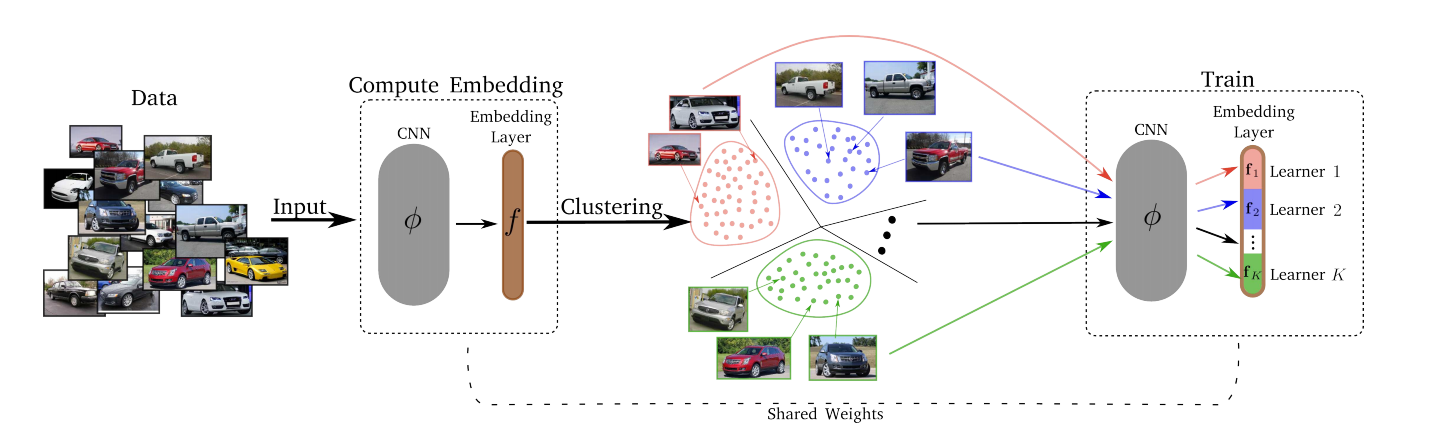
2. Divide.
   - k-means. . . Embedding layer K . – . d/K (d – ).
3. जीत।
   डिवाइड चरण के बाद, प्रत्येक K समूहों को K Lerners में से एक को सौंपा गया है। लर्नर्स बदले में ट्रेन करते हैं, अर्थात् किसी भी समय, हम एक क्लस्टर का चयन करते हैं, जिस पर प्रशिक्षण होता है, एक मिनी-बैच से इसका नमूना लिया जाता है, और संबंधित लर्नर इसके मापदंडों को अपडेट करके अपने नुकसान को कम करता है। एम्बेडिंग का स्थान समय के साथ अपडेट किया जाता है, ताकि हर टी युग, क्लस्टरिंग (डिवाइड) नए सिरे से हो।
4. मर्जिम - हम सभी लर्नर (एंबेडिंग परत के स्लाइस) को समेटते हैं। फिर हम Lerners को मित्र बनाने के लिए संपूर्ण डेटासेट पर एम्बेडिंग परत को प्रशिक्षित करते हैं।

प्रायोगिक परिणाम: सभी ने कई डेटासेट पर जीत हासिल की।

नुकसान कुछ भी हो सकता है - ट्रिपल लॉस, मार्जिन लॉस, प्रॉक्सी-एनसीए, आदि।

K लर्नर की इष्टतम संख्या 8 निकली (संपूर्ण एम्बेडिंग स्पेस का आयाम 128 था, ताकि प्रत्येक Lerner ने 16-आयामी अंतरिक्ष में अपने सबटस्क को हल किया)।

1 से 10 तक टी में बदलाव से कुछ भी प्रभावित नहीं हुआ, इसलिए टी = 2 का उपयोग किया गया।