जूलियन क्लिंटन स्प्रोट के एक लेख के आधार पर। प्यार के गतिशील मॉडल। Nonlinear गतिशीलता मनोविज्ञान और जीवन विज्ञान, अगस्त 2004।
मेरा मानना था कि बीजगणित में सामंजस्य ...
मेरे मित्र का सिद्धांत सूखा है, लेकिन जीवन का पेड़ हमेशा हरा रहता है ...जो सिर्फ इस "समस्या" के बारे में नहीं लड़े ...। यह प्राचीन ग्रीक त्रासदियों में ध्वस्त हो गया था, महान शेक्सपियर ने हमें रोमियो और जूलियट की कहानी सुनाई, आंद्रेजेज वाजदा ने इसे एनाटॉमी ऑफ लव में दोनों तरफ से नष्ट कर दिया। लेकिन जब तक वैज्ञानिकों ने फैसला नहीं लिया तब तक लोग सच्चाई की तह तक नहीं गए। सच है, नहीं सब कुछ मनोवैज्ञानिकों के लिए काफी आश्वस्त लगता है। वे खुद कभी-कभी अपने तलाक के बाद भी अपने दिवंगत प्रेम के इतिहास का विश्लेषण करना शुरू करते हैं। खैर, किताबें लिखें जो कभी-कभी गर्म केक की तरह जाती हैं। वे विशेषज्ञों द्वारा लिखे गए हैं! मैं क्या कह सकता हूं? लगभग कुछ भी नहीं व्यक्तिगत - बस व्यापार ...
और अंत में, लेखकों और मनोवैज्ञानिकों के साथ कवियों ने गले से प्यार नहीं लिया। गणित विज्ञान की रानी है। क्या वह एक शाश्वत समस्या का सामना करने में सक्षम है? किताबें प्रकाशित होती हैं, उदाहरण के लिए, जॉन गॉटमैन, "द मैथमेटिक्स ऑफ मैरिज" और अन्य लेखक। गणितज्ञ रोमांटिक संबंधों के विकास को एक गतिशील प्रक्रिया मानते हैं ...
और यह सब शुरू होता है, जैसा कि उम्मीद थी, परिभाषाओं के साथ। गुणात्मक और मात्रात्मक रूप से प्यार की पहचान कैसे करें? शोधकर्ता समस्या को प्रकार से वर्गीकृत करते हैं: प्रेम संबंध, जुनून, निष्ठा। इसके अलावा, प्रत्येक प्रजाति में भावनाओं का एक जटिल समूह होता है। लेकिन दूसरे व्यक्ति के लिए प्यार के अलावा, खुद के लिए, जीवन के लिए, मानवता के लिए प्यार है ...
एक ही समय में, गणितीय मॉडल में प्यार के विपरीत - नफरत नहीं की जा सकती, क्योंकि ये दोनों भावनाएं एक ही समय में सह-अस्तित्व में आ सकती हैं। उदाहरण के लिए, कोई व्यक्ति साथी की कुछ अभिव्यक्तियों को पसंद कर सकता है, लेकिन अन्य लोग बुरा हो सकते हैं। इसलिए, यह मानना अवास्तविक है कि किसी व्यक्ति का प्रेम केवल उसकी स्वयं की भावनाओं से प्रभावित होता है, और दूसरे साथी की भावनाएं अन्य प्रभावों पर निर्भर नहीं होती हैं, और यह कि दो लोगों की परस्पर क्रिया करने वाले पैरामीटर अपरिवर्तित रहते हैं और इस प्रकार सीखने और अनुकूलन की संभावना को बाहर कर देते हैं।
एक न्यूनतम प्रतिबंधित मॉडल में भी जटिलता नाटकीय रूप से बढ़ जाती है जब तीन या अधिक चर को अशुद्धता और / या के समीकरणों में पेश किया जाता है।
* नोट: अनुवादक मेरी राय में, इस तरह के अध्ययन गणित को भी पुनर्जीवित कर सकते हैं, जनता का ध्यान आकर्षित कर सकते हैं, आमतौर पर इस अमूर्त विज्ञान से।
सरल रैखिक मॉडलरोमियो और जूलियट की प्रेम कहानी को समय (t) में कार्यों का उपयोग करके दर्शाया जा सकता है * R (t) - जूलियट के लिए रोमियो का प्रेम और J (t) - रोमियो के लिए जूलियट का प्रेम।
तब समीकरणों द्वारा उनके संबंधों का एक सरल रैखिक मॉडल व्यक्त किया जाता है (1)
ए और बी - रोमियो की रोमांटिक शैली के पैरामीटर
सी और डी - जूलियट शैली विकल्प
a - यह दर्शाता है कि रोमियो अपनी भावनाओं में कैसे ढंका है
b - जूलियट की भावनाओं से रोमियो कितना आलिंगनबद्ध है
लेखों में से एक (गॉटमैन एट अल।, 2002) पहले और दूसरे पैरामीटर के लिए "प्रभाव समारोह" के लिए शब्द "व्यवहार जड़ता" का उपयोग करता है। यद्यपि एक = 0 पर, जड़ता सबसे बड़ी हो जाती है। ऐसी परिस्थितियों में गतिशील मॉडल दो आयामी और प्रारंभिक परिस्थितियों और चार मापदंडों द्वारा चलाया जा सकता है, जो सकारात्मक या नकारात्मक हो सकता है।
रिनाल्डी, 1998 ए द्वारा एक सरल रैखिक मॉडल प्रस्तावित किया गया था। उसी समय, एक व्युत्पन्न शब्द को प्रत्येक व्युत्पन्न में जोड़ा जाता है ताकि आकर्षण (या नकारात्मक मूल्य के साथ प्रतिपदार्थ) को ध्यान में रखा जाए, जो कि प्रत्येक साथी अन्य भावनाओं के अभाव में दूसरे को दिखाता है। ऐसा मॉडल अधिक यथार्थवादी है क्योंकि यह भावनाओं को उदासीनता से बढ़ने की अनुमति देता है और एक संतुलन प्रदान करता है जो पूर्ण उदासीनता की विशेषता नहीं है। यह सब केवल दो अतिरिक्त मापदंडों में प्रवेश करके इस तरह वर्णित है। जबकि गैर-उदासीन संतुलन की स्थिति प्रश्न में व्यक्तियों के लिए बहुत महत्वपूर्ण हो सकती है, यह राज्य अंतरिक्ष आरजे को स्थानांतरित करने की तुलना में अन्यथा गतिशीलता को नहीं बदलता है।
रोमांटिक शैलीरोमियो काम के लेखक द्वारा दिए गए अंकन (स्ट्रोगेट्ज, 1994) और उनके छात्रों के आधार पर चार रोमांटिक शैलियों में से एक को प्रदर्शित कर सकता है।
- भावुक इच्छा: ए> 0, बी> 0 (रोमियो जूलियट की अपनी भावनाओं और भावनाओं में लिप्त है।)
- Narcissistic प्रकार: a> 0, b <0 (रोमियो अपनी भावनाओं में अधिक ढला हुआ है, वह जूलियट की भावनाओं से अलग है।)
- सतर्क (या विश्वसनीय प्रेमी): एक <0, b> 0 (रोमियो अपनी भावनाओं से दूर जाता है, लेकिन वह जूलियट की भावनाओं से उबर जाता है।)
- हरमिट: एक <0, b <0 (रोमियो जूलियट की अपनी भावनाओं और भावनाओं से अलग है)।
चूँकि जूलियट के लिए व्यवहार की चार शैलियाँ भी संभव हैं, प्रत्येक जोड़े की 16 गतियाँ हैं, जिनमें से प्रत्येक की अपनी गतिशीलता है, हालाँकि उनमें से आधे आर और जे के क्रमपरिवर्तन के अनुरूप हैं।
समीकरण (1) R = J = 0 के लिए एक एकल संतुलन बिंदु निर्धारित करते हैं, जो परस्पर उदासीन संबंध या तथाकथित "प्रेम का पठार" (रिनाल्डी मॉडल, 1988 में), आइजनवेल्यूज़ (2) के माध्यम से व्यवहार के वर्णन के साथ मेल खाता है
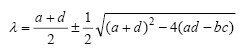
फोकस फोर्किंग सैडल
अंजीर। 1. समीकरण 1 के अनुसार दो-आयामी अंतरिक्ष में संतुलन बिंदु के पास गतिशील स्थिति।प्रेम का त्रिकोणएक और अधिक गणितीय रूप से समृद्ध मॉडल प्राप्त किया जाता है जब एक तीसरे व्यक्ति को एक साधारण मॉडल में जोड़ा जाता है, विशेष रूप से क्योंकि यह संभव है कि गठबंधन बन सकते हैं जिसमें दो व्यक्ति तीसरे के खिलाफ एकजुट हो सकते हैं। मान लीजिए कि रोमियो का एक और प्रेमी है, जेनेवीव, हालांकि सवाल में तीसरा व्यक्ति एक बच्चा या अन्य रिश्तेदार हो सकता है। इस स्थिति में, राज्यों का स्थान दो-आयामी की तुलना में छह-आयामी हो जाता है, क्योंकि तीन में से प्रत्येक में अन्य दो के लिए भावनाएं होती हैं, और बारह पैरामीटर उत्पन्न होते हैं यदि प्रत्येक दूसरे के संबंध में विभिन्न शैलियों को ले सकता है, भले ही प्राकृतिक आकर्षण को अनदेखा कर दिया जाए, रिनाल्डी द्वारा समीक्षा, 1998a)।
सबसे सरल मामले में, जूलियट और जेनेविव एक दूसरे के अस्तित्व के बारे में नहीं जानते हैं, और रोमियो दोनों के संबंध में एक ही रोमांटिक शैली दिखा सकता है। परिणामी चार-आयामी प्रणाली तब दो विभाजित दो-आयामी प्रणालियों में बदल जाती है, जब तक कि जूलियट के लिए रोमियो की भावनाएं किसी तरह से उसके लिए जिनेविव की भावनाओं से प्रभावित होती हैं, और वही जिनेविव के लिए सच है।
नॉनलाइनर प्रभावगैर-रेखीय प्रभाव इनपुट करने के लिए अनंत तरीके हैं। कल्पना कीजिए कि रोमियो जूलियट के प्यार का सकारात्मक जवाब देता है, लेकिन अपने प्यार की अत्यधिक अभिव्यक्ति के साथ, उसे ऐसा लगता है जैसे उसका गला घोंटा गया है और प्रतिकूल प्रतिक्रिया प्रदर्शित करता है। इसके विपरीत, अगर जूलियट काफी नापसंदगी दिखाता है, तो रोमियो उसके लिए सुखद बनने की कोशिश कर सकता है।
इस मामले में, लॉजिस्टिक फ़ंक्शन bJ (1 - | J |) के साथ समीकरण 1 में bJ को प्रतिस्थापित करना संभव है। J से मापी गई इकाइयों में J की माप के अनुरूप है कि J = 1 उस मूल्य से मेल खाता है जिस पर उसका प्रेम प्रतिशोधात्मक हो जाता है। गुणात्मक रूप से समान परिणाम फ़ंक्शन बीजे (1 - जे 2) से आते हैं, जो कि 14 वीं शताब्दी के इतालवी कवि प्लेटोनिक प्रेम मॉडल के लिए रिनाल्डी (1998 बी) द्वारा विचार किया गया है, जो शादी के लिए बाध्य है। जूलियट के लिए समान मानते हुए, हम प्राप्त करते हैं:
(4)
मूल में एक सहित 4 संतुलन राज्य हैं। चित्रा 3 जूलियट जिस पर स्थिर ध्यान केंद्रित दिखाता है। "भावुक इच्छाओं" के रूप में (c = d = 1) रोमियो के "hermit" (a = b = –2) को R = J = 2. पर आपसी प्रेम की स्थिति में ले जाता है। सिग्मोएडल नॉनलाइनिटी के लिए सतर्क (विश्वसनीय) प्रेमियों के लिए एक समान मॉडल भी होता है। स्थिर संतुलन (रिनाल्डी और ग्रैगनानी 1998)। समीकरण 4 स्पष्ट रूप से सीमा चक्र की अनुमति नहीं देते हैं, और अराजकता तब नहीं होती है जब सिस्टम दो आयामी होता है।
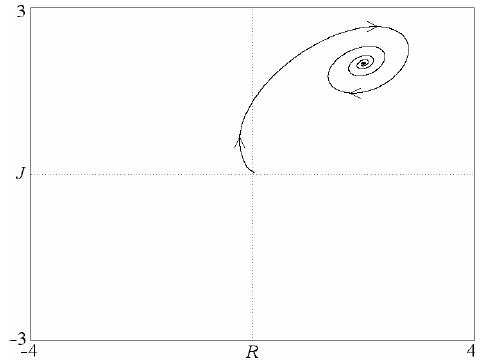अंजीर। 3. समीकरण 4 के अनुसार नॉनलाइन मॉडल के समाधानों में से एक।शायद प्रेम के त्रिकोण के लिए nonlinear प्रभाव का अनुप्रयोग।
अंतभाषणप्यार के कुछ रैखिक गतिशील मॉडल आश्चर्यजनक रूप से जटिल गतिशीलता का प्रदर्शन करते हैं, जबकि उनमें से अधिकांश रिश्तों में ज्ञात अनुभव के समान प्रतीत होते हैं। यदि तीन या अधिक चर हैं और यहां तक कि सबसे सरल nonlinear प्रभाव पेश किए जाते हैं, तो अराजकता हो सकती है। मॉडल के एक दिलचस्प विस्तार की कल्पना तब की जा सकती है जब एक बड़े परिवार या कम्यून के मामलों के लिए, बातचीत करने वाले व्यक्तियों के समूह पर विचार किया जाए। इस तरह के मॉडल, ज़ाहिर है, बहुत सरल होते हैं, क्योंकि प्यार को एक साधारण स्केलर चर के रूप में ध्यान में रखा जाता है, और अपने स्वयं के प्यार के संबंध में व्यक्तियों की प्रतिक्रियाएं और उनके लिए अन्य व्यक्तित्वों का प्यार बाहरी प्रभाव कारकों को ध्यान में रखे बिना सुसंगत और यंत्रवत हैं।
पीएस लव गणित के बिना रह सकता है, लेकिन गणित उन लोगों के लिए स्वयं के प्यार को उजागर करता है जो सच्चे सद्भाव को महत्व देते हैं।
संदर्भ:
जूलियन क्लिंटन स्प्रोट। प्यार के गतिशील मॉडल। Nonlinear गतिशीलता मनोविज्ञान और जीवन विज्ञान • अगस्त 2004
रिनाल्डी, एस (1998 ए)। लव डायनामिक्स: रैखिक जोड़ों का मामला। अनुप्रयुक्त गणित और संगणना, 95, 181-192।
रिनाल्डी, एस। और गगनानी, ए (1998)। सुरक्षित व्यक्तियों के बीच प्रेम की गतिशीलता: एक मॉडलिंग दृष्टिकोण। नॉनलाइनियर डायनेमिक्स, मनोविज्ञान और जीवन विज्ञान, 2, 283-301।
रिनाल्डी, एस (1998 बी)। लौरा और पेट्रार्क: चक्रीय प्रेम की गतिशीलता का एक पेचीदा मामला। एप्लाइड गणित पर SIAM जर्नल, 58, 1205-1221