अभाज्य संख्याओं की गणना के लिए सूत्र और जानवर बल विभाजकों का अनुकूलन

नमस्ते! मैंने प्राइम नंबर खोजने की समस्या पर शोध करने के लिए अपने अवकाश पर फैसला किया। विषय व्यापक और रोचक है। मैं उस पर कुछ विचार साझा करना चाहता हूं जो दिमाग में आया। इंटरनेट पर एक खोज ने उनकी मौलिकता की ओर इशारा करते हुए ऐसा नहीं बताया।

सबसे पहले, मैं क्रम में primes की गणना के लिए एक गणितीय सूत्र कभी नहीं मिला। लेकिन आखिरकार, अगर एल्गोरिदम हैं, तो निश्चित रूप से तार्किक कार्यों या ऑपरेटरों का उपयोग करके सूत्रों की रचना करना संभव है। मैं सबसे संक्षिप्त सूत्र नीचे देता हूं जो निकला।

संख्याओं के कुछ अनुक्रम के लिए $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {अधिकतम}}$ हम एक के बराबर पहली संख्या का पता लगाने के ऑपरेटर का परिचय देते हैं:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ बाएँ \ {\ {शुरू करना {मैट्रिक्स} m \ \ mathbf {अगर} \ \ अस्तित्व \ m: \ forall \, k <m \ x_ / k } \ neq a \ \ mathbf {और} \ x_ {m} = a \\ 0 \ \ \ mathbf {अन्यथा} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ \ "\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ अंत \"}}$$

5 से शुरू होने वाली सभी प्रमुख संख्याओं की गणना सूत्र द्वारा की जा सकती है:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1}} 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {_ \ _ \ _} \ _ \ _ \ अल्फ़ा -1}} {2} +10 \ _, \ \ 2 \ leqslant \ Alpha \ leqslant n-1; \ \ j_ {अधिकतम} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

ऑपरेटर $$$\ mathbf {Dt_ {0} ^ {j}}$ पर निर्भर करता है $$$ज$ प्रत्येक उम्मीदवार संख्या को सरलता से विभाजित करने के शेष $$$मैं$ वें नंबर $$$(P_ {n-1} + 2i)$ पहले से सीमा में पाए जाने वाले अपराधों तक $$$P_ {j_ {अधिकतम} +1}$ । पिछली संख्या से अधिक विषम संख्याओं के सेट से क्रम में उम्मीदवारों की संख्या का चयन किया जाता है $$$P_ {n-1}$ । $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ एक पीआई फ़ंक्शन है जो प्राइम की संख्या दिखा रहा है $$$\ leqllant \ sqrt {P_ {n-1} + 2i}$ ।
ऑपरेटर $$$\ mathbf {Dt_ {0} ^ {i}}$ पर निर्भर करता है $$$मैं$ ऑपरेटर आउटपुट मान $$$\ mathbf {Dt_ {0} ^ {j}}$ जब तक यह नहीं मिल जाता है 0. जब से अपराधों की श्रृंखला अनंत है, यह जल्दी या बाद में होगा। ऑपरेटर के बाहर निकलने पर $$$\ mathbf {Dt_ {0} ^ {i}}$ इसलिए हमेशा कुछ नम्बर रहेगा $$$मैं$ । नीचे की ओर बँधा हुआ $$$i_ {अधिकतम}$ वांछित की तुलना में आसन्न primes के अधिकतम अंतर से निर्धारित होता है। इस अंतर में वृद्धि लघुगणकीय रूप से होती है। नीचे दिया गया ग्राफ़ अधिकतम और औसत वृद्धि की निर्भरता को दर्शाता है $$$\ Delta P _ {\ Alpha}$ एन से पहले 100,000 primes के लिए। अधिकतम मूल्य प्रत्येक हजार संख्या के लिए नमूना और औसत था।
Primes के अंतर में अधिकतम वृद्धि $$$\ डेल्टा _ {अधिकतम} (\ डेल्टा पी _ {\ अल्फा})$ पिछले अधिकतम मूल्य के लिए $$$अधिकतम (\ Delta P _ {\ alpha})$ 20 के बराबर (primes के अंतर के लिए 31397-31469 = 72 के अंतर के साथ 25523-25471 = 52)। यह उस क्षेत्र में है जहां लिफाफा लघुगणक के व्युत्पन्न है $$$\ Delta P _ {\ Alpha}$ अभी भी काफी बड़ा है, और अभाज्य संख्याएँ अब बहुत छोटी नहीं हैं। इस मूल्य के आधार पर, के लिए शर्त $$$i_ {अधिकतम}$ । समय सारिणी $$$\ डेल्टा _ {अधिकतम} (\ डेल्टा पी _ {\ अल्फा})$ नीचे दिए गए पहले 50,000 अपराधों के लिए। मूल्यों की गणना हर हजार के लिए की जाती थी।
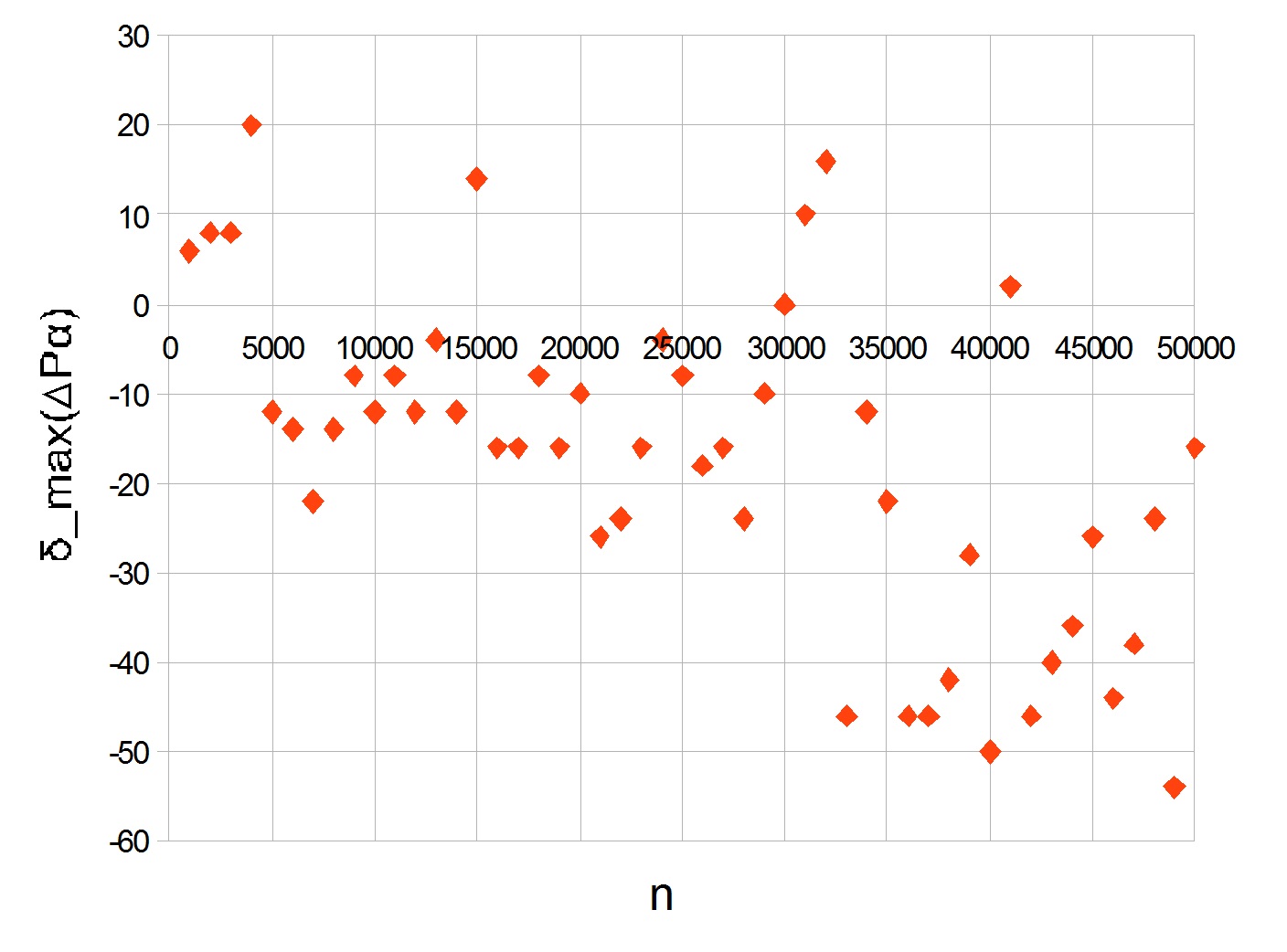
शिखर 20 पर दिखाई देता है। बढ़ते हुए n के साथ , ग्राफ माइनस में चला जाता है, जो बड़े अपराधों की वृद्धि दर में कमी दर्शाता है।

दूसरा विचार primes के अनुक्रम की गणना का अनुकूलन करना है।
ऊपर दिए गए सूत्र में निर्धारित एल्गोरिथ्म डिवाइडरों को एन्यूमरेट करने के लिए एक बेहतर तरीका है। सुधार को विचार से भी संख्याओं को बाहर करना है और वर्ग से छोटे केवल अपराधों की विभाज्यता की जांच करना है। उम्मीदवार संख्या की जड़ें। एल्गोरिथ्म का सबसे कठिन हिस्सा शेष मॉड कार्यों के सेट की गणना है। इस फ़ंक्शन को अनुकूलित करके जटिलता को कम किया जा सकता है। हालाँकि, एक और भी प्रभावी तरीका है। चलो $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}}})}$ अवशेषों के अनुक्रम को अंतिम पाया गया अभाज्य संख्या 3 से मूल में विभाजित करने से है। हम प्रपत्र के अनुक्रम बनाएंगे

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$$

से शुरू करने के क्रम में $$$i = 1$ । अंतिम अवधि की गणना की जाती है यदि $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ । जब गणना के कुछ चरणों में शेष $$$r_ {i, j + 1} ^ {n}$ 0 के बराबर हो जाता है, अगले क्रम पर जाएं। यह तब तक किया जाता है जब तक कि मुझे नहीं मिल जाता है, जिस पर सभी अवशेष नॉनजेरो हैं। इसका मतलब है अगली प्राइम नंबर ढूंढना। अनुक्रम $$$(r_ {j + 1} ^ {n})$ अगले प्राइम नंबर मिलने तक इसे सहेज कर रखना होगा। इस तरह से अभाज्य संख्याओं की गणना के लिए आवर्तक सूत्र निम्न में परिवर्तित होता है:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1) ^ {} n})), \ \ \ forall \, n \ geqslant 3$$

प्रस्तुत एल्गोरिथ्म में, ऑपरेशन मॉड की सुविधा है: विभाज्य द्वारा $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ अधिक डिवाइडर। एकमात्र अपवाद नए सरल भाजक की घटना है। कंप्यूटर मेमोरी में, एल्गोरिथ्म को लागू करते समय, मांग की जड़ में सरणी के एक सरणी को संग्रहीत करना आवश्यक है, साथ ही साथ अवशिष्ट के एक चर सरणी। सामान्य ज्ञान में एल्गोरिथ्म की जटिलता (काम की मात्रा) अन्य ज्ञात विधियों की तुलना में कम हो सकती है। इसमें सबसे जटिल ऑपरेशन वर्गमूल की निकासी, अवशेषों और गुणा की गणना है। जड़ को निकटतम पूर्णांक तक निकाला जा सकता है। अवशेष प्राप्त करने के लिए, आप विभाजन के सामान्य नियम के आधार पर एक प्रभावी एल्गोरिथ्म का उपयोग कर सकते हैं। गुणन केवल 2 अपेक्षाकृत छोटी संख्याओं द्वारा उपयोग किया जाता है i । एल्गोरिथ्म की समय जटिलता को i के मूल्यों के अनुसार कार्य वितरित करके कम किया जा सकता है। इस तरह प्राप्त खंडित छलनी बहु-थ्रेडेड कंप्यूटरों पर तेजी से काम करना चाहिए। हालांकि, लाभांश में वृद्धि के कारण प्रदर्शन किया गया कार्य बड़ा होगा। आप एल्गोरिथ्म पर पहिया पेंच भी कर सकते हैं। पहियों के इष्टतम आकार के साथ, यह n की एक निश्चित सीमा में जटिलता को कम कर सकता है - जब तक कि हार्डवेयर "wilds" इसे धीमा नहीं करता।

शायद कोई मेरे विचारों में काम आएगा।