सब कुछ जो आप पेंडुलम के बारे में जानना चाहते थे

लेख उन लोगों के लिए एक धोखा पत्रक के रूप में कार्य करता है जो अपने रिवर्स पेंडुलम बनाना चाहते हैं। यहां समस्याएं हैं जिनके कारण मैंने कई बार पुन: काम किया, सिस्टम को स्थिर करने के तरीके को समझने के लिए सिद्धांत का एक संक्षिप्त अवलोकन आवश्यक है।

मुझे इसकी आवश्यकता क्यों थी?

संक्षेप में: मैं अपनी सीएनसी मशीन का विस्तार करना चाहता था, लेकिन कुछ गलत हो गया ...

असफल प्रयास

परियोजना को लगभग दो साल का परीक्षण और त्रुटि मिली, फिर से डिज़ाइन करना, विवरणों की प्रतीक्षा करना और अधूरे दिन बंद करना ताकि जो लोग दोहराना चाहते हैं उन्होंने अपना समय और तंत्रिकाओं को बचाया, मैं असफल निर्णयों के बारे में बात करना आवश्यक समझता हूं।

• एक एनकोडर के बजाय एक जाइरोस्कोप (MPU6050) - इसके खिलाफ मूल रूप से कुछ भी नहीं है, लेकिन सेंसर को एक घूर्णन रॉड पर स्थित होना चाहिए, यह अक्ष के चारों ओर कई बार रॉड को स्क्रॉल करने में असमर्थता प्रभाव और असमर्थता का परिचय देता है।
  
• पूर्ण एनकोडर - यदि यह एक पोटेंशियोमीटर है, यहां तक ​​कि तारों की आवाजाही (मुख्य रूप से आर्डिनो में संपर्कों के कारण) माप में शोर का परिचय देता है, तो 10-बिट एडीसी अभी भी पर्याप्त नहीं है; यदि यह अधिक महंगा सेंसर है, तो पढ़ना एक सीरियल इंटरफ़ेस के माध्यम से होता है, और यह सिस्टम में देरी का परिचय देता है, खासकर एक स्टेपर मोटर के साथ संयोजन में।
  
• प्रणाली की कठोरता - कुछ बिंदु पर मैंने अंत में एक लोड के साथ एक एल्यूमीनियम ट्यूब लिया, जब गाड़ी हिल गई, उसमें मजबूत कंपन शुरू हो गया, और यह तुरंत स्पष्ट नहीं था कि हम किस प्रणाली को स्थिर कर रहे थे। हमें यह सुनिश्चित करने के लिए प्रयास करना चाहिए कि भौतिक प्रणाली मॉडल के जितना संभव हो उतना करीब हो।
  
• घर्षण - इस घटना को अक्सर उपेक्षित किया जाता है, मैंने छोटी गेंदों के साथ स्लाइडर्स के साथ रेल के विपरीत बड़े गाड़ी के पहियों और वी-स्लॉट प्रोफाइल का उपयोग करके इसे कम करने की कोशिश की, क्योंकि रोलिंग घर्षण त्रिज्या के विपरीत आनुपातिक है।
  
• स्टेपर मोटर का उपयोग - मैंने इस मार्ग पर जाने में बहुत समय बिताया है, यह सूत्रों को सरल बनाने के लिए भ्रामक है (वास्तव में, हम तुरंत पेंडुलम के आधार के त्वरण को नियंत्रित करते हैं) और डिजाइन की सादगी (हम रेल में घर्षण के बारे में भूल सकते हैं, अगर हम मानते हैं कि मोटर कदमों को नहीं छोड़ता है) , लेकिन ... गति को सही ढंग से नियंत्रित करने के लिए, चरणों के बीच का समय दसियों माइक्रोसेकंड होना चाहिए, जिसका अर्थ है कि आप कंसोल को राज्य आउटपुट के बारे में भूल सकते हैं। प्रतिक्रिया के बिना, आप यह सुनिश्चित नहीं कर सकते हैं कि मोटर ने कदमों को याद नहीं किया है और गति वास्तव में है कि सिस्टम क्या सोचता है। मैं यह दावा नहीं करता हूं कि यह एक मृत अंत समाधान है, अगर कोई स्टेपर मोटर के साथ पेंडुलम को स्थिर करने में सफल होता है, तो मुझे इसे देखकर खुशी होगी।
  

मुक्त पेंडुलम

तस्वीर को पूरा करने के लिए, हम बिना किसी घर्षण के एक मुफ्त गाड़ी पर एक पेंडुलम का अनुकरण करते हैं।

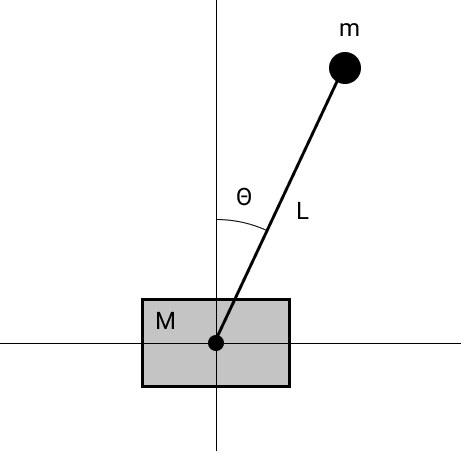
गति के समीकरणों को सामान्यीकृत निर्देशांक के संबंध में लैग्रैनिजियम को विभेदित करके प्राप्त किया जा सकता है। हम निम्नलिखित समीकरण प्राप्त करते हैं:

$$

$$\ _ {मामले} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ _ \ _ \ _ ddot {x} + m \ cdot \ ddot {\ cta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot / sin (\ theta) )} = 0 \ end {मामले}$$

जिससे आप पा सकते हैं कि राज्य वेक्टर कैसे बदलता है:

$$

$$\ _ {केस} \ _ \ _ थीटा = w \\ \ डॉट {w} = \ frac {g \ cdot {sin (\ थीटा)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos ((theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ dot {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {पाप (थीटा)} - g \ cdot {sin (\ थीटा)} \ cdot {cos (\ थीटा)} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {मामले}, b = \ frac {m} {M + m}$$

और सिस्टम का अनुकरण करें। कोड यहाँ है ।

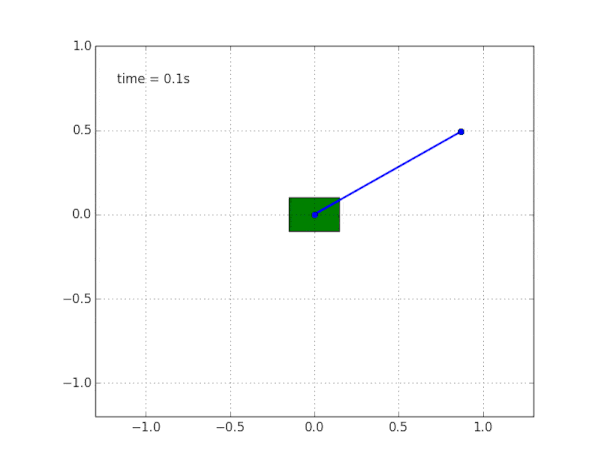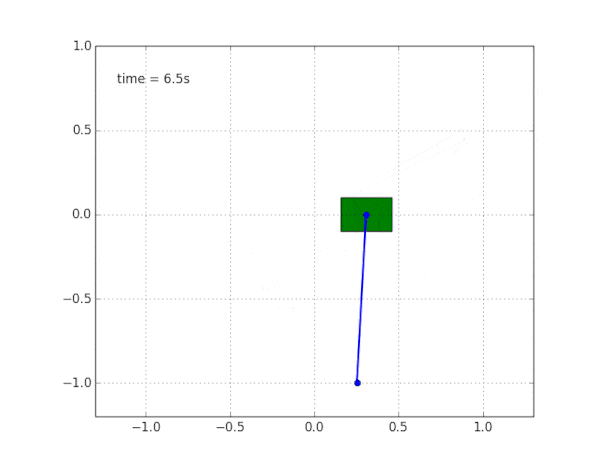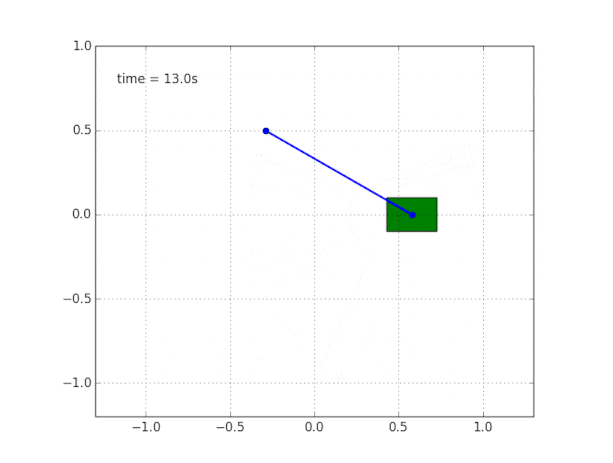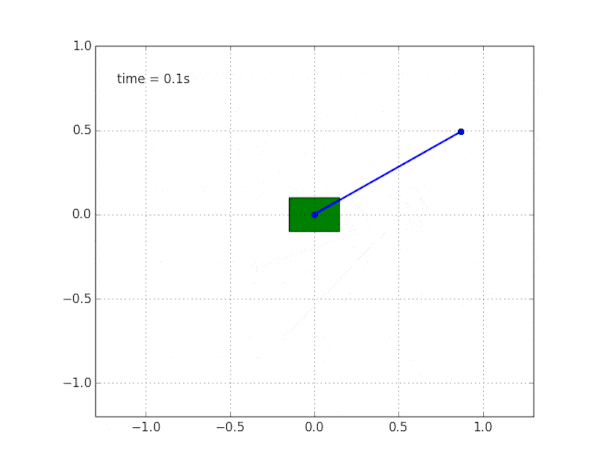
सिस्टम अस्थिर क्यों है?

सामान्य ज्ञान और दृश्य हमें बताते हैं कि पेंडुलम स्वयं खड़ा नहीं होगा। लेकिन इस गणितीय रूप से कैसे सत्यापित करें?
सामान्य शब्दों में, रैखिककृत प्रणाली और समाधान इस प्रकार हैं:

$$

$$\ dot {\ mathbf {x}} = A \ mathbf {x}, \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$$

मैट्रिक्स की शक्ति में एक प्रतिपादक स्पष्ट दिखता है, अगर हम eigenvectors से समन्वय प्रणाली में जाते हैं, तो मैट्रिक्स $$$ए$विकर्ण हो जाएगा ( $$$डी$), और प्रदर्शक की तरह दिखेगा:

$$

$$e ^ {Dt} = \ start {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$$

अब यह देखा जाता है, आइजेनवेल्स की उपस्थिति में ( $$$\ lambda_i$) एक सकारात्मक वास्तविक भाग के साथ, राज्य वेक्टर का संगत घटक अनन्तता की ओर बढ़ेगा, और सिस्टम अलग हो जाएगा। उपरोक्त निरंतर प्रणालियों पर लागू होता है, स्थिरता के बारे में अधिक इस वीडियो व्याख्यान में वर्णित है।
जांचें कि क्या यह रिवर्स पेंडुलम के लिए मामला है। हम के लिए संतुलन की स्थिति के पास हमारे सिस्टम को रैखिक करते हैं $$$\ theta = 0, sin (\ theta) \ अनुमानित \ theta, cos (\ theta) \ लगभग 1, w ^ 2 \ लगभग 0$:

$$

$$\ start {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ _ {bmatrix} 0 & 1 & 0 और 0 \ 0 \\ शुरू करें \ frac {g} {L (1 + b)} {\ थीटा} और 0 & 0 & 0 \\ 0 & 0 और 0 & 1 \\ -g \ frac {b} {1 + b} \ थीटा & 0 & 0 & 0 \ end {bmatrix} \ start {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$$

नॉनजरो आइजेनवेल्यूज का रूप है $$$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$, इस प्रकार हम अस्थिरता के प्रति आश्वस्त हो गए।

प्रतिक्रिया जोड़ें

अब बल गाड़ी पर कार्रवाई करेगा $$$च$, समीकरणों में से एक फार्म में फिर से लिखा जा सकता है: $$$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ _ \ _ \ _ta} ^ 2 \ cdot {sin (\ theta)} = f$ , और लीनियराइज़्ड सिस्टम रूप लेगा:

$$

$$\ start {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ start {bmatrix} 0 & 1 & 0 & 0 \ _ \\ \ frac {g} {L (1 + b)} {\ थीटा} और 0 & 0 & 0 \\ 0 & 0 और 0 & 1 \\ -g \ frac {b} {1 + b} \ थीटा & 0 & 0 & 0 \ end {bmatrix} \ start {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ start {bmatrix} 0 \\ \ frac {1} {L} \ frac {१} {२ मी + एम} \ ० \ ० एल ० \ ० फ्राक {१} {२ एम + एम} \ एंड {बमेटिक्स} \ सीडॉट {एफ}$$

अब प्रणाली ( $$$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$) नियंत्रणीय बन गया, यह जाँचकर कि मैट्रिक्स की रैंक को सत्यापित किया जा सकता है $$$\ start {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}$ राज्य वेक्टर के आयाम के बराबर, अर्थात 4. एक सीधी स्थिति में पेंडुलम रखने के लिए, मैंने एक रैखिक-द्विघात राज्य नियंत्रक का उपयोग किया, अर्थात नियंत्रण (यू या एफ) राज्य वेक्टर का उत्पाद है $$$[\ theta, \ dot {\ theta}, x, \ dot {x}]$द्विघात कार्यात्मक को कम करके एक बार मिलने वाले मापदंडों के वेक्टर द्वारा। सिमुलेशन कोड यहाँ है ।

इंजन नियंत्रण

अब आपको डीसी मोटर को नियंत्रित करने की आवश्यकता है, इसमें कई पैरामीटर हैं जो मुझे नहीं पता हैं, इसलिए मैंने इसे एक "ब्लैक बॉक्स" के लिए लिया, जो कि निम्नलिखित समीकरणों द्वारा वर्णित है, इसे घर्षण में लिया गया है:

$$

$$\ _ {केस} \ _ \ _ {एक्स} = v \\ \ डॉट {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {साइन (v)} \ एंड {केस}$$

आप समीकरण और पैरामीटर अनुमान की व्युत्पत्ति के बारे में यहां पढ़ सकते हैं। नीचे मैं वोल्टेज के आधार पर गाड़ी के साथ मोटर के त्वरण के अपने रेखांकन देता हूं (वास्तव में, पीडब्लूएम सिग्नल कंट्रोलर से आउटपुट है) और फिट किए गए घुमाव।

मुझे ब्रूट फोर्स, कोड द्वारा मॉडल गुणांक भी मिला।
इस प्रकार, नियंत्रक हमें आवश्यक त्वरण देता है, और दूसरे समीकरण से, सभी स्थिरांक को जानने के बाद, हम वोल्टेज पाते हैं।

असली डिवाइस को एक साथ रखना

अब हमारे पास पेंडुलम को इकट्ठा करने और स्थिर करने के लिए सभी ज्ञान हैं। मैंने निम्नलिखित लोहे का उपयोग किया:

• Arduino Mega 2560 UNO नहीं है, क्योंकि दो एनकोडर को व्यवधान के लिए 4 पिन की आवश्यकता होती है
• पेंडुलम के लिए एनकोडर - OMRON E6B2-CWZ6C 2500 दालों प्रति क्रांति - हमें कोण देता है, हम कोणीय वेग की गणना करते हैं, संकल्प काफी अधिक है, इसलिए चौरसाई और औसत के बिना पर्याप्त परिमित अंतर थे
• मोटर के लिए एनकोडर - LPD3806-600BM-G5-24C प्रति क्रांति 600 दालों - गाड़ी की स्थिति देता है, गति की गणना करें
• 5: 1 गियरबॉक्स के साथ 12 वी डीसी मोटर
• 10Amp 5V-30V मोटर चालक

इस प्रकार, हम स्पष्ट रूप से पेंडुलम के कोण को मापते हैं, गाड़ी की स्थिति, पेंडुलम के कोणीय वेग और गाड़ी की गति की गणना करते हैं - हमें पूर्ण स्थिति मिलती है, मुझे इस स्क्रिप्ट के साथ नियंत्रक पैरामीटर मिला। हैरानी की बात है, सब कुछ जल्दी से काम के रूप में यह था। मैं परिणाम से संतुष्ट हूं, यह खड़ा है और यहां तक ​​कि एक गिलास भी रखता है!


Arduino के लिए कोड यहाँ है
यूट्यूब पर पाए जाने वाले कई विकल्पों की तुलना में क्या सुधार किया जा सकता है - यह पेंडुलम शांत है क्योंकि पीडब्लूएम श्रवण सीमा के बाहर ट्यून किया गया है और प्लास्टिक के पहियों का उपयोग किया जाता है।
अब यह कार्य प्रयोगशाला के काम की तरह दिखता है: मोटर के मापदंडों को मापने के लिए और नियामक के गुणांकों को खोजने के लिए, एक साथ यह समझना कि क्या हो रहा है।

आगे क्या है?

मेरी योजना एक पेंडुलम बनाने की है: एक स्विंग बनाएं, तारों के एक तार से छुटकारा पाएं, सुविधाजनक कनेक्टर के साथ एक ढाल बनाएं ताकि किसी स्कूल या संग्रहालय को दान करना शर्म की बात न हो। यदि कोई शामिल होना चाहता है, तो मुझे खुशी होगी कि कई और महत्वाकांक्षी विचार हैं।

संदर्भ

• उलटे पेंडुलम समस्या का विस्तृत विवरण
• हम एक उल्टे पेंडुलम को नियंत्रित करने के लिए एक रैखिक-द्विघात नियामक को चबाते हैं - इस लेख ने मुझे अपना पेंडुलम बनाते समय बहुत समय बचाया
• महान TAU वीडियो व्याख्यान

आपका ध्यान के लिए धन्यवाद!