श्रम अर्थशास्त्रियों की सेवा में बेजियर वक्र

(उद्यम में स्थापित वेतन के लिए एक तर्क विकसित करने के प्रयास का परिणामी प्रतिनिधित्व)

एनोटेशन के बजाय

यदि आपने कभी उद्यम के कर्मचारियों के वेतन के हिस्से के आकार को सही ठहराने की आवश्यकता के बारे में सोचा, तो आपको ऐसे निर्णय लेने में स्पष्टता और सरलता की आवश्यकता थी, तो आप अकेले नहीं हैं और आपके लिए कटौती के तहत सामग्री है। एक बिंदु-रेटिंग प्रणाली और बेज़ियर घटता को प्राप्त करने के लिए आधुनिक एकीकृत मूल्यांकन तंत्र का उपयोग करके एक उद्यम में एक वेतन औचित्य प्रणाली को लागू करने का एक मामूली प्रयास, जिसके परिणामस्वरूप अंकों को परिवर्तित करने के लिए आधार यहां प्रस्तुत किया जाएगा।

समस्या का संक्षिप्त विवरण

एक आधुनिक उद्यम के कुल पारिश्रमिक की संरचना विविध है, सामान्यीकृत रूप में इसमें विभिन्न घटक शामिल हो सकते हैं (छवि 1)। इस प्रकाशन में, हम मूल वेतन में रुचि लेंगे। यह भी ध्यान दिया जा सकता है कि काम की प्रक्रिया में, अधिकांश भाग के लिए, संरचनाओं पर विचार किया गया था जहां समय-आधारित मजदूरी प्रबल होती है।


चित्रा 1. कुल पारिश्रमिक की संरचना।

मैं विशेष रूप से ध्यान देना चाहूंगा कि समस्या पर विचार करते समय, लेखकों का दृष्टिकोण, अधिकांश भाग के लिए, गैर-उत्पादन कर्मियों के लिए, जिसका काम मापना और डिजिटाइज़ करना बहुत मुश्किल है।

शुद्ध समय मजदूरी एक उत्तेजक कारक नहीं है, लेकिन अगर निष्पक्षता और पारदर्शिता के सिद्धांत का उल्लंघन किया जाता है, तो यह प्रेरणा में कमी को काफी प्रभावित कर सकता है। न्याय के सिद्धांत का उल्लंघन निम्नलिखित में व्यक्त किया गया है:

1. भुगतान पर सामान्य स्थानीय कार्य औपचारिक हैं और वेतन की वास्तविक स्थापना और परिवर्तन का निर्धारण नहीं करते हैं।
2. टैरिफ ग्रिड बनाया गया है ताकि एक श्रेणी के बिना एक विशेषज्ञ विभाग के प्रमुख (मेष धुंधला) के रूप में प्राप्त कर सके।
3. भुगतान की श्रेणी में एकजुट किए गए पदों के समूह, प्रदर्शन किए गए कार्यों की जटिलता में काफी भिन्न हो सकते हैं।
4. वेतन उस विभाजन पर निर्भर करता है जिसमें कर्मचारी काम करता है, न कि अपने काम की जटिलता पर।

हम कुछ अतिरिक्त शर्तें भी लगाते हैं:

ग्रेडिंग प्रत्येक व्यक्ति कर्मचारी (या कार्यस्थल) की गतिविधियों के मूल्यांकन के आधार पर एक समान दर निर्धारित करने का एक तरीका है, जो समान मानदंडों के अनुसार, संगठन के लिए उनके महत्व (मूल्य) के अनुसार वितरित किया जाता है।

दूसरे शब्दों में:

- यह कंपनी में उच्चतम से लेकर सबसे कम तक की श्रेणियों के सभी पदों का टूटना है, जिनमें से प्रत्येक को एक विशिष्ट वेतन, या वेतन का "कांटा" सौंपा गया है, जो प्रत्येक स्थिति के लिए न्यूनतम और अधिकतम शुल्क दर निर्धारित करता है।

हमारे श्रम कानून को व्यावसायिक संरचनाओं के लिए स्टाफिंग और टैरिफ अनुसूची की आवश्यकता नहीं है, और इन दोनों को सबसे पहले नियोक्ता द्वारा खुद को श्रम संसाधनों के प्रबंधन के लिए एक उपकरण के रूप में आवश्यक है।

इस क्षेत्र में विकास, प्रसिद्ध लेखकों के वैज्ञानिक कार्य, निर्विवाद रूप से मौजूद हैं। इसके अलावा, आवेदकों की सीमा व्यापक है। सबसे प्रसिद्ध, शायद, हे ग्रुप का विकास है। महान बात है, मैं सुंदर और अंधेरे को अपनी तरह के, प्रणालियों में से एक के लिए आलोचना नहीं करूंगा। मैं केवल इस बात पर ध्यान देता हूं कि उद्यम में जहां इस तरह की प्रणाली शुरू की गई थी, अप्रशिक्षित कर्मियों को यह नहीं पता था कि इसका उपयोग कैसे करना है, और इसलिए, जब श्रम और मजदूरी विभाग में पदों पर लोगों को बदलते हुए, कोई भी पूरी तरह से बदलती परिस्थितियों के लिए प्रणाली को अनुकूलित नहीं कर सकता है। इसलिए उन्होंने इसे एक महान प्राचीन कलाकृति की तरह रखा, जिसे ओल्ड बिलीवर्स के अलावा कोई नहीं पढ़ सकता था, और वे अब नहीं रह गए थे।

परिवर्तन करें

(मॉडल विकास)
आमतौर पर, मल्टीफॉर्मर मॉडल के कार्यान्वयन के लिए, जिन्हें अंततः एक संख्यात्मक परिणाम प्राप्त करने की आवश्यकता होती है, मैं मानदंड पेड़, कन्वेंशन मैट्रिसेस और एक पैमाने पर मानदंडों को कम करने के लिए एक प्रणाली के आधार पर जटिल मूल्यांकन की विधि को प्राथमिकता देता हूं।

संक्षेप में, ऐसे निर्माणों के लाभ की संभावनाएं हैं:

• मूल्यांकन कारकों की एक असीमित संख्या के आवेदन;
• गैर-रैखिकता की प्राप्ति और कारकों के प्रभाव की डिग्री की परिवर्तनशीलता;
• विभिन्न प्रकार के कारकों को शामिल करना (शारीरिक परिवर्तन, विशेषज्ञ अनुमान, पत्राचार टेबल, आदि के साथ);
• परिणामों की भविष्यवाणी करना और एक निश्चित सीमा में मूल्यों की अपेक्षा करना।

इस तरह के तंत्र के उपयोग में आसानी से परिणामी अनुमान के बहुपरत के साथ सफलतापूर्वक संयुक्त है, यहां तक ​​कि 1-4 की एक सीमित संख्यात्मक सीमा में, जो एक व्यापक मूल्यांकन लेता है, आप पर्याप्त विविधता प्राप्त कर सकते हैं।


चित्रा 2. ग्रेड रसीद का ब्लॉक आरेख और कर्मचारियों के वेतन में उनका स्थानांतरण।
यह विचार था कि, कई मानदंडों के अनुसार, संरचनात्मक इकाई के व्यवसाय के लिए "महत्व" और इस इकाई के लिए विशिष्ट स्थिति का एक मूल्यांकन किया गया था।

सामान्य तौर पर, इस योजना के अनुसार, यह नोट करना आवश्यक है:

• प्रत्येक इकाई के लिए, इसकी अपनी गणना एकल एकीकृत मूल्यांकन मॉडल के अनुसार बनाई गई है;
• एकीकृत मूल्यांकन के मॉडल में, मात्रात्मक रूप से मापने योग्य कारक और विशेषज्ञ दोनों का उपयोग किया जा सकता है;
• प्रत्येक विभाग और प्रत्येक स्थिति के लिए सभी मॉडल मान प्राप्त करने के बाद, मैट्रिक्स गुणा किया जाता है, जहां समग्र परिणाम बनता है;
• वेतन के आकार में ग्रेड लाने के लिए, विभाग के कर्मचारियों के वेतन में ग्रेड लाने के लिए एक मॉडल लागू किया जाता है।

विभाग के महत्व का आकलन करने में, निम्नलिखित मानदंडों का उपयोग किया गया था:

1. प्रक्रियाओं के स्तर के अनुसार: मुख्य, सहायक, सेवा;
2. हल किए जा रहे कार्यों की सार्वभौमिकता की डिग्री से: सार्वभौमिक, विशिष्ट, स्थितिजन्य;
3. बातचीत के स्तर तक: संगठनों के बीच; संगठनात्मक इकाइयों के बीच; आंतरिक बातचीत।

प्रस्तुत मूल्यांकन मानदंडों में, प्रत्येक मानदंड के लिए हमेशा 3 विकल्प होते हैं। इन विकल्पों को रेटिंग 4 से रेटिंग 1 के महत्व के "अवरोही क्रम" में व्यवस्थित किया गया है। औसत विकल्प 2.5 की रेटिंग से मेल खाता है। इस कमी को लागू करते हुए, सभी अनुमानों को मानक जटिल मूल्यांकन पैमाने 1-4 में अनुवादित किया जा सकता है (यहां आपको बस स्वीकार करने की आवश्यकता है ... हम सहमत हुए)।
स्थिति के महत्व का आकलन करने के लिए पेड़ का मूल प्रकार निम्नानुसार बनाया गया था:

1. स्थिति स्तर: प्रबंधक, विशेषज्ञ, कलाकार;
2. कार्यों के प्रकार: संगठनात्मक, रचनात्मक, विनियमित;
3. कार्यों की कनेक्टिविटी: बाहरी वातावरण के साथ, इकाइयों के बीच, इकाइयों के भीतर।

इसका एक उदाहरण एकीकृत मूल्यांकन का मॉडल है, जो कि, हम एक्सेल में "ड्राइव" करने में कामयाब रहे, अर्थात। उपलब्ध कराएं, दिखाता है कि मूल्यांकन प्रक्रिया का संचालन करना कितना आसान है।


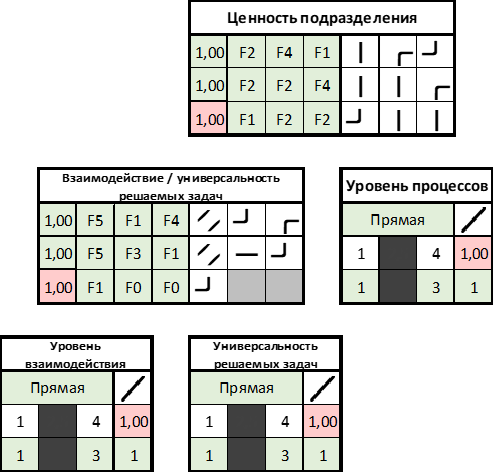चित्रा 3. एकीकृत मूल्यांकन मॉडल "यूनिट वैल्यू" का सामान्य दृश्य।
एक मॉडल को संकलित करने के बाद, प्रत्येक इकाई के लिए प्रत्येक मानदंड (और क्रमशः पदों के लिए, इसका अपना मॉडल है) को अपनी रेटिंग दी जाती है, और सिस्टम बस इसे मानता है। यह इन मूल्यों को लिखने के लिए बना हुआ है।

ग्रेड का "सारांश" अंत में कैसा दिखता है?


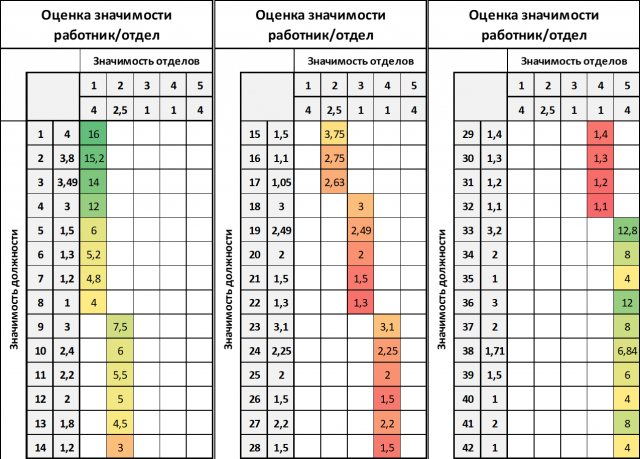चित्रा 4. "विभाग महत्व / स्थिति महत्व" के एक ग्रेड की गणना का एक उदाहरण।

इस मामले में, इष्टतम "विभाग महत्व" और "स्थिति महत्व" का गुणन प्रतीत होता है। परिणाम काफी भिन्न था और इसका उपयोग टैरिफ पैमाने को निर्धारित करने के लिए किया जा सकता है।

अंतिम घटक

जैसा कि आपको याद है, चित्र 2 के अनुसार, अब बॉल-रेटिंग को वेतन में बदलना आवश्यक है।

यह मूल रूप से माना जाता था कि यह एक सरल रैखिक फ़ंक्शन का उपयोग करके किया जा सकता है। इन उद्देश्यों के लिए, निर्णय निर्माता (निर्णय निर्माता) को केवल उद्यम में न्यूनतम और अधिकतम वेतन का संकेत देने के लिए आमंत्रित किया जाता है। काफी सरल और तार्किक कदम, जैसा कि लग रहा था।

पहला और स्पष्ट प्रयास एक रैखिक सर्किट के साथ तस्वीर करना है। संकेतित मापदंडों के साथ, निर्णय निर्माता (विश्वविद्यालयों में से एक के प्रमुख) ने ऐसा परिणाम प्राप्त किया कि संरचनात्मक इकाई के प्रमुख को 13 का ग्रेड बिंदु प्राप्त हुआ, उसे 200 हजार से अधिक (विभाग प्रमुख) का वेतन मिलना चाहिए।


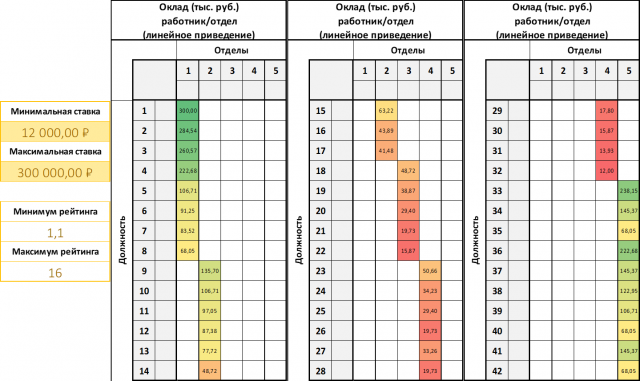चित्रा 5. एक रेखीय डाली पैमाने का उपयोग कर मजदूरी करने के लिए "उजागर" ग्रेड का एक उदाहरण।

वेतन / ग्रेड की गैर-रेखीय कमी के गठन के लिए एक सरल प्रणाली को लागू करने की आवश्यकता स्पष्ट हो गई है। इस मामले में, यथासंभव अधिकतम कमी के "चयन" की प्रक्रिया को सरल बनाने की आवश्यकता थी।

हादसे से बेज़ियर कर्व्स काफी समझ में आया। चूंकि वक्र के लिए चरम बिंदु स्वचालित रूप से (न्यूनतम और अधिकतम ग्रेड / न्यूनतम और अधिकतम वेतन) निर्धारित किए जाते हैं, इसलिए निर्णय निर्माता को वांछित प्रकार की वक्र प्राप्त करने के लिए बस एक / दो अंक स्थानांतरित करना होगा।


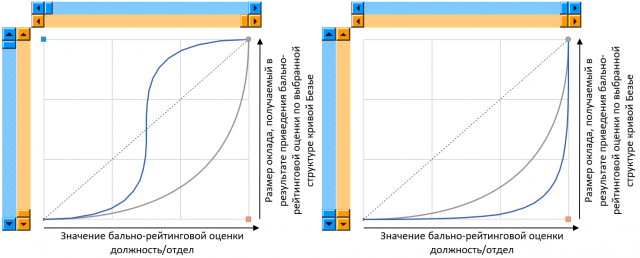चित्र 6. एक्सेल में लागू बेजियर कर्व ग्राफिकल कंट्रोल
प्रारंभ में, वक्र के केवल एक द्विघात संस्करण को प्राप्त करने का प्रयास किया गया था, हालांकि, निर्माण करने की कोशिश करने के बाद, यह स्पष्ट हो गया कि वे चारों ओर नहीं मिल सकते हैं और फ़ंक्शन के क्यूबिक संस्करण को लागू करना आवश्यक था।

एक्सेल में एक बेजियर वक्र उत्पन्न करने के लिए, निम्नलिखित क्रियाओं की आवश्यकता होती है:

• निर्देशांक X, Y: (1; 1) और (4; 4) द्वारा ग्राफ पर चरम बिंदुओं को इस उदाहरण में निर्दिष्ट करें। ग्राफ को स्पष्ट दिखाने के लिए इस तरह के चरम निर्देशांक लिए जाते हैं। उसे वास्तविक संबंध दिखाने की आवश्यकता नहीं है, लेकिन केवल निर्भरता दिखाने के लिए;
• एलपीआर द्वारा विस्थापित बिंदुओं के लिए निर्देशांक निर्दिष्ट करें: एक द्विघात वक्र के लिए एक बिंदु और एक घन के लिए दो बिंदु;
• वक्र के लिए गणना चरण निर्धारित करें (हमारे उदाहरण में - 0.5) और वक्र के लिए बिंदुओं के जोड़े की गणना करें।

घटता के निर्माण के बाद, निर्णय निर्माता को एक दृश्य नियंत्रण उपकरण प्राप्त हुआ। हालाँकि, घटता लगाने के लिए, संकेतित Y निर्देशांक से Y निर्देशांक प्राप्त करने की प्रक्रिया को लागू करना आवश्यक है। यहाँ बड़ी समस्या स्वयं थी। हालांकि, वीबीए कोड लागू करना संभव था जो आपको इस तरह के संचालन करने की अनुमति देता है।

एक द्विघात समारोह के लिए:

Function __Y__X__( _ X As Double, _ X1 As Double, _ X2 As Double, _ X3 As Double, _ Y1 As Double, _ Y2 As Double, _ Y3 As Double) As Double Dim aX, bX, cX, aY, bY, cY, Temp, dis, X_1, X_2, X_f, Y_f As Double aX = X1 - 2 * X2 + X3 bX = -2 * X1 + 2 * X2 cX = X1 - X aY = Y1 - 2 * Y2 + Y3 bY = -2 * Y1 + 2 * Y2 cY = Y1 dis = bX * bX - 4 * aX * cX If aX <> 0 Then X_1 = (-bX + (dis ^ (1 / 2))) / (2 * aX) X_2 = (-bX - (dis ^ (1 / 2))) / (2 * aX) Else X_1 = -cX / bX End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 Y_f = ((1 - X_f) ^ 2) * Y1 + 2 * (1 - X_f) * X_f * Y2 + (X_f ^ 2) * Y3 '=(1-R[-1]C[-1];2)*R58C2+2*(1-R[-1]C[-1])*R[-1]C[-1]*R58C3+(R[-1]C[-1];2)*R58C5 a = a __Y__X__ = Y_f End Function 

घन समारोह के लिए:

 Function __Y__X__( _ X As Double, _ X1 As Double, _ X2 As Double, _ X3 As Double, _ X4 As Double, _ Y1 As Double, _ Y2 As Double, _ Y3 As Double, _ Y4 As Double) As Double Dim myPi, aX, bX, cX, dX, aY, bY, cY, dY, Q, P, S, Temp, fi, dis, X_1, X_2, X_3, X_f, Y_f As Double 'Exit Function 'If X1 = 1.5 Or X = 0 Or X1 = 0 Or X2 = 0 Or X3 = 0 Or X4 = 0 Then Exit Function 'Application.Volatile True myPi = WorksheetFunction.Acos(-1) aX = -X1 + (3 * X2) - (3 * X3) + X4 bX = 3 * X1 - 6 * X2 + 3 * X3 cX = -3 * X1 + 3 * X2 dX = X1 - X aY = -Y1 + 3 * Y2 - 3 * Y3 + Y4 bY = 3 * Y1 - 6 * Y2 + 3 * Y3 cY = -3 * Y1 + 3 * Y2 dY = Y1 If aX < 0.000001 And aX > -0.000001 Then _ aX = 0 If CDbl(CStr(aX)) <> 0 Then Temp = aX aX = aX / Temp bX = bX / Temp cX = cX / Temp dX = dX / Temp Q = (bX ^ 2 - 3 * cX) / 9 P = (2 * (bX ^ 3) - 9 * bX * cX + 27 * dX) / 54 S = Q ^ 3 - P ^ 2 'X1 = -1 'X2 = -1 'X3 = -1 T = T If S < 0.00000001 And S > -0.00000001 Then _ S = 0 If P < 0.00000001 And P > -0.00000001 Then _ P = 0 If Q < 0.00000001 And Q > -0.000000001 Then _ Q = 0 If S > 0 Then fi = (1 / 3) * WorksheetFunction.Acos(P / ((Q ^ 3) ^ (1 / 2))) X_1 = -2 * (Q ^ (1 / 2)) * Cos(fi) - bX / 3 X_2 = -2 * (Q ^ (1 / 2)) * Cos(fi + 2 * myPi / 3) - bX / 3 X_3 = -2 * (Q ^ (1 / 2)) * Cos(fi - 2 * myPi / 3) - bX / 3 ElseIf S = 0 Then fi = 0 X_1 = -2 * (P ^ (1 / 3)) - bX / 3 X_2 = (P ^ (1 / 3)) - bX / 3 Else If Q > 0 Then fi = (1 / 3) * WorksheetFunction.Acosh(Abs(P) / ((Q ^ 3) ^ (1 / 2))) X_1 = -2 * Sgn(P) * (Q ^ (1 / 2)) * WorksheetFunction.Cosh(fi) - bX / 3 ElseIf Q = 0 Then fi = 0 T = (dX - (bX ^ 3) / 27) X_1 = -((Abs(T) ^ (1 / 3)) * (2 * (T < 0) + 1)) - bX / 3 'T = (dX - (bX ^ 3) / 27) 'T = (Abs(T) ^ (1 / 3)) * ((T < 0) + 1) 'X_1 = -T - bX / 3 Else fi = (1 / 3) * WorksheetFunction.Asinh(Abs(P) / ((Abs(Q) ^ 3) ^ (1 / 2))) X_1 = -2 * Sgn(P) * (Abs(Q) ^ (1 / 2)) * WorksheetFunction.Sinh(fi) - bX / 3 End If End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 If Not IsEmpty(X_3) Then If ((CDbl(CStr(X_3)) >= 0) And (CDbl(CStr(X_3)) <= 1)) Then X_f = X_3 a = a Else dis = cX * cX - 4 * bX * dX If bX < 0.000001 And bX > -0.000001 Then _ bX = 0 If bX <> 0 Then X_1 = (-cX + (dis ^ (1 / 2))) / (2 * bX) X_2 = (-cX - (dis ^ (1 / 2))) / (2 * bX) Else X_1 = -dX / cX End If If Not IsEmpty(X_1) Then If ((CDbl(CStr(X_1)) >= 0) And (CDbl(CStr(X_1)) <= 1)) Then X_f = X_1 If Not IsEmpty(X_2) Then If ((CDbl(CStr(X_2)) >= 0) And (CDbl(CStr(X_2)) <= 1)) Then X_f = X_2 End If a = a Y_f = ((1 - X_f) ^ 3) * Y1 + 3 * ((1 - X_f) ^ 2) * X_f * Y2 + 3 * (1 - X_f) * (X_f ^ 2) * Y3 + (X_f ^ 3) * Y4 'Debug.Print (Y_f) __Y__X__ = Y_f End Function 

इस प्रक्रिया में, नेटवर्क पर तैयार किए गए विकल्प को खोजने और रीसायकल करने का प्रयास किया गया, लेकिन ऐसा नहीं हुआ। यह भी गलती से पता चला था कि VBA एक नकारात्मक संख्या से विषम डिग्री जड़ को सही ढंग से निकालने में सक्षम नहीं है। केवल एक निश्चित संयोजन स्थिति को ठीक करने की अनुमति देता है:

 T = (dX - (bX ^ 3) / 27) X_1 = -((Abs(T) ^ (1 / 3)) * (2 * (T < 0) + 1)) - bX / 3 

* - कोड में संभवतः इस तरह की गणना के साथ जुड़ा एक पल कहीं और रहता है। लेख लिखने के दौरान एक बग की खोज की गई थी)

परिणाम स्वरूप निर्माण

इसलिए, परिणामों की तुलना करें (चित्र 6 (दाएं ग्राफ) में घटता के प्रकार के अनुसार निर्मित):


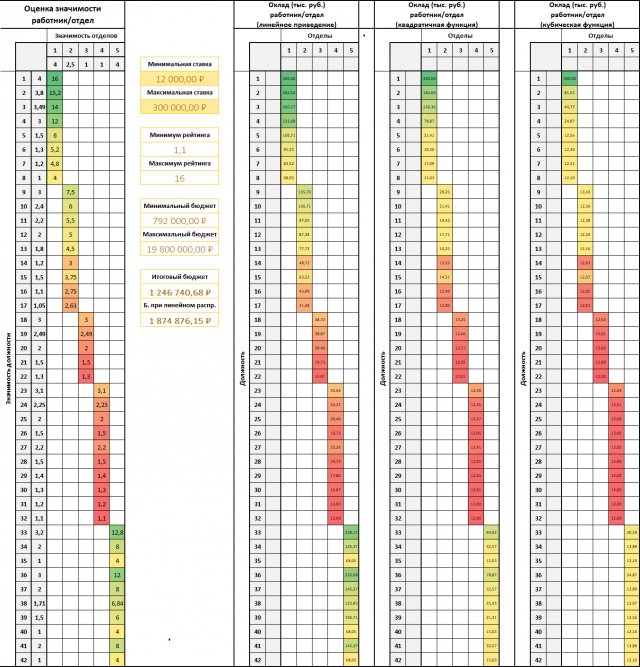चित्रा 7. वास्तविक वेतन (ग्रेड के लचीलेपन का प्रतिबिंब) को ग्रेड के कलाकारों की तुलना

यह उस आंकड़े से देखा जा सकता है कि क्यूबिक फ़ंक्शन गेंद की रेटिंग और वास्तविक वेतन की निर्भरता को "मोड़" करने की अनुमति देता है (प्रबंधक, दुर्भाग्य से, इस विकल्प से संतुष्ट था)।

किसी भी मामले में, यह काम, हालांकि यह प्रकृति में विशुद्ध रूप से प्रायोगिक है, वास्तव में कहीं भी लॉन्च नहीं किया गया है, लेकिन जैसा कि लेखकों को लगता है, यह वास्तविक विकास में उपयोगी हो सकता है।

मुझे आशा है कि वह "शेल्फ पर झूठ" नहीं करेगी, लेकिन किसी की ज़रूरत होगी।