🚣🏼 📙 👩🏿‍🎓 3 डी ग्राफिक्स में विभाजन, सबसे स्वचालित विकल्प 🈴 🔺 🥑

लगभग एक महीने पहले, मैंने डावसन किताब से पायथन सीखना शुरू किया और pygame के तहत अपने खेल को लिखने की प्रक्रिया में गहराई से जाग गया। टीके ऐसा था कि 3 डी स्प्लिन की सहेजी गई सतहों को स्प्राइट में भरकर छद्म-त्रि-आयामी ग्राफिक्स के साथ एक गेम बनाने का सबसे आशाजनक लग रहा था। मैं बाद के बारे में लिखूंगा।

तो, बहुभुज हैं (यह क्वाड्रांगल्स के साथ काम करना सबसे आसान है) जिस पर हम क्यूबिक सतहों को फैलाना चाहते हैं ताकि वे एक साथ काफी सुचारू रूप से फिट हों - ये सतह स्प्लिन हैं।

एक फ़ंक्शन के रूप में एक बहुभुज के लिए एक पट्टी पेश करना सबसे सुविधाजनक है

g (u, v) = v c d o t g_{1} (u) + (1 - v) c d o t g_{2} (u) + u c d o t g_{3} (v) + (१ - u) c d o t g_{4} (v) (१)

$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (१-u) \ cdot g_4 (v) (१)$

यहां

g_{1}, g_{2}, g_{3}, g_{4}

$g_1, g_2, g_3, g_4$

- क्यूबिक बहुपद कुछ सीमा स्थितियों (नीचे के चित्र में - हल्के हरे और लाल घटता, और व्युत्पन्न-प्रारंभिक स्थिति - बकाइन और नीले वैक्टर) को संतुष्ट करते हैं; यू और वी 0 से 1 तक भिन्न होते हैं।

इस व्याख्या में, कुछ डिग्री खो जाती हैं (मापदंडों के 2 और 3 डिग्री के उत्पाद), लेकिन बहुपद गुणांक प्रारंभिक स्थितियों के केवल 12 वैक्टर (प्रत्येक बिंदु के लिए यू और वी के संबंध में 4 बहुभुज बिंदु और व्युत्पन्न वैक्टर) निर्दिष्ट करके पाया जा सकता है। जंक्शनों पर, स्प्लीन संयोग करते हैं यदि पड़ोसी पॉलीगोन के लिए समान प्रारंभिक शर्तें निर्धारित की जाती हैं (व्युत्पन्न वैक्टर को समतल होना चाहिए, तो सतह बहुभुज के समान बिंदुओं से गुजरती है)।

एक समस्या - पूरी सीमा पर समस्या के इस तरह के बयान के साथ व्युत्पन्न संयोग नहीं हो सकता है - जंक्शनों पर छोटी कलाकृतियां होंगी। आप इसे ठीक करने के लिए 4 और शर्तें सोच सकते हैं और ध्यान से सूत्र में एक और शब्द जोड़ सकते हैं

u c d o t v c d o t (u - 1) c d o t (v - 1) c d o t g_{5} (u, v)

$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$

जो सीमाओं को खराब नहीं करता है, लेकिन यह एक अलग लेख के लिए एक विषय है।

एक विकल्प बेज़िएर सतह है , लेकिन यह असंगत (मेरे लिए) गणितीय अर्थ के 16 मापदंडों को निर्धारित करने का प्रस्ताव करता है, अर्थात। यह माना जाता है कि कलाकार अपने हाथों से काम करेगा। यह मेरे लिए बहुत उपयुक्त नहीं है, इसलिए बैसाखी के साथ एक साइकिल इस प्रकार है।

गुणांक (1) कोनों और मूल्यों के मैट्रिक्स के व्युत्क्रम मैट्रिक्स को खोजने और इनपुट स्थितियों से गुणा करके (प्रत्येक समन्वय के लिए तीन बार) आसानी से गणना की जाती है। मैट्रिक्स यह हो सकता है:

छिपा हुआ पाठ

[[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], #g (0%)
[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0], #g (1,0)
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], #g (0,1)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # 1 (1,1)
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], # dg / du (0,0)
[0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 3, 0], # dg / du (1,0)
[0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], # dg / du (0,1)
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3], # dg / du (1,1)
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,], # dg / DV (0,0)
[0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1], # dg / DV (1,0)
[0, 1, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0], # dg / DV (0,1)
[0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 0, 1]] # डीजी / डीवी (1,1)

NumPy इसका एक उत्कृष्ट कार्य करता है।

एक सवाल रहता है - डेरिवेटिव के वैक्टर कहां से लाएं। यह माना जाता है कि उन्हें पड़ोसी की स्थिति के आधार पर (बहुभुज के लिए) अंक और चिकनाई कारणों के लिए किसी न किसी रूप में चुना जाना चाहिए।
मेरे लिए व्यक्तिगत रूप से, यह अभी भी पूरी तरह से प्रतिगामी था कि व्युत्पन्न वेक्टर की लंबाई से कैसे निपटें। दिशा समझ में आती है, लेकिन लंबाई?

परिणामस्वरूप, निम्नलिखित एल्गोरिथ्म का जन्म हुआ:

1. पहले चरण में, कुछ बिंदुओं का वर्गीकरण होता है। ग्राफ में (जो बहुभुज के बिंदु और उनके कनेक्शन निर्दिष्ट करते हैं), लंबाई 4 के चक्रों को खोजा और संग्रहीत किया जाता है, और इसके अलावा, पड़ोसी जो बहुभुज के किनारों को विस्तारित करने की भूमिका के लिए सबसे उपयुक्त हैं, वे दर्ज किए गए हैं (यह पहले से निर्धारित किया जाता है कि यह पैरामीटर पैरामीटर यू में परिवर्तन के अनुरूप हैं और जो v के अनुरूप है)। यहाँ कोड का एक टुकड़ा है जो खोजता है, सॉर्ट करता है, और एक चक्र के 0 वें बिंदु के लिए पड़ोसियों को याद करता है:

छिपा हुआ पाठ

"""   : cykle[5] cykle[7] cykle[4]--cykle[0] --u-- cykle[1]-cykle[6] |v |v cykle[10]-cykle[3] --u-- cykle[2]-cykle[8] cykle[11] cykle[9] """ sosed = [] for i in range(0, N): if self.connects[i][ind] == 1 and i != cykle[0] and i != cykle[1] and i != cykle[3]: sosed += [i] #    ... if(len(sosed) < 2): continue #    else: #      cykle[0] vs0c3 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[3]]) vs1c1 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[1]]) #        vs0c1 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[1]]) vs1c3 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[3]]) Rvsc = [ScalMult(vs0c3,vs0c3),ScalMult(vs1c1,vs1c1),ScalMult(vs0c1,vs0c1),ScalMult(vs1c3,vs1c3) ] n1 = Rvsc.index(max(Rvsc)) if n1 < 2: cykle += [sosed[1],sosed[0]] #  u   v else: cykle += [sosed[0],sosed[1]]

इसके अलावा, जब तख़्ते का निर्माण होता है, तो किनारे के साथ व्युत्पन्न (उदाहरण के लिए, पैरामीटर यू के संबंध में) बहुभुज के बिंदु पर किनारे के दो बिंदुओं और एक आसन्न बिंदु के आधार पर चयन किया जाता है (इसे अंक vec1, vec2 और vec3 होने दें; वह बिंदु जिस पर व्युत्पन्न दूसरा है)

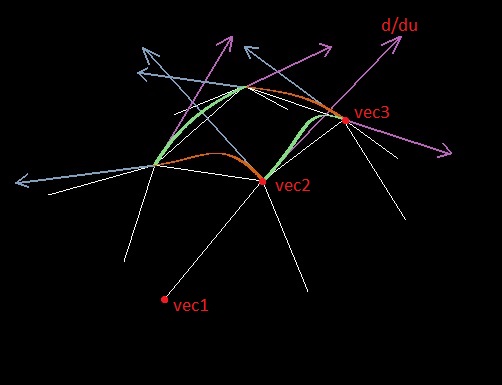
पहले तो मैंने इस भूमिका के लिए सामान्यीकृत वेक्टर vec3 - vec1 (जैसे मैंने लाग्रेंज प्रमेय लागू किया) का उपयोग करने की कोशिश की, लेकिन व्युत्पन्न वेक्टर की लंबाई के साथ समस्याएं ठीक-ठीक उत्पन्न हुईं - यह एक स्थिर विचार था।

गीतात्मक विषयांतर:

व्युत्पन्न वेक्टर पैरामीट्रिक संस्करण में क्या है, इसके एक छोटे से चित्रण के लिए, हम एक सरल दो-आयामी सादृश्य की ओर मुड़ते हैं - यहाँ एक वृत्त के चाप का एक टुकड़ा है:

g (u) = (र ु । (u p i / २), R c o s (u p i / २))

$g (u) = (रु। (u \ pi / २), Rcos (u \ pi / २))$

g^{'} (u) = (R p i / 2 c d o t c o s (u p i / 2), - R p i / 2 c d o t s i n (u p i / 2))

$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$

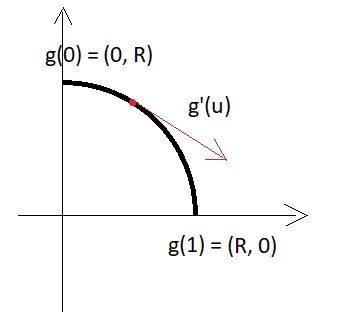
यानी व्युत्पन्न मापांक = आर * पी / 2 और, आम तौर पर बोलना, चाप के टुकड़े के आकार पर निर्भर करता है, जिसे हम पैरामीटर के माध्यम से निर्धारित करते हैं।

अब इसका क्या करें? लियो निकोलाइविच टॉल्स्टॉय ने हमसे कहा कि सब कुछ गोल = अच्छा है, इसलिए, यदि हम एक बिंदु पर व्युत्पन्न सेट करते हैं जैसे कि हम वहां एक चाप बनाना चाहते हैं, तो हमें एक सुंदर सुंदर वक्र मिलेगा।

विषयांतर का अंत।

व्युत्पन्न खोज का दूसरा चरण:

2. हमारे तीन बिंदुओं vec1, vec2, vec3 के माध्यम से हम एक विमान का निर्माण करते हैं, इस विमान में हम एक वृत्त की तलाश करते हैं जो तीनों बिंदुओं से होकर गुजरता है। वांछित व्युत्पन्न बिंदु vec2 पर वृत्त के स्पर्शरेखा के साथ निर्देशित किया जाएगा, और व्युत्पन्न के वेक्टर के मापांक सर्कल के त्रिज्या के उत्पाद और क्षेत्र के कोण के बराबर होना चाहिए, जो बहुभुज चेहरे के कुछ बिंदुओं का निर्माण करते हैं (गीतात्मक खुदाई से हमारे सरल फ्लैट सादृश्य के समान)।

g^{'} = R c d o t p h i

$g '= R \ cdot \ phi$

सब कुछ सरल प्रतीत होता है, यहाँ फ़ंक्शन कोड है, उदाहरण के लिए (NumPy का फिर से उपयोग किया जाता है):

कोड नहीं, लेकिन ...

 def create_dd(vec1, vec2, tuda, vec3): """     1-2       3   == 1""" #0.         -         :( vecmult = VecMult(MinusVecs(vec2,vec1),MinusVecs(vec3,vec1)) #  vec2-vec1 x vec3 - vec1 if vecmult[0]*vecmult[0] + vecmult[1]*vecmult[1] + vecmult[2]*vecmult[2] < 0.000001: #  0 if tuda == 1: return NormVec(MinusVecs(vec3,vec2)) else: return NormVec(MinusVecs(vec1,vec2)) #1.   ,     #           2   M = np.zeros((3,3),float) C = np.zeros((3,1),float) M[0][0] = 2*vec2[0] - 2*vec1[0] M[0][1] = 2*vec2[1] - 2*vec1[1] M[0][2] = 2*vec2[2] - 2*vec1[2] C[0] = -vec1[0]*vec1[0] - vec1[1]*vec1[1] - vec1[2]*vec1[2] + vec2[0]*vec2[0] + vec2[1]*vec2[1] + vec2[2]*vec2[2] M[1][0] = 2*vec3[0] - 2*vec2[0] M[1][1] = 2*vec3[1] - 2*vec2[1] M[1][2] = 2*vec3[2] - 2*vec2[2] C[1] = -vec2[0]*vec2[0] - vec2[1]*vec2[1] - vec2[2]*vec2[2] + vec3[0]*vec3[0] + vec3[1]*vec3[1] + vec3[2]*vec3[2] #   ,   4     M[2][0] = vecmult[0] M[2][1] = vecmult[1] M[2][2] = vecmult[2] C[2] = vecmult[0]*vec1[0] + vecmult[1]*vec1[1] + vecmult[2]*vec1[2] # M *    = C Mobr = np.linalg.inv(M) Rvec = np.dot(Mobr,C) res = NormVec(VecMult(MinusVecs(Rvec,vec2), vecmult)) #    ka #R = math.sqrt((Rvec[0]-vec1[0])**2 + (Rvec[1]-vec1[1])**2 + (Rvec[2]-vec1[2])**2) #   = 3.14*2*asin(l/(2*R))/180 * R,      l  ,    l = 1.2*math.sqrt((vec1[0]-vec2[0])**2 + (vec1[1]-vec2[1])**2 + (vec1[2]-vec2[2])**2) if ScalMult(res, MinusVecs(vec2, vec1)) > 0: #     return MultVxC(res, tuda*l) else: return MultVxC(res, -tuda*l)

खैर, सामान्य तौर पर, यह सभी किसी न किसी तरह से काम करता है। प्रदर्शन के लिए, मैंने 5x5x5 क्यूब लिया और एक रैंडमाइज़र के साथ बिंदुओं की स्थिति बदल दी:

GIF, 8Mb

3 डी ग्राफिक्स में विभाजन, सबसे स्वचालित विकल्प

More articles: