कार्यात्मक निर्भरता का परिचय

इस लेख में हम डेटाबेस में कार्यात्मक निर्भरता के बारे में बात करेंगे - यह क्या है, यह कहां लागू होता है और उनकी खोज के लिए क्या एल्गोरिदम मौजूद हैं।

हम रिलेशनल डेटाबेस के संदर्भ में कार्यात्मक निर्भरता पर विचार करेंगे। बहुत ही अशिष्टता से बोलते हुए, ऐसे डेटाबेस में जानकारी तालिकाओं के रूप में संग्रहीत की जाती है। इसके अलावा, हम अनुमानित अवधारणाओं का उपयोग करते हैं, जो एक सख्त संबंधपरक सिद्धांत में विनिमेय नहीं हैं: हम तालिका को स्वयं एक संबंध कहेंगे, कॉलम - विशेषताएँ (उनका सेट एक संबंध आरेख है), और विशेषताओं के सबसेट पर पंक्ति मानों का एक सेट - टपल।



उदाहरण के लिए, ऊपर दी गई तालिका में, (बेन्सन, एम, एम ऑर्गन ) विशेषताओं का एक प्रकार है (रोगी, लिंग, डॉक्टर) ।
औपचारिक रूप से, यह इस प्रकार लिखा जाता है: $$$t_ {1}$ [ रोगी, पॉल, डॉक्टर ] = (बेन्सन, एम, एम अंग) ।
अब हम कार्यात्मक निर्भरता (FZ) की अवधारणा को प्रस्तुत कर सकते हैं:

परिभाषा 1. संबंध R संघीय कानून को संतुष्ट करता है X → Y (जहां X, Y if R) यदि और केवल यदि किसी ट्यूपल्स के लिए $$$t_ {1}$ । $$$t_ {2}$ ∈ R धारण: यदि $$$t_ {1}$ [एक्स] = $$$t_ {2}$ [एक्स] फिर $$$t_ {1}$ [य] = $$$t_ {2}$ [Y]। इस मामले में, यह कहा जाता है कि एक्स (एक निर्धारक, या विशेषताओं का एक परिभाषित सेट) कार्यात्मक रूप से वाई (एक आश्रित) को परिभाषित करता है।

दूसरे शब्दों में, फेडरल लॉ एक्स → वाई की उपस्थिति का मतलब है कि अगर हमारे पास आर में दो ट्यूपल हैं और वे एक्स की विशेषताओं में मेल खाते हैं, तो वे वाई की विशेषताओं में भी मेल खाएंगे।
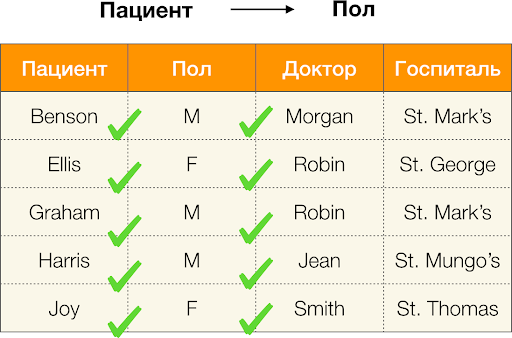
और अब क्रम में। रोगी और लिंग विशेषताओं पर विचार करें जिसके लिए हम यह पता लगाना चाहते हैं कि उनके बीच निर्भरताएं हैं या नहीं। इतनी सारी विशेषताओं के लिए, निम्नलिखित निर्भरताएँ मौजूद हो सकती हैं:

1. रोगी → लिंग
2. लिंग → रोगी

उपरोक्त परिभाषा के अनुसार, पहली निर्भरता रखने के लिए, रोगी स्तंभ के प्रत्येक अनूठे मूल्य के अनुरूप लिंग स्तंभ का केवल एक मूल्य होना चाहिए। और नमूना तालिका के लिए, यह सच है। हालांकि, यह विपरीत दिशा में काम नहीं करता है, अर्थात, दूसरी निर्भरता पूरी नहीं होती है, और पॉल विशेषता रोगी के लिए एक निर्धारक नहीं है। इसी तरह, अगर आप निर्भरता डॉक्टर → रोगी को लेते हैं, तो आप देख सकते हैं कि इसका उल्लंघन किया गया है, क्योंकि इस विशेषता के लिए रॉबिन मूल्य में कई अलग-अलग मूल्य हैं - एलिस और ग्राहम ।

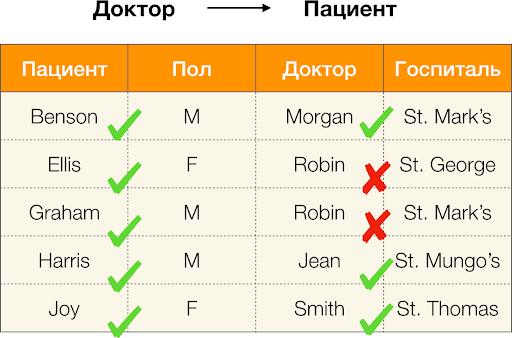
इस प्रकार, कार्यात्मक निर्भरताएं तालिका विशेषताओं के सेट के बीच मौजूदा संबंधों को निर्धारित करना संभव बनाती हैं। इसके बाद, हम सबसे दिलचस्प रिश्तों पर विचार करेंगे, या एक्स → वाई जैसे कि वे हैं:

• nontrivial, अर्थात् , निर्भरता के दाईं ओर बाईं ओर का उपसमूह नहीं है (Y ̸⊆ X) ;
• न्यूनतम, अर्थात्, ऐसी कोई निर्भरता नहीं है Z → Y जैसे कि Z there X।

इस बिंदु तक मानी जाने वाली निर्भरताएं सख्त थीं, अर्थात्, उन्होंने मेज पर किसी भी उल्लंघन को शामिल नहीं किया था, लेकिन उनके अलावा ऐसे भी हैं जो ट्यूपल्स के मूल्यों के बीच कुछ असंगति की अनुमति देते हैं। इस तरह की निर्भरता को एक अलग वर्ग में रखा जाता है, जिसे अनुमानित कहा जाता है, और एक निश्चित संख्या में ट्यूपल्स पर उल्लंघन की अनुमति दी जाती है। यह राशि अधिकतम इमैक्स त्रुटि संकेतक द्वारा विनियमित होती है। उदाहरण के लिए, त्रुटि का अनुपात $$$e_ {अधिकतम}$ = 0.01 का मतलब यह हो सकता है कि विशेषताओं के निर्धारित सेट पर उपलब्ध ट्यूपल्स के 1% द्वारा निर्भरता का उल्लंघन किया जा सकता है। यानी 1000 रिकॉर्ड के लिए, अधिकतम 10 ट्यूपल संघीय कानून का उल्लंघन कर सकते हैं। हम तुलनात्मक टुपल्स के जोड़ी-अलग-अलग मूल्यों के आधार पर थोड़ा अलग मीट्रिक पर विचार करेंगे। संबंध r पर निर्भरता X → Y के लिए , इसे निम्नानुसार माना जाता है:

$$

$$e (X \ rightarrow Y, r) = \ frac {| \ {(t_1, t_2) \ r in 2 \ _ | \ t_1 [X] = t_2 [X] \ wedge t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ २ | - - आर |}}$$

हम डॉक्टर के लिए त्रुटि की गणना करते हैं → उपरोक्त उदाहरण से रोगी । हमारे पास दो ट्यूपल हैं, जिनमें से रोगी की विशेषता के मूल्य भिन्न हैं, लेकिन डॉक्टर पर मेल खाते हैं: $$$t_ {1}$ [ डॉक्टर, रोगी ] = ( रॉबिन, एलिस ) और $$$t_ {2}$ [ डॉक्टर, रोगी ] = ( रॉबिन, ग्राहम )। त्रुटि की परिभाषा के बाद, हमें सभी परस्पर विरोधी जोड़े को ध्यान में रखना चाहिए, जिसका अर्थ है कि उनमें से दो होंगे: $$$t_ {1}$ । $$$t_ {2}$ ) और इसका उलटा ( $$$t_ {2}$ । $$$t_ {1}$ )। सूत्र में स्थानापन्न और प्राप्त करें:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0.1$$

अब आइए इस प्रश्न का उत्तर देने का प्रयास करें: "यह सब क्यों है?"। वास्तव में, संघीय कानून अलग हैं। पहला प्रकार निर्भरताएं हैं जो डेटाबेस डिज़ाइन चरण में व्यवस्थापक द्वारा निर्धारित की जाती हैं। आमतौर पर वे कम हैं, वे सख्त हैं, और मुख्य अनुप्रयोग डेटा सामान्यीकरण और संबंध योजना का डिज़ाइन है।

दूसरा प्रकार निर्भरता है जो "छिपी" डेटा का प्रतिनिधित्व करता है और विशेषताओं के बीच पहले से अज्ञात संबंध। यही है, डिजाइन के समय ऐसी निर्भरता के बारे में नहीं सोचा गया था और पहले से ही मौजूद डेटा सेट के लिए पाए जाते हैं, ताकि, पहचाने गए संघीय कानूनों के सेट के आधार पर संग्रहीत जानकारी के बारे में कोई निष्कर्ष निकाला जा सके। यह इतनी निर्भरता के साथ है कि हम काम कर रहे हैं। वे अपने आधार पर निर्मित विभिन्न खोज तकनीकों और एल्गोरिदम के साथ खनन डेटा के एक पूरे क्षेत्र में लगे हुए हैं। आइए समझते हैं कि किसी भी डेटा में कार्यात्मक निर्भरता (सटीक या अनुमानित) कैसे उपयोगी हो सकती है।



आज, डेटा सफाई निर्भरता के उपयोग के मुख्य क्षेत्रों में से एक है। इसमें उनके बाद के सुधार के साथ "गंदे डेटा" की पहचान के लिए प्रक्रियाओं का विकास शामिल है। "गंदे डेटा" के उज्ज्वल प्रतिनिधि डुप्लिकेट, डेटा त्रुटियां या टाइपोस, लापता मूल्य, पुराने डेटा, अतिरिक्त स्थान और पसंद हैं।

उदाहरण डेटा त्रुटि:



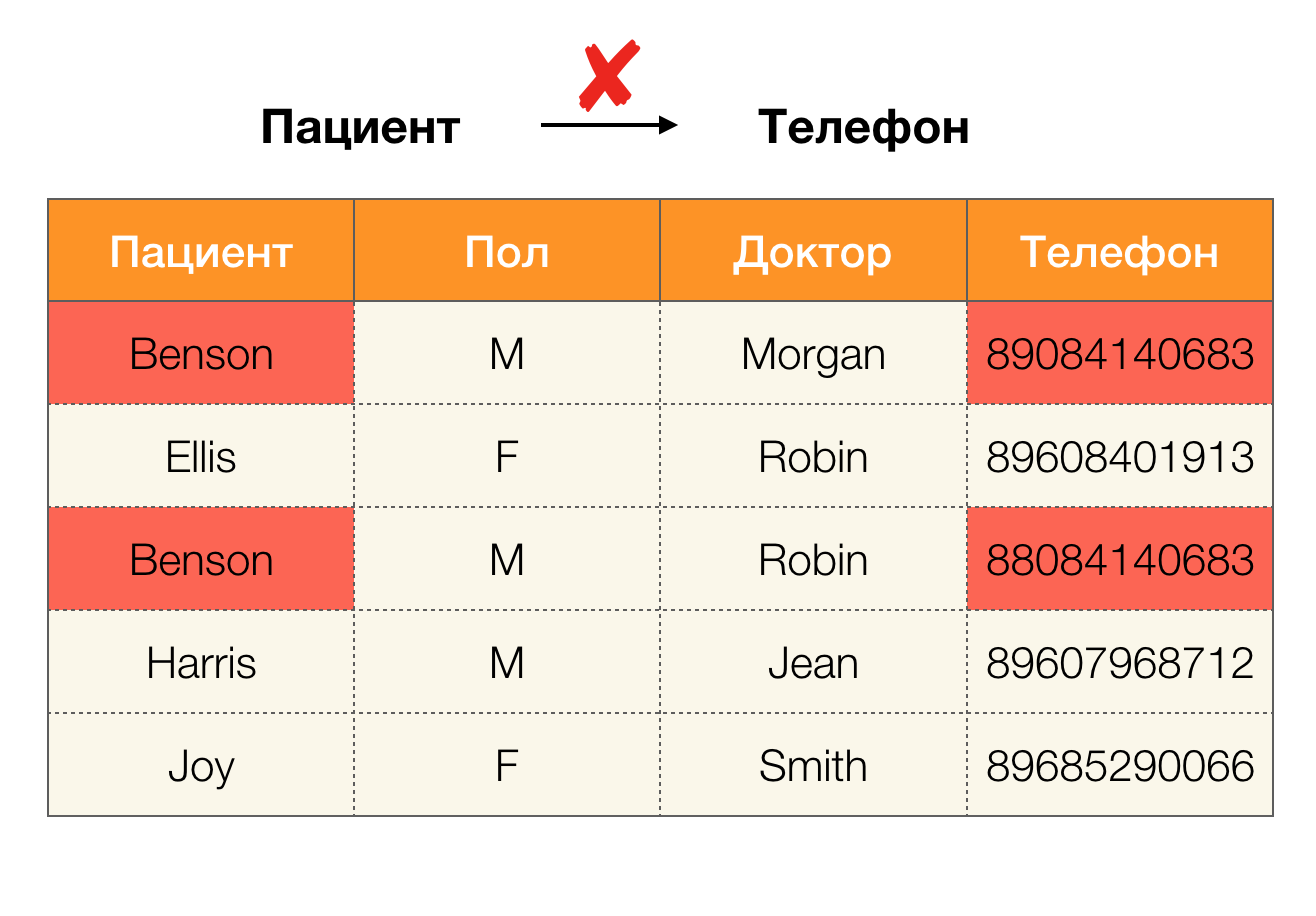
उदाहरण डेटा में डुप्लिकेट:



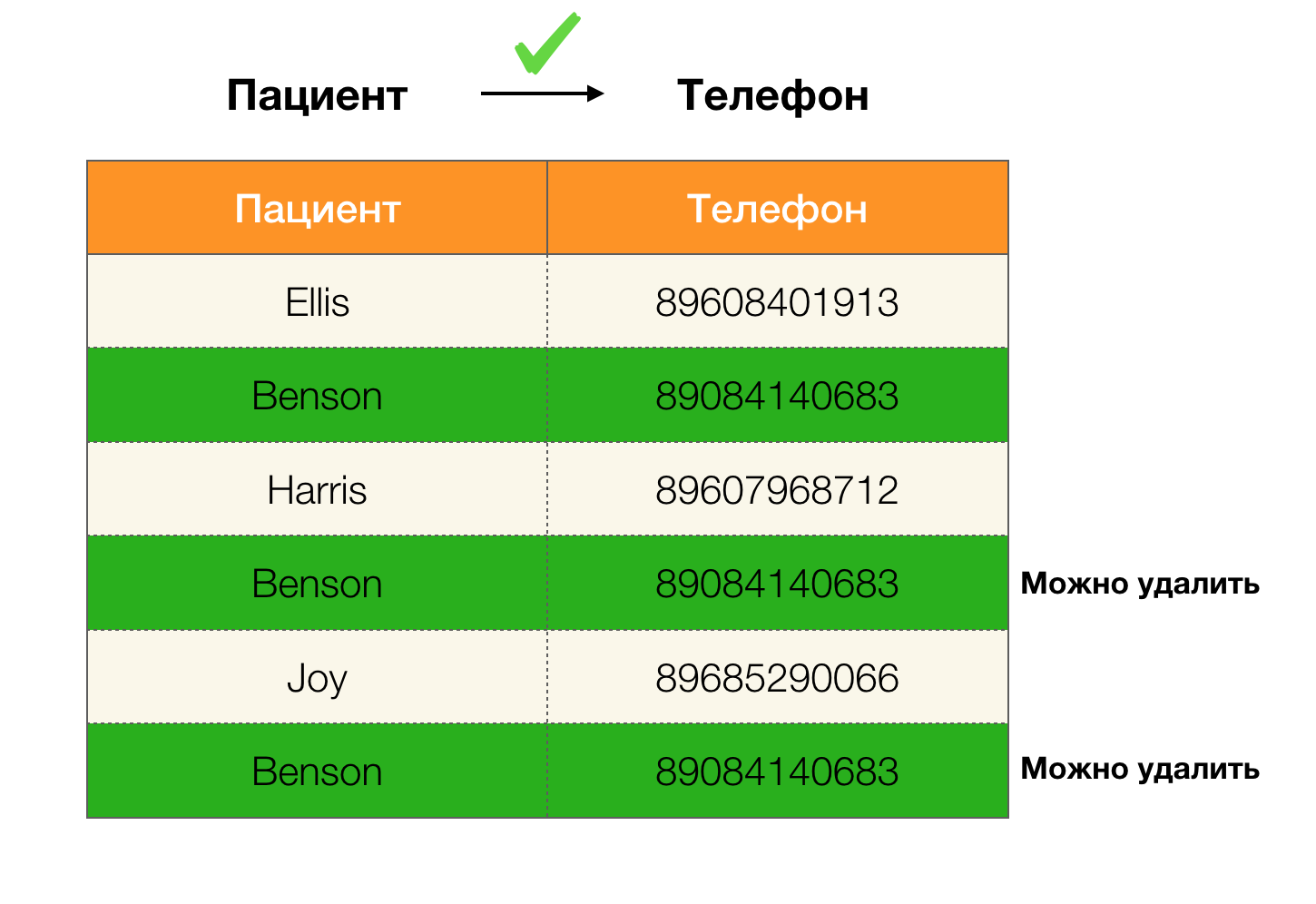
उदाहरण के लिए, हमारे पास एक तालिका और संघीय कानूनों का एक सेट है जिसे निष्पादित किया जाना चाहिए। इस मामले में डेटा की सफाई में डेटा को बदलना शामिल है ताकि संघीय कानून सही हों। उसी समय, संशोधनों की संख्या न्यूनतम होनी चाहिए (इस प्रक्रिया के लिए, ऐसे एल्गोरिदम हैं जिन पर हम इस लेख में ध्यान केंद्रित नहीं करेंगे)। निम्नलिखित ऐसे डेटा रूपांतरण का एक उदाहरण है। बाईं ओर प्रारंभिक संबंध है, जिसमें, जाहिर है, आवश्यक संघीय कानून पूरे नहीं होते हैं (संघीय कानून के उल्लंघन का एक उदाहरण लाल रंग में हाइलाइट किया गया है)। दाईं ओर एक अद्यतन संबंध है जिसमें हरे रंग की कोशिकाएं परिवर्तित मान दिखाती हैं। इस तरह की प्रक्रिया के बाद, आवश्यक निर्भरताएं आयोजित होने लगीं।



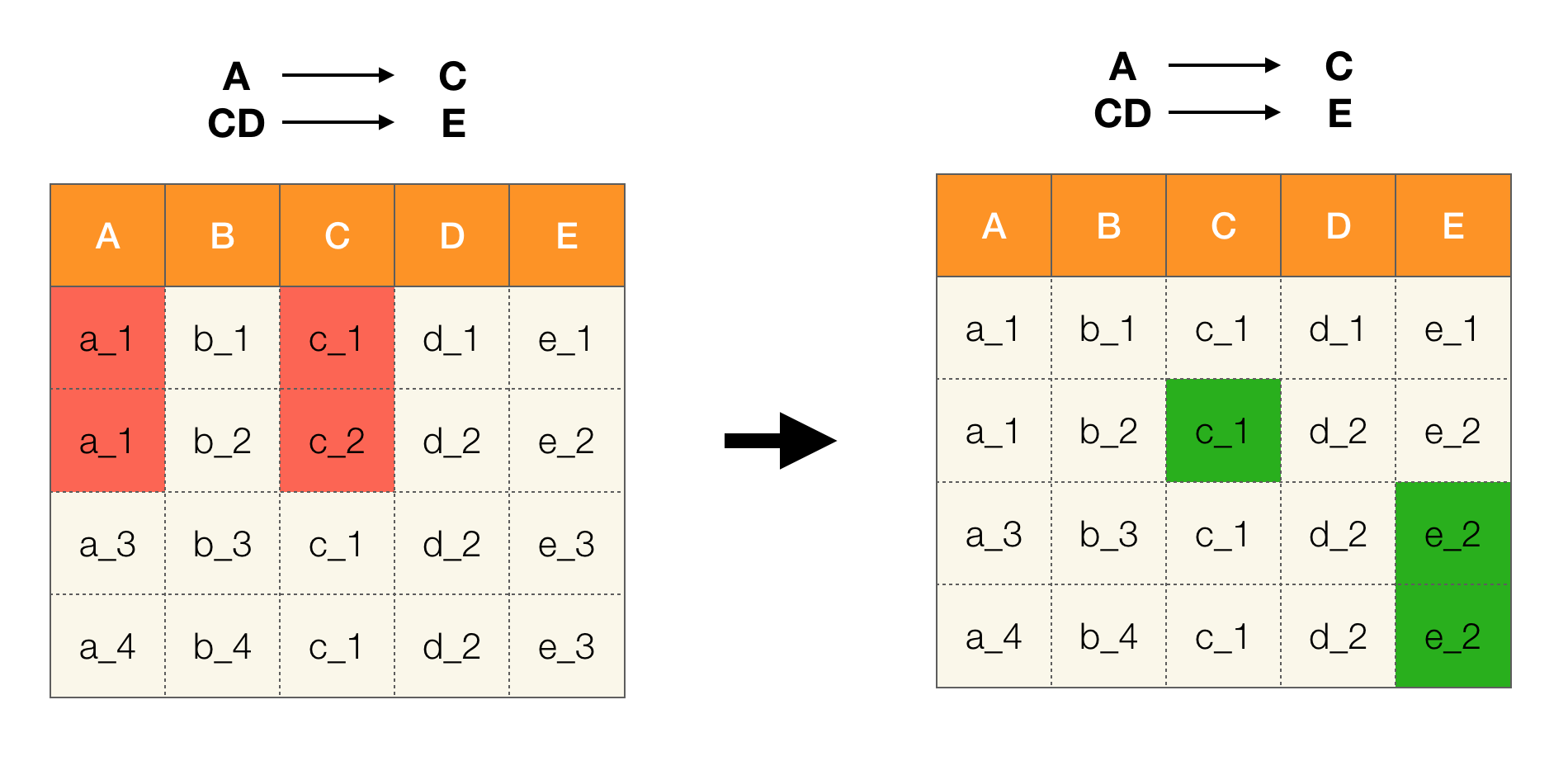
एक अन्य लोकप्रिय अनुप्रयोग डेटाबेस डिज़ाइन है। यहां यह सामान्य रूपों और सामान्यीकरण के बारे में याद रखने योग्य है। सामान्यीकरण एक निश्चित आवश्यकताओं के अनुरूप संबंध बनाने की प्रक्रिया है, जिनमें से प्रत्येक को सामान्य रूप से अपने तरीके से निर्धारित किया जाता है। हम विभिन्न सामान्य रूपों की आवश्यकताओं को नहीं लिखेंगे (यह शुरुआती लोगों के लिए डीबी पाठ्यक्रम पर किसी भी पुस्तक में किया गया है), लेकिन हम केवल यह ध्यान देते हैं कि उनमें से प्रत्येक अपने तरीके से कार्यात्मक निर्भरता की अवधारणा का उपयोग करता है। दरअसल, संघीय कानून स्वाभाविक रूप से अखंडता बाधाएं हैं जो एक डेटाबेस को डिजाइन करते समय ध्यान में रखी जाती हैं (इस कार्य के संदर्भ में, संघीय कानून कभी-कभी सुपरकी कहलाते हैं)।

नीचे दिए गए चित्र में चार सामान्य रूपों के लिए उनके आवेदन पर विचार करें। याद रखें कि सामान्य बॉयस-कोडड फॉर्म तीसरे रूप की तुलना में अधिक कठोर है, लेकिन चौथे की तुलना में कम कठोर है। हम अभी तक उत्तरार्द्ध पर विचार नहीं करते हैं, क्योंकि इसके सूत्रीकरण के लिए बहु-मूल्यवान निर्भरता की समझ की आवश्यकता होती है, जो इस लेख में हमारे लिए कोई दिलचस्पी नहीं है।






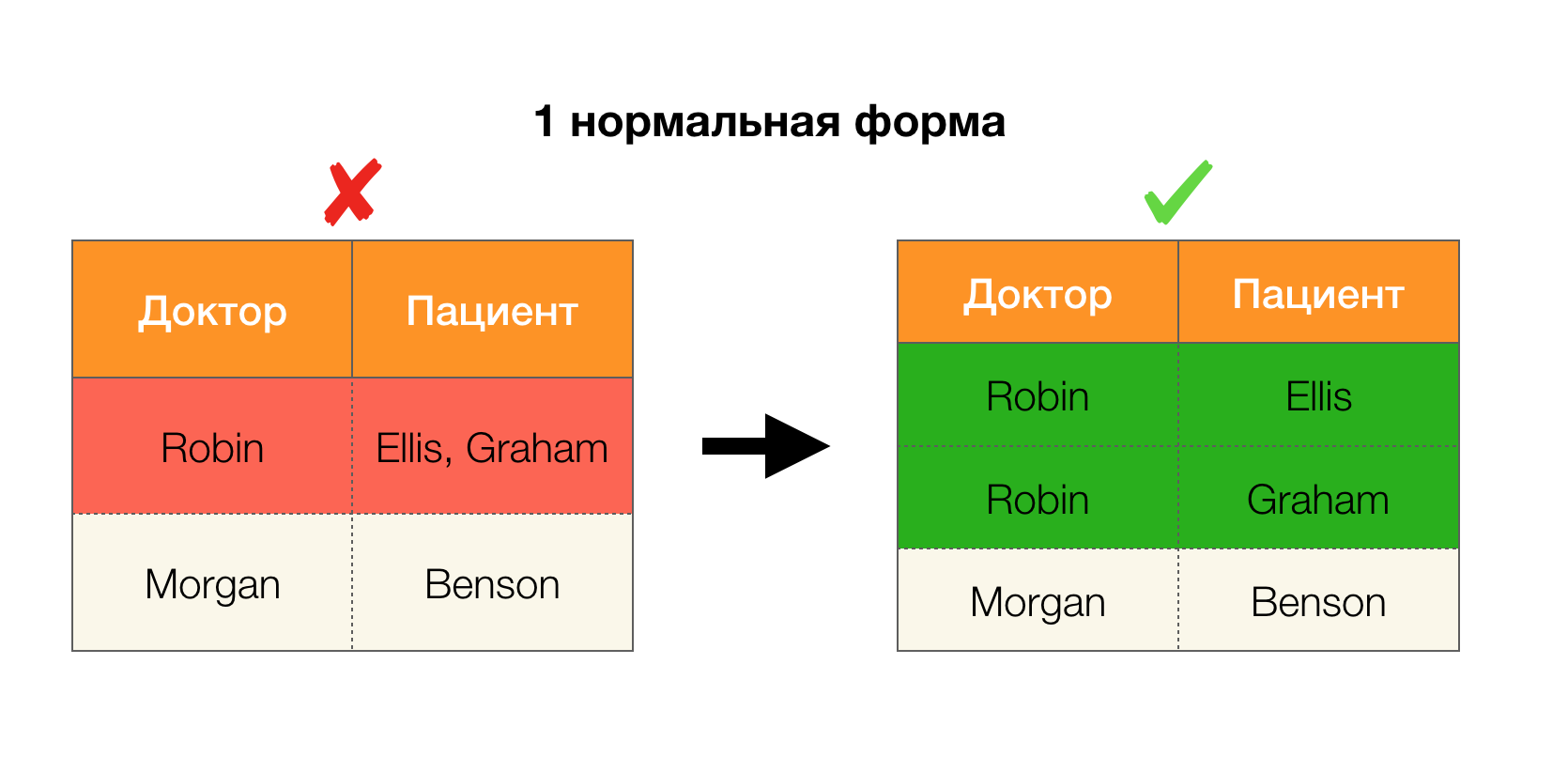
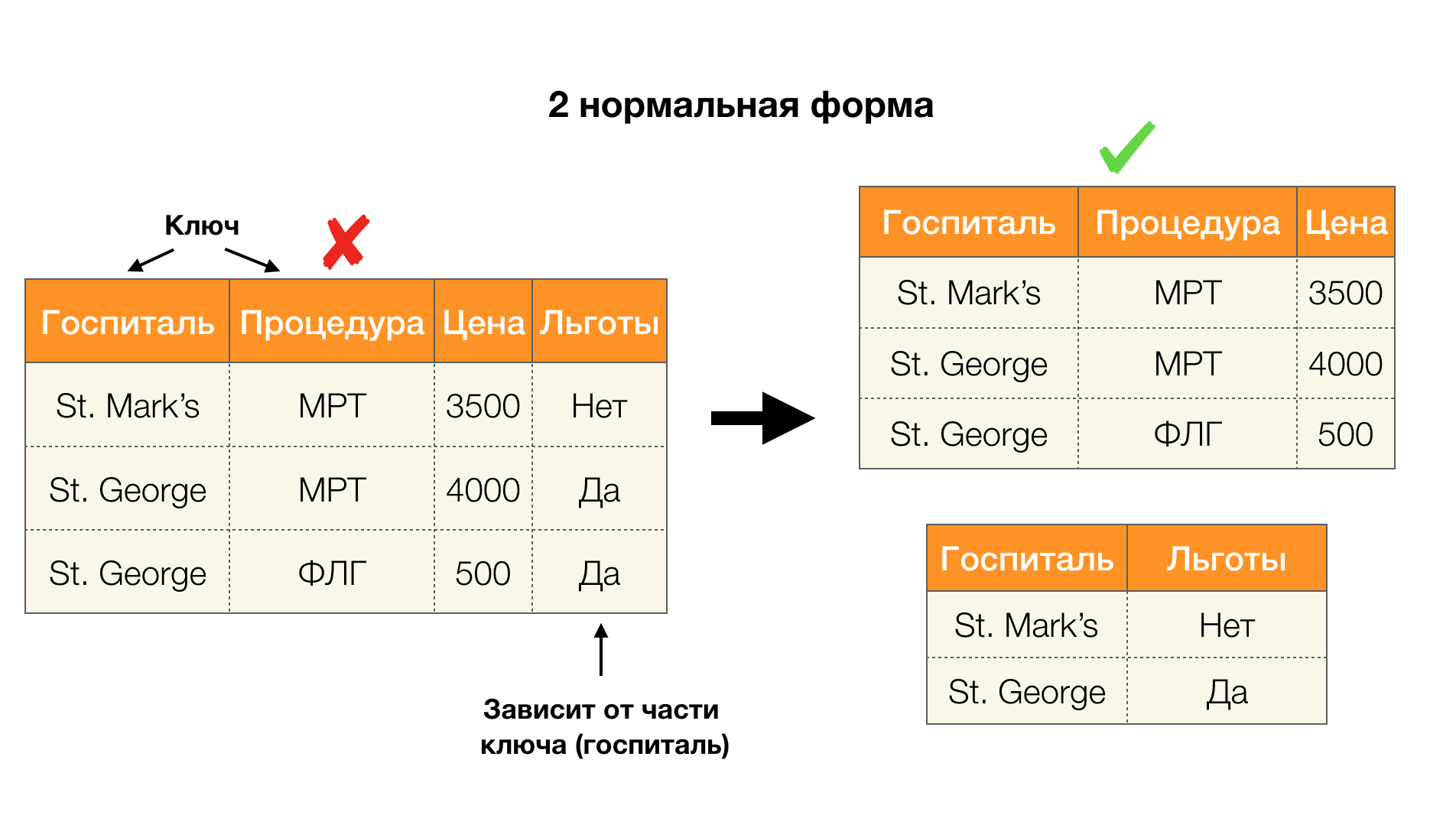
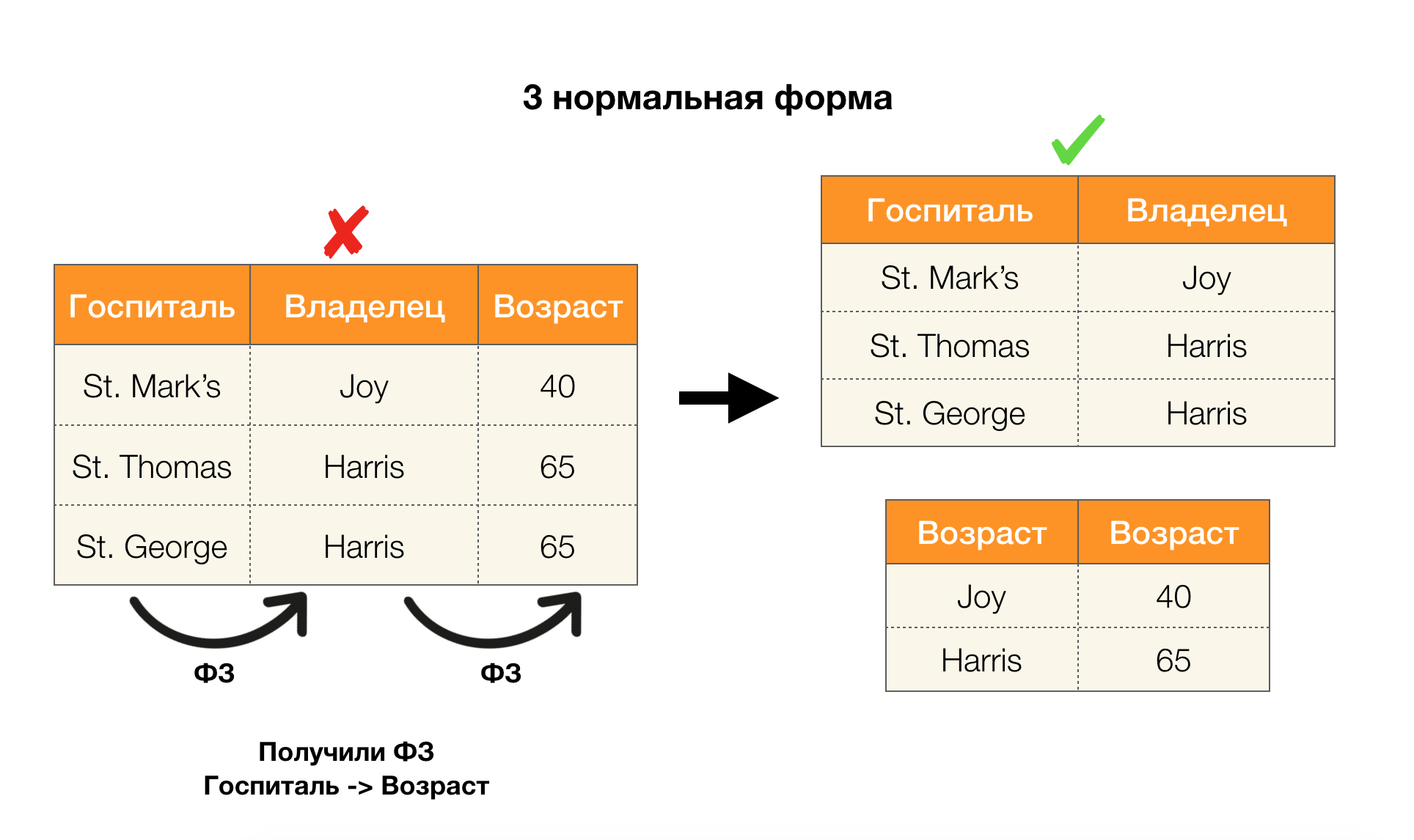
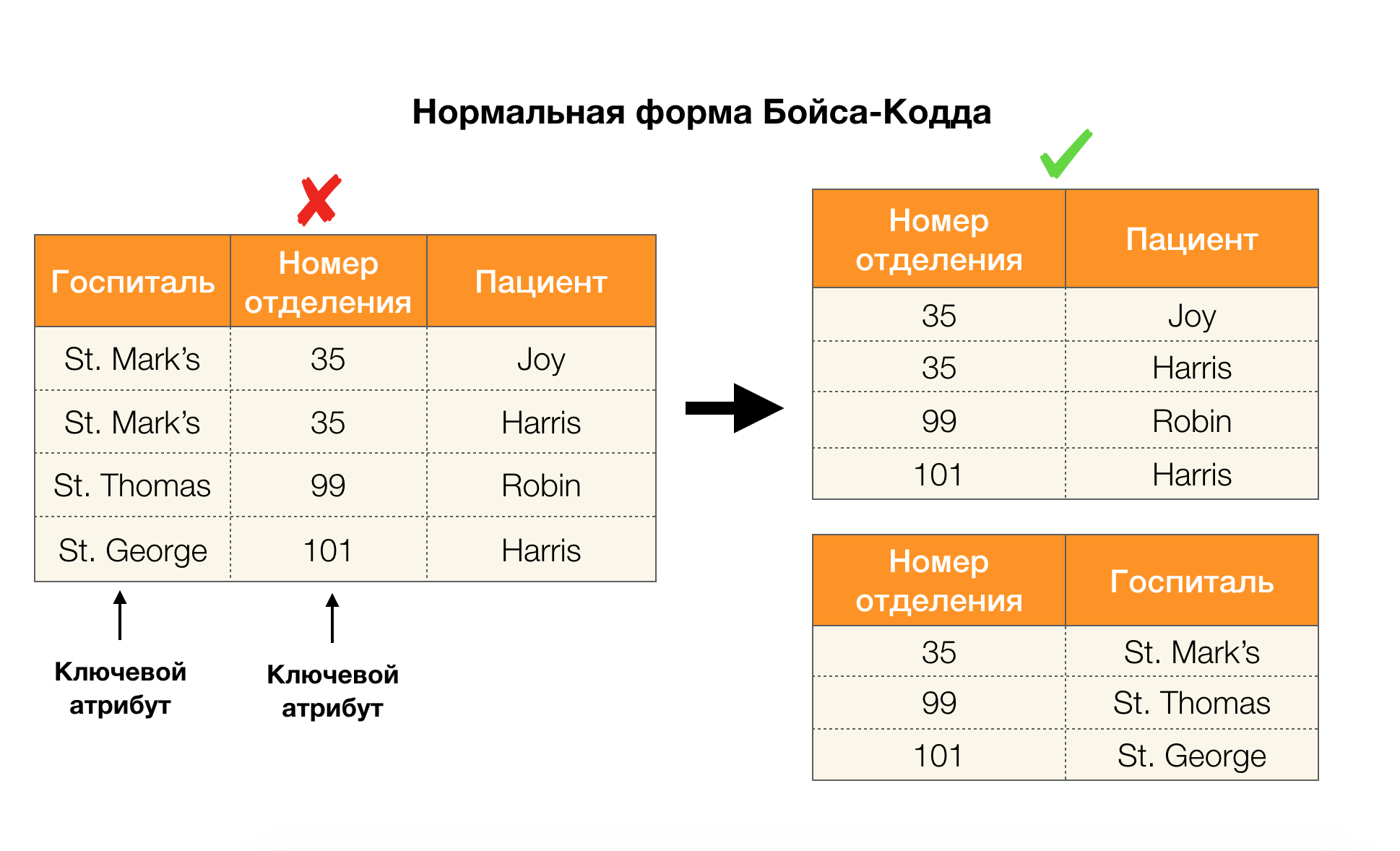
एक अन्य क्षेत्र जिसमें निर्भरता ने अपना आवेदन पाया है, ऐसे कार्यों में फ़ीचर स्पेस के आयाम को कम करना है जैसे कि एक भोले बेसेसियन क्लासिफायर का निर्माण, महत्वपूर्ण विशेषताओं की पहचान, और प्रतिगमन मॉडल का पुनर्समीक्षाकरण। मूल लेखों में, इस समस्या को निरर्थक विशेषताओं और सुविधा प्रासंगिकता [5, 6] का निर्धारण कहा जाता है, और इसे डेटाबेस अवधारणाओं के सक्रिय उपयोग के साथ हल किया जाता है। ऐसे कार्यों के आगमन के साथ, हम कह सकते हैं कि आज समाधान के लिए एक अनुरोध है जो डेटाबेस, विश्लेषण और उपरोक्त अनुकूलन समस्याओं के संयोजन को एक उपकरण [7, 8, 9] में लागू करने की अनुमति देता है।

डेटा सेट में संघीय कानून की खोज करने के लिए कई एल्गोरिदम (आधुनिक और बहुत दोनों नहीं) हैं। ऐसे एल्गोरिदम को तीन चरणों में विभाजित किया जा सकता है:

• बीजीय अक्षांशों के ट्रैवर्सल का उपयोग कर एल्गोरिदम (जाली ट्रैवर्सल एल्गोरिदम)
• संगत मानों की खोज के आधार पर एल्गोरिदम (Di-erence- और सहमत-सेट एल्गोरिदम)
• पेयरवाइज़ कम्पेरिजन एल्गोरिथम (डिपेंडेंसी इंडक्शन एल्गोरिदम)
  

प्रत्येक प्रकार के एल्गोरिथ्म का संक्षिप्त विवरण नीचे तालिका में प्रस्तुत किया गया है:


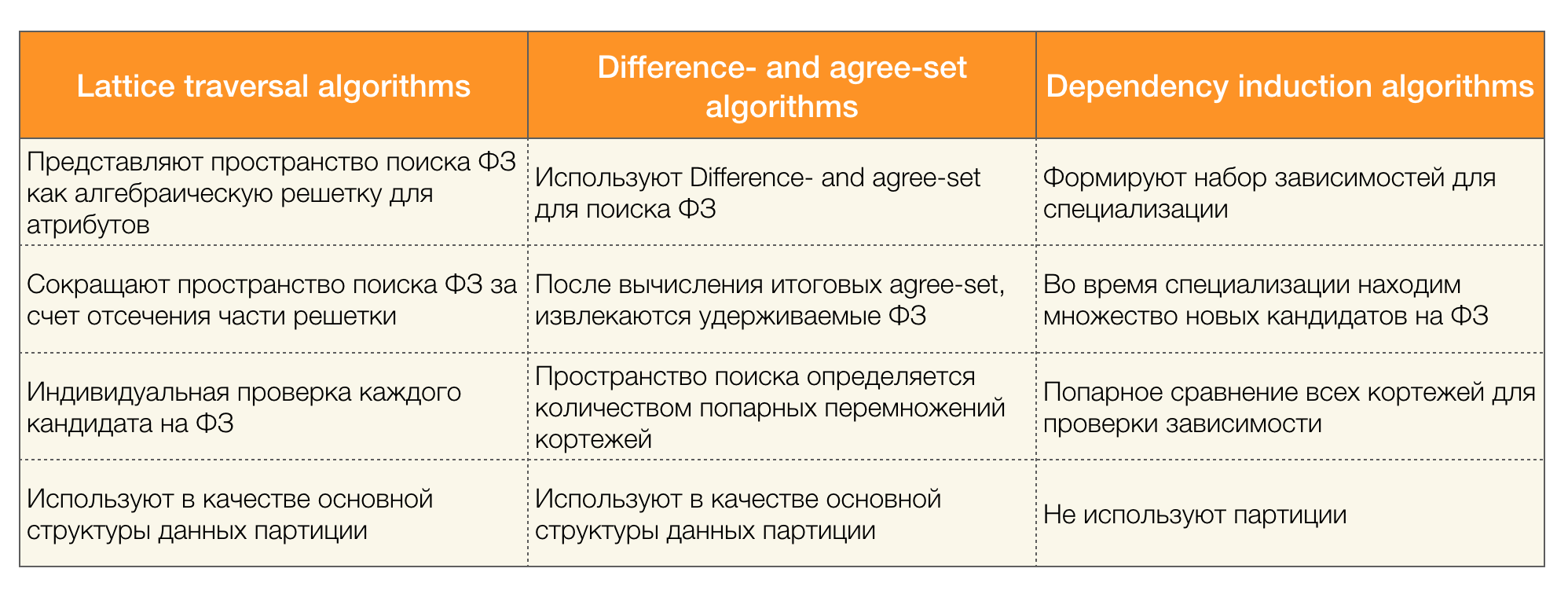
इस वर्गीकरण के बारे में अधिक जानकारी [4] पढ़ी जा सकती है। नीचे प्रत्येक प्रकार के एल्गोरिदम के उदाहरण दिए गए हैं:





वर्तमान में, नए एल्गोरिदम दिखाई दे रहे हैं जो कार्यात्मक आश्रितों की खोज के लिए कई दृष्टिकोणों को एक साथ जोड़ते हैं। ऐसे एल्गोरिदम के उदाहरण Pyro [2] और HyFD [3] हैं। इस श्रृंखला के निम्नलिखित लेखों में उनके काम का विश्लेषण अपेक्षित है। इस लेख में, हम केवल उन मूल अवधारणाओं और लेम्मा का विश्लेषण करेंगे जो निर्भरता का पता लगाने के लिए तकनीकों को समझने के लिए आवश्यक हैं।

आइए एक सरल एक - di ff erence- और सहमत-सेट के साथ शुरू करें, जिसका उपयोग दूसरे प्रकार के एल्गोरिदम में किया जाता है। डि up एरेन्स-सेट टुपल्स का एक सेट है जो मूल्यों में मेल नहीं खाता है, और सहमत-सेट, इसके विपरीत, टुपल्स है जो मूल्य में मेल खाते हैं। यह ध्यान दिया जाना चाहिए कि इस मामले में हम केवल निर्भरता के बाईं ओर पर विचार करते हैं।

इसके अलावा एक महत्वपूर्ण अवधारणा जो ऊपर से मिली थी, बीजीय जाली है। चूंकि कई आधुनिक एल्गोरिदम इस अवधारणा पर काम करते हैं, इसलिए हमें यह पता लगाने की आवश्यकता है कि यह क्या है।

एक जाली की अवधारणा को पेश करने के लिए, आंशिक रूप से ऑर्डर किए गए सेट (या आंशिक रूप से ऑर्डर किए गए सेट, शॉर्ट - पॉसेट के लिए) को परिभाषित करना आवश्यक है।

परिभाषा 2. यह कहा जाता है कि सेट एस को आंशिक रूप से द्विआधारी संबंध द्वारा आदेश दिया जाता है any यदि किसी भी, बी, सी following एस के लिए निम्नलिखित गुण संतुष्ट हैं:

1. रिफ्लेक्सिटी, यानी ivity ए
2. एंटीसिममेट्री, अर्थात्, यदि b बी और बी then ए, तो ए = बी
3. ट्रांज़िटिविटी, यानी ⩽ b और b follows c के लिए यह इस प्रकार है कि that c
   

इस तरह के संबंध को (गैर-सख्त) आंशिक आदेश का संबंध कहा जाता है, और सेट को आंशिक रूप से आदेशित सेट कहा जाता है। औपचारिक संकेतन: ,S, ⟨।

आंशिक रूप से ऑर्डर किए गए सेट के सबसे सरल उदाहरण के रूप में, हम ऑर्डर के सामान्य संबंध के साथ सभी प्राकृतिक संख्याओं एन का सेट ले सकते हैं। यह सत्यापित करना आसान है कि सभी आवश्यक स्वयंसिद्ध संतुष्ट हैं।

अधिक सार्थक उदाहरण। समावेशन संबंध the द्वारा आदेशित सभी उप-समूहों {1, 2, 3} के सेट पर विचार करें। वास्तव में, यह संबंध आंशिक आदेश की सभी शर्तों को पूरा करता है; इसलिए, {P ({1, 2, 3}), ly आंशिक रूप से आदेशित सेट है। नीचे दिया गया आंकड़ा इस सेट की संरचना को दर्शाता है: यदि एक तत्व से आप तीर के साथ दूसरे तत्व तक चल सकते हैं, तो वे क्रम के संबंध में हैं।



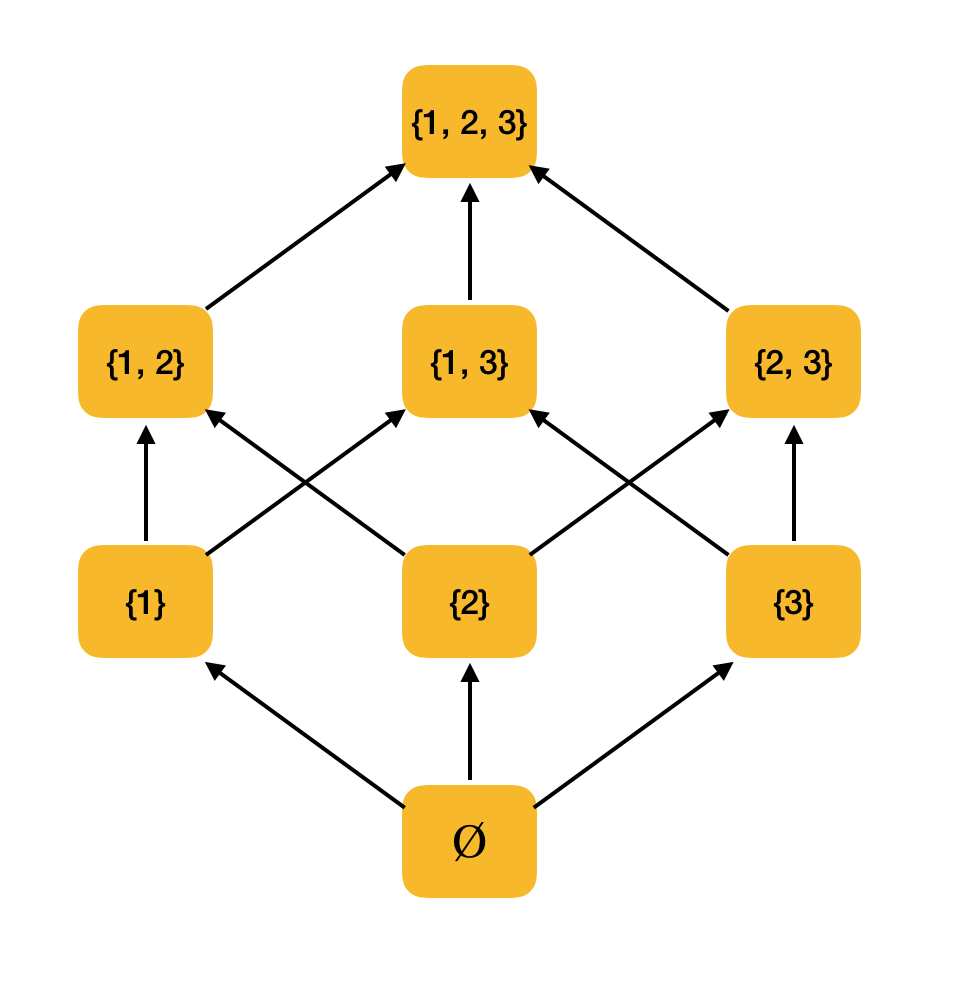
हमें गणित के क्षेत्र से दो और सरल परिभाषाओं की आवश्यकता होगी - सर्वोच्च और अनंत।

परिभाषा 3. orderedS, Let एक आंशिक रूप से आदेशित सेट हो, A upper S. A की ऊपरी सीमा एक तत्व u element S है जो कि ∈x: A: x। U है। यू को ए के सभी ऊपरी सीमा के सेट होने दें। यदि यू में सबसे छोटा तत्व है, तो इसे सुपरमम कहा जाता है और सुपर ए द्वारा निरूपित किया जाता है।

इसी तरह, एक सटीक निचले बाउंड की अवधारणा पेश की जाती है।

परिभाषा 4. orderedS, Let एक आंशिक रूप से आदेशित सेट हो, A lower S. A की निचली सीमा एक तत्व l element S है जो कि ⟨x: A: l। X है। L को A के सभी निचले सीमाओं का सेट माना जाता है। यदि L के पास सबसे बड़ा तत्व है, तो इसे एक infimum कहा जाता है और A द्वारा अस्वीकार कर दिया जाता है।

एक उदाहरण के रूप में, ऊपर दिए गए आंशिक रूप से दिए गए सेट (P ({1, 2, 3}) पर विचार करें, और इसमें सर्वोच्च और अनंत खोजें:



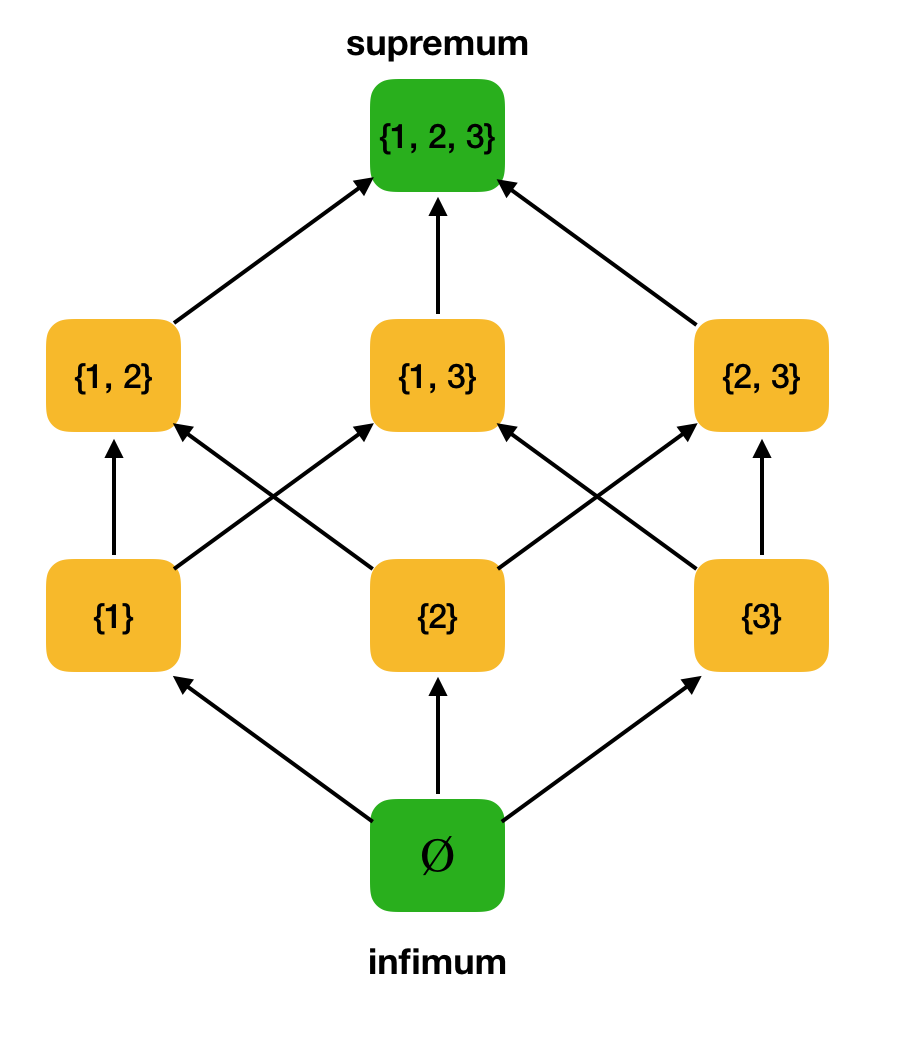
अब हम एक बीजीय जाली की परिभाषा तैयार कर सकते हैं।

परिभाषा 5. आज्ञा दें 5.P, Let आंशिक रूप से आदेशित सेट हो, जैसे कि प्रत्येक दो-तत्व वाले उपसमूह में ऊपरी और निचले सीमाएं हों। तब P को बीजगणितीय जाली कहा जाता है। इसके अलावा, sup {x, y} को x and y, और inf {x, y} - के रूप में x। Y लिखा जाता है।

हम सत्यापित करते हैं कि हमारा कार्य उदाहरण (P ({1, 2, 3}), example एक जाली है। वास्तव में, किसी के लिए, बी (पी ({1, 2, 3}), a∨b = a ,b, और a∩b = a∧b। उदाहरण के लिए, सेट्स {1, 2} और {1, 3} पर विचार करें और उनके असीम और सर्वोच्च को खोजें। यदि हम उन्हें पार करते हैं, तो हम सेट {1} प्राप्त करते हैं, जो कि सबसे अनुकूल होगा। हमें उनके संघ द्वारा सर्वोच्चता मिलती है - {1, 2, 3}।

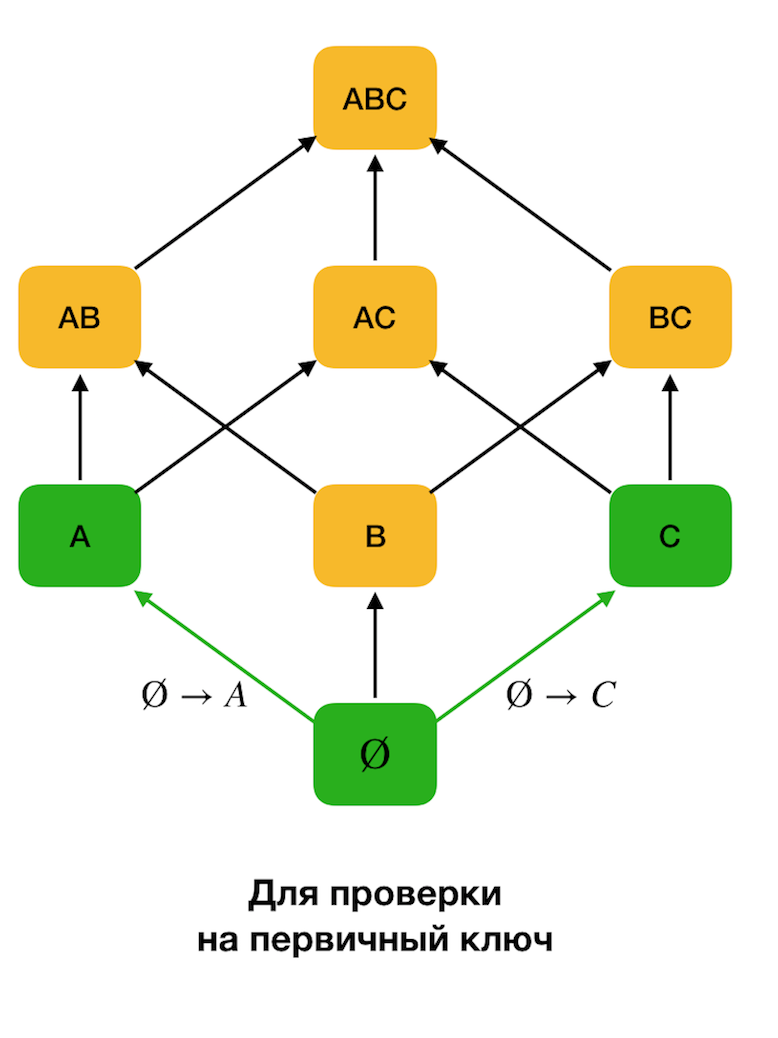
एफडी डिटेक्शन एल्गोरिदम में, खोज स्थान को अक्सर एक जाली के रूप में दर्शाया जाता है, जहां एक तत्व के सेट (खोज जाली का पहला स्तर पढ़ें, जहां निर्भरता के बाएं हिस्से में एक विशेषता होती है) मूल संबंध के प्रत्येक गुण हैं।
शुरुआत में, फार्म attribute → एकल विशेषता की निर्भरता पर विचार किया जाता है। यह चरण आपको यह निर्धारित करने की अनुमति देता है कि कौन सी विशेषताएँ प्राथमिक कुंजी हैं (ऐसी विशेषताओं के लिए कोई निर्धारक नहीं हैं, और इसलिए बाईं ओर खाली है)। इसके अलावा, इस तरह के एल्गोरिदम जाली को ऊपर ले जाते हैं। यह ध्यान देने योग्य है कि जाली को सभी को बायपास नहीं किया जा सकता है, अर्थात, यदि बाएं भाग का वांछित अधिकतम आकार इनपुट को प्रेषित किया जाता है, तो एल्गोरिथ्म इस आकार के साथ स्तर से परे नहीं जाएगा।

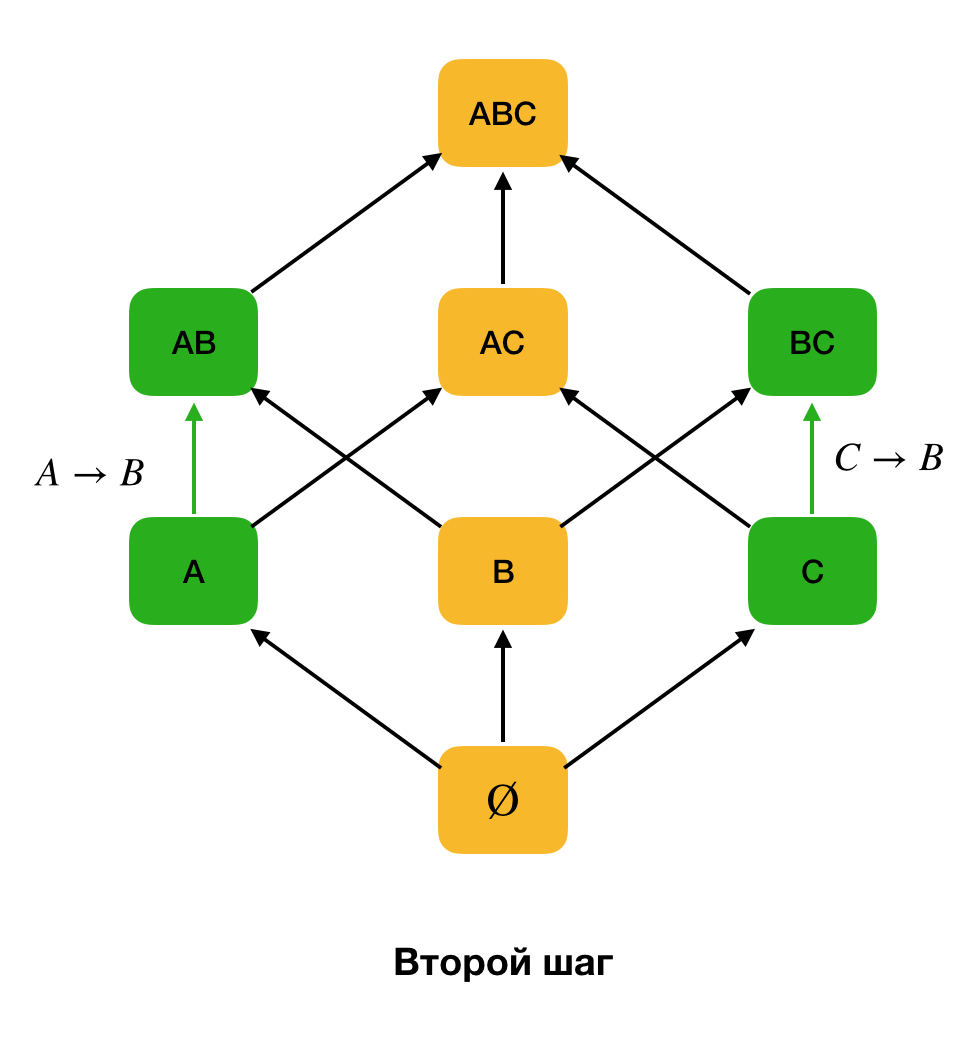
नीचे दिया गया आंकड़ा दिखाता है कि आप संघीय कानून के लिए खोज समस्या में बीजीय जाली का उपयोग कैसे कर सकते हैं। यहाँ, प्रत्येक किनारे ( X, XY ) एक निर्भरता X → Y का प्रतिनिधित्व करता है । उदाहरण के लिए, हम पहले स्तर से गुजरे हैं और हम जानते हैं कि निर्भरता ए → बी रखी गई है (हम इसे ए और बी के बीच हरे रंग के कनेक्शन द्वारा प्रदर्शित करेंगे)। इसलिए, जब हम जाली को ऊपर की ओर बढ़ाते हैं, तो हम निर्भरता ए, सी → बी की जांच नहीं कर सकते, क्योंकि यह अब न्यूनतम नहीं होगी। इसी तरह, अगर हम निर्भरता C → B रखते हैं तो हम इसका परीक्षण नहीं करेंगे।




इसके अलावा, एक नियम के रूप में, सभी आधुनिक एफजेड खोज एल्गोरिदम इस तरह के डेटा संरचना का उपयोग विभाजन के रूप में करते हैं (मूल स्रोत में विभाजन [1])। विभाजन की औपचारिक परिभाषा इस प्रकार है:

परिभाषा 6. चलो X be R संबंध आर के लिए विशेषताओं का समूह है। एक क्लस्टर r से tuples के सूचकांकों का एक सेट है जिसका X के लिए समान मान है, अर्थात, c (t = = {i। Ti [X] = t [X]} | विभाजन समूहों का एक समूह है, जो इकाई लंबाई के समूहों को छोड़कर है:

$$

$$\ pi (X): = \ {c (t) | t \ r r \ wedge में | c (t) | > 1 \}$$

सरल शब्दों में, विशेषता X के लिए विभाजन सूचियों का एक समूह है, जहां प्रत्येक सूची में X के लिए समान मानों के साथ पंक्ति संख्याएं होती हैं। आधुनिक साहित्य में, विभाजन का प्रतिनिधित्व करने वाली संरचना को स्थिति सूची सूचकांक (पीएलआई) कहा जाता है। पीएलआई संपीड़न के लिए यूनिट की लंबाई वाले समूहों को बाहर रखा गया है क्योंकि वे एक अद्वितीय मूल्य के साथ केवल एक रिकॉर्ड संख्या वाले क्लस्टर हैं जो हमेशा सेट करना आसान होगा।

एक उदाहरण पर विचार करें। आइए मरीजों के साथ उसी तालिका में वापस जाएं और रोगी और पॉल कॉलम के लिए विभाजन बनाएं (बाईं ओर एक नया कॉलम दिखाई दिया, जिसमें तालिका की पंक्ति संख्याएं चिह्नित हैं):





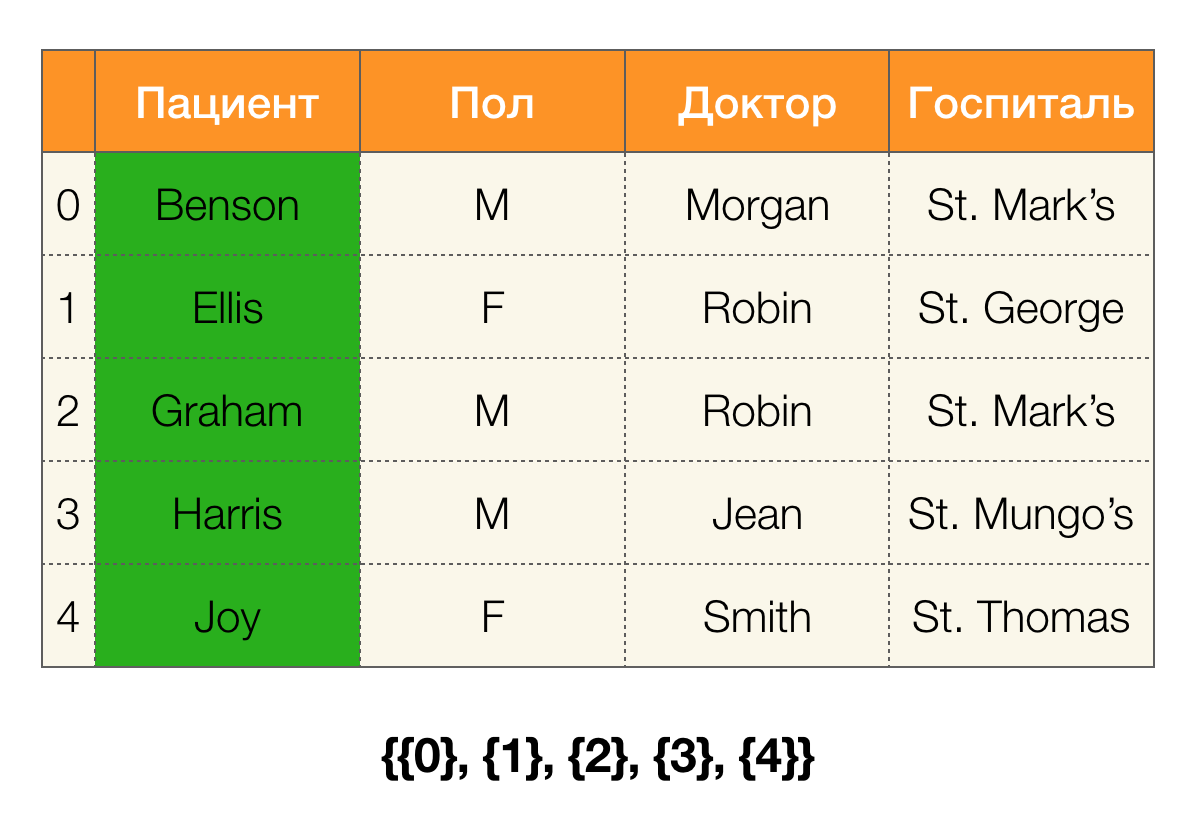
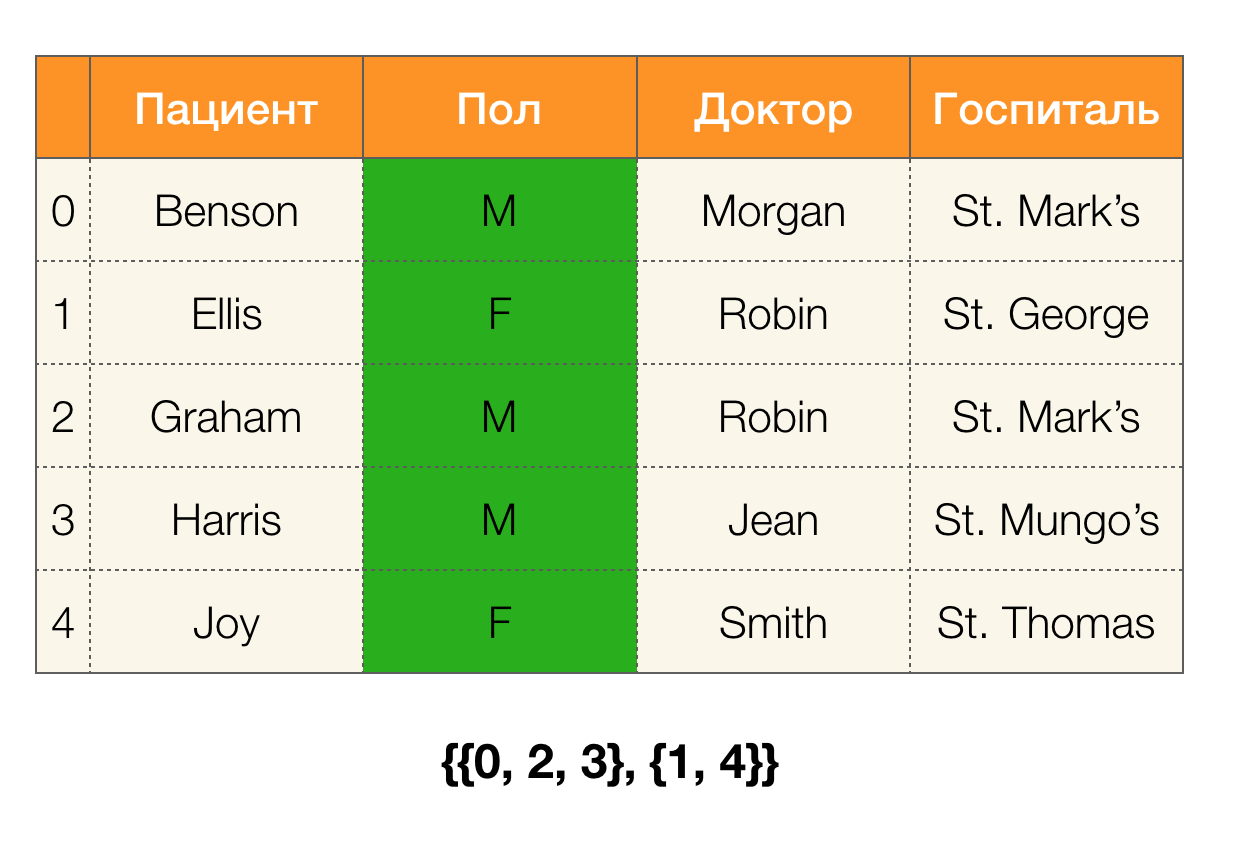
इसके अलावा, परिभाषा के अनुसार, रोगी स्तंभ के लिए विभाजन वास्तव में खाली होगा, क्योंकि एकल समूहों को विभाजन से बाहर रखा गया है।

विभाजन कई विशेषताओं द्वारा प्राप्त किया जा सकता है। और इसके लिए दो तरीके हैं: तालिका के माध्यम से, सभी आवश्यक विशेषताओं के अनुसार एक बार में एक विभाजन का निर्माण करें, या विशेषताओं के सबसेट के साथ विभाजन को पार करने के संचालन का उपयोग करके इसका निर्माण करें। FZ खोज एल्गोरिदम दूसरे विकल्प का उपयोग करते हैं।

सरल शब्दों में, उदाहरण के लिए, एबीसी कॉलम द्वारा एक विभाजन प्राप्त करने के लिए, आप एसी और बी (या किसी अन्य उपसमूह के सेट) के लिए विभाजन ले सकते हैं और उन्हें एक दूसरे के साथ जोड़ सकते हैं। दो विभाजनों के प्रतिच्छेदन का संचालन दोनों विभाजनों के लिए सबसे बड़ी लंबाई के समूहों की पहचान करता है।

आइए एक उदाहरण देखें:





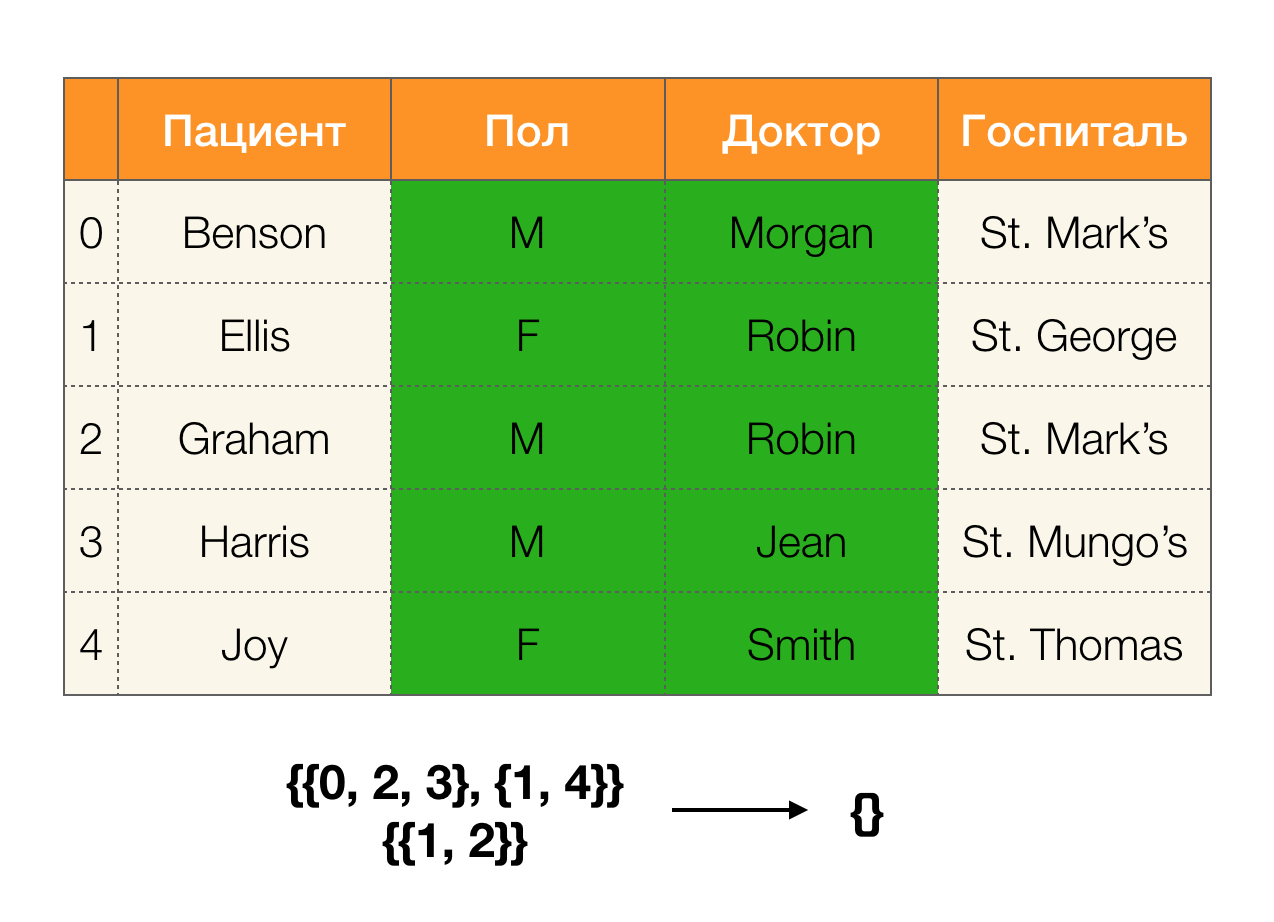
पहले मामले में, हमें एक खाली विभाजन प्राप्त हुआ। यदि आप तालिका को करीब से देखते हैं, तो वास्तव में, दो विशेषताओं के समान मूल्य नहीं हैं। यदि हम तालिका (दाईं ओर मामला) को थोड़ा संशोधित करते हैं, तो हमें पहले से ही एक गैर-रिक्त चौराहा मिलता है। उसी समय, लाइनों 1 और 2 में वास्तव में पॉल और डॉक्टर की विशेषताओं के समान मूल्य शामिल हैं।

अगला, हमें विभाजन आकार के रूप में ऐसी अवधारणा की आवश्यकता है। औपचारिक रूप से:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

सीधे शब्दों में, विभाजन आकार विभाजन में शामिल समूहों की संख्या है (याद रखें कि विभाजन में व्यक्तिगत क्लस्टर शामिल नहीं हैं!):





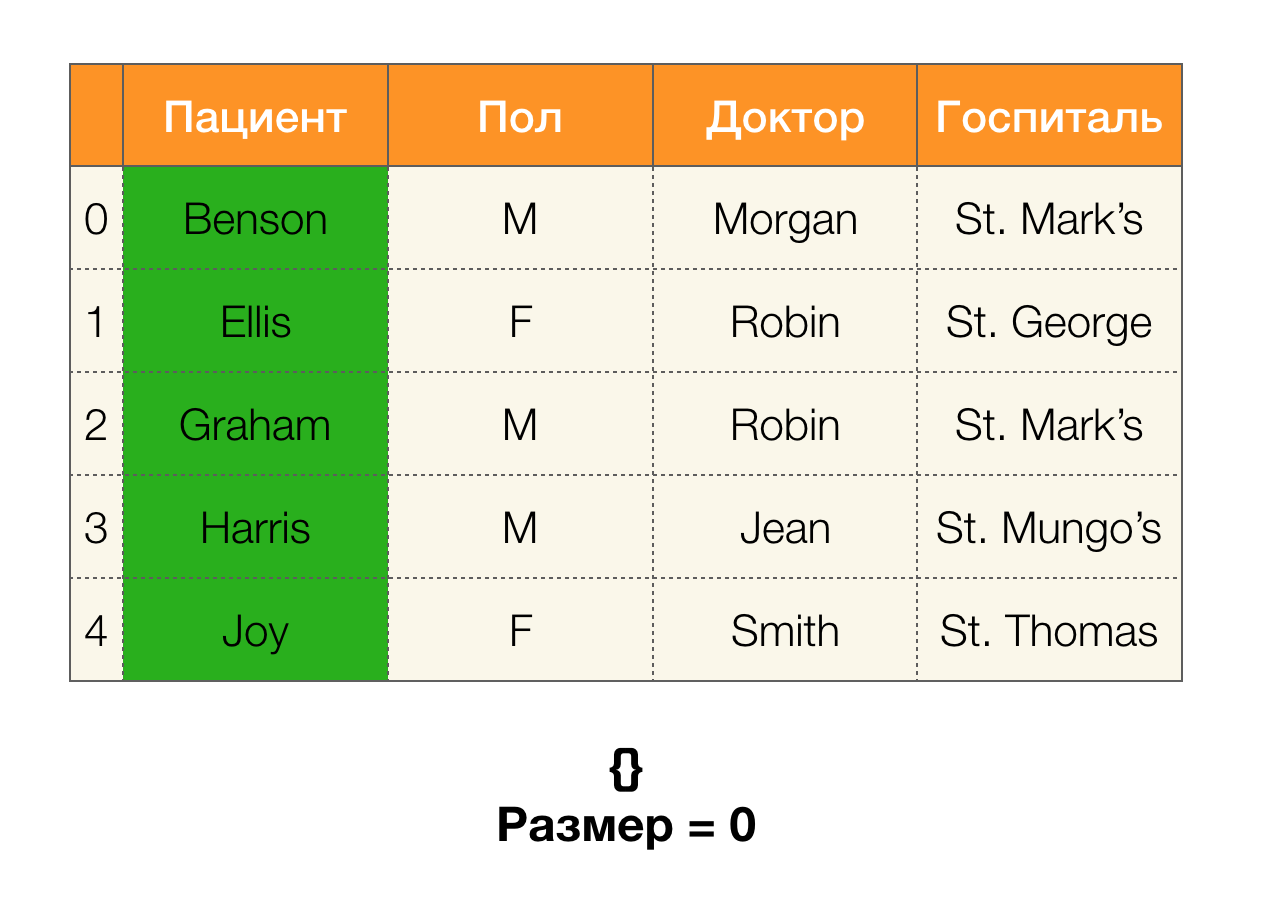
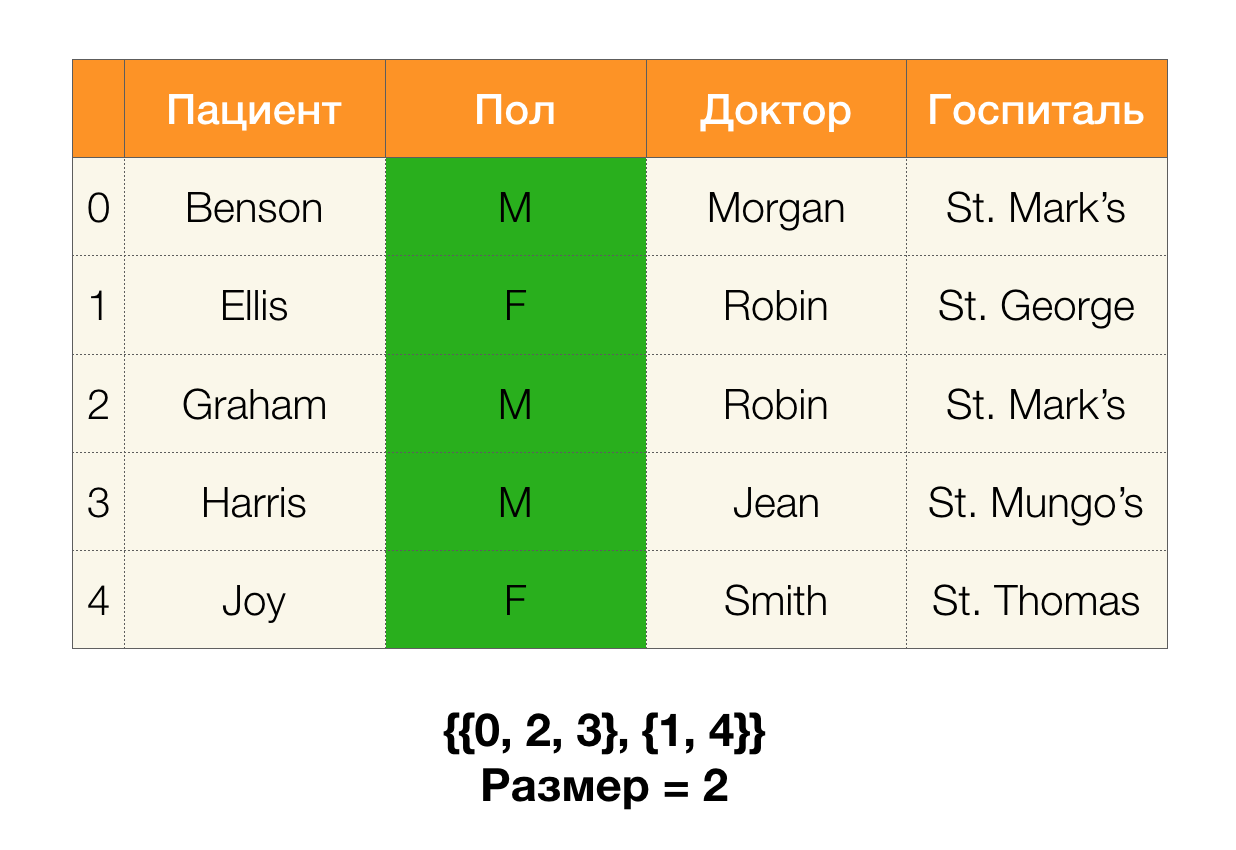
अब हम उन प्रमुख लीमाओं में से एक को परिभाषित कर सकते हैं, जो दिए गए विभाजन से हमें यह स्थापित करने की अनुमति मिलती है कि निर्भरता है या नहीं:

लेम्मा 1 । निर्भरता ए, बी → सी अगर और केवल अगर आयोजित की जाती है

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

लेम्मा के अनुसार, यह निर्धारित करने के लिए कि क्या एक निर्भरता आयोजित की जाती है, चार चरण करना आवश्यक है:

1. निर्भरता के बाईं ओर विभाजन की गणना करें
2. निर्भरता के दाईं ओर विभाजन की गणना करें
3. पहले और दूसरे चरण के उत्पाद की गणना करें
   
4. पहले और तीसरे चरण में प्राप्त विभाजन के आकार की तुलना करें
   

निम्नलिखित जाँच करने का एक उदाहरण है कि क्या निर्भरता इस लेम्मा द्वारा बनाए रखी गई है:






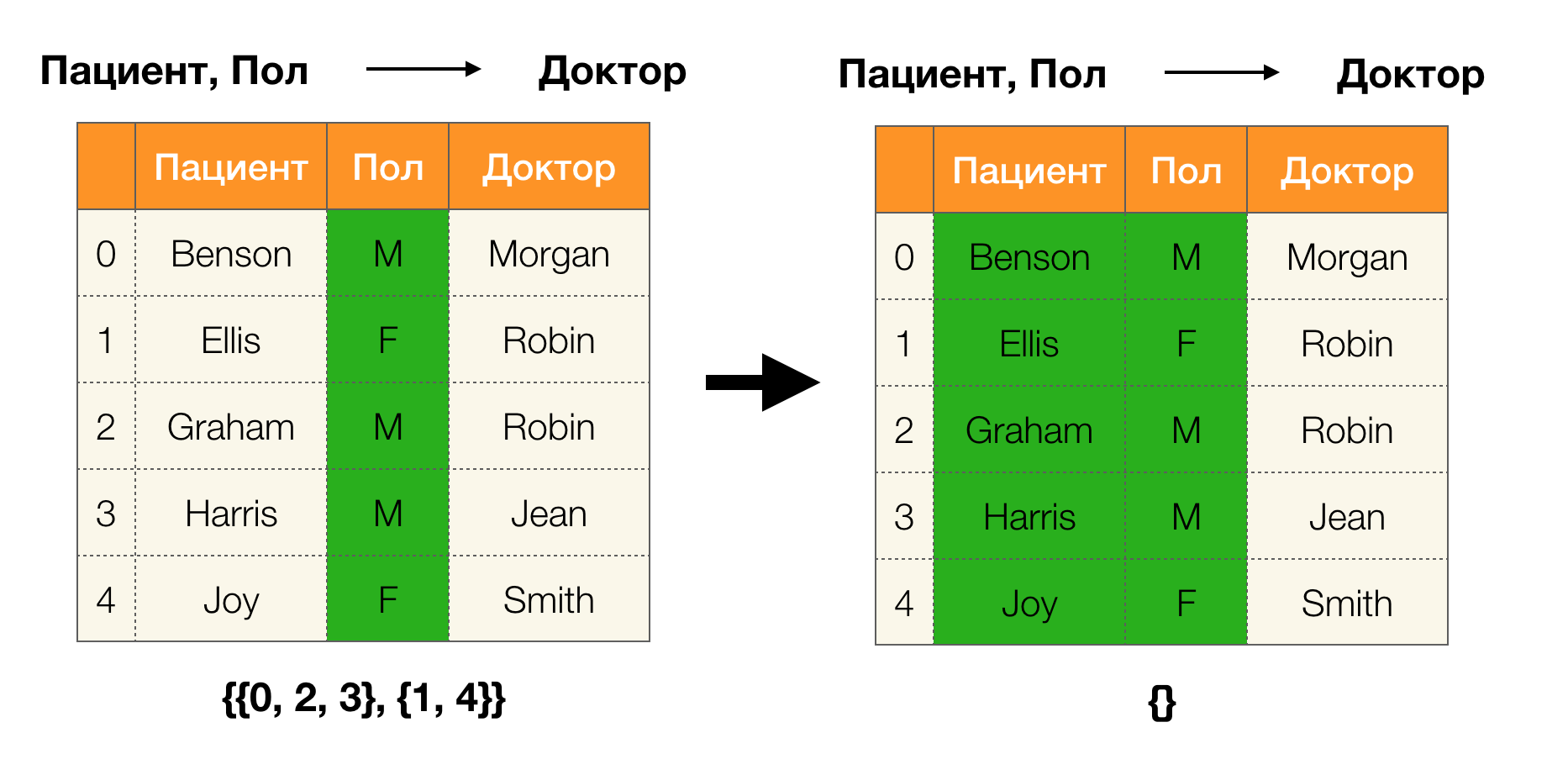
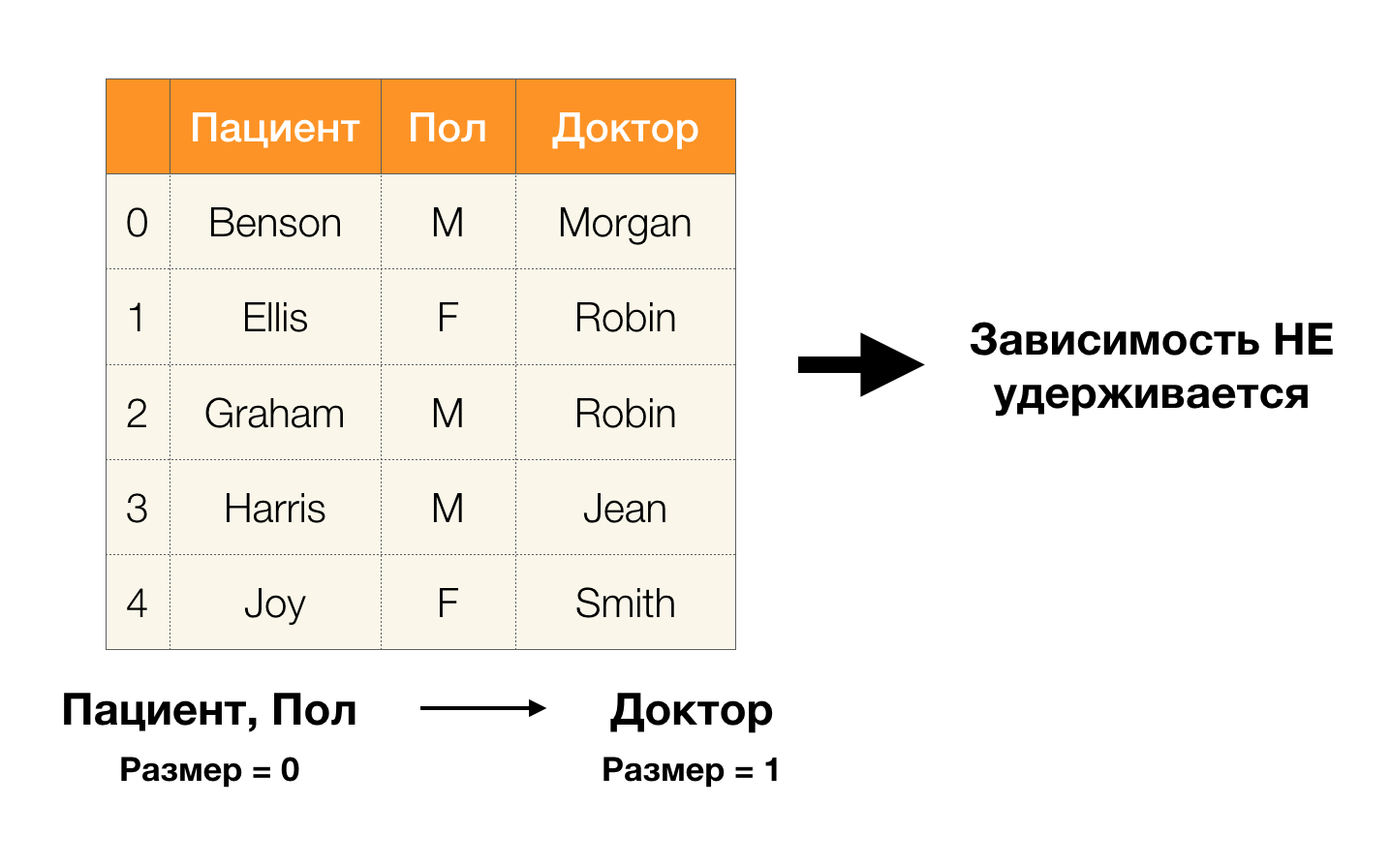
इस लेख में, हमने कार्यात्मक निर्भरता, अनुमानित कार्यात्मक निर्भरता जैसी अवधारणाओं की जांच की, जहां उनका उपयोग किया जाता है, साथ ही साथ संघीय कानून के लिए खोज एल्गोरिदम मौजूद हैं। हमने संघीय कानून की खोज के लिए आधुनिक एल्गोरिदम में सक्रिय रूप से उपयोग किए जाने वाले बुनियादी, लेकिन महत्वपूर्ण अवधारणाओं की विस्तार से जांच की।

साहित्य के संदर्भ:

1. हुहताला वाई। एट अल। TANE: कार्यात्मक और अनुमानित निर्भरता की खोज के लिए एक कुशल एल्गोरिथ्म // कंप्यूटर जर्नल। - 1999. - टी। 42. - नहीं। 2. - एस। 100-111।
2. क्रूस एस।, नौमन एफ। अनुमानित निर्भरता की कुशल खोज // वीएलडीबी बंदोबस्ती की कार्यवाही। - 2018. - टी। 11. - नहीं। 7. - एस। 759-772।
3. Papenbrock T., Naumann F. A hybrid approach to functional dependency discovery //Proceedings of the 2016 International Conference on Management of Data. – ACM, 2016. – . 821-833.
4. Papenbrock T. et al. Functional dependency discovery: An experimental evaluation of seven algorithms //Proceedings of the VLDB Endowment. – 2015. – . 8. – №. 10. – . 1082-1093.
5. Kumar A. et al. To join or not to join?: Thinking twice about joins before feature selection //Proceedings of the 2016 International Conference on Management of Data. – ACM, 2016. – . 19-34.
6. Abo Khamis M. et al. In-database learning with sparse tensors //Proceedings of the 37th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems. – ACM, 2018. – . 325-340.
7. Hellerstein JM et al. The MADlib analytics library: or MAD skills, the SQL //Proceedings of the VLDB Endowment. – 2012. – . 5. – №. 12. – . 1700-1711.
8. Qin C., Rusu F. Speculative approximations for terascale distributed gradient descent optimization //Proceedings of the Fourth Workshop on Data analytics in the Cloud. – ACM, 2015. – . 1.
9. मेंग एक्स। एट अल। Mllib: Apache स्पार्क में मशीन सीखना // मशीन लर्निंग रिसर्च जर्नल। - 2016. - टी। 17. - नहीं। १ .-- एस। १२३५-१२४१

लेख के लेखक: एनस्तासिया बिरिलो , जेटब्रेन्स रिसर्च के शोधकर्ता , सीएस सेंटर के छात्र और निकिता बोबरोव , जेटब्रेन रिसर्च के शोधकर्ता