सरल रैखिक प्रतिगमन के समीकरण को हल करें

लेख एक सरल (जोड़ीदार) प्रतिगमन रेखा के गणितीय समीकरण को निर्धारित करने के लिए कई तरीकों पर चर्चा करता है।

यहां चर्चा किए गए समीकरण को हल करने के सभी तरीके कम से कम वर्ग विधि पर आधारित हैं। हम निम्न तरीकों का उल्लेख करते हैं:

• विश्लेषणात्मक समाधान
• धीरे-धीरे उतरना
• स्टोचैस्टिक ग्रेडिएंट डिसेंट

सीधी रेखा के समीकरण को हल करने के लिए प्रत्येक विधि के लिए, लेख विभिन्न कार्यों का वर्णन करता है जो मुख्य रूप से उन में विभाजित होते हैं जो बिना NumPy लाइब्रेरी का उपयोग किए बिना लिखे जाते हैं और जो गणना के लिए NumPy का उपयोग करते हैं। माना जाता है कि NumPy का कुशल उपयोग कंप्यूटिंग लागत को कम करने के लिए किया जाता है।

इस आलेख के सभी कोड अजगर 2.7 में Jupyter नोटबुक का उपयोग करके लिखे गए हैं। स्रोत कोड और नमूना डेटा फ़ाइल github पर पोस्ट की गई है

लेख दोनों शुरुआती और उन लोगों पर केंद्रित है जो पहले से ही बहुत कम हैं, जिन्होंने कृत्रिम बुद्धिमत्ता - मशीन सीखने में बहुत व्यापक खंड के अध्ययन में महारत हासिल की है।

सामग्री का वर्णन करने के लिए, हम एक बहुत ही सरल उदाहरण का उपयोग करते हैं।

उदाहरण की स्थिति

हमारे पास पाँच मान हैं जो X पर Y की निर्भरता को दर्शाते हैं (तालिका संख्या 1):

तालिका संख्या 1 "उदाहरण की शर्तें"



हम मान लेते हैं कि मूल्य $$$x_i$ वर्ष का महीना है, और $$$y_i$ - इस महीने में राजस्व। दूसरे शब्दों में, राजस्व वर्ष के महीने पर निर्भर करता है, और $$$x_i$ - एकमात्र संकेत जिस पर राजस्व निर्भर करता है।

एक उदाहरण ऐसा है, इसलिए वर्ष के महीने में राजस्व की सशर्त निर्भरता के संदर्भ में, और मूल्यों की संख्या के संदर्भ में - उनमें से बहुत कम हैं। हालांकि, यह सरलीकरण अनुमति देगा कि उंगलियों पर क्या समझाया जाता है, हमेशा आसानी से नहीं, शुरुआती द्वारा अवशोषित सामग्री। और संख्याओं की सादगी भी महत्वपूर्ण श्रम लागतों के बिना, जो लोग कागज पर उदाहरण को हल करना चाहते हैं, की अनुमति देगा।

मान लें कि उदाहरण में दर्शाई गई निर्भरता, फार्म के एक साधारण (युग्म) प्रतिगमन रेखा के गणितीय समीकरण द्वारा काफी अच्छी तरह से अनुमानित की जा सकती है:

$$

$$वाई = ए + बीएक्स$$

जहाँ $$$x$ - यह वह महीना है जिसमें राजस्व प्राप्त हुआ था, $$$य$ - महीने के अनुसार राजस्व, $$$एक$ और $$$ब$ - अनुमानित रेखा का प्रतिगमन गुणांक।

ध्यान दें कि गुणांक $$$ब$ अक्सर अनुमानित रेखा का ढलान या ढाल कहा जाता है; उस राशि का प्रतिनिधित्व करता है जिसके द्वारा बदलना है $$$य$ जब बदल रहा हो $$$x$ ।

जाहिर है, उदाहरण में हमारा काम समीकरण में ऐसे गुणांक का चयन करना है $$$एक$ और $$$ब$ जिसके लिए सही उत्तरों से हमारे अनुमानित मासिक राजस्व का विचलन, अर्थात्। नमूने में प्रस्तुत मूल्य न्यूनतम होंगे।

कम से कम वर्ग विधि

कम से कम वर्गों की विधि के अनुसार, विचलन की गणना इसे चुकता करके की जानी चाहिए। इस तरह की तकनीक विचलन के आपसी पुनर्भुगतान से बचती है, अगर उनके विपरीत संकेत हैं। उदाहरण के लिए, यदि एक मामले में, विचलन +5 (प्लस पांच) है, और अन्य -5 (शून्य से पांच) में है, तो विचलन का योग पारस्परिक रूप से चुकाया जाएगा और 0 (शून्य) होगा। आप विचलन को दरकिनार नहीं कर सकते हैं, लेकिन मॉड्यूल संपत्ति का उपयोग करें और फिर सभी विचलन सकारात्मक होंगे और हम में जमा होंगे। हम इस बिंदु पर विस्तार से ध्यान केंद्रित नहीं करेंगे, लेकिन केवल यह इंगित करते हैं कि गणना की सुविधा के लिए, यह विचलन को चौकोर करने के लिए प्रथागत है।

यह वह सूत्र है जिसकी सहायता से हम छोटे विचलन (त्रुटियों) के सबसे छोटे योग का निर्धारण करते हैं:

$$

$$ERR (x) = \ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ sum \ limit_ {i = 1} ^ n (f (x_i) -y_i) 2 \ rightarrow मिनट$$

जहाँ $$$f (x_i) = a + bx_i$ सही उत्तरों को अनुमानित करने का एक कार्य है (यानी, हमारे द्वारा गणना की गई आय),

$$$y_i$ - ये सही उत्तर हैं (नमूने में दिया गया राजस्व),

$$$मैं$ नमूना सूचकांक (उस महीने की संख्या जिसमें विचलन निर्धारित होता है)

हम फ़ंक्शन को अलग करते हैं, आंशिक अंतर समीकरणों को परिभाषित करते हैं, और विश्लेषणात्मक समाधान के लिए आगे बढ़ने के लिए तैयार हैं। लेकिन पहले, आइए इस बात पर एक छोटा सा विषयांतर करें कि भेदभाव क्या है और व्युत्पन्न के ज्यामितीय अर्थ को याद करें।

भेदभाव

भेदभाव एक फ़ंक्शन के व्युत्पन्न को खोजने का ऑपरेशन है।

व्युत्पन्न क्या है? एक फ़ंक्शन का व्युत्पन्न एक फ़ंक्शन के परिवर्तन की दर को दर्शाता है और इसकी दिशा को इंगित करता है। यदि किसी दिए गए बिंदु पर व्युत्पन्न सकारात्मक है, तो फ़ंक्शन बढ़ता है, अन्यथा, फ़ंक्शन कम हो जाता है। और व्युत्पन्न मोडुलो का मूल्य जितना बड़ा होता है, फ़ंक्शन के मूल्यों के परिवर्तन की दर उतनी ही अधिक होती है, साथ ही साथ फ़ंक्शन के ग्राफ का कोण भी स्थिर होता है।

उदाहरण के लिए, कार्टेशियन कोऑर्डिनेट सिस्टम की शर्तों के तहत, बिंदु M पर व्युत्पन्न का मान (0,0) के बराबर है जिसका अर्थ है कि किसी दिए गए बिंदु पर, जब मूल्य को स्थानांतरित किया जाता है $$$x$ मनमानी इकाई, मूल्य का अधिकार $$$य$ 25 पारंपरिक इकाइयों की वृद्धि। ग्राफ पर, यह ऊंचाई के एक काफी खड़ी कोण जैसा दिखता है $$$य$ एक दिए गए बिंदु से।

एक और उदाहरण। -0.1 के व्युत्पन्न मूल्य का मतलब है कि जब ऑफसेट $$$x$ प्रति पारंपरिक इकाई, मूल्य $$$य$ केवल 0.1 पारंपरिक इकाई द्वारा घट जाती है। उसी समय, फ़ंक्शन ग्राफ पर, हम नीचे मुश्किल से ध्यान देने योग्य झुकाव का निरीक्षण कर सकते हैं। पहाड़ के साथ एक सादृश्य आकर्षित करते हुए, हम पिछले उदाहरण के विपरीत, पहाड़ से कोमल ढलान पर बहुत धीरे-धीरे उतरते हुए प्रतीत होते हैं, जहाँ हमें बहुत खड़ी चोटियाँ लेनी थीं :)

इस प्रकार, फ़ंक्शन को विभेदित करने के बाद $$$ERR (x) = \ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ गुणांकों द्वारा $$$एक$ और $$$ब$ , हम पहले आदेश के आंशिक व्युत्पन्न के समीकरणों को परिभाषित करते हैं। समीकरणों को परिभाषित करने के बाद, हम दो समीकरणों की एक प्रणाली प्राप्त करते हैं, यह तय करते हुए कि हम गुणांक के ऐसे मूल्यों को चुन सकते हैं $$$एक$ और $$$ब$ जिस पर दिए गए बिंदुओं पर संबंधित व्युत्पत्ति के मान बहुत, बहुत कम मूल्य से बदलते हैं, और विश्लेषणात्मक समाधान के मामले में वे बिल्कुल भी नहीं बदलते हैं। दूसरे शब्दों में, पाया गया गुणांक में त्रुटि समारोह एक न्यूनतम तक पहुंच जाता है, क्योंकि इन बिंदुओं पर आंशिक डेरिवेटिव का मान शून्य होगा।

इसलिए, भेदभाव के नियमों के अनुसार, गुणांक के संबंध में 1 आदेश के आंशिक व्युत्पन्न का समीकरण $$$एक$ फार्म लेंगे:

$$

$$2na + 2b \ _ \ _ सीमाएं {{i = 1} ^ nx_i - 2 \ योग \ सीमाएं {{1 = 1} ^ ny_i = 2 (na + b \ sum \ limit_ {i = 1} ^ nn_i - \ योग \ _] {i = 1} ^ ny_i)$$

1 आदेश आंशिक व्युत्पन्न समीकरण के संबंध में $$$ब$ फार्म लेंगे:

$$

$$2a \ sum \ limit_ {i = 1} ^ nx_i + 2b \ sum \ limit_ {i = 1} ^ nx ^ 2_i - 2 \ sum \ limit_ {i = 1} ^ nx_iy__ = 2 \ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i)$$

नतीजतन, हमें समीकरणों की एक प्रणाली मिली जिसका एक काफी सरल विश्लेषणात्मक समाधान है:

\ {{समीकरण *} शुरू
\ शुरू {मामलों}
na + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i = 0
\\
\ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i) = 0
\ अंत {मामलों}
\ अंत {समीकरण *}

समीकरण को हल करने से पहले, पूर्व लोड करें, सही लोडिंग की जांच करें और डेटा को प्रारूपित करें।

डाउनलोड करें और डेटा स्वरूपित करें

यह ध्यान दिया जाना चाहिए कि विश्लेषणात्मक समाधान के लिए, और बाद में ढाल और स्टोकेस्टिक ग्रेडिएंट वंश के लिए, हम दो भिन्नताओं में कोड का उपयोग करेंगे: NumPy लाइब्रेरी का उपयोग करना और इसका उपयोग किए बिना, हमें तदनुसार डेटा प्रारूपित करने की आवश्यकता होगी (देखें कोड)।

दृश्य

अब, हमारे बाद, सबसे पहले, डेटा डाउनलोड किया, दूसरे, हमने सही लोडिंग की जाँच की और अंत में डेटा को स्वरूपित किया, हम पहले दृश्य का संचालन करेंगे। अक्सर, इसके लिए सीबोर्न लाइब्रेरी के युग्मक विधि का उपयोग किया जाता है। हमारे उदाहरण में, सीमित संख्या के कारण, यह सीबोर्न पुस्तकालय का उपयोग करने के लिए कोई मतलब नहीं है। हम नियमित Matplotlib लाइब्रेरी का उपयोग करेंगे और केवल स्कैटरप्लॉट को देखेंगे।


अनुसूची नंबर 1 "वर्ष के महीने पर राजस्व की निर्भरता"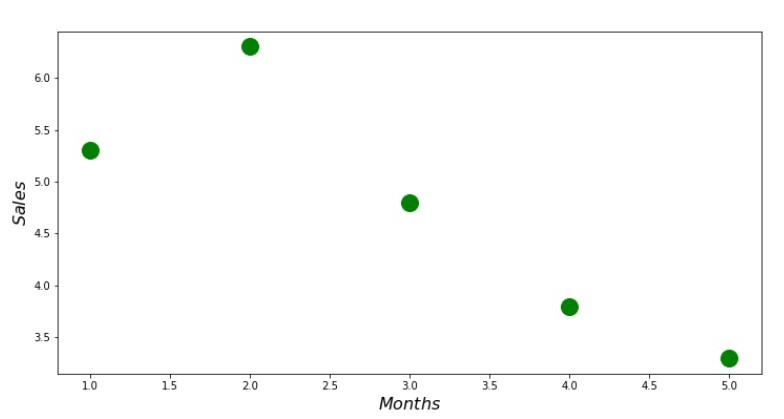

विश्लेषणात्मक समाधान

हम अजगर में सबसे आम उपकरण का उपयोग करेंगे और समीकरणों की प्रणाली को हल करेंगे:

\ {{समीकरण *} शुरू
\ शुरू {मामलों}
na + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i = 0
\\
\ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i) = 0
\ अंत {मामलों}
\ अंत {समीकरण *}

Cramer के नियम के अनुसार, हम एक सामान्य निर्धारक के साथ-साथ निर्धारक भी पाते हैं $$$एक$ और इसके द्वारा $$$ब$ , जिसके बाद, निर्धारक को विभाजित करके $$$एक$ सामान्य निर्धारक पर - हम गुणांक पाते हैं $$$एक$ इसी तरह, गुणांक पाते हैं $$$ब$ ।


यहाँ हमें क्या मिला है:



तो, गुणांक मान पाए जाते हैं, चुकता विचलन का योग निर्धारित होता है। हम पाए गए गुणांक के अनुसार बिखरने वाले हिस्टोग्राम पर एक सीधी रेखा खींचते हैं।


अनुसूची नंबर 2 "सही और अनुमानित उत्तर"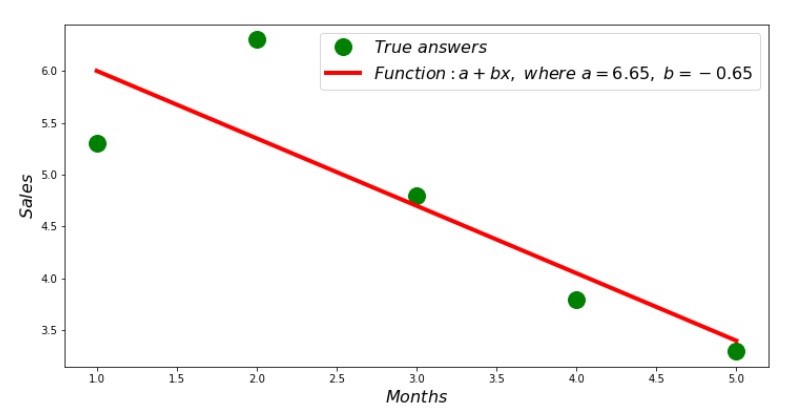



आप प्रत्येक माह के विचलन कार्यक्रम को देख सकते हैं। हमारे मामले में, हम इसमें से कोई महत्वपूर्ण व्यावहारिक मूल्य नहीं ले सकते हैं, लेकिन हम इस उत्सुकता को पूरा करेंगे कि साधारण रेखीय प्रतिगमन समीकरण कितनी अच्छी तरह से वर्ष के महीने में राजस्व की निर्भरता की विशेषता है।


अनुसूची संख्या 3 "विचलन,%"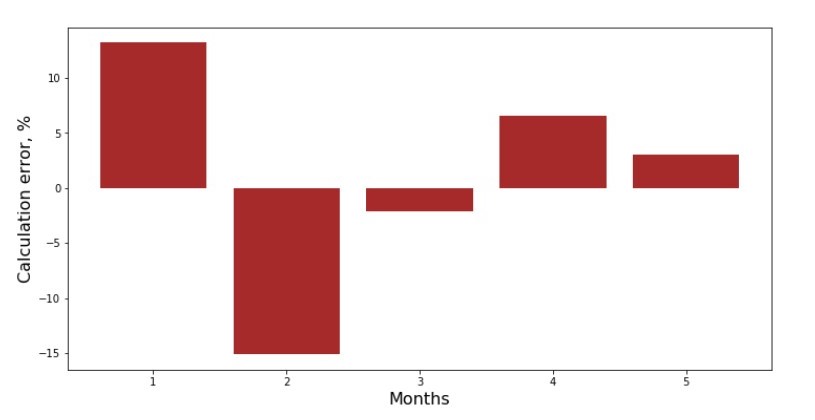



पूर्ण नहीं है, लेकिन हमने अपना कार्य पूरा कर लिया है।

हम एक फ़ंक्शन लिखते हैं, जो गुणांक निर्धारित करने के लिए है $$$एक$ और $$$ब$ NumPy लाइब्रेरी का उपयोग करता है, अधिक सटीक रूप से, हम दो फ़ंक्शन लिखेंगे: एक छद्म उलटा मैट्रिक्स का उपयोग करके (अभ्यास में अनुशंसित नहीं है, क्योंकि प्रक्रिया कम्प्यूटेशनल रूप से जटिल और अस्थिर है), दूसरा मैट्रिक्स समीकरण का उपयोग करके।


गुणांकों को निर्धारित करने में लगने वाले समय की तुलना करें $$$एक$ और $$$ब$ , प्रस्तुत 3 विधियों के अनुसार।




डेटा की एक छोटी राशि पर, एक "स्व-लिखित" फ़ंक्शन आगे आता है जो Cramer पद्धति का उपयोग करके गुणांक पाता है।

अब आप गुणांक खोजने के अन्य तरीकों पर आगे बढ़ सकते हैं $$$एक$ और $$$ब$ ।

धीरे-धीरे उतरना

सबसे पहले, आइए परिभाषित करें कि एक ढाल क्या है। एक सरल तरीके से, एक ढाल एक खंड है जो किसी फ़ंक्शन की अधिकतम वृद्धि की दिशा को इंगित करता है। एक चढ़ाई के साथ सादृश्य द्वारा, जहां ढाल दिखती है, पहाड़ की चोटी पर सबसे ऊंची चढ़ाई है। पहाड़ के उदाहरण को विकसित करते हुए, हम याद करते हैं कि वास्तव में हमें तराई में जल्द से जल्द पहुँचने के लिए सबसे कम वंश की आवश्यकता होती है, यानी न्यूनतम - वह स्थान जहाँ फ़ंक्शन नहीं बढ़ता या घटता है। इस बिंदु पर, व्युत्पन्न शून्य होगा। इसलिए, हमें एक ढाल नहीं, बल्कि एक विरोधी ढाल की आवश्यकता है। एंटी-ग्रेडिएंट को खोजने के लिए, आपको बस ग्रेडिएंट को -1 (माइनस वन) से गुणा करना होगा।

हम इस तथ्य पर ध्यान आकर्षित करते हैं कि एक फ़ंक्शन में कई मिनीमा हो सकते हैं, और नीचे प्रस्तावित एल्गोरिथ्म के अनुसार उनमें से एक में उतरते हुए, हम एक और न्यूनतम नहीं पाएंगे जो संभवतः पाए गए से कम है। आराम करो, हम खतरे में नहीं हैं! हमारे मामले में, हम अपने कार्य के बाद से एक न्यूनतम के साथ काम कर रहे हैं $$$\ _ \ _ सीमाएं {{i = 1} ^ n (a + bx_i - y_i) ^ 2$ ग्राफ पर एक साधारण परवलय है। और जैसा कि हम सभी को गणित के स्कूल पाठ्यक्रम से अच्छी तरह से पता होना चाहिए, परवलय केवल एक न्यूनतम है।

यह पता लगाने के बाद कि हमें एक ढाल की आवश्यकता क्यों है, और यह भी कि ढाल एक खंड है, यानी दिए गए निर्देशांक के साथ एक वेक्टर, जो वास्तव में समान गुणांक हैं $$$एक$ और $$$ब$ हम ढाल वंश को लागू कर सकते हैं।

शुरू करने से पहले, मैं वंश एल्गोरिथ्म के बारे में कुछ वाक्य पढ़ने का सुझाव देता हूं:

• हम छद्म यादृच्छिक तरीके से गुणांक के निर्देशांक निर्धारित करते हैं $$$एक$ और $$$ब$ । हमारे उदाहरण में, हम गुणांक को शून्य के पास निर्धारित करेंगे। यह एक सामान्य अभ्यास है, लेकिन प्रत्येक अभ्यास का अपना अभ्यास हो सकता है।
• समन्वय से $$$एक$ बिंदु पर 1 आदेश के आंशिक व्युत्पन्न के मूल्य को घटाएं $$$एक$ । इसलिए, यदि व्युत्पन्न सकारात्मक है, तो फ़ंक्शन बढ़ जाता है। इसलिए, व्युत्पन्न के मूल्य को दूर करते हुए, हम विकास की विपरीत दिशा में, यानी वंश की दिशा में आगे बढ़ेंगे। यदि व्युत्पन्न ऋणात्मक है, तो इस बिंदु पर कार्य घटता है और व्युत्पन्न के मूल्य को हटाते हुए हम वंश की ओर बढ़ते हैं।
• हम समन्वय के साथ एक समान ऑपरेशन करते हैं $$$ब$ : बिंदु पर आंशिक व्युत्पन्न के मूल्य को घटाएं $$$ब$ ।
• न्यूनतम कूदने और दूर स्थान में नहीं उड़ने के लिए, वंश की ओर कदम का आकार निर्धारित करना आवश्यक है। सामान्य तौर पर, आप गणना की लागत को कम करने के लिए वंश को सही ढंग से कैसे सेट करें और इसे कैसे बदलना है, इस पर एक संपूर्ण लेख लिख सकते हैं। लेकिन अब हमारे पास थोड़ा अलग काम है, और हम "पोकिंग" की वैज्ञानिक विधि द्वारा चरण आकार स्थापित करेंगे या, जैसा कि वे आम लोगों में कहते हैं, अनुभवजन्य रूप से।
• हम दिए गए निर्देशांक से हैं $$$एक$ और $$$ब$ डेरिवेटिव के मूल्यों को घटाकर, हम नए निर्देशांक प्राप्त करते हैं $$$एक$ और $$$ब$ । हम अगले कदम (घटाव) लेते हैं, पहले से ही गणना निर्देशांक से। और इसलिए चक्र फिर से शुरू होता है, जब तक आवश्यक अभिसरण प्राप्त नहीं होता है।

वह सब है! अब हम मारियाना ट्रेंच के सबसे गहरे कण्ठ की खोज में जाने के लिए तैयार हैं। नीचे उतरना।




हम मारियाना ट्रेंच के बहुत नीचे तक गिर गए और वहाँ हमें गुणांक के सभी समान मूल्य मिले $$$एक$ और $$$ब$ , जो वास्तव में अपेक्षित था।

चलो एक और गोता लगाते हैं, केवल इस बार, हमारे गहरे समुद्र के वाहन को भरने के लिए अन्य प्रौद्योगिकियां होंगी, अर्थात् न्यूमपी लाइब्रेरी।



गुणांक मान $$$एक$ और $$$ब$ अपरिवर्तित।

आइए देखें कि ग्रेडिएंट डिसेंट के दौरान त्रुटि कैसे बदल गई, अर्थात, प्रत्येक चरण के साथ चुकता विचलन का योग कैसे बदल गया।


चार्ट dev4 "ढाल वंश में विचलन के वर्गों का योग"



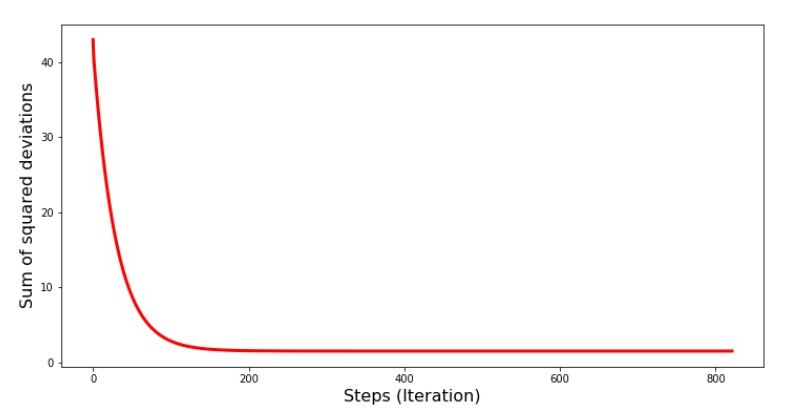
ग्राफ़ पर हम देखते हैं कि प्रत्येक चरण के साथ त्रुटि कम हो जाती है, और निश्चित संख्या में पुनरावृत्तियों के बाद हम व्यावहारिक रूप से क्षैतिज रेखा का निरीक्षण करते हैं।

अंत में, हम कोड के निष्पादन समय में अंतर का अनुमान लगाते हैं:




शायद हम कुछ गलत कर रहे हैं, लेकिन फिर से, एक सरल "स्व-लिखित" फ़ंक्शन जो कि NumPy लाइब्रेरी का उपयोग नहीं करता है, समय से पहले NumPy लाइब्रेरी का उपयोग करके फ़ंक्शन का उपयोग करता है।

लेकिन हम अभी भी खड़े नहीं हैं, लेकिन सरल रेखीय प्रतिगमन के समीकरण को हल करने के लिए एक और रोमांचक तरीके के अध्ययन की ओर बढ़ते हैं। मुझसे मिलो!

स्टोचैस्टिक ग्रेडिएंट डिसेंट

स्टोचस्टिक ढाल वंश के संचालन के सिद्धांत को जल्दी से समझने के लिए, साधारण ढाल वंश से इसके अंतर को निर्धारित करना बेहतर है। हम, व्युत्पन्न के मामले में, के व्युत्पन्न के समीकरणों में $$$एक$ और $$$एक$ सभी चिह्नों के मानों और नमूने में उपलब्ध सही उत्तरों (यानी, के योग) का उपयोग किया $$$x_i$ और $$$y_i$ )। स्टोकेस्टिक ग्रेडिएंट वंश में, हम नमूने में उपलब्ध सभी मूल्यों का उपयोग नहीं करेंगे, लेकिन इसके बजाय, छद्म यादृच्छिक तरीके से, हम तथाकथित नमूना सूचकांक का चयन करेंगे और इसके मूल्यों का उपयोग करेंगे।

उदाहरण के लिए, यदि सूचकांक संख्या 3 (तीन) द्वारा निर्धारित किया जाता है, तो हम मान लेते हैं $$$x_3 = 3$ और $$$y_3 = $ 4.$ , फिर हम डेरिवेटिव के समीकरणों में मूल्यों को प्रतिस्थापित करते हैं और नए निर्देशांक निर्धारित करते हैं। फिर, निर्देशांक निर्धारित करने के बाद, हम फिर से छद्म-यादृच्छिक रूप से नमूने के सूचकांक का निर्धारण करते हैं, आंशिक अंतर समीकरणों में सूचकांक के अनुरूप मानों को प्रतिस्थापित करते हैं, और निर्देशांक को एक नए तरीके से निर्धारित करते हैं $$$एक$ और $$$एक$ आदि हरियाली से पहले अभिसरण। पहली नज़र में, ऐसा लग सकता है कि यह काम कर सकता है, लेकिन यह काम करता है। सच है, यह ध्यान देने योग्य है कि प्रत्येक चरण के साथ त्रुटि कम नहीं होती है, लेकिन प्रवृत्ति निश्चित रूप से मौजूद है।

सामान्य पर स्टोकेस्टिक क्रमिक वंश के फायदे क्या हैं? यदि हमारे नमूने का आकार बहुत बड़ा है और हजारों मानों में मापा जाता है, तो इसे संसाधित करना बहुत आसान है, पूरे नमूने की तुलना में उनमें से एक यादृच्छिक हजार कहें। इस मामले में, स्टोचैस्टिक ग्रेडिएंट वंश लॉन्च किया गया है। हमारे मामले में, ज़ाहिर है, हम एक बड़ा अंतर नहीं देखेंगे।

हम कोड को देखते हैं।




हम गुणांक को ध्यान से देखते हैं और खुद को इस सवाल पर पकड़ते हैं कि "ऐसा कैसे?"। हमें गुणांक के अन्य मूल्य मिले $$$एक$ और $$$ब$ । शायद स्टोचैस्टिक ग्रेडिएंट डिसेंट ने समीकरण के अधिक इष्टतम पैरामीटर पाए? काश, नहीं। यह चौकोर विचलन के योग को देखने के लिए पर्याप्त है और देखें कि गुणांक के नए मूल्यों के साथ, त्रुटि अधिक है। निराशा में जल्दबाजी न करें। हम त्रुटि परिवर्तन की साजिश करते हैं।


चार्ट dev5 "स्टोचस्टिक ढाल वंश में विचलन के वर्गों का योग"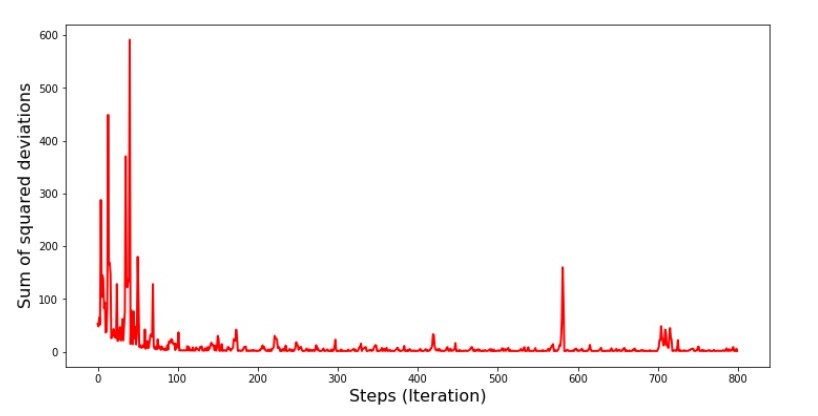



शेड्यूल को देखते हुए, सब कुछ ठीक हो गया है और अब हम सब कुछ ठीक कर देंगे।

तो क्या हुआ? निम्नलिखित हुआ।जब हम अनियमित रूप से एक महीने का चयन करते हैं, तो यह चयनित महीने के लिए होता है कि हमारा एल्गोरिथ्म राजस्व की गणना में त्रुटि को कम करना चाहता है। फिर हम एक और महीने का चयन करते हैं और गणना को दोहराते हैं, लेकिन हम पहले से ही चयनित दूसरे महीने के लिए त्रुटि को कम करते हैं। और अब हमें याद दिलाना चाहिए कि पहले दो महीनों के लिए हमने सरल रेखीय प्रतिगमन के समीकरण की रेखा से काफी विचलन किया है। इसका मतलब है कि जब इन दो महीनों में से किसी का चयन किया जाता है, तो उनमें से प्रत्येक की त्रुटि को कम करके, हमारे एल्गोरिथ्म पूरे नमूने में त्रुटि को गंभीरता से बढ़ाता है। तो क्या करें? उत्तर सरल है: आपको वंश कदम को कम करने की आवश्यकता है। सब के बाद, वंश कदम को कम करने से, त्रुटि भी "कूद" ऊपर और नीचे बंद हो जाएगी। बल्कि, त्रुटि "स्किप" बंद नहीं होगी, लेकिन यह इतनी जल्दी नहीं करेगा :) हम जाँच करेंगे।




चार्ट i6 "स्टोचस्टिक ढाल वंश (80 हजार कदम) में चौकोर विचलन का योग"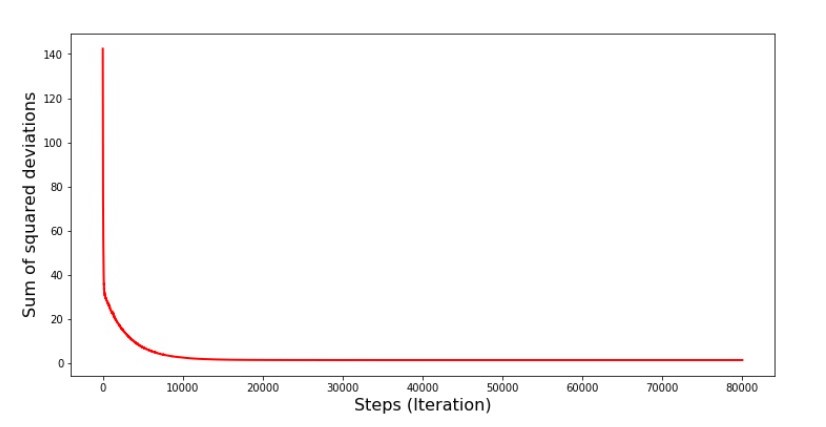



गुणांक के मूल्यों में सुधार हुआ, लेकिन अभी भी आदर्श नहीं है। Hypothetically, यह इस तरह से सुधारा जा सकता है। उदाहरण के लिए, पिछले 1000 पुनरावृत्तियों पर, हम गुणांक के मूल्यों को चुनते हैं, जिसके साथ न्यूनतम त्रुटि हुई थी। सच है, इसके लिए हमें गुणांक मूल्यों को स्वयं लिखना होगा। हम ऐसा नहीं करेंगे, बल्कि शेड्यूल पर ध्यान देंगे। यह सुचारू दिखता है, और त्रुटि समान रूप से घटती है। वास्तव में ऐसा नहीं है। आइए पहले 1000 पुनरावृत्तियों को देखें और अंतिम के साथ उनकी तुलना करें।


अनुसूची नंबर 7 "SGD के विचलन के वर्गों का योग (पहले 1000 कदम)"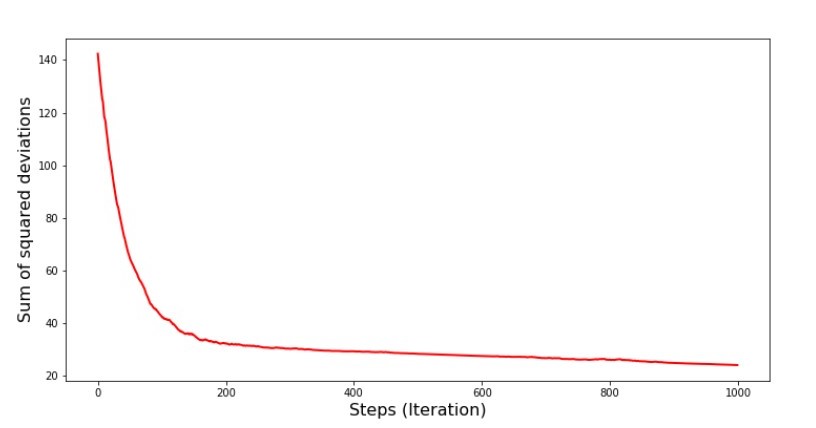



ग्राफ नंबर 8 "SGD के विचलन के वर्गों का योग (अंतिम 1000 कदम)"



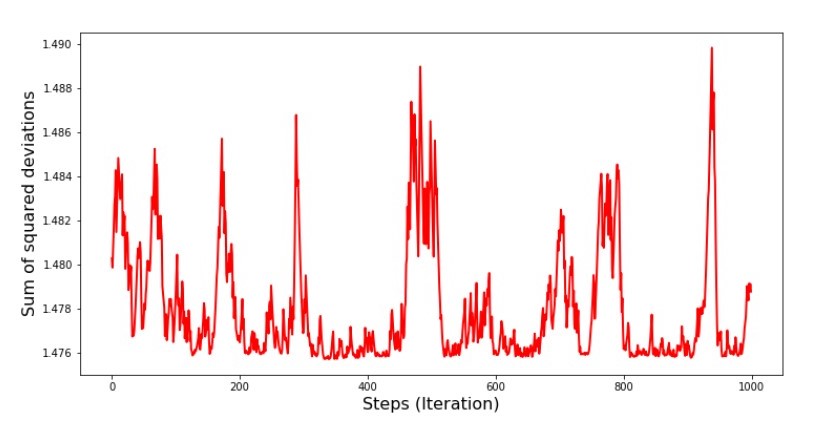वंश की शुरुआत की शुरुआत में, हम त्रुटि में काफी समान और तेज कमी का निरीक्षण करते हैं। अंतिम पुनरावृत्तियों पर, हम देखते हैं कि त्रुटि 1.475 के मान के आसपास और आसपास जाती है और कुछ बिंदुओं पर इस इष्टतम मूल्य के बराबर भी होती है, लेकिन फिर यह वैसे भी बढ़ जाती है ... फिर से, मैं गुणांक के मूल्यों को लिख सकता हूं$$$एक$ और $$बी , और फिर उन का चयन करें जिनके लिए त्रुटि न्यूनतम है। हालाँकि, हमें एक और अधिक गंभीर समस्या थी: हमें इष्टतम के करीब मूल्यों को प्राप्त करने के लिए 80 हजार कदम (कोड देखें) लेना था। और यह पहले से ही ढाल के सापेक्ष स्टॉचस्टिक ढाल वंश के साथ कम्प्यूटेशनल समय को बचाने के विचार का खंडन करता है। क्या सुधारा और सुधारा जा सकता है? यह नोटिस करना मुश्किल नहीं है कि पहले पुनरावृत्तियों में हम आत्मविश्वास से नीचे जाते हैं और इसलिए, हमें पहले पुनरावृत्तियों में एक बड़ा कदम छोड़ना चाहिए और कदम को कम करना चाहिए क्योंकि हम आगे बढ़ते हैं। हम इस लेख में ऐसा नहीं करेंगे - यह पहले से ही घसीटा हुआ है। जो लोग चाहते हैं वे खुद सोच सकते हैं कि यह कैसे करना है, यह मुश्किल नहीं है :)अब हमNumPyलाइब्रेरी का उपयोग करके स्टोकेस्टिक क्रमिक वंश का प्रदर्शन करेंगे।$ब$

(और हम उन पत्थरों पर ठोकर नहीं खाएंगे जिन्हें हमने पहले पहचाना था)




मूलांक के दौरान, NumPy का उपयोग किए बिना मान लगभग समान थे । हालाँकि, यह तर्कसंगत है।

हम यह पता लगाएंगे कि स्टोकेस्टिक ग्रेडिएंट अवरोहियों ने हमें कितना समय दिया।




जंगल में दूर, बादलों को गहरा: फिर से "स्व-लिखित" सूत्र सबसे अच्छा परिणाम दिखाता है। यह सब बताता है कि NumPy लाइब्रेरी का उपयोग करने के लिए और भी अधिक सूक्ष्म तरीके होने चाहिए , जो वास्तव में गणनाओं के संचालन को गति देते हैं। इस लेख में हम उनके बारे में नहीं जान पाएंगे। अपने अवकाश के बारे में सोचने के लिए कुछ होगा :)

संक्षेप में प्रस्तुत करना

संक्षेप करने से पहले, मैं इस प्रश्न का उत्तर देना चाहूंगा कि हमारे प्रिय पाठक से सबसे अधिक संभावना है। क्यों, वास्तव में, इस तरह के "पीड़ा" अवरोह के साथ, हमें क़ीमती तराई खोजने के लिए पहाड़ (मुख्य रूप से नीचे) क्यों जाना पड़ता है, अगर हमारे पास एक ऐसा शक्तिशाली और सरल उपकरण है, जो एक विश्लेषणात्मक समाधान के रूप में है, जो हमें तुरंत टेलीपोर्ट करता है। सही जगह है?

इस सवाल का जवाब सतह पर है। अब हमने एक बहुत ही सरल उदाहरण की जाँच की है जिसमें सही उत्तर है$$y मैं एक विशेषता पर निर्भर करता है$y_i$$$$x_i$ ।जीवन में, यह अक्सर नहीं देखा जाता है, इसलिए कल्पना करें कि हमारे पास 2, 30, 50 या अधिक के संकेत हैं। प्रत्येक विशेषता के लिए इस हजारों, या यहां तक ​​कि हजारों मूल्यों में जोड़ें। इस मामले में, विश्लेषणात्मक समाधान परीक्षण पास नहीं कर सकता और विफल हो सकता है। बदले में, धीरे-धीरे वंश और इसके रूपांतर धीरे-धीरे लेकिन निश्चित रूप से हमें लक्ष्य के करीब लाएंगे - फ़ंक्शन का न्यूनतम। और गति के बारे में चिंता न करें - हम शायद उन तरीकों का भी विश्लेषण करेंगे जो हमें कदम की लंबाई (यानी गति) को सेट और समायोजित करने की अनुमति देंगे।

और अब वास्तव में एक संक्षिप्त सारांश।

सबसे पहले, मुझे उम्मीद है कि लेख में प्रस्तुत सामग्री शुरुआती "तिथि वैज्ञानिकों" को समझने में मदद करेगी कि सरल (और न केवल) रेखीय प्रतिगमन के समीकरणों को कैसे हल किया जाए।

दूसरे, हमने समीकरण को हल करने के कई तरीकों की जांच की। अब, स्थिति के आधार पर, हम उस समस्या को हल करने के लिए सबसे उपयुक्त चुन सकते हैं।

तीसरा, हमने अतिरिक्त सेटिंग्स की शक्ति देखी, अर्थात् ढाल के चरण की लंबाई। इस पैरामीटर की उपेक्षा नहीं की जा सकती। जैसा कि ऊपर उल्लेख किया गया है, गणना की लागत को कम करने के लिए, कदम की लंबाई को वंश के साथ बदलना चाहिए।

चौथा, हमारे मामले में, "स्व-लिखित" कार्यों ने गणनाओं का सबसे अच्छा लौकिक परिणाम दिखाया। यह संभवतः NumPy लाइब्रेरी की क्षमताओं का सबसे अधिक पेशेवर उपयोग नहीं करने के कारण है। लेकिन जैसा कि यह हो सकता है, निष्कर्ष इस प्रकार है। एक ओर, कभी-कभी यह स्थापित राय पर सवाल उठाने लायक होता है, और दूसरी ओर, यह हमेशा जटिल चीजों के लायक नहीं होता है - इसके विपरीत, कभी-कभी किसी समस्या को हल करने का एक सरल तरीका अधिक प्रभावी होता है। और चूंकि हमारा लक्ष्य सरल रेखीय प्रतिगमन के समीकरण को हल करने में तीन दृष्टिकोणों का विश्लेषण करना था, इसलिए "स्व-लिखित" कार्यों का उपयोग हमारे लिए काफी पर्याप्त था।

← लेखक की पिछला काम - "घातीय वितरण का उपयोग कर केंद्रीय सीमा प्रमेय के बयान का अध्ययन"$\leftarrow$
→ लेखक का अगला काम - "हम रैखिक प्रतिगमन के समीकरण को मैट्रिक्स रूप में लाते हैं"$\rightarrow$

साहित्य (या ऐसा कुछ)

1. रैखिक प्रतिगमन

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. कम से कम वर्गों की विधि

mathprofi.ru/metod_naimenshih_kvadratov.html

3. व्युत्पन्न

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. ढाल

mathprofi.ru /proizvodnaja_po_napravleniju_i_gradient.html

5. स्नातक वंशज

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com/-12-12-31/linear_regression

6. NumPy लाइब्रेरी

डॉक्स। scipy.org/doc/ numpy-१.१०.१ / संदर्भ / जनरेट /

numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.ythyworld.ru/numpy/2। एचटीएमएल