हमने मोंटे कार्लो विधि की जांच की , आज हम देखेंगे कि कैसे 2048 में कंप्यूटर का दिमाग अल्फा-बीटा लंघन के साथ अच्छे पुराने मिनिमैक्स का उपयोग करता है।

लेख EDISON, एक कंपनी के समर्थन के साथ लिखा गया था जो मोबाइल एप्लिकेशन विकसित करता है और सॉफ्टवेयर परीक्षण सेवाएं प्रदान करता है।
समाधान उपयोगकर्ता stackoverflow द्वारा पर जासूसी की
 ओवोल्यूड
ओवोल्यूड , जिन्होंने
एआई खेल 2048 को सिखाने के लिए चर्चा में उल्लेख किया।
Ovolve से टिप्पणी अनुवादमैं इस सूत्र में वर्णित कार्यक्रम का लेखक हूं। आप एआई
को कार्रवाई में देख सकते हैं या
कोड देख सकते हैं।
वर्तमान में, कार्यक्रम मेरे लैपटॉप पर एक ब्राउज़र में जावा स्क्रिप्ट को निष्पादित करके लगभग 90% मामलों में जीतता है, पाठ्यक्रम के बारे में सोचने के लिए 100 मिलीसेकंड खर्च करते हुए, हालांकि, पूरी तरह से नहीं, लेकिन बहुत अच्छी तरह से।
चूंकि खेल पूरी जानकारी के साथ एक असतत राज्य स्थान है, वास्तव में शतरंज और चेकर्स जैसे बारी-आधारित खेल होने के कारण, मैंने उन्हीं तरीकों का इस्तेमाल किया, जिन्होंने इन खेलों में अपना प्रदर्शन दिखाया, अर्थात्
अल्फ़ा-बीटा क्लिपिंग के साथ
न्यूनतम खोज । चूंकि लिंक इस एल्गोरिदम के बारे में बहुत सारी जानकारी प्रदान करते हैं, मैं सिर्फ उन दो मुख्य आंकड़ों के बारे में बात करूंगा, जिनका मैंने
स्थैतिक आकलन समारोह में उपयोग किया था और यहां अन्य लोगों द्वारा बनाई गई कई सहज मान्यताओं को औपचारिक रूप दिया।

एकरसता
यह अनुमानवादी यह सुनिश्चित करने की कोशिश करता है कि सभी टाइल मूल्य बाएं या दाएं और ऊपर / नीचे दोनों में वृद्धि या कमी करते हैं। अकेले यह अनुमान अनुमान को दर्शाता है कि कई अन्य लोगों ने उल्लेख किया है कि एक कोने में अधिक मूल्यवान टाइलें समूहीकृत की जानी चाहिए। यह, एक नियम के रूप में, कम मूल्यवान टाइलों के संचय को रोकता है और बोर्ड को व्यवस्थित रखता है, क्योंकि छोटी टाइलें बड़े लोगों में कैस्केड होती हैं।
यहाँ पूरी तरह नीरस ग्रिड का एक स्क्रीनशॉट है। अन्य अवगुणों को नजरअंदाज करने और केवल एकरसता को ध्यान में रखने के लिए मैंने इंस्टाल फंक्शन के साथ एक एल्गोरिथ्म चलाकर यह स्थिति प्राप्त की।

चिकनाई (चिकनाई, शाम)
उपरोक्त अपने आप में अनुमानी संरचनाएं बनाने के लिए जाता है जिसमें पड़ोसी कोशिकाओं को मूल्य में कम किया जाता है, हालांकि, निश्चित रूप से, पड़ोसियों को गठबंधन करने का एक ही अर्थ होना चाहिए। इसलिए, सहजता का अनुमानी, आसन्न टाइल्स के बीच के मूल्यों में अंतर को मापता है, उनकी संख्या को कम करने की कोशिश करता है।
हैकर न्यूज के एक टिप्पणीकार ने ग्राफ सिद्धांत के संदर्भ में इस विचार
का एक
दिलचस्प औपचारिकरण प्रदान किया।
हैकर समाचार के साथ औपचारिकता का अनुवादकल मैंने इस गेम को एक सहकर्मी, ग्राफ सिद्धांत के एक प्रेमी को दिखाया, और हमने यह भी सोचने का फैसला किया कि एआई का उपयोग करके इस गेम को कैसे हल किया जाए।
सबसे सरल समाधान न्यूनतम है, जो, जैसा कि मैं इसे देखता हूं, बहुत अच्छी तरह से लागू किया गया है। अगर यहां कोई मिनिमैक्स से परिचित नहीं है, तो ओपी ने बहुत ही सुरुचिपूर्ण और अच्छी तरह से टिप्पणी की गई कोड लिखा जो एक महान ट्यूटोरियल होगा।
कम कम्प्यूटेशनल रूप से गहन दृष्टिकोण जो हमने प्रस्तावित किया था वह खेल राज्य को एक ग्राफ जी (वी, ई) के रूप में मॉडल करने के लिए था, जहां वी सक्रिय टाइल्स का एक सेट है और ई किनारों का एक समूह है जो फ़ंक्शन सी द्वारा भारित आसन्न टाइल्स को जोड़ता है। (v1, v2) , जो दो टाइलों के बीच के अंतर का पूर्ण मान लौटाता है। प्रत्येक समाधान के लिए, AI एक ऐसा कदम चुनता है जो नए गेम स्टेट में सभी किनारों के वजन को कम करता है।
इसका कारण यह है कि खेल में प्रगति करने का एकमात्र तरीका एक दूसरे के बगल में समान मूल्यों के साथ टाइलें हैं, जिसके लिए जी में वजन 0. होगा। इस प्रकार, एआई को कुल वजन को कम करने का प्रयास करना चाहिए। अंत में, किनारों पर बड़ी संख्या में किनारों पर आसन्न टाइलों के साथ एक बड़ी संख्या होगी, इसलिए AI अंतर को कम करने के लिए इन टाइलों को अन्य बड़ी टाइलों के बगल में रखने की कोशिश करेगा।
चूंकि खेल स्टोचस्टिक है, मैंने जो दृष्टिकोण वर्णित किया है वह सबसे खराब स्थिति में काम नहीं कर सकता है, लेकिन इसे पेड़ में प्रत्येक नोड के लिए एक वजन समारोह के रूप में मौजूदा न्यूनतम समाधान पर भी लागू किया जा सकता है।
यहाँ एक पूरी तरह से चिकनी जाल का एक स्क्रीनशॉट है, कृपया इस उत्कृष्ट
नकली कांटा द्वारा प्रदान किया गया है।
(वेब संग्रह के लिए लिंक, जबकि पृष्ठ पर जावा स्क्रिप्ट काम करती है और आप कीबोर्ड का उपयोग किसी भी दिशा में - अनुवादक द्वारा नोट करने के लिए कर सकते हैं)।ढीली टाइल्स
और अंत में, बहुत कम मुफ्त टाइल होने के लिए एक जुर्माना है, क्योंकि विकल्प जल्दी से समाप्त हो सकते हैं जब खेल का मैदान बहुत तंग हो जाता है।
और वह सब है! इन मानदंडों का अनुकूलन करते हुए खेल स्थान की खोज आश्चर्यजनक रूप से अच्छा प्रदर्शन देती है। स्पष्ट रूप से एन्कोडेड चाल रणनीति के बजाय इस तरह एक सामान्य दृष्टिकोण का उपयोग करने का एक लाभ यह है कि एल्गोरिथ्म अक्सर दिलचस्प और अप्रत्याशित समाधान पा सकता है। यदि आप उसकी प्रगति का निरीक्षण करते हैं, तो वह अक्सर आश्चर्यजनक लेकिन प्रभावी आंदोलन करता है, जैसे कि दीवारों या कोनों का अचानक परिवर्तन, जिसके पास वह अपना खेल बनाता है।

छोटा सा बदलाव
स्क्रीनशॉट इस दृष्टिकोण की शक्ति को प्रदर्शित करता है। मैंने टाइल सीमा को हटा दिया (ताकि वे 2048 तक पहुंचने के बाद भी बढ़ते रहें), और यहां आठ परीक्षणों के बाद सबसे अच्छा परिणाम है।
हां, यह 2048 के साथ 4096 है। =) इसका मतलब है कि वह एक बोर्ड पर मायावी 2048 टाइल तक पहुंच गया है।
अल्फा-बीटा क्लिपिंग और स्टैकओवरफ्लो यूजर ओवोल्यूशन से स्थैतिक मूल्यांकन फ़ंक्शन के साथ न्यूनतम के लिए जावा-स्क्रिप्ट कोड लेख में नीचे दिया गया है।
मिनिमैक्स विधि कई उत्कृष्ट हब्र-लेखों के लिए समर्पित है, इसलिए हम इसमें जो भी शामिल है, उसके अकादमिक विस्तृत विवरण को छोड़ देते हैं।
आईटी समुदाय में शामिल होने वालों के लिए
, मैंने हाल ही में सुंदर शब्द "मिनिमैक्स" और "अल्फा-बीटा क्लिपिंग" सुना है, लेकिन इसका मतलब यह नहीं है, इसका अर्थ है, चलो कोशिश करते हैं, सबसे सामान्य अर्थ समझाने के लिए, अनुच्छेदों के एक जोड़े में शाब्दिक अर्थ।
अल्पमहिष्ठ
कुछ खेलों में, दो खिलाड़ियों के बीच एक खेल की प्रक्रिया (जो बदले में एक चाल है) को विकल्पों के तथाकथित पेड़ के रूप में दर्शाया जा सकता है। प्रत्येक विशिष्ट स्थिति में, प्रत्येक खिलाड़ी के पास आमतौर पर उसकी चाल के लिए विभिन्न विकल्पों में से एक विकल्प होता है। और इन विकल्पों में से प्रत्येक के जवाब में, एक प्रतिद्वंद्वी भी कई मायनों में पसंद कर सकता है।
विकल्पों के एक पेड़ का टुकड़ाचूंकि खेल के किसी भी क्षण में खेल के मैदान की स्थिति के बारे में पूरी जानकारी होती है, इसलिए स्थिति की वर्तमान स्थिति का हमेशा सटीक अनुमान लगाया जा सकता है। ऐसे कार्य को
स्थैतिक मूल्यांकन फ़ंक्शन या संक्षिप्त
एसएफओ कहा जाता है। इसके अलावा, यह महत्वपूर्ण है कि एक विशिष्ट स्थिति का मूल्यांकन करते समय यह अधिक महत्वपूर्ण है, उतना ही लाभप्रद एक खिलाड़ी के लिए स्थिति है (चलो इसे
अधिकतम खिलाड़ी कहते हैं )। किसी स्थिति का मूल्यांकन करते समय इस फ़ंक्शन का संख्यात्मक मान जितना छोटा होता है, उतना ही लाभप्रद दूसरे खिलाड़ी के लिए स्थिति होती है (इसे
न्यूनतम खिलाड़ी कहते हैं )।
प्रत्येक चाल के बाद, स्थिति बदल जाती है, और इसलिए इसका स्कोर बदल जाता है। विकल्पों के वृक्ष पर विचार करते समय, प्रत्येक खिलाड़ी को केवल उन शाखाओं को पसंद करने की आवश्यकता नहीं होती है जिनमें रेटिंग उसके लिए सबसे अधिक अनुकूल होती है। आपको उन शाखाओं से भी बचना चाहिए जिनमें प्रतिद्वंद्वी के लिए स्थिति का मूल्यांकन अनुकूल है।
यह माना जाता है कि प्रतिद्वंद्वी तर्कवाद द्वारा भी निर्देशित होता है और उन विकल्पों से भी बचता है जो उसे हारने के लिए प्रेरित कर सकते हैं। अर्थात्, प्रत्येक खिलाड़ी, जब कोई विकल्प चुनते हैं, तो अपने स्वयं के लाभ को अधिकतम करने और एक ही समय में प्रतिद्वंद्वी के लाभ को कम करने से आगे बढ़ता है।
यह न्यूनतम है।
अल्फा बीटा कतरन
यह काफी स्पष्ट है: जो एक पेड़ को एक बड़ी स्थिति से अधिक गहराई तक गणना करता है, उसके पास जीतने की अधिक संभावना है। लेकिन एक उपद्रव है - खेलों में विकल्पों के वृक्ष को घोंसले के प्रत्येक स्तर के साथ शाखाओं में बंटने और तेजी से बढ़ने की एक आदत है। कार्यक्रमों की गिनती की क्षमता, और इससे भी अधिक लोग सीमित हैं, "सही चटाई तक" गिनती हमेशा से संभव है। यह आसानी से पता लगा सकता है कि खिलाड़ी एक ऐसी स्थिति में गिना जाता है, जहां उसके पास खेल के मैदान का अच्छा आकलन है, लेकिन शाब्दिक रूप से अगले (अपठनीय) स्तर पर, प्रतिद्वंद्वी के पास ऐसा कदम उठाने का अवसर होता है जो मौलिक रूप से स्थिति के विपरीत को बदल देता है।
किसे दोष देना है और क्या करना है? कम्प्यूटेशनल जटिलता पूर्ण ट्री ट्रैवर्सल के लिए दोषी है, यह अनावश्यक शाखाओं को काटकर लड़ने का प्रस्ताव है। यदि स्थिति का मूल्यांकन करने वाला खिलाड़ी देखता है कि विकल्प ट्री की कुछ शाखा:
या पहले से ही विश्लेषण की गई अन्य शाखाओं की तुलना में इसके लिए कम लाभदायक,
या विरोधी के लिए अन्य शाखाओं की तुलना में अधिक लाभदायक जिनका पहले ही विश्लेषण किया जा चुका है,
तब खिलाड़ी इस शाखा को छोड़ देता है, उसके लिए स्पष्ट रूप से बदतर शाखा से उप-विकल्पों पर विचार करने में समय और संसाधन बर्बाद नहीं करता है।
यह आपको विकल्प पेड़ में एक बड़ी प्रतिपादन गहराई के लिए अधिक अनुकूल शाखाओं की गणना के लिए अधिक कंप्यूटिंग संसाधनों को आवंटित करने की अनुमति देता है। विकल्प के पेड़ के विभिन्न स्तरों पर खेल के मैदान का मूल्यांकन करने की प्रक्रिया में, खिलाड़ी दो गतिशील रूप से बदलते गुणांकों के साथ संचालित होता है -
अल्फा (एसएफडी का मूल्य जो शाखा में न्यूनतम रूप से सामना किया जाता है - यानी न्यूनतम खिलाड़ी के लिए अधिक अनुकूल) और
बीटा (एसएफडी का मूल्य जो शाखा में सबसे अधिक सामना करना पड़ता है - i.e. अधिक से अधिक खिलाड़ी के लिए अनुकूल)। प्रत्येक स्तर पर,
अल्फा और
बीटा गुणांक के साथ वर्तमान स्थिति के SFD की तुलना करने से आपको स्वीप करने की अनुमति मिलती है (उन्हें पूरी तरह से गणना किए बिना) शाखाएं जो उस खिलाड़ी के लिए
कम फायदेमंद होती हैं जो स्थिति का मूल्यांकन करती हैं और / या अपने प्रतिद्वंद्वी के लिए
अधिक फायदेमंद होती हैं।
यह अल्फा बीटा क्लिपिंग है।
अल्फा बीटा क्लिपिंग के साथ रिकर्सिव मिनिमैक्स फंक्शन
एआई के साथ 2048 को वीबीए मैक्रोज़ के साथ एक्सेल एप्लिकेशन के रूप में लागू किया गया है, यह है कि अल्फा बीटा क्लिपिंग के साथ मिनिमैक्स एल्गोरिथ्म एक तुच्छ दृश्य मूल जैसा दिखता है। जावा-स्क्रिप्ट में ओव्यूलेशन कोड function AI(grid) { this.grid = grid; }
स्थैतिक मूल्यांकन समारोह
चूंकि विकल्पों के वृक्ष में प्रत्येक स्तर पर आपको खेल के मैदान का मूल्यांकन करना होता है (खिलाड़ियों के लिए यह तय करने के लिए कि अनुमानित स्थिति वास्तव में अधिक लाभप्रद है), आपको यह तय करने की आवश्यकता है कि किसी अच्छे पद को एक बुरे से अलग करने के लिए क्या मापदंड हैं।
हम मानते हैं कि अधिकतम खिलाड़ी वह व्यक्ति (या एआई) है जो सभी टाइलों को स्थानांतरित करने के लिए 4 दिशाओं (ऊपर, बाएं, दाएं, नीचे) में से कौन तय करता है। एक न्यूनतम खिलाड़ी वह कपटी सबरूटीन होता है जो सबसे अनुचित स्थानों में अनियमित रूप से 2 या 4 उत्पन्न करता है।
एसएफओ एक अधिकतम खिलाड़ी के दृष्टिकोण से संकलित है। खेल मैदान के लिए एसएफडी रेटिंग जितनी अधिक होगी, "मैक्सिममिस्ट" के लिए बेहतर स्थिति होगी। निचला - "न्यूनतावादी" के लिए बोर्ड पर अधिक सुखद स्थिति।
2048 के मामले में - टाइल्स को स्थानांतरित करने वाले के लिए कौन से कारक अनुकूल माने जाते हैं?
एकरसता
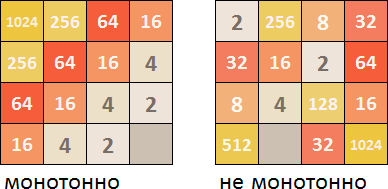
सबसे पहले, यह वांछनीय है कि टाइल्स को कुछ दिशाओं में आरोही / अवरोही क्रम में व्यवस्थित किया जाता है। यदि ऐसा नहीं किया जाता है, तो जब नई टाइलें उत्पन्न होती हैं, तो खेल का मैदान जल्दी से विभिन्न आकारों के यादृच्छिक रूप से व्यवस्थित टाइलों से भरा हो जाएगा, जो तुरंत एक दूसरे से सामान्य रूप से जुड़ा नहीं हो सकता है।
साइबेरियाई संघीय जिले में, आपको सभी 4 दिशाओं (ऊपर-नीचे, बाएं-से-दाएं, दाएं-बाएं, नीचे-ऊपर) में देखना होगा और गणना करना होगा कि टाइल कहां घट रही है या प्रगति बढ़ रही है। यदि प्रगति में ऐसी टाइलें हैं जो सामान्य श्रृंखला में फिट नहीं होती हैं, तो यह एकरसता के संख्यात्मक गुणांक को कम करता है। फिर, सभी दिशाओं के लिए 4 गुणांक से, सबसे अच्छा एक का चयन किया जाता है, जिसे साइबेरियाई संघीय जिले के कुल मूल्य में ध्यान में रखा जाता है।
चिकनाई

इसके अलावा, यह अधिक बेहतर होगा यदि टाइल्स की एक पंक्ति में खड़े होने से प्रगति केवल बढ़ती नहीं थी, लेकिन गैर-घटती है (या पंक्ति को कम करने के बजाय, यह गैर-वृद्धि के लिए बेहतर है), अर्थात, यह अच्छा है जब एक ही टाइल पास हो, जो उन्हें एक में ढहने की अनुमति देता है, और अंक प्राप्त कर रहा है। खेल के मैदान पर खाली स्थान बढ़ाना।
इसलिए, साइबेरियाई संघीय जिला खेल के मैदान पर एक ही आसन्न टाइल की तलाश में है और एक विशेष गुणांक में इस तरह के जोड़े की संख्या को ध्यान में रखता है।
खाली सेल

जाहिर है, अधिक खाली स्थान, पैंतरेबाज़ी के लिए अधिक जगह और जल्दी से कम खो जाने की संभावना।
SFO मैदान पर खाली कोशिकाओं को मानता है और इनमें से अधिक, स्थिति को अधिकतम करने वाले खिलाड़ी के लिए अधिक लाभदायक माना जाता है।
अधिकतम टाइल
चूंकि इस खेल में मुख्य बात यह है कि मैदान पर एक बड़ी टाइल प्राप्त की जाए, तो अधिक बेहतर है - 2048, 4096, 8192 (या आपके लिए जो भी शक्ति और धैर्य है), उन विकल्पों पर जहां अधिकतम टाइल मूल्य अधिक है उन्हें सबसे अधिक लाभदायक SFD माना जाना चाहिए।
2048 के लिए साइबेरियाई संघीय जिला
VBA मैक्रो के रूप में साइबेरियाई संघीय जिले का कार्यान्वयन जावा-स्क्रिप्ट में ओव्यूलेशन कोड function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
एक्सेल एप्लिकेशन को स्वयं
Google से डाउनलोड किया
जा सकता है ।
आवेदन की कार्यक्षमता
पिछले लेख में वर्णित
है, जहां एआई मोंटे कार्लो पद्धति का उपयोग करके खेलता है । आज का समाधान मौजूदा मोंटे कार्लो में जोड़ा गया है।
एआई और 2048 श्रृंखला के सभी लेख
- मोंटे कार्लो
- मिनीमैक्स + अल्फा बीटा क्लिपिंग
- अधिकतम की प्रतीक्षा कर रहा है
- तंत्रिका नेटवर्क